A SAS Macro for a Clustered Permutation Test

Abstract

The clustered permutation test is a nonparametric method of significance testing for correlated data. It is often used in cluster randomized trials where groups of patients rather than individuals are randomized to either a treatment or control intervention. We describe a flexible and efficient SAS macro that implements the 2-sample clustered permutation test. We discuss the theory and applications behind this test as well as details of the SAS code.

1. Introduction

The permutation test is an analytical method for significance testing in clinical trials. The method involves permuting the treatment assignment to estimate the distribution of the test statistic under the null hypothesis of no treatment effect. It is a nonparametric technique limited to significance testing rather than estimation of effects. Generally it is applied to study designs with only two comparison groups.

The permutation test is an exact test. It is a more conservative choice than tests based on asymptotic distributions and yields Type I error values close to the nominal level. [1] The permutation test may be selected as a method of analysis when the usual asymptotic theory may not hold, for example, in studies where there are few observations or in unconventional designs.

Several recent publications have applied clustered permutation tests to the analysis of cluster randomized trials. [2, 3, 4] Unlike the usual permutation test, the clustered permutation test permutes clusters of observations rather than individual observations. In these studies the clusters are inherent in the data and are incorporated into the design (examples of cluster identifiers include geographic location, family, and primary care physician.) Appropriate methods are necessary to preserve Type I error rates in clustered study designs. Methods such as Generalized Estimating Equations or random effects models can be used to account for the clustering. However, these methods impose assumptions on the distribution of the data. The clustered permutation test has an advantage over these methods in that it yields correct inference without making the same distributional assumptions. [5]

Although the clustered permutation test has been widely discussed in the literature, to our knowledge no SAS procedure for it is available for public use. Balasubramani et al. developed a SAS program to perform a permutation test for unclustered data. [6] Here we have extended the Balasubramani method to sample clusters allowing the user a choice of sampling methods without compromising computational efficiency.

In Sections 2.1–2.2 we describe the permutation test and how it has been adapted to clustered data. In Sections 2.3 and 2.4 we describe the clustered permutation test algorithm and an approximation. In Sections 2.5–2.6 we detail code and efficiency issues. In Section 3 an example study illustrates use of the macro. The Clustered Permutation Test Macro (©2008 Margaret Stedman) and example data are freely distributed under the terms of the GNU General Public License and available to download from our website: http://www.drugepi.info/links/downloads.php.

2. Methods

2.1. The Permutation Test

The permutation test is an exact nonparametric test introduced by R.A. Fisher. [5] See Lehmann for a full explanation. [7] In brief, the purpose of this test is to compare outcomes from a treatment group to outcomes from a control group. Assume for the treated group there is a sample z of size n drawn from an unknown distribution F, and for the control group there is a sample y of size m drawn from unknown distribution G. To determine whether the outcomes from the treatment group are different from the outcomes from the control group, we perform the permutation test of the null hypothesis that F=G. Under the null hypothesis an observation is equally likely to have occurred from F or G, so the observed treatment assignment in samples z and y has a probability $\frac{1}{\left(\begin{array}{c}n+m\\ n\end{array}\right)}$. Similarly, any test statistic, S, which is a function of treatment assignment and the observed outcome, has a permutation distribution in which each combination of observations occurs with probability $\frac{1}{\left(\begin{array}{c}n+m\\ n\end{array}\right)}$.[5]

2.2. The Clustered Permutation Test

In cluster randomized study designs, randomization occurs at the cluster level. The data violate the assumptions of the usual permutation test, because we cannot assume that all observations are independent and equally likely to have been given either treatment assignment. However, if we define each unit to be a cluster rather than an observation, then in fact all clusters are independent and equally likely to have either treatment assignment. Since we define the unit of observation to be a cluster of observations, the test assumes equal probability for all permutations of the clusters. Unlike the unclustered test, the clustered permutation test restricts the number of permutations to those that keep the clusters intact. Gail et al. [3] examined the utility of the permutation test in cluster randomized trials and found that the Type I error was close to nominal when the number of clusters was balanced across treatment groups and when there was not considerable imbalance in the variances of the treatment groups.

2.3. Clustered Permutation Test Algorithm

To implement the clustered permutation test, assume there are two treatment groups with unknown outcome distributions F and G, with M and N clusters, respectively. Let X be a vector of the treatment assignment. Let V be a vector of the outcome values. To test whether F and G are in fact different distributions, perform a permutation test using statistic S, a function of X and V. S can be any test statistic (e.g. t test statistic, or χ² test statistic.) In the steps below, Ŝ represents the observed test statistic, while Ŝ^* refers to the test statistic computed for a permutation of the data. [5]

In each step keep all clusters intact. When a cluster is given a treatment assignment, all observations belonging to the cluster must receive the same treatment assignment. The following algorithm has been adapted from Efron. [5]

1. Combine all M + N clusters.

2. Generate all possible permutations of X. There are $B=\left(\begin{array}{c}N+M\\ N\end{array}\right)$ possible ways to partition X into two groups of size N and M. Let i = 1, 2, .., B index a specific permutation of X, denoted X_i.

3. Compute the test statistic ${\widehat{S}}_i^{\ast }$ as a function of V and X_i for i = 1, …, B (all permutations of X.)

4. Compare the distribution of the permuted Ŝ^* to the observed Ŝ found in the original arrangement of the data. The achieved significance level (ASL) is measured by the probability under the null hypothesis that the permuted Ŝ^* is more extreme than the original Ŝ.

$$AS{L}_{\mathit{perm}}={\mathit{Prob}}_{\mathit{perm}}\{\mid {\widehat{S}}^{\ast }\mid \ge \mid \widehat{S}\mid \}=\frac{\#(\mid {\widehat{S}}^{\ast }\mid \ge \mid \widehat{S}\mid )}{B}$$ (1)

where Ŝ^* is the permuted test statistic (a random value) and Ŝ is the observed test statistic (a fixed value). B is the number of permutations. Note that the outlined steps yield a two-sided p-value.

2.4. Approximate Clustered Permutation Test

When the number of clusters is large, the standard permutation test may be computationally infeasible. We propose a modified version of the clustered permutation test that takes a sample of the full permutation distribution. In this case the approximate clustered permutation test is performed with a random sample, B′ permutations, where B′ is less than all possible permutations. To determine how many samples B′ are needed to adequately approximate the full permutation distribution, we describe the following algorithm adapted from Efron. [5]

1. Perform the clustered permutation test (described above) using a sample of B=100 permutations.

2. Calculate the achieved significance level (A) based on results from B permutations.

3. Specify E, the acceptable percentage of Monte Carlo error around A.

4. Solve for the number of permutations needed:

   $$B^{\prime }=\frac{(1-A)/A}{E^2}$$ (2)

5. Perform the clustered permutation test using B′ permutations.

In Table 1 we present the results from permutations of a χ² test. As the number of permutations increase the estimate, Â, stabilizes. This is also reflected by the decline in the coefficient of variation, E. If we are only interested in determining if the p-value is less than .05, the answer is found with as few as 100 permutations.

Table 1.

Permutations of a χ² test: results and computation time

Permutations:	1	10	100	1,000	5,000	10,000
Elapsed Time (seconds):	13	14	29	185	997	2,192
Â	0.5000	0.1000	0.0200	0.017	0.0164	0.0185
E	1	.95	.70	.24	.11	.07

2.5. SAS Macro

The SAS program performs a 2-sample clustered permutation test. The program is intended only for bivariate tests. It is written in SAS version 9.1 and may not operate correctly in earlier versions. Users should confirm that the IML package has been installed prior to use. The full code for the clustered permutation test has been posted to our website: http://www.drugepi.info/links/downloads.php.

At the start of the program the test statistic is computed on the original dataset. The number of rows of output is counted corresponding to the selected procedure and reported back to the user. An error message is issued if the procedure output contains more than one row. If the number of permutations requested is greater than or equal to the number of permutations possible, it resets the number of requested permutations to equal the number of possible permutations (“all”).

The algorithm continues in one of two directions determined by the input from the user. The user can either request all possible permutations (clustered permutation test) or a specific number of permutations (approximate clustered permutation test). If the approximate permutation test is requested, then the permutations are generated within the IML step. It is possible that a duplicate sample will be produced in the IML step, so the user may also request that the permutations be sorted to remove duplicate samples. If duplicates are removed, the resulting number of permutations performed will be slightly smaller than the number requested. Alternatively, if all possible permutations are requested, then the permutations are generated using “proc plan” as described in the Balasubramani [6] method.

The results file will contain the observed result from the original orientation of the data and all permuted results. The observed result is then compared to each of the permuted results. An indicator marks the permutations with test statistics larger than the observed result. Finally, it computes the probability that the observed test statistic is more extreme than the permuted test statistics to determine the significance of the result.

The SAS program requires nine macro variables to be inputted by the user. All nine variables require entries from the user. See table 2 in Appendix A for a full description of the macro variables.

The input dataset should be structured so that each record contains a unique observation allowing for multiple records per cluster. The SAS program does not require an equal number of observations per cluster or equal number of clusters per treatment group. When there is only one observation per cluster, the program resolves to the standard unclustered permutation test. The input dataset should include (but is not limited to) at least the following variables: cluster I.D., treatment group, and outcome. Any unnecessary variables should be removed from the dataset to improve the efficiency of the program. The input dataset should be a permanent SAS dataset saved to the subdirectory specified by the user at the top of the program.

The SAS procedure to be permuted is requested at the top of the program within the procedure macro (“procmacro”). Some SAS procedures require sorting prior to use; if this is the case, a sort statement should be included before the procedure. Do not include the name of the dataset (i.e. data=…); if the dataset name is included, the statistic will not be permuted. The code should also collapse the output so that there is only one record in the output dataset.

Output from the macro will display the observed result (without permutations) and a p-value for the permuted test statistic. The user provides the name and path to store the permuted output permanently. The dataset of the permuted output contains the observed result and all permutations of the test statistic. The following system checks will also be reported in the printed output: total number of clusters, number of clusters per treatment group, and number of output records generated by the procedure.

2.6. Macro Performance

The macro processing time will be affected by the choice of test statistic to permute and the size of the dataset. The runtime of a procedure can also affect the execution time of the macro. Some procedures such as “proc freq” may take less than a second to run, while others such as proc NLMixed can require several minutes per iteration. Table 1 contains elapsed times for the permutation of a χ² test. The test was performed using UNIX SAS v. 9.1 on a SUN OS 5.9 platform with 8 GB RAM, and 4 Ultra Spark IIIi CPUs. On this type of server a single χ² test of a dataset with 1,973 observations and 435 clusters requires 0.06 seconds of runtime. For an example of the SAS code used, see example 2 at the end of the macro program.

3. Example study

We present an example of the use of the clustered permutation test by analyzing a randomized controlled trial of an education program for physicians to improve osteoporosis management. Physicians were randomized to a one-on-one educational session versus no education. Those in the intervention group were provided information on how best to prevent osteoporosis in high-risk patients. Patients of the randomized physicians were followed for ten months to determine whether they received either a bone mineral density test or osteoporosis medication. The outcome was binary for osteoporosis management. Since the treatment was randomized at the physician level, the individual patient outcomes were considered clustered within the physician. A total of 435 physicians were enrolled in the study. The number of patients at risk per physician varied between 1 and 148. [9]

To demonstrate use of the macro, we simulated data to replicate the structure of this trial. We assumed a random intercept model with a normally distributed random effect. For the sake of simplicity we simulated 458 clusters (229 per treatment group) with 8 observations per cluster. We have posted the code used to generate the data on our website: http://www.drugepi.info/links/downloads.php. In this example we performed an approximate clustered permutation test with the Wald Chi-Square Statistic from logistic regression to determine whether there was a significant difference between the intervention and control observations.

To perform the approximate clustered permutation test we first ran a sample of B=100 permutations of the chi-square statistic to get a rough estimate of the ASL. Based on 100 permutations we find the estimate of the ASL to be .05 with a coefficient of variation of 44%. Since we would prefer a more precise estimate of the p-value, we specify the coefficient of variation to be less than 5%. Applying formula (2) we solve for the number of permutations: (1 −.05)/(.05 × .05²) = 7, 600.

The permutation test is repeated with B=7,600 permutations. This test required approximately 20 minutes to complete, and the results from the output are summarized in Table 3, appendix B. The first half of the output (not shown) displays the observed result from logistic regression without permutation testing. The p-value for the unclustered treatment effect is 0.0122. The output next confirms that there is only one record of data exported from the logistic regression procedure, and there are 458 clusters in the dataset. There are 2.77 × 10¹³⁶ possible permutations. We chose to approximate the result with 7,600 permutations. At the bottom of the output, the result from the clustered permutation test is reported (p= 0.06).

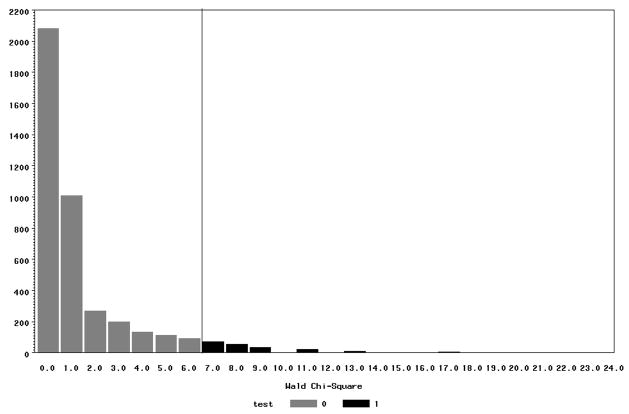
In figure 1 we have generated a histogram of the permuted data. The original Wald Statistic (χ² = 6.83) is marked along the horizontal axis. The area above it (test=1) is the achieved significance level (p=.06) for the permutation test. In this case the usual logistic regression found a significant result, and the clustered permutation test did not show a significant difference. The usual logistic regression procedure incorrectly assumes the data are independent and underestimates the variance. The permutation test is more conservative, because the standard errors have been adjusted to correct for the correlations in the data.

Figure 1.

Histogram of 7,600 permutations of the χ² statistic

4. Discussion

The clustered permutation test is a sampling method to perform exact nonparametric significance testing for correlated data. It can be used to determine the cluster-adjusted significance level for almost any test statistic. The current method available in SAS (proc multtest) does not allow the flexibility to test any procedure, nor does it permit clustered data. [10] We have developed efficient and flexible code to address this problem. The user may decide on the optimal test statistic, the number of permutations, and the method (approximate or all possible permutations). We have provided examples of its use with a simple χ² test and a more complex procedure for regression analysis.

The Clustered Permutation Test Macro (©2008 Margaret Stedman) is freely available under the terms of the GNU General Public License for download from our website. It uses the proc plan procedure and IML to create thousands of permutations of the data. Although the focus of this program was to permute clustered data, the code may be used to permute data that are not clustered as long as there is an unique identifier for independent observations. The modified permutation test makes it possible to run the permutation test on larger datasets with hundreds of clusters. Any SAS procedure can be selected for the permutation test as long as the output can be collapsed to one row of data with a single test statistic.

The clustered permutation test macro has some limitations. Since the algorithm temporarily stores all requested permutations, the program is limited by the memory allocated and dimensions permitted for a dataset. Our method was developed for a 2-sample test. Expansion to three or more treatment groups would require additional alterations to the program. The method is limited to crude comparisons of treatment groups rather than multivariable adjusted comparisons. Though it is uncommon to perform a multivariable adjusted permutation test, some methods are available. [4]

It is unlikely that the permutation test will be as powerful as optimal parametric methods that leverage distributional assumptions. Previous studies have demonstrated that the clustered permutation test preserves Type I error and is a more conservative approach than the available parametric methods. [11] Braun and Feng found that even the best permutation test (with a Type I error close to the nominal level) had less power than other parametric tests for clustered data. [8] Some of this lost power is impossible to regain because, unlike asymptotic tests, the permutation test can measure only discrete probabilities. Berger recommends considering the length of interval around the p-value to determine whether the loss in power is due to the discreteness of the permutation test. He argues that the parametric methods may seem more powerful due to a shift in the power curve from inflation in the Type I error. [1] Gail found that the discreteness of the permutation test was less of an issue when large numbers of clusters were included in the study. [3]

The flexibility of this macro was inspired by the various data structures of cluster randomized trials. Physician-randomized trials typically enroll large numbers of physician clusters with practices of small cluster size. Conversely, community intervention trials typically enroll a few community clusters with a large cluster size. Because of this variability in design, the macro was created to accommodate sampling methods in which all possible combinations are included for studies with few clusters as well as approximate sampling needed for efficient testing of studies with many clusters.

6. Appendix

Table 2.

Macro Variable Definitions

Variable Name	Definition
datain	Name of the input dataset containing the data to be tested.
noperm	Number of permutations to be performed. If set equal to “all,” then all possible permutations are performed If set to a number, then the modified permutation test is performed
dups	Duplicates allowed yes/no.
treat	The treatment group or independent variable that will be permuted.
clusterid	Identifies each unique cluster.
seed	Number used to generate a stream of reproducible random numbers.
procout	Name of the output dataset created by the program.
testname	Name of the variable containing the test statistic included in the output dataset (“procout”.)
permuteout	Name of SAS dataset containing all permutation results.

Table 3.

Summary of results from Example Data

Usual logistic regression p-value:	0.0122
Number of rows in output dataset:	1
Number of clusters in dataset:	458
Number of clusters per treatment group	229 229
Number of possible permutations	2.77 × 10136
Number of permutations performed	7600
P-value for permutation test	0.0584