A Comparison of Four Models of Delay Discounting in Humans

Abstract

The present study compared four prominent models of delay discounting: a one-parameter exponential decay, a one-parameter hyperbola (Mazur, 1987), a two-parameter hyperboloid in which the denominator is raised to a power (Green and Myerson, 2004), and a two-parameter hyperbola in which delay is raised to a power (Rachlin, 2006). Sixty-four college undergraduates made choices between hypothetical monetary rewards, one immediate and one delayed, and the fit of the four models to their data was assessed. All four equations accounted for a large proportion of the variance at both the group and the individual levels, but the exponents of both two-parameter models were significantly less than 1.0 at the group level, and frequently so at the individual level. Taken together, these results strongly suggest that more than one parameter is needed to accurately describe delay discounting by humans. Notably, both the Rachlin and the Green and Myerson models accounted for more than 99% of the variance at the group level and for 96% of the variance in the median individual. Because both models provide such good descriptions of the data, model selection will need to be based on other grounds.

1. Introduction

In behavior analysis and behavioral economics, the term discounting refers to the decrease in the value of a reward as a function of increasing delay or decreasing probability. That is, when subjects are given a choice between two rewards that differ in delay, they often choose the one that would be delivered sooner, even when it has a lower objective value. Similarly, when subjects are given choices between two rewards that differ in probability, they tend to choose the more certain one, even when it has a lower objective value. In such cases involving delayed or probabilistic rewards, the value of the more delayed or less certain reward is said to be discounted (for a review, see Green and Myerson, 2004; for a broader conceptualization, see Rachlin, 2006).

Experimental procedures to gauge the quantitative and qualitative characteristics of discounting typically adjust either the time to the delayed reward or the amount of the immediate reward (e.g., Green et al., 2007; Mazur, 1987; Rachlin et al., 1991). Data obtained from humans as well as a number of nonhuman species (e.g., rats, pigeons, rhesus monkeys, mice) using both types of procedures have shown that the discounting of a variety of delayed rewards (e.g., water, food, cocaine) is well described by Mazur’s (1987) hyperbola (e.g., Green et al., 2007; Helms et al., 2006; Madden et al., 1999; Rachlin et al., 1991; Richards et al., 1997; Woolverton et al., 2007):

$$V=A/(1+\mathit{kD}),$$ (1)

where V is the subjective value of the delayed reward, A is the amount of the delayed reward, D is the delay, and k is a parameter that reflects the discounting rate.

The finding that discounting by nonhumans and humans follows a hyperbolic function, however, is at odds with the discounted utility model of standard economic theory (Samuelson, 1937), which posits exponential discounting:

$$V=A{e}^{­\mathit{kD}},$$ (2)

where V, A, k, and D are as in Eq. 1. Exponential discounting predicts that individuals will have time-consistent preferences that are independent of reward amount. In contrast, behavioral psychologists have typically favored the hyperbolic form expressed in Eq. 1, which predicts time-inconsistent preferences as evidenced by the well-established finding of preference reversals in both humans and nonhumans (e.g., Ainslie and Haendel, 1983; Green et al., 1981; Green et al., 1994; for more on this issue, see Ainslie, 1975; Green and Myerson, 1993).

With humans, Eq. 1 tends to overpredict subjective value at shorter delays, while underpredicting it at longer delays (Green and Myerson, 2004; see, e.g., Odum et al., 2006). As a result, alternative models have been proposed to more adequately describe the discounting of delayed rewards by humans. Perhaps the most prominent alternative model of discounting is a generalized form of Eq. 1 described by Myerson and Green (1995):

$$V=A/{(1+\mathit{kD})}^s.$$ (3)

In this equation, s is a free parameter that may reflect individual differences in the scaling of delay and/or amount (Green, Fry, and Myerson, 1994; Myerson and Green, 1995). Note that when s = 1.0, Eq. 3 reduces to Eq. 1. When s is less than 1.0, however, subjective value is more sensitive to changes at shorter delays and less sensitive to changes at longer delays than is predicted by Eq. 1. (For earlier discussions of Eq. 3, see Loewenstein and Prelec, 1992; Rachlin, 1989).

Because Eq. 3, a two-parameter model, will almost always provide a better fit than a one-parameter model, statistical procedures are used to assess whether the relative complexity of Eq. 3 is necessary when describing discounting by humans. One approach has been to determine whether the proportion of variance accounted for (R²) by Eq. 3 is significantly greater than that of Eqs. 1 and 2. A second approach has been to test whether the s parameter of Eq. 3 deviates significantly from 1.0 (e.g., Myerson and Green, 1995; Simpson and Vuchinich, 2000). Significant deviations from an s value of 1.0 suggest the need for the more general form of hyperbolic discounting represented by Eq. 3. Overall, the results obtained using these approaches at both the individual and group level indicate that a hyperboloid model of the form of Eq. 3 often describes the discounting of various rewards displayed by humans more accurately than does Eq. 1 (e.g., Green et al., 1999; Myerson and Green, 1995; Simpson and Vuchinich, 2000).

Rachlin (2006) has proposed a different two-parameter model of discounting. His model is similar to Mazur’s (1987) hyperbola except that delay is raised to a power (see also, Rodriguez and Logue, 1988):

$$V=A/(1+{\mathit{kD}}^s).$$ (4)

Like Eq. 3, Rachlin’s power-function form of hyperbolic discounting is derived explicitly from Stevens’s (1957) psychophysical power law. According to Rachlin, the s parameter reflects the sensitivity of subjective value to the variable D, delay. Rachlin found that both Eqs. 3 and 4 accounted for a similarly high proportion of the variance in delay discounting data at the group level for various magnitudes ($100, $1,000, and $1,000,000) of delayed gains (R²s of .99).

Although Rachlin (2006) compared the fits of Eqs. 3 and 4 to group median data, the ability of these models to describe data at the individual level has not been compared. A good model of discounting should not only be able to describe the aggregate behavior of any particular group, but should also accurately describe the behavior of the individuals in that group (Green and Myerson, 2004; see Estes, 1956; Sidman, 1952). Accordingly, the major aim of the present work was to compare the two hyperboloid models of delay discounting, Eq. 3 (Green and Myerson, 2004) and Eq. 4 (Rachlin, 2006), at the individual as well as the group level. It has been shown that Eq. 3 provides a better description than Eq. 1 of the data from many, but not all individuals (e.g., Myerson et al., 2003). However, the proportion of individuals for whom Eq. 4 provides a better description than Eq. 1 is not known. Eq. 2 was studied because of its status in standard economic theory as a normative model of intertemporal choice.

2. Materials and methods

2.1. Participants

Sixty-four participants (41 female) were recruited from an introductory psychology course at a regional university in Northeast Alabama. The average age and education (and standard deviation) of the participants was 21.6 (± 3.8) and 12.6 (± 0.9) years, respectively. The ethnic breakdown was: 61% Caucasian, 33% African-American, and 6% Hispanic or Other. There were no eligibility criteria and participation was voluntary. Participants were tested individually in a quiet room. The university’s Institutional Review Board approved study procedures prior to their conduct.

2.2 Procedure

Participants sat in front of a desktop computer that presented them with a series of choices between a smaller, immediate and a larger, delayed hypothetical monetary gain. An adjusting-amount procedure was used. In each series of choices, the amount of the larger, later reward and the delay until its receipt were held constant (e.g., $1000 in one year). The smaller, immediate reward was adjusted according to a “double-limit” algorithm (see Richards et al., 1999) until it converged on an immediate amount that was deemed subjectively equivalent to the larger, later reward (i.e., the participant was relatively indifferent between them). Then the delay to the larger, later reward was changed, and the smaller, immediate reward was repeatedly adjusted again until another indifference point was determined. This procedure was repeated for each of seven delays (1 day, 1 week, 1 month, 6 months, 1 year, 5 years, and 25 years), which were studied in ascending order. The larger, later amount was always $1000, and the smaller, immediate amounts ranged from $40 to $960.

2.3 Data Analysis

The amount of immediate money judged equal in subjective value to the $1000 delayed amount was expressed as a proportion of the objective value of the delayed amount. Eqs. 1 through 4 were fit to the individual and group data using nonlinear regression techniques (GraphPad Prism^®), which provided appropriate parameter estimates and R² values. A t-ratio statistic was used to determine whether the s values in Eq. 3 and 4 deviated significantly from 1.0. Specifically, the estimate of s was subtracted from 1.0, and then divided by the standard error of s. The resulting t ratio has (n – p) degrees of freedom where n is the number of data points and p is the number of model parameters (Myerson and Green, 1995). To assess whether the fits at the individual level differed significantly between equations with the same number of parameters (i.e., Eq. 1 vs. Eq. 2, and Eq. 3 vs. Eq. 4), the R² values were subjected to Wilcoxon signed-ranks tests.

3. Results

The top panel of Fig. 1 shows the median indifference points and the best-fitting discounting functions for Eqs. 1 through 4. The data appear to be relatively well described by all four equations, but compared with the one-parameter exponential and hyperbolic equations (Eqs. 1 and 2, respectively), the two-parameter equations (i.e., Eqs. 3 and 4) provide visually superior fits to the median data. The bottom panel of Fig. 1 depicts the same data, but the x-axis is scaled logarithmically to provide more detail of the fit at the shorter delays. As may be seen, both of the one-parameter equations (and especially Eq. 2) overestimate the indifference points at the shorter delays and underestimate them at the longer delays. In contrast, neither of the two-parameter equations exhibited such systematic bias.

Fig. 1.

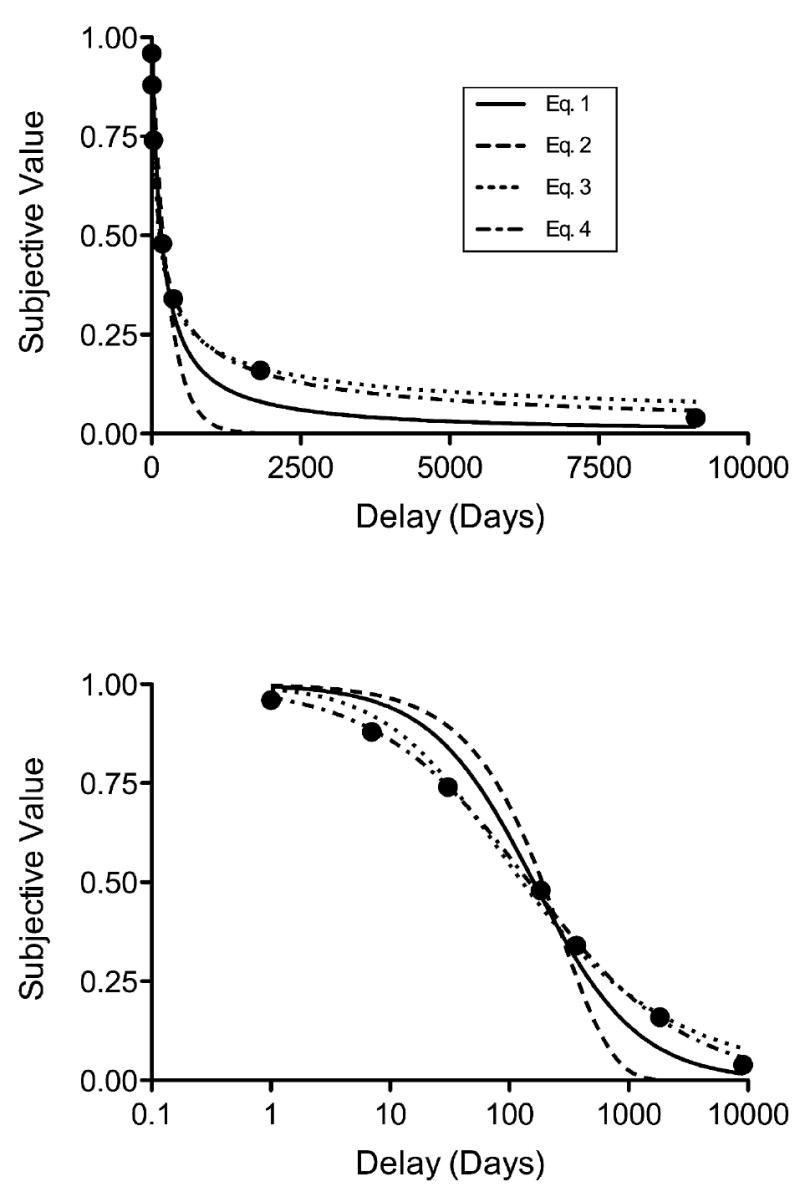
Subjective value expressed as a proportion of the $1,000 delayed amount. The top panel shows the four delay discounting functions (Eqs. 1 through 4) fit to the median indifference points. The bottom panel shows the same data and functions, but the x-axis is scaled logarithmically to provide more detail at the shorter delays.

Table 1 shows the parameter values and R²s for the discounting functions fit to the group median data depicted in Fig. 1, as well as (in italics) the median parameter values and R²s based on fits of the discounting functions to individual data. With respect to the fits to the data shown in Fig. 1, the values of the s parameter for Eqs. 3 and 4 (0.45 and 0.67) both were significantly less than 1.0; t(5) = 8.55, and t(5) = 16.10, respectively, both ps < .01. At the individual level, the value of the s parameter in Eq. 3 differed significantly from 1.0 in 37 (58%) of the 64 cases, all t(5)s > 2.57, ps < .05, and was significantly less than 1.0 in all but one of these 37 cases; the value of the s parameter in Eq. 4 differed significantly from 1.0 in 40 (63%) of the 64 cases, all t(5)s > 2.57, ps < .05, and was significantly less than 1.0 in 34 of these 40 cases.

Table 1.

Parameter estimates and fit statistics for the discounting functions (Eqs. 1 through 4). Values in regular font are based on fits to the group median data depicted in Figure 1; values in italics are the medians based on fits to individual data.

Discounting Equation	k	s	R2
Eq. 1 (Hyperbolic)	0.0062 0.0069	- -	.967 .929
Eq. 2 (Exponential)	0.0037 0.0038	- -	.911 .892
Eq. 3 (Green & Myerson)	0.0281 0.0423	0.45 0.42	.992 .956
Eq. 4 (Rachlin)	0.0346 0.0435	0.67 0.66	.999 .963

Note: Dashes indicate parameter was not applicable to the particular equation.

In terms of variance accounted for, all four discounting models provided good-to-excellent fits to the group median data (see Table 1). The one-parameter models both accounted for a high proportion of the variance, but Eq. 1 accounted for notably more variance than did Eq. 2 (R² = .967 and .911, respectively). Not surprisingly, the two-parameter models, Eqs. 3 and 4, both provided even better fits to the median data (R² = .992 and .999, respectively).

With respect to fits at the individual level, in many cases the one-parameter models did not provide a better description of an individual’s data than did the mean of that individual’s subjective values (i.e., the sum of the squared residuals was greater than the variance about the mean of the individual’s subjective values for the different delays). Specifically, the hyperbolic equation (Eq. 1) provided a poorer description than the mean of the individual’s subjective values in 10 cases (16%), and the exponential equation (Eq. 2) provided a poorer description than the mean in 14 cases (22%). With regard to the two-parameter models, in contrast, there was only 1 case in which Eq. 3 fared worse than an individual’s mean, and there were no cases in which Eq. 4 accounted for less variance than an individual’s mean.

Comparing the one-parameter models, the R² for Eq. 1 was higher than that for Eq. 2 in 43 (67%) of the 64 participants, and the difference between these models was significant according to a Wilcoxon signed-rank test (p < .01). Comparing the two-parameter models, Eq. 4 accounted for more variance than did Eq. 3 in slightly more than half (53%) of the cases, and the difference between these models was not significant according to a Wilcoxon signed-ranks test.

4. Discussion

The primary aim of the present study was to compare the ability of four different models to describe the discounting of delayed monetary rewards at both the group and individual levels. With regard to the one-parameter models, the data clearly supported the simple hyperbola (Mazur, 1987) over an exponential model at the group level and in a substantial majority of the participants. These results are consistent with prior findings that call into question the adequacy of exponential discounting as an appropriate model of intertemporal choice (e.g., Kirby and Herrnstein, 1995; Madden et al., 1999; Myerson and Green, 1995).

The present results also are consistent with a growing number of studies indicating that an additional sensitivity parameter often is warranted when describing delay discounting by human participants. With both the Green and Myerson model, Eq. 3, and the Rachlin model, Eq. 4, we found that s deviated significantly from 1.0 in the majority of individual participants as well as at the group level. With respect to Eq. 3, these results are consistent with previous findings (e.g., Green and Myerson, 2004; Myerson et al., 2003; Myerson and Green, 1995; Simpson and Vuchinich, 2000). With respect to Eq. 4, the present results replicate Rachlin’s (2006) findings regarding delay discounting at the group level and are the first to support his model at the individual level.

Notably, when s was significantly different from 1.0, it was less than 1.0 in all but one case with Eq. 3, and in 85% of the cases with Eq. 4. Whether s is greater or less than 1.0 is important from a theoretical perspective, particularly that of the Rachlin (2006) model. This is because the s parameter in the Rachlin model represents the exponent of the power function that scales delay, and previous studies have shown that the relation between subjective and objective time is negatively accelerated, particularly over the range studied here (e.g., Zauberman, Kim, Malkoc, and Bettman, in press). Therefore, the exponent in the power function component of Eq. 4 should be less than 1.0, as indeed it was in the majority of cases when Eq. 4 was fit to the data from individual participants. With respect to the Green and Myerson model, the s parameter represents the exponent of the power function scaling time divided by the exponent of the power function scaling amount (Myerson and Green, 1995). Although both exponents would be expected to be less than 1.0 in this model, there is no basis for predicting which is smaller, particularly at the individual level. Nevertheless, the finding that s < 1.0 is important because it implies that the exponent of the power function scaling time is typically less than the exponent of the power function scaling amount.

Rachlin (2006) found that that there was little difference in R² between Eqs. 3 and 4 at the group level, and our results replicate this finding and extend it to delay discounting by individual participants. Thus, our results support Rachlin’s contention that it may be difficult to distinguish between these models solely on the basis of their fits to data. Instead, one may need to choose a model based on theoretical reasons, rather than empirical ones.

Rachlin (2006) pointed out that the extent to which models fit into a larger theoretical network provides an important basis for their evaluation. In this context, he showed that the generalized matching law (Baum, 1974) and a form of utility maximization could be rewritten in the hyperboloid form of Eq. 4. It should be noted, however, that Eq. 3 also is consistent with the matching law. In contrast to Baum’s equation, Eq. 3 yields a form of generalized matching in which amount and delay have separate exponents. This is because Myerson and Green’s (1995) derivation of Eq. 3 assumes that Stevens’s power law describes the scaling of amount as well as time. Indeed, utility functions, which describe the relation between value and amount, are generally assumed to be well described by power functions. Thus, both Eq. 3 and Eq. 4 have the desirable attribute of fitting into larger theoretical networks, and future work will be needed to determine an appropriate basis for choosing between them.