Model-based Automatic Detection of the Anterior and Posterior Commissures on MRI Scans

Abstract

The projections of the anterior and posterior commissures (AC/PC) on the mid-sagittal plane of the human brain are important landmarks in neuroimaging. They can be used, for example, during MRI scanning for acquiring the imaging sections in a standard orientation. In post-acquisition image processing, these landmarks serve to establish an anatomically-based frame of reference within the brain that can be extremely useful in designing automated image analysis algorithms such as image segmentation and registration methods. This paper presents a fully automatic model-based algorithm for AC/PC detection on MRI scans. The algorithm utilizes information from a number of model images on which the locations of the AC/PC and a reference point (the vertex of the superior pontine sulcus) are known. This information is then used to locate the landmarks on test scans by template matching. The algorithm is designed to be fast, robust, and accurate. The method is flexible in that it can be trained to work on different image contrasts, optimized for different populations, or scanning modes. To assess the effectiveness of this technique, we compared automatically and manually detected landmark locations on 84 T₁-weighted and 42 T₂-weighted test scans. Overall, the average Euclidean distance between automatically and manually detected landmarks was 1.1 mm. A software implementation of the algorithm is freely available online at www.nitrc.org/projects/art.

Introduction

The anterior and posterior commissures are bundles of transverse white matter fibers that connect the two cerebral hemispheres of the brain. Intersection points of these fibers (AC/PC) with the mid-sagittal plane (MSP) are important landmarks in neuroimaging. For example, during magnetic resonance imaging (MRI) scans, these landmarks may be used for acquiring the imaging sections parallel to the standard AC-PC plane. In post-acquisition computerized image analysis, the AC/PC serve to establish an anatomically-based frame of reference in the brain. Such a standard coordinate system is extremely useful in designing automated image analysis algorithms such as brain image segmentation and registration methods. These landmarks are also bases for widely-used standard stereotactic brain atlases (Schaltenbrand and Wahren, 1977; Talairach and Tournoux, 1988).

In most current neuroimaging applications, these landmarks are determined manually on MRI scans by expert observers. This paper presents an algorithm for fully automatic detection of the AC/PC. Automated AC/PC detection has the advantages of being faster, more reproducible (i.e., no inter-observer variability), and independent of operator expertise. These are important features when dealing with large numbers of images from multiple subjects, and multi-center studies. It also automates algorithms that would otherwise require manual intervention. For example, we routinely use this method to obtain an initial rigid-body linear transformation between a test volume and a template volume before performing non-linear image registration using the Automatic Registration Toolbox (ART) package (Klein et al., 2009). We have also applied the algorithm during MRI acquisition, allowing 2D image sections to be scanned exactly perpendicular to the MSP and parallel to the AC-PC plane.

Several previously published algorithms exist for automatic location of the AC/PC on 3D MRI scans (Vérard et al., 1997; Han and Park, 2004; Prakash et al., 2006). All of these algorithms rely on a successful localization of the corpus callosum (CC), which can be a problem (Lee et al., 2000; van Ginneken et al., 2002). These methods are also limited to operating on T₁-weighted (T1W) images. Some of the algorithms rely on edge detection, which can pose a problem when dealing with noisy images, or images with motion artifacts. Some of these algorithms involve setting over 30 parameters.

The algorithm presented in this technical note does not rely on CC localization. Instead, we first find a highly prominent landmark (MPJ) on the midbrain-pons junction, located at the vertex of the superior pontine sulcus, and then proceed to search for the AC/PC based on their relative locations with respect to the MPJ as obtained from the training data set. The algorithm also does not rely on edge enhancement. Since the algorithm is model-based, it does not rely on any particular contrast, and can be trained for data other than T1W. Another main advantage of this approach is that it is flexible, in that it follows the examples provided to it in the training set in defining the AC/PC (e.g., center versus edges). In other words, it adapts to the particular landmark definitions and images properties on which it is trained.

Materials and Methods

Image data

Three sets of scans were used for training and evaluation of the algorithm presented in this paper. The Nathan Kline Institute (NKI) set consisted of forty-eight 3D T1W anatomical MRI volumes, acquired from 33 healthy subjects and 15 patients with chronic schizophrenia. Six of these volumes were used for training the algorithm and the remaining 42 were used to evaluate the accuracy of the method. All subjects were participants in research projects approved by the local Institutional Review Board and provided written informed consent. The MRI scans were performed using a 1.5 T Siemens Vision system (Siemens AG, Erlangen, Germany). High-resolution sagittal 3D T1W volumes were acquired from each subject using a magnetization-prepared rapid acquisition gradient echo (MPRAGE) sequence with the following parameters: TR=11.6 ms, TE=4.9 ms, flip angle=8°, FOV=256×256×190 mm³, matrix size=256×256×190, 1 mm³ isotropic voxel size.

The second set of data that were used exclusively for evaluating the accuracy of the algorithm (not for training) were 42 standard anatomical 3D T1W MPRAGE scans obtained from the publically available IXI database (www.ixi.org.uk). These volumes had a matrix size of 256×256×150 voxels (2 volumes had 146 slices) and a voxel size of 0.9375×0.9375×1.2 mm³. The images were acquired at three different sites with 1.5 T and 3.0 T scanners. Subject ages ranged from 22 to 86 years old. The 42 volumes were selected randomly in a way that each decade of life from 20’s to 80’s was represented by three male and three female subjects. More details about these data and subjects can be found at the IXI database website. The data accession numbers are given in Appendix A.

The third set of volumes used for evaluating the algorithm, also downloaded from the IXI database, consisted of 42 T₂-weighted (T2W) fast spin echo scans, acquired from the same subjects listed in Appendix A, with overlapping slices to produce a densely sampled “pseudo-volume”. These volumes had a matrix size of 256×256×130 voxels (one volume had 120 and three volumes had 136 slices) and a voxel size of 0.9375×0.9375×1.25 mm³ (4 volumes had a voxel size of 0.9375×0.9375×1.2 mm³).

Manual location of landmarks

For both training and evaluation of the algorithm, we manually located the AC/PC on all of the 132 volumes (48 T1W NKI, 42 T1W IXI, 42 T2W IXI) described above using the following procedure. Manual location of landmarks was performed using a program that displayed three orthogonal slices through a selected point. Zooming, contrast enhancement and position stepping by single voxels was also available.

Landmark location generally started with a view of the approximate MSP. The MPJ point was located by following the superior edge of the pons until the recess at the juncture of the pons with the tegmentum of the mesencephalon was found. The AC can generally be found at the tip of the sagittal image of the fornix in the MSP. The arc of the commissure in the axial slice provided the signature of the AC. Since the AC is only about 2 mm wide, larger slice thicknesses can dim its image in the sagittal plane and make it difficult to locate. It may also appear to be either 2 or 3 voxels wide. Generally we tried to locate the most intense voxel, but where necessary, estimated the position to 0.5 voxel. The PC is located at the top of the superior colliculus, about 2 mm in diameter. It is more difficult to locate the AC and PC in T2W images. Landmarks were measured twice at least a day apart. Any image for which a coordinate was different by more than one voxel was remeasured. In this particular data set, this was only necessary on T2W images.

Training phase

The algorithm introduced in this paper is model-based. This involves a training phase, which is performed once for a particular class of data, using a number of images with known landmark locations. The information extracted from the training data is then used to locate the landmarks on test images. Below, we will present details of the training and landmark detection phases separately. All coordinates in the procedures described in this paper are in physical space in units of millimeters.

Let us assume that we have available a set of M model images on which we know the index locations of the AC, PC, and MPJ. The training procedure involves the following steps:

1. The MSP is automatically located on each model image using the algorithm described by Ardekani et al. (1997). The MSP is defined by equation: Ax+By+Cz = 1. The three parameters (A, B, C) are determined using an optimization procedure that maximizes the symmetry between image halves on either side of the plane. Several other specific approaches to automatic MSP detection have been reported that also appear to be reliable and can be used for this purpose (Liu et al., 2001; Prima et al., 2002; Hu and Nowinski, 2003).

2. A small rotation and translation are applied to the detected MSP so that the transformed plane passes through the AC and PC. Henceforth, MSP refers to this slightly adjusted plane. Note that the MPJ will not necessarily lie on this plane, but it will be close to it.

3. A linear rigid-body transformation is applied to each of the model images so that the following conditions are met: the AC to PC line is parallel to the image x-axis; the image y-axis points towards subject’s feet; the z-axis points towards left; and the MSP lies on the z = 0 plane. We refer to these transformed images as being in “PIL” (posterior-inferior-left) coordinates (note that PIL is a left-handed coordinates system). The MSP’s from the six PIL orientated model images are shown in Figure 1. At this stage, the image is also resampled to have isotropic voxel dimensions. The voxel dimension is specified as a parameter to the model building program, with a default value of 1 mm.

4. The linear transformation in step (3) is also applied to the manually identified position vectors of the AC, PC, and MPJ on the original image. Let P⃗_ai, P⃗_pi, and P⃗_mi respectively correspond to the position vectors of AC, PC, and MPJ of the i^th model image after undergoing this transformation. These position vectors are measured in physical space in units of millimeters in the PIL-orientated coordinates system (x = posteior, y = inferior, z = left) with its origin located at the center of the image FOV.

5. The mean MPJ position vector, P⃗_m, and two mean displacement vectors, P⃗_ma and P⃗_mp, are computed as follows:

   $${\overrightarrow{P}}_m=\frac{1}{M}\sum _{i=1}^M{\overrightarrow{P}}_{mi}$$ (1)

   $${\overrightarrow{P}}_{ma}=\frac{1}{M}\sum _{i=1}^M({\overrightarrow{P}}_{ai}-{\overrightarrow{P}}_{mi})$$ (2)

   $${\overrightarrow{P}}_{mp}=\frac{1}{M}\sum _{i=1}^M({\overrightarrow{P}}_{pi}-{\overrightarrow{P}}_{mi})$$ (3)

   Note that the displacement vectors P⃗_ma and P⃗_mp, connect the mean MPJ location to the mean AC and PC locations, respectively.

6. Small cylindrical regions centered around the three position vectors P⃗_ai, P⃗_pi, and P⃗_mi are considered (Figure 1). The axes of these cylinders are parallel to the z-axis (subjects’ left).

7. Each PIL oriented model image i = 1, 2, ···, M is rotated by N pitch angles α ∈ {α₁, α₂, ···, α_N} about the axes of each of the cylinders in step (6). For each rotation, the voxel values that fall in the cylindrical region are organized as vectors, denoted by: T⃗_aiα, T⃗_piα, and T⃗_miα corresponding to the cylinders centered around the AC, PC, and MPJ, respectively. Thus, for example, the elements of vector T⃗_piα are voxel values inside the cylinder centered around the PC in model i after undergoing a rotation of α degrees about the axis of the cylinder.

8. Finally, average template vectors over all model images are computed as follows:

   $${\overrightarrow{T}}_{a\alpha }=\frac{1}{M}\sum _{i=1}^M{\overrightarrow{T}}_{ai\alpha }$$ (4)

   $${\overrightarrow{T}}_{p\alpha }=\frac{1}{M}\sum _{i=1}^M{\overrightarrow{T}}_{pi\alpha }$$ (5)

   $${\overrightarrow{T}}_{m\alpha }=\frac{1}{M}\sum _{i=1}^M{\overrightarrow{T}}_{mi\alpha }$$ (6)

   To summarize, the results of the training procedure are the mean position vector of the MPJ: P⃗_m the mean displacement vector between the MPJ and the AC: P⃗_ma, the mean displacement vector between the MPJ and PC: P⃗_mp, and N average template vectors for different pitch angles α for the AC, PC, and the MPJ: T⃗_aα, T⃗_pα, and T⃗_mα. This information is saved in a “model file” that is recalled during automatic AC/PC detection.

Figure 1.

Mid-sagittal planes of AC/PC aligned PIL images of the 6 scans used as the training set. The circles represent cross-sections of the AC, PC, and MPJ cylindrical templates.

AC/PC detection phase

The following steps are applied to automatically detect the AC/PC on test images:

1. The MSP is automatically detected as in the training phase.

2. The test image is transformed to PIL orientation and resampled to have an isotropic voxel size equal to the voxel size used in the modeling phase. The transformation to PIL orientation is such that the detected MSP in step 1 would lie on the z = 0 plane.

3. The PIL oriented test image is thresholded using Otsu’s method (Otsu, 1979). Only the supra-threshold voxels are considered as candidates for the landmarks.

4. The mean position vector P⃗_m and the set of templates T⃗_mα are read from the model file. A cylindrical region, centered around P⃗_m whose axis parallel is to the z-axis, is searched on the PIL oriented test image for the MPJ. The search is based on template matching by normalized cross-correlation (NCC). For each supra-threshold voxel v in the search cylinder, a vector F⃗_v is formed whose element are the voxel values on the test image inside a cylindrical region centered around v and parallel with the z-axis, exactly similar in shape and size to the one that was used in defining the template T⃗_mα during the training phase. The maximum NCC (over all angles α ∈ {α₁, α₂, ···, α_N}) is computed for all voxels v in the search region. The voxel with the largest maximum NCC is taken provisionally to be the location of the MPJ, denoted by v_m. The operations described here can be written in a concise mathematical form as follows:

   $$v_m=\underset{v}{\text{argmax}}\left[\underset{\alpha }{max}\frac{{\overrightarrow{T}}_{m,\alpha }·{\overrightarrow{F}}_v}{\parallel {\overrightarrow{T}}_{m\alpha }\parallel \parallel {\overrightarrow{F}}_v\parallel }\right]$$ (7)

   Let Q⃗_m denote the position vector of v_m, and s_m denote the corresponding value of the NCC.

5. The mean displacement vector P⃗_mp and the set of templates T⃗_pα are read from the model file. A cylindrical region, centered about point (Q⃗_m + P⃗_mp) whose axis is parallel to the z-axis is searched for the PC. Again, the search mechanism is based on template matching by NCC, as detailed in step (4). This search yields an estimated location for the PC. Let s_p denote the maximum NCC corresponding to this position.

6. The mean displacement vector P⃗_ma and the set of templates T⃗_aα are read from the model file. A cylindrical region, centered about point (Q⃗_m + P⃗_ma) whose axis is parallel to the z-axis is searched for the AC. This search yields an estimated location for the AC, and a corresponding maximum NCC denoted by s_a.

7. Steps (4)–(6) are repeated by selecting the second most likely MPJ candidate voxel in step (4). This step yields a second set of three landmark MPJ, PC, and AC. We accept the set with the larger sum of maximum similarity measures (s_m + s_p + s_a) as the final answer. This can be repeated for other possible MPJ points. But in practice, we have not found a case in which this was necessary. This is due to the prominence of the MPJ as a brain landmark, which limits the possibility of finding false positives when detecting the MPJ. It should be noted that after finding the most likely candidate MPJ point in step (4), we impose a cylindrical exclusion zone around this point to ensure that the second most likely candidate MPJ point is not in the immediate neighborhood of the first one. We set the radius of this exclusion zone equal to the radius of templates T⃗_mα and its height equal to the height of the MPJ search region. The point with the next highest NCC in this procedure usually turns out to be the cerebellum fourth ventricle notch, which can be seen inside the MPJ research region (blue circle) on Figure 2.

8. The MSP is adjusted slightly by a translation and a rotation so that it passes through the detected AC/PC points.

9. Finally, the inverse of the PIL transformation applied in step (2) above is applied to the AC/PC and the MSP so that these landmarks are given in the coordinate system of the original test image.

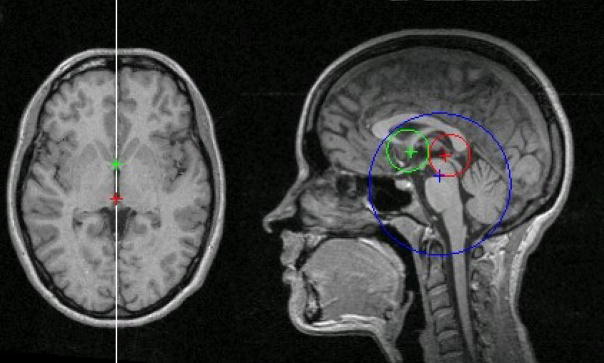
Figure 2.

An example of successful AC/PC detection from a healthy subject. The red, green, and blue indicate detected AC, PC, and MPJ points. The circles indicate cross-sections of the cylindrical search regions for the three landmarks. The line on the axial image indicates the detected MSP.

Quantitative evaluation

In order to evaluate the accuracy of the algorithm, we compared the manually determined AC/PC locations on the 42 T1W NKI volumes (48 original volumes minus 6 used for training), the 42 T1W IXI, and the 42 T2W IXI volumes with those detected automatically by the algorithm. We used the 3D Euclidean distance between the automatically and manually determined landmarks as a measure of discrepancy (“error”) between the two methods.

To evaluate the intra- and inter-observer reproducibility of the manual method used to identify landmark points, manual AC/PC detection was repeated one month later on the 42 T1W IXI images by the same observer (AHB) who had identified the AC/PC for training and testing on all images. In addition, a second rater (BAA) manually identified these landmarks on the same data set to assess inter-observer variability.

Results

Training

We used 6 of the 48 T1W NKI volumes from 3 normal subjects and 3 patients with schizophrenia to train the algorithm. The only criterion used for selecting the 6 volumes in the training set was lack of obvious imaging artifacts such as motion. The (x, y, z) coordinates of the centers of the AC, PC, and MPJ were manually identified on these scans by an expert observer (AHB) using the method described above. The radii of the cylindrical templates were set to 8.0, 6.0, and 14.0 mm for the AC, PC, and MPJ, respectively. The cylindrical template heights were set to 5.0 mm for all three landmarks. Templates T⃗_aα, T⃗_pα, and T⃗_mα were determined for 5 pitch angles α ∈{−10°, 0°, 10°, 20°, 30°}.

Figure 1 shows the MSP of the training scans in AC/PC aligned PIL orientation. The cross-sections of the three cylindrical AC, PC, and MPJ templates are shown on these images, as are the manually identified AC and PC locations and the projection of the manually identified MPJ on the MSP. Images on the first row are from healthy subjects, and the second row images are from patients with schizophrenia. Note the considerable variability of the shape of the corpus callosum on these images, while the MPJ structure is relatively invariant across subjects. Also note the prominence of this landmark which makes it relatively easy to detect.

We did not train a separate model for T2W volumes. Since the contrast on T2W images is approximately the inverse of T1W contrast, we simply used the negative of the templates obtained from training on T1W volumes when detecting the AC/PC on T2W volumes.

Quantitative evaluation

Using the model trained from the 6 NKI volumes, we applied the algorithm to the remaining 126 volumes (42 NKI, 84 IXI). Figure 2 shows the result of a successful detection of the AC/PC in the MSP. The detected AC, PC, and the projection of the detected MPJ on the MSP are shown in red, green, and blue colors, respectively. The corresponding color circles are cross-sections of the respective search regions. In this case, the radii of the cylindrical search regions were the program defaults of 15.0, 15.0, and 50.0 mm for the AC, PC, and MPJ, respectively. The heights of the cylindrical search regions were also program defaults set at 7.0 mm for the AC and PC, and 1.0 mm for the MPJ. Figure 2 also shows the axial plane containing the AC/PC and the intersection of the MSP on this plane.

For a quantitative evaluation of the algorithm accuracy, we compared the 3D coordinates between the landmarks detected automatically and those identified manually by an expert observer (AHB) on the 126 volumes. The 3D Euclidean distance in millimeters was calculated between the automatically detected and manually identified landmarks. The results are summarized in Table 1. The overall average discrepancy between the automatically and manually detected landmarks was 1.1 mm.

Table 1.

Statistics of discrepancies (errors) between manually and automatically detected AC/PC landmarks.

Error (ε):	Cases with ε<1 mm	Cases with 1≤ε<2 mm	Cases with 2≤ ε<3 mm	Cases with 3≤ε mm	Average (mm)	Maximum (mm)
NKI data (AC)	34	8	0	0	0.9	1.6
NKI data (PC)	31	11	0	0	0.9	1.8
IXI T1 data (AC)	18	23	1	0	1.1	2.2
IXI T1 data (PC)	28	14	0	0	0.9	1.8
IXI T2 data (AC)	18	18	5	1	1.3	3.5
IXI T2 data (PC)	9	25	7	1	1.5	4.5
All data (AC & PC)	138	99	13	2	1.1	4.5

Table 2 shows the results inter-observer (AHB vs. BAA) and intra-observer (AHB vs. AHB) reproducibility of the manual method used to identify the AC/PC. Average (maximum) inter-observer variability was 0.8 (2.4) mm for the AC, and 0.9 (1.7) mm for the PC. The intra-observer variability was 0.5 (1.6) mm for the AC, and 0.4 (1.3) mm for the PC.

Table 2.

Statistics of discrepancies (errors) between manually detected AC/PC landmarks within and between observers on the 42 T1W IXI image set.

Error (ε):	Cases with ε<1 mm	Cases with 1≤ε<2 mm	Cases with 2≤ε<3 mm	Average (mm)	Maximum (mm)
Inter-rater (AC)	26	15	1	0.8	2.4
Inter-rater (PC)	23	19	0	0.9	1.7
Intra-rater (AC)	36	6	0	0.5	1.6
Intra-rater (PC)	39	3	0	0.4	1.3

Discussion

Quantitative evaluation of the algorithm (Table 1) showed average error of 1.1 mm over all data sets and both landmarks. These is comparable with inter-rater variability reported in this paper, as well as those reported by Boesen et al. (2005), who noted variations from mean of 0.82 mm (AC) and 0.69 mm (PC) between four raters that independently detected the AC/PC on the same set of scans. The errors on all 42 T1W NKI test volumes were below 2 mm. This was also true for the 42 T1 WIXI test volumes, expect for one case where the error in locating the PC was 2.2 mm. These errors are smaller that the results of Prakash et al. (2006) who reported that over 10% of their localizations exceeded 3 mm when compared to each of two experts.

Discrepancies between manually and automatically detected landmarks on the T2W IXI dataset were higher than those on T1W data. The averages for the AC and PC were 1.3 mm and 1.5 mm, respectively. In all T2W scans, the discrepancy was below 3 mm, except in one case where the distance between the manually and automatically detected AC was 3.5 mm, and in another case where the error was 4.5 mm. Discrepancy can arise when there is an error in manual or automatic detection or both. We looked carefully back into the case with the 3.5 mm AC error and judged that the landmark detected automatically by the algorithm appears to be in the correct location. Therefore, in this case we concluded that the discrepancy was due to error in manual detection. On the other hand, for the case in which there was a 4.5 mm discrepancy in PC location, we concluded that the algorithm failed.

The fact that the errors in T2W data are generally larger may be attributed to several factors. (1) The T2W images were not truly 3D scans, rather interleaved 2D acquisitions. In some cases, there appears to be subject motion between the two acquisitions (e.g., cases 36, 51, and 132 amongst others). (2) Distance between slices was slightly higher in T2W data (1.25 mm vs. 1.2 mm in T1W IXI and 1.0 mm in T1W NKI). (3) The algorithm was not directly trained for T2W data. Instead, we used the templates derived from T1 W data and searched for negative correlations. (4) In general, it appears to be more difficult to manually identify the AC/PC on T2W scans.

The training and testing results presented in this paper are intended to provide a proof of concept for the algorithm. In principle, it is recommended that custom-made models be trained for specific pulse sequences, patient populations, field strengths, etc. Usually, at least in neuroimaging research laboratories, the protocol for anatomical scans is fixed after a period of optimization and repeated when scanning different subjects. Therefore, it may be worthwhile to train the algorithm on the characteristics of the images at specific sites. From the results presented here, it appears that a small number of images (e.g., 6) are sufficient to train a successful model.

An interesting application of the automatic AC/PC detection algorithm presented here can be in field-of-view (FOV) placement during MRI acquisition (Weiss et al., 2003). Image acquisition protocols in neuroimaging research involving multiple subjects often include acquisition of a 3D T1W scan such as an MPRAGE or SPGR. This scan is used, for example, to register images from multiple subjects in functional MRI (fMRI) and diffusion tensor imaging (DTI) studies before voxelwise statistical analysis (Ardekani et al., 2002). We have developed a system, whereby after the acquisition of the 3D scan, the present algorithm is applied to automatically detect the MSP and the AC/PC. This information is then used to determine the necessary FOV placement parameters (rotations and translations) so that the subsequent axial 2D fMRI or DTI scans are AC-PC aligned, perpendicular to the MSP, with zero roll angle. This ensures that fMRI and DTI data from different subjects are acquired as much as possible in a standard orientation. This technique is also extremely useful in longitudinal studies when the same subject is scanned multiple times. This procedure is much more accurate, reproducible, and faster than manual attempts by MRI technicians for AC-PC alignment.

The training and AC/PC detection algorithms together require specification of 14 parameters. These are: radii of the AC, PC, and MPJ cylindrical templates; heights of the three templates; radii of the AC, PC, and MPJ cylindrical search regions; heights of the AC and PC search regions; initial pitch angle α; number of pitch angles N; and pitch angle step size Δα All of these parameters are set at default values and are transparent to the user. The default values were used to obtain the results presented in this paper and on many other scans on which we have successfully tested the algorithm. If necessary, however, any of the default values can be overridden by the operator.

In principle, the algorithm presented in this paper may be trained to detect brain landmarks other than AC/PC. In addition, different laboratories may prefer these landmarks to be defined differently. For example, in the original Talairach coordinate system, the inferior-to-superior axis is supposed to be tangent to the posterior aspect of the AC. Assuming that image resolution allows distinguishing this point, one can train the algorithm to detect this aspect of the AC by simply identifying this point during manual landmark selection on the training data set. In the experiments reported here, we trained the algorithm to detect the centers of the AC and PC structures (Schaltenbrand and Wahren, 1977).

It should be mentioned that in general there is a problem with using the AC/PC as basis for brain coordinates systems (Sandor et al, 1994). The use of these landmarks is limited by their separation of only about 30 mm, compared to the approximately 150 mm sagittal width of the brain. This means that a transverse error of 1 mm on one of the landmarks results in a 2-degree angular error and a misalignment of several millimeters at the cortex. However, once these landmarks are identified, they can still provide a useful starting point for more precise algorithms.

The algorithm proposed in this paper was implemented in C++ on a Linux workstation. For the image volumes described above, this implementation takes approximately 6 seconds to run on a computer with an Intel Pentium 4 CPU with a speed of 3.0 GHz and 2 GB RAM. Of this time, approximates 4.5 seconds are spent locating the MSP and the remaining 1.5 seconds are spent on AC/PC detection. This implementation of the algorithm is freely available online at www.nitrc.org/projects/art.

Conclusions

We presented a new model-based algorithm for automatic AC/PC detection on 3D structural MRI scans. Test results presented indicate that the landmarks detected by this algorithm are very close (usually within 1 mm) to points determined manually on the same scans by an experienced operator. The algorithm has a number of advantages over previously published methods. It does not rely on locating the corpus callosum. It also does not rely on edge-detection, which can pose problems, for example in images that have been blurred due to motion. It uses 3D templates that are derived from multiple model images. The detection algorithm can be custom trained to detect the landmarks in ways that are preferable for particular applications. Since the method is model-based, it does not make any assumptions about the image contrast. Thus, it can be trained, for example, to locate the AC/PC on T2W scans. If necessary, this approach allows development of separate models for special populations, such as young children. The algorithm is fast and only takes a few seconds to run on an average speed workstation.

Appendix A

The IXI data accession numbers used in this study were: 2, 16, 36, 43, 51, 56, 57, 84, 91, 101, 105, 119, 121, 131, 132, 139, 142, 158, 161, 163, 168, 169, 172, 180, 193, 229, 237, 251, 305, 313, 344, 353, 391, 455, 464, 473, 497, 499, 538, 539, 639, 640.