Variation in the Phase of Response to Low-Frequency Pure Tones in the Guinea Pig Auditory Nerve as Functions of Stimulus Level and Frequency

Abstract

The directionality of hair cell stimulation combined with the vibration of the basilar membrane causes the auditory nerve fiber action potentials, in response to low-frequency stimuli, to occur at a particular phase of the stimulus waveform. Because direct mechanical measurements at the cochlear apex are difficult, such phase locking has often been used to indirectly infer the basilar membrane motion. Here, we confirm and extend earlier data from mammals using sine wave stimulation over a wide range of sound levels (up to 90 dB sound pressure level). We recorded phase-locked responses to pure tones over a wide range of frequencies and sound levels of a large population of auditory nerve fibers in the anesthetized guinea pig. The results indicate that, for a constant frequency of stimulation, the phase lag decreases with increases in the characteristic frequency (CF) of the nerve fiber. The phase lag decreases up to a CF above the stimulation frequency, beyond which it decreases at a much slower rate. Such phase changes are consistent with known basal cochlear mechanics. Measurements from individual fibers showed smaller but systematic variations in phase with sound level, confirming previous reports. We found a “null” stimulation frequency at which little variation in phase occurred with sound level. This null frequency was often not at the CF. At stimulation frequencies below the null, there was a progressive lag with sound level and a progressive lead for stimulation frequencies above the null. This was maximally 0.2 cycles.

Introduction

When stimulated with low-frequency sounds auditory nerve fibers generate action potentials that occur at specific times with respect to the stimulus waveform (e.g., first seen in the earliest recordings of Galambos and Davis 1943; Johnson 1980; Kiang et al. 1965; Palmer and Russell 1986; Rose et al. 1967). This “phase locking” is a consequence of the mechanical stimulation of the hair cells of the cochlea (see Ruggero and Rich 1987 for review) and has been used to infer the nature of the driving forces in the cochlea. Obviously, a more direct way to determine the vibration of the cochlear partition is by direct measurement and a wealth of such measurements have been produced in a variety of species (see review by Robles and Ruggero 2001). These measurements have repeatedly demonstrated the nonlinear nature of the vibration patterns. The pioneering work of Rhode (1971) showed that the vibration of the basilar membrane (BM) at any point is linear at low sound levels and becomes compressive at moderate sound levels resulting in an extended dynamic range. The tuning of the vibration pattern also becomes broader with sound level (Robles and Ruggero 2001). However, mechanical measurements of the cochlear vibration have been limited in two ways. First, because of difficulty in accessing the apex of the cochlear spiral, most measurements have been made at basal locations, with high characteristic frequencies (CFs). Published accounts of measurements in the low CF apex of the guinea pig cochlea (Cooper 2006; Cooper and Dong 2003; Cooper and Rhode 1995; Hao and Khanna 1996; Zinn et al. 2000) are not entirely consistent but suggest a different mechanical response than at more basal locations. All the studies indicate that the active processes are also present at the apex, but their action is somewhat different, even producing expansion rather than compression under some conditions. Second, the measurements have tended to be point measurements and the longitudinal vibrations are then inferred. Only quite recently have extensive longitudinal measurements been made and these were at high frequency via the round window (Nilsen and Russell 2000; Nilsen and Russell 1999; Ren 2002; Russell and Nilsen 1997). In this paper, we measure the phase response of low-frequency auditory nerve fibers and compare them to the mechanical measurements of basilar membrane motion at the apex. It is clear that auditory nerve firing times are dictated, not only by the motion of the basilar membrane but also by any nonlinear elements in the pathway to the spike generation. This is quite obvious in the distorted shape of tone evoked cycle histograms at high sound level (e.g., Ruggero et al. 1996). Because auditory nerve fiber cycle histograms are much less sinusoidal than BM motion, the “best phase” of the histograms can never be a completely accurate metric of the phase of BM motion. Even using methods that minimize such distortion, taking a single value for the delay imposed by processes such as neurotransmission at the hair cell base is probably an oversimplification. The data we present therefore provide a valuable insight into BM mechanics but cannot be taken to be a direct surrogate.

The phase of response of auditory nerve fibers were measured near threshold of chinchilla using pure tones by Ruggero and Rich (1987) and within 35 dB of threshold in cat by van der Heijden and Joris (2006). This latter study used a special stimulus (“zwuis”) designed to extract the linear components of the phase locking comprising a complex tone with nonharmonically related partials. These data were used to make direct inferences about the nature of the vibration at the cochlear apex. In this paper, we extend these measurements to a much wider range of sound levels, from 40 to 90 dB sound pressure level (SPL), using pure tone stimulation to allow both a “panoramic” view of the phase response of the auditory nerve, and the effects of nonlinearities on the phase response. Such nonlinearities were shown by Anderson et al. (1971) at isolated CFs in the squirrel monkey and had been demonstrated repeatedly in a variety of species since (e.g., cat, Allen 1983; bird, Gleich and Narins 1988; frog, Hillery and Narins 1987). We have repeated these measurements in an extensive population of auditory nerve fibers and confirm and extend these earlier observations. Furthermore, our measurements are in the guinea pig, a species for which direct measurements of apical cochlear mechanics are available.

Methods

Anesthesia and surgical preparation

Adult pigmented guinea pigs (n = 12, 304–932 g) were anesthetized by intraperitoneal injection of urethane (0.9–1.3 g kg⁻¹ in a 20% solution, Sigma) supplemented when necessary by intramuscular injections of 0.2 ml Hypnorm (Fentanyl citrate 0.315 mg ml⁻¹, fluanisone 10 mg ml⁻¹, Janssen) to maintain areflexia. Atropine sulfate was administered subcutaneously to suppress bronchial secretions. All animals were tracheotomized and mounted in a stereotaxic frame with hollow ear bars. The animals’ core temperature was maintained at 38°C by a heating blanket controlled by a rectal thermistor. End-tidal CO₂ was monitored and kept within normal physiological limits by artificially respiring with oxygen and the electrocardiogram was monitored via a pair of electrodes inserted into the skin to either side of the animal’s thorax.

After a midline incision and retraction of the skin, the temporalis muscle was removed on the left side. The left auditory bulla was exposed and a small hole was made in the posterolateral aspect through which an insulated silver wire was introduced onto the rim of the round window. The bulla was resealed using petroleum jelly (Vaseline, Unilever) including a long small bore nylon tube to allow static pressure equalization, while maintaining closed bulla acoustic conditions. The threshold of the cochlear action potential (CAP) recorded from the round window, as a function of the frequency of a short tone pip (10 ms duration, 2 ms linear rise/fall), was monitored periodically using an automated PEST procedure (see Palmer and Russell 1986; Taylor and Creelman 1967). The CAP audiogram so obtained was assessed every few hours or if single unit thresholds increased. An increase in CAP threshold at all frequencies often indicated fluid buildup in the bulla; drainage of this fluid frequently reestablished CAP and unit thresholds. If CAP thresholds below 10 kHz were elevated by more than 10 dB and no recovery was affected by drainage the experiment was concluded.

A craniotomy was performed which extended from midline 5 mm laterally and from below the nuchal ridge 7–8 mm anteriorly. The flocculus was removed by aspiration, the cerebellum was displaced with a spatula, and 2.7-M KCl filled micropipettes (impedances 20–100 MΩ) were introduced into the auditory nerve under direct visual control. The craniotomy was filled with 1.5% agar in 0.9% saline to prevent desiccation and to aid stability. For all analyses, the microelectrode signals (recorded with an Axon Instruments Axoprobe 1A) were amplified by 60 dB, filtered (300–2,000 Hz) and the time of occurrence of spikes were recorded with 1 μs accuracy (using TDT spike conditioner PC1, spike discriminator SD1, and event timer ET1; Tucker-Davis Technologies, Alachua, FL, USA).

Sound presentation

Experiments were carried out in a sound-attenuated booth. Stimuli were delivered monaurally via a closed-field system (modified Radioshack 40-1377 tweeters; M. Ravicz, Eaton Peabody Laboratory, Boston, MA, USA) coupled to a damped 4-mm diameter probe tube, which fitted into the hollow ear bars. The maximum output level of the system was limited to approximately 100 dB SPL and the response was flat to within ±10 dB from 100 to 35,000 Hz. A probe tube microphone (Brüel and Kjaer 4134 with a calibrated 1-mm probe tube) was used to calibrate the sound system close to the tympanic membrane. Although during the experiment sound levels were defined in terms of attenuation from the maximum, in subsequent analysis and throughout this paper (with the exception of Fig. 1A), all sound levels were converted to dB SPL (dB re 20 μPa) by using the calibration curve for that experiment. The phase of the tone stimuli varied smoothly by only ±0.1 cycles maximum between 100 Hz and 2.5 kHz (the range relevant for the data in this paper). This variation in phase response will not affect the data in those figures plotted at a constant signal frequency (i.e., all those plotted as a function of CF) since it will only shift entire curves up or down slightly. After unwrapping the phase (see below), the only other manipulation of the phases reported was to ensure that the phase-frequency plots intersected the axes at or near zero (to remove any whole cycle phase errors caused by the unwrapping process). All stimuli were generated by an array processor (TDT AP2; Tucker-Davis Technologies, Alachua, FL, USA), which was housed in a personal computer. The stimuli were output via a digital-to-analog converter and waveform reconstruction filter at rates of at least 100 kHz (TDT System II).

FIG. 1.

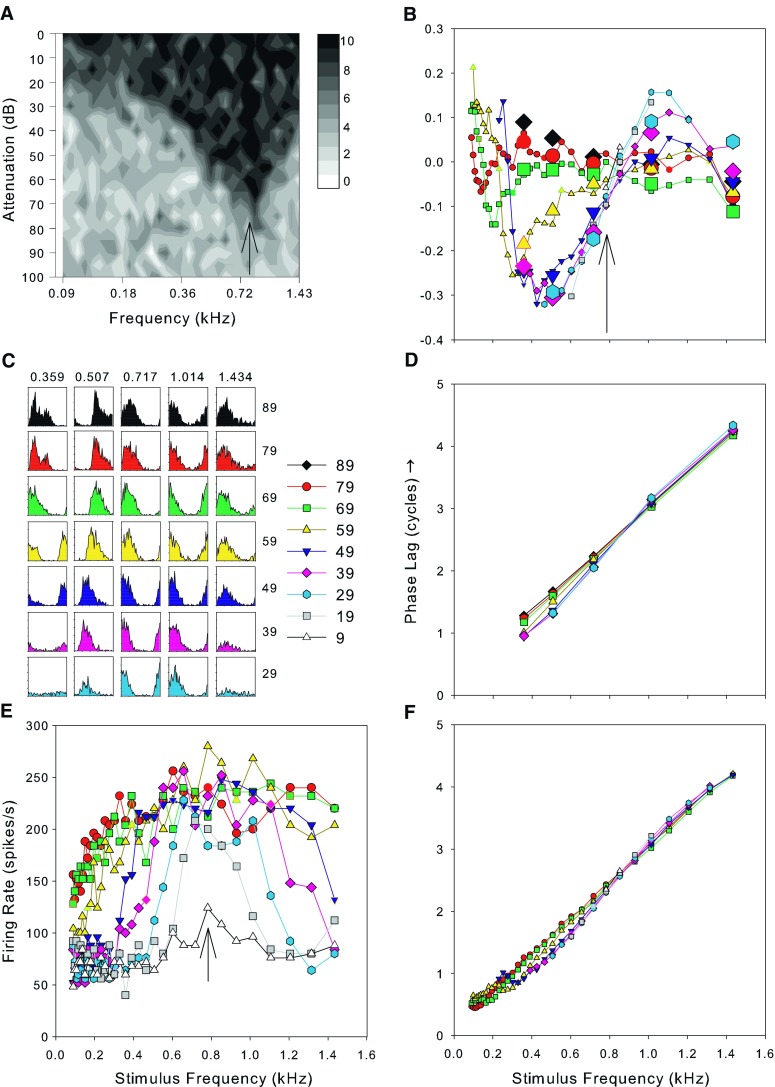
A The frequency response area as a grayscale plot. The CF of this fiber was 0.717 kHz and its spontaneous rate was 58.5 spikes/s. The sound levels are shown as attenuations: The mean maximum sound level over the range of this response area was 91 dB SPL with a standard deviation of 1.7 dB. B The variation of the compensated phase of phase locking as a function of stimulus frequency and sound level (compensated by subtracting the best fitting linear function to the phase curve measured from the FRA derived data at 79 dB SPL). C Period histograms from 50 repeats of tones at half-octave intervals (frequencies across the top, sound levels in dB SPL at the right). D The variation of raw phase values obtained from the histograms in C after unwrapping the phase. E The mean discharge rate as a function of the level and frequency of pure tones (frequency response area). F. The unwrapped raw phase data obtained from period histograms computed from the same data as E. Symbols used in B and D–F represent data for sound levels from 9–89 dB SPL as indicated in the key next to C. The arrow in A, B, and E indicated the frequency of the peak at the lowest sound level in E.

All stimuli in this study were pure tones of 50 ms duration and 2 ms rise fall time presented every 200 ms. The driven rate was calculated within a 50-ms window after stimulus onset and the spontaneous rate was calculated within a 100-ms window beginning 50 ms after stimulus offset. After audiovisual estimation of the fiber minimum threshold and characteristic frequency, three different data sets were collected although not generally all three for each fiber. In the early experiments, the full frequency/level response area was measured using single presentations of tones spanning 0–100 dB attenuation in 5 dB steps and frequencies from 3 octaves below to 1 octave above audiovisual CF in 1/8 octaves steps. The number of spikes evoked by each tone was counted and displayed as a block of grayscale at the appropriate level and frequency (Fig. 1A). To estimate phase, we initially used the same protocol as an earlier study in the inferior colliculus (Palmer et al. 2007) which comprised 50 repetitions of tones at 0–40 dB above audiovisual threshold at five frequencies spanning the CF in 0.5 octave steps. These data yielded very reliable estimates of phase, but with only a coarse sampling of frequency, and, together with the response area, were time consuming to obtain.

In later experiments, we collected more repeats of the response area with fewer levels which allowed simultaneous collection of the phase response using more fine grained frequency steps. We presented five repetitions of tones from 3 octaves below to 1 octave above audiovisual CF in 1/8 octave steps at a range of sound levels separated by 10 dB steps (Fig. 1E). We term these plots the frequency response area (FRA), and off-line, we reestimated the CF from these plots as the frequency at which a peak was distinguishable at the lowest sound level (see arrow in Fig. 1E); for convenience, this is termed the best frequency (BF).

From the spike times, we constructed period histograms locked to the period of the stimulus waveform and from these calculated the vector strength and mean phase (after Goldberg and Brown 1969). In this paper, we report only mean phase values for which the period histogram showed statistically significant (p < 0.001) phase locking (Rayleigh test of uniformity, Buunen and Rhode 1978; Mardia 1972). Using a wide frequency range results in large changes in mean phase and when constructing period histograms, this resulted in phase wrapping to within a single cycle. The phase was unwrapped by manually adding whole cycles to produce the best straight line function of phase against frequency. We obtained identical results when we reanalyzed all the data using automatic phase unwrapping. Throughout this paper, we use a single convention, a positive phase indicates a phase lag (i.e., delay) relative to the stimulus; however, in some figures, positive phase is plotted downwards to match similar figures in the literature. The unwrapped phases are shown in Figure 1D for the coarse frequency steps and Figure 1F for the fine steps.

We fitted a linear regression function to the data as close to 90 dB SPL as we had data for and corrected each point in Figure 1D, F by subtracting this function. In fitting the regression, we used the phase data from the highest level FRA available even if we also had data using coarse frequency steps at a higher level, so in Figure 1, the regression was fitted to the FRA data at 79 dB. Generally, the function had a small phase offset of less than 0.25 cycles from zero so this procedure is equivalent to subtracting the mean group delay and a small constant phase from all the data. Using this technique, the mean of the corrected 90 dB data is zero. We preferred this technique to following Anderson et al. (1971) by subtracting the raw phase values at 90 dB SPL as there is a possibility, when doing this, that any systematic variations in phase at this level would be imposed on the data at other sound levels. Additionally, this manner of correction allows us to also use the 90 dB SPL data which would otherwise be reduced, by definition, to a completely flat line. An example of this procedure is shown in Figure 1B. There is a frequency close to the CF in Figure 1B where the variation of phase with level is minimal, and phase changes in different directions with level on either side. We term this the “null” frequency, and we estimated its value by eye from plots such as in Figure 1B.

Results

Data were collected from 185 auditory nerve fibers in 12 guinea pigs although other data reported elsewhere were also collected from higher CF fibers. For the present study, we specifically targeted fibers with CFs within the range of phase locking of the guinea pig (up to about 3.5 kHz; see Palmer and Russell 1986), and therefore, the CF range in our sample was from 0.071 to 3.227 kHz. We collected the half-octave spaced, 50-repetition data for 134 fibers and the data with finer frequency steps, but only five repetitions for 125 fibers. Both sets of data were collected for 74 fibers.

An example of the data from a single fiber which was held for long enough to obtain a comprehensive data set is shown in Figure 1. There is clear evidence of good phase locking in the period histograms taken at half-octave spacing around the CF (Fig. 1C). Figure 1D shows the mean phase derived from the histograms as a function of stimulus frequency, after unwrapping the phase. The curves for all sound levels are very similar and the slope of the curve indicates the fixed delay to this recording place (see Palmer and Russell 1986 for discussion). Frequency response areas showing the discharge rate as a function of stimulus frequency at a range of different sound levels, as in Figure 1E, have been published many times before (see for example Anderson et al. 1971; and the extensive data in Geisler et al. 1974). The phase versus stimulus frequency curves derived from these data are shown in Figure 1F and, not surprisingly, look very like those in Figure 1D with extra frequency resolution. Finally, in Figure 1B, we show the deviation in the phase compensated for the linear regression fit at 90 dB SPL as a function of sound level for both sets of data. The large symbols represent the half-octave data and these clearly give similar phase estimates to those from Figure 1F.

Estimation of characteristic frequency

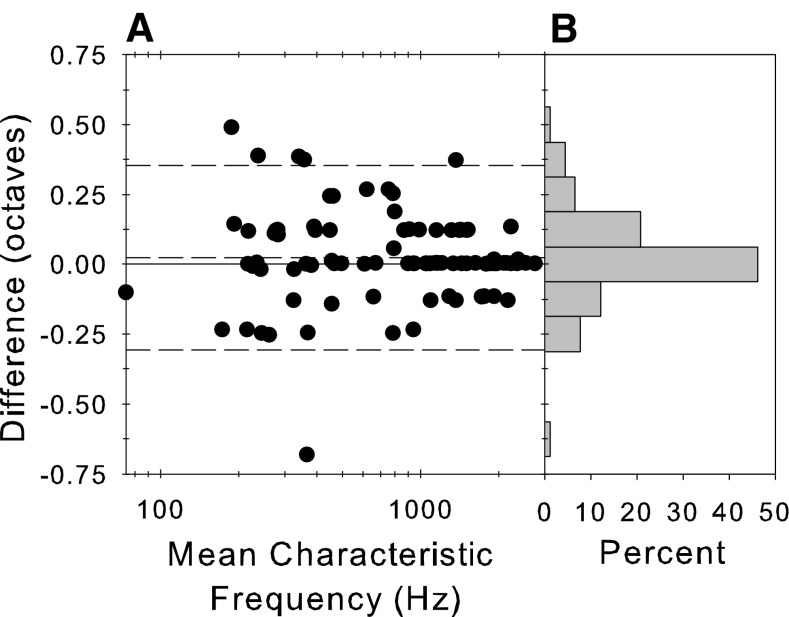
Figure 1A shows the full frequency level response area for an example fiber and illustrates one issue with our data collection that needs to be taken into account when considering effects of sound level. Our estimate of the audiovisual CF was 0.717 kHz and the response area was constructed around this frequency (1 octave above and 3 octaves below CF). It is clear from this plot, however, that a better estimate of CF would have been slightly higher in frequency. An alternative measure of the CF would be the frequency of a definite peak at the lowest sound level in the FRA (Fig. 1E), called the BF here for convenience. This frequency is shown by the arrows on the response area (Fig. 1A), the FRA (Fig. 1E), and the corrected phase versus frequency plots (Fig. 1B). The difference between the two estimates of CF is shown in Figure 2 along with a histogram of the difference. The dashed lines show the 95% limits of agreement (Bland and Altman 1999). In many instances, the CF estimates were the same, but the BF could vary symmetrically above and below the audiovisual CF. The measurements were not significantly different (paired t test, t = 1.57, p = 0.12, df = 90; two-sample Kolmogorov–Smirnov goodness of fit test D = 0.059, p = 0.999). To homogenize variance in this test, we transformed the frequencies into equivalent rectangular bandwidth (ERB) rate (a measure of frequency in units of filter bandwidth, Moore and Glasberg 1983) by integrating the ERB function for the guinea pig derived from behavioral and physiological measurements (Evans 2001). In later sections, we compare the position of the null frequency with the CF. In principle, the pattern of results could be different depending upon which definition of CF was used. However, there was no difference in the patterns of these results depending upon the definition of CF, so we only show the results plotted relative to the audiovisual CF.

FIG. 2.

A Difference between two estimates of CF in octaves as a function of the mean of those estimates. B Histogram of the difference measure pooled across CF. The CF measures were estimated by (a) the audiovisual threshold during the experiment and (b) the peak of the frequency response function (e.g., Fig. 1E) at the lowest level presented.

Variation of the mean phase along the basilar membrane

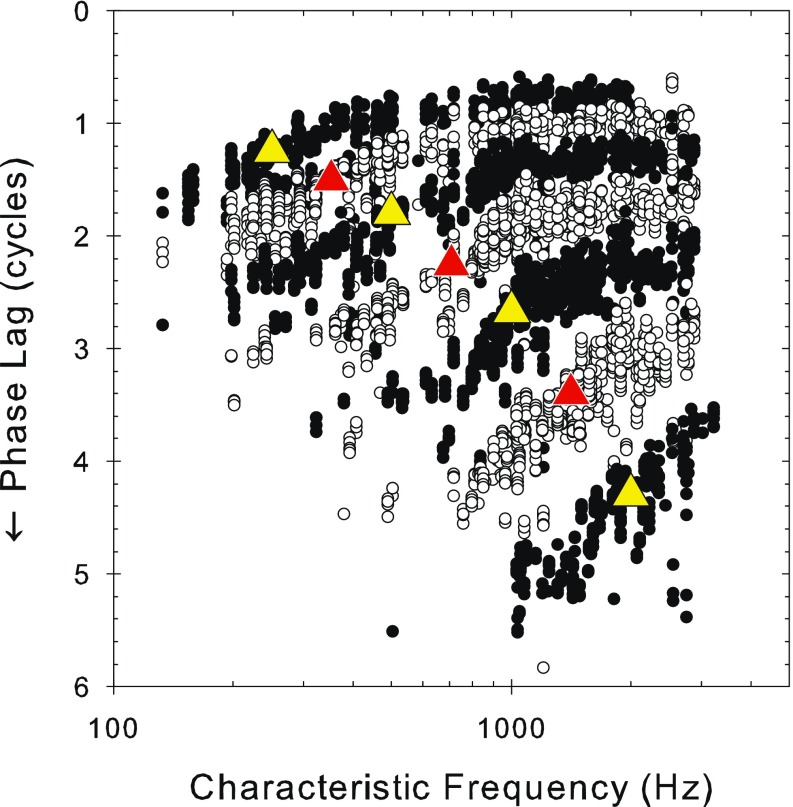
From plots of phase as a function of frequency and level such as those in Figure 1D, F, we extracted the mean phase at a series of individual frequencies. These are shown over 3 octaves of stimulus frequency from 250–2,000 Hz in half-octave steps as a function of the fiber CF (i.e., basilar membrane position) in Figure 3. The data for different signal frequencies are shown as alternating black and white circles, with the signal frequencies marked by superimposed large triangles in a contrasting color. For all stimulus frequencies, the general trend is a gradually decreasing phase lag, as CF increases, of maximally about 1.5 to two cycles beyond which the curves become flat. As the stimulus frequency increases, the phase lag at any CF increases, and the slope of the function increases (c.f. Kim et al. 1980).

FIG. 3.

Pooled plots of the variation of raw phase lag against CF in which the phase values at all sound levels measured are overplotted (note, there is no added shift in this figure, unlike Figs. 4 and 11). The frequencies displayed are at one quarter octave intervals starting at 250 Hz (250, 353, 500, 707, 1,000, 1,414, and 2,000 Hz). The top black symbols represent the 250-Hz data and the bottom black symbols represent the 2000-Hz data. The triangles indicate the stimulus frequency for the different plots and are placed by eye at the middle of the appropriate data and given the contrasting color.

In Figure 3, the data were pooled over sound level to emphasize the major effects of CF and signal frequency. However, there is also a smaller but systematic effect of signal level which is revealed by plotting the mean phase as a function of CF separately for each signal frequency with signal level as parameter in Figure 4 (separated by one cycle for clarity). In this format, it is clear that the transition between the sloping part of the function and the flat portion is quite abrupt, as previously demonstrated by van der Heijden and Joris (2006). A “knee point” and slope were determined by “broken stick” fits to the data (comprising a linear portion of variable slope at low CFs breaking to a flat portion at a variable CF knee point; fit by “nlinfit” in MATLAB, Mathworks) as shown by the superimposed lines. At each stimulus frequency, this “knee-point” shifts to higher CFs with increasing sound level and the low-CF slope becomes shallower. Unfortunately, there are insufficient data at higher CFs to be able to properly delineate the shape of the function for higher stimulus frequencies, but if a knee point exists for stimulus frequencies of 2,000 Hz, it is above CFs of 3,000. Figure 5 shows the variation in the knee-point CF and in the low-CF slope of the data from the first three panels of Figure 4. The variation in knee-point CF and slope with level are clear as are the variations with stimulus frequency. The knee point in response to 250 Hz stimulation, for example, starts off at about 500 Hz at 50 dB SPL and ends up at almost 1,250 Hz at 90 dB SPL.

FIG. 4.

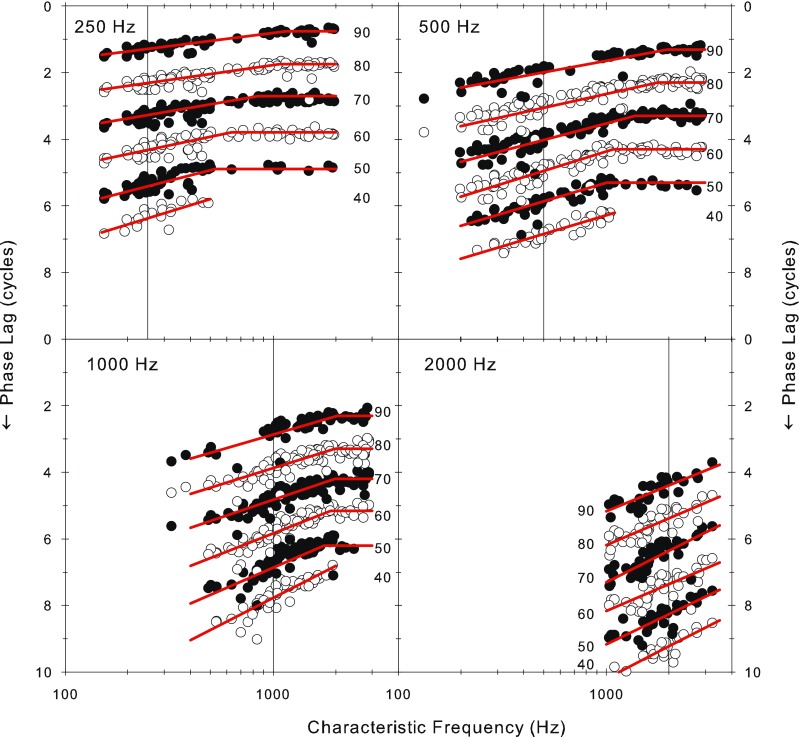
Variation in phase of phase locking as a function of the fiber CF and the sound level. The curves for the different sound levels in each panel have been offset by one cycle and alternated shading for clarity. Each panel represents a different stimulus frequency. The vertical lines indicate the stimulus frequency. “Broken stick” fits are overplotted (see “Methods” for details).

FIG. 5.

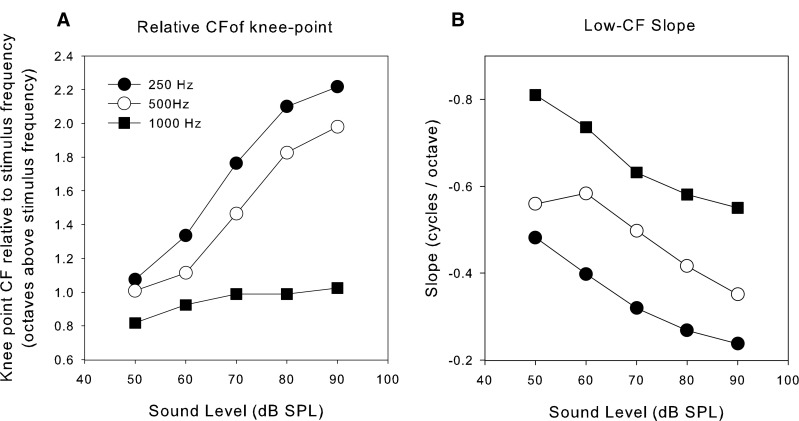
Variation of the knee-point and low-frequency slope with sound level and stimulus frequency. The data points were obtained by fitting a broken stick (two linear parts) to the data shown in three of the panels in Figure 3 and extracting the parameters of the fit. A Position of the knee point for three stimulus frequencies (legend) as a function of sound level. The knee-point CF is expressed in octaves with respect to the stimulus frequency so that all three frequencies could be conveniently represented. B Slope of the low-CF part of the phase versus CF plot expressed in cycles/octave as a function of sound level.

Figure 6 shows the variation in the discharge rate over the same range of frequencies and levels. We show here normalized driven rates between spontaneous and saturation. At low stimulus levels (40 dB SPL; bottom row in Fig. 6), the locus of activity at each of the four frequencies is relatively well defined and centered at the stimulus frequency (vertical line in all panels of Fig. 6). This locus widens with level due to broadening of the tuning and saturation effects, and the frequency at which it is maximal shifts upward away from low stimulus frequencies or downwards from high stimulus frequencies (as has been demonstrated before, see Palmer 1995, Figure 4). At the highest levels, most of this population of low-frequency fibers is active and firing at near saturation rates. The phase versus characteristic frequency pattern shown in Figure 3 is similar at all sound levels despite the fact that at 90 dB SPL, the firing rates are saturated and at 40–60 dB SPL, the majority of fibers are firing within their spike dynamic range. The phase measured is therefore largely independent of the firing rate provided sufficient spikes are evoked to determine the phase and is little affected by saturation.

FIG. 6.

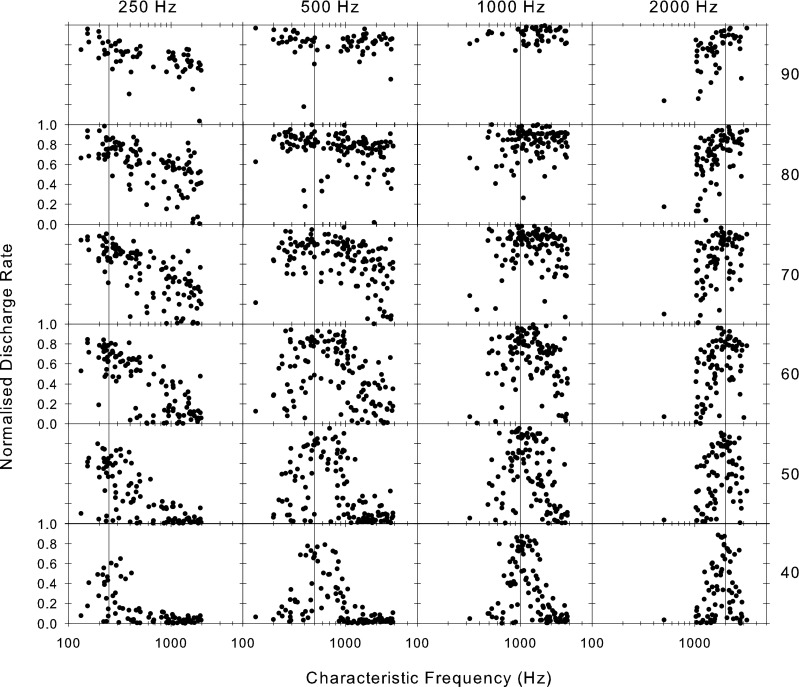
Distribution of discharge rate across the fiber array for stimuli of four different frequencies (across the top) and six sound levels (in dB SPL as shown at the right). Each point is from a different fiber plotted at its CF. The rate has been normalized by subtracting the spontaneous rate and expressing it as a proportion of the maximum driven rate.

Estimates of delay from the phase frequency plots

Figure 7A shows selected examples of phase versus frequency plots at the highest level used in each fiber (usually about 90 dB SPL). The plots are approximately straight lines, showing a nearly constant group delay. Taking the slopes of these plots for all fibers, at each SPL, gives the mean group delay to the recording electrode shown in Figure 7B (open symbols in Fig. 8 taken from Palmer and Russell 1986). On Figure 7B, we also plot the function from Siegel et al. (2005, Figure 7) that they used to summarize the group delays in the guinea pig data of Evans (1972). The function they used was of the same form as that they used to model their more comprehensive chinchilla data but fitted to isolated measurements at low (400 Hz) and high (18–40 kHz) frequencies in the guinea pig data. The close match of this function to our present, much more finely sampled, delay data validates this fit and allows us to infer that the present data set is likely to be very representative of mammals in general.

FIG. 7.

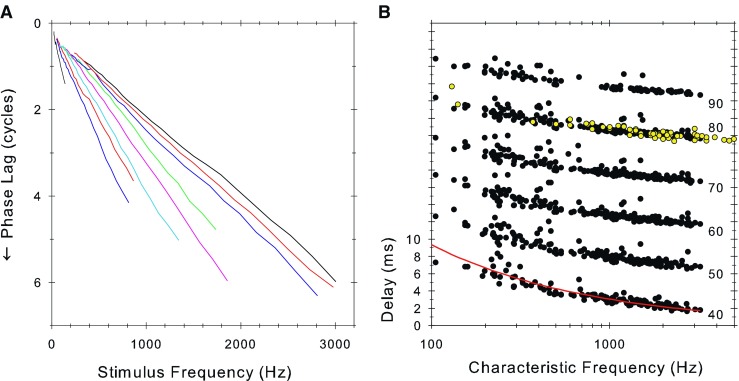
A Raw phase lag versus stimulus frequency curves for nine fibers at the highest sound level presented (approximately 90 dB SPL). B Delay to the recording site computed as the slope of the raw phase-frequency plots (as in A), plotted as a function of fiber characteristic frequency and sound level (in dB SPL as shown to the right). The y-axis is correct for the 40-dB SPL data and each subsequent plot is displaced by 5 ms for clarity. The open symbols are from a previous study in guinea pig (Palmer and Russell 1986). The solid line is the equation 87.56 × CF_(Hz)^−0.486 described in Figure 7 of Siegel et al. (2005).

FIG. 8.

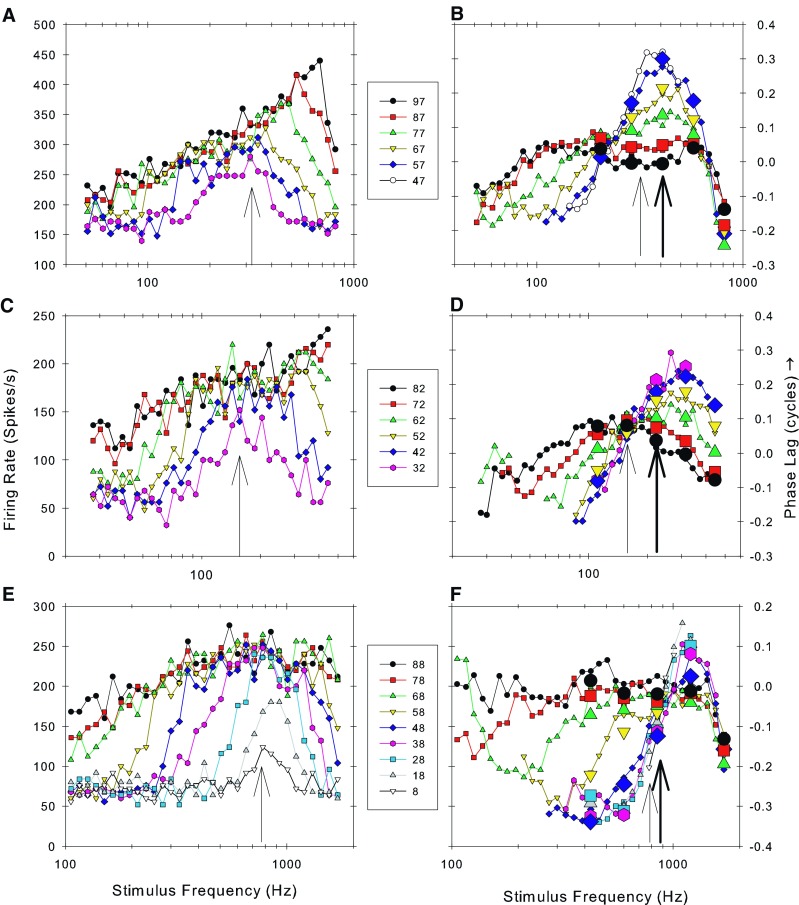
A, C, E show the mean discharge rate of three fibers as a function of the stimulus frequency and sound level (FRA; as in Fig. 1B). The arrows indicate the frequency at which a peak occurred at the lowest sound level. B, D, F show the corrected phase of phase locking as a function of stimulus frequency and sound level derived from the data in A, C, and E. The data were corrected by subtracting the linear regression fit to the phase data derived from the highest level FRA. The thick arrows show the on-line audiovisual estimate of CF while the thin arrows show the frequency of the peaks at the lowest level in the FRA (A, C, E). Symbols used for different sound levels apply to both parts of the figure for each of the three fibers. The large symbols represent phase values obtained from period histograms after 50 stimulus repeats (see Fig. 1C, D). CFs and spontaneous rates of the fibers were A 0.407 kHz, 140 spikes/s; C 0.222 kHz, 49.5 spikes/s; and E 0.849 kHz, 58.6 spikes/s. Sound levels are shown in the key.

Variation in phase with sound level

Figure 8 shows examples for individual AN fibers of the variation with stimulus frequency and level of firing rate (Fig. 8A, C, E) and phase (Fig. 8B, D, F) after compensating for the regression fit to the data at 90 dB SPL. On the left (Fig. 8A, C, E) is the FRA from which the phase data shown on the right (Fig. 8B, D, F) were derived. For these three fibers, both the limited frequency resolution data with 50 repeats and the data at the higher frequency resolution were obtained. Phase data from the former one are shown by large symbols. The phase values obtained from both data sets are extremely consistent in all cases giving confidence to conclusions based solely upon the smaller number of repeats. The data are consistent with similar plots that have been previously published in several species including the classical study of Anderson et al. (1971) in the squirrel monkey. The arrows on the phase plots in each case show the audiovisual CF (thick arrow) and the BF estimated from the FRA (thin arrows on both plots). It is clear that these values are somewhat divergent (but, as shown in Fig. 2, not systematically so). In the central panel (Fig. 8D), the phase shows a progressive lag with sound level at frequencies below CF and a progressive lead for frequencies above CF. This is the pattern shown in the earlier studies. The null frequency in this case was at the CF as estimated from the FRA (Fig. 8C). In the plots shown above and below (Fig. 8B and F), the position of the null frequency does not correspond to the CF derived by either estimate. The null is below the CF in Figure 8B and above the CF in Figure 8F. In every case where we could identify a null frequency, the phase progressively lagged at higher levels for frequencies below the null and lead at higher levels for frequencies above the null. Null frequencies were identified in 152/185 fibers. In cases where we were unable to identify a null frequency, this was because (1) most often the fiber CF was above about 1.4 kHz and the functions at different levels had not converged at the limit of useful phase locking, (2) paucity of data when fibers were lost before sufficient repeats were obtained, or (3) the phase curves did not vary in a systematic fashion with sound level.

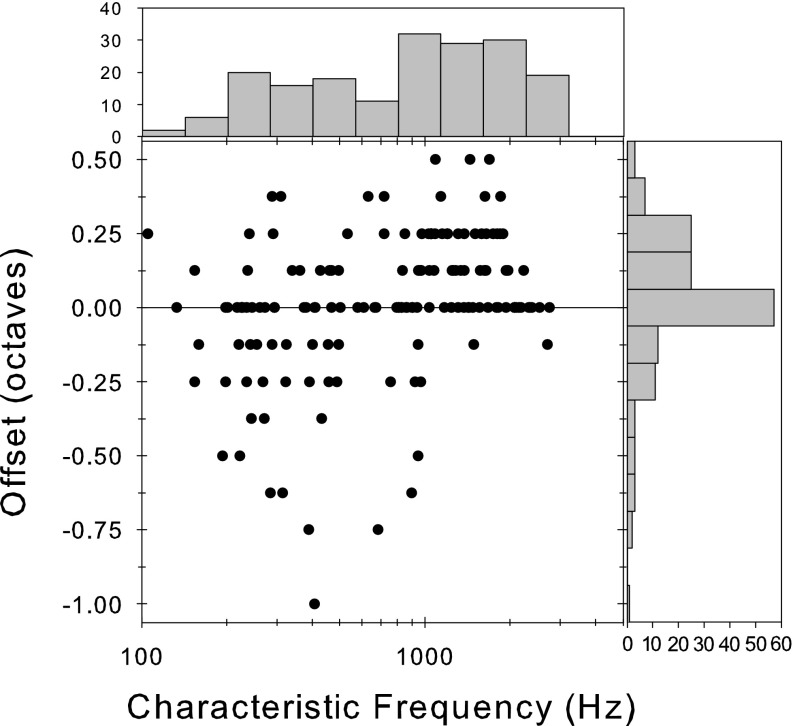
In Figure 9, we show the offset of the null frequency from the CF as a function of the CF. Null frequencies that occur at the CF were found throughout the CF range. Null frequencies above the CF are also found throughout the CF range but were more prevalent at CFs above 1,000 Hz. Null frequencies below CF were mostly found at CFs below 1,000 Hz. While the accuracy of the estimate of this offset is limited in resolution by the size of the frequency steps used, values of as much as + 0.5 and −1 octaves can be found.

FIG. 9.

Offset of the null frequency (see text for explanation) from the CF as a function of the CF. The bar graph to the right shows the distribution of offsets collapsed across CF. The bar graph at the top shows the distribution of CFs sampled (in half-octave bands).

It is clear from Figure 9 that offsets of different sizes and directions can occur at the same CF. This is not due to pooling across animals, as shown in the left hand column of Figure 10, where data for the three animals with most recordings are shown along with the data for all animals pooled together. It is clear that the individual animals show the same pattern as the pooled data, in particular the null offset can vary at the same CF within the same animal.

FIG. 10.

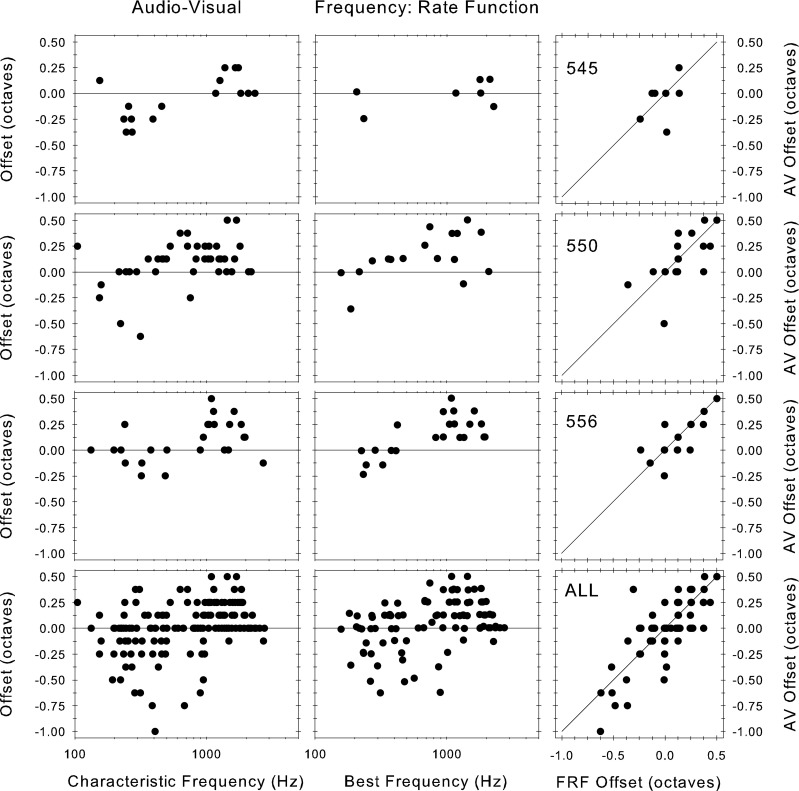
Offset of the null frequency from: left column, the audiovisually measured CF, and middle column, the BF estimated from the FRA measured at the lowest SPL tested. The right column shows a comparison of these two offsets. The top three rows show the data from three individual animals (the number in the right hand column is the animal ID#); the fourth row shows the data for all animals pooled.

It is possible that the offset of the null from the CF shown is due to error in estimating the CF; however, a different method of estimating the CF yields similar results. In the center column of Figure 10, we also show the offset of the nulls from the estimate of the BF derived from the FRA. The patterns of offsets are the same as those obtained from audiovisual CF estimates. The estimate of BF should be largely independent of the estimate of audiovisual CF, so if the null offset were merely due to error in estimating CF, then we would expect the null offsets from the audiovisual CF and the BF to be randomly distributed; however, the right-hand column of Figure 10 shows a clear correlation, indicating that the null offset from CF is a genuine phenomenon and not an artifact of inaccurate measurement of CF.

Variation of the corrected mean phase along the basilar membrane

Finally, in Figure 11, we show the variation in compensated phase across the population as a function of level and stimulus frequency. To obtain this figure, we extracted the phase from plots such as those in Figure 8B, D, F at each of four stimulus frequencies and six sound levels and plotted these against fiber CF. Perhaps surprisingly, given the diversity that we have seen in some of these corrected phase curves, these measures are systematic across the population. The data for the three animals with most data are highlighted. At the highest level shown (90 dB SPL), the phase in nearly all fibers irrespective of CF and stimulus frequency is at zero. This is not surprising since we adjusted the phase for each nerve fiber individually so its mean phase at 90 dB SPL was zero and the best fitting linear function to the fibers’ data at 90 dB was flat. At sound levels below 90 dB SPL, a deviation from the flat zero phase line become apparent. At 40 to 70 dB SPL, these deviations occur for CFs above and below the stimulus frequency, which stays at zero phase. The largest deviation occurs at the lowest levels, where the phase transition is the sharpest. The transition is sharper for high stimulus frequencies than for low stimulus frequencies. These deviations reach a maximum of ±0.2 cycles, matching the stereotypical maximum deviations shown in individual fibers. In all cases, phase lags occur for fibers with CFs below stimulus frequency, while phase leads occur for fibers with CFs above the stimulus frequency mirroring in the population the pattern seen in individual fibers

FIG. 11.

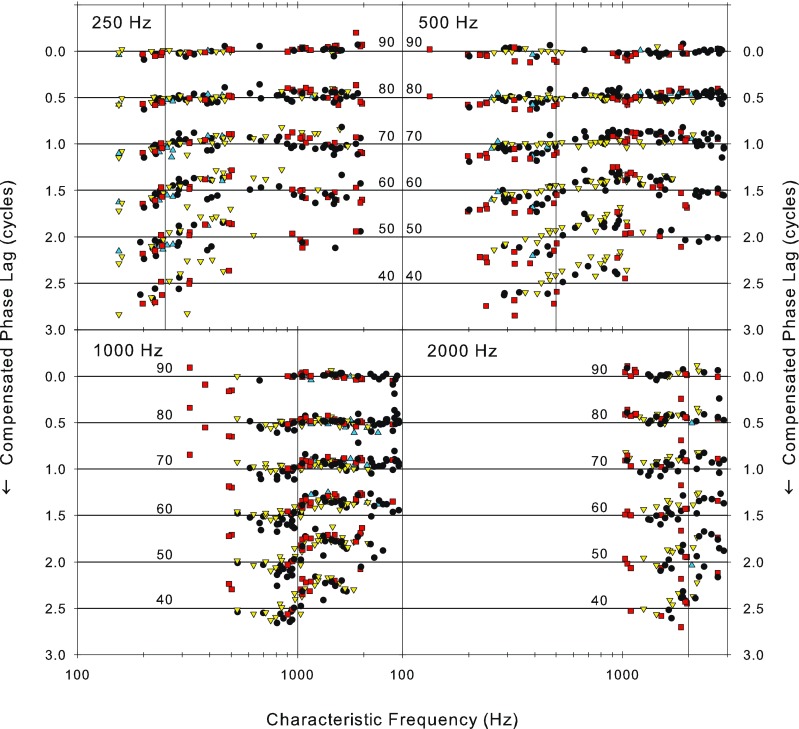
Variation of the compensated phase as a function of CF for four stimulus frequencies (above each panel) and six sound levels (in dB SPL as shown in each panel). The data at different sound levels have been offset by 0.5 cycles. The data for the same three animals as shown in Figure 10, from which most fibers were isolated, are highlighted by different symbols (squares and upward and downward triangles) and the data for the remaining animals are plotted as solid circles. The horizontal lines provide a zero-phase reference for each sound level. The vertical lines indicate the stimulus frequency.

Discussion

We have described phase locking in the auditory nerve of the guinea pig as a function of the frequency and level of a pure tone stimulus. We show that, for a stimulus consisting of a single frequency, the phase lag at which the spikes in the auditory nerve are evoked progressively decreases as the CF of the fiber increases and then decreases at a much slower rate above a knee point (Figs. 4 and 5). Since CF is related directly to cochlear position (Greenwood 1990), these data give an indirect measure of the phase of the mechanical events along the length of the basilar membrane. Similar extensive data have also been obtained very near threshold using pure tones in the chinchilla auditory nerve (Ruggero and Rich 1987) and recently in the cat auditory nerve (van der Heijden and Joris 2006) at levels within 35 dB of threshold using broadband stimuli. Our data are directly comparable with these, showing the same characteristics. Both previous studies found that at high CFs relative to the signal frequency, the phase function was nearly flat, whereas at low CFs, the function had a significant slope. As in our data, the slope decreased as the signal frequency decreased. In our data and those of van der Heijden and Joris (2006), the point of transition (knee point) is smooth and varies in CF as signal frequency changes. However, in Ruggero and Rich’s (1987) data, there is a local peak, which is fixed in CF at around 3.5 kHz. This is not necessarily an inconsistency, however, because both our and van der Heijden and Joris’s (2006) data are suprathreshold, whereas that of Ruggero and Rich (1987) was measured at threshold. Our lowest level data generally do not extend to sufficiently high enough CFs to be able to define a knee point, and our highest CF fiber was only just above 3 kHz. van der Heijden and Joris (2006) showed that the knee-point CF was about an octave above the signal frequency at low frequencies and got closer to the signal frequency as it increased. We showed the same effect at the lowest level we tested, with the further finding that the knee point moved even further from the signal frequency as level increased (c.f. Figure 11 in van der Heijden and Joris 2006, with Fig. 5). In other words, despite the differences in species, stimuli, and techniques, the phase functions across CF and signal frequency are consistent.

These phase changes can be interpreted as indicative of a fast-traveling wave near the base of the basilar membrane (high CFs) such as that measured routinely in animal preparations (see Robles and Ruggero 2001 for review), which exponentially slows down as it progresses toward the cochlear apex where the lower frequencies are transduced. The fast wave activates disparate regions in close temporal synchrony and hence with little phase lag; however, the slower wave gives rise to rapidly increasing phase lag as it propagates along the basilar membrane. We identify the point of transition between the fast and slow waves as the knee point in our phase data. From our data, it appears that, as sound level is increased, the point of transition between the fast and slow components of the traveling wave moves more basally (to higher CFs) and the speed of the traveling wave at the characteristic place increases. Since there is a smooth transition between the fast and slow components, with no evidence of any interference effects, van der Heijden and Joris (2006) suggest that both are part of the same traveling wave rather than the fast component being the plateau region sometimes observed in basilar membrane vibrations (see for example Cooper and Rhode 1995; Robles and Ruggero 2001; Wilson and Johnstone 1975).

Comparison with the phase of apical mechanical measurements

Our cochlear nerve data are consistent in that, in the vast majority of nerve fibers (152/185), a null frequency was evident below which there was an increased phase lag with level and above which there was an increasing phase lead with level. This relatively simple picture seems at odds with guinea pig (Cooper and Rhode 1995; Zinn et al. 2000) and chinchilla (Rhode and Cooper 1996a, b) mechanical measurements which taken together are somewhat inconsistent. The mechanical measurements show quite complicated phase changes with level that are frequency dependent and radically influenced by various notches in the amplitude transfer functions (see Figures 3 and 4 in Cooper and Rhode 1995). In one published measurement in chinchilla (Fig. 1B; Rhode and Cooper 1996b; the raw data for which was kindly supplied for reanalysis by Rhode and Cooper) and one in guinea pig (Figures 3 and 4 of Cooper and Rhode 1995), the behavior was very similar to that shown by us if only the mechanical data near CF, at low sound levels, and away from notches were considered. However, at higher sound levels and at frequencies away from CF the phase changes were much larger and could go in opposite directions with further increase in sound level. The range of levels over which the simple pattern existed was quite limited (below 60 dB SPL in the chinchilla data and below 100 dB in the guinea pig). This suggests that it is at high levels and at frequencies well away from the CF that discrepancies occur. However, other data by the same authors in both chinchilla and guinea pig (see Rhode and Cooper 1996a; Figs. 6 and 7) appear to show relatively simple phase behavior with level dependent phase changes that are in exactly the opposite direction to those we show in this paper (i.e., increasing leads with level below CF and increasing lags above). Other mechanical data from the guinea pig apex from Zinn et al. (2000) also show a complex phase behavior with level, particularly above about 80 dB SPL, but even below this the phase is level dependent and shows an accumulating lead at frequencies away from CF on either side. Recent data from Dong and Cooper (2006) suggest that unlike basal mechanical measurements, those in the apex are radically affected by the measurement conditions (specifically obtaining a cochlear pressure seal). While such factors might contribute to these discrepancies, the phase effects shown by Dong and Cooper (2006) were relatively small and probably do not account for the large phase changes shown in earlier measurements. Interestingly, Rhode and Cooper (1996b) report quite complicated phase behavior with level in auditory nerve fibers of the chinchilla, measured under conditions nearly identical to their mechanical measurements. For the two fibers illustrated (Fig. 3), the phase behavior was opposite that which we show (i.e., increasing phase lead below CF and either no level dependency or accumulating phase lag above CF). It is difficult to reconcile the internal consistency of our measurements and other measurements from the auditory nerve (Allen 1983; Anderson et al. 1971; Gleich and Narins 1988; Hillery and Narins 1987) with the wide divergence of effects seen in the mechanical measurements.

Consistency of phase measurement across species

The phase as a function of signal frequency plots for different CFs shown in Figure 7A is approximately straight lines, showing a nearly constant group delay, in agreement with data already published in the literature for several species including the guinea pig (see Anderson et al. 1971; Geisler et al. 1974; Pfeiffer and Molnar 1970; Ronken 1986), although van der Heijden and Joris (2006) found nonlinear functions (comprised of two to three linear sections). The open circles plotted alongside the present data in Figure 7B are from Palmer and Russell (1986) who concluded that their data were consistent with those from other species (e.g., Anderson et al. 1971; Gleich and Narins 1988; Hillery and Narins 1987; Ruggero and Rich 1987) and show good agreement with the present data set even though obtained under different anesthesia in another laboratory. More recently, the cochlear delays measured in a variety of preparations (different species, in vivo and postmortem) and using a variety of different methods have been compared (Ruggero and Temchin 2007). These authors concluded that all mammals and indeed some nonmammals that even lacked a basilar membrane gave delays that were of the same magnitude. These comparisons showing consistency across species are based only on the cochlear delays. However, since these delays are derived from the slope of the phase frequency plots such as in Figure 7A, it is reasonable to infer that the other measures of phase locking that we show here are likely to be generalizable across species as well. The known exception to this is the high-frequency limit of phase locking which, as reported by Palmer and Russell (1986), is lower than in some other mammals such as the cat.

Relationship of null frequency to CF

We have replicated here in a large population of guinea pig auditory nerve fibers the level dependency of the phase of phase locking that was originally reported by Anderson et al. (1971) and repeated several times since in a variety of species (e.g., cat, Allen 1983; bird, Gleich and Narins 1988; frog, Hillery and Narins 1987). For many nerve fibers, there is a null frequency at which no change in the phase of phase locking occurs as a function of the level of a tone stimulus. Below this null frequency, the phase shows a progressive lag with sound level and above the null frequency the phase progressively leads. These phase changes have been attributed to the nonlinearities in the basilar membrane motion: The tuning of the vibration becomes wider with sound level. Such phase changes might be expected simply because of the changes in the filter shape with level (see Figure 2 in Carney 1994 and Figure 11 in Tan and Carney 2003). Here, we show that the null frequency is often well displaced from the CF as previously reported in the barn owl (Koppl 1997). Careful study of a variety of earlier publications shows that this is not a novel finding in mammals, although it has largely gone unremarked. In the paper of Anderson et al. (1971) while all examples in the figures look to have the null frequency at or near the CF, they mention at least one (in a sample of only 22 fibers) that has the null 0.4 octaves away from CF. Other authors also report disparities between the CF and the null frequency or other phase anomalies (for examples, see Allen 1983, Figure 21; Ronken 1986). Similar, but smaller, deviations of the null from CF can be found in the mechanical measurements of the basilar membrane motion (see for example Robles and Ruggero 2001, Figure 8, even though these are mostly at frequencies well above the limit of phase locking). The level dependence of the phase of the receptor potential in inner hair cells in the low CF region of the guinea pig cochlea has been measured by Cheatham and Dallos (2001). The patterns of phase variation over wide ranges of sound level are exactly like those shown here and in the previous auditory nerve and mechanical data. In these hair cell data, the null frequency occurs at CF only at cochlear positions corresponding to about 1,000 Hz. At higher and lower CFs, the null frequency is displaced from CF.

The data in Figures 8, 9, and 10 show that sound level induced phase deviation is not centered on CF, but on a null frequency which may be some distance away. This will result in an increased variance in the phase distribution of small ensembles of neurons at a particular CF as sound level is changed. Across CF in the neural ensemble (Fig. 11), we see the complement of the stereotypical pattern seen in individual fibers across signal frequency. Thus, the functions are flat at high levels, become increasingly steep through the CF at the signal frequency as level is reduced, and then return to zero for CFs away from the signal frequency. Some of the variability shown in Figure 11 may be due to pooling across animals; however, each of the highlighted animals has variability which is only just less than that of the pooled data; they also show the same pattern as the ensemble. Figure 11 thus provides a valid reflection of the variation of phase across the ensemble of nerve fibers as sound level is varied. One possible function for this variation is suggested by Carney and colleagues (Carney 1994; Heinz et al. 2001) who have proposed monaural coincidence detection making use of the variation in the phase that occurs with sound level as a means of overcoming the limited dynamic range of auditory nerve fibers. As level is increased, the relative variation in phase across frequency decreases. In these models, the null frequency occurs at the CF. The deviation of the null from CF shown here (Figs. 8, 9, and 10) would likely manifest as an additional source of internal noise in these models (Heinz et al. 2001) which would bring them more in line with human performance. The data in Figure 11 do, however, indicate that the variation in the null frequency does not materially disrupt the patterns of phase variation with level across frequency within the population.

As mentioned earlier, the level dependent phase changes have been generally attributed to the widening of mechanical and auditory nerve fiber tuning curves with level (Carney 1994; Tan and Carney 2003): The phase transition through the filter takes place over a wider frequency range in broad filters than in narrow filters. One method that has been used many times to reveal the changes in filter shape with level in mammalian auditory nerve fibers is reverse correlation and the related Wiener kernel analysis (Carney and Yin 1988; de Boer and de Jongh 1978; Evans 1977; Harrison and Evans 1982; Kim and Young 1994; Lewis et al. 2002; Moller 1977; Recio-Spinoso et al. 2005). Reverse correlation techniques yield the filter impulse response, and thus, phase can also be computed, but in most studies, only one or two noise levels were used. Generally, the first order Wiener kernel in response to low level noise is comparable with the tuning curve measured using tones for low CF fibers and the second order for high CFs. Notably, the study of Reccio computed first and second order Weiner kernels and used a range of noise levels in both low and high CF fibers. The variation in phase with level in their study showed the same level dependency in fibers with CFs of 1.35 and 12.1 kHz as in the present paper, with a progressive phase lag with level below CF and a progressive lead above CF (Recio-Spinoso et al. 2005, Figure 13). Other less extensive data from reverse correlation studies appear to show the same trends (Carney and Yin 1988; Moller 1977).

An initial impetus for this study was an investigation of the effect of interaural level differences (ILDs) on the encoding of interaural time differences (ITDs) at the level of the inferior colliculus (Palmer et al. 2007). In that study, we showed (as had Kuwada and Yin 1983; Yin and Kuwada 1983) that the phase shifts with sound level that occur in the auditory nerve (known from such papers as Anderson et al. 1971) affects the ITD sensitivity as would be expected from the coincidence detection mechanism in the medial superior olive (MSO). Based upon earlier studies such as from Anderson et al. (1971), our expectation was that there should be no shift in ITD sensitivity for tones at CF, corresponding to the null frequency. In fact, this was true only for less than one third of our sample of ITD sensitive IC neurons. Equally often, ITD sensitivity independent of sound level occurred below and less often above CF which is consistent with the rather more complicated pattern of null frequencies shown in Figures 9 and 10. Thus, although taken in isolation the IC results could have implied some processing after the MSO coincidence detector or that the simple notion of a coincidence detector was insufficient, the similarity in patterns of null frequencies between auditory nerve and IC means that no such adjustment to the theory is necessary.

In summary, we have detailed the phase at which spikes occur in response to tone stimulation as a function of sound level and stimulus frequency. These data, like those of earlier studies, provide some noninvasive insight into the operation of the mechanics at the apex of the cochlea where few direct measurements have been made. These data from the guinea pig are remarkably consistent with those from other species and particularly recent data from the cat. Finally, the phase shifts with level shown here are consistent with most of the sensitivity of ITD to ILDs (Palmer et al. 2007).