When in doubt, chimpanzees rely on estimates of past reward amounts

Summary

Many animals can repeatedly judge the larger of two sets of food items. However, it remains unclear as to what information might accrue regarding the relative rates of return from these repeated responses. Information about overall rates of return is, in fact, unnecessary to perform well at the task itself. However, if an uncertain situation arose, such as when the quantity in one set was unknown, that information would be useful in determining whether to select a known quantity or an unknown quantity. We gave chimpanzees this test. First, they made multiple judgements between two visible food sets that varied in the number of items across trials. Then, they were faced with the same combinations of set sizes, but only one set was revealed while the other remained unknown. Rather than using a specific quantity as a threshold for choosing the known or the unknown set, the chimpanzees' choice of the unknown set varied in relation to the rate of return from responses in the first phase (when both sets were known). This indicated that the chimpanzees' decisions in the face of uncertainty were guided by a sense of how well they were rewarded overall during the session.

1. Introduction

Animals are faced with many types of decision each day. These include where to travel, when to eat, what to eat and how to interact with other members of their species or even other species. One important type of decision pertains to comparing quantities of food. Assuming that more food is always preferred to less food, researchers have shown that animals perform very well (although not perfectly) in discriminating among food quantities. The primates are particularly well studied in these kinds of tests, and they accurately judge discrete quantities and continuous quantities (e.g. Boysen & Berntson 1995; Brannon & Terrace 2000; Hauser et al. 2000; Beran & Beran 2004; Cantlon & Brannon 2006; Suda & Call 2006; vanMarle et al. 2006; Hanus & Call 2007; Tomonaga 2007; Beran et al. 2008a).

Typically, these studies of relative quantity judgement show that animals perform well in comparing sets provided the relative difference between the sets is larger as opposed to smaller, and the magnitude of the sets is smaller rather than larger (e.g. Call 2000; Beran 2001). Thus, judgements rely on an approximate sense of the true quantity in these sets, and this type of approximate representation is adaptive and appropriate for the task of increasing caloric intake without requiring the kind of exactness that is necessary to support more abstract mathematical and quantitative reasoning (see Brannon & Roitman 2003). Although it is now clear how animals make judgements between quantities, less attention has been given to how individual judgements of quantities during these decision-making sessions may influence each other. We know that animals can track the rates of return from multiple food sources within foraging bouts (e.g. Stephens & Krebs 1986). They also track the relative reinforcement rates for multiple response schedules (Herrnstein 1961), providing strong evidence for matching responses to probabilities of reward on those schedules (Herrnstein 1997; Sugrue et al. 2004). Thus, animals are sensitive to the expected value of response options in the environment, and we are now learning how the nervous system supports this behaviour (e.g. McCoy & Platt 2005). In most studies, however, response options and rewards for those responses were relatively stable across blocks of trials or even sessions (e.g. in assessments of the matching law, typically two response options each have a set probability of reward for their selection that does not change until the end of the trial block or the end of the session). Or, in the case of foraging bouts, food patches were stable with the exception of depletion by the organism. We know less about how repeated experience with discrete judgements that are each unique along a quantitative dimension might lead to the formation of an expected value (or some other measure related to the approximate average number of items they had received across each of these unique experiences).

The basis for the present experiments came from the observations of the first author during a series of experiments. In those experiments, chimpanzees were presented with sequential sets of food items placed into opaque containers. After both sets had been presented, the chimpanzees chose one and they received the contents of that set. Chimpanzees performed well in these experiments, judging accurately among a large range of quantities and even comparing sets after additional items had been added or removed (e.g. Beran 2001, 2004). After a few dozen trials, chimpanzees began to exhibit anticipatory responses where they tried to point to a container that had received a large number of food items even before seeing how many items were placed into the other container. Or they would point towards the second (still empty) container after seeing only a small number of items placed into the first container. This seemed to indicate that the chimpanzees were using information beyond that available in the present trial to guide their responses. They seemed to anticipate the likelihood that the already presented set would be the larger or smaller set even though they had only partial information on that given trial.

The present study formally investigated this aspect of decision making during quantity judgements. To do this, we separated each daily test session of 30 trials into two phases. The training phase consisted of a fairly easy comparison task during which the chimpanzees saw two discrete food quantities and then chose between them. Unlike in most other studies assessing how expected reward is used, however, each trial of this procedure involved a unique comparison between two quantities. Therefore, the chimpanzees could not learn to select a specific response location or a specific quantity. Then, in the test phase, the chimpanzees were shown only one of the quantities, and the other remained hidden up to and including the point of responding. In that case, the chimpanzees had to choose between a set they had seen and one that was unknown, and we were interested in knowing what might determine their selection of the unknown quantity.

We assessed four hypotheses regarding the rule that the chimpanzees might use. The first hypothesis was that they would have an absolute threshold quantity that separated responses of the known set and the unknown set. For example, a given chimpanzee might always choose a known set of four or more items and always avoid a known set of three items or less. Primates sometimes show indifference between sets of identical food items that differ only in amount, if both amounts are sufficiently large (Silberberg et al. 1998). Presumably, this is because both sets exceed some threshold that produces indifference, not due to failure to perceive the quantitative difference. This also might represent a form of satisficing, in which an alternative is chosen because it exceeds a ‘good enough’ threshold independent of other available information that could contribute to the decision-making process (Simon 1955; Todd & Gigerenzer 2003; Gigerenzer 2008).

The second hypothesis was that the chimpanzees' selection of the unknown quantity would be based on the most recent trial and the number of items obtained on that trial. In accordance with this explanation, if the known set was smaller than the set just received on the last trial, the chimpanzees would choose the unknown set. If the known set was larger, the chimpanzees would choose it. This would be similar to a contrast effect (Crespi 1942).

The third hypothesis was that the chimpanzees would respond differentially to known quantities based on the last outcome of a risk-taking response in which they chose the unknown quantity. Specifically, we were interested in knowing whether the chimpanzees would use some form of a win–stay, lose–shift strategy that was not responsive to the known quantity itself but rather was responsive to the outcome of choosing the unknown quantity. Such strategies are well established in many species in discrete choice situations and also in foraging-like situations (e.g. Schusterman 1963; Shimp 1976; Randall & Zentall 1997; MacDonald & Agnes 1999; Bicca-Marques 2005).

The fourth hypothesis was that the chimpanzees would use information beyond that obtained on the most recent trial (or the most recent few trials) so that they would estimate something similar to the average amount of food items they had obtained during all trials in the training phase. In other words, they might base their responses in the face of uncertainty on some measure related to the average number of items they had received throughout the training, and they would choose the known or unknown quantity based on that information. They might do this even though such information was not relevant or necessary on a trial-by-trial basis for maximizing the amount of food obtained during the training phase. This hypothesis would be supported only if the previous three hypotheses did not account for the performance of the chimpanzees. It would require showing that the choice of unknown sets varied as a function of both the known set size and the range of set sizes used during training because the different ranges would create different expectations for the chimpanzees about the average reward rate for the task during that session.

2. Material and methods

(a) Participants

We tested three chimpanzees: Lana (female, 37 years of age); Sherman (male, 34 years of age); and Mercury (male, 21 years of age). All were highly experienced in a variety of different cognitive tests, including judgements of food quantities (e.g. Beran & Beran 2004).

(b) Apparatus

We hid food items under opaque tin containers positioned at opposite ends of a black wooden bench (48 cm high, 67 cm wide and 36 cm deep). The bench had a sliding drawer on top that allowed us to move both quantities towards a chimpanzee at the same time.

(c) Procedure

Each experimental session consisted of 30 trials. For the first 15 trials, the chimpanzee saw both quantities in sequence. An experimenter placed a blind between the apparatus and the chimpanzee. He placed two quantities of mini-marshmallows on opposite ends of the bench and then covered them with the containers. He removed the blind and then lifted the tin container on his left, allowing the chimpanzee to look at the quantity of marshmallows underneath for approximately 2 s before re-covering it. He then revealed and re-covered the other set (on his right) in the same manner. Finally, he closed his eyes and lowered his head (so as not to influence the chimpanzee's choice) and immediately pushed the bench shelf forward so that the chimpanzee could make a selection by sticking a finger through the cage mesh and pressing one of the containers. A second experimenter, out of view of the chimpanzees, called out which container was selected so the first experimenter would know which quantity to uncover and give to the chimpanzee. The barrier was then lowered again and the next trial was prepared.

In the test phase, a second block of 15 trials was presented. Trials were prepared in the same way (out of view of the chimpanzee) and the experimenter revealed the first set in the same way. However, he never revealed the second set. Instead, he paused for 2 s and then pushed the bench shelf forward. This meant that the second set contained a quantity unknown to the chimpanzee at the point of its response. All other aspects of trial presentation were the same.

Each chimpanzee completed 10 sessions. They received one session per day for 2 or 3 days each week. In each session, six different quantities were presented during trials, and each possible combination was presented one time during the 15 training trials and one time during the 15 test trials. The order in which these 15 comparisons were presented was randomly determined for both phases. Across two consecutive test sessions, each comparison was presented one time in the training phase and one time in the test phase with the smaller quantity on the left and one time in each phase with the smaller quantity on the right. Therefore, position of the larger set was counterbalanced in both phases across these two sessions. We presented three quantity ranges: 1–6 (1, 2, 3, 4, 5 and 6); 2–10 (2, 3, 5, 6, 8 and 10); and 5–12 (5, 6, 7, 8, 10 and 12). Each quantity range was presented for two consecutive sessions. The ranges were presented in the following order across the experiments: 1–6; 2–10; 1–6; 5–12; and 1–6. This allowed us to assess how the chimpanzees varied their selections of the unknown quantity as a function of the known quantity and as a function of the overall rate of reward they had received during the training phase. Each chimpanzee completed a total of 30 test trials with the range 2–10, 30 test trials with the range 5–12 and 90 test trials with the range 1–6.

3. Results

During training, the chimpanzees selected the larger quantity in 256 of 270 trials (94.8%) when the range was 1–6 items, 87 of 90 trials (96.7%) when the range was 2–10 items and 77 of 90 trials (85.5%) when the range was 5–12 items. Each of these performance levels was significantly higher than chance levels of responding as assessed with a two-tailed binomial test (p<0.01).

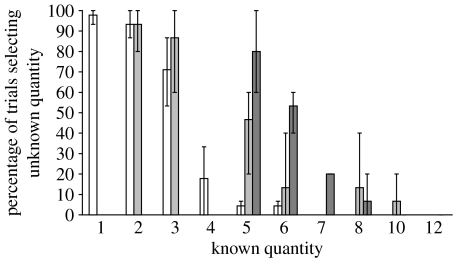
Figure 1 presents the percentage of all test trials in which the chimpanzees selected the unknown quantity as a function of the known quantity for each range of values presented during the training phase. The three blocks of trials with the quantity range of one to six items were combined. Chimpanzees' overall selection frequencies of the unknown quantity differed from chance levels (50%) in nearly all cases, either because the chimpanzees were significantly more likely than chance to choose the unknown quantity or significantly less likely than chance to choose the unknown quantity (all p<0.05 as assessed with a two-tailed binomial test). The two exceptions were for the quantity 5 when the training range was 2–10 and the quantity 6 when the training range was 5–12.

Figure 1.

The percentage of trials in which the chimpanzees selected the unknown quantity during the test phase. All data are combined across chimpanzees. Each series shows performance for a different range of quantities presented during individual sessions. Error bars show the range of performance across all three chimpanzees (the highest and lowest performing animals are indicated by the extremes of this range, and the third chimpanzee performed between those two values). White bars, 1–6; light grey bars, 2–10; dark grey bars, 5–12.

(a) Assessing the use of an absolute threshold quantity versus a relative threshold based on the training phase and some measure related to the average reward rate

Assessing whether the chimpanzees had a threshold quantity that determined the choice of the known or unknown set required us to look at selection patterns across the three quantity ranges. The critical data for this analysis came from the chimpanzees' selection patterns of the quantities that were presented in all three ranges (quantities 5 and 6). We first assessed the overall performance of all three chimpanzees using a Friedman test to determine whether selections of the known quantities 5 and 6 differed across the three training ranges. The percentages of choosing those known quantities were significantly different across the three ranges, Χ₂²=6.00, p=0.05.

Given the small sample size, we also assessed whether each chimpanzee showed this effect individually. To do this, we conducted a series of 3×2 chi-square analyses for each chimpanzee and each known quantity. All three chimpanzees showed a statistically significant difference in their choice of known quantity 5 across the three ranges: Lana Χ₂²=11.52, p=0.003; Mercury Χ₂²=20.61, p<0.001; and Sherman Χ₂²=10.45, p=0.005. All three chimpanzees also showed a statistically significant difference in their choice of known quantity 6 across the three ranges: Lana Χ₂²=9.13, p=0.010; Mercury Χ₂²=7.14, p=0.028; and Sherman Χ₂²=9.13, p=0.010.

These results indicate that the choice of the unknown set was not made on the basis of an absolute threshold across all quantity ranges. This supports the hypothesis that the chimpanzees may have used some measure related to the average reward rate to guide responses in the face of uncertainty about one set. However, the two remaining alternative hypotheses needed to be assessed.

(b) Assessing the role of the last consumed quantity on subsequent selections

We next assessed the likelihood that responses during the test phase were the result of trial-by-trial comparisons of the known quantity to the previously consumed quantity (the contrast effect hypothesis). This hypothesis predicted that, if the current known quantity was larger than the previously obtained quantity, the chimpanzees would select it, but if it were smaller, they would choose the unknown quantity.

For every test trial, we recorded the number of food items that the chimpanzees obtained from their selections and then compared that quantity with the known set for the next trial. We then examined the number of times the chimpanzees chose the known set even though it was smaller than the set obtained on the previous trial. We also examined how often the chimpanzees chose the unknown set even though the known set was larger than the set obtained on the previous trial. If the chimpanzees were using trial-by-trial comparisons of the last obtained quantity and the current known quantity, they should have rarely made these types of responses. However, they did so on 40.2 per cent of the trials overall (Lana: 32.1%; Sherman: 38.5%; and Mercury: 50%).

(c) Assessing the outcome of the last risk-taking response on subsequent selections

Finally, we were interested in situations in which the chimpanzees chose an unknown quantity that, when revealed, was smaller than the known quantity that was not chosen (i.e. trials that involved the chimpanzees making a ‘losing’ response). We then examined what response the chimpanzees made the next time they saw that same known quantity paired with an unknown option. If animals were using a win–stay, lose–shift strategy regarding the outcomes of their responses to the unknown quantity, we would expect the chimpanzees to be more likely to choose the known quantity in that situation (as part of the lose–shift strategy). However, if a more general sense of the rate of reward overall during the session guided responses, they should again choose the unknown quantity as long as the known quantity was smaller than the approximate mean number of rewards received during the training phase.

There were a total of 32 trials (approx. 17% of the total test trials) in which the chimpanzees chose the unknown set and received a quantity smaller than the known set. When next faced with the known quantity that they had given up, the chimpanzee again chose the unknown set on 21 of those trials (65.6%). This percentage did not differ from chance (as assessed with a sign test, p=0.110), indicating that losing on a trial in which the unknown set was chosen did not lead to the chimpanzees then preferentially choosing or avoiding that same known quantity the next time it was presented.

4. Discussion

The chimpanzees showed clear differences in preference for the quantities common across the ranges used in this experiment when faced with one known quantity and one unknown quantity. This confirmed that the chimpanzees did not respond solely on the basis of an absolute threshold amount that triggered a response in selecting either the known set or the unknown set. This experiment also discounted two cues the chimpanzees might have used to adjust their preference for certain quantities. First, they were not responding solely on a trial-by-trial basis by comparing the current known set with the quantity they had just received. Second, when the chimpanzees chose the unknown quantity and received a smaller number of rewards than was contained in the known set, they showed no bias to then choose or to avoid that same known quantity at the next opportunity. To predict whether the chimpanzees would take the known quantity or the unknown quantity, one had to know what occurred during the training phase because the chimpanzees appeared to be keeping track of the relative rates of return from their selections across trials rather than just responding to the comparison currently before them. They responded to the test trials, in which they could not know the contents of the unknown set, by using information gathered from their previous responses during the training phase.

The chimpanzees had never been required to remember anything from one trial to the next to be successful in this type of task. In fact, previous studies explicitly involved showing the chimpanzees that containers were empty at the outset of each trial to minimize the interference from one trial to the next that might occur if they failed to reset whatever mechanism they employed to assist in making these judgements. However, in the present study, they seemed to attend not only to the present comparison in front of them but also to some cumulative sense of how well they were rewarded overall for doing these trials. This suggests that quantitative information was encoded in a way that may have evoked a spontaneous (albeit probably implicit) measure related to the average reward rate. This measure may make the task of comparing sets easier because general evaluations of sets (e.g. ‘better than usual’, ‘worse than usual’) would allow for easy and fast comparisons when perceived sets are immediately classified according to that type of scale (a type of heuristic that would be useful when faced with uncertainty about one of the choices; Gigerenzer 2008). The next question was what form this measure of average reward might have taken.

One possibility is that average reward rate was based on the outcome of all trial comparisons. For the range of one to six items, the mean number of items obtained per trial during the training phase was 4.64 for Lana, 4.62 for Sherman and 4.54 for Mercury. However, the chimpanzees rarely selected an unknown quantity over a known quantity of four items. This was even more pronounced for the other ranges. For the range of 2–10 items, the mean number of items obtained per trial during training was 7.53 for Lana, 7.50 for Sherman and 7.47 for Mercury, but the chimpanzees consistently selected known sets of six items, and they were basically indifferent between the two choices when the known set had only five items. For the range of 5–12 items, the mean number of items obtained per trial during training was 9.43 for Lana, 9.20 for Sherman and 9.40 for Mercury, but the chimpanzees rarely selected the unknown set even when the known set consisted of six or seven items.

Although the above analysis used the arithmetic mean as a potential guide for how the chimpanzees may have structured their decisions in the face of uncertainty, another possibility exists. Animals often respond on the basis of a different form of central tendency called the geometric mean (the square root of the product of the anchor values; Roberts 2005; Jordan & Brannon 2006; Beran et al. 2008b). If the chimpanzees attended to the largest and smallest quantities seen during the training phase and used those as a guide to responding in the face of uncertainty about one quantity, their approximations of the average reward rate may have been related to the geometric mean. In that case, the 1–6 range had a geometric mean of 2.45, the 2–10 range had a geometric mean of 4.47 and the 5–12 range had a geometric mean of 7.75. These values fit more closely to the quantities at which the chimpanzees shifted from choosing the known set to choosing the unknown set (figure 1). However, it remains possible that some other measure would produce an even better fit to the data, and not necessarily a measure of central tendency.

Although we believe that these results are interesting for what they might illustrate about chimpanzees' decision making in the face of uncertainty, we want to carefully qualify what we think the chimpanzees may be experiencing during the task. We do not believe that the chimpanzees are capable of arithmetically calculating the mean number of items they receive over multiple trials. This is a highly complicated mathematical feat, particularly in a situation where the time course extends to 15 min or more, and it seems unlikely that chimpanzees could form such exact representations of the average reward quantity from all of their selections combined. In fact, the data suggest that they cannot, both from the underestimation that occurred and the increase in that underestimation as a function of the true mean number obtained during training. These aspects of performance indicate a ‘fuzzy’ sense of the average reward rate that matches other reports from quantity comparison tasks used with animals (e.g. Emmerton 1998; Brannon & Terrace 2000; Beran 2004, 2007; Judge et al. 2005; Cantlon & Brannon 2006; Agrillo et al. 2008). We believe that the chimpanzees attended to the outcomes of each trial and used trial-by-trial feedback of the quantity obtained to modify some representation1 of their overall reward rate for that day.

Perhaps the most interesting question is why this information about relative reward rate is generated at all. As noted, it is unnecessary to retain any information about how well one is doing overall to make correct responses throughout the training phase. One could even argue that such information is detrimental to making good choices during the training phase because the chimpanzees had to remember the quantity of items in each set and then make a choice based on their memory of each quantity. Information about past trial quantities could interfere with a current judgement if that information disrupted accurate recall of the current quantities.

Learning something about the overall reward structure of a task offers a source of information that could be used in the face of uncertainty. These chimpanzees appeared to use this type of information to support their decision making. However, these chimpanzees were very highly trained in these kinds of tasks, and we tested only three chimpanzees. It will be important to determine whether other research groups find similar performances with their chimpanzees and also to assess the performance of other non-human species in this task. This will provide a broader assessment of this possible capacity for spontaneously estimating relative rates of return and using that information in the face of uncertainty during successive quantity judgements.