The Effects of Anisotropy on the Stress Analyses of Patient-Specific Abdominal Aortic Aneurysms

Abstract

The local dilation of the infrarenal abdominal aorta, termed an abdominal aortic aneurysm (AAA), is often times asymptomatic and may eventually result in rupture —an event associated with a significant mortality rate. The estimation of in-vivo stresses within AAAs has been proposed as a useful tool to predict the likelihood of rupture. For the current work, a previously-derived anisotropic relation for the AAA wall was implemented into patient-specific finite element simulations of AAA. There were 35 AAAs simulated in the current work which were broken up into three groups: elective repairs (n = 21), non-ruptured repairs (n = 5), and ruptured repairs (n = 9). Peak stresses and strains were compared using the anisotropic and isotropic constitutive relations. There were significant increases in peak stress when using the anisotropic relationship (p<0.001), even in the absence of the ILT (p = 0.014). Rutpured AAAs resulted in elevated peak stresses as compared to non-ruptured AAAs when using both the isotropic and anisotropic simulations, however these comparisons did not reach significance (p_ani = 0.55, p_iso = 0.73). While neither the isotropic or anisotropic simulations were able to significantly discriminate ruptured vs. non-ruptured AAAs, the lower p-value when using the anisotropic model suggests including it into patient-specific AAAs may help better identify AAAs at high risk.

INTRODUCTION

Rupture of abdominal aortic aneurysms (AAA) occurs when the continuous and cyclic pressure acting on the lumen of the AAA creates a wall stress which eventually overcomes the ability of the wall to withstand those forces (the wall strength). Thus, the biomechanical point of view of AAA rupture states that there are two primary factors influencing AAA rupture—AAA wall stress and wall strength. By taking this point of view, it is easy to recognize that the risk of AAA rupture will increase with increasing wall stress as well as decreasing wall strength. It is not surprising then, that the prediction of stress in aneurysms has been reported by several researchers in the literature. ^{5,7,9,12,16,17,24,30,33,40,42,46} Some of these studies utilize the finite element method, which is able to model aneurysms with varying degrees of complexity.

Early finite element models of aneurysms in the literature utilized simplistic geometries (e.g., spherical) and small deformation constitutive relations.^6,16,17 Later work demonstrated that the complex shape (e.g., local curvatures) are an important factor in determining the peak stress acting on an individual AAA.^12,24,42 The isotropic constitutive model developed by Raghavan and Vorp represented the first large strain relation for the AAA wall.²³ Several other researchers have since utilized this relation when estimating the stresses acting on patient-specific AAA finite element simulations. ^7,8,40,46 One of the more recent advances in the finite element analyses of AAA was the inclusion of the intra-luminal thrombus by Wang et al.,⁴⁶ whose simulations demonstrated that the presence of the ILT can significantly effect both the magnitude and distribution of stress within a AAA. More recently Raghavan et al. investigated the effect of variable wall thickness on AAA stresses and demonstrated that this may be a very important factor in predicting the rupture risk using finite element analyses.²¹ The effect of localized calcification on peak AAA wall stress was also investigated recently by Speelman et al. who reveal a unique dependence of AAA wall stress on the location and stiffness of mineralized plaques in patient-specific AAA simulations.²⁹

The present work addresses the assumption of isotropy for the AAA wall. Nearly all biological materials display some amount of anisotropy due to their nonuniform composition and structure. Recent work by Nicosia et al. demonstrated the anisotropy present in the porcine ascending aorta.¹⁸ They conclude that the utilization of an isotropic constitutive relation for the ascending aorta is insufficient in providing a physiologically realistic prediction of stress. Kyriacou and Humphrey also recently underscored the importance of including multiaxial constitutive relations into finite element stress analyses of intracranial saccular aneurysms, especially given their unique 3D shape.¹⁴ The anterior bulging present in the aneurysmal formation of the abdominal aorta also suggests that this region may indeed be in a state of multiaxial stress.

Appropriate stress approximation has been proposed as an important component in AAA rupture prediction. Previous work in our laboratory has shown anisotropy is present in the aneurysmal abdominal aorta in the multiaxial stress state.³⁸ In addition, the general constitutive relation for the AAA wall was also shown to be different for uniaxially vs. biaxially tested specimens. The implementation of an anisotropic constitutive relation for the AAA wall may lead to a more appropriate estimation of stress within patient-specific AAAs. This improvement may also be important in noninvasively identifying those AAAs which have a high risk of rupture.

METHODS

Boundary Conditions

Blood Pressure

An increase in the blood pressure acting on the interior of a AAA would obviously cause an increase in the stress acting on the AAA wall. It is therefore not surprising that hypertension has been identified as a major risk factor for AAA rupture.² Since the interest here is to isolate the effects of including an anisotropic constitutive relation into patient-specific stress predictions, a systolic pressure of 120 mmHg was applied either to the luminal contour of the ILT and/or to AAA wall when ILT was not present.

Longitudinal Tethering

The abdominal aorta is in a unique and complex physical environment, especially in the presence of an aneurysm. Several studies have investigated the longitudinal stretch present in blood vessels and shown them to be under a state of longitudinal tethering in-vivo.^10,19,20,32 For the current work, the nodes comprising the proximal and distal ends of each AAA were constrained in all three displacement degrees of freedom. This was done to mimic the in-vivo longitudinal tethering thought to be present in the abdominal aorta. It was found in the current study that constraining the radial displacement of nodes on the ends of the AAA did not result in localized stress concentrations, but did result in faster convergence of the finite element solution. The boundary conditions utilized here have also been used by several other researchers in the patient specific finite element simulation of AAA.^7,9,24,40

Reference Configuration

For the purposes of the finite element simulation of AAA, the systolic pressure should be applied to the unloaded state with longitudinally tethering force already present. Since the geometry in a CT scan represents a time-averaged loaded state configuration, the geometry of the AAAs in the completely unloaded state was not available. Therefore, in the current study the systolic pressure was applied to the time-averaged loaded state (CT-configuration). The error associated with using the loaded configuration as the unloaded state has been investigated previously by Raghavan et al.,²² who demonstrated that using the CT-configuration will generate minimal differences in predicted wall stress (0.7–2.7% error). It should be noted that despite this admitted error, the conclusions of this study will most likely not change as we are herein focused on isolating differences in stress estimates between using an isotropic and anisotropic constitutive model for the AAA wall.

Implementation of the Constitutive Relation into ABAQUS

Despite the changes in stress resulting from the in homogeneities known to be present in AAAs,²⁹ many researchers assume a homogenous mechanical response for the AAA wall.^7,9,24,40,46 The AAA wall will be assumed to act as a nonlinearly elastic homogenous material for the simulations in the present work.

Constitutive Relationship and Finite Element Model

The anisotropic constitutive relation derived previously ³⁸ was implemented into the finite element software with the use of the user-defined material function (UMAT) available in ABAQUS. In a finite strain environment, the ABAQUS constitutive relationship is expressed in a rate form defined by

$${\tau }^{\nabla J}={\mathbf{C}}^{J\tau }:\mathbf{D}$$ (1)

This form is based on Jaumann rate of the Kirchoff stress (τ^∇J) as an objective stress rate, and the rate of deformation tensor (D). The associated material Jacobian (C^Jτ) characterizes the material stiffness.

The strain energy assumption is defined by the following form

$$\begin{array}{c}W=b_0(e^{\frac{1}{2}{b}_1{E}_{\theta \theta }^2}+e^{\frac{1}{2}{b}_2{E}_{LL}^2}+e^{b_3{E}_{\theta \theta }{E}_{LL}}+e^{\frac{1}{2}{b}_4{E}_{\theta L}^2}\\ +e^{b_5{E}_{\theta \theta }{E}_{\theta L}}+e^{b_6{E}_{LL}{E}_{\theta L}}-6)\end{array}$$ (2)

where b₀, b₁, b₂, and b₃ where 0.14, 477.0, 416.4, and 408.3 kPa, respectively.³⁸ The strain energy terms involving the constants b₄, characterize material shear and b₅, and b₆ the shear-normal behaviors, respectively. Although these terms are not required to fit the experimental stress–strain data, as shear strains in the AAA wall are negligible, they were included solely to address computational concerns. By including both a shear term and two shear-normal terms, zero energy modes related to in-plane stiffness are avoided in the finite element simulation. Constants for these terms were selected on the basis of providing numerical stability without impacting physiological relevance. Note that unlike the traditional Fung-type elastic strain energy, the constitutive relation given by (2) avoids model parameter covariance by separating out each of the individual exponential terms and allowing each strain tensor component to independently contribute to the total strain energy.

ABAQUS linear shell elements (S4R) were used to model the AAA wall. These elements require the definition of out-of-plane transverse shear stiffness apart from the user-defined material function. Given the membrane nature and flexural rigidity of the AAA wall, a transverse stiffness of 10 kPa was used in the simulations. Transverse stiffness values of this order were shown to have insignificant impact on the resulting AAA wall strain field.

Definition of Local Material Coordinates

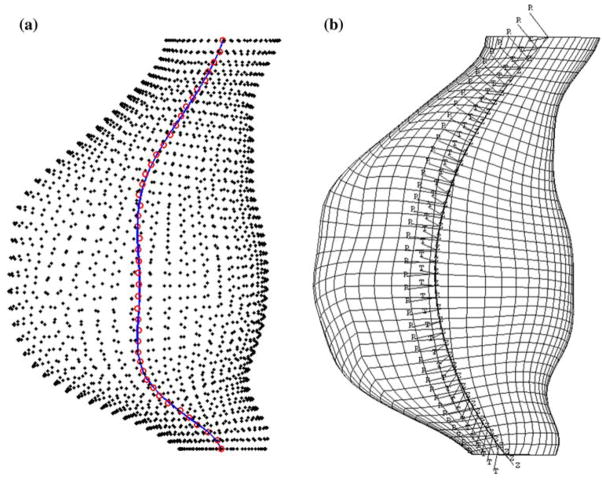
For the majority of AAAs, the presence of the ILT and the tortuous path of blood flow within an AAA results in an asymmetrical geometry. This tortuosity does not allow a simple interpretation for the locally acting material coordinates (circumferential and longitudinal). The 3D path of the centerline of the AAA wall is in general a reliable indication of the local longitudinal direction of the AAA wall. For this reason, each AAA wall mesh was divided up into several (e.g., ³⁰) longitudinal slices, allowing the center of each slice to be found (Fig. 1a). 3D spline tools were then utilized in Matlab to create a spline through the centerline points along the AAA (Fig. 1a). The projection of this 3D spline onto the surface of each AAA wall element was then used to define the local longitudinal direction of the shell. The normal direction of the shell is automatically defined in ABAQUS using the ordering of nodes within an element. Once the local longitudinal and normal directions of the shell element are defined, the final local circumferential direction of the shell is computed using the right hand rule. The above formulation provided an accurate, repeatable, and mesh-independent definition of the local material directions for a given slice along the AAA (Fig. 1b).

FIGURE 1.

(a) 3D spline defining centerpoint of each longitudnal slice of elements. (b) Definition of local material coordinates.

Biaxial Simulations

In order to test the accuracy of the UMAT subroutine, the equibiaxial protocol of several AAA wall biaxial tensile tests were simulated. The computational results of the anisotropic simulations were compared with the biaxial experimental data as well as simulations utilizing an isotropic constitutive relation previously used in the literature to model the AAA wall.²⁴ Patient specific data from a uniaxial tested specimen were fit to the equation,²³ which gave the parameters for the patient specific isotropic, or PT ISO, simulation. Constitutive model parameters for the average isotropic, or AVE ISO, simulation were previously derived by fitting data from 69 uniaxial tested specimens.²³

A subset of AAA wall biaxial specimen (n = 14) were constructed in ABAQUS using their respective dimensions from the experimental biaxial test. Each node along both sides of the biaxial specimen was assigned a force boundary condition in order to mimic the experimental biaxial setup (120 N/m tension per side). Patient specific data from one biaxially tested specimen were fit to the anisotropic constitutive model which yielded parameters for the patient specific anisotropic, or PT ANI, simulation. The constitutive model parameters derived for an averaged dataset were used for the average anisotropic, or AVE ANI, simulations. It should be noted that the uniaxial and biaxial specimens used to derive the constitutive relations used in the PT ANI and PT ISO simulations were taken from adjacent locations within the same AAA patient.

The stress–strain relationships for the biaxial experiments were compared to the computational results of the PT ISO and PT ANI simulations. The strain at 60 kPa for the biaxial data was compared with the strain at 60 kPa for both the isotropic and anisotropic simulations. A tangential modulus, TM, at ~3% strain was calculated by

$$\text{TM}=\frac{S_2-S_1}{E_2-E_1}$$ (3)

where S₁ and S₂ are the Second-Piola Kirchhoff stresses occurring 5 data points above and below 3% strain, respectively and E₁ and E₂ are the Green strains occurring 5 data points above and below 3% strain, respectively. All statistical comparisons were performed using a one-way ANOVA (Sigma Stat, v. 3.0) with a significance of p<0.05.

Cylindrical Simulation

As a first step to 3D simulations, the UMAT was used in the simulation of a pressurized cylinder. For this simulation, a 9 cm long cylinder of 3.0 cm diameter and 2 mm thickness was pressurized to 120 mmHg, with each end of the cylinder being constrained in all degrees of freedom. The analytical solution for the hoop stress due to the pressurization of a thick walled cylinder (thickness/radius = 0.13> 0.05) takes the form

$$t_{\theta }(r)=\frac{a^2{P}_{\text{i}}-b^2{P}_{\text{o}}}{b^2-a^2}+\frac{(P_{\text{i}}-P_{\text{o}})a^2{b}^2}{(b^2-a^2)r}$$ (4)

where t_θ(r) is the hoop stress as a function of the radial coordinate r, P_i is the internal pressure (120 mmHg), P_o is the external pressure (0 mmHg), a is the internal radius (1.4 cm), and b is the external radius (1.6 cm). The hoop stress at the luminal, mid-wall, and adventitial integration points of the shell element were compared to the analytical solution for the pressurization of a thick-walled cylinder.

Patient-Specific AAA Finite Element Simulations

There were 35 AAAs simulated in the current work which were broken up into three groups: elective repairs (n = 21, AAA1–AAA21), non-ruptured repairs (n = 5, N1–N5), and ruptured repairs (n = 9, R1–R9). Elective repair simulations were derived from CT scans from AAA patients who underwent scheduled elective open repair of their AAA. Non-ruptured simulations consisted of AAA simulations for which there existed a set of CT scans at least 1 year apart, with the latter scan providing evidence the AAA remained quiescent. For these simulations, the images from the earlier CT scan were used to reconstruct the AAAs. Ruptured repair simulations were derived from CT scans taking place no more than one year prior to AAA rupture.

The electively repaired AAAs (n = 21) were utilized to investigate the differences in stress due to the implementation of the anisotropic constitutive relation for the AAA wall³⁸ and biaxially-derived isotropic constitutive relation for the ILT.³⁷ AAA simulations including the anisotropic relation for the AAA wall and the uniaxially-derived isotropic relation for the ILT⁴⁵ were denoted as ANI. Simulations utilizing the previously developed isotropic constitutive relations for the AAA wall²³ and ILT⁴⁵ were labeled ISO. Finally, the influence of anisotropy in the absence of the ILT was investigated with simulations utilizing the anisotropic (ANI_NOILT) and isotropic (ISO_NOILT) relations for the AAA wall with no ILT present. For each individual simulation, the peak maximum principal stress and strain within the AAA was recorded and compared across groups. In addition, the mean stresses acting on each AAA were also recorded and compared.

Ruptured vs. Electively-Repaired Simulations

The ruptured and non-ruptured AAAs (n = 9, n = 5, respectively) were used to investigate whether or not the peak and average stresses within a AAA are different between these two groups. The presence of a statistically larger stress for the ruptured group would indicate that stress may be an important factor in determining a given AAAs risk of rupture. The fact that the non-ruptured AAAs remained quiescent for an entire year would suggest this group of AAAs may have a decreased stress acting on the AAA wall. Of course, since rupture is mechanically dependent on stress and strength, the lack of a statistical difference between these groups may be due to large differences in the strengths of each of these AAAs.^39,43 For all of the ruptured (R1–R9) and non-ruptured AAAs (N1–N5), the peak and mean maximum principal stresses and strains acting on the AAA wall were recorded and compared.

RESULTS

Biaxial Simulations

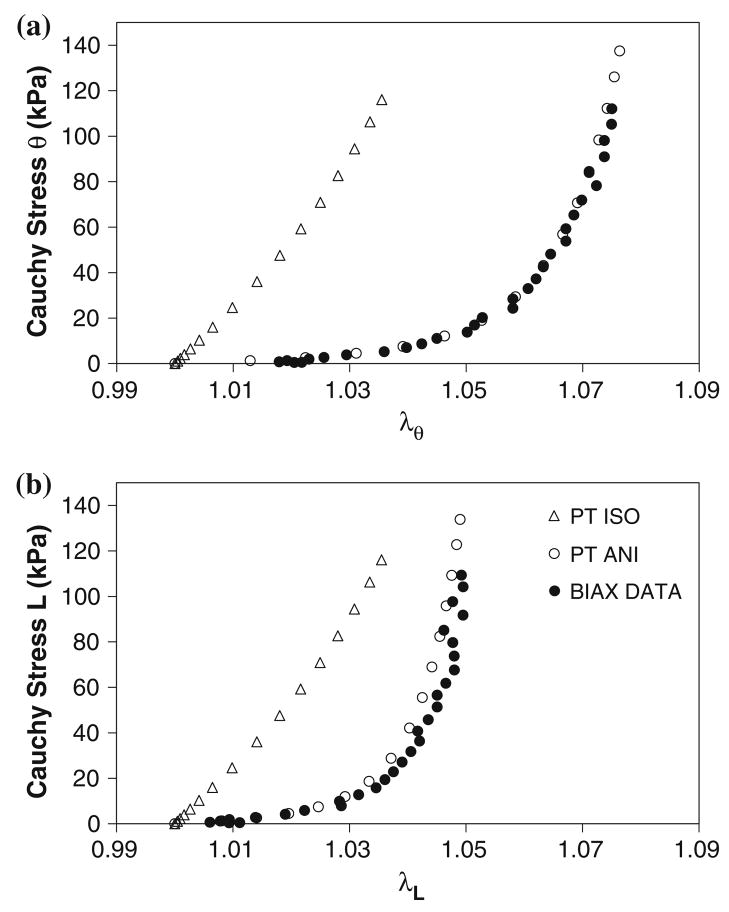
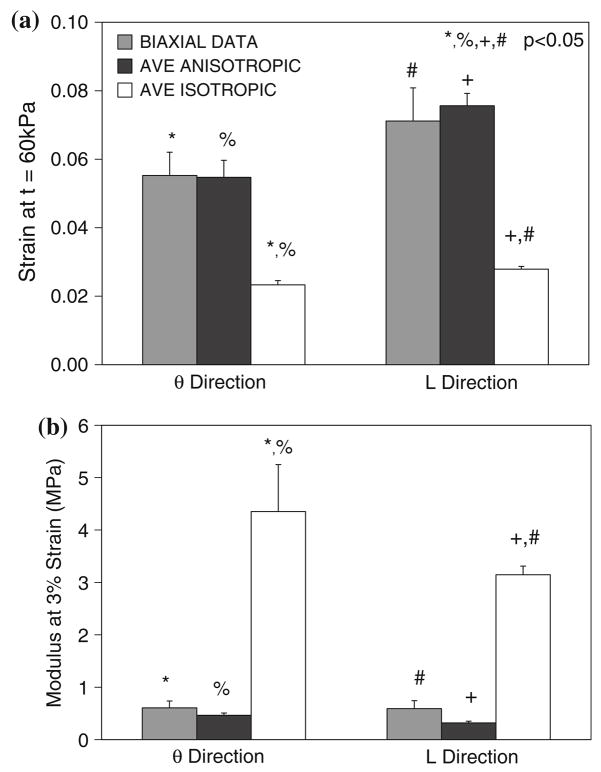
Plots of the experimental and computational Cauchy stress vs. stretch ratio for a representative biaxial specimen are shown in Fig. 2. Note the stiffer response for the PT ISO as compared to the PT ANI simulation. Note also that the similarity between the PT ANI computational data and the experimental biaxial data. Since both of the constitutive relations utilized in the PT ANI and PT ISO simulations were derived from tissue from similar locations within a AAA patient, this plot displays the differences in stress prediction resulting from constitutive relations derived from uniaxial and biaxial testing, which was previously observed by our group.^36,38 The biaxial data and average anisotropic simulations yielded significantly greater strain values compared to the average isotropic simulations at a given stress of 60 kPa (Fig. 3a). At a given strain of ~3%, the TM of the average isotropic simulations were significantly greater than those of the biaxial data and average anisotropic simulations (Fig. 3b).

FIGURE 2.

Circumferential (a) and longitudinal (b) Cauchy stress vs. stretch ratio for the PT ISO and PT ANI simulations and the corresponding biaxial experimental data.

FIGURE 3.

(a) The strain values at t = 60 kPa and (b) TM for 14 biaxial simulations. AVE ISOTROPIC simulations utilize the uniaxially-derived isotropic model previously reported by Raghavan et al.²⁴

Cylindrical Simulation

The results of the cylindrical simulation utilizing the anisotropic UMAT and the analytical stresses using Eq. (4) are summarized in Table 1. The percent error in the hoop stress at the luminal (r = 1.4 cm), mid-wall (r = 1.5 cm), and adventitial (1.6 cm) integration points were 0.41, 1.96, and 5.30%, respectively.

TABLE 1.

Hoop stress for the analytical and computational solution of the pressurization of a thick walled cylinder.

	Stress (N/cm2)
	r = 1.4 cm	r = 1.5 cm	r = 1.6 cm
Analytical	12.05	11.17	10.45
Computational	12.00	10.95	9.90
% Error	0.41	1.96	5.30

Patient-Specific Anisotropic Finite Element Simulations

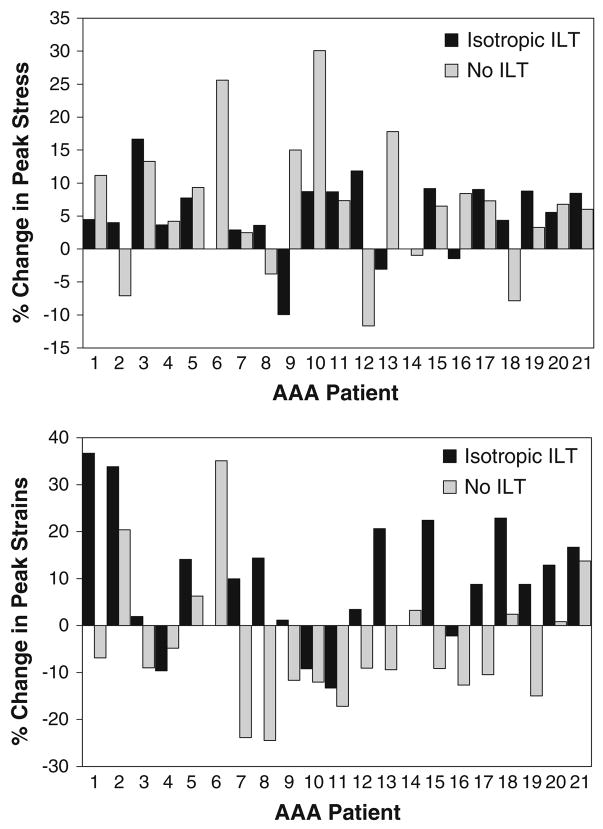
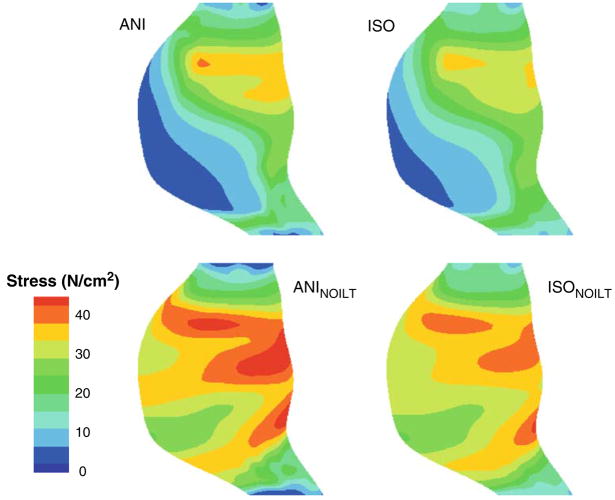
The peak maximum principal stresses and strains for each of the electively repaired simulations are shown in Fig. 4. Note that AAA6 and AAA14 did not have any ILT, so only the ANI_NOILT and ISO_NOILT simulations were run for these AAAs. The average of the peak maximum principal stresses for the electively repaired simulations were 38.30 ± 3.04, 36.06 ± 2.73, 54.70 ± 2.44, and 51.27 ± 2.09 N/cm² for the ANI, ISO, ANI_NOILT, and ISO_NOILT simulations, respectively. Using a paired t-test, there were significant differences between the ANI and ISO peak stresses (p<0.001) as well as between the ANI_NOILT and ISO_NOILT peak stresses (p = 0.014). Using a Wilcoxon Signed Rank test, there were no statistically differences between the peak stresses of the ANI and ISO simulations. Whether the anisotropic or isotropic relation was used for the AAA wall, the peak stresses were statistically larger for simulations neglecting the presence of the ILT (p<0.001 for ANI vs. ANI_NOILT and ISO vs. ISO_NOILT). In general, the presence of the anisotropic constitutive relation elevated the peak stress within a given AAA. It is interesting to note, however, that this was not true for all of the electively repaired AAA simulations as 3 out of the 21 simulations had an elevated peak stress for simulations utilizing the isotropic relation for the AAA wall (AAA9, AAA13, and AAA16). This was even more pronounced in the absence of the ILT, as 5 out of the 21 isotropic simulations had higher maximum principal stresses than their anisotropic counterparts (AAA2, AAA8. AAA12, AAA14, and AAA18). The maximum principal stress distribution for a representative electively repaired AAA is shown in Fig. 5.

FIGURE 4.

(Top) Percent change in peak maximum principal stress when using the anisotropic constitutive model for the AAA wall. Differences were investigated both with and without ILT present. (Bottom) Percent change in maximum principal strains when using the anisotropic model.

FIGURE 5.

Maximum principal stress distributions for AAA17. ANI = anisotropic AAA wall; ISO = isotropic AAA wall; ANI_NOILT = anisotropic wall no ILT; ISO_NOILT = isotropic wall with no ILT.

In addition to the peak maximum principal stress acting within a given AAA, the peak maximum principal strain was also quantified for each electively repaired AAA. The peak strains in the ANI simulations were statistically larger than for the ISO simulations (0.139 ± 0.005 vs. 0.127 ± 0.005, p = 0.012). There was no significant change in the peak strain when neglecting the presence of the ILT (ANI_NOILT vs. ISO_NOILT, 0.142 ± 0.005 vs. 0.150 ± 0.003, p = 0.152).

Ruptured vs. Electively-Repaired Simulations

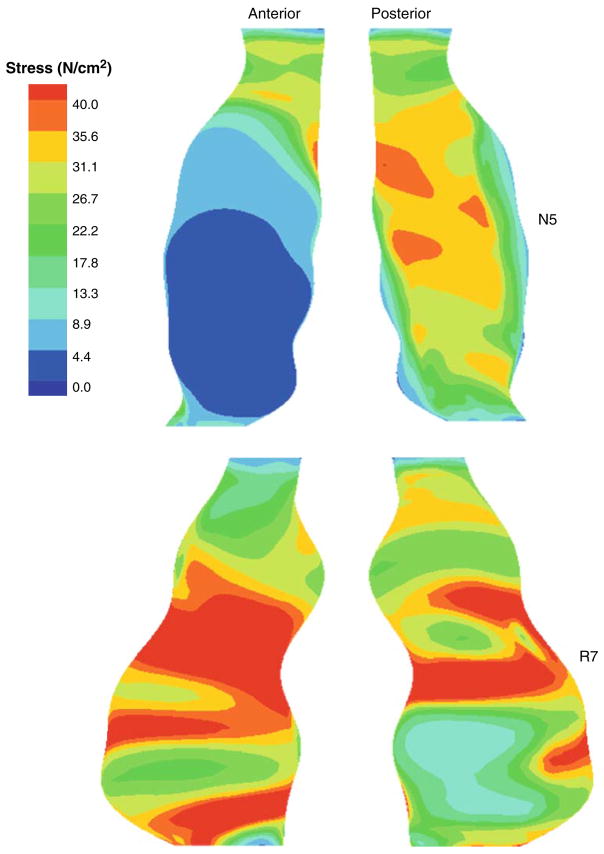
The peak maximum principal stresses for each of the non-ruptured and ruptured simulations are shown in Tables 2 and 3, respectively. In this dataset, there were two AAAs which did not have any ILT (N2 and R2). As detailed in this table, the mean peak stresses for the non-ruptured and ruptured AAAs were 45.98 ± 4.26 and 49.89 4.02 N/cm², respectively (p = 0.55). There was no significant difference between the mean stresses for the non-ruptured and ruptured AAAs (20.39 ± 1.66 vs. 20.65 ± 2.61 N/cm², p = 0.95). There were also no statistical differences in the peak and mean maximum principal strains between each of the groups (0.143 ± 0.008 vs. 0.161 ± 0.009, p = 0.20 and 0.088 ± 0.005 vs. 0.085 ± 0.007, p = 0.75, respectively). Maximum principal stress distributions for a pair of representative AAAs are shown in Fig. 6. The mean peak maximum principal stresses for the non-ruptured and ruptured AAAs when utilizing the isotropic constitutive relation for the AAA wall were 43.76 ± 3.41 and 46.36 ± 5.0 N/cm², respectively (p = 0.73).

TABLE 2.

Peak and mean maximum principal stresses and strains for the non-ruptured AAA simulations.

	Non-ruptured
Simulation	Tmax (N/cm2)	Tmean (N/cm2)	Emax	Emean
N1	53.02	15.83	0.129	0.075
N2	41.40	23.67	0.156	0.099
N3	58.93	24.04	0.144	0.097
N4	36.49	21.13	0.166	0.093
N5	40.06	17.28	0.121	0.078
Mean	45.98	20.39	0.143	0.088
SEM	4.26	1.66	0.008	0.005

TABLE 3.

Peak and mean maximum principal stresses and strains for the ruptured AAA simulations.

	Ruptured
Simulation	Tmax (N/cm2)	Tmean (N/cm2)	Emax	Emean
R1	33.50	7.42	0.124	0.049
R2	54.47	31.76	0.189	0.123
R3	63.99	24.87	0.158	0.078
R4	53.72	18.17	0.195	0.085
R5	55.05	22.46	0.164	0.090
R6	44.40	16.65	0.169	0.085
R7	67.30	31.05	0.186	0.105
R8	42.25	18.84	0.137	0.073
R9	34.32	14.57	0.130	0.078
Mean	49.89	20.65	0.161	0.085
SEM	4.02	2.61	0.009	0.007

FIGURE 6.

Maximum principal stress distributions for N5 and R7.

DISCUSSION

An anisotropic constitutive relation was successfully implemented into the commercially available finite element package ABAQUS. The user-defined FORTRAN subroutine (UMAT) was tested and validated using biaxial tensile simulations and a simulation of the pressurization of a 3D cylinder. The user-defined anisotropic relation was then applied to patient-specific AAA simulations. The results for maximum principal stress and strain for the anisotropic simulations were compared to simulations utilizing a previously derived isotropic constitutive relation (n = 21, AAA1–AAA21). These results suggest that the peak wall stress is, in general, significantly increased when using the anisotropic constitutive relation. This was not the case for all simulations, as for some simulations the isotropic relation resulted in a higher peak stress. When comparing the ruptured to non-ruptured AAAs, there were no significant differences between the peak stress, mean stress, peak strain, and mean strain.

Abdominal aortic aneurysm simulations using axisymmetric hypothetical geometries have previously been created and analyzed in the literature. ^{6,11–13,16,17,30} Such analyses fail to take into account the unique and patient-specific geometry known to be present in AAAs.^25–27 Several studies have since investigated the stresses acting on realistic patient-specific AAAs reconstructed from noninvasive imaging techniques.^{4,7,9,24,40,46} These studies revealed that the mechanical stress acting on the AAA wall cannot be estimated using simplistic hypothetical geometries or other crude analyses such as the Law of LaPlace. Raghavan et al. were the first to estimate the stresses acting on patient-specific AAAs using a geometry derived from CT scan images.²⁴ Wang et al. improved upon this reconstruction technique with the inclusion of the ILT into the patient-specific modeling of AAAs.⁴⁶ The reconstruction technique utilized herein is an updated version of this reconstruction protocol, with decreases in reconstruction time and user to user variability as well as improvements in computational efficiency via a more automated reconstruction protocol.

The estimation of stress using the finite element method requires the identification of an accurate constitutive relation for the AAA wall and ILT. Early finite element simulations of AAA assumed the wall and ILT to act as linear isotropic materials, such that these materials could be modeled with the definition of a Young’s modulus and Poisson’s ratio.^{6,13,16,17,30,42} Such engineering analyses are appropriate for materials undergoing small strains (e.g., steel), while for materials undergoing large strains a more rigorous finite strain constitutive model must be derived. The AAA wall has been shown to undergo large strains in-vivo,^28,41 rendering significant error in the application of a small strain relation into finite element analyses of AAA. Raghavan et al. were the first to develop a large strain constitutive relation for the AAA wall,²³ while Wang et al. did the same for the ILT.⁴⁵ The constitutive relations for both of these investigations can easily be implemented into most commercially available finite element packages. However, both of these relations are also isotropic relations derived from the uniaxial tensile testing of excised aneurysm contents.

Our group has recently shown that the aneurysmal wall displays an anisotropic mechanical response.³⁸ The implementation of this anisotropic constitutive relation into patient-specific AAA results in a significant increase in peak stress in most AAAs (Fig. 4). The use of an anisotropic relation did not, however, result in an increased peak stress level for all AAAs, suggesting that the effect of anisotropy on the peak AAA stress is patient-specific. Differences in the stress distributions within a given AAA were also more amplified in cases where the ILT is neglected. It is interesting to note that the presence of an anisotropic relation for the AAA wall resulted in larger strains in the presence of ILT, while the anisotropic simulations had lower peak strains when neglecting the presence of the ILT. This result was not true, however, for all AAA simulations. This result further confirms the idea that the stresses and strains within an individual AAA are largely a function of the locally varying geometrical parameters such as ILT thickness and local curvature.

The effect of the intra-luminal thrombus on the stresses acting on finite element simulations of AAA has been investigated previously.^{5,17,34,38,46} Mower et al. showed that the presence of the ILT can reduce the stresses acting on an AAA up to 51%.¹⁷ Wang et al. were the first to implement a large strain constitutive relation into patient specific AAA simulations. Their results agree with Mower et al., showing the ILT acts as a stress cushion and can reduce wall stress up to 38%.⁴⁶ In contrast, work by Thubrikar et al. has shown that the pressures acting at the AAA wall are 91% of those in the lumen.³⁴ Similar findings were recently reported by Takagi et al.³¹ Results reported here corroborate the work done by Mower et al. and Wang et al., in that the presence of the ILT (ANI_UNIAXIAL vs. ANI_NOILT and ISO_UNIAXIAL vs. ISO_NOILT) significantly decreased the peak stress acting on the AAA wall.

When comparing the ruptured vs. non-ruptured AAA simulations, it was found there was no significant difference in the peak stress and strain between these two groups. Figure 7 shows the mean peak stress acting on all ruptured and non-ruptured AAAs for simulations utilizing both of the anisotropic and isotropic constitutive relations for the AAA wall. The previously derived isotropic constitutive model for the ILT was used in all of these simulations.⁴⁵ While both constitutive relations showed a trend towards increased peak stress in the ruptured group, neither group reached significance. While not significant, the smaller p-value for the anisotropic comparison may be evidence for an improvement in stress prediction using this relation. These results are in contrast to work done by Fillinger et al., who showed a significant increase peak wall stress for ruptured and symptomatic AAAs compared to non-symptomatic AAAs who were electively repaired.⁷ This difference may in fact be due to the relatively smaller sample sizes used in the current study.

FIGURE 7.

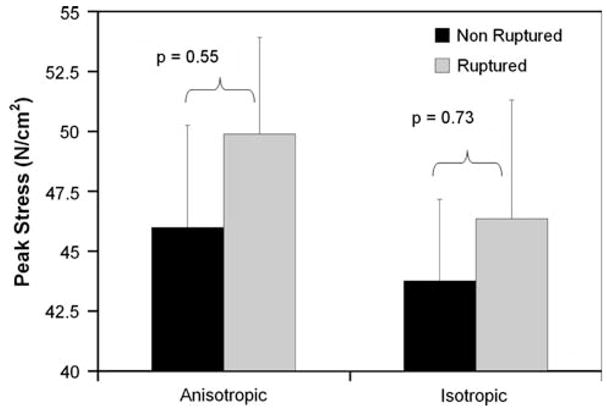
Comparison of anisotropic and isotropic simulations for ruptured and non-ruptured groups.

Some of the limitations in the current work result from the assumptions applied in deriving a noninvasive estimation of AAA wall stress. One of these assumptions is that the material properties for all AAA patients can be modeled using one constitutive relation. This assumption stems from the inability to noninvasively derive a constitutive relation on a patient-specific basis. While such a relation would be ideal, the error arising from using a population-wide anisotropic constitutive model can be assessed by analyzing the stresses on AAA simulations in which the upper and lower 95% confidence interval constitutive models (see Ref. 38) are utilized. Using a representative AAA in the current work, the error in peak wall stress was found to be 2.4% for the upper and 1.8% for the lower 95% confidence interval. These results are similar to results reported previously in which the upper and lower 95% confidence interval variations in isotropic AAA wall constitutive parameters resulted in less than 4% change in peak wall stress.²³ The same type of analysis was performed by Di Martino et al. on the ILT which resulted in a maximum variation of 10% on the AAA wall stress due to large yet physically reasonable variations in mean ILT model parameters. These results suggest that the peak stress acting on an individual AAA are relatively insensitive to the errors introduced using a set of mean or population-wide model parameters.

Another limitation of the current work is the assumption that the CT configuration from which the AAA models are derived is the “stress free” configuration. This assumption may lead to significant error in wall stress estimation as the state of stress within a blood vessel has previously been shown to be in a state of stress even in the unloaded configuration (due to residual stresses/strains).^1,3,10,35 There currently exist no experimental information on the residual stresses and strains present in the aneurysmal abdominal aorta. Such information would provide for a better understanding of the location on the stress–strain curve the AAA acts in-vivo. In order to quantify the error associated with using the CT geometry as the “stress free” configuration the following analysis was performed. An asymmetrical hypothetical AAA was used to mimic the stress free configuration. This AAA was pressurized to 100 mmHg in ABAQUS, from which the deformed geometry was extracted and assumed to correspond to the configuration of the AAA during a CT scan. A 120 mmHg was then applied to this deformed geometry to mimic the boundary conditions utilized in the current work. Of course, the “true stress” acting on the AAA can be modeled with the pressurization (0–120 mmHg) of the zero stress state configuration. Comparing the nodal stresses between the “true stress” simulations and the simulation assuming the CT configuration was the stress free state revealed a maximum and mean difference in stress of 1.0 and 0.7%, respectively.

These results are in contrast to a similar investigation reported previously in our laboratory for the isotropic constitutive relation which showed a maximum error in peak stress of 8% (range 2–10%).⁴⁴ Recent work by Marra et al. estimated the zero-stress state geometry of a patient-specific AAA using dynamic magnetic resonance imaging.¹⁵ Their results indicate an error of 8.2% in peak wall stress when comparing the pressurization of the zero-pressure geometry to the diastolic dynamic magnetic resonance geometry pressurized to the systolic blood pressure. While the results reported above indicate this assumption seems to introduce modest error in the stress estimation of a hypothetical AAA, the effect of this assumption on stress estimations of patient-specific AAA requires further investigation.

On average, the presence of an anisotropic constitutive relation in patient-specific finite element simulations of AAA increased the peak stress acting on most AAAs. The lack of a consistent increase in peak stress in anisotropic vs. isotropic AAA simulations suggests that this effect may be patient-specific. While peak stress in simulations using both relations was not found to be a significant predictor of AAA rupture, the anisotropic relation utilized here may provide a better estimate of stress as evidenced by the larger difference in peak stress when comparing ruptured and non-ruptured AAAs. The presence of a multiaxial stress-state for the AAA wall in-vivo suggests that implementing anisotropy into patient-specific models of AAA provides a more accurate state of stress for the AAA wall.