Evaluation of Reproducibility for Paired Functional Data

Abstract

Evaluation of reproducibility is important in assessing whether a new method or instrument can reproduce the results from a traditional gold standard approach. In this paper, we propose a measure to assess measurement agreement for functional data which are frequently encountered in medical research and many other research fields. Formulae to compute the standard error of the proposed estimator and confidence intervals for the proposed measure are derived. The estimators and the coverage probabilities of the confidence intervals are empirically tested for small to moderate sample sizes via Monte Carlo simulations. A real data example in physiology study is used to illustrate the proposed statistical inference procedures.

1 Introduction

Evaluation of reproducibility is needed for many scientific research problems. For example, when a new instrument is developed, it is of interest to assess whether the new instrument can reproduce the results obtained by using a traditional gold standard criterion. Indeed, the need to quantify agreement arises in many research fields when two approaches or two raters simultaneously evaluate a response. There are some traditional criteria for measuring agreement between two rating approaches, such as Pearson’s correlation coefficient and paired t-test when the responses are continuous. Even though these criteria had been used in practice, they fail to detect poor agreement in some situations (see, for example, Lin, 1989). Thus, the topic of assessing agreement for measurements by two approaches has become an interesting research topic. Lin, Hedayat, Sinha and Yang (2002) gives a review and comparison of various measures of recent developments in this area. Some measures to evaluate reproducibility include intraclass correlation (Fleiss, 1986, Quan and Shih, 1996) and within-subject coefficient of variation (Lee, Koh and Ong, 1989). Lin (1989) introduced the concordance correlation coefficient which assesses the linear relationship between two variables under the constraint that the intercept is zero and the slope is one. This measure is more appropriate for assessing reproducibility of continuous outcomes. King and Chinchilli (2001b) proposed a generalized concordance correlation coefficient for categorical data and continuous data. They also show that the generalized concordance correlation coefficient is actually equivalent to the weighted kappa coefficient (Cohen, 1968) for ordinal data and equivalent to the kappa coefficient (Cohen, 1960) for binary data.

The concordance correlation coefficient has been widely applied to various research fields since its introduction. Several extensions have been proposed to address different problems recently. Extending Lin’s ideas, Chinchilli, Martel, Kumanyika and Lloyd (1996) suggested a weighted concordance correlation coefficient for repeated measures design. Vonesh, Chinchilli and Pu (1996) used the concordance correlation coefficient to assess goodness-of-fit for generalized nonlinear mixed-effects models. King and Chinchilli (2001a) developed a robust version of the concordance correlation coefficient. To accommodate covariate adjustment, Barnhart and Williamson (2001) proposed a generalized estimating equations approach to model the concordance correlation coefficient via three sets of estimating equations.

This paper deals with the problem when paired data of repeated measures are curves, and proposes a measure to evaluate the reproducibility of repeated-paired curve data. Such data are also called functional data. Image data and growth curve data are special cases thereof. Analysis of functional data is becoming an important topic in the statistical literature. Many interesting applications can be found in the excellent book by Ramsey and Silverman (1997) and references therein. The method in this paper is developed to analyze an actual data set collected in the Noll Physiological Research Center at The Pennsylvania State University (courtesy of Dr. W. L. Kenney). This study was designed to assess agreement of measurement by two different approaches to measure body core temperature.

Body core temperature refers to the temperature of tissues located at sufficient depth within the body so that it is minimally affected by the environmental temperature. The core temperature may be monitored by measuring the temperature at different locations in the body. Both the esophageal temperature (Tes) and rectal temperature (Tre) have been used for measuring indices of core temperature for research purposes. The Tes probe is a thermometer sealed inside a plastic feeding tube, which is inserted into the esophagus via the nostril to the level of the right atrium. The Tre probe is a thermometer sealed in soft vinyl tubing and is inserted into the rectum 8–10 cm beyond the anal spincter. It is known that the Tes probe includes the temperature of the saliva swallowed by the subject and changes with depth of the probe in the esophagus and Tre has a slower response time than Tes in the case of rapid storage of heat during intense thermal stress of a short duration. During this study, temperatures for each subject were observed by the two approaches every minute over 90 minutes of an experiment period. The researchers would like to have an overall index of agreement over the whole time period. They also want to have an index which can summarize the degree of agreement during different conditions. The experiment consists of using the two methods to measure core temperature when the subjects will enter a chamber set at 36 degree Celsius and 50humidity. The subjects will sit quietly for 10 minutes and then exercise on a motor-driven treadmill for 20 minutes. The experiment will end when the subject has undergone 3 cycles of 10-minute rest/20-minute exercise. To address the researcher’s need, we propose a measure of agreement for repeated-paired curve data. We name it concordance correlation coefficient since it is motivated by the concordance correlation coefficient proposed by Lin (1989) which is a measure of agreement at a single time point. When the observations are taken over different time points, the concordance correlation coefficient proposed by Lin (1989) cannot be used for the data set. The weighted concordance correlation coefficient for repeated measures may not be appropriate for this situation because an observation for each subject is very dense, more like a pair of curves over time rather than a multi-dimensional vector or a set of repeated measurements.

Since functional data arise frequently, there is strong need for a generalization of concordance correlation coefficient for such data. In this paper, we deal with this problem and propose an estimate for it. (Since Pearson correlation coefficient is such a frequently encountered coefficient, we also provide a generalization of Pearson correlation coefficient for functional data and propose an estimate for it.) The consistency and asymptotic normality of the proposed estimator are established. Based on the asymptotic normality, we provide a formula to compute the standard error of the resulting estimate. The small sample performance of the proposed standard error formula is investigated via Monte Carlo simulation, and we found that it is good for practical use. Statistical inferences on the concordance correlation coefficient are also discussed. A physiological data set is used to illustrate the proposed methodology.

This paper is organized as follows. In Section 2, we give the motivation and introduce a concordance correlation coefficient for curve data and image data. We then propose an estimator for the coefficient. The consistency and asymptotic normality of the proposed estimator are established. Section 3 contains simulation results and illustration of the proposed method by analyzing the physiology data set aforementioned. Conclusions are given in Section 4. Regularity conditions, technical lemmas and proof of Theorem 2.1 are given in the Appendix.

2 Concordance correlation coefficient for functional data

Let x and y denote scores from two raters or measurements from two instruments. Let us first consider that both x and y are univariate. Suppose that (x₁, y₁), ···, (x_n, y_n) are independent and identically distributed paired observations from (x, y). Denote x = (x₁, ···, x_n) and y = (y₁, ···, y_n). It is said that x and y are in perfect agreement if x_i = y_i for i = 1, ···, n. Therefore, if x and y are in perfect agreement, then the angle between x and y, denoted by θ(x, y), is 0, which implies that cosθ = 1. It is well known that

$$cos\theta =\frac{<\mathbf{x},\mathbf{y}>}{\parallel \mathbf{x}\parallel \parallel \mathbf{y}\parallel },$$

where <·, ·> denotes the inner product, and || · || is the Euclidean norm in Rⁿ. In other words, $<\mathbf{x},\mathbf{y}>={\sum }_{i=1}^n{x}_i{y}_i$, and $\parallel \mathbf{x}\mid {\mid }^2={\sum }_{i=1}^n{x}_i^2$ for any n-dimensional vectors x and y. However, cosθ is not a good measure for agreement because for any positive constant c,

$$cos\theta (c\mathbf{x},\mathbf{y})=cos\theta (\mathbf{x},c\mathbf{y})=cos\theta (\mathbf{x},\mathbf{y}).$$

This implies that cosθ cannot detect a scale change on either x or y.

The sample correlation coefficient between x and y can be written as

$$\rho (\mathbf{x},\mathbf{y})=\frac{<\mathbf{x}-\overline{x},\mathbf{y}-\overline{y}>}{\parallel \mathbf{x}-\overline{x}\parallel \parallel \mathbf{y}-\overline{y}\parallel },$$

where x̄ and ȳ are the sample means of x and y, respectively. If x and y are in perfect agreement, then ρ(x, y) = 1. However, it cannot detect a location shift on either x or y and a scale change on either x or y because for any constants a > 0 and b

$$\rho (a\mathbf{x}+b,\mathbf{y})=\rho (\mathbf{x},a\mathbf{y}+b)=\rho (\mathbf{x},\mathbf{y}).$$

The degree of concordance between x and y can be characterized by the expected value of the squared difference E(x − y)². Using this characterization, Lin (1989) proposed the concordance correlation coefficient

$${\rho }_c(x,y)=\frac{2cov(x,y)}{var(x)+var(y)+{\{E(x)-E(y)\}}^2}.$$ (2.1)

The concordance correlation coefficient strikes a balance between a correlation measure insensitive to location differences and a measure of location discrepancy. It can be further written as the product of the accuracy and the precision coefficients ρ_c = ρC_b. The accuracy coefficient C_b is a bias correction factor that measures how far the best-fit line deviates from the identity line. $C_b=\frac{2}{w+1/w+v^2}$, where $w=\sqrt{var(y)/var(x)}$ and $v^2={\{E(x)-E(y)\}}^2/\sqrt{var(x)var(y)}$. Note that 0 < C_b ≤1. The further C_b, is from 1, the greater the deviation from the identity line. The precision coefficient is the Pearson correlation coefficient ρ. It measures how far are the observations from the best-fit line. See Lin (1989) for more detailed discussion.

Evaluation of reproducibility for functional data is a frequently encountered practical problem. In this section, we propose a concordance correlation coefficient for functional data to address the problem. To get more insights into the concordance correlation coefficient and for ease of presentation, we first concentrate on the case when data are collected over an interval of a real line.

Suppose that X(t) and Y(t), t ∈ ℐ, a finite closed real interval, are measurements from two instruments. Regard X(·) and Y(·) as two random elements in some probability functional space . For the probability functional space , define an inner product

$$<X(·),Y(·)>=E{\int }_{\mathcal{I}}X(t)Y(t)w(t)dt,$$ (2.2)

where w(·) is a weight function and takes non-negative values over ℐ.

Using the notion of inner product, define the correlation coefficient for two random elements X and Y in 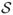as:

$$\rho (X,Y)=\frac{<X-E(X),Y-E(Y)>}{\parallel X-E(X)\parallel \parallel Y-E(Y)\parallel },$$ (2.3)

where $\parallel X\parallel =\sqrt{<X,X>}$, both E(X) = EX(t) and E(Y) = EY(t) are functions of t.

Define a concordance correlation coefficient for X(·) and Y(·) to be

$${\rho }_c(X,Y)=\frac{2<X-E(X),Y-E(Y)>}{\parallel E(X)-E(Y)\mid {\mid }^2+\parallel X-E(X)\mid {\mid }^2+\parallel Y-E(Y)\mid {\mid }^2}.$$ (2.4)

Both ρ and ρ_c depend on the weight function w(·). The weight function allows one to assign importance to different parts of t. The choice of the weight function will be discussed in Section 2.2. No matter what the weight function is, the concordance correlation coefficient possesses the following characteristics, same as those for ρ_c defined on two random variables (see Lin, 1989):

1. |ρ_c| ≤ |ρ| ≤ 1. Also, ρ_c and ρ have the same sign.

2. ρ_c = ρ if and only if ||E(X) − E(Y)|| = 0 and ||X − E(X)|| = ||Y−E(Y)||.

3. ρ_c = 0 if and only if ρ = 0.

4. ρ_c = ±1 if and only if ρ = ±1, ||X − E(X)|| = ||Y−E(Y)||, and ||E(X) − E(Y)|| = 0.

Using the Cauchy-Schwarz inequality and the definition of ρ_c, the proofs of these characteristics are straightforward and are omitted here.

2.1 Statistical inferences

In this section, we propose statistical inference procedures for ρ and ρ_c defined in (2.3) and (2.4). Without loss of generality, we assume that the interval ℐ = [0,1]. For ease of presentation, suppose that for subject i, i = 1, ···, n, (X_i(t), Y_i(t)) was observed at t = t_j, j = 1, ···, N with 0 ≤ t₁ < ··· < t_N ≤ 1 This implies that all subjects were observed at the same t_j, j = 1, ···, N. In practice, different subjects may be observed at different time t. In such a situation, one may use interpolation to compute the sample means in (2.5) and (2.6) defined below. Thus, the proposed estimation procedure is still applicable. See, for instance, Fan and Zhang (2000) for implementation with linear interpolation. When sampling rate is high, the bias caused by the approximation is small and asymptotically negligible.

Denote Δ_j = t_j+1 − t_j, the gap size between t_j+1 and t_j. Using the sample counterparts to estimate ρ and ρ_c, we have

$$\widehat{\rho }=\frac{\frac{1}{n}{\sum }_{i=1}^n{\sum }_{j=1}^N\{X_i(t_j)-\overline{X}(t_j)\}\{Y_i(t_j)-\overline{Y}(t_j)\}w(t_j){\mathrm{\Delta }}_j}{{\{\frac{1}{n}{\sum }_{i=1}^n{\sum }_{j=1}^N{(X_i(t_j)-\overline{X}(t_j))}^{2}w(t_j){\mathrm{\Delta }}_j\}}^{1/2}{\{\frac{1}{n}{\sum }_{i=1}^n{\sum }_{j=1}^N{(Y_i(t_j)-\overline{Y}(t_j))}^{2}w(t_j){\mathrm{\Delta }}_j\}}^{1/2}},$$ (2.5)

and

$${\widehat{\rho }}_c=\frac{\frac{2}{n}{\sum }_{i=1}^n{\sum }_{j=1}^N\{X_i(t_j)-\overline{X}(t_j)\}\{Y_i(t_j)-\overline{Y}(t_j)\}w(t_j){\mathrm{\Delta }}_j}{{\sum }_{j=1}^N{\{\overline{X}(t_j)-\overline{Y}(t_j)\}}^{2}w(t_j){\mathrm{\Delta }}_j+\frac{1}{n}{\sum }_{i=1}^n{\sum }_{j=1}^N[{\{X_i(t_j)-\overline{X}(t_j)\}}^2+\{Y_i(t_j)-\overline{Y}(t_j){\}}^2]w(t_j){\mathrm{\Delta }}_j},$$ (2.6)

where $\overline{X}(t_j)=n^{-1}{\sum }_{i=1}^n{X}_i(t_j)$ and $\overline{Y}(t_j)=n^{-1}{\sum }_{i=1}^n{Y}_i(t_j)$ are the sample means of X(t_j) and Y(t_j), respectively. We establish the asymptotic normality of the newly proposed estimator in the following theorem, whose proof is given in Appendix.

Theorem 2.1

Suppose, that {(X_i(t), Y_i(t)), t = t_j, j = 1, ···, N, i = 1, ···, n} is a random realization from {(X(t), Y(t))} at t = t_j, j = 1, ···, N. If Conditions (A)—(D) given in the Appendix hold, then ρ̂_c is a consistent estimator for ρ_c, and when |ρ_c| < 1, $\sqrt{n}({\widehat{\rho }}_c-{\rho }_c)$ has an asymptotic normal distribution with zero mean and variance ${\sigma }_{{\rho }_c}^2=a^T\mathrm{\sum }a$, where

$$a=\frac{{(2,-{\rho }_c,-{\rho }_c,2{\rho }_c)}^T}{E{\int }_{\mathcal{I}}{X}^2(t)w(t)dt+E{\int }_{\mathcal{I}}{Y}^2(t)w(t)dt-2E{\int }_{\mathcal{I}}X(t)Y(t)w(t)dt},$$ (2.7)

and

$$\mathrm{\sum }=\mathit{cov}\left\{\left(\begin{array}{c}{\int }_{\mathcal{I}}\{X(t)-EX(t)\}\{Y(t)-EY(t)\}w(t)dt\\ {\int }_{\mathcal{I}}{X}^2(t)w(t)dt\\ {\int }_{\mathcal{I}}{Y}^2(t)w(t)dt\\ {\int }_{\mathcal{I}}\{(X(t)-EX(t))EY(t)+Y(t)EX(t)\}w(t)dt\end{array}\right)\right\}.$$ (2.8)

To estimate the standard error of ρ̂_c, we estimate ${\sigma }_{{\rho }_c}^2$ by its sample counterparts:

$${\widehat{\sigma }}_{{\rho }_c}^2={\widehat{a}}^T\widehat{\mathrm{\sum }}\widehat{a},$$

where â and Σ^ are the corresponding sample counterparts. Thus, using Theorem 2.1, standard error formulae for ρ̂_c is

$$\text{SE}({\widehat{\rho }}_c)={\widehat{\sigma }}_{{\rho }_c}/\sqrt{n-3},$$ (2.9)

where we use the factor $1/\sqrt{n-3}$ rather than $1/\sqrt{n-2}$ for small sample correction in practice. The accuracy of these two standard error formulae for small to moderate sample sizes will be examined in Section 3, and we find that they perform well even for small sample sizes.

Since the range of ρ_c is [−1,1], one can improve upon the normal approximation by using Fisher’s Z-transformation. That is,

$${\widehat{Z}}_c=\frac{1}{2}ln\frac{1+{\widehat{\rho }}_c}{1-{\widehat{\rho }}_c}.$$

Using the δ-method, it can be shown that $\sqrt{n}({\widehat{Z}}_c-\frac{1}{2}ln\frac{1+{\rho }_c}{1-{\rho }_c})$ has asymptotic normal distributions with zero means and variance

$${\sigma }_{z_c}^2={\sigma }_{{\rho }_c}^2/{(1-{\rho }_c^2)}^2.$$

Thus,

$${\widehat{\sigma }}_{z_c}^2={\widehat{\sigma }}_{{\rho }_c}^2/{(1-{\widehat{\rho }}_c^2)}^2.$$

Furthermore, asymptotic 100(1 − α)% confidence intervals for Z_c = 2⁻¹ ln{(1 + ρ_c)/(1 − ρ_c)} is

$${\widehat{Z}}_c\pm t_{n-3}(1-\alpha /2){\widehat{\sigma }}_{z_c}/\sqrt{n-3}.$$ (2.10)

Using (2.10), we may construct asymmetric confidence intervals for ρ_c. The performance of the standard error formula will be examined in Section 3.

Remark

The consistence and asymptotic normality of ρ̂ can be derived in the same manner as those of ρ̂_c. Furthermore, standard error formula can be derived and confidence interval for ρ can be constructed in the same approach as those for ρ_c. See Li and Chow (2001) for details.

2.2 Choice of weight function

The definition of inner product (2.2) over the probability space 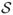involves a weight function. In this section, we briefly discuss how to determine the weight function for the proposed procedures.

The weight function allows us to assign importance to different time t. Therefore, when some prior information on the importance of different time intervals is available, one may determine the weight function accordingly. We call this kind of approach subjective approach because it is based on experience of data analysts or prior information.

In some pilot studies, there is no prior information, and hence a data-driven approach to choosing the weight function is desirable. We refer to this type of approach as objective approach. The points t₁, ···, t_N at which data were collected are regarded as realizations of a random variable. In other words, regard t as a random variable defined on ℐ. We choose the density function of t as the weight function. Thus, the inner product defined in (2.2) is indeed an expectation of XY, which is consistent with the definition of an inner product in a probability space. Thus, to estimate the weight function, we need to estimate the density of t based on the data t₁, ···, t_N. There are a large amount of literature on the topic of density estimation. See the reference book, for example, Silverman (1986) for details. Here we estimate the density function via a kernel estimator:

$$\widehat{w}(t)=\frac{1}{Nh}\sum _{j=1}^{N}K\{(t_j-t)/h\},$$

where K(·) is a kernel density function, such as the Gaussian density function, and h is a bandwidth to be chosen. A rule of thumb suggests taking h = 1.06s_tN^−1/5 for the Guassian kernel, where s_t is the sample standard deviation of t₁, ··· t_N.

In many case studies, such as the example in Section 3.2, the data were evenly collected over time. Without subjective information, the objective approach implies taking a uniform weight function. This will be implemented in Section 3.

2.3 Concordance correlation coefficient for image data

Suppose that X(t) and Y(t), t ∈ I, a closed rectangle of the plane R², are image data produced by two instruments. Let X(t) and Y(t) be two elements in a probability functional space 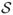, and define an inner product for 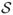as:

$$<X,Y>=E{\int }_{\mathbf{I}}X(\mathbf{t})Y(\mathbf{t})w(\mathbf{t})d\mathbf{t}.$$

Thus, we can define a correlation coefficient and a concordance correlation coefficient in the same manner as (2.3) and (2.4).

$$\rho (X,Y)=\frac{<X-E(X),Y-E(Y)>}{\parallel X-E(X)\parallel \parallel Y-E(Y)\parallel },$$ (2.11)

and

$${\rho }_c(X,Y)=\frac{2<X-E(X),Y-E(Y)>}{\parallel X-E(X)\mid {\mid }^2+\parallel Y-E(Y)\mid {\mid }^2+\parallel E(X)-E(Y)\mid {\mid }^2}.$$ (2.12)

The characteristics of ρ_c in Section 2 are still valid.

Here we focus on the estimation of ρ and ρ_c. Without loss of generality, it is assumed that the rectangle I = [0,1]². Suppose that X_i(t), Y_i(t) was observed at t_kl = (t_1k, t_2l), k = 1, ···, K and l = 1, ···, L with 0 ≤ t₁₁ < ··· < t_1K ≤ 1 and 0 < t₂₁ < ··· < t_2L ≤ 1. Define N = KL and Δ_kl = (t_1,k+1−t_1,k) (t_2,j+1−t_2,j. Using the sample counterparts to estimate ρ and ρ_c, we have

$$\widehat{\rho }=\frac{\frac{1}{n}{\sum }_{i,k,l}\{X_i({\mathbf{t}}_{kl})-\overline{X}({\mathbf{t}}_{kl})\}\{Y_i({\mathbf{t}}_{kl})-\overline{Y}({\mathbf{t}}_{kl})\}w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}}{{\{\frac{1}{n}{\sum }_{i,k,l}{(X_i({\mathbf{t}}_{kl})-\overline{X}({\mathbf{t}}_{kl}))}^{2}w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}\}}^{1/2}{\{\frac{1}{n}{\sum }_{i,k,l}{(Y_i({\mathbf{t}}_{kl})-\overline{Y}({\mathbf{t}}_{kl}))}^{2}w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}\}}^{1/2}},$$ (2.13)

and

$${\widehat{\rho }}_c=\frac{\frac{2}{n}{\sum }_{i,k,l}\{X_i({\mathbf{t}}_{kl})-\overline{X}({\mathbf{t}}_{kl})\}\{Y_i({\mathbf{t}}_{kl})-\overline{Y}({\mathbf{t}}_{kl})\}w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}}{\frac{1}{n}{\sum }_{i,k,l}\left[{\{X_i({\mathbf{t}}_{kl})-\overline{X}({\mathbf{t}}_{kl})\}}^2+{\{Y_i({\mathbf{t}}_{kl})-\overline{Y}({\mathbf{t}}_{kl})\}}^2\right]w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}+{\sum }_{k,l}{\{\overline{X}({\mathbf{t}}_{kl})-\overline{Y}({\mathbf{t}}_{kl})\}}^{2}w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}},$$ (2.14)

Similar to Theorem 2.1, ρ̂_c is consistent and has an asymptotic normal distribution.

Theorem 2.2

Suppose that {(X_i(t_kl), Y_i(t_kl))}, i = l, ···, n, k= 1, ···, K, l = 1, ··· L is a random sample from {X(t), Y(t)} at t_kl for k = 1, ···, K, l = 1, ···, L. If Conditions (A), (B), (C′) and (D′) given in the Appendix hold, then the ρ̂_c, defined in (2.14), is a consistent estimator for ρ_c, and $\sqrt{n}({\widehat{\rho }}_c-{\rho }_c)$ has an asymptotic normal distribution with zero mean and variance ${\sigma }_{{\rho }_c}^2=b^T{\mathrm{\sum }}_{2}b$, where

$$b=\frac{{(2,-{\rho }_c,-{\rho }_c,2{\rho }_c)}^T}{E{\int }_{\mathbf{I}}{X}^2(\mathbf{t})w(\mathbf{t})dt+E{\int }_{\mathbf{I}}{Y}^2(\mathbf{t})w(\mathbf{t})d\mathbf{t}-2E{\int }_{\mathbf{I}}X(\mathbf{t})Y(\mathbf{t})w(\mathbf{t})d\mathbf{t}},$$ (2.15)

and

$${\mathrm{\sum }}_2=\mathit{cov}\left\{\left(\begin{array}{c}{\int }_{\mathbf{I}}\{X(\mathbf{t})-EX(\mathbf{t})\}\{Y(\mathbf{t})-EY(\mathbf{t})\}w(\mathbf{t})d\mathbf{t}\\ {\int }_{\mathbf{I}}{X}^2(\mathbf{t})w(\mathbf{t})d\mathbf{t}\\ {\int }_{\mathbf{I}}{Y}^2(\mathbf{t})w(\mathbf{t})d\mathbf{t}\\ {\int }_{\mathbf{I}}\{(X(\mathbf{t})-EX(\mathbf{t}))EY(\mathbf{t})+Y(\mathbf{t})EX(\mathbf{t})\}w(\mathbf{t})d\mathbf{t}\end{array}\right)\right\}.$$ (2.16)

Proof

Using Lemma A.2 in the Appendix, Theorem 2.2 follows by similar arguments in the proof of Theorem 2.1.

As discussed in Section 2, we may apply the Fisher Z-transformation for ρ̂ and ρ̂_c to obtain a better normal approximation. Furthermore, one may construct an asymptotic confidence interval using the asymptotic properties in Theorem 2.1.

3 Simulation study and applications

In this section, we investigate the small sample performance of the proposed estimators and test the accuracy of proposed standard error formulae in (2.9) when the sample size is small. We also investigate the performance of the confidence interval in (2.10) in terms of coverage probability via Monte Carlo simulations. We then apply the proposed method to a real data set. In our simulations and analysis of the real data set, the weight function w(t) involved in the definition of ρ and ρ_c is taken to be 1.

3.1 Simulation study

To assess the performance of proposed estimators in (2.5) and (2.6) and their standard error formulae, a Monte Carlo simulation was conducted for four underlying K-dependent Gaussian processes (see Li and Chow (2001) for an algorithm to generate the simulated data) and four underlying K-dependent non-Gaussian processes (X(t), Y(t)) with mean (μ_x(t), μ_y(t)), variance $({\sigma }_x^2(t),{\sigma }_y^2(t))$ and covariance cov(X(t), Y(t)) = σ_xy(t). For the non-Gaussian processes, both X(t) and Y(t) are generated from a t-distribution with 10 degrees of freedom with a location shift and a scale change. For each of the K-dependent process, we take K = 20,40 and set the sample size n = 10, 20. We generate N = 50,100 sample points over a period of time [0,1]. Thus, for each case of 64(= 2×4×2×2×2) situations, we conduct 1000 Monte Carlo simulations using MATLAB.

Case 1

In this case, μ_x(t) = μ_y(t) = 0, ${\sigma }_x^2(t)={\sigma }_y^2(t)=1$ and σ_xy = 0.95. In this setting, ρ = ρ_c = 0.95 with no difference in location and scale parameters.

Case 2

Let ${\mu }_x(t)=-\sqrt{0.05t},{\mu }_y(t)=\sqrt{0.05t},{\sigma }_x^2={\sigma }_y^2(t)=1$ and σ_xy(t) = 0.95. In this case, both the pointwise correlation coefficient and the pointwise concordance correlation coefficient are close to 1. Moreover, ρ = 0.95 and ρ_c = 0.9048 with a slight location shift.

Case 3

Let ${\mu }_x(t)=-\sqrt{0.1}/2,{\mu }_y(t)=\sqrt{0.1}/2,{\sigma }_x^2(t)={1.1}^2,{\sigma }_y^2(t)={0.9}^2$, σ_xy(t) = 1.1 × 0.9 × {sin(2πt) + 1}/2. In this example, ρ = 0.5 and ρ_c = 0.4670 with slight constant differences in both locations and variance and a varying covariance function. Furthermore, both the pointwise correlation coefficient and the pointwise concordance correlation coefficient vary between 0 to 1.

Case 4

Let ${\mu }_x(t)=-\sqrt{0.05t},{\mu }_y(t)=\sqrt{0.05t},{\sigma }_x^2(t)={1.1}^2,{\sigma }_y^2(t)={0.9}^2$, and σ_xy = 1.1 × 0.9 × {sin(2πt) + 3}/4. In this case, the difference in location and covariance between X(t) and Y(t) are varying in t, but the difference in variance is a constant. In the example, we have ρ = 0.75 and ρ_c = 0.7005. The pointwise correlation coefficient and the pointwise concordance correlation coefficient vary between 0.5 and 1.

These four simulation settings were motivated by actual situations that arise in practice. Cases 1 and 2 correspond to highly correlated and highly agreed paired functional data and were motivated from the real example studied in Li and Chow (2001); and the means and variances in Cases 3 and 4 were taken the same as those of Cases 3 and 4 in Lin (1989). The pointwise correlation function in Cases 3 and 4 periodically changes over time, which was also motivated by the actual data example in Section 3.2. Table 1 summarizes the simulation results of the case in which the (X(t), Y(t)) is K-Guassian process with K = 20, N = 50 and n = 10. The simulation results for some other cases are similar. See Li and Chow (2001) for more simulation results.

Table 1.

Simulation Results

The column labeled “mean(std)” presents the mean and standard deviation of the 1000 estimates of the coefficients in the 1000 simulations. The column labeled “SE(std)” lists the mean and standard deviation of the 1000 estimates of standard errors defined in (2.9). CP stands for the coverage probability of the confidence interval in (2.10) at the significance level α = 0.05.

	mean(std)	SE(std)		mean(std)	SE(std)	CP
Case 1:	ρ = ρc = 0.95			Z = Zc = 1.832
ρ̂	.950(.017)	.016(.007)	Ẑ	1.853(.169)	.159(.042)	.954
ρ̂c	.943(.018)	.017(.007)	Ẑc	1.791(.162)	.157(.042)	.954
Case 2:	ρ = 0.95, ρc = 0.905			Z = 1.832, Zc = 1.498
ρ̂	.950(.017)	.016(.007)	Ẑ	1.853 (.169)	.159(.042)	.954
ρ̂c	.899(.030)	.029(.011)	Ẑc	1.491 (.158)	.155(.040)	.954
Case 3:	ρ = 0.5, ρc = 0.467			Z = 0.549, Zc = 0.506
ρ̂	.497(.139)	.125(.041)	Ẑ	.563 (.187)	.169(.043)	.935
ρ̂c	.442(.128)	.121(.036)	Ẑc	.486 (.161)	.153(.041)	.949
Case 4:	ρ = 0.75, ρc = 0.701			Z = 0.973, Zc = 0.868
ρ̂	.747(0.084)	.074(.031)	Ẑ	.993(.191)	.169(.044)	.939
ρ̂c	.678(0.091)	.082(.030)	Ẑc	.845(.172)	.154(.041)	.938

From Table 1, we can see that the averages of estimates of ρ̂, Ẑ, ρ̂_c and Ẑ_c are very close to the true values, although we notice that ρ̂_c slightly underestimate ρ_c. The average of estimated standard errors (SE) is very close to the standard deviation of 1000 estimates, which can be regarded as the true value of the standard deviation of ρ̂ and ρ̂_c. The difference between the average of the estimated standard errors and the true value is less than half standard deviation of the estimated standard errors. This implies that the standard error formulae proposed in (2.9) are fairly accurate even for small sample sizes. We also notice that the SE is always less than the true standard deviation. This may imply that the standard error formulae proposed in (2.9) slightly underestimate the true standard error. Note that the Monte Carlo standard error for the coverage probability is 0.0069. It can be seen from the last column of Table 1 that most of the coverage probabilities are very close to the true probability 0.95. This implies that the proposed confidence interval formula in (2.10) work well even for small sample sizes.

3.2 An Application

Example

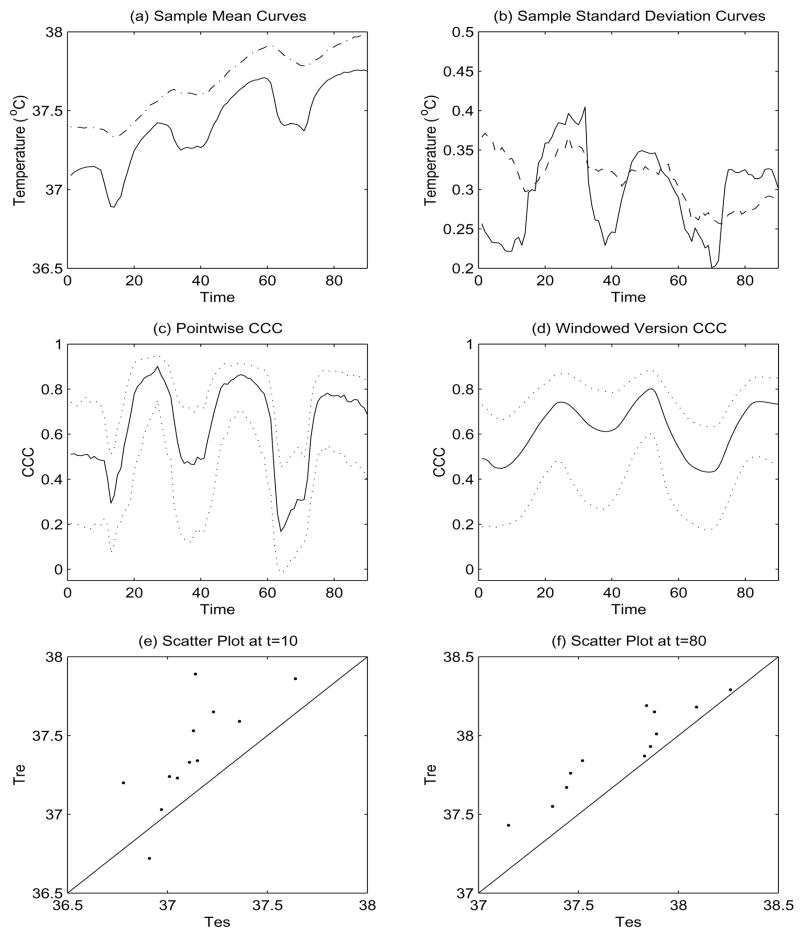
In this example, we illustrate the proposed method in Section 2 by application to an actual data set collected in the Noll Physiological Research center at the Pennsylvania State University. The researchers of study is interested in measuring body core temperature and to compare agreement of measurement by two different methods under the active heating condition. Data had been collected to compare the temperature recorded by the esophageal temperature (Tes) approach and the rectal temperature (Tre) approach. There are 12 subjects in this study. During this study, temperatures for each subject were observed by the two approaches every minute over one and half hour of an experiment period. The subjects will sit quietly for 10 minutes and then exercise on a motor-driven treadmill for 20 minutes. The subjects will alternate rest with exercise on a treadmill for 3 cycles in an environmental chamber. Figure 1(a), (b) display the sample mean and standard deviation curves of subjects under the active heating condition, from which we can see that the two means and standard deviation functions do not agree with each other well. The sample mean curves have tended to increase over time since the experiment was performed under the active heating condition. The effect of the three rest and exercise cycles was shown clearly in the sample mean curve. The pointwise concordance correlation coefficient, depicted in Figure 1(c), changes over time dramatically. That coincides with the researchers’ expectation since Tre has a slower response time than Tes during the heating condition. Furthermore, the time points where the concordances are high or low roughly correspond to the changing points in the sample mean curve. Again this is as expected since the response time to temperature change of the two instruments are different.

Figure 1.

Plots for Example 1. (a) and (b) are plots of the sample mean and standard deviation curves, respectively. The solid line stands for the Tes, and the dash-dotted line for the Tre. In (c) and (d), the solid line is plot of pointwise and windowed version concordance correlation coefficient, respectively, and dotted lines are the 2.5th and 97.5th percentiles of 1000 bootstrap estimates, respectively, (e) and (f) are scatter plots at t = 10 and 80, respectively.

We further computed the windowed version of concordance correlation coefficient at time t, using all datum points between t − h and and t + h. The idea is similar to that of moving average, and h is referred to as the window size. Figure 1(d) depicts a windowed version concordance correlation coefficient, using h = 9. Such a window size is decided such that we use about 20% datum points around time t to estimate concordance correlation coefficient at time t. We also computed the concordance correlation coefficient using about 10% and 30% datum points around t. The shape of concordance correlation coefficient is similar to that in Figure 1(d). We further construct a confidence interval for the windowed version concordance correlation coefficient using bootstrap method. Here we bootstrap 1000 subject-based samples rather than observations-based samples. The dotted lines are the 2.5th and 97.5th percentiles of the 1000 bootstrap estimates and provide us a 95% confidence interval. One may construct an asymptotic pointwise confidence interval for pointwise concordance correlation coefficient (see Lin, 1989), but the confidence interval depicted in Figure 1(c) is the bootstrap confidence interval due to the small sample size.

Figure 1(e) and (f) display the scatter plot at two typical time points: t = 10 and t = 80. To assess overall agreement of these two approaches, we compute ρ̂ and ρ̂_c and obtain that ρ̂ = 0.8637 with standard error 0.0574, and ρ̂_c = 0.6162 with standard error 0.1222. Although the correlation coefficient is pretty high, the low value of ρ̂_c implies the the measurements by the two approaches do not agree with each other. This is also evidenced by Figure 1(a), (b), (e) and (f). This example shows that ρ_c is more effective than ρ in detecting non-agreement of measurement.

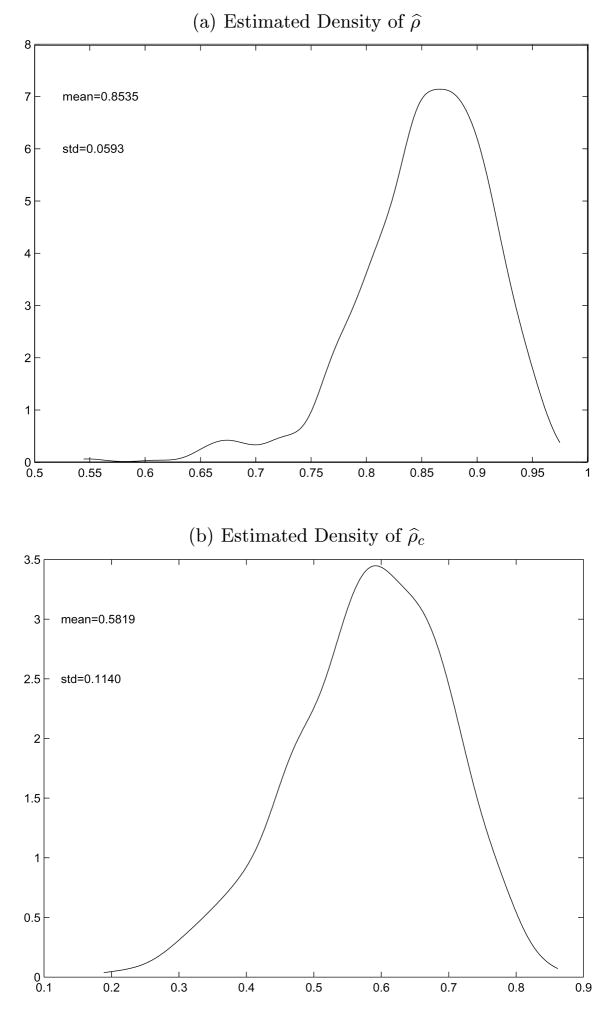
We now employ bootstrap samples to estimate the sampling distributions of ρ̂ and ρ̂_c. Figure 2 depicts the densities of ρ̂ and ρ̂_c using kernel density estimation with Guassian kernel and bandwidth chosen using the plug-in method proposed by Sheather and Jones (1991). The sample mean and standard deviation of the 1000 bootstrap estimate for ρ̂_c are 0.5819 and 0.1140, respectively. They approximately equal to the estimate and standard error of ρ_c. Result for ρ̂ is similar. Based on the 1000 bootstrap estimates, a 95% confidence interval for ρ̂_c and ρ̂ is [0.3261,0.7803] and [0.7011,0.9481], respectively. Since the sampling distributions for ρ̂_c and ρ̂ are skew, the sample means are not the center of the confidence intervals.

Figure 2.

Plot of Estimated Densities of ρ̂ and ρ̂_c Based on 1000 Bootstrap Estimates.

4 Conclusions

In this paper, we proposed a concordance correlation coefficient for curve data and image data. Its characteristics have been investigated. We proposed an estimator for the concordance correlation coefficient and established the asymptotic normality of the proposed estimator. A standard error formula for the resulting estimate is derived and empirically tested. An application to an actual data set illustrates the proposed methodology.

Appendix

We first present the regularity conditions for Theorem 2.1.

Definition A.1

Let 0 = t₀ < ··· < t_l = 1 be any partition 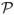of [0,1], and f(t) be a real function defined on [0,1]. If the variation

$$V_{\mathcal{P}}=\sum _{l=1}^l\mid f(t_{j+1})-f(t_j)\mid$$

has an upper bound which is independent of the choice of 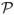, then f is called a function of bounded variation. The least upper bound of V 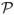is called the total variation of f and is denoted by V(f).

For a function of bounded variation, it has been shown that

$$\mid {\int }_0^{1}f(t)dt-\sum _{j=1}^{N}f(t_j){\mathrm{\Delta }}_j\mid \le V(f)\underset{0\le j\le N-1}{max}\mid t_{j+1}-t_j\mid .$$ (A.1)

See, for example, Theorem 5.3 of Hua and Wang (1981).

The equation (A.1) tells us how to impose assumptions on V(f) and max_{0≤j≤N−1} |t_j+1 − t_j| in a natural way. Let 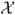and 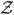denote the space consisting of paths X(·) and Y(·). Further, define

$$\begin{array}{l}{\mathcal{Z}}_1=\{X(·)Y(·):X\in \mathcal{X}\text{and}Y\in \mathcal{Y}\},\\ {\mathcal{Z}}_2=\{X^2(·):X\in \mathcal{X}\},\\ {\mathcal{Z}}_3=\{Y^2(·):Y\in \mathcal{Y}\}.\end{array}$$

Conditions

1. For ℱ = 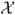, , 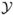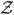_i, i = 1, 2 and 3,

   $$\underset{f\in \mathcal{F}}{sup}V(f)<\infty \text{a}.\text{s}.$$ (A.2)

2. The weight function w(t) is a function of bounded variation.

3. There exists a constant Δ such that

   $$\underset{0\le j\le N-1}{max}\mid t_{j+1}-t_j\mid \le \frac{\mathrm{\Delta }}{N}$$

   and $\sqrt{n}/N\to 0$ as n → ∞.

4. $$\begin{array}{l}E{[{\int }_{\mathcal{I}}{X}^2(t)w(t)dt]}^2<\infty ,\\ E{[{\int }_{\mathcal{I}}{Y}^2(t)w(t)dt]}^2<\infty ,\\ E{[{\int }_{\mathcal{I}}X(t)Y(t)w(t)dt]}^2<\infty .\end{array}$$

To prove Theorem 2.1, we need the following lemma.

Lemma A.1

Under the conditions of Theorem 2.1, we. have

$$\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^N{X}_i(t_j)Y_i(t_j)w(t_j){\mathrm{\Delta }}_j=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathcal{I}}{X}_i(t)Y_i(t)w(t)dt+O_P(\frac{1}{N}).$$ (A.3)

$$\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^N{X}_i^2(t_j)w(t_j){\mathrm{\Delta }}_j=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathcal{I}}{X}_i^2(t)w(t)dt+O_P(\frac{1}{N}),$$ (A.4)

$$\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^N{Y}_i^2(t_j)w(t_j){\mathrm{\Delta }}_j=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathcal{I}}{Y}_i^2(t)w(t)dt+O_P(\frac{1}{N}),$$ (A.5)

$$\sum _{j=1}^N{\overline{X}}^2(t_j)w(t_j){\mathrm{\Delta }}_j={\int }_{\mathcal{I}}{\overline{X}}^2(t)w(t)dt+O_P(\frac{1}{N}),$$ (A.6)

$$\sum _{j=1}^N{\overline{Y}}^2(t_j)w(t_j){\mathrm{\Delta }}_j={\int }_{\mathcal{I}}{\overline{Y}}^2(t)w(t)dt+O_P(\frac{1}{N}),$$ (A.7)

$$\sum _{j=1}^N\overline{X}(t_j)\overline{Y}(t_j)w(t_j){\mathrm{\Delta }}_j={\int }_{\mathcal{I}}\overline{X}(t)\overline{Y}(t)w(t)dt+O_P(\frac{1}{N}).$$ (A.8)

Proof

Denote

$$\mathcal{G}=\{X(·)Y(·)w(·):X\in \mathcal{X},Y\in \mathcal{Y}\}.$$

Since w(t) is a function of bounded variation, using (A.2), it can be shown that

$$\underset{f\in \mathcal{G}}{sup}V(f)<\infty ,\text{a}.\text{s}.$$

Thus, by Condition (C), it follows that

$$\begin{array}{l}\mid \frac{1}{n}\sum _{i=1}^n\sum _{j=1}^N{X}_i(t_j)Y_i(t_j)w(t_j){\mathrm{\Delta }}_j-\frac{1}{n}\sum _{i=1}^n{\int }_{\mathcal{I}}{X}_i(t)Y_i(t)w(t)dt\mid \\ \le \frac{1}{n}\sum _{i=1}^n\mid \sum _{j=1}^N{X}_i(t_j)Y_i(t_j)w(t_j){\mathrm{\Delta }}_j-{\int }_{\mathcal{I}}{X}_i(t)Y_i(t)w(t)dt\mid \\ \le \frac{1}{n}\sum _{i=1}^{n}V(X_i{Y}_{i}w)\underset{0\le j\le N-1}{max}\mid t_{j+1}-t_j\mid \\ \le \underset{f\in \mathcal{G}}{sup}V(f)\frac{\mathrm{\Delta }}{N}.\end{array}$$

So (A.3) follows. Along the same lines as the proof of (A.3), it can be shown that (A.4) to (A.8) hold. This completes the proof of Lemma A.1.

Proof of Theorem 2.1

Denote

$$A_n=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^N\{X_i(t_j)-\overline{X}(t_j)\}\{Y_i(t_j)-\overline{Y}(t_j)\}w(t_j){\mathrm{\Delta }}_j.$$

Using Lemma A.1 in the Appendix, it follows that

$$\begin{array}{l}{A}_n=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathcal{I}}{X}_i(t)Y_i(t)w(t)dt-{\int }_{\mathcal{I}}\overline{X}(t)\overline{Y}(t)w(t)dt+O_P(\frac{1}{N})\\ =\frac{1}{n}\sum _{i=1}^n{\int }_{\mathcal{I}}\{X_i(t)-EX(t)\}\{Y_i(t)-EY(t)\}w(t)dt\\ -{\int }_{\mathcal{I}}\{\overline{X}(t)-EX(t)\}\{\overline{Y}(t)-EY(t)\}w(t)dt+O_P(\frac{1}{N}).\end{array}$$

Since

$$E{\int }_{\mathcal{I}}\{\overline{X}(t)-EX(t)\}\{\overline{Y}(t)-EY(t)\}w(t)dt=O_P(\frac{1}{n}),$$

and

$$var\{{\int }_{\mathcal{I}}\{\overline{X}(t)-EX(t)\}\{\overline{Y}(t)-EY(t)\}w(t)dt\}=O_P(\frac{1}{n^2}),$$

we have

$$A_n=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathcal{I}}\{X_i(t)-EX(t)\}\{Y_i(t)-EY(t)\}w(t)dt+O_P(\frac{1}{n})+O_P(\frac{1}{N})$$ (A.9)

which tends to E ∫_ℐ{X(t) − EX(t)}{Y(t) − EY(t)}w(t) dt in probability by the weak law of large numbers and N → ∞. Similarly, we can show that all other terms involved in ρ̂_c are convergent in probability, and therefore ρ̂_c is consistent.

To establish the asymptotic normality of ρ̂_c, we rewrite ρ̂_c as

$${\widehat{\rho }}_c=\frac{\frac{2}{n}{\sum }_{i=1}^n{\sum }_{j=1}^N\{X_t(t_j)-\overline{X}(t_j)\}\{Y_i(t_j)-\overline{Y}(t_j)\}w(t_j){\mathrm{\Delta }}_j}{\frac{1}{n}{\sum }_{i=1}^n{\sum }_{j=1}^N{X}_i^2(t_j)w(t_j){\mathrm{\Delta }}_j+\frac{1}{n}{\sum }_{i=1}^n{\sum }_{j=1}^N{Y}_i^2(t_j)w(t_j){\mathrm{\Delta }}_j-2{\sum }_{j=1}^N\overline{X}(t_j)\overline{Y}(t_j)w(t_j){\mathrm{\Delta }}_j}.$$

Denote

$$\begin{array}{l}{B}_n=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^N{X}_i^2(t_j)w(t_j){\mathrm{\Delta }}_j,\\ C_n=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^N{Y}_i^2(t_j)w(t_j){\mathrm{\Delta }}_j,\end{array}$$

and

$$D_n=\sum _{j=1}^N\overline{X}(t_j)\overline{Y}(t_j)w(t_j){\mathrm{\Delta }}_j.$$

By straightforward calculation, we have

$$\begin{array}{l}{B}_n=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathcal{I}}{X}_i^2(t)w(t)dt+O_P(\frac{1}{N}),\\ C_n=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathcal{I}}{Y}_i^2(t)w(t)dt+O_P(\frac{1}{N}).\end{array}$$

Next we deal with D_n. It is not difficult to show that

$$D_n={\int }_{\mathcal{I}}\overline{X}(t)\overline{Y}(t)w(t)dt+O_P(\frac{1}{N})$$

which equals

$${\int }_{\mathcal{I}}\{\overline{X}(t)-EX(t)\}\{\overline{Y}(t)-EY(t)\}w(t)dt+{\int }_{\mathcal{I}}\{(\overline{X}(t)-EX(t))EY(t)+EX(t)\overline{Y}(t)\}w(t)dt+O_P(\frac{1}{N}).$$

This is equal to

$$D_n=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathcal{I}}\{(X_i(t)-EX(t))EY(t)+EX(t)Y_i(t)\}w(t)dt+O_P(\frac{1}{n})+O_P(\frac{1}{N})$$

Define V_n = (A_n, B_n, C_n, D_n)^T and

$$V=\left(\begin{array}{c}E{\int }_{\mathcal{I}}\{X(t)-EX(t)\}\{Y(t)-EY(t)\}w(t)dt\\ E{\int }_{\mathcal{I}}{X}^2(t)w(t)dt\\ E{\int }_{\mathcal{I}}{Y}^2(t)w(t)dt\\ {\int }_{\mathcal{I}}EY(t)EX(t)\}w(t)dt\end{array}\right).$$

By Condition (C), the multivariate central limit theorem and the Slutsky theorem, $\sqrt{n}(V_n-V)$ has an asymptotic normal distribution with mean zero and variance Σ given by (2.8).

Define h(v₁, v₂, v₃, v₄) = 2v₁/(v₂ + v₃ − 2v₄). Thus, ρ̂_c = h(A_n, B_n, C_n, D_n). Using the delta method, $\sqrt{n}({\widehat{\rho }}_c-{\rho }_c)$ has an asymptotic normal distribution with mean zero and variance a^TΣa, where a and Σ are defined in (2.7) and (2.8), respectively. This completes the proof.

Let us present the regularity conditions for Theorem 2.2.

Definition A.3

Let 0 = t₁₀ < ···< t_1m1 = 1 and 0 = t₂₀ < ··· <t_2m2 = 1 be any partition 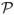of [0,1]², and f(t₁, t₂) be a real function defined on [0,1]². Define

$$\begin{array}{l}{\mathrm{\Delta }}_{10}f(t_{1i},t_2)=f(t_{1(i+1)},t_2)-f(t_{1i},t_2),\\ {\mathrm{\Delta }}_{01}f(t_1,t_{2j})=f(t_1,t_{2(j+1)})-f(t_1,t_{2j}),\\ {\mathrm{\Delta }}_{11}f(t_{1i},t_{2j})=f(t_{1i},t_{2j})-f(t_{1(i+1)},t_{2j})-f(t_{1i},t_{2(j+1)})+f(t_{1(i+1)},t_{2(j+1)}).\end{array}$$

If the variation

$$V_{\mathcal{P}}=\sum _{i=1}^{m_1-1}\sum _{j=0}^{m_2-1}\mid {\mathrm{\Delta }}_{11}f(t_{1i},t_{2j})\mid +\sum _{i=0}^{m_1-1}\mid {\mathrm{\Delta }}_{10}f(t_{1i},1)\mid +\sum _{j=0}^{m_2-1}\mid {\mathrm{\Delta }}_{01}f(1,t_{2j})\mid$$

has an upper bound which is independent of the choice 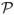, then f is called a function of bounded variation (see, for example, Hua and Wang, 1981). The least upper bound of V 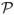is called the total variation of f and is denoted by V(f).

Condition

(C′) There exists Δ₁ and Δ₂ such that

$$\underset{0\le k\le K}{max}\mid t_{1(k+1)}-t_{1k}\mid \le \frac{{\mathrm{\Delta }}_1}{K},$$

and

$$\underset{0\le l\le L}{max}\mid t_{2(l+1)}-t_{2l}\mid \le \frac{{\mathrm{\Delta }}_2}{L}.$$

Further, $\sqrt{n}/N\to 0$ as n → ∞, where N = KL.

(D′)

$$\begin{array}{l}E{[{\int }_{\mathbf{I}}{X}^2(\mathbf{t})w(\mathbf{t})d\mathbf{t}]}^2<\infty ,\\ E{[{\int }_{\mathbf{I}}{Y}^2(\mathbf{t})w(\mathbf{t})d\mathbf{t}]}^2<\infty ,\\ E{[{\int }_{\mathbf{I}}X(\mathbf{t})Y(\mathbf{t})w(\mathbf{t})dt]}^2<\infty .\end{array}$$

Lemma A.2

Under the conditions of Theorem 4.1, we. have

$$\frac{1}{n}\sum _{i,k,l}{X}_i({\mathbf{t}}_{kl})Y_i({\mathbf{t}}_{kl})w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathbf{I}}{X}_i(\mathbf{t})Y_i(\mathbf{t})w(\mathbf{t})dt+O_P(\frac{1}{N}).$$ (A.10)

$$\frac{1}{n}\sum _{i,k,l}{X}_i^2({\mathbf{t}}_{kl})w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathbf{I}}{X}_i^2(\mathbf{t})w(\mathbf{t})dt+O_P(\frac{1}{N}),$$ (A.11)

$$\frac{1}{n}\sum _{i,k,l}{Y}_i^2({\mathbf{t}}_{kl})w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}=\frac{1}{n}\sum _{i=1}^n{\int }_{\mathbf{I}}{Y}_i^2(\mathbf{t})w(\mathbf{t})dt+O_P(\frac{1}{N}),$$ (A.12)

$$\sum _{k,l}{\overline{X}}^2({\mathbf{t}}_{kl})w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}={\int }_{\mathbf{I}}{\overline{X}}^2(\mathbf{t})w(\mathbf{t})dt+O_P(\frac{1}{N}),$$ (A.13)

$$\sum _{k,l}{\overline{Y}}^2({\mathbf{t}}_{kl})w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}={\int }_{\mathbf{I}}{\overline{Y}}^2(\mathbf{t})w(\mathbf{t})d\mathbf{t}+O_P(\frac{1}{N}),$$ (A.14)

$$\sum _{k,l}\overline{X}({\mathbf{t}}_{kl})\overline{Y}({\mathbf{t}}_{kl})w({\mathbf{t}}_{kl}){\mathrm{\Delta }}_{kl}={\int }_{\mathbf{I}}\overline{X}(\mathbf{t})\overline{Y}(\mathbf{t})w(\mathbf{t})d\mathbf{t}+O_P(\frac{1}{N}).$$ (A.15)

Proof

The proof is similar to that of Lemma A.1. We omit it here. A rigorous proof is given in Li and Chow (2001).