Abstract
Internal and external fluctuations are ubiquitous in cellular signaling processes. Because biochemical reactions often evolve on disparate time scales, mathematical perturbation techniques can be invoked to reduce the complexity of stochastic models. Previous work in this area has focused on direct treatment of the master equation. However, eliminating fast variables in the chemical Langevin equation is also an important problem. We show how to solve this problem by utilizing a partial equilibrium assumption. Our technique is applied to a simple birth-death-dimerization process and a more involved gene regulation network, demonstrating great computational efficiency. Excellent agreement is found with results computed from exact stochastic simulations. We compare our approach with existing reduction schemes and discuss avenues for future improvement.
INTRODUCTION
With the decoding of the genomes and proteomes of various organisms, a key focus of cell biology has shifted to uncovering the organization and functioning principles of regulatory and signaling networks. Recent high throughput approaches have accelerated this transition not only by identifying biomolecular species involved in various cellular processes but also by revealing and quantifying the complex interactions between genes, proteins, and metabolites that compose these systems.1, 2 The analysis and interpretation of these data pose a great challenge to theoreticians working in the area of systems biology. Novel analysis and simulation techniques based on physical and chemical principles are needed to uncover the design principles of signaling and regulatory networks. At the mesoscopic level, many different techniques are used to characterize the activity of these systems, including inference networks, Boolean maps, differential equations, and stochastic models, the latter playing a special role.3, 4, 5, 6, 7, 8, 9, 10
Cells live in noisy environments and are subject to constant internal and external fluctuations. To maintain normal function in the face of these changing conditions, regulatory networks must possess a certain level of robustness while retaining enough sensitivity to pick up useful signals from the noisy background.11, 12, 13, 14, 15 When molecular species are present in low abundances, fluctuations in molecule number can generate large variability in the cell’s response to an external or internal signal.16, 17, 18 Such intrinsic fluctuations have been suggested to play important roles in evolution and embryonic development.19, 20 Thus, describing and evaluating the effects of molecular level noise are important problems in cell modeling.
The chemical master equation describes how the probabilities for the number of molecules of each chemical species evolve in time.21, 22 In the limit of large particle numbers, the law of mass action for chemical kinetics is recovered from the master equation as a set of ordinary differential equations (ODEs).23, 24 At intermediate particle numbers, the chemical Langevin equations or the equivalent Fokker–Planck equation can be derived under quite general assumptions.21, 23 The analysis of these equations provides an important approach for characterizing noisy cellular behavior.6, 25, 26
Only in a few special cases21, 27 can stochastic models be solved analytically. Therefore, numerical simulations have been the approach used to analyze and quantitatively explain many biochemical processes.3, 21 The large size of the interaction networks determined by new experimental approaches and the vastly different time scales associated with the biochemical processes that make up the network often necessitate large amounts of computer time and memory. Thus, in many modeling studies the computational load turns out to be the bottleneck for fruitful analysis. Consequently, model reduction and simplification techniques are a necessity.
In physics and chemistry, many techniques have been developed to treat small amplitude fluctuations or noise with short correlation times.21, 27, 28 More recently, considerable effort has been devoted to accelerating stochastic simulations.5, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 38 In this paper, we report on a new reduction technique for the chemical Langevin equation, which is widely used in modeling the stochastic behavior of biochemical processes and has been studied extensively in previous work. The chemical Langevin equations consist of a deterministic part plus associated noise terms. Its derivation is based on the assumption that the fluctuations occur on a much faster time scale than the deterministic motion. Hence, in the chemical Langevin equation, the noise is taken to be white because its correlation time is assumed to be negligible relative to the deterministic time scale.21, 23 Nevertheless, when time scale separations exist in the fluctuations, it may be necessary to distinguish noise from different sources to achieve model reduction.
When using ODEs derived from the law of mass action,2, 21, 22, 39, 40 singular perturbation techniques that take advantage of separation of time scales can be used to eliminate fast variables that are entrained to the slow variables. This type of reduction is not directly applicable to Langevin equations because the noise terms always represent fast motions and cannot be formally separated into groups with different time scales. Here we propose a practical approach to achieve the desired simplification that is based on physical considerations of chemical reactions. For intrinsic fluctuations in chemical reactions, not only the deterministic motion but also the fluctuations evolve on separate time scales: fast motions are associated with fast intrinsic noise and slow motions with slow intrinsic noise. The chemical Langevin equation masks this distinction. Partial equilibrium assumptions in the context of the master equation have been widely used to reduce multiscale systems.30, 31, 35, 36, 38, 41 Similarly, in order to take advantage of separations in time scale within the Langevin formalism, we first determine the slow degrees of freedom and assume that the fast variables reach a quasisteady state, where an adiabatic steady probability distribution exists and parametrically evolves with the slow variables. Chemical Langevin equations are written for the slow variables in which only averages of fast variables appear and the noise term comes purely from the slow motion. This reduction ensures that we only need to simulate the slow reactions, achieving high computational efficiency. Total fluctuations, which include the fast noise, may be computed at any desired time instant from the adiabatic steady state distribution.
In Sec. 2, we use a simple birth-death-dimerization process to illustrate our technique. The slow variables are constructed and the associated chemical Langevin equation is derived. Through solution of the steady state dimerization reaction, the adiabatic probability distribution for the fast variable is derived containing the slow variable as a parameter. In Sec. 3, we compare the results from our reduction with exact Gillespie simulations. Next, a related gene regulation model is introduced in which the dimers act as transcriptional activators for the protein and thus change the production rate of the monomers. After a small modification in the reduction scheme to account for the discrete states of the promoter, our model shows excellent agreement with the benchmark computations. In Sec. 4, separation of time scale and model reduction problems are discussed, and our scheme is compared with existing methods. In Sec. 5, we summarize our work and point to possible future directions.
FORMULATING THE PROBLEM THROUGH A SIMPLE DIMERIZATION PROCESS
Consider the following simple dimerization process to be used later as part of a gene regulatory network,
| (1) |
The monomers M are produced at a rate g by a Poisson process. The monomers dimerize into D with a rate μ. At the same time, M and D decay back to their original reactants with rates k and λ, respectively. In the limit of large molecular abundances, the deterministic evolution of the molecule numbers evolves according to the following chemical kinetic equations:
| (2) |
where n denotes the number of D and m the number of M. It turns out that the deterministic dynamics given by Eq. 2 can be simplified by projecting the dynamics onto a slow manifold42, 43, 44, 45, 46 which is a smooth hypersurface of lower dimension than the original phase space. However, for stochastic dynamics dictated by the corresponding chemical Langevin equations the reduction is not obvious due to the mixing of deterministic and stochastic time scales, and therefore must be done very carefully. Below, we elaborate on such a reduction technique.
To eliminate the fast variable, it is necessary to define the variables that correspond to the slow manifold. The total particle number N=m+2n is a good slow variable31 and satisfies a simpler equation,
| (3) |
However, Eq. 3 is not closed because it contains m, the monomeric protein number. To close this equation, we need to find an algebraic relation between m and N. If μ,λ⪢g,k, an adiabatic assumption may be made that the dimerization reactions always reach a quasisteady state (i.e., dn∕dt=0 in the lowest order approximation). Under this assumption, we have the identity
| (4) |
which defines the slow manifold in the phase space of Eq. 2 and also gives a relation between the time evolution of m and N,
| (5) |
Substituting Eq. 3 into Eq. 5 results in a closed equation for m. Thus, we have successfully eliminated the fast variable by utilizing the slow manifold represented by Eq. 4.
Can the same elimination techniques be applied in the presence of noise? Caution must be exercised because the approximation given by Eq. 4 is only valid near the slow manifold which is determined by the deterministic part of the equation. Noise coming from the fast dimerization reactions can potentially drive the solution away from the manifold, which makes Eq. 4 and thus Eq. 5 inapplicable. With noise, we have to use a probabilistic description. When all species are present in large quantities, the chemical Langevin equations23 accurately generate individual realizations of the reaction trajectories. In the limit of fast dimerization, the distribution for the monomers M can be assumed to be in steady state for each value of the slowly evolving N. Although the monomer number m itself fluctuates rapidly, , the average conditioned on N, remains close to the slow manifold, i.e., Eqs. 4, 5 are still satisfied with high accuracy if m is replaced by . On the other hand, the slow birth-death reaction effectively only sees the average , which leads to the chemical Langevin equation
| (6) |
where Γi(t), i=1,2, are Gaussian white noise terms with ⟨Γi⟩=0, ⟨Γi(t)Γj(t′)⟩=δij(t−t′). Although the noise in Eq. 6 seems to have zero time correlation, we have to keep in mind that it is a mathematical abstraction of the stochasticity intrinsic to the chemical reactions and it is “slow” compared with fluctuations from the dimerization process. Substituting Eq. 5 into Eq. 6 results in
| (7) |
which gives the time evolution of the conditional average and includes the slow noise generated in the birth-death process. To produce the full stochastic trajectory, we have to include the “fast” noise generated in the dimerization process which we assume is in steady state.
We concentrate on the dimerization reaction for fixed N to study the effects of the fast noise. To obtain an analytic expression for the steady state probability distribution we use a generating function formalism, which has been widely used in describing random process in physics and chemistry.21, 47, 48 The generating function Ψ(x)=∑mP(m)xm, where P(m) denotes the probability of having m monomer M, satisfies
| (8) |
which has the steady state solution
| (9) |
where C is a normalization constant to ensure Ψ(1)=1 and HeN is an Nth order Hermite polynomial:
| (10) |
where [N∕2] denotes the greatest integer not bigger than N∕2. Thus, explicitly, for even N,
| (11) |
which gives the steady probability distribution
| (12) |
Using the Sterling approximation
and taking the logarithm of Eq. 12, we have
| (13) |
In the limit of large particle numbers, we may use a Gaussian approximation for the probability distribution and, thus, we calculate the first and second derivatives of Eq. 13,
| (14) |
| (15) |
The condition d ln P(N−2n)∕dn=0 then gives an equation for the average,
| (16) |
to leading order. If we write m=N−2n, then Eq. 16 is almost equivalent to Eq. 4. Therefore, the average of the stationary distribution is well approximated by the deterministic result for , which stays close to the slow manifold. If we define , then we get a Gaussian approximation of the probability distribution
| (17) |
which describes the fast noise distribution conditional on N.
Consequently, the random variable m is well approximated by
| (18) |
where ξN is a random variable with the distribution given by Eq. 17. In this way, we achieve the desired reduction. To get the stochastic trajectory of m(t), we first solve the slow Langevin equation 7 to get and hence N(t) by Eq. 4. Next, this N(t) is used to generate a random number ξN according to the probability distribution equation 17 and m(t) is obtained through Eq. 18. In practice, computational resources can be directed to evolve the slow variable, considering the full stochasticity of m(t) only when necessary.
NUMERICAL IMPLEMENTATION AND COMPARISON WITH THE GILLESPIE ALGORITHM
In this section, we examine the validity of our technique using two examples. First, we compare the simulation results from Eqs. 7, 18 with exact discrete stochastic simulations. Next a gene regulatory network is introduced and a similar reduction is carried out. This example requires a modification to the reduction method to accommodate the discrete dynamics of the gene promoter. Numerical solutions of the simplified model are also compared with discrete stochastic simulations. The Gillespie algorithm3 is used to produce exact results for both systems. A second-order forward integration scheme49, 50, 51, 52, 53 is invoked to evolve the chemical Langevin equations. In both simulations we used 4×104 trajectories to compute the averages. The probability distribution functions (PDFs) at particular times and time series for the average and variance of the monomer number are plotted. As above, we use to denote the conditional average of m for fixed N and introduce the angular bracket notation ⟨⋅⟩ to denote the overall average of a variable.
The birth-death-dimerization problem
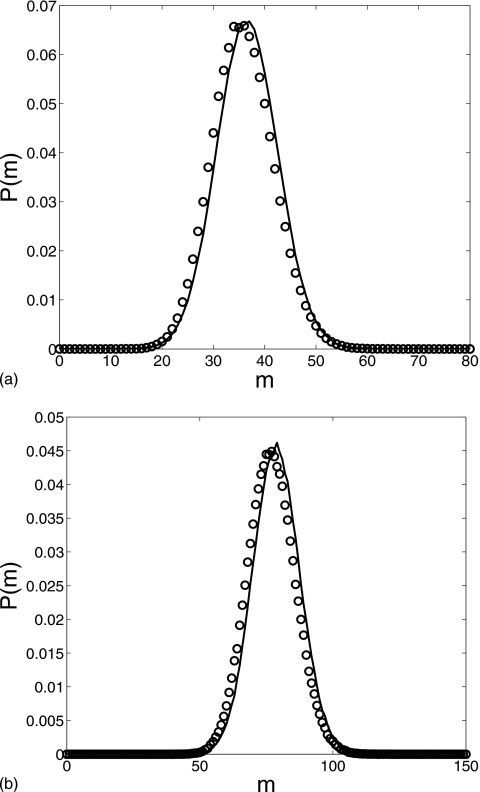
To satisfy the fast dimerization condition, we choose g=0.2, k=0.001, μ=0.002, and λ=30. The initial condition is (m,n)=(0,0). Figure 1 shows a comparison of the distributions for M at t=200 and t=500 obtained from our reduced Langevin approximation (solid line) and Gillespie simulations (circles), indicating excellent agreement. The reduced equation captures the characteristic features of the distribution. Although the figure only shows the distribution at two specific snapshots, the distributions are in good agreement throughout the time evolution.
Figure 1.
Comparison of the m distribution for the two-step cascade at times (a) t=200 and (b) t=500: Gillespie simulation (circles) and reduced Langevin approximation (solid line). g=0.2, k=0.001, μ=0.002, and λ=30 with the initial condition (m,n)=(0,0).
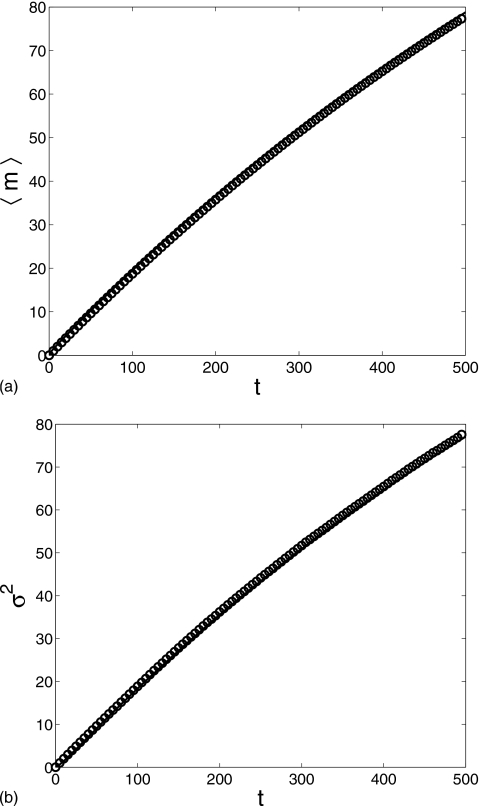
Figure 2 displays the average and the variance of protein number m in the time interval [0,500]. The reduced equation produced a result in perfect agreement with the Gillespie result. Both the average and the variance grow monotonically with time. One interesting observation is that the average is approximately equal to the variance, which is a characteristic feature of the Poisson process and can be explained by Eq. 7. With the current parameter values, the first factor on the right hand side of Eq. 7 is very close to 1 since . Thus, to a very good approximation, the conditional average satisfies a usual birth-death equation which describes a Poisson process. The dimerization in Eq. 1 rarely happens in the interval t=[0,500] since ⟨n⟩≈0.2 when ⟨m⟩≈80 at t=500.
Figure 2.
Comparison of the m average and variance computed for the two-step cascade in the time interval t=[0,500]: Gillespie simulation (circle) and reduced Langevin approximation (solid line). g=0.2, k=0.001, μ=0.002, and λ=30 with the initial condition (m,n)=(0,0).
Positive autoregulation
We now turn to a more complex system involving a genetic switch.17, 54, 55, 56, 57, 58, 59, 60, 61 In addition to the birth-death-dimerization process, the switch involves a positive feedback loop in which the dimer form of the protein acts a transcriptional activator by binding to the promoter region of the gene. As the time scales become even more entangled60, 62 in this model, we test the validity of the reduction scheme in this new context.
The reactions for this system are as follows:63
| (19) |
| (20) |
| (21) |
| (22) |
The above equations describe a simplified version of an autoregulated gene. The promoter is denoted by Os, where s∊{0,1} denotes the states of the promoter, unoccupied and dimer bound, respectively. The constitutive production rate of the promoter is very small compared to the production rate of the activated gene when a dimer bounds to the promoter. The transitions in the promoter state are represented by Eq. 22, where k is the forward rate and β is the dimensionless dissociation constant. For simplicity, we lump the transcription step and the translation step into one production rate 20 with a rate αs that depends on the state of the promoter. When s=0, α0 is small and marks the constitutive production rate of the monomer; when s=1, α1 is much larger than α0 and represents the active state of the gene. The protein M decays at a constant rate δ in Eq. 19 while it dimerizes to D at a rate Λ in Eq. 21. The dissociation rate is θΛ.
This system is more complicated than the previous one because now the number n of the dimer D affects the production rate of the monomer M by binding to the gene promoter. Furthermore, the promoter has only two discrete states O0 and O1, which cannot be approximated by a continuously varying random number. Thus, the Gaussian noise approximation is not applicable here, and we have to keep the original discrete stochastic process to model transitions in the state of the promoter.
If the dimerization is much faster than other reactions, we may use the steady state approximation as in the previous example; specifically,
| (23) |
where and denote the conditional averages of the monomer number m and the dimer number n, respectively, under the fast reaction 21. Let N=2n+m denote the slow variable; from
| (24) |
we derive
| (25) |
which shows how changes with N. For the slow variable N, we may write the corresponding chemical Langevin equation,
| (26) |
The primary difference between Eqs. 6, 26 is that here αs is a two-state random variable with a Poisson switching probability determined by the equations
| (27) |
where P0 and P1 denote the probabilities for the state variable s having a value of 0 or 1.
We use a fixed time-step method to integrate Eq. 26 and simulate the random switching event of the promoter. For sufficiently small time step dt, the transition probability from O0 to O1 in the time interval dt is and βkP1dt is the probability for the reverse transition. In each time interval, we fix the promoter state and allow it to change only at the end of each step according to the transition probability. As long as dt is much smaller than the average switching time, this numerical scheme is relatively accurate. Within each time interval, we used a second-order stochastic integrator to update as in the previous example. Based on this scheme, we carried out simulations with two sets of parameter values and calculated the averages, variances, and PDFs. We also carried out Gillespie simulations with identical parameters to compare with our reduced system. In the plots below, the Gillespie results are depicted with open circles and the chemical Langevin results with solid lines (or dashed lines). All results consist of averages over 40 000 trajectory realizations.
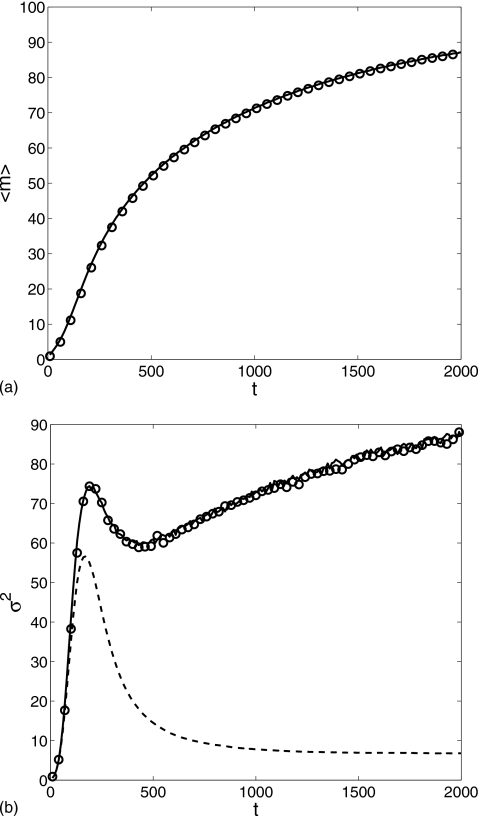
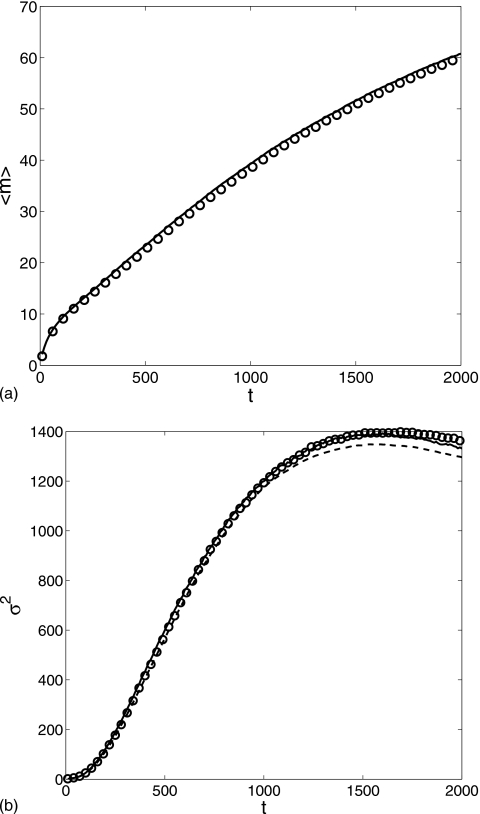
Simulation results shown in Fig. 3, were obtained in the time interval t∊[0,2000] with parameter values δ=0.01, α0=0.1, α1=1.0, λ=0.2, θ=15, k=0.05, and β=3 and the initial condition (m,Nϕ0,Nϕ1,n)=(0,1,0,0). We see that the evolution of the average and the variance of two different calculations agree extremely well. The average is a monotonically increasing function of time, saturating at long times, while the variance shows a fast initial rise to a peak and after a small drop starts a second slowly growing stage. The peak in the variance arises due to the discreteness of the dimers at the initial stage. The dashed lines in Fig. 3 display the results for the reduced model without fast noise, i.e., with only in Eq. 18. The average overlaps with the full noise approximation as expected while the variance shows large discrepancies at later times. Initially, dimerization rarely happens, and thus contributes little to the variance. After that, however, the monomers dimerize more frequently and the dimerization process starts to dominate the fluctuations. At t=2000, taking , we get by Eq. 23. According to Eqs. 16, 17, the contribution of the fast noise to the variance is
which accounts for the difference between the solid and the dashed line in Fig. 3b.
Figure 3.
Comparison of (a) the average and (b) the variance of the monomer M number computed for the gene regulation cascade in the time interval t=[0,2000]: the Gillespie simulation (circle), the reduced Langevin approximation (solid line), and without fast noise (dashed line). δ=0.01, α0=0.1, α1=1.0, λ=0.2, θ=15, k=0.05, and β=3 with the initial condition (m,Nϕ0,Nϕ1,n)=(0,1,0,0).
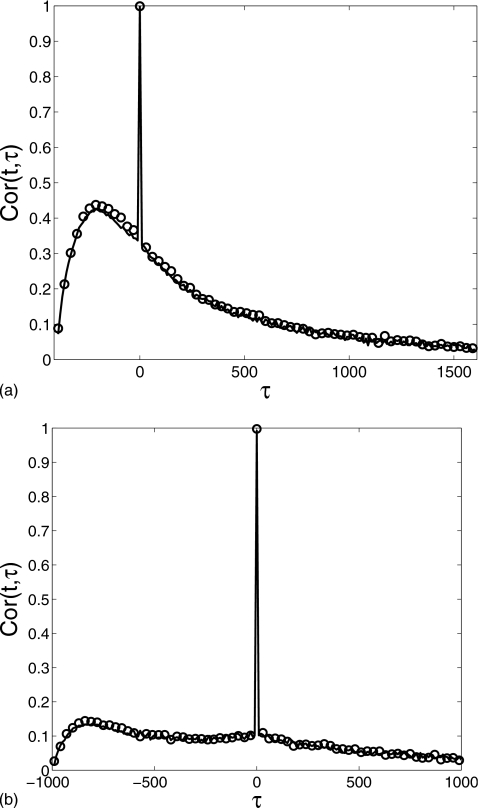
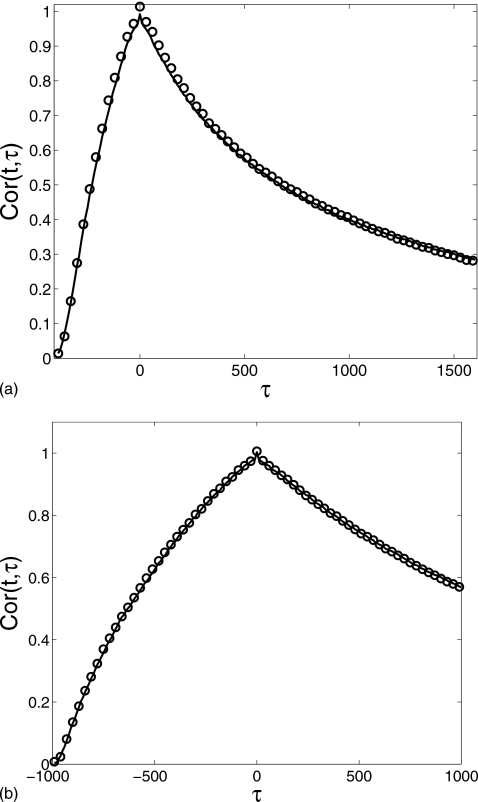
To further demonstrate that the reduced method captures the dynamic behavior of the full system, in Fig. 4 we compare the temporal autocorrelation function
which is a function of two variables t and τ representing two time instants t and t+τ (where indicates variance at time t). When the system reaches equilibrium, Cor(t,τ) depends only on the time difference τ. In the transient phase, however, the correlation function also has a strong dependence on the variable t. This is clearly exhibited in Fig. 4a for t=400 and Fig. 4b for t=1000. The graphs look similar and both have a sharp protrusion near τ=0 due to the short decorrelation time. For t=1000 (Fig. 4), the profile becomes more symmetric around τ=0 than for t=400 since the system approaches equilibrium with increasing time. In both figures, the reduced method (solid lines) agrees with the Gillespie result (circles) extremely well.
Figure 4.
Comparison of the autocorrelation function Cor(t,τ) at (a) t=400 and (b) t=1000 of the monomer M number computed for the gene regulation cascade: the Gillespie simulation (circle) and the reduced Langevin approximation (solid line). δ=0.01, α0=0.1, α1=1.0, λ=0.2, θ=15, k=0.05, and β=3 with the initial condition (m,Nϕ0,Nϕ1,n)=(0,1,0,0).
Figure 5 shows similar calculations but with a different set of parameter values, δ=0.02, α0=0.2, α1=2.0, λ=0.4, θ=50, k=0.001, and β=10, where we significantly increased the backward reaction rate θ and dissociation constant β but decreased the promoter switching rate k. The agreement with Gillespie calculation is still very good, but small discrepancies exist, especially in the variance near the end of the simulation. The average is still a monotonic function, but the variance displays a broad peak which is very different from the one depicted in Fig. 3b. The computation without fast noise now agrees quite well with the full noise approximation in both averages and variances. In the current case, the birth-death fluctuations resulting from switching in the promoter state dominates. The dimerization noise becomes relatively insignificant. Also note the large values of the variance, which indicate a strong deviation from the Poisson process. Thus, the dynamics for the two chosen sets of parameters differ significantly. The PDFs shown below reveal additional differences.
Figure 5.
Comparison of (a) the average and (b) the variance of the monomer M number computed for the gene regulation cascade in the time interval t∊[0,2000]: the Gillespie simulation (circle), the reduced Langevin approximation (solid line), and without fast noise (dashed line). δ=0.02, α0=0.2, α1=2.0, λ=0.4, θ=50, k=0.001, and β=10 with the initial condition (m,Nϕ0,Nϕ1,n)=(0,1,0,0).
We compare the time correlation function Cor(t,τ) in Fig. 6 again for t=400 and t=1000 with the new set of parameter values. They continue to show the t dependence of Cor(t,τ) out of equilibrium. The profile around the peak in both (a) and (b) seems to display a cusp at the peak. The sharp protrusion at the origin in Fig. 4 is not obvious here because the fast noise is subordinate to the fluctuations induced by the slow changes in the state of the promoter. Still, the agreement between the reduced method and the exact Gillespie simulations is nearly perfect, demonstrating that the temporal dynamics of the original system is very well captured by the reduced equations.
Figure 6.
Comparison of the autocorrelation function Cor(t,τ) at (a) t=400 and (b) t=1000 of the monomer M number computed for the gene regulation cascade: the Gillespie simulation (circle) and the reduced Langevin approximation (solid line). δ=0.02, α0=0.2, α1=2.0, λ=0.4, θ=50, k=0.001, and β=10 with the initial condition (m,Nϕ0,Nϕ1,n)=(0,1,0,0).
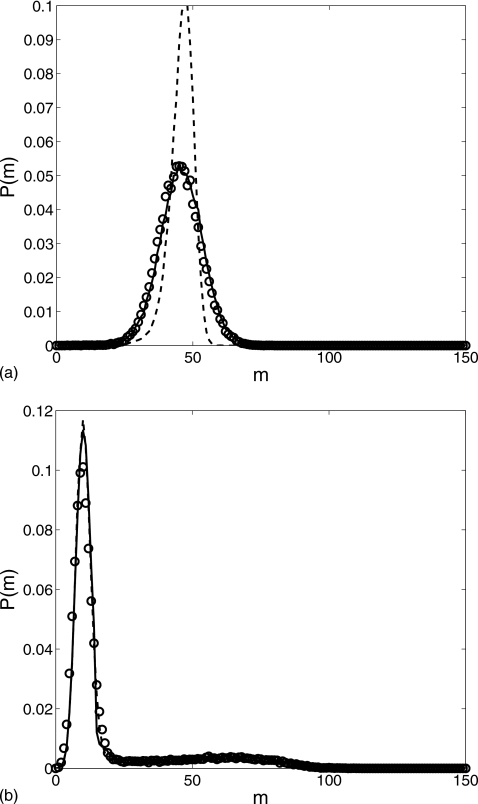
Figure 7 shows the probability distributions at time t=400 calculated with the two sets of parameter values. Our reduced Langevin approximation captures the distribution function very well. In Fig. 7a, the distribution is close to a Gaussian centered around m=50 while in Fig. 7b the distribution has a peak at m=10 plus a broad elevation near m=70. For both sets of parameters, when s=0, the monomer number is approximately 10 but is approximately 100 when s=1. The values of θ and β in Fig. 7a are considerably smaller than those in Fig. 7b; thus, it is a lot easier for the first system to retain the s=1 state than the second.
Figure 7.
Comparison of the probability distributions for the gene regulation cascade at t=400: the Gillespie simulation (circle), the reduced Langevin approximation (solid line), and without fast noise (dashed line) for parameter values (a) δ=0.01, α0=0.1, α1=1.0, λ=0.2, θ=15, k=0.05, and β=3 and (b) δ=0.02, α0=0.2, α1=2.0, λ=0.4, θ=50, k=0.001, and β=10, with the initial condition (m,Nϕ0,Nϕ1,n)=(0,1,0,0).
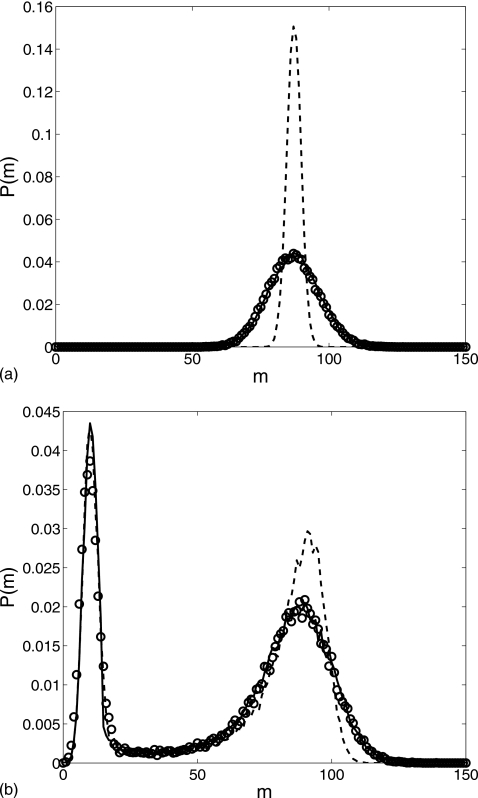
We let the two systems further evolve to t=2000 resulting in the probability distributions depicted in Fig. 8. Our reduced model still perfectly matches the exact simulations. The Gaussian profile of the first distribution is retained but its center moved to m≈90 which means that most of the trajectories reach the s=1 state. In Fig. 8b, a large second peak appears near m=100 while the first peak is considerably lower when compared to Fig. 7b. The second peak corresponds to the s=1 state while the trajectories in the first peak mainly stay at the s=0 state.
Figure 8.
Comparison of the probability distributions for the gene regulation cascade at t=2000: the Gillespie simulation (circle), the reduced Langevin approximation (solid line), and without fast noise (dashed line) for parameter values (a) δ=0.01, α0=0.1, α1=1.0, λ=0.2, θ=15, k=0.05, and β=3 and (b) δ=0.02, α0=0.2, α1=2.0, λ=0.4, θ=50, k=0.001, and β=10, with the initial condition (m,Nϕ0,Nϕ1,n)=(0,1,0,0).
The dashed lines in Figs. 78 depict the results of the reduced model without fast noise. For the first set of parameter values, the PDF profiles are considerably narrower than the exact ones while there are only small discrepancies for the second set of parameter values. In fact, in Fig. 3b the dashed line shows a variance of , which is much smaller than the value produced by a pure birth-death process with the corresponding average value ⟨m⟩≈87. The dimers act as a reservoir to buffer fluctuations in the monomer number. When monomers decay, some dimers subsequently dissociate to keep the monomer number from decreasing; when monomers are born, dimers are subsequently formed to reduce the monomer number. Thus, the dimer reservoir has the effect of damping fluctuations generated in the birth-death process. Of course, at short time scales, the fluctuations caused by dimerization could be very large. For the second parameter set, the fluctuations are mainly due to the slow promoter state switching, so the dashed lines in Figs. 7b, 8b are closer to the exact profiles.
DISCUSSION
Since the introduction of the Gillespie exact stochastic simulation algorithm,3 much effort has been devoted to accelerate its implementation. The first reaction method4 was improved by the next reaction method,5 which also is exact and requires only one random number for each reaction event. The τ-leap method24 determines the number of transitions that occur in a fixed time interval with the approximation that the propensities of all the reactions do not change significantly during that time. In order to avoid negative protein numbers in the τ-leap method with large step size, binomial sampling scheme can be invoked.32 If all species exist in large quantities, the chemical Langevin equations provide a continuous approximation to the underlying discrete process. In real reaction networks, however, there often coexist species with large and small copy numbers, as well as reactions with very different rates. The approximations needed in these schemes do not hold uniformly across the whole system and may not significantly reduce the computation load in many practical situations. Consequently, further reduction methods have been developed that partition the species or the reactions into different groups.7, 8, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38 Fast reactions are assumed to reach partial equilibrium30, 31, 35, 38 such that effective reaction rates for the slow reactions can be estimated conditional on the averages of the fast variables. Alternatively, if the fast species assume large populations, deterministic equations, chemical Langevin equations, or the τ-leap method7, 8, 29, 33, 37 can be used to evolve these species while the original or slightly modified Gillespie algorithm is used to advance the slow reactions.
The reduction scheme introduced here is related to the acceleration schemes mentioned above. Our contribution resides in treating the chemical Langevin equation instead of the chemical master equation as all the above schemes did. Therefore, our scheme deals with reaction species with large population. The chemical Langevin equations are a reduction in the master equation and the treatment here can be regarded as a second reduction. It turns out that even with the chemical Langevin equation, the partial equilibrium assumption30, 31, 35, 41 is still applicable as long as the reaction rates are well separated. In this sense, the current scheme is an extension of the partition scheme for the master equation. Many techniques such as the hybrid integration method developed for the master equation are also applicable here. In our second example, the promoter switches between two discrete states. We retained this discreteness in our reduced system and utilized a simple hybrid scheme. The excellent agreement of the results from this method with exact Gillespie simulations convincingly verifies the validity of the scheme.
In the examples considered here, our reduction scheme takes only 2% or 3% of the computational time as the exact Gillespie algorithm, demonstrating considerable efficiency. The main advantage of the reduction is that it removes the stiffness64 embedded in the chemical Langevin equations. The fast dimerization process contributes stiff terms to both the monomer and dimer equations such that very small steps need to be taken in order to avoid instabilities when integrating these equations. Our reduction scheme preprocesses the fast reactions, and thus retains only the slow variables. This allows for much larger time steps. The increase in the integration step size is approximately proportional to the ratio of the fast and the slow reaction rates to maintain the integration stability kdt∼1, where k is a reaction rate and dt is the integration step size. Note that only a forward integration scheme64 was considered because such methods are the most popular and convenient schemes for integrating the chemical Langevin equations.
An interesting question is whether it is possible to incorporate the fast reaction distribution equation 17 into the slow Langevin equation 7 to forge a single Langevin equation for m. The answer seems to be negative. Equation 7 is the core of the whole reduction but is only valid for the conditional average as we argued in Sec. 2. Thus, to write an equation purely in terms of m, we have to deduce the average from the known full random m at each time instant in order to make use of the slow manifold property. This is impossible without simulating the fast noise which breaks our original goal of reducing computational load. In the literature discussed above, the slowest and the fastest motions including fluctuations are always treated separately. If there are more than two time scales, the fastest reactions should reach steady state first, followed by the second fastest, and then the remaining reactions. Our reduction scheme evolves only the slowest set of reactions and is able to sequentially generate the distributions of fast variables based on the values of the slower variables.
SUMMARY
In this paper, we proposed a new scheme for performing model reduction using a separation of time scales in the chemical Langevin equation. In the reduced model, a Langevin equation is used to advance the slow variables while assuming the fast variables remain in a quasisteady state. A stochastic numerical simulation technique is devised to implement the proposed scheme. Two examples are used to demonstrate the effectiveness of our method. The first one is a birth-death-dimerization process and the second is a simple gene regulation network. In these examples, reactions involved in the dimerization reactions are assumed to be faster than other processes, and thus represent fast degrees of freedom. However, the monomer participates in both the slow and the fast reactions, thus mixing time scales. We introduced an auxiliary variable to successfully separate reaction components with different time scales and achieved significant computation efficiency in the resulting reduced model. The approximate solutions agree extremely well with the results computed from exact Gillespie simulations.
Although more sophisticated integration techniques are available that would further improve the efficiency of the current scheme, the main goal here was to demonstrate our scheme’s validity and usefulness. We chose to use a simple method to integrate Eq. 26. The time step dt is required to be much smaller than the average switching time between promoter states. This restriction can be removed by using hybrid integration schemes like those employed in treating the master equation.7, 8, 33, 37 Furthermore, these integration schemes are able to handle time-dependent noise and may be used in our reduction technique to treat nonautonomous systems.
The reduction scheme has been shown to be very effective in the two examples in which the network structures are relatively simple and the slow and fast variables are easy to identify. In more realistic situations, the cellular network could be much more complicated and the time scales are more entangled. Defining slow variables and separating different time scales in a systematic way is essential for the implementation of the current technique. Furthermore, often in realistic large-scale networks, there exists a span of time scales, where there is no clear-cut distinction between the slow and fast processes. Systematically extending our technique to model systems with multiple time scales is a challenging and interesting problem. Recent work by Ball et al.36 provides a possible avenue for pursuing this problem.
ACKNOWLEDGMENTS
This work was supported through National Science Foundation (NSF) Grant No. 0715225 and National Institutes of Health (NIH) Grant No. R01-GM079271.
References
- Hartwell L. H., Hopfield J. J., Leibler S., and Murray A. W., Nature (London) 10.1038/35011540 402, C47 (1999). [DOI] [PubMed] [Google Scholar]
- Foundations of Systems Biology, edited by Kitano H. (MIT Press, Cambridge, 2001). [Google Scholar]
- Gillespie D. T., J. Phys. Chem. 10.1021/j100540a008 81, 2340 (1977). [DOI] [Google Scholar]
- Gillespie D. T., J. Comput. Phys. 10.1016/0021-9991(76)90041-3 22, 403 (1976). [DOI] [Google Scholar]
- Gibson M. A. and Bruck J., J. Phys. Chem. A 10.1021/jp993732q 104, 1876 (2000). [DOI] [Google Scholar]
- Rao C. V., Wolf D. M., and Arkin A. P., Nature (London) 10.1038/nature01258 420, 231 (2002). [DOI] [PubMed] [Google Scholar]
- Kiehl T. R., Mattheyses R. M., and Simmons M. K., Bioinformatics 10.1093/bioinformatics/btg409 20, 316 (2004). [DOI] [PubMed] [Google Scholar]
- Pucha̱lka J. and Kierzek A. M., Biophys. J. 86, 1357 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lan Y. and Papoian G., Biophys. J. 10.1529/biophysj.107.123778 94, 3839 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lan Y. and Papoian G., Phys. Rev. Lett. 10.1103/PhysRevLett.98.228301 98, 228301 (2007). [DOI] [PubMed] [Google Scholar]
- Barkai N. and Leibler S., Nature (London) 10.1038/43199 387, 913 (1997). [DOI] [PubMed] [Google Scholar]
- Rieke F. and Baylor D. A., Biophys. J. 75, 1836 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vilar J. M. G., Kueh H. Y., Barkai N., and Leibler S., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.092133899 99, 5988 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barkai N. and Leibler S., Nature (London) 10.1038/35002255 403, 267 (2000). [DOI] [PubMed] [Google Scholar]
- Swain P. S., J. Mol. Biol. 10.1016/j.jmb.2004.09.073 344, 965 (2004). [DOI] [PubMed] [Google Scholar]
- Weinberger L. S., Burnett J. C., Toettcher J. E., Arkin A. P., and Schaffer D. V., Cell 10.1016/j.cell.2005.06.006 122, 169 (2005). [DOI] [PubMed] [Google Scholar]
- Thattai M. and van Oudenaarden A., Genetics 10.1534/genetics.167.1.523 167, 523 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korobkova E., Emonet T., Vilar J. M. G., Shimizu T. S., and Cluzel P., Nature (London) 10.1038/nature02404 428, 574 (2004). [DOI] [PubMed] [Google Scholar]
- Zandstra P. W., Lauffenburger D. A., and Eaves C. J., Blood 96, 1215 (2000). [PubMed] [Google Scholar]
- Süel G. M., Kulkarni R. P., Dworkin J., Garcia-Ojalvo J., and Elowitz M. B., Science 10.1126/science.1137455 315, 1716 (2007). [DOI] [PubMed] [Google Scholar]
- van Kampen N. G., Stochastic Processes in Physics and Chemistry (North Holland Personal Library, Amsterdam, 1992). [Google Scholar]
- Reichl L. E., A Modern Course in Statistical Physics (Wiley, New York, 1998). [Google Scholar]
- Gillespie D. T., J. Chem. Phys. 10.1063/1.481811 113, 297 (2000). [DOI] [Google Scholar]
- Gillespie D. T., J. Chem. Phys. 10.1063/1.1378322 115, 1716 (2001). [DOI] [Google Scholar]
- Meng T. C., Somani S., and Dhar P., In Silico Biology 4, 0024 (2004). [Google Scholar]
- Hasty J. and Collins J. J., Nat. Genet. 10.1038/ng0502-13 31, 13 (2002). [DOI] [PubMed] [Google Scholar]
- Gardiner C. W., Handbook of Stochastic Methods (Springer, New York, 2002). [Google Scholar]
- Risken H., The Fokker-Planck Equation (Springer, Berlin, 1984). [Google Scholar]
- Haseltine E. L. and Rawlings J. B., J. Chem. Phys. 10.1063/1.1505860 117, 6959 (2002). [DOI] [Google Scholar]
- Rao C. V. and Arkin A. P., J. Chem. Phys. 10.1063/1.1545446 118, 4999 (2003). [DOI] [Google Scholar]
- Bundschuh R., Hayot F., and Jayaprakash C., Biophys. J. 84, 1606 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian T. and Burrage K., J. Chem. Phys. 10.1063/1.1810475 121, 10356 (2004). [DOI] [PubMed] [Google Scholar]
- Salis H. and Kaznessis Y., J. Chem. Phys. 10.1063/1.1835951 122, 054103 (2005). [DOI] [PubMed] [Google Scholar]
- Erban R., Kevrekidis I. G., Adalsteinsson D., and Elston T. C., J. Chem. Phys. 10.1063/1.2149854 124, 084106 (2005). [DOI] [PubMed] [Google Scholar]
- Cao Y., Gillespie D. T., and Petzold L., J. Comput. Phys. 10.1016/j.jcp.2004.12.014 206, 395 (2005). [DOI] [Google Scholar]
- Ball K., Kurtz T. G., Popovic L., and Rempala G., J. Appl. Probab. 16, 1925 (2006). [Google Scholar]
- Hellander A. and Lötstedt P., J. Comput. Phys. 227, 100 (2007). [Google Scholar]
- Morelli M. J., Allen R. J., Tănase-Nicola S., and ten Wolde P. R., J. Chem. Phys. 10.1063/1.2821957 128, 045105 (2008). [DOI] [PubMed] [Google Scholar]
- Hornberg J. J., Binder B., Bruggeman F. J., Schoeberl B., Heinrich R., and Westerhoff H. V., Oncogene 24, 5533 (2005). [DOI] [PubMed] [Google Scholar]
- Ross J. and Vlad M. O., Annu. Rev. Phys. Chem. 10.1146/annurev.physchem.50.1.51 50, 51 (1999). [DOI] [PubMed] [Google Scholar]
- Ackers G. K., Johnson A. D., and Shea M. A., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.79.4.1129 79, 1129 (1982). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temam R., Infinite-Dimensional Dynamical Systems in Mechanics and Physics, Appl. Math. Sci. No. 68 (Springer-Verlag, New York, 1988). [Google Scholar]
- Foias C., Jolly M. S., Kevrekidis I. G., Sell G. R., and Titi E. S., Phys. Lett. A 10.1016/0375-9601(88)90295-2 131, 433 (1988). [DOI] [Google Scholar]
- Kevrekidis I. G., Gear C. W., and Hummer G., AIChE J. 10.1002/aic.10106 50, 1346 (2004). [DOI] [Google Scholar]
- Valorani M., Creta F., Goussis D. A., Lee J. C., and Najm H. N., Combust. Flame 10.1016/j.combustflame.2006.03.011 146, 29 (2006). [DOI] [Google Scholar]
- Lam S. H. and Goussis D. A., Int. J. Chem. Kinet. 10.1002/kin.550260408 26, 461 (1994). [DOI] [Google Scholar]
- Lan Y. and Papoian G. A., J. Chem. Phys. 10.1063/1.2358342 125, 154901 (2006). [DOI] [PubMed] [Google Scholar]
- Lan Y., Wolynes P., and Papoian G. A., J. Chem. Phys. 10.1063/1.2353835 125, 124106 (2006). [DOI] [PubMed] [Google Scholar]
- Honeycutt R. L., Phys. Rev. A 10.1103/PhysRevA.45.600 45, 600 (1992). [DOI] [PubMed] [Google Scholar]
- Lehn J., Rößler A., and Schein O., J. Comput. Appl. Math. 138, 297 (2002). [Google Scholar]
- Brańka A. C. and Heyes D. M., Phys. Rev. E 10.1103/PhysRevE.58.2611 58, 2611 (1998). [DOI] [Google Scholar]
- Wilkie J., Phys. Rev. E 10.1103/PhysRevE.70.017701 70, 017701 (2004). [DOI] [PubMed] [Google Scholar]
- Fox R. F., J. Stat. Phys. 10.1007/BF01044719 54, 1353 (1989). [DOI] [Google Scholar]
- Elowitz M. B., Levine A. J., Siggia E. D., and Swain P. S., Science 10.1126/science.1070919 297, 1183 (2002). [DOI] [PubMed] [Google Scholar]
- Ozbudak E. M., Thattai M., Kurtser I., Grossman A. D., and van Oudenaarden A., Nat. Genet. 10.1038/ng869 31, 69 (2002). [DOI] [PubMed] [Google Scholar]
- Kaern M., Blake W. J., and Collins J. J., Annu. Rev. Biomed. Eng. 10.1146/annurev.bioeng.5.040202.121553 5, 179 (2003). [DOI] [PubMed] [Google Scholar]
- Sasai M. and Wolynes P. G., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.2627987100 100, 2374 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blake W. J., Kaern M., Cantor C. R., and Collins J. J., Nature (London) 10.1038/nature01546 422, 633 (2003). [DOI] [PubMed] [Google Scholar]
- Walczak A. M., Sasai M., and Wolynes P. G., Biophys. J. 10.1529/biophysj.104.050666 88, 828 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walczak A. M., Onuchic J. N., and Wolynes P. G., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0509547102 102, 18926 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Süel G. M., Garcia-Ojalvo J., Liberman L. M., and Elowitz M. B., Nature (London) 10.1038/nature04588 440, 545 (2006). [DOI] [PubMed] [Google Scholar]
- Okabe Y., Yagi Y., and Sasai M., J. Chem. Phys. 10.1063/1.2768353 127, 105107 (2007). [DOI] [PubMed] [Google Scholar]
- Kepler T. B. and Elston T. C., Biophys. J. 81, 3116 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press W. H., Teukolsky S. A., Vetterling W. T., and Flannery B. P., Numerical Recipes in C (Cambridge University Press, Cambridge, England, 1992). [Google Scholar]