Multiple-Interval Mapping for Quantitative Trait Loci With a Spike in the Trait Distribution

Abstract

For phenotypic distributions where many individuals share a common value—such as survival time following a pathogenic infection—a spike occurs at that common value. This spike affects quantitative trait loci (QTL) mapping methodologies and causes standard approaches to perform suboptimally. In this article, we develop a multiple-interval mapping (MIM) procedure based on mixture generalized linear models (GLIMs). An extended Bayesian information criterion (EBIC) is used for model selection. To demonstrate its utility, this new approach is compared to single-QTL models that appropriately handle the phenotypic distribution. The method is applied to data from Listeria infection as well as data from simulation studies. Compared to the single-QTL model, the findings demonstrate that the MIM procedure greatly improves the efficiency in terms of positive selection rate and false discovery rate. The method developed has been implemented using functions in R and is freely available to download and use.

MANY statistical methods for mapping quantitative trait loci (QTL) have been developed for traits with regular distributions. These include single-interval mapping (Lander and Botstein 1989), marker-based regression (Cowen 1989; Moreno-Gonzalez 1992), composite-interval mapping (Jansen 1993; Jansen and Stam 1994; Zeng 1994), multiple-interval mapping (Kao et al. 1999; Kao and Zeng 2002), and methods especially for binary traits (see, e.g., Xu and Atchley 1996; Visscher et al. 1996; Xu et al. 1998; Yi and Xu 2000; McIntyre et al. 2001).

Recently, Broman (2003) considered the traits with distribution having a spike, i.e., a mixture of a regular distribution and a single-point mass. This type of trait is common in survival analysis and tumor studies (see, e.g., Boyartchuk et al. 2001; Hunter et al. 2001). Broman (2003) studied several single-QTL methods. The common feature of these methods is that putative QTL are considered one at a time. The single-QTL methods can be efficient for identifying QTL-bearing chromosomes. But if they are used to identify individual QTL, there is a potential to commit a high false discovery rate due to the existence of spurious genotype correlations between loci not in linkage disequilibrium (LD) with QTL and those in LD with QTL.

A natural alternative to single-QTL methods is to consider multiple QTL simultaneously. In this article, we consider a multiple-interval mapping (MIM) procedure based on mixture generalized linear models (GLIM) for traits with the spike feature. An EM algorithm for the mixture GLIM and a forward procedure using an extended Bayesian information criterion (EBIC) (see Chen and Chen 2008) are developed. The MIM procedure is illustrated with the Listeria data (Boyartchuk et al. 2001) that were analyzed by Broman (2003), using the single-QTL methods mentioned above. Simulation studies are carried out to compare the MIM procedure with the single-QTL methods.

METHODS

For simplicity, we consider backcross designs without loss of generality. Let the marker genotypes of an interval be coded by x as follows: x = 1, if both markers are homozygous; x = 2, if the left one is homozygous and the right one is heterozygous; x = 3, if the left one is heterozygous and the right one is homozygous; and x = 4, if both markers are heterozygous. Let y_i be the trait value of individual i and x_ij be its genotype code on interval j. Denote by δ_ij the unobservable genotype of individual i at a putative QTL on interval j, where δ_ij = 1, if the genotype is homozygous, and 0 otherwise. The probability that δ_ij = 1 is determined by x_ij and r_j, where r_j is the recombination fraction between the left marker and the putative QTL of interval j. Let p(r_j, x_ij) denote this probability.

The multiple-QTL mixture GLIM:

Consider any m intervals. Let 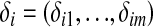. Assume that the conditional density function of y_i given 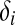is

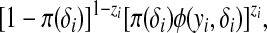(1)

where z_i = I{y_i ≠ 0}, 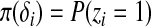, and φ is the density function of an exponential family distribution. Then the joint density of 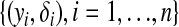is given by

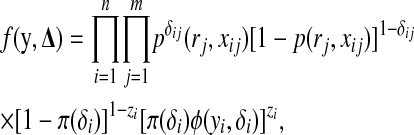(2)

where 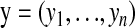and 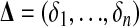. The marginal density of 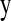is obtained by summing up the second product over all possible values of the δ_ij's, which gives rise to a mixture of 2^m components of form (1).

Consider the general exponential family form of ,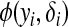

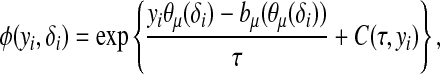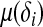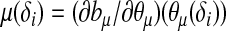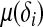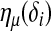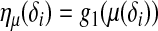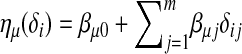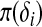where τ is a dispersion parameter common to all i, and b_μ is a monotone function related to the mean of the distribution by . Let g₁(μ(δ_i)) be the link function that connects with a linear predictor as . If only the main effects of the QTL are considered, . If epistasis effects among the QTL are considered, . Similarly, let be related to a linear predictor η_π(δ_i) through another link function g₂. The linear predictor η_π has the same structure as η_μ. For example, in the main-effect-only model, 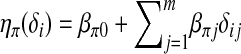. A common choice for g₂ is the logistic link .

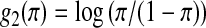The mixture GLIM described above forms the basis of the MIM procedure. For details on GLIM, the reader is referred to McCullagh and Nelder (1989).

The EM algorithm:

In the EM algorithm, the unobservable QTL genotypes 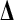are treated as missing data. The pair 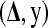is considered as the complete data and 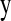as the incomplete data. The parameters to be estimated are 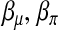, the coefficient vectors in the two linear predictors, and 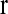, the vector of recombination fractions, as well as τ, the dispersion parameter. The EM algorithm alternates iteratively between an E-step and an M-step. In an E-step, the conditional expectation of the log likelihood of the complete data, 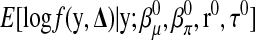, is computed at the most updated values of 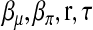. In an M-step, the conditional expectation is maximized with respect to the parameters. Let 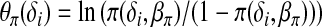and b_π(θ_π) = ln(1 + exp(θ_π)). The log density of the complete data, 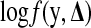, is expressed as follows:

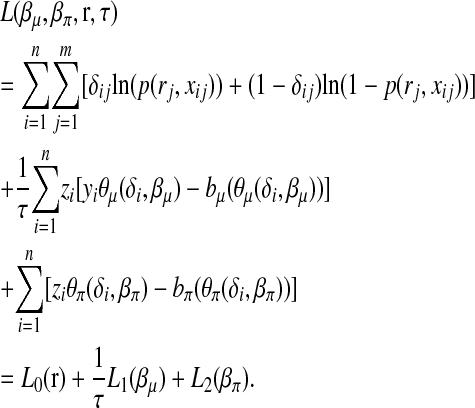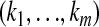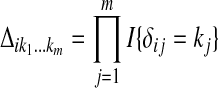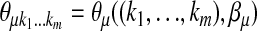Let be an m-tuple with k_j's taking values 0 or 1. Define . Let and 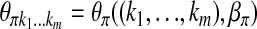. Then 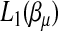and 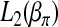can be expressed as

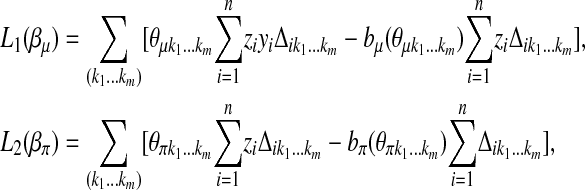where the sums are taken over all possible m-tuples 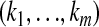. The E-step thus is reduced to the computation of the conditional expectations 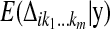, and the M-step is broken down into three separate maximization problems. For ease of notation, in what follows, we use the same notation for 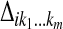, δ_ij, and their respective conditional expectations. Since 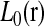is the sum of m sums, each of them involving a different position parameter, the maximization of 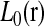is further broken down into m maximization problems. Each of them can be solved easily by a grid-point search procedure. The maximization of 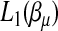and 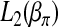can be carried out by two separate iterated weighted least-squares procedures that we describe as follows.

Let 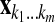be the row vector of the covariate values in the linear predictors with 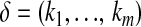. Let X be the matrix obtained by stacking the 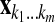's one above another in lexicographical order; i.e., the indexes 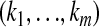are in the order (00 … 00), (00 … 01), (00 … 10), 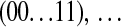, 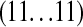. Define 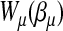as the diagonal matrix with diagonal elements 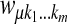given by 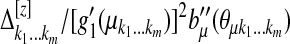, where 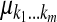is the mean value corresponding to 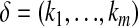, , 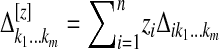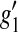is the first derivative of g₁, and 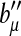is the second derivative of b_μ. Define 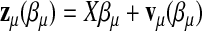, where 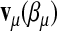is the vector with its (k₁ … k_m)th component given by 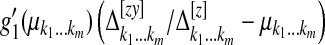, where . Similarly, define 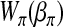and 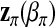by replacing 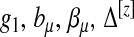, and Δ^[zy] with 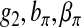, Δ^[1], and Δ^[z], respectively, where 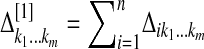. The M-step for updating 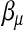and 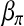is then realized by iteratively solving the following equations:

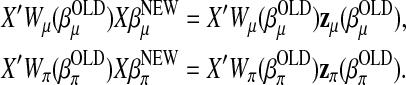After 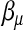is updated, the dispersion parameter τ is updated by the average squared Pearson's residuals associated with L₁. The EM algorithm above is developed along the same line as that in Chen and Liu (2009).

Multiple-interval mapping procedure:

The MIM procedure makes use of a model selection criterion adapted from the EBIC recently developed by Chen and Chen (2008). For a model with m intervals, the adapted criterion is given by

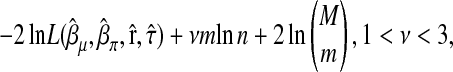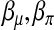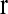where M is the total number of intervals under study. The number νm is considered as the effective number of unknown parameters in the model. For a model with m intervals, there are m components in each of , and . But 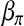does not play the same role as 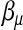. Furthermore, only a portion of the data involve 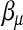, and a position parameter cannot be counted fully as a free parameter in terms of its effect on the likelihood. For example, most backcross progenies have flanking markers that are either both homozygous or both heterozygous. In this case, the position of a putative QTL has little effect on the likelihood. A definite effective number, which is in fact dependent on the data, is difficult to determine. The ν adjusts the effective number according to the data. The choice of ν should be data dependent. In the discussion, some ad hoc rules and an outline of a data-driven approach to the choice of ν are provided.

We use EBIC as the model selection criterion because, as has been shown, it is consistent if the number of covariates under consideration is of the order O(n^κ) for any κ where n is the sample size, but the ordinary BIC fails to be consistent if κ > 0.5 (see Chen and Chen 2008).

The MIM procedure starts with models containing only one interval. The model with the minimum EBIC is compared with the null model with no QTL at all. If the minimum is smaller than the EBIC of the null model, the interval contained in the model is selected and the procedure continues; otherwise, it stops. At a general step, suppose m intervals have already been selected. Then all the models containing these m intervals plus an additional one are assessed. The minimum EBIC of these models is compared with that of the previous model consisting of m intervals. If the minimum is still smaller, the additional interval corresponding to the minimum EBIC is selected, and the procedure continues; otherwise, it stops. In the above procedure, if an additional interval to be added is adjacent to any one already selected, it is skipped to avoid potential colinearity that might cause nonconvergence of the EM algorithm. To summarize, the procedure sequentially adds intervals to a tentative model if the EBIC of the model decreases. The procedure stops when the EBIC begins to increase. The intervals contained in the final model are taken as QTL-bearing ones.

EXAMPLE

The Listeria data of Boyartchuk et al. (2001) are reanalyzed to illustrate the MIM procedure. The data consist of the time to death following infection with Listeria monocytogenes of 116 F₂ mice from an intercross between the BALB/cByJ and C57BL/6ByJ strains and the mice's genotypes at 133 markers on 20 chromosomes. The result obtained is compared with that of the single-QTL two-part model method considered by Broman (2003).

The single-QTL two-part model method is implemented with threshold value of 4.93 for the LOD score. This threshold value is obtained by 10,000 permutation replicates. The intercross version of the MIM procedure is applied with ν = 2.5 in EBIC. The exponential family distribution φ in the GLIM is taken as the normal distribution.

In the following, we use [k, d] to denote a locus on chromosome k with a genetic distance d cM from the left end of that chromosome. The single-QTL two-part model method detects chromosomes 1, 5, and 13 as QTL-bearing ones. The loci at which the LOD score attains its maximum over each of the three chromosomes are, respectively, [1, 81], [5, 30.9], and [13, 26.16]. The MIM procedure detects chromosome 1, 2, 5, 6, 8, and 13 as QTL-bearing ones. The detected loci in the last step of the MIM procedure are [1, 81], [2, 3.5], [5, 29.0], [6, 13.0], [8, 10.0], [13, 26.5], and [13, 13.05]. These results are summarized in Table 1. The loci and the EBIC value at each step of the MIM procedure are given in Table 2. The positions of the loci are slightly different from step to step because they are reestimated at each step. We cannot judge which result is better in this example. In the next section, we evaluate these two methods by simulation studies.

TABLE 1.

Loci (genetic distance in centimorgans from the left end of each chromosome) indicating evidence of QTL detected by the single-QTL two-part model (TPM) and multiple interval-mapping (MIM) in the example

	Loci detected
Chromosome	TPM	MIM
1	81	81
2	—	3.5
5	30.90	29
6	—	13
8	—	10
13	26.16	13.05, 26.5

TABLE 2.

The loci included and the corresponding EBIC value at each step of the MIM procedure in the example

Step	Loci included	EBIC
1	[13, 27]	153.02
2	[13, 26.5] [5, 28]	141.11
3	[13, 26.5] [5, 28] [1, 81]	138.78
4	[13, 26.5] [5, 28] [1, 81] [6, 14]	136.88
5	[13, 26.5] [5, 28] [1, 81] [6, 14] [2, 4]	136.74
6	[13, 26.5] [5, 29] [1, 81] [6, 14] [2, 3.5] [8, 8.5]	128.31
7	[13, 26.5] [5, 29] [1, 81] [6, 13] [2, 3.5] [8, 10] [13, 13.05]	124.48

SIMULATIONS

The genetic map of the mouse genome in the example section is used to generate the data in simulation studies; that is, the number and lengths of chromosomes and the number and positions of markers on each chromosome are kept the same as those in the mouse genome. The genetic map is provided in supporting information, File S1.

Backcross progenies are generated according to the genetic map. In each replicate of the simulation, 5 chromosomes are randomly chosen from the first 19 chromosomes (the 20th chromosome is ignored since there are only two markers on it); on each of them, a QTL location is generated at random, and then the genotypes at these 5 QTL together with the 133 markers of 200 backcross progenies are generated. The trait values are generated under the assumption of no epistasis effect. The 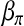is set at

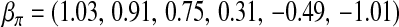and kept unchanged throughout. It is designed such that ∼25% of the progenies will survive. Three settings of 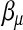are considered:

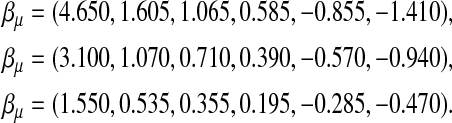The survival times are generated by a normal distribution with mean equal to η_μ and variance 1. The three 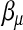-values correspond to the survival time heritabilities 0.63, 0.43, and 0.16, respectively.

The 95% threshold value for the LOD is simulated as 3.35 by 10,000 replicates and used in all three settings. The LOD scores are calculated at grid points spaced 1 cM apart. Three values of ν, 1.5, 2, and 2.5, are used in the EBIC. The MIM procedure and the single-QTL two-part model method are applied to the same data. Their performances are assessed by positive selection rate (PSR) and false discovery rate (FDR). To make the comparison fair to the single-QTL two-part model method, we consider only whether or not a QTL-bearing chromosome is correctly identified, since single-QTL methods have been used mainly for this purpose. A chromosome is claimed as a QTL-bearing one if at least one of the selected loci falls in that chromosome. A claimed QTL-bearing chromosome is said to be a positive discovery if that chromosome does contain QTL. Otherwise, it is said to be a false discovery. The PSR and the FDR are defined as follows:

The simulation results over 500 replicates are given in Table 3. The findings are summarized as follows. With heritability 0.63, the MIM procedure has a much higher PSR with all the three ν-values, a lower FDR when ν = 2 or 2.5, and a comparable FDR when ν = 1.5. With heritability 0.43, the MIM procedure has higher PSR and lower or comparable FDR when ν = 2 or 1.5 and lower FDR and comparable PSR when ν = 2.5. We may claim that the MIM procedure is better than the single-QTL two-part model method when the heritability is moderate or high. However, in the case of heritability 0.16, the single-QTL two-part model method is better than the MIM procedure in terms of either PSR or FDR. An explanation is given below. The heritability considered in the simulation accounts only for the nonsurvival portion and the QTL effect on the survival proportion is fixed. Any QTL with a heritability as low as 0.16 is hard to detect no matter what approach is used. The fairly sizeable PSR in this case is mainly due to the QTL effect on the survival proportion. In the EBIC criterion of the MIM procedure, an overpenalization arises when the effect on the survival time is in fact negligible. This explains why the PSR of the MIM procedure is lower in this case. A remedy for the problem of overpenalization is discussed in the next section.

TABLE 3.

The average positive selection rate (PSR), false discovery rate (FDR), number of positive discoveries (NPD), and number of false discoveries (NFD) of the two approaches: the single-QTL two-part model (TPM) and the multiple-interval mapping (MIM), over 500 replicates in the simulation study

Heritability	Method	ν	PSR	FDR	NPD	NFD
0.63	TPM	—	0.614	0.018	3.072	0.056
	MIM	1.5	0.839	0.026	4.196	0.112
		2.0	0.778	0.008	3.888	0.030
		2.5	0.722	0.003	3.610	0.010
0.43	TPM	—	0.509	0.017	2.538	0.044
	MIM	1.5	0.626	0.026	3.130	0.082
		2.0	0.547	0.008	2.734	0.022
		2.5	0.471	0.002	2.354	0.004
0.16	TPM	—	0.293	0.033	1.112	0.038
	MIM	1.5	0.269	0.059	1.346	0.084
		2.0	0.224	0.054	1.118	0.064
		2.5	0.208	0.053	1.038	0.058

DISCUSSION

We have demonstrated that the MIM procedure compares favorably with the single-QTL two-part model method when being used to identify QTL-bearing chromosomes. It has the further advantage of identifying individual QTL with accurately estimated positions. We discuss some further issues in this section.

In the MIM procedure considered in the previous sections, we do not distinguish between the QTL effects on the spike probability and on the survival time. This might lead to an overpenalization of the EBIC if only one type of effect exists and hence result in a reduced power for QTL detection. The procedure can be modified such that, when a new interval is considered, two substeps are taken, one for the effect on the spike probability and the other for the effect on the survival time. Correspondingly, the term νm ln n in the EBIC is replaced by νq ln n, where q counts the number of parameters of the model. When a new interval is considered, if only one type of effect is included, q increases by 1, and if both types of effect are included, q increases by 2.

In the simulation studies, we used different ν-values in EBIC. For smaller ν, the PSR is higher but the FDR is also higher, and vice versa. We give some ad hoc rules for the choice of ν here. First, different ν-values should be used and the results compared. It is usually the case that, if the heritability is relatively high, the results will be similar in a range of ν-values. If this is the case, the smallest ν in this range produces the highest PSR and comparable FDR compared with other values in the range and should be used for a final decision. If there is a big discrepancy among different values, the choice should be based on the purpose of the study. If the study is for confirmation, the FDR is a more serious concern, and a larger ν should be taken. If the study is a preliminary step to detect regions for further investigation, a smaller ν should be taken.

A data-driven approach based on the idea of model averaging and bootstrapping can be used. The approach is outlined as follows. Starting with a moderate ν-value, a set of claimed QTL together with their estimated effects is obtained. Then the following bootstrap-like procedure is carried out. A random number, say m*, is generated from a Poison distribution with the mean as the number of claimed QTL. Then m* loci, each on a different interval, are randomly selected from the genetic map and assigned as QTL, the effects of the QTL are generated using the estimated effects of the claimed QTL, and the trait values of individuals are generated by using the GLIM. Finally, the MIM procedure with different ν-values is applied to the generated data, and the positive discoveries and false discoveries are obtained by comparing the claimed QTL with the assigned QTL. This process is repeated for a large number of times. The numbers of positive discoveries and false discoveries are averaged to provide estimates for PSR and FDR for each of the ν-values. Then with the estimated PSR and FDR, the user can make a choice on the basis of a balanced consideration of PSR and FDR. A full development of the data-driven approach in more general settings is underway, which is beyond the scope of this article. We will report the general data-driven approach elsewhere.

The MIM procedure has been implemented using functions in the R package migtlm. The package will be updated soon to include a general function for the MIM procedure. The package can be downloaded from www.stat.nus.edu.sg/∼stachenz.