In the article by L. E. Bauman, J. S. Sinsheimer, E. M. Sobel and K. Lange (Genetics 180: 1743–1761) entitled “Mixed Effects Models for Quantitative Trait Loci Mapping With Inbred Strains,” recurrence (7) describing the calculation of the strain coefficient matrix for an individual with itself should read
 |
where diag(γ) denotes a diagonal matrix whose diagonal entries coincide with the entries of the vector γ and k and l are the parents of i.
In appendix b, recurrence (B3) should read
 |
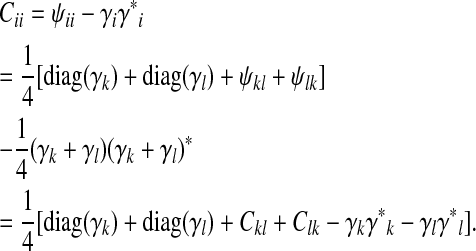Proposition 1e should read
Proposition 1. In addition to satisfying the recurrences (B1), (B2), and (B3), the matrix Cij
e. has entries Cij(m, n) confined to the interval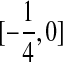 
for n ≠ m and to the interval 
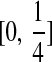for n = m.
In the next paragraph, the constant aij for s = 2 strains should satisfy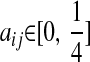 
. Furthermore, for the assertion since αij = 0 whenever i or j is a founder or an F1 individual, straightforward recursive arguments show that within any strictly linear mating designs like Fn, αij = 0 for all i ≠ j is not true.
Finally, in Proposition 2 the bound on the coefficients aij,mn is slightly changed. The coefficients aij,mn are nonnegative dyadic rationals satisfying
 |
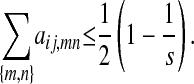The proofs for Proposition 1e and for Proposition 2 remain essentially the same, as do all numerical examples.