Asymmetric control of inspiratory and expiratory phases by excitability in the respiratory network of neonatal mice in vitro

Abstract

Rhythmic motor behaviours consist of alternating movements, e.g. swing-stance in stepping, jaw opening and closing during chewing, and inspiration–expiration in breathing, which must be labile in frequency, and in some cases, in the duration of individual phases, to adjust to physiological demands. These movements are the expression of underlying neural circuits whose organization governs the properties of the motor behaviour. To determine if the ability to operate over a broad range of frequencies in respiration is expressed in the rhythm generator, we isolated the kernel of essential respiratory circuits using rhythmically active in vitro slices from neonatal mice. We show respiratory motor output in these slices at very low frequencies (0.008 Hz), well below the typical frequency in vitro (∼0.2 Hz) and in most intact normothermic mammals. Across this broad range of frequencies, inspiratory motor output bursts remained remarkably constant in pattern, i.e. duration, peak amplitude and area. The change in frequency was instead attributable to increased interburst interval, and was largely unaffected by removal of fast inhibitory transmission. Modulation of the frequency was primarily achieved by manipulating extracellular potassium, which significantly affects neuronal excitability. When excitability was lowered to slow down, or in some cases stop, spontaneous rhythm, brief stimulation of the respiratory network with a glutamatergic agonist could evoke (rhythmic) motor output. In slices with slow (<0.02 Hz) spontaneous rhythms, evoked motor output could follow a spontaneous burst at short (≤1 s) or long (∼60 s) intervals. The intensity or timing of stimulation determined the latency to the first evoked burst, with no evidence for a refractory period greater than ∼1 s, even with interburst intervals >60 s. We observed during inspiration a large magnitude (∼0.6 nA) outward current generated by Na⁺/K⁺ ATPase that deactivated in 25–100 ms and thus could contribute to burst termination and the latency of evoked bursts but is unlikely to control the interburst interval. We propose that the respiratory network functions over a broad range of frequencies by engaging distinct mechanisms from those controlling inspiratory duration and pattern that specifically govern the interburst interval.

Rhythmic behaviours such as breathing, locomotion and mastication are organized into mechanically different phases that are optimized, often moment-to-moment, in a task-specific manner. The characteristics of these movements are subject to, and reflect, the organization of spinal and brainstem central rhythm- and pattern-generating circuits. For example, ipsilateral inhibitory neurons between antagonist motor pools (Stein, 1997; Grillner, 2006), and inhibitory commissural interneurons between half-centre oscillators (Butt & Kiehn, 2003), respectively underlie the obligatory swing–stance and left–right alternating limb movements of stepping. A similar coordination of left–right body flexions in the swimming pattern of lamprey can be traced to bilateral oscillatory networks with reciprocal inhibitory connections (Grillner, 2006). Moreover, different phases of a motor pattern can be subject to distinct control mechanisms. A notable example is in mastication, where there is no jaw-closing reflex yet a potent jaw-opening reflex serves to minimize the likelihood of tooth damage if an unanticipated hard object is present when chewing (Lund & Olsson, 1983; Lund, 1991).

How does the neural control of breathing reflect alternating inspiration and expiration? In mammals, the mechanics of inspiration are fundamentally different from those of expiration. At rest under normal conditions active contraction of the diaphragm is necessary to expand the lung for inspiration, whereas the elasticity of the diaphragm and thorax is sufficient to deflate the lung and produce expiration. Thus, at rest, inspiration requires active muscle contraction; expiration does not. Given the mechanical and physiological asymmetries, the changes in inspiratory and expiratory patterns are different when ventilation changes. For example, modest increases in ventilation near resting values in humans are typically accomplished by increasing inspiratory flow and decreasing expiratory duration, without affecting inspiratory duration (Gardner, 1980). With further elevation of metabolic demand, e.g. with exercise, expiration becomes an active process, and abdominal, internal intercostal, and other muscles contract to expel air (West, 2007). In extreme conditions of low metabolic demand as in hypothermia or hibernation, expiratory durations during intermittent breathing are dramatically prolonged while inspiratory durations do not change as drastically (Milsom, 1991, 1992). Inspiratory and expiratory duration are also modulated differentially in the Hering–Breuer reflex, where lung inflation shortens inspiration but prolongs expiration (West, 2007).

We addressed whether the kernel of the central neural circuits generating respiratory rhythm incorporates these asymmetries using an in vitro approach in which active expiration is absent. The preBötzinger Complex (preBötC) plays an essential role in inspiratory rhythm generation, and, when expiration is passive, expiratory duration corresponds to the interval between inspiratory bursts (Feldman & Del Negro, 2006; West, 2007). We specifically examined the relationship between inspiratory motor bursts and the interburst (expiratory) interval in brainstem slice preparations from neonatal rodents that isolate the inspiratory rhythm-generating preBötC as well as respiratory-related hypoglossal (XII) motoneurons and premotoneurons (Smith et al. 1991; Koizumi et al. 2008), but do not contain the retrotrapezoid nucleus/parafacial respiratory group hypothesized to underlie generation of active expiration (Feldman & Del Negro, 2006; Janczewski & Feldman, 2006). The absence of sensory, descending and ascending inputs as well as reduced temperature typically yield slices that can generate respiratory rhythms with a frequency of ∼0.2 Hz at 27°C.

Here, in the absence of active expiration, we show evidence of a mechanism in the preBötC affecting expiratory duration that does not affect inspiratory duration or inspiratory motor nerve burst amplitude. We propose that this mechanism influences expiratory timing as breathing changes in response to metabolic need.

Methods

We used neonatal C57BL/6 mice (P0–5) for experiments in vitro. The Office for the Protection of Research Subjects (University of California Animal Research Committee) and the Institutional Animal Care and Use Committee (The College of William and Mary) approved all protocols. Transverse slices, 550 μm thick, were cut from the neonatal mouse brainstem, which contained the specialized rhythm-generating preBötC (Smith et al. 1991) as well as respiratory premotoneurons and hypoglossal (XII) respiratory motoneurons that discharge in phase with inspiratory rhythm (Koizumi et al. 2008). To obtain slices with the preBötC at the surface, the rostral cut was made above the first set of XII nerve rootlets at the level of the dorsomedial cell column and principal lateral loop of the inferior olive, and the caudal cut captured the obex (Ruangkittisakul et al. 2006). Normal ACSF contained (in mm): 124 NaCl, 3 KCl, 1.5 CaCl₂, 1 MgSO₄, 25 NaHCO₃, 0.5 NaH₂PO₄, and 30 d-glucose, equilibrated with 95% O₂ and 5% CO₂ (27°C, pH 7.4).

Slices were perfused with 27°C ACSF at 4 ml min⁻¹ in a 0.5 ml chamber mounted rostral side up in a fixed-stage microscope (Axioskop FS-1, Carl Zeiss, Inc., Thornwood, NY, USA) set up for Koehler illumination. Infrared-enhanced differential interference contrast (IR-DIC) videomicroscopy was performed using a DAGE-MTI IR-series charge-coupled device (CCD) video camera (Michigan City, IN, USA) coupled to a Hamamatsu C-2400 analog camera controller (USA contact: Bridgewater, NJ, USA) connected to the video-in jack on a television monitor. Extracellular potassium concentration ([K⁺]_o) was raised to 9 mm and respiratory motor output was recorded from XII nerve roots using suction electrodes and a differential amplifier (Dagan Instruments, Minneapolis, MN, USA). The XII discharge was full-wave rectified and smoothed.

Electrical recordings were performed on inspiratory preBötC neurons, selected visually with IR-DIC videomicroscopy in the region ventral to the semicompact division of the nucleus ambiguus, and then confirmed via recording to exhibit an inspiratory discharge pattern.

Whole-cell current-clamp experiments were performed using either an Axoclamp-2A amplifier (Molecular Devices, Sunnyvale, CA, USA) or an IX2-700 amplifier (Dagan Instruments). Voltage-clamp experiments utilized a Model 2400 patch-clamp amplifier (A-M Systems, Sequim, WA, USA). Continuous data were acquired in current- or voltage-clamp using an analog-to-digital converter (Powerlab 8/30, ADInstruments, Colorado Springs, CO, USA or Digidata 1322, Molecular Devices) and either Chart 5 software (ADInstruments) or pCLAMP (Molecular Devices). A computer controlled digital-to-analog converter (LabJack U3, Lakewood, CO, USA) delivered custom voltage waveform commands to the voltage-clamp amplifier through C/C++ software written by the authors (J.A.H.) for a G4 PowerBook (Apple Inc., Cupertino, CA, USA).

Patch electrodes with a 3–6 MΩ tip resistance were fabricated using a four-stage custom program on a Flaming–Brown micropipette puller (P-97, Sutter Instruments, Novato, CA, USA) and filled with solution containing (in mm): 140 potassium gluconate, 5 NaCl, 0.1 EGTA, 10 Hepes, 1 Mg-ATP, and 0.3 Na₃-GTP (pH 7.25). Access resistance was compensated using adjustable bridge balance in current clamp and analog feedback compensation in voltage clamp. To stimulate neurons in the preBötC we pressure-ejected 500 μm (±)-α-amino-3-hydroxy-5-methylisoxazole-4-propionic acid (AMPA) dissolved in ACSF from a patch pipette (10 μm tip diameter) at 20 p.s.i. using a Picospritzer (General Valve Division, Parker Hannifin, Cleveland, OH, USA) or the Pressure System IIe (Toohey Co., Fairfield, NJ, USA). Pulses were 5 ms in duration. Multiple pulses were separated by 5 ms pauses to reduce tissue deformation by continuous pressure application. To block ionotropic excitatory and inhibitory synaptic transmission we bath-applied (in μm): 10 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX), 50 dl-2-amino-5-phosphonovaleric acid (APV), 100 picrotoxin, and 1 strychnine (Sigma-Aldrich, St Louis, MO, USA). We also bath-applied 10 μm strophanthidin (Sigma) to block Na⁺/K⁺ ATPase pumps.

We measured the peak amplitude and half-width, and computed the area of respiratory-related full-wave rectified XII motor output using the Peak Parameters analysis tool available as an extension of Chart 5 software (ADInstruments). This software selects a time window containing an event such as the XII burst and then quantitatively analyses the event. For respiratory analyses we focus on the full-wave rectified XII output and use Peak Parameters to move sequentially from burst to burst, recording the timing of each XII burst, placing all burst measurements in a spreadsheet that can be analysed with statistics or plotted offline. Peak Parameters computes the baseline from the average voltage during a user-defined interval preceding the burst, which is generally 200–400 ms. XII burst termination is defined by the time point at which the signal crosses baseline and remains at baseline for the same 200–400 ms period of time. A peak-detection algorithm then defines burst amplitude from the difference between peak and baseline. Half-width (burst duration) is defined as the time that the XII discharge exceeded 50% of the peak amplitude. In experiments where the XII burst had a fragmented appearance (e.g., Fig. 3A) we applied a sliding window average of 33–111 points to a duplicate XII-analysis channel, which smoothes the peaks and valleys and yields a more accurate measurement of XII half-width. XII burst area is computed as the integral of the full-wave rectified XII burst discharge in units of V s, which is calculated from the area under the curve of XII output referenced to baseline. The smoothed and unsmoothed channels yielded identical area measurements for XII bursts with fragmented appearance. These three measures, which typically provide commensurate information regarding motor output, were employed to assess whether any experimental challenge affected XII bursts. Therefore, we refer to the ‘magnitude’ or ‘pattern’ of XII output, when amplitude, half-width, and area provide equivalent measures of respiratory-related motor discharge from the XII nerve rootlet. It is important to note that, unlike intracellular recordings, suction electrodes have no absolute scale and the XII discharge signal varies between experiments. Therefore, for comparison, XII motor output in each nerve rootlet was normalized to its own maximum discharge in control conditions. The effects of experimental tests were expressed as a fraction of control. Lastly, the three measurements of amplitude, half-width and duration do not exclude the possibility that XII bursts may differ with respect to the declining phase or the power spectrum of intraburst oscillations attributable to the relative discharge synchrony of XII motoneurons (Sebe et al. 2006; Sebe & Berger, 2008).

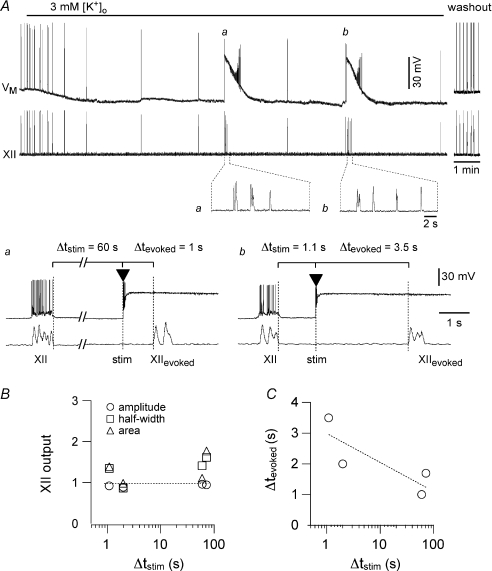
Figure 3. Transient local stimulation with AMPA pulses evokes XII motor output (XII_evoked) following short (∼1 s) and long (60 s) intervals following endogenous XII output.

The interval of stimulation following endogenous XII output is defined as Δt_stim. A, lowering [K⁺]_o from 9 to 3 mm slowed the respiratory rhythm to 0.008 Hz. The top trace (V_M) shows a whole-cell recording from a neuron in the preBötC. Baseline voltage was −60 mV at the start of the sweep. The lower trace shows XII output. Lower insets show XII_evoked cycles at higher sweep speed following long (a) and short (b) stimulation. The 2 s calibration bar applies to both inset traces. a, after two successive cycles with a period of ∼120 s, local AMPA stimulation was applied 60 s after the endogenous XII output (i.e. Δt_stim= 60 s), which evoked three rapid cycles of XII_evoked with a latency (Δt_evoked) of 1 s. b, after the first stimulation protocol (a), the cycle period returned to ∼120 s, and after two consecutive cycles, another local AMPA stimulation was applied 1.1 s following the endogenous XII output (i.e. Δt_stim= 1.1 s), which evoked four rapid cycles of XII_evoked with a latency (Δt_evoked) of 3.5 s. B, the normalized amplitude (open circles), half-width (open squares), and area (open triangles), of XII_evoked from the experiment in A are plotted versus Δt_stim. C, Δt_evoked of the bursts from the experiment shown in A are plotted versus Δt_stim. The dotted line in B is a horizontal reference for normalized XII output = 1; dotted line in C is a linear regression fit to the data.

To study respiratory frequency we manipulated [K⁺]_o as an index of neural excitability. While excitability is a broad concept that encompasses the entire complement of active and passive membrane properties and their influence on firing behaviour, the level of [K⁺]_o modulates baseline membrane potential, even when its effects are non-Nernstian at [K⁺]_o≤ 3 mm (Forsythe & Redman, 1988). Therefore, changing [K⁺]_o provides an experimentally advantageous means of rapidly and reversibly changing baseline membrane potential throughout the preBötC network, which has previously been used in studies of respiratory rhythmogenesis (Del Negro et al. 2001; Johnson et al. 2001).

The coefficient of variation (CV) of the period was calculated by dividing the standard deviation of the periods for a given [K⁺]_o by the value of the mean period for the same [K⁺]_o. Measures of XII output and the CV were compared at multiple [K⁺]_o levels using a one-way ANOVA with Tukey–Kramer post hoc analysis to detect pairwise disparities among [K⁺]_o levels. We compared the cycle period/frequency of respiratory rhythm as well as the amplitude, half-width, and area of XII bursts in control and following blockade of Cl⁻-mediated inhibition using a two-way ANOVA with control vs. disinhibition and [K⁺]_o level as independent variables and multiple comparison tests in follow-up analyses. Statistical significance was uniformly set at a minimum of P < 0.05.

Before beginning each experiment we monitored the slice preparation for 30 min to ensure that the XII frequency and magnitude reached steady state in 9 mm K⁺. In assessing the effect of [K⁺]_o on XII output we changed the [K⁺]_o in the ACSF and allowed 5–10 min to elapse before collecting any data. We then recorded for a minimum of 2–10 min at steady state to capture at least five consecutive cycles of XII output for offline analysis of burst amplitude, half-width and area, as well as frequency, at each level of [K⁺]_o. For 3 mm K⁺, we recorded the minimum of five cycles in n= 3 slices, 6 cycles in n= 1 slice, 7–9 cycles in n= 6 slices, and 10 or more cycles in all other slices in the data set. To document low-frequency rhythmic states at 4 and 5 mm K⁺ we recorded 15–60 min to measure far more than five cycles (minimum of 12 cycles, n= 17 slices in standard conditions, n= 9 disinhibited slices). In all experiments where [K⁺]_o exceeded 5 mm, the minimum number of consecutive XII cycles analysed was 25 and the maximum was 50 per increment in [K⁺]_o. In n= 13 experiments we applied the [K⁺]_o levels in random order and in n= 13 experiments we increased [K⁺]_o in sequence from 3 to 10–12 mm. In all cases the experiments began and ended with 9 mm K⁺ serving as control and washout.

Results

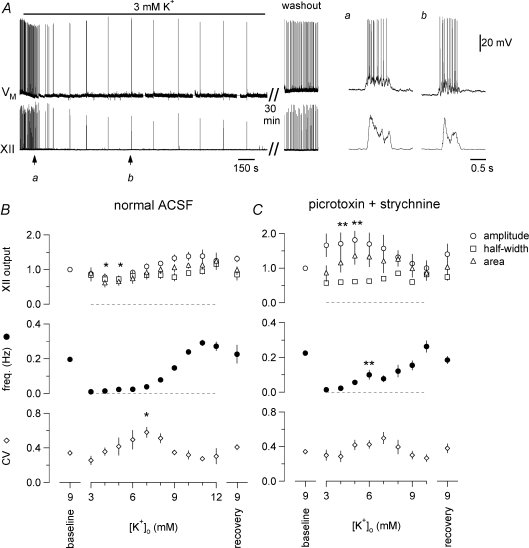
The frequency of respiratory rhythm in control conditions in vitro (9 mm K⁺) was 0.20 ± 0.02 Hz at 27°C (period: 5.7 ± 0.5 s). Lowering [K⁺]_o in a single step from 9 to 3 mm hyperpolarized the baseline membrane potential of preBötC inspiratory neurons by 5–10 mV (baseline was defined as the average voltage during the final third of the interburst interval) and decreased frequency to 0.008 ± 0.002 Hz (period: 143.2 ± 3.9 s, Fig. 1A, n= 14 out of 17 slices tested) or stopped the rhythm (n= 3 out of 17 slices tested) at steady state. The drop in frequency for the 14 slices active at 3 mm K⁺ compared to the frequency at 9 mm K⁺ was statistically significant (P < 0.0001), yet there was no significant decrease in the amplitude, half-width, or area of the XII output and inspiratory bursts in preBötC neurons (P > 0.05 for all measures). Figure 1Aa and b show the inspiratory bursts and XII output for a representative experiment.

Figure 1. The effects of [K⁺]_o on respiratory rhythm and burst characteristics in vitro.

A, [K⁺]_o was lowered from 9 to 3 mm for 35 min, which reversibly caused baseline membrane potential (−60 mV) to hyperpolarize 5 mV in this representative preBötC neuron (V_M, upper trace) and slowed respiratory frequency to ∼0.008 Hz. XII output is shown in the lower trace. Duration of exposure to 3 mm K⁺ is shown in the bar above V_M. a and b show inspiratory bursts at 9 vs. 3 mm K⁺ at higher sweep speed. Separate time calibrations of 150 s and 0.5 s are shown below the XII trace. The voltage calibration (in b) applies to all V_M traces. B, effects of [K⁺]_o on XII output are shown in the upper graph, measured as burst amplitude (open circles), area (open triangles), half-width (open squares). The effects of [K⁺]_o on respiratory frequency (filled circles) and the coefficient of variation (CV) of period (open circles) are shown in the middle and lower graphs, respectively. Data plotted are means ± standard error of the mean (s.e.m.) (n= 17). C, effects of [K⁺]_o on XII output, frequency and the CV of period in the absence of fast synaptic inhibition (100 μm picrotoxin, 1 μm strychnine, n= 9). Statistical significance is indicated by symbols as follows: *P < 0.05, **P < 0.01.

In 17 slices, increasing [K⁺]_o in 1 mm increments from 3 mm monotonically increased respiratory frequency, which reached a plateau asymptotically at 11–12 mm where peak frequency measured 0.29 ± 0.02 Hz, corresponding to a minimum period of 3.5 ± 0.2 s (Fig. 1B, middle). At both 4 and 5 mm K⁺ the XII amplitude and area, but not half-width, were less than in 9 mm K⁺: amplitude measured 0.7 ± 0.1 and area measured 0.6 ± 0.1 of XII bursts in 9 mm K⁺. These changes were statistically significant (P < 0.05, Fig. 1B, top). However, for 3 mm K⁺ and all other [K⁺]_o exceeding 5 mm, the peak amplitude, half-width, and area of the inspiratory-modulated XII output were statistically indistinguishable from the same measures in 9 mm K⁺ (P > 0.05 for amplitude, half-width, and area, Fig. 1B, top).

The stability of cycle period was similar at 3 and 9 mm K⁺. The coefficient of variation (CV) decreased from 0.34 ± 0.02 in 9 mm K⁺ to 0.26 ± 0.05 at 3 mm K⁺, but the change was not statistically significant (Fig. 1B, bottom). CV increased from 3 to 7 mm K⁺, and then decreased for [K⁺]_o exceeding 7 mm. More irregular rhythms, judged by higher CV, were seen at intermediate [K⁺]_o levels. At 7 mm K⁺ the CV peaked at 0.58 ± 0.06, which was significantly higher than the CV at 9 mm K⁺ and at 3 mm K⁺ (P < 0.05 for both, Fig. 1B, bottom). In every slice tested, returning [K⁺]_o to 9 mm restored rhythms back to baseline, indistinguishable from the first application of 9 mm K⁺ ACSF on the basis of XII burst amplitude, half-width, area, period/frequency and CV (all P > 0.05).

In many neural oscillator circuits, fast inhibitory synaptic transmission can mediate or influence network behaviour. While inhibition is not essential for respiratory rhythmogenesis in vitro, inhibitory neurons in the preBötC are rhythmically active and can shape network output (Feldman & Smith, 1989; Shao & Feldman, 1997; Brockhaus & Ballanyi, 1998; Ritter & Zhang, 2000; Ren & Greer, 2006). Therefore, we tested the effects of changes in [K⁺]_o (1 mm increments) in the presence of 100 μm picrotoxin, an antagonist of GABA_A receptor-mediated neurotransmission, and 1 μm strychnine, an antagonist of glycine receptor-mediated neurotransmission (Fig. 1C, n= 9), to examine how inhibitory synaptic activity influences rhythm generation over a wide range of frequencies (but see Ren & Greer, 2006 and Discussion). The frequency monotonically increased from a minimum of 0.013 ± 0.004 Hz at 3 mm (period: 100 ± 14 s) to a maximum of 0.24 ± 0.04 Hz at 10 mm K⁺ (period: 4.18 ± 0.49 s, Fig. 1C, middle). Compared to control slices, the addition of picrotoxin and strychnine (i) increased frequency at 6 mm K⁺ (P < 0.01), with frequency at all other [K⁺]_o unchanged (P > 0.05), (ii) increased XII amplitude at 4 and 5 mm K⁺ (P < 0.01) with no effect on amplitude at 3 mm and from 6–10 mm K⁺ (P > 0.05), and (iii) had no effect on the half-width and area of XII bursts, nor on the CV, at any [K⁺]_o (P > 0.05, Fig. 1C).

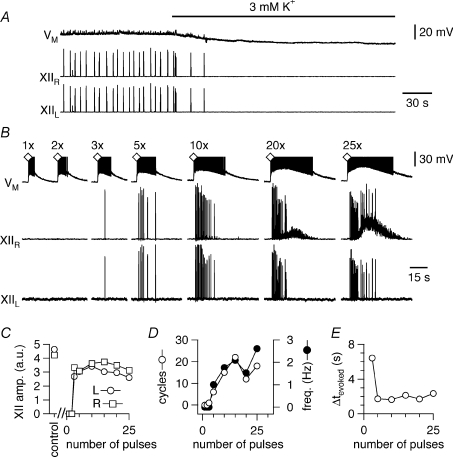
Three preparations (of 17) became quiescent after changing from 9 to 3 mm K⁺ (Fig. 2A). We posited that these silent preparations were nonetheless excitable (analogous to a neuron at resting potential). To test this, we unilaterally applied 5 ms pressure pulses of 500 μm AMPA within the preBötC. Single AMPA pulses depolarized preBötC neurons but did not evoke XII output. However, pulse trains consisting of at least three consecutive AMPA pulses (separated by 5 ms) evoked XII output. Control XII burst activity was defined as the mean spontaneous motor output from 10 consecutive cycles at steady state in 9 mm K⁺. The amplitude, half-width, and area of the evoked XII bursts in 3 mm K⁺ measured 0.8 ± 0.2, 0.8 ± 0.2 and 0.8 ± 0.1 of control (all P > 0.05, n= 3). The evoked XII output occurred synchronously on both left and right nerve roots, even though the stimulus was unilateral (Fig. 2B and C), with burst pattern similar to control. Increasing the number of pulses in the train produced more cycles of XII discharge in the evoked response (Fig. 2D, open circles) and increased their peak frequency (Fig. 2D, filled circles). With pulse trains of ≥20 pulses, tonic motor activity was seen in the ipsilateral but not the contralateral XII output. For 3–10 pulses per train, the latency to the first evoked XII output decreased as the number of stimuli increased, i.e. barely suprathreshold stimuli evoked XII output with long onset latency (∼6 s) whereas stronger stimuli evoked cycles of XII output with shorter latency (Fig. 2E). For 15–25 pulses per train, latency was ∼2 s.

Figure 2. Excitable properties of the preBötC network in slice preparations without spontaneous rhythm at 3 mm K⁺.

A, [K⁺]_o was lowered from 9 to 3 mm, which silenced the respiratory rhythm in 3 out of 17 slices and hyperpolarized the baseline voltage of −60 mV in this preBötC neuron (V_M, upper trace) by 8 mV. Bilateral XII output is shown in the middle and lower traces. B, in the same slice as A, single unilateral AMPA stimulation in the right preBötC depolarized the preBötC neuron (V_M, the voltage axis was truncated for display) but did not evoke XII output unless three or more pulses were applied (see Methods). Tonic XII discharge occurred in the side ipsilateral to the AMPA injection when 20–25 AMPA pulses were applied in rapid succession. C, the amplitude of the evoked XII output in arbitrary units (a.u.) plotted versus the number of successive AMPA pulses from B. XII area and half-width measurements yielded commensurate plots (not shown). D, the number of cycles of XII_evoked plotted versus number of AMPA pulses from B (left y-axis, open circles) and the frequency of XII_evoked (right y-axis, filled circles). E, the latency Δt_evoked in seconds of XII_evoked plotted versus number of AMPA pulses from B.

The influence of stimulation intensity on the latency and frequency of evoked XII bursts in slices quiescent at 3 mm K⁺ led us to question whether the network was refractory after XII bursts in rhythmically active slices, and whether refractoriness influenced periodicity. If refractoriness were relevant, we reasoned that the effect of stimulation would depend on when the stimulus was delivered in the interburst interval. We tested this prediction in rhythmically active slices at 3 mm and 9 mm K⁺ (Figs. 3 and 4).

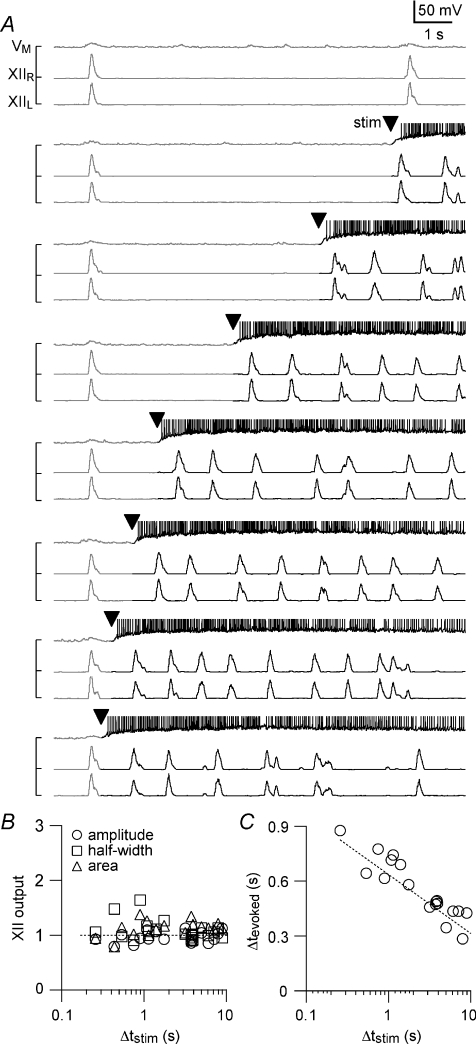
Figure 4. Transient local stimulation with AMPA pulses evokes XII output, similar to bursts recorded endogenously, at a range of intervals following endogenous XII output.

A, the interval of stimulation following endogenous XII output is defined as Δt_stim. The experiment was performed with [K⁺]_o= 9 mm such that the endogenous frequency was ∼0.1 Hz in this slice. The top trace (V_M) shows a whole-cell recording from a neuron in the preBötC with baseline voltage at −60 mV at the start of each sweep. The voltage axis was truncated for display such that action potentials are not shown in their entirety. The lower traces show left and right XII output. Moving from the top to the bottom of the panel, transient local AMPA stimulation (5× pulses, arrowhead) was applied at progressively shorter Δt_stim, starting with Δt_stim= 9 s and finishing with Δt_stim= 0.2 s. Endogenous rhythmic activity is displayed with grey whereas the evoked activity is black for emphasis. B, the amplitude (open circles), half-width (open squares), and area (open triangles) of XII_evoked from the experiment shown in A are plotted versus Δt_stim. C, Δt_evoked from the experiment shown in A is plotted versus Δt_stim. The dotted line in B is a horizontal reference for normalized XII output = 1; dotted line in C is a linear regression fit to the data.

Figure 3 shows a typical experiment at 3 mm K⁺. Based on the variability data in Fig. 1B, we surmised that if two consecutive cycles with periods ∼120 s differed by less than 5 s per cycle, then the preparation was at steady-state, or near it, with a low frequency. In this condition, we applied unilateral AMPA stimulation (typically 5 pulses, e.g. Fig. 2B) within the preBötC at either long (∼60 s) or short (∼1 s) delays following an endogenous XII burst. We called this delay Δt_stim, defined as the interval from the termination of an endogenous XII burst to the time of stimulation (see Fig. 3Aa and b). Both short and long Δt_stim evoked approximately the same number of cycles of XII output (XII_evoked). For example, in Fig. 3 the long and short Δt_stim were each applied two times. The insets below the XII trace at the top of Fig. 3, and panels a and b, show one example of each stimulation interval. For the long Δt_stim, the first bout evoked three XII_evoked (Fig. 3Aa) and the second bout evoked four XII_evoked (not shown). For the short Δt_stim, the first bout evoked four XII_evoked (Fig. 3Ab) and the second bout evoked three XII_evoked (not shown). Using the preceding spontaneous XII bursts as control, the XII_evoked were similar in amplitude, half-width, and area (P > 0.05 for all measures, Fig. 3B). Group data for three slices tested at 3 mm K⁺ are plotted in Fig. 5A. The technical challenges of the experiment precluded data from a larger number of slices. These limitations notwithstanding, as a fraction of control, XII_evoked amplitude, half-width, and area of the data collected measured 1.0 ± 0.1, 1.1 ± 0.2 and 1.2 ± 0.1, respectively (all P > 0.05).

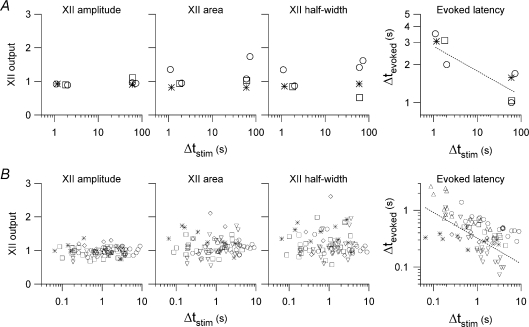
Figure 5. Group data for experiments in Figs 3 and 4.

A and B, XII amplitude, area and half-width are plotted versus Δt_stim for multiple experiments in the left graphs, which share the same y-axis and scaling. The right graphs plot Δt_evoked versus Δt_stim for the same experiments. Panels in A show 4 experiments in 3 slices at 3 mm K⁺; open circles, open squares and asterisks mark different slice preparations. Panels in B show 84 experiments in 6 slices at 9 mm K⁺; open circles, open squares, asterisks, upward and downward triangles, as well as open diamonds mark different slice preparations. All graphs are plotted with linear-log axes except the Δt_evokedversusΔt_stim, which are plotted with log-log axes. Evoked latency graphs in A and B (right) are shown with fitted regression lines.

We determined the relationship between Δt_stim and the latency of the first evoked XII output. We called this latency Δt_evoked, defined as the interval from the time of stimulation to XII_evoked (Fig. 3Aa and b illustrate Δt_stim and Δt_evoked). As shown in Fig. 3C, Δt_evoked and Δt_stim were inversely related: when stimulation followed a spontaneous XII output by 60 s, then XII_evoked emerged in 1 s, whereas when stimulation followed the spontaneous XII output by 1 s, then XII_evoked emerged in 3.5 s. This relationship was consistent in all slices tested (Fig. 5A, right). Regardless of latency, the XII_evoked collected from the three slices was not significantly different in amplitude, area, or half-width with respect to baseline (all P > 0.05, Figs. 3B and 5A).

We used a range of Δt_stim to examine the magnitude and latency of XII_evoked in greater detail (Figs. 4 and 5B). Threshold AMPA stimulation was determined using the protocol shown in Fig. 2B but the experiment was performed at 9 mm K⁺. The higher endogenous respiratory frequency at 9 mm K⁺ ensured that the slice returned to steady state more rapidly after each AMPA injection, which enabled us to test a greater number of Δt_stim particularly at progressively shorter intervals, i.e., Δt_stim < 10 s. We started very close to (but less than) the endogenous period (Fig. 4A, top trace). To illustrate the effects of stimulation we shaded each sweep such that the endogenous activity was grey and the response to AMPA puffs in black, with an arrowhead to mark the onset of the AMPA puff (Fig. 4A). We decreased Δt_stim incrementally to ∼100 ms. With [K⁺]_o at 9 mm, the threshold stimulus induced multiple cycles of motor output with a frequency of ∼1 Hz that returned to the control frequency in ∼10 s. Measurements of the evoked XII magnitude did not differ significantly from control (P > 0.05 for amplitude, half-width, and area, Fig. 4B), where control was again defined as the spontaneous XII burst preceding the XII_evoked. After each bout of AMPA injection we waited 2 min before changing Δt_stim to ensure that the effects of the previous stimulus dissipated. Δt_evoked increased monotonically as Δt_stim decreased: the shorter the stimulus interval, the longer the latency (Fig. 4C).

Group data for six slices tested at 9 mm K⁺ are plotted in Fig. 5B. As a fraction of control, XII_evoked amplitude measured 1.0 ± 0.1, half-width measured 1.1 ± 0.2, and area measured 1.2 ± 0.1 (all P > 0.05). These data show that stimulation always caused XII_evoked similar to endogenous XII bursts regardless of how short the Δt_stim, which suggests the lack of a measureable absolute refractory period <65 ms, the minimum Δt_stim we could deliver. We were also not able to detect a relative refractory period for Δt_stim≥ 65 ms in which XII_evoked emerged with magnitude different from control, i.e. the peak amplitude, half-width, and area of XII_evoked were statistically indistinguishable from the spontaneous XII bursts serving as control (P > 0.05). However, the latency to evoke the XII burst depended on the elapsed time since the preceding endogenous XII burst: Δt_evoked was negatively correlated with Δt_stim (Fig. 5B, right), which could be considered a form of relative refractoriness in a network context. These data suggest that intrinsic cellular properties, sensitive to timing of preceding spontaneous inspiratory burst, influence the temporal recruitment of preBötC neurons that take part in evoking the motor output, XII_evoked. Nevertheless, once suprathreshold AMPA stimulation was present, e.g. Fig. 2B, the network produced a XII burst indistinguishable in amplitude, area, and half-width from endogenous bursts (Fig. 5A and B).

One mechanism that might contribute to burst termination and influence subsequent XII_evoked bursts is an outward current generated by Na⁺/K⁺ ATPase pumps (I_pump). Inspiratory bursts depend heavily on a Ca²⁺-activated, non-specific cation current (I_CAN) in which Na⁺ is the dominant inward charge carrier (Pace et al. 2007a; Mironov, 2008). Since Ca²⁺-dependent K⁺ currents (I_K-Ca) are not obligatory for, and do not play a major role in, terminating inspiratory bursts (Onimaru et al. 2003; Crowder et al. 2007; Zavala-Tecuapetla et al. 2008), we conjectured that Na⁺ accumulation during the inspiratory burst might recruit electrogenic Na⁺/K⁺ ATPase pumps to produce I_pump. I_pump activation can aid in burst termination and influence network excitability in spinal networks (Darbon et al. 2003). I_pump may play a similar role in the preBötC and thus be relevant to the control of the interburst interval.

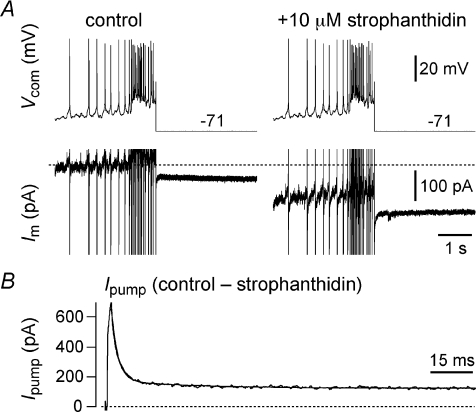
We applied the I_pump blocker strophanthidin (10 μm) to rhythmically active slice preparations in 9 mm K⁺, which depolarized baseline membrane potential in preBötC neurons during the interburst interval by 21 ± 2 mV and increased respiratory frequency to 0.47 ± 0.1 Hz within 71 ± 5 s of drug application (n= 6). The amplitude of inspiratory bursts decreased 4.8 ± 0.2 mV (data not shown) during strophanthidin application, measured at the peak frequency response. By 243 ± 35 s the rhythm stopped and preBötC neurons spiked tonically (1–5 Hz) at a depolarized baseline voltage of −39 ± 2 mV (n= 6, not shown). These data suggest that I_pump may influence inspiratory rhythm. However, these experiments are difficult to interpret without knowing the relative contribution of I_pump to burst termination versus its role in maintaining the Na⁺ and K⁺ gradients and the baseline membrane potential.

To measure I_pump directly we first recorded an inspiratory burst in current clamp that lasted ∼750 ms with an underlying drive potential of 10 mV, and then used this waveform as the basis for a voltage command in subsequent experiments on isolated preBötC neurons after bath-applying ionotropic receptor antagonists (see Methods). Figure 6A shows the modified protocol wherein the burst waveform was terminated 50 ms early by clamping the voltage to E_K (−71 mV in 9 mm K⁺). This allowed us to measure non-K⁺ currents. We repeated the protocol 1–2 min after application of 10 μm strophanthidin to minimize the effects of changes in ionic gradients and obtained I_pump by subtraction (Fig. 6B). I_pump peaked at ∼600 pA in the first 20 ms after clamping to E_K and then decayed bi-exponentially with a fast (τ∼ 25 ms) and slow (τ∼ 100 ms) component; I_pump also exhibited ∼100 pA of outward current at steady-state (n= 3). We also performed this experiment in current clamp, using 500 ms current steps to evoke 30–50 zHz spiking in synaptically isolated preBötC neurons. We repeated these step currents in 10 μm strophanthidin and obtained the contribution of the Na⁺/K⁺ ATPase pump by subtraction. The pump contributed 8 ± 2 mV of membrane hyperpolarization that decayed with a time constant of 50 ± 9 ms (n= 4). These data suggest that I_pump has a dynamic and a tonic component. The dynamic component of I_pump develops during the inspiratory phase and is relevant during burst termination, but its contribution is brief, decaying significantly within 25–100 ms. The tonic component of I_pump may influence network excitability through its tonic ∼100 pA contribution to baseline membrane potential.

Figure 6. Na⁺/K⁺ ATPase pump current (I_pump) in preBötC neurons.

A, inspiratory burst waveforms applied in voltage clamp in control and 10 μm strophanthidin conditions. The burst was terminated 50 ms early and clamped to E_K (−71 mV). B, I_pump obtained by subtraction plotted on an expanded time scale and fitted with a bi-exponential curve (superimposed).

Discussion

We show that in vitro respiratory rhythm driven by the preBötC operates with frequencies spanning 0.008–0.3 Hz (Fig. 1) and can transiently run at frequencies as high as ∼1 Hz following local stimulation with AMPA puffs (Fig. 4) with similar XII output at nearly all frequencies. We observed stable rhythms with very long periods (≥2 min) by decreasing [K⁺]_o to hyperpolarize baseline membrane potential in preBötC neurons. Lowering [K⁺]_o appeared to sweep the respiratory network through low frequency states and in some cases into a quiescent regime without respiratory-related oscillations. Yet, the quiescent preBötC was excitable, so that transient local stimuli, i.e. AMPA pulses, evoked XII output. Conversely, raising [K⁺]_o increased respiratory frequency. XII bursts were remarkably stable over the broad range of frequencies, being statistically indistinguishable in amplitude, area and half-width from control bursts (at 9 mm K⁺) at most [K⁺]_o and modestly decreased at 4 and 5 mm K⁺. Burst frequency was modulated by [K⁺]_o in a graded fashion, due almost exclusively to changes in the interburst interval. What do these results suggest about the underlying mechanisms?

Given the presence of recurrent connections between preBötC neurons (Rekling et al. 2000a; Guyenet et al. 2002; Hartelt et al. 2008), we propose that the dynamics of recurrent excitation between rhythmogenic neurons (Rekling et al. 1996; Hayes & Del Negro, 2007), control – at least in part – the interburst interval in the preBötC. This process is likely to culminate when excitation reaches an as yet unknown critical fraction of rhythmogenic neurons in the preBötC and results in a synchronous inspiratory burst in the preBötC that drives XII output.

Changes in [K⁺]_o primarily affect baseline membrane potential. [K⁺]_o could thus control frequency by governing the number of excitatory preBötC neurons at or near threshold and influence how long it takes for regenerative recurrent excitation to envelop the preBötC and initiate XII output. This type of frequency control is predicted for networks akin to the preBötC, according to the speed of propagation in random graphs with recurrent connectivity (Watts, 2002). In mathematical models of networks encapsulated in low dimensional ordinary differential equations that are amenable to geometric analyses by certain approximations (Wilson & Cowan, 1972; Rinzel & Ermentrout, 1998), recurrent excitation is a slow moving trajectory in the vicinity of a threshold defined for networks (the ‘ghost of a saddle point’, Strogatz, 1994). The proximity to this threshold, which is directly regulated by excitability parameters, forms a simple mechanism for frequency control that can operate stably at very low frequencies but is also exquisitely sensitive to perturbations that can rapidly reinitiate (reset) network burst cycles (Hoppensteadt & Izhikevich, 1997; Rinzel & Ermentrout, 1998).

Whereas frequency monotonically increased with [K⁺]_o, the stability of the rhythm was a biphasic function of [K⁺]_o. At low [K⁺]_o, the stability indicated by low CV could result from reduced background spiking activity. Stochastic fluctuations in neuronal activity are decreased, and therefore less likely to perturb the regular low frequency of recurrent excitatory cascades. At intermediate [K⁺]_o, the lower stability indicated by higher CV may result from spurious bursts triggered by a growing subset of preBötC neurons with baseline membrane potential at or near threshold. Thus, [K⁺]_o elevation enlarges the subset of neurons able to initiate recurrent excitation, causing stochastic fluctuations of cycle period (De Felice & Isaac, 1993). At higher [K⁺]_o levels, when the CV decreases again, a large fraction of preBötC neurons has baseline voltage at or above spike threshold. With widespread tonic activity (transiently stopped by burst-terminating currents), recurrent excitation could begin with practically any neuron and the random activity of single cells would be less likely to lead to burst generation. These changes in the initiation and dynamics of recurrent excitation, however, apparently do not affect the actual burst-generating mechanisms and ultimately result in termination of a burst and resetting of the cycle. In this way a reliable oscillator arises from a large number of fluctuating, less-reliable components (Enright, 1980). These factors that influence the initiation of recurrent excitation apparently do not affect the shape or duration of the burst-once it is initiated.

Varying [K⁺]_o, however, is not the only means of affecting the frequency or excitability of the motor nerve output of the slice. The frequency of rhythm generation is highly sensitive to [Ca²⁺]_o. While we employed 3 mm K⁺ to produce stable low frequency rhythms in our 550 μm thick slices, 3 mm K⁺ is sufficient to transiently support faster, i.e. ∼0.1 Hz, rhythms in neonatal rat slice preparations of similar thickness, but in lower extracellular Ca²⁺ (Ruangkittisakul et al. 2006). At the [Ca²⁺]_o employed in our preparation (1.5 mm), rhythm generation stops, while the use of lower [Ca²⁺]_o (<1.2 mm) results in rhythms that start at frequencies of ∼0.1 Hz, but decline slowly over several hours (Ruangkittisakul et al. 2007). The mechanism of this Ca²⁺ modulation may be related to surface charge screening by divalent ions (Hille, 2001) or long-term effects on the Ca²⁺ buffering capacity of respiratory neurons (Alheid et al. 2002).

Stimulation of ionotropic glutamate receptors can also increase excitability independent of [K⁺]_o. Acute unilateral AMPA injection into the preBötC appears to evoke XII bursts similar to spontaneous XII bursts without regard to [K⁺]_o and the ongoing frequency of the rhythm. We propose that the XII_evoked also results from recurrent excitation. Local AMPA receptor activation in the preBötC excites interconnected glutamatergic interneurons (Rekling et al. 2000b; Hartelt et al. 2008; Mironov, 2008). For unilateral AMPA injections in the preBötC to generate network bursts in a recurrent excitatory network where approximately half of the neurons in the preBötC are glycinergic (Hulsmann et al. 2007; Gray et al. 2008), we propose that excitatory neurons are more highly interconnected, connected with stronger synapses, and/or have higher excitability, e.g. higher glutamate sensitivity, than inhibitory neurons.

Indeed, GABAergic and glycinergic inputs have significant effects only at specific [K⁺]_o and do not mediate the strong modulation of frequency by [K⁺]_o. Removing fast synaptic inhibition significantly raised the frequency only at 5 and 6 mm K⁺ and nearly doubled the XII amplitude at 3–6 mm K⁺, with no significant effect on frequency at 3 and 4 mm K⁺. Inhibition exhibited a significant influence on motor output only within a limited range of [K⁺]_o (Rekling et al. 2000a). Although we did not observe a significant increase in XII output under our standard conditions (9 mm K⁺), disinhibition has been shown to enhance the XII burst amplitude, while reducing its relative power, in neonatal and juvenile mice in vitro (Sebe et al. 2006). These effects are consistent with synaptic inhibition influencing recurrent excitation and the interburst interval, which is significant at some [K⁺]_o levels, but not others.

In neonatal rats, activation of Cl⁻-mediated conductances such as those produced by GABA and glycine receptors can have disparate effects at different [K⁺]_o, by affecting the activity of Cl⁻ cotransporters to change the Cl⁻ reversal potential. Thus, activation of Cl⁻ conductances at 3 mm K⁺ is inhibitory while at 9 mm K⁺ activation of Cl⁻ conductances is excitatory (Ren & Greer, 2006). However, also in neonatal rats, blocking Cl⁻-mediated synaptic conductances increased the frequency and amplitude of XII activity at 9 mm K⁺ in slices (Shao & Feldman, 1997) and increased the burst frequency in isolated preBötC ‘islands’ in a range of K⁺ from 4 to 15 mm (Johnson et al. 2001). These data suggest that the Cl⁻ gradient was in its mature form and that Cl⁻ conductances were inhibitory during the neonatal period even in the presence of 9 mm (or higher) K⁺. While preBötC neurons may express a mature Cl⁻ reversal potential, the Cl⁻ reversal potential in hypoglossal motoneurons, which relay and shape the preBötC output, is not stable during the neonatal period and may also contribute to disparate effects of GABA and glycine antagonists on inspiratory burst shape (Singer et al. 1998). Our present results are consistent with [K⁺]_o having some effect on the Cl⁻ reversal potential because disinhibition had a greater effect on XII burst amplitude and frequency at lower [K⁺]_o, i.e. 3–6 mm, where the Cl⁻ gradient would be expected to be inhibitory (Ren & Greer, 2006). Whether this applies to the XII nucleus as well as the preBötC in neonatal mice remains to be determined. While the role of GABAergic and glycinergic transmission in medullary slices of neonatal rats remains equivocal, antagonism of both receptors did not abolish the strong modulation of frequency by [K⁺]_o.

The latency changes in XII_evoked during AMPA stimulation in the preBötC suggest a key role for the Type 1 class of preBötC neurons (Rekling et al. 1996; Rekling & Feldman, 1998). The latency of the first burst evoked by AMPA puffs varied inversely as a function of stimulus delay within each cycle even as XII_evoked magnitude was conserved, i.e. Δt_evoked was long when Δt_stim was short. Type 1 preBötC neurons, which are hypothesized to be important in rhythm generation, show 5–10 mV afterhyperpolarizations (AHP) following inspiratory bursts that lasts ∼2 s and gives rise to a ramp-like trajectory during the interburst interval (Rekling et al. 1996; Gray et al. 1999). While these neurons constitute a subset of the entire population of preBötC neurons, we propose that at short Δt_stim it takes longer for recurrent excitation to depolarize a sufficient number of preBötC neurons to threshold because Type 1 neurons are in their AHP phase. However, this AHP is unlikely to underlie an absolute refractory state for the network, since depolarizing current pulses applied during the AHP in Type 1 neurons can rapidly evoke spiking activity (Rekling et al. 1996). As the interburst interval evolves, Type 1 neurons steadily depolarize, and progressively less time is required for stimuli, e.g. AMPA microinjections, to evoke spiking activity that we postulate triggers recurrent excitation in the preBötC to evoke the next XII burst. Thus, longer Δt_stim allow for shorter latencies because more rhythmogenic Type 1 preBötC move closer to threshold.

We explored mechanisms contributing to burst termination and the influence of Δt_stim on the latency to onset of the next XII burst. Since Na⁺ is the main charge carrier for the burst-generating current I_CAN (Pace et al. 2007a), we posit that an activity-dependent outward current like I_pump, which we measured, or an ATP-dependent K⁺ current (I_K-ATP) that responds to I_pump-mediated ATP depletion, could contribute to burst termination (Ballerini et al. 1997; Haller et al. 2001; Darbon et al. 2003). A parallel Na⁺-dependent K⁺ current (I_K-Na) might also contribute (Wallen et al. 2007). While the tonic component of I_pump likely contributes to baseline membrane potential, it does not play an active role in burst termination. The removal of the tonic component is probably responsible for the initial depolarization and acceleration of the respiratory rhythm when strophanthidin was bath applied to slices. To isolate a dynamic component of I_pump, we employed a voltage-clamp protocol that mimicked the endogenous burst shape, but terminated the burst at baseline E_K. Because I_pump participates in the maintenance of ionic gradients across neuronal membranes, strophanthidin block of I_pump could result in rundown of these gradients and changes in the reversal potentials of Na⁺ and K⁺, possibly affecting our measurements of I_pump. To minimize this effect, we ran these experiments 1–2 min following strophanthidin application when the predominant consequence of blocking the Na⁺/K⁺ ATPase is membrane potential depolarization due to the loss of the tonic outward current from electrogenic activation of the pump. Our measurements show that I_pump contributes a large transient outward current at burst termination that decays almost completely within 50–200 ms. A change in ionic gradients during this time frame is unlikely to account for the large magnitude of the dynamic component of I_pump. This transient current reflects the dynamic component of I_pump that could participate in burst termination, being strong enough to countervail the inward currents that underlie inspiratory drive, yet decaying rapidly enough such that another XII burst can be evoked within ∼1 s by an adequate stimulus.

Our results are consistent with the group-pacemaker hypothesis in which the respiratory network collectively functions like an excitable unit (Rekling et al. 1996; Rekling & Feldman, 1998; Feldman & Del Negro, 2006; Pace et al. 2007a), regardless of whether or not individual neurons have pacemaker properties (Rekling et al. 1996; Rekling & Feldman, 1998). In this model, distributed excitatory synaptic coupling forms the essential mechanism governing the period between inspiratory bursts. Thus, a critical fraction of interconnected neurons with spiking activity can initiate a cascade of recurrent excitation. Glutamatergic excitation ultimately evokes robust inspiratory bursts that then reset by multiple mechanisms that include I_pump (Pace et al. 2007a; Mironov, 2008). Systems with these properties are excitable, with the ability to evoke full amplitude bursts from their quiescent state, and also to support stable burst oscillations activity over a large range of frequencies (Hoppensteadt & Izhikevich, 1997; Rinzel & Ermentrout, 1998).

In other contemporary models of respiratory rhythm generation, the duration of the expiratory phase is determined by a variable directly related to inspiration. Models based on voltage-dependent pacemaker neurons rely on the deinactivation kinetics of persistent Na⁺ current (I_NaP) during the expiratory phase (Butera et al. 1999b; Del Negro et al. 2001; Purvis et al. 2007; Smith et al. 2007). In these models, the rhythmogenic kernel in the preBötC cannot generate cellular- or network-level bursts while I_NaP remains inactivated. Moreover, during the expiratory phase, evoked bursts at the cellular and network level are graded functions of recovery time because they depend on I_NaP deinactivation (Butera et al. 1999a,b). These properties are inconsistent with evoked XII bursts that emerged at full magnitude. This suggests that intrinsic properties like I_NaP are not well suited biophysically to influence the interburst interval despite being widely expressed in the preBötC (Ptak et al. 2005; Pace et al. 2007b) and that mechanisms of burst generation are separate from mechanisms that can specifically control expiratory phase duration.

While ionic mechanisms for inspiratory burst generation and mechanism(s) that control interburst interval may interact, we suggest that they are fundamentally different processes that can be separately regulated. Such independent regulation of inspiratory and expiratory durations occurs under physiological conditions in amphibians and during hibernation in mammals (Milsom, 1992; Gargaglioni & Milsom, 2007), and with modest changes in ventilation from rest in humans (Gardner, 1980). In fact, that respiratory rhythmogenic circuits can operate stably at very low frequencies well below the usual minima may reflect physiological changes seen in hypothermia and/or during hibernation (Milsom, 1991, 1992). We propose that the respiratory circuit can utilize a distinct mechanism to control the interburst interval, which operates stably over a broad range of frequencies, without an obligatory effect on inspiratory pattern.

Because breathing is a continuous behaviour in mammals, accounting for ∼6% of basal metabolism, controlling phases independently in respiration may offer an energetic advantage (Milsom, 1989). Respiratory pattern appears optimized at rest to minimize energy expenditure, which is consumed principally by the activity of the respiratory pump muscles driving the movement of air. At rest, inspiration is the power stroke of breathing, and the activation of inspiratory pump muscles the principal source of energy expenditure. Thus, the resting pattern of inspiratory muscle activity is probably highly optimized, and modest changes in ventilation can be produced without affecting its energetics simply by affecting the interburst period, i.e. expiratory duration (Milsom, 1989).

Our data suggest that during active inspiratory-dominated respiratory rhythm, when expiration is passive, changes in expiratory duration are effected in the preBötC. While additional respiratory-related areas of the brainstem or pons, or sensory afferents, almost certainly provide afferent drive to modulate mechanisms determining expiratory duration within the preBötC, these areas are not required for the expression of such changes. The situation is likely to change as ventilation is further increased and expiration becomes active.