Medical Geography: a Promising Field of Application for Geostatistics

Abstract

The analysis of health data and putative covariates, such as environmental, socio-economic, behavioral or demographic factors, is a promising application for geostatistics. It presents, however, several methodological challenges that arise from the fact that data are typically aggregated over irregular spatial supports and consist of a numerator and a denominator (i.e. population size). This paper presents an overview of recent developments in the field of health geostatistics, with an emphasis on three main steps in the analysis of areal health data: estimation of the underlying disease risk, detection of areas with significantly higher risk, and analysis of relationships with putative risk factors. The analysis is illustrated using age-adjusted cervix cancer mortality rates recorded over the 1970–1994 period for 118 counties of four states in the Western USA. Poisson kriging allows the filtering of noisy mortality rates computed from small population sizes, enhancing the correlation with two putative explanatory variables: percentage of habitants living below the federally defined poverty line, and percentage of Hispanic females. Area-to-point kriging formulation creates continuous maps of mortality risk, reducing the visual bias associated with the interpretation of choropleth maps. Stochastic simulation is used to generate realizations of cancer mortality maps, which allows one to quantify numerically how the uncertainty about the spatial distribution of health outcomes translates into uncertainty about the location of clusters of high values or the correlation with covariates. Last, geographically-weighted regression highlights the non-stationarity in the explanatory power of covariates: the higher mortality values along the coast are better explained by the two covariates than the lower risk recorded in Utah.

1 Introduction

Since its early development for the assessment of mineral deposits, geostatistics has been used in a growing number of disciplines dealing with the analysis of data distributed in space and/or time. One field that has received little attention in the geostatistical literature is medical geography or spatial epidemiology, which is concerned with the study of spatial patterns of disease incidence and mortality and the identification of potential “causes” of disease, such as environmental exposure or socio-demographic factors (Waller and Gotway 2004). This lack of attention contrasts with the increasing need for methods to analyze health data following the emergence of new infectious diseases (e.g. West Nile Virus, bird flu), the higher occurrence of cancer mortality associated with longer life expectancy, and the burden of a widely polluted environment on human health.

The first initiative to tailor geostatistical tools to the analysis of disease rates must be credited to Christian Lajaunie (1991) from the Center of geostatistics in Fontainebleau, France. He developed an approach that accounts for spatial heterogeneity in the population of children to estimate the semivariogram of the “risk of developing cancer” from the semivariogram of observed mortality rates. Binomial cokriging was then used to produce a map of the risk of childhood cancer in the West Midlands of England (Oliver et al 1993, 1998; Webster et al. 1994). Later, the same methodology was used in the mapping of lung cancer mortality across the US (Goovaerts 2005a). In his book (p.385–402), Cressie (1993) analyzed the spatial distribution of the counts of sudden-infant-death-syndromes (SID) for 100 counties of North Carolina. He proposed a two-step transform of the data to remove first the mean-variance dependence of the data and next the heteroscedasticity. Traditional variography was then applied to the transformed residuals. In contrast, Christakos and Lai (1997) incorporated directly the fuzziness or softness of the data into the computation of the sample semivariogram and into the kriging equations using the BME (Bayesian Maximum Entropy) formalism. More recently, geostatistics was used for mapping the number of low birth weight (LBW) babies at the Census tract level, accounting for county-level LBW data and covariates measured over different spatial supports, such as a fine grid of ground-level particulate matter concentrations or tract population (Gotway and Young 2007).

Individual humans represent the basic unit of spatial analysis in health research. However, because of the need to protect patient privacy publicly available data are often aggregated to a sufficient extent to prevent the disclosure or reconstruction of patient identity. The information available for human health studies thus takes the form of disease rates, e.g. number of deceased or infected patients per 100,000 habitants, aggregated within areas that can span a wide range of scales, such as census units, counties or states. Associations can then be investigated between these areal data and environmental, socio-economic, behavioral or demographic covariates. Figure 1 shows an example of datasets that could support a study of the impact of demographic and socioeconomic factors on cervix cancer mortality. The top map shows the spatial distribution of age-adjusted mortality rates recorded over the 1970–1994 period for 118 counties of four states in the Western USA. The corresponding population at risk is displayed in the middle maps. The population size, which is available for each census block and assumed uniform within these census units, was aggregated at two levels: counties and 25 km² cells. The bottom maps show two putative explanatory variables: percentage of habitants living below the federally defined poverty line, and percentage of Hispanic females. Indeed, Hispanic women tend to have elevated risk of cervix cancer, while poverty reduces access to health care and to early detection through the Pap smear test in particular (Friedell et al. 1992). These socio-demographic data are available at the census block level and were assigned to the nodes of a 5km spacing grid for the purpose of this study (same resolution as the population map).

Figure 1.

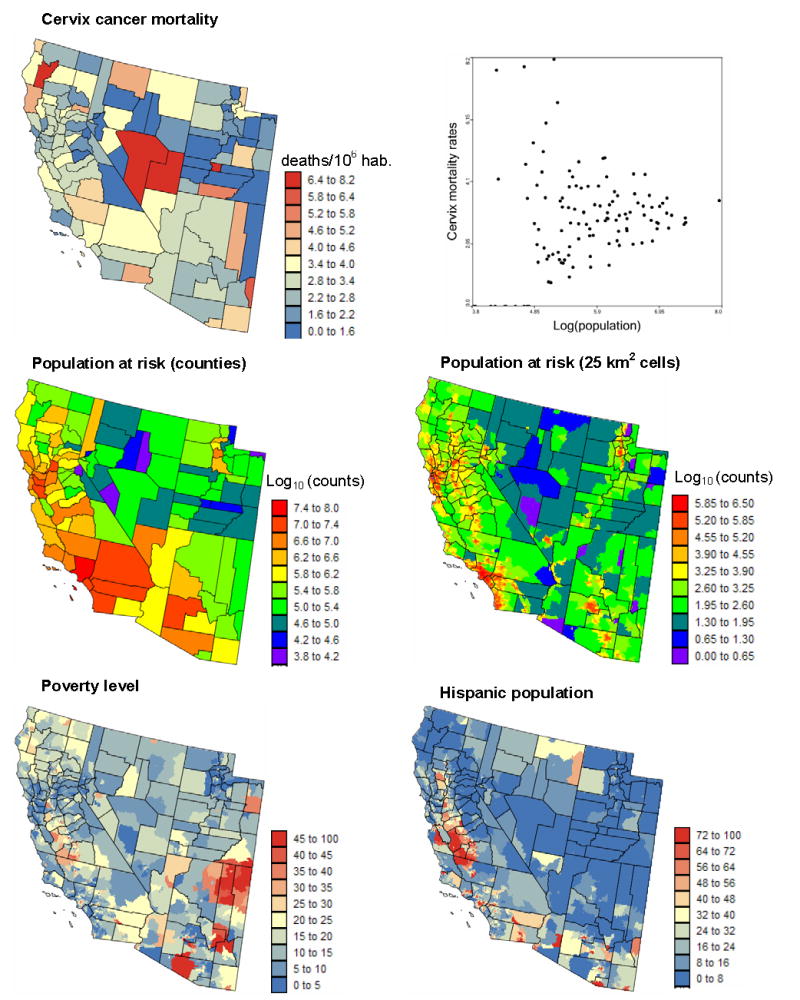
Geographical distribution of cervix cancer mortality rates recorded for white females over the period 1970–1994, and the corresponding population at risk (aggregated within counties or assigned to 25 km² cells). Scatterplot illustrates the larger variance of rates computed from sparsely populated counties. Bottom maps show two putative risk factors: percentage of habitants living below the federally defined poverty line, and percentage of Hispanic females.

A visual inspection of the cancer mortality map conveys the impression that rates are much higher in the centre of the study area (Nye and Lincoln Counties), as well as in one Northern California county. This result must however be interpreted with caution since the population is not uniformly distributed across the study area and rates computed from sparsely populated counties tend to be less reliable, an effect known as “small number problem” and illustrated by the top scattergram in Fig. 1. The use of administrative units to report the results (i.e. counties in this case) can also bias the interpretation: had the two counties with high rates been much smaller in size, these high values likely would have been perceived as less problematic. Last, the mismatch of spatial supports for cancer rates and explanatory variables prevents their direct use in correlation analysis. Unlike datasets typically analyzed by geostatisticians, the attributes of interest are here measured exhaustively. Ordinary kriging, the backbone of any geostatistical analysis, thus seems of little use. Yet, one can envision at least three main applications of geostatistics for the analysis of such areal data:

1. Filtering of the noise caused by the small number problem using a variant of kriging with non-systematic measurement errors.

2. Modeling of the uncertainty attached to the map of filtered rates using stochastic simulation, and propagation of this uncertainty through subsequent analysis, such as the detection of aggregate of counties (clusters) with significantly higher or lower rates than neighboring counties.

3. Disaggregation of county-level data to map cancer mortality at a resolution compatible with the measurement support of explanatory variables.

Goovaerts (2005b, 2006a, b) introduced a geostatistical approach to address all three issues and compared its performances to empirical and Bayesian methods which have been traditionally used in health science. The filtering method is based on Poisson kriging and semivariogram estimators developed by Monestiez et al. (2005, 2006) for mapping the relative abundance of species in the presence of spatially heterogeneous observation efforts and sparse animal sightings. In addition, Poisson kriging can be combined with stochastic simulation to generate multiple realizations of the spatial distribution of disease risk, which allows one to quantify numerically how the uncertainty about the spatial distribution of health outcomes translates into uncertainty about the location of disease clusters (Goovaerts 2006a), the presence of significant boundaries (Goovaerts 2008b), or the relationship between health outcomes and putative risk factors. A limitation of all these studies is the assumption that the size and shape of geographical units, as well as the distribution of the population within those units, are uniform, which is clearly not adequate in the example of Fig. 1. The last issue of change of support was addressed recently in the geostatistical literature (Gotway and Young 2002, 2005; Kyriakidis 2004; Goovaerts 2008a). In its general form kriging can accommodate different spatial supports for the data and the prediction, while ensuring the coherence of the predictions so that disaggregated estimates of count data are non-negative (Yoo and Kyriakidis, 2006) and their sum is equal to the original areal count. The coherence property needs however to be tailored to the current situation where areal rate data have various degree of reliability depending on the size of the population at risk (Goovaerts 2006b).

Geostatistics represents an attractive alternative to increasingly popular Bayesian spatial models in that: 1) it is easier to implement and less CPU intensive since it does not require lengthy and potentially non-converging iterative estimation procedures, and 2) it accounts for the size and shape of geographical units, avoiding the limitations of conditional auto-regressive (CAR) models commonly used in Bayesian algorithms while allowing for the prediction of the risk over any spatial support. Goovaerts and Gebreab (2008) conducted a simulation-based evaluation of performance of geostatistical and full Bayesian disease-mapping models, using the BYM model (Besag et al. 1991) as benchmark for Bayesian methods. They found that the geostatistical approach yields smaller prediction errors, more precise and accurate probability intervals, and allows a better discrimination between counties with high and low mortality risks. The BYM model also generates smoother risk surfaces, leading to a much larger proportion of false negatives than the geostatistical model in particular as the risk threshold raises. The benefit of Poisson kriging increases as the county geography becomes more heterogeneous and when data beyond the adjacent counties (i.e. 1^st order CAR neighborhood) are used in the estimation.

This paper discusses how geostatistics can benefit three main steps of the analysis of areal health data: estimation of the underlying disease risk, detection of areas with significantly higher risk, and analysis of relationships with putative risk factors. The different concepts are illustrated using the cervix cancer data of Fig. 1.

2 Estimating mortality risks from observed rates

2.1 Area-to-Area (ATA) Poisson Kriging

For a given number N of geographical units v_α (e.g. counties), denote the observed mortality rates (areal data) as z(v_α)=d(v_α)/n(v_α), where d(v_α) is the number of recorded mortality cases and n(v_α) is the size of the population at risk. The disease count d(v_α) is interpreted as a realization of a random variable D(v_α) that follows a Poisson distribution with one parameter (expected number of counts) that is the product of the population size n(v_α) by the local risk R(v_α), see Goovaerts (2005b) for more details. The noise-filtered mortality rate for a given area v_α, called mortality risk, is estimated as a linear combination of the kernel rate z(v_α) and the rates observed in (K-1) neighboring entities v_I:

$$\widehat{r}(v_{\alpha })=\sum _{i=1}^K{\lambda }_{i}z(v_i)$$ (1)

The weights λ_i assigned to the K rates are computed by solving the following system of linear equations; known as “Poisson kriging” system:

$$\begin{array}{l}\sum _{j=1}^K{\lambda }_j\left[{\overline{C}}_R(v_i,v_j)+{\delta }_{ij}\frac{m^{\ast }}{n(v_i)}\right]+\mu (v_{\alpha })={\overline{C}}_R(v_i,v_{\alpha })\text{i}=1,\dots ,K\\ \sum _{j=1}^K{\lambda }_j=1.\end{array}$$ (2)

where δ_ij=1 if i=j and 0 otherwise, and m* is the population-weighted mean of the N rates. The “error variance” term, m*/n(v_i), leads to smaller weights for less reliable data (i.e. rates measured over smaller populations). In addition to the population size, the kriging system accounts for the spatial correlation among geographical units through the area-to-area covariance terms C̄_R(v_i, v_j) =Cov{R(v_i), R(v_j)} and C̄_R(v_i, v_α). Those covariances are numerically approximated by averaging the point-support covariance C_R(h) computed between any two locations discretizing the areas v_i and v_j:

$${\overline{C}}_R(v_i,v_j)=\frac{1}{{\displaystyle \sum _{s=1}^{P_i}}{\displaystyle \sum _{s^{\prime }=1}^{P_j}}{w}_{s{s}^{\prime }}}\sum _{s=1}^{P_i}\sum _{s^{\prime }=1}^{P_j}{w}_{s{s}^{\prime }}{C}_R({\mathbf{u}}_s-{\mathbf{u}}_{s^{\prime }})$$ (3)

where P_i and P_j are the number of points used to discretize the two areas v_i and v_j, respectively. The weights w_ss′ are computed as the product of population sizes assigned to each discretizing point u_s and u_s′:

$$w_{s{s}^{\prime }}=n({\mathbf{u}}_s)\times n({\mathbf{u}}_{s^{\prime }})\text{with}\sum _{s=1}^{P_i}n({\mathbf{u}}_s)=n(v_i)\text{and}\sum _{s^{\prime }=1}^{P_i}n({\mathbf{u}}_{s^{\prime }})=n(v_j)$$

In this study the discretizing points were identified with the nodes of a 5 km grid, yielding a total of 11 to 2,082 discretizing per county; see Fig. 2. The population size, which is available for each census block, was aggregated within each 25 km² cell under the assumption of uniform distribution within these small census units. If the cell size becomes smaller than the census blocks and land use heterogeneity invalidates the assumption of uniform population repartition, a disaggregation procedure might be necessary and could be conducted using area-to-point interpolation (Liu et al. 2008).

Figure 2.

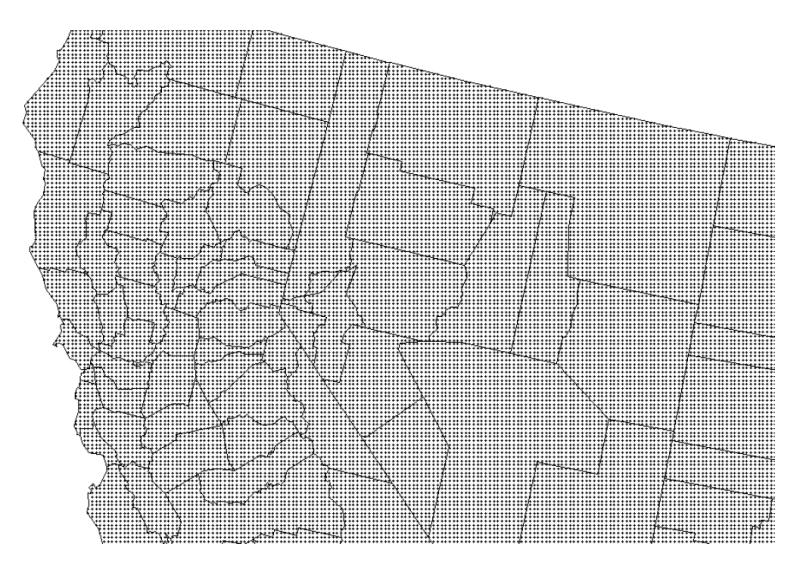
Example of discretization geography used to compute county-to-county covariance terms for area-to-area kriging.

Except if spectral methods are used for integration (Equation 3) it is not computationally efficient to use the same discretizing level for each geographical unit when they differ by several orders of magnitude like in the West coast. One solution is to use flexible discretizing grids that ensure a constant number of discretizing points within each unit. For example, in TerraSeer’s STIS software (Avruskin et al. 2004) a given number of discretization points is distributed uniformly within each polygon according to a stratified random design.

The uncertainty about the cancer mortality risk prevailing within the geographical unit v_α can be modeled using the conditional cumulative distribution function (ccdf) of the risk variable R(v_α). Under the assumption of normality of the prediction errors, that ccdf is defined as:

$$F(v_{\alpha };r\mid K))=\text{Prob}\left\{R(v_{\alpha })\le r\mid (K)\right\}=G\left(\frac{r-\widehat{r}(v_{\alpha })}{\widehat{\sigma }(v_{\alpha })}\right)$$ (4)

G(.) is the cumulative distribution function of the standard normal random variable, and σ̂(v_α) is the square root of the kriging variance estimated as:

$${\widehat{\sigma }}^2(v_{\alpha })={\overline{C}}_R(v_{\alpha },v_{\alpha })-\sum _{i=1}^K{\lambda }_i{\overline{C}}_R(v_i,v_{\alpha })-\mu (v_{\alpha })$$ (5)

where C̄_R(v_α, v_α) is the within-area covariance that is computed according to Equation (3) with v_i = v_j = v_α. The notation “|(K)” expresses conditioning to the local information, say, K neighboring observed rates. The function (4) gives the probability that the unknown risk is no greater than any given threshold r. It is modeled as a Gaussian distribution with the mean and variance corresponding to the Poisson kriging estimate and variance.

2.2 Area-to-Point (ATP) Poisson Kriging

A particular case of ATA kriging is when the prediction support is so small that it can be assimilated to a point u_s, leading to the following area-to-point Poisson kriging estimator and kriging variance:

$${\widehat{r}}_{PK}({\mathbf{u}}_s)=\sum _{i=1}^K{\lambda }_i({\mathbf{u}}_s)z(v_i)$$ (6)

$${\widehat{\sigma }}_{PK}^2({\mathbf{u}}_s)=C_R(0)-\sum _{i=1}^K{\lambda }_i({\mathbf{u}}_s){\overline{C}}_R(v_i,{\mathbf{u}}_s)-\mu ({\mathbf{u}}_s)$$ (7)

The kriging weights and the Lagrange parameter μ(u_s) are computed by solving the following system of linear equations:

$$\begin{array}{l}\sum _{j=1}^K{\lambda }_j({\mathbf{u}}_s)\left[{\overline{C}}_R(v_i,v_j)+{\delta }_{ij}\frac{m^{\ast }}{n(v_i)}\right]+\mu ({\mathbf{u}}_s)={\overline{C}}_R(v_i,{\mathbf{u}}_s)\text{i}=1,\dots ,K\\ \sum _{j=1}^K{\lambda }_j({\mathbf{u}}_s)=1.\end{array}$$ (8)

The ATP kriging system is similar to the ATA kriging system (2), except for the right-hand-side term where the area-to-area covariances C̄_R(v_i, v_α) are replaced by area-to-point covariances C̄_R(v_i, u_s) that are approximated as:

$${\overline{C}}_R(v_i,{\mathbf{u}}_s)=\frac{1}{{\displaystyle \sum _{s^{\prime }=1}^{P_i}}{w}_{s^{\prime }s}}\sum _{s^{\prime }=1}^{P_i}{w}_{s^{\prime }s}{C}_R({\mathbf{u}}_{s^{\prime }},{\mathbf{u}}_s)$$ (9)

where P_i is the number of points used to discretize the area v_i and the weights w_s′s are computed as for expression (3). ATP kriging can be conducted at each node of a grid covering the study area, resulting in a continuous (isopleth) map of mortality risk and reducing the visual bias that is typically associated with the interpretation of choropleth maps. Another interesting property of the ATP kriging estimator is its coherence: the population-weighted average of the risk values estimated at the P_α points u_s discretizing a given entity v_α yields the ATA risk estimate for this entity:

$${\widehat{r}}_{PK}(v_{\alpha })=\frac{1}{n(v_{\alpha })}\sum _{s=1}^{P_{\alpha }}n({\mathbf{u}}_s){\widehat{r}}_{PK}({\mathbf{u}}_s)$$ (10)

Constraint (10) is satisfied if the same K areal data are used for the ATP kriging of the P_α risk values.

2.3 Deconvolution of the Semivariogram of the Risk

Both ATA and ATP kriging require knowledge of the point support covariance of the risk C_R(h), or equivalently the semivariogram γ_R(h). This function cannot be estimated directly from the observed rates, since only areal data are available. Thus, only the regularized semivariogram of the risk can be estimated as:

$${\widehat{\gamma }}_{Rv}(\mathbf{h})=\frac{1}{2{\displaystyle \sum _{\alpha ,\beta }^{N(\mathbf{h})}}\frac{n(v_{\alpha })n(v_{\beta })}{n(v_{\alpha })+n(v_{\beta })}}\sum _{\alpha ,\beta }^{N(\mathbf{h})}\left\{\frac{n(v_{\alpha })n(v_{\beta })}{n(v_{\alpha })+n(v_{\beta })}{\left[z(v_{\alpha })-z(v_{\beta })\right]}^2-m^{\ast }\right\}$$ (11)

where N(h) is the number of pairs of areas (v_α,v_β) whose population-weighted centroids are separated by the vector h. The different spatial increments [z(v_α)−z(v_β)]² are weighted by a function of their respective population sizes, n(v_α)n(v_β)/[n(v_α)+n(v_β)], a term which is inversely proportional to their standard deviations (Monestiez et al 2006). More importance is thus given to the more reliable data pairs (i.e. smaller standard deviations).

Derivation of a point-support semivariogram from the experimental semivariogram γ̂_Rv(h) computed from areal data is called “deconvolution”, an operation that has been the topic of much research (Journel and Huijbregts 1978; Mockus 1998; Gotway and Young 2007; Kyriakidis 2004). In this paper, we adopted the iterative procedure introduced for rate data measured over irregular geographical units (Goovaerts 2006b) whereby one seeks the point-support model that, once regularized, is the closest to the model fitted to areal data This innovative algorithm starts with the derivation of an initial deconvolved model γ⁽⁰⁾(h); for example the model γ_Rv(h) fitted to the areal data. This initial model is then regularized using the following expression:

$${\gamma }_{\mathrm{regul}}(\mathbf{h})={\overline{\gamma }}^{(0)}(v,v_h)-{\overline{\gamma }}_h^{(0)}(v,v)$$ (12)

where γ̄⁽⁰⁾(v, v_h) is the area-to-area semivariogram value for any two counties separated by a distance h. It is approximated by the population-weighted average (3), using γ⁽⁰⁾(h) instead of C(h). The second term, ${\overline{\gamma }}_h^{(0)}(v,v)$, is the within-area semivariogram value. Unlike the expression commonly found in the literature, this term varies as a function of the separation distance since smaller areas tend to be paired at shorter distances. To account for heterogeneous population density, the distance between any two counties is estimated as a population-weighted average of distances between locations discretizing the pair of counties:

$$\mathrm{Dist}(v_i,v_j)=\frac{1}{{\displaystyle \sum _{s=1}^{P_i}}{\displaystyle \sum _{s^{\prime }=1}^{P_j}}n({\mathbf{u}}_s)n({\mathbf{u}}_{s^{\prime }})}\sum _{s=1}^{P_i}\sum _{s^{\prime }=1}^{P_j}n({\mathbf{u}}_s)n({\mathbf{u}}_{s^{\prime }})\mid \mid {\mathbf{u}}_s-{\mathbf{u}}_{s^{\prime }}\mid \mid$$ (13)

where n(u_s) is the population size assigned to the discretizing point u_s. In other words, what matters is the distance between individuals living in these counties, not the distance between the centroids of these geographical units. Note that the block-to-block distances (13) are numerically very close to the Euclidian distances computed between population-weighted centroids (Goovaerts 2006b). The theoretically regularized model,γ_regul(h), is compared to the model fitted to experimental values, γ_Rv(h), and the relative difference between the two curves, denoted D, is used as optimization criterion. A new candidate point-support semivariogram γ⁽¹⁾(h) is derived by rescaling of the initial point-support model γ⁽⁰⁾(h), and then regularized according to expression (12). Model γ⁽¹⁾(h) becomes the new optimum if the theoretically regularized semivariogram model ${\gamma }_{\mathrm{regul}}^{(1)}(\mathbf{h})$ gets closer to the model fitted to areal data, that is if D⁽¹⁾ < D⁽⁰⁾. Rescaling coefficients are then updated to account for the difference between ${\gamma }_{\mathrm{regul}}^{(1)}(\mathbf{h})$ and γ_Rv(h), leading to a new candidate model γ⁽²⁾(h) for the next iteration. The procedure stops when the maximum number of allowed iterations has been tried (e.g. 35 in this paper) or the decrease in the D statistic becomes negligible from one iteration to the next. The use of lag-specific rescaling coefficients provides enough flexibility to modify the initial shape of the point-support semivariogram and makes the deconvolution insensitive to the initial solution adopted. More details and simulation studies are available in Goovaerts (2006b, 2008a).

2.4 Application to the Cervix Cancer Mortality Data

Figure 3 (top graph, dark gray curve) shows the experimental and model semivariograms of cervix cancer mortality risk computed from areal data using estimator (11) and the distance measure (13). This model is then deconvolved and, as expected, the resulting model (light gray curve) has a higher sill since the punctual process has a larger variance than its aggregated form. Its regularization using expression (12) yields a semivariogram model that is close to the one fitted to experimental values, which validates the consistency of the deconvolution.

Figure 3.

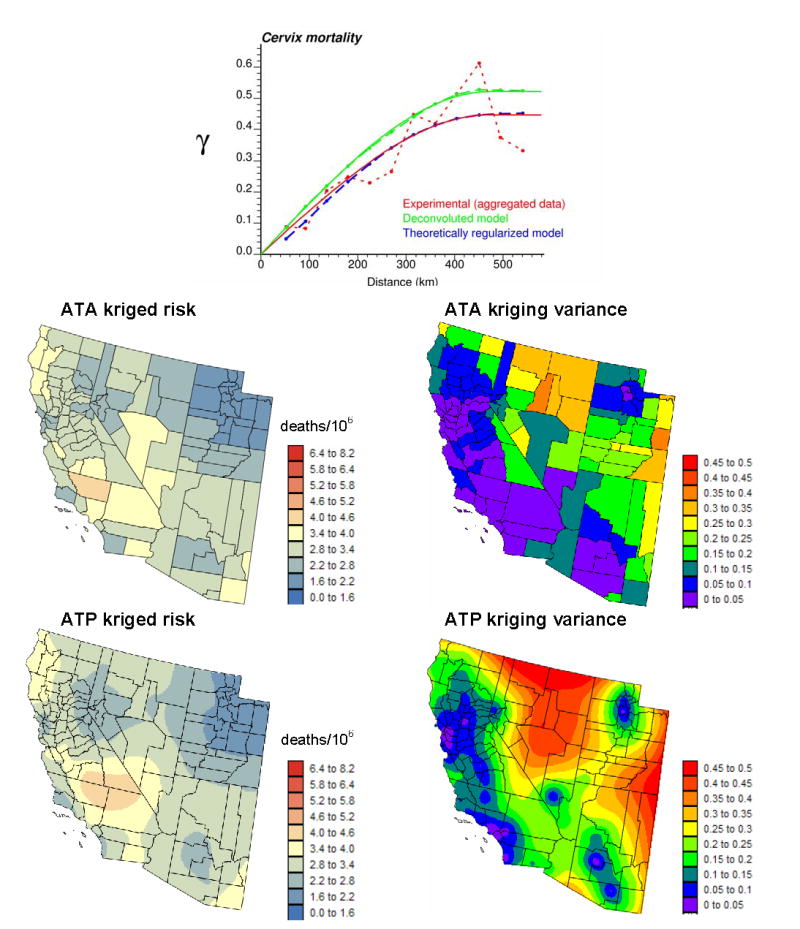
Experimental semivariogram of the risk estimated from county-level rate data, and the results of its deconvolution (top curve). The regularization of the point support model yields a curve (black dashed line) that is very close to the experimental one. The model is then used to estimate the cervix cancer mortality risk (deaths/100,000 habitants) and associated prediction variance at the county level (ATA kriging) or at the nodes of a 5 km spacing grid (ATP kriging).

The deconvolved model was used to estimate areal risk values at the county level (ATA kriging) and to map the spatial distribution of risk values within counties (ATP kriging). Both maps are much smoother than the map of raw rates since the noise due to small population sizes is filtered. In particular, the high risk area formed by two central counties in Fig. 1 disappeared, which illustrates how hazardous the interpretation of the map of observed rates can be. The highest risk (4.081 deaths/100,000 habitants) is predicted for Kern County, just west of Santa Barbara County. ATP kriging map indicates that the high risk is not confined to this sole county but potentially might spread over four counties, which is important information for designing prevention strategies. By construction, aggregating the ATP kriging estimates within each county using the population density map of Fig. 1 (right medium graph) yields the ATA kriging map.

The map of ATA kriging variance essentially reflects the higher confidence in the mortality risk estimated for counties with large populations. The distribution of population can however be highly heterogeneous in large counties with contrasted urban and rural areas. This information is incorporated in the ATP kriging variance map that shows clearly the location of urban centers, such as Los Angeles, San Francisco, Salt Lake City, Las Vegas or Tucson. The variance of point risk estimates is much larger than the county-level estimates, as expected.

3 Detection of Spatial Clusters and Outliers

Mapping cancer risk is a preliminary step towards further analysis that might highlight areas where causative exposures change through geographic space, the presence of local populations with distinct cancer incidences, or the impact of different cancer control methods.

3.1 Local Cluster Analysis (LCA)

The local Moran test (Anselin 1995) aims to detect the existence of local clusters or outliers of high or low cancer risk values (Jacquez and Greiling 2003; Goovaerts 2005c). For each county, the so-called LISA (Local Indicator of Spatial Autocorrelation) statistic is computed as:

$$\mathrm{LISA}(v_{\alpha })=\left[\frac{z(v_{\alpha })-m}{s}\right]\times \left(\sum _{j=1}^{J(v_{\alpha })}\frac{1}{J(v_{\alpha })}\times \left[\frac{z(v_j)-m}{s}\right]\right)$$ (14)

where z(v_α) is the mortality rate for the county being tested, which is referred to as the “kernel” hereafter; z(v_j) are the rates for the J(v_α) neighboring counties that are here defined as units sharing a common border or vertex with the kernel v_α (1st order queen adjacencies). All values are standardized using the mean m and standard deviation s of the set of risk estimates. Since the standardized values have zero mean, a negative value for the LISA statistic indicates a negative local auto-correlation and the presence of spatial outlier where the kernel value is much lower (higher) than the average of surrounding values. Cluster of low (high) values will lead to positive values of the LISA statistic. Note that as any local statistics of spatial association, the value of the LISA statistic, hence the conclusion about the presence of clusters and outliers, is tied to the neighborhood structure. For example, the use of a 2^nd versus a 1^st adjacency neighborhood structure could lead to the detection of different outliers or clusters.

In addition to the sign of the LISA statistic, its magnitude informs on the extent to which kernel and neighborhood values differ. To test whether this difference is significant or not, a Monte Carlo simulation is conducted, which traditionally consists of sampling randomly and without replacement the global distribution of rates (i.e. sample histogram) and computing the corresponding simulated neighborhood averages. This operation is repeated many times (e.g. M=999 draws) and these simulated values are multiplied by the kernel value to produce a set of M simulated values of the LISA statistic for the entity v_α. This set represents a numerical approximation of the probability distribution of the LISA statistic at v_α, under the assumption of spatial independence. The observed statistic (Equation 14) is compared to the probability distribution, enabling the computation of the probability of not rejecting the null hypothesis of spatial independence. The so-called p-value is compared to the significance level chosen by the user and representing the probability of rejecting the null hypothesis when it is true (Type I error). Every county where the p-value is lower than the significance level is classified as a significant spatial outlier (HL: high value surrounded by low values, and LH: low value surrounded by high values) or cluster (HH: high value surrounded by high values, and LL: low value surrounded by low values). If the p-value exceeds the significance level, the county is declared non-significant (NS).

Figure 4A shows the results of the LCA of the observed cervix cancer mortality rates. Only two counties are declared significant HL outliers, a result that must be interpreted with caution given their small population sizes. Indeed, these two counties become non-significant when the analysis is conducted on the map of kriged risks, see Fig. 4B. Accounting for population size in the analysis reveals a cluster of low risk values in Utah, which likely reflects cultural or religious influence on sexual practices resulting in reduced transmission of human papillomavirus. Yet, the smoothing effect of kriging tends to enhances spatial autocorrelation in the risk map, with the risk of inflating artificially cluster sizes. For example, the one-county HH cluster detected in the middle of the mortality map grows to become an aggregate of seven counties on the map of kriged risks. Another weakness is that the uncertainty attached to the risk estimates (i.e. kriging variance) is ignored in the analysis.

Figure 4.

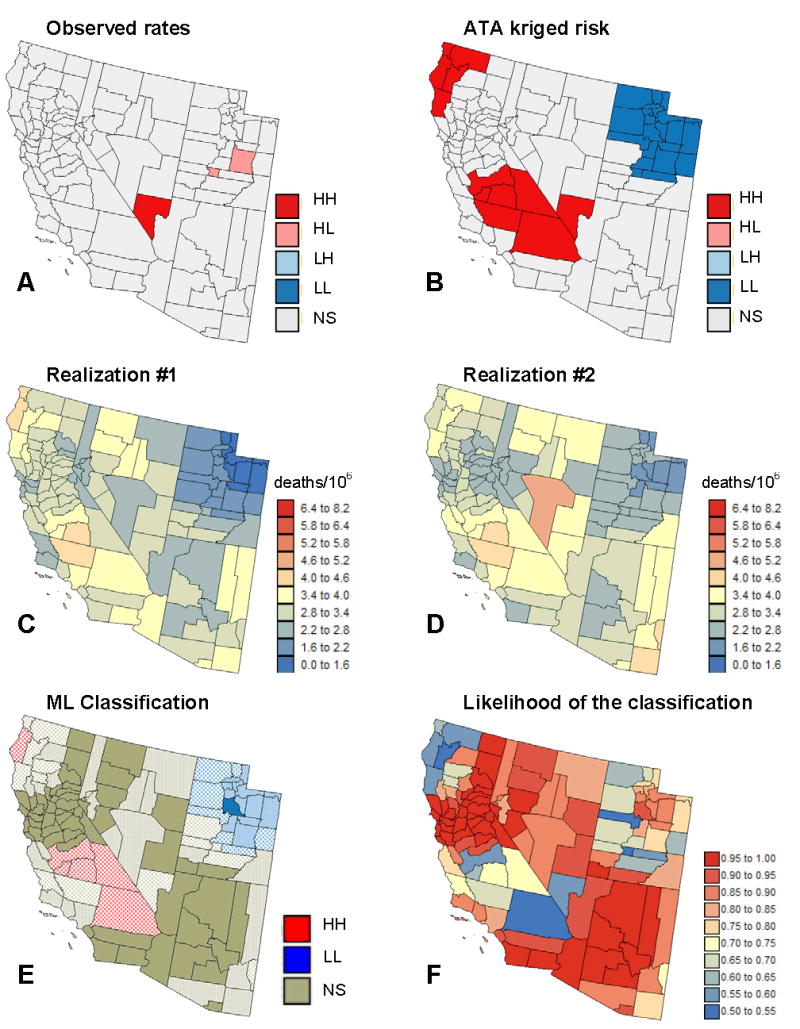
Results of the local cluster analysis conducted on cervix cancer mortality rates and estimated risks (A,B); see legend description in text. (C,D) Two realizations of the spatial distribution of cervix cancer risk. (E) Most likely (ML) classification inferred from 500 realizations. The intensity of the shading increases as the classification becomes more certain, i.e. the likelihood (F) increases.

3.2 Stochastic simulation of cancer mortality risk

Static maps of risk estimates and the associated prediction variance fail to depict the uncertainty attached to the spatial distribution of risk values and do not allow its propagation through local cluster analysis. Instead of a unique set of smooth risk estimates {r̂_PK(v_α), α = 1,…,N}, stochastic simulation aims to generate a set of L equally-probable realizations of the spatial distribution of risk values, {r^(l)(v_α), α=1,…,N; l=1,…,L}, each consistent with the spatial pattern of the risk as modeled using the function γ_R(h). Goovaerts (2006a) proposed the use of p-field simulation to circumvent the problem that no risk data (i.e. only risk estimates), hence no reference histogram, is available to condition the simulation. The basic idea is to generate a realization {r^(l)(v_α), α=1,…,N} through the sampling of the set of local probability distributions (ccdf) by a set of spatially correlated probability values {p^(l)(v_α), α = 1,…,N}, known as a probability field or p-field. Assuming that the ccdf of the risk variable is Gaussian, each risk value can be simulated as:

$$r^{(l)}(v_{\alpha })={\widehat{r}}_{PK}(v_{\alpha })+{\widehat{\sigma }}_{PK}(v_{\alpha })y^{(l)}(v_{\alpha })$$ (15)

where y^(l)(v_α) is the quantile of the standard normal distribution corresponding to the cumulative probability p^(l)(v_α). r̂_PK (v_α) and σ̂_PK(v_α) are the ATA kriging estimate and standard deviation, respectively. The L sets of random deviates or normal scores, {y^(l)(v_α), α = 1,…N}, are generated using non-conditional sequential Gaussian simulation with the distance metric (13) and the semivariogram of the risk, γ_R(h), rescaled to a unit sill; see Goovaerts (2006a) for a detailed description of the algorithm.

Figures 4C–D show two realizations of the spatial distribution of cervix cancer mortality risk values generated using p-field simulation. The simulated maps are more variable than the kriged risk map of Fig. 3, yet they are smoother than the map of potentially unreliable rates of Fig. 1. Differences among realizations depict the uncertainty attached to the risk map. For example, Nye County in the center of the map, which has a very high mortality rate (recall Fig. 1) but low population, has a simulated risk that is small for realization #1 but large in the next realization. Five hundreds realizations were generated and underwent a local cluster analysis. The information provided by the set of 500 LCAs is summarized at the bottom of Fig. 4. The color code indicates the most frequent classification (maximum likelihood = ML) of each county across the 500 simulated maps. The shading reflects the probability of occurrence or likelihood of the mapped class, see Fig. 4F. Solid shading corresponds to classifications with high frequencies of occurrence (i.e. likelihood > 0.9), while hatched counties denote the least reliable results (i.e. likelihood < 0.75). This coding is somewhat subjective but leads to a clear visualization of the lower reliability of the clusters of high values relatively to the cluster of low risk identified in Utah. Only one county south of Salt Lake City is declared a significant low-risk cluster with a high likelihood (0.906).

4 Correlation Analysis

Once spatial patterns, such as clusters of high risk values, have been identified on the cancer mortality map, a critical step for cancer control intervention is the analysis of relationships between these features and putative environmental, demographic, socioeconomic and behavioral factors. The major difficulty is the choice of a scale for quantifying correlations between variables that are typically measured over very different supports, e.g. counties and census blocks in this study.

4.1 Ecological Analysis

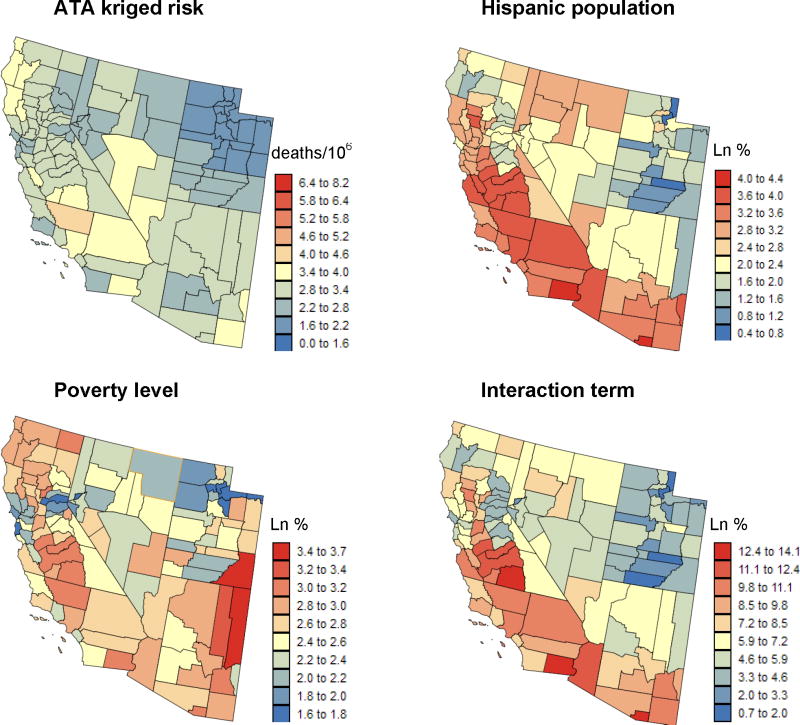
The most straightforward approach is to aggregate the finer data to the level of coarser resolution data, resulting in a common spatial support for the correlation analysis. For example, Figure 5 shows the county-level kriged risk and the two covariates of Fig. 1 aggregated to the same geography: percentage of habitants living below the federally defined poverty line, and percentage of Hispanic females. Both variables were logarithmically transformed, and their product defines the interaction term. Table 1 (first two rows) shows the correlation coefficient between each of the three covariates and the mortality rates before and after application of Poisson kriging. Filtering the noise due to the small number problem clearly enhances the explanatory power of the covariates: the proportion of variance explained (R²) increases by almost one order of magnitude (6.2% to 48.8%) and all correlation coefficients become highly significant. The uncertainty attached to the risk estimates can be accounted for by weighting each estimate according to the inverse of its kriging variance, leading to slightly larger correlation coefficients and R² (Table 1, 3rd row).

Figure 5.

Maps of cancer mortality risk estimated by Poisson kriging and the logtransformed values of three putative covariates aggregated to the county-level for conducting the ecological analysis.

Table 1.

Results of the correlation analysis of cervix cancer mortality rates and kriged risks with two putative covariates, as well as their interaction. Kriging estimates are weighted according to the inverse of their kriging variance. The use of neutral models allows one to incorporate the spatial uncertainty attached to cancer risk estimates into the computation of the correlation coefficients and testing of their significance (*= significant, **=highly significant). The last two rows show the results obtained after disaggregation.

	Correlation with covariates			R2 (%)
Regression models	Hispanic	Poverty	Interaction
County-level correlation
Rates	0.210*	0.144	0.240**	6.2
ATA kriging	0.625**	0.473**	0.690**	48.8
ATA kriging (weighted)	0.641**	0.613**	0.729**	54.1
ATA kriging (neutral model)	0.247–0.703**	0.173–0.590**	0.347–0.716**	14.4–52.0
Point-level (25 km2 cells) correlation
ATP kriging	0.096**	−0.036**	0.188**	9.8
ATP kriging (weighted)	0.239**	0.090**	0.321**	14.0

Instead of computing the correlation between each covariate and the smoothed risk map, the correlation was quantified for each of the 500 risk maps generated by p-field simulation in Section 3.2. This propagation of uncertainty leads to a range of correlation coefficients and R² that can be fairly wide, see Table 1 (4th row). Next, this distribution must be compared to the one expected under the assumption of no correlation between mortality risk and each covariate. So far the significance of the correlation coefficient has been tested using the common assumption of independence of observations, which is clearly inappropriate for most spatial datasets. A reference distribution, which accounts for the spatial correlation of the data, was obtained empirically using the following two-step procedure:

1. The maps of covariates are modified using the spatially ordered shuffling procedure proposed by Goovaerts and Jacquez (2004). The idea is to generate a standard normal random field with a given spatial covariance, e.g. the covariance of the demographic variable in this paper, using non-conditional sequential Gaussian simulation. Each simulated normal score is then substituted by the value of same rank in the distribution of proportion of Hispanic females. To maintain the correlation among covariates, all three covariate maps were modified simultaneously. The operation was repeated 100 times, yielding 100 sets of covariate maps.

2. The correlation between each of the re-ordered covariate maps and each of the 500 simulated risk maps is assessed, leading to a distribution of 50,000 correlation coefficients that corresponds to a hypothesis of no correlation, since the covariate maps were modified independently of the risk maps.

For this case study, this more realistic testing procedure does not change the conclusions drawn from the classical analysis.

Correlations computed between health outcomes and risk factors averaged over geographical entities, such as counties, are referred to as ‘ecological correlations’. The unit of analysis is a group of people, as opposed to individual-based studies that relies on data collected for each cancer case. A limitation of ecological analyses is the resolution available which might be too coarse to obtain a detailed view of geographical patterns in disease mortality or incidence. The aggregation may also distort or mask the true exposure/response relationship for individuals, a phenomenon called the ecological fallacy (Waller and Gotway 2004). The disaggregation performed by ATP Poisson kriging eliminates the need for using averaged values, and the correlation coefficients between both risk and covariates estimated at the nodes of the 5-km spacing grid are listed in Table 1 (last rows). The correlation is much weaker than for county-level data, which might be due to the noise in the map of socio-demographic variables and/or reflects the scale-dependence of the relationship.

4.1 Geographically-weighted Regression

The analysis in Table 1 is aspatial and makes the implicit assumption that the impact of covariates is constant across the study area. This assumption is likely unrealistic for large areas which can display substantial geographic variation in demographic, social, economic, and environmental conditions. Several local regression techniques have been developed to account for the non-stationarity of relationships in space (Fotheringham et al. 2002; Congdon 2006). In geographically-weighted regression (GWR) the regression is performed within local windows centred on each observation or the nodes of a regular grid, and each observation is weighted according to its proximity to the centre of the window. This weighting scheme avoids abrupt changes in the local statistics computed in adjacent windows. Local regression coefficients and associated statistics (i.e. proportion of variance explained, correlation coefficients) can then be mapped to visualize how the explanatory power of covariates changes spatially (Goovaerts 2005d). It is noteworthy that the geostatistical method of kriging with an external drift (KED) accomplishes a similar re-evaluation of local relationships, while accounting for data clustering and pattern of correlation (Wackernagel 1998, Goovaerts 1999). GWR is however easier to implement than KED and empirical comparisons have demonstrated the good correspondence between the results of both methods (Goovaerts 2009a).

GWR regression was conducted using as dependent variable the mortality risk estimated by ATA and ATP kriging (20 km spacing grid). The centers of the local windows were identified to either the county population-weighted centroids or the nodes of the 5 km spacing grid. The window size was defined as the set of 50 closest observations for both county-level and point-level data (as for the LISA statistic, results are tied to the rather subjective choice of a local neighborhood structure). The weight assigned to each observation u_α was computed as ${\text{C}}_{\text{sph}}(h_{0\alpha })/{\widehat{\sigma }}_{PK}^2({\mathbf{u}}_a)$, where C_sph(h_0α) is the value of the spherical covariance at a distance h_0α to the center u₀ of the window, and ${\widehat{\sigma }}_{PK}^2({\mathbf{u}}_a)$ is the kriging variance of the ATA or ATP kriged estimate. The range of C_sph(h) was set to the distance between the center of the window and the most distant observation. Two statistics are displayed in Fig. 6: the proportion of variance explained within each window (left column) and the covariate with the highest significant correlation coefficient (right column).

Figure 6.

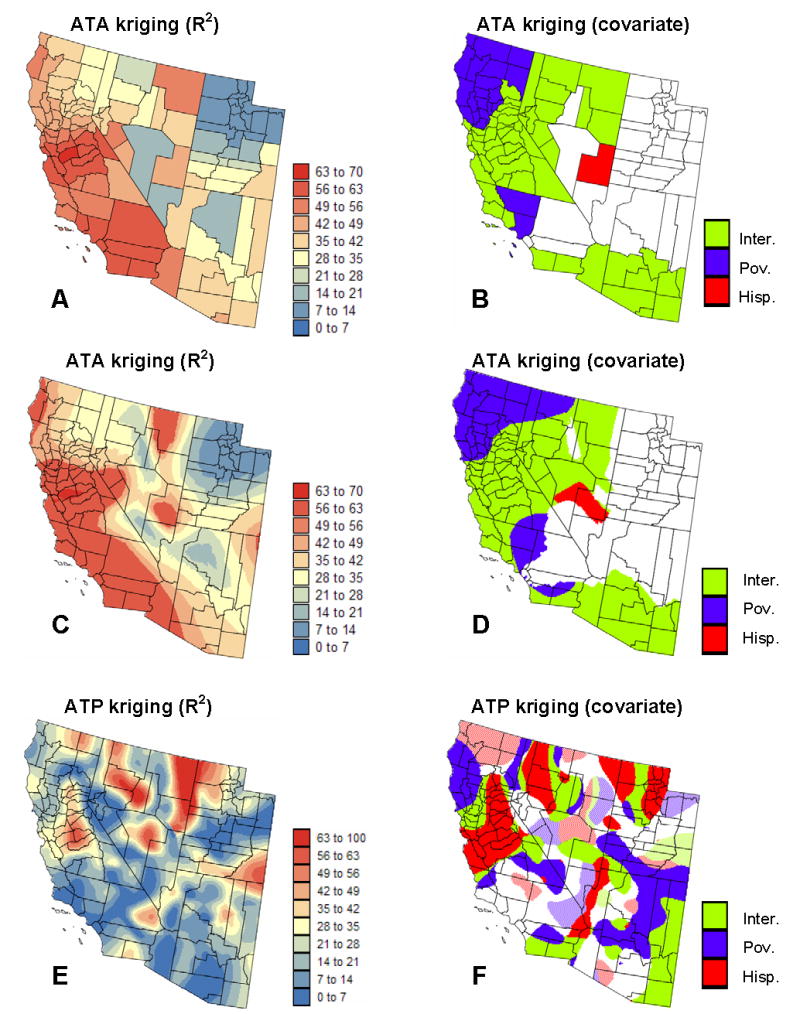
Results of the geographically-weighted regression applied to the ATA and ATP kriged risk values. Left column displays the maps of the local proportion of variance explained, whereas the right maps show, for each county or node of the 5km spacing grid, the covariate (Hispanic population, poverty level, and interaction) that has the highest significant correlation (hatched areas = negative correlation) with cancer mortality risk. Maps (C,D) show the analysis of county-level data conducted at each node of the 5 km spacing grid.

The analysis of county-level data (Figs. 6A–B) shows a clear SW-NE trend in the explanatory power of the local regression models: the higher mortality values along the coast are better explained by the two covariates than the lower risk recorded in Utah. In this state, none of the covariates displays significant correlation with cancer mortality. Poverty level is the best correlated covariate in Northern California while the interaction between economic and demographic variables is the most significant factor in Central California and in the South of the study area. The proportion of Hispanic females is the most significant covariate in a very small transition area between the coast where higher mortality rates and proportion of Hispanic females are observed and Utah where the same two variables have lower values. The computation of the GWR statistics over a regular grid allows one to visualize the within-county variability (Figs. 6C–D), yet the analysis is still based on county-level aggregates of socio-demographic variables which can be overly simplistic for some counties, recall Fig. 1 (bottom maps). For example, the largest R² observed in the Northeast corner of the study area (Fig. 6E) corresponds to the Eastern border of a county that display great variation for both proportion of Hispanic females and habitants below the poverty level. Differences between the GWR of county-level and point-support data are even more striking for the map of significantly correlated covariates. The pattern becomes much more complex and correlations are locally negative, see hatched areas in Fig. 6F. These maps are mainly used for descriptive purpose and should guide further individual-level studies to interpret these local relationships.

5 Conclusions

The analysis of health data and putative covariates, such as environmental, socio-economic, behavioral or demographic factors, is a promising application for geostatistics. It presents, however, several methodological challenges that arise from the fact that data are typically aggregated over irregular spatial supports and consist of a numerator and a denominator (i.e. population size). Common geostatistical tools, such as semivariograms or kriging, thus cannot be blindly implemented in environmental epidemiology. This paper demonstrated how recent developments in other disciplines, such as ecology for Poisson kriging or remote sensing for area-to-point kriging, can foster the advancement of health geostatistics. Capitalizing on these results and an innovative approach for semivariogram deconvolution, this paper presented one of the first studies where the size and shape of administrative units, as well as the population density, is incorporated into the filtering of noisy mortality rates and the mapping of the corresponding risk at a fine scale (i.e. disaggregation).

Like in other disciplines, spatial interpolation is rarely a goal per se; rather it is a step along the decision-making process. In epidemiology one main concern is to establish the rationale for targeted cancer control interventions, including consideration of health services needs, and resource allocation for screening and diagnostic testing. It is thus important to delineate areas with significantly higher mortality or incidence rates, as well as to analyze relationships between health outcomes and putative risk factors. The uncertainty attached to cancer maps needs however to be propagated through this analysis, a task that geostatisticians have been tackling for several decades using stochastic simulation. Once again the implementation of this approach in epidemiology faces specific challenge, such as the absence of measurements of the target attribute. This paper introduced the application of p-field simulation to generate realizations of cancer mortality maps, which allows one to quantify numerically how the uncertainty about the spatial distribution of health outcomes translates into uncertainty about the location of clusters of high values or the correlation with covariates. Last, this study demonstrated the limitation of a traditional aspatial regression analysis, which ignores the geographic variations in the impact of covariates.

In the future, the approach should be generalized to the multivariate case to analyze jointly multiple diseases or the rates of the same disease recorded for different categories of individuals (e.g. different genders or ethnic groups). Analysis of spatial relationships among diseases should facilitate the identification of common stressors, such as poverty level, lack of access to health care or environmental pollution. A multivariate approach would also enable the mapping and detection of health disparities, such as the delineation of areas where cancer mortality rates are significantly higher for minority groups. Another avenue of research is the incorporation of the temporal dimensions into the analysis (Goovaerts 2005d). The study of temporal changes in spatial patterns would provide useful information for cancer control strategies, for example through the identification of areas where current prevention (e.g. screening for cancers) is deficient. Secondary information, such as socio-demographic variables, could also be incorporated in the disaggregation of disease rates using recent developments in area-to-point residual kriging (Liu et al 2008) and Poisson kriging with spatial drift (Bellier et al 2009).

In contrast to the well-developed methods for mapping aggregated epidemiologic data, the spatial mapping of individual-level data has received much less attention (Webster et al., 2006). In addition to the greater accuracy in the location of health outcomes, the analysis of geocoded data however can often capitalize on detailed information on residential history and a large number of potential risk factors. A straightforward mapping approach is to use ‘kernel density estimation methods’, whereby the number of cases and the total number of individuals at risk (or number of controls) are summed within sliding windows and their ratio defines the rate (or odd ratio) assigned to the center (i.e. grid node) of that window (Rushton et al 2004). The operation is repeated for each grid node, allowing the creation of isopleth maps of, for example, late-stage cancer rates (ratio of number of late-stage cancer cases to total number of people diagnosed with that cancer) or cancer odds ratios (ratio of number of cases to the number of controls). Unlike kernel density estimation, geostatistics has the potential to take into account the spatial support of the data and the pattern of spatial dependence (e.g. anisotropy, range of autocorrelation) in the computation of the weights assigned to neighboring data. Each observation represents the probability (0 or 1) that the individual is a case (e.g. late stage cancer, birth defect), hence indicator kriging (Journel 1983) seems well suited to the analysis of such data. Non-parametric geostatistics was recently applied to individual-level epidemiologic data to map the risk for late stage breast cancer diagnosis using patient residences across Michigan (Goovaerts 2009b).

Last, in addition to methodological developments, critical components to the success of health geostatistics include the publication of applied studies illustrating the merits of geostatistics over spatial statistical methods commonly used in health departments and cancer registries, training through short courses and updating of existing curriculum, as well as the development of user-friendly software.