A Parametric Approach to Numerical Modeling of TKR Contact Forces

Abstract

In vivo knee contact forces are difficult to determine using numerical methods because there are more unknown forces than equilibrium equations available. We developed parametric methods for computing contact forces across the knee joint during the stance phase of level walking. Three-dimensional contact forces were calculated at two points of contact between the tibia and the femur, one on the lateral aspect of the tibial plateau, and one on the medial side. Muscle activations were parametrically varied over their physiologic range resulting in a solution space of contact forces. The obtained solution space was reasonably small and the resulting force pattern compared well to a previous model from the literature for kinematics and external kinetics from the same patient. Peak forces of the parametric model and the previous model were similar for the first half of the stance phase, but differed for the second half. The previous model did not take into account the transverse external moment about the knee and could not calculate muscle activation levels. Ultimately, the parametric model will result in more accurate contact force inputs for total knee simulators, as current inputs are not generally based on kinematics and kinetics inputs from TKR patients.

INTRODUCTION

Preclinical testing of total knee replacements (TKRs) with knee joint simulators and computational models require accurate in vivo contact force, muscle force, and joint angle input data. Kinematics can be obtained using gait analysis, but in vivo force data from instrumented TKRs (D’Lima et al., 2006; Zhao et al., 2007a; Zhao et al., 2007b; Mündermann et al., 2008) are just beginning to become available from one patient. For TKR patients, there is considerable inter-subject variability of patient kinetics (Andriacchi and Hurwitz, 1997) and kinematics (Ngai et al., 2007) making computational modeling a necessity for obtaining contact force and muscle force data for a larger patient population.

Muscle forces cannot be directly measured in vivo. Solving for contact forces and muscle forces at the knee joint is an indeterminate problem with more unknown variables than equations. Therefore, contact forces across the knee have traditionally been determined by reduction (Morrison, 1969; Schipplein and Andriacchi, 1991; Sharma et al., 2007, Wimmer and Andriacchi, 1997) or optimization methods (Röhrle et al., 1984; Seireg and Arvikar, 1975; Taylor et al., 2004). Reduction methods require reducing the number of unknown muscle forces to the number of equations, resulting in a determinate problem. Optimization methods minimize an objective function subject to a criterion but have historically tended to result in the overestimation of knee contact forces.

A parametric model for calculating hip contact forces was developed by Hurwitz et al. (2003). The parametric method allows for variation of individual muscle activation levels across their physiologic range resulting in a solution space of three-dimensional contact forces at each activation level. The method also allows muscles to have three-dimensional lines of action consistent with joint anatomy. Our goal was to develop a tool that could be used to determine the physiologic solution space of patient specific TKR contact and muscle forces. In this paper we present the modeling methods, and compare knee forces with those obtained from a previously published model (Wimmer and Andriacchi, 1997) using the same input data.

METHODS

A coordinate system was first defined for the tibial plateau where the positive x, y, and z axes pointed laterally, anteriorly, and superiorly, respectively (Figure 1). The coordinate system originated at the intersection of mid-anterior-posterior (AP) and medial-lateral lines on the surface of the tibial plateau. Knee contact forces were defined at two different points of contact between the femur and tibia, one on the medial aspect of the tibial plateau (contact force components ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{x}}$, ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{y}}$, and ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{z}}$), and another on the lateral aspect of the tibial plateau (contact force components ${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{x}}$, ${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{y}}$, and ${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{z}}$). The location of the points of contact were defined by variables ${\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{x}}$, ${\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{x}}$, ${\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{y}}$, and ${\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{y}}$ in the coordinate system (Figure 1, Table 1). The coordinates for the points of contact had unique values at each instance of stance that corresponded to the movement of the femur on the tibia and defined the moment arms of the contact forces about the center of the tibial plateau.

Figure 1.

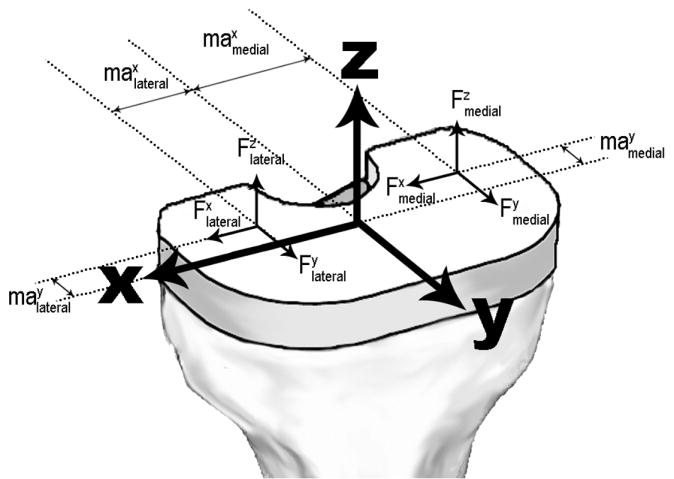
Coordinate system and location of the contact force components on the proximal tibia. The x-axis pointed laterally, the y-axis pointed anteriorly, and the z-axis pointed in the superior direction. The coordinate system originated at the intersection of mid-sagittal and mid-frontal planes on the surface of the tibial plateau. Contact forces ( ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{x}}$, ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{y}}$, ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{z}}$, ${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{x}}$, ${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{y}}$, and ${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{z}}$) were located at two points on the tibia, with locations defined by the contact point between the tibia and the femur ( ${\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{x}}$, ${\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{x}}$, ${\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{y}}$, and ${\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{y}}$).

Table 1.

Definition of variables used in the equations for calculating contact forces across the knee joint.

Variable	Definition	Method of Obtaining
${\mathrm{M}}_{\mathrm{external}}^{\mathrm{x}}$, ${\mathrm{M}}_{\mathrm{external}}^{\mathrm{y}}$, ${\mathrm{M}}_{\mathrm{external}}^{\mathrm{z}}$	external moment about the x, y, and z-axis of the knee joint	gait analysis
${\mathrm{F}}_{\mathrm{external}}^{\mathrm{x}}$, ${\mathrm{F}}_{\mathrm{external}}^{\mathrm{y}}$, ${\mathrm{F}}_{\mathrm{external}}^{\mathrm{z}}$	external force about the x, y, and z-axis of ihe knee joint	gait analysis
${\mathrm{M}}_{\mathrm{i}}^{\mathrm{x}}$, ${\mathrm{M}}_{\mathrm{i}}^{\mathrm{y}}$, ${\mathrm{M}}_{\mathrm{i}}^{\mathrm{z}}$	maximum x, y, and z-direction moment for the ith muscle or passive structure in each group	SIMM output and Matlab software
${\mathrm{F}}_{\mathrm{i}}^{\mathrm{x}}$, ${\mathrm{F}}_{\mathrm{i}}^{\mathrm{y}}$, ${\mathrm{F}}_{\mathrm{i}}^{\mathrm{z}}$	maximum x, y, and z-direction force for the ith muscle or passive structures in each group	SIMM output and Matlab software
${\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{x}}$, ${\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{x}}$	x-direction distance from the origin of the coordinate system to the contact point (x-direction moment arm for z-direction contact forces).	coordinate of contact point
${\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{y}}$, ${\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{y}}$	y-direction distance from the origin of the coordinate system to the contact point (y-direction moment arm for z-direction contact forces).	coordinate of contact point
ml_ratio	ratio defining the percent load transferred through the medial versus lateral side of the tibial plateau	set by the user
ai, bi, ci	relative activation level for the ith muscle in each agonist group	parametrically varied
A, B, C	group activation levels for each muscle agonist group	unknown, solve using equations
D	activation level for passive structures	0 (on) or 1 (off)
E	activation level for antagonist muscles	set by the user
${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{x}}$, ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{x}}$	x-direction contact forces	unknown, solve using equations
${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{y}}$, ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{y}}$	y-direction contact forces	unknown, solve using equations
${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{z}}$, ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{z}}$	z-direction contact forces	unknown, solve using equations

¹lateral and medial indicate the lateral or medial side of the tibial plateau, respectively

Equilibrium equations for moments (Equations 1, 2, and 3) and forces (Equations 4, 5, and 6) as well as equations that defined the relationship between the medial and lateral contact forces (Equations 7, 8, and 9) were written for the x, y, and z axes of the coordinate system.

$$\begin{array}{ll}{\mathrm{M}}_{\mathrm{external}}^{\mathrm{x}}& =\mathrm{A}\sum _{\mathrm{primary\; agonists}}{\mathrm{a}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{x}}+\mathrm{B}\sum _{\mathrm{secondary\; agonists}}{\mathrm{b}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{x}}+\mathrm{C}\sum _{\mathrm{min\; or\; agonists}}{\mathrm{c}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{x}}\\ & +\mathrm{D}\sum _{\mathrm{passive\; structures}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{x}}+\mathrm{E}\sum _{\mathrm{antagonists}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{x}}+{\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{y}}{\mathrm{F}}_{\mathrm{medial}}^{\mathrm{z}}+{\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{y}}{\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{z}}\end{array}$$ (1)

$$\begin{array}{ll}{\mathrm{M}}_{\mathrm{external}}^{\mathrm{y}}& =\mathrm{A}\sum _{\mathrm{primary\; agonists}}{\mathrm{a}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{y}}+\mathrm{B}\sum _{\mathrm{secondary\; agonists}}{\mathrm{b}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{y}}+\mathrm{C}\sum _{\mathrm{min\; or\; agonists}}{\mathrm{c}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{y}}\\ & +\mathrm{D}\sum _{\mathrm{passive\; structures}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{y}}+\mathrm{E}\sum _{\mathrm{antagonists}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{y}}-{\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{x}}{\mathrm{F}}_{\mathrm{medial}}^{\mathrm{z}}-{\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{x}}{\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{z}}\end{array}$$ (2)

$$\begin{array}{ll}{\mathrm{M}}_{\mathrm{external}}^{\mathrm{z}}& =\mathrm{A}\sum _{\mathrm{primary\; agonists}}{\mathrm{a}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{z}}+\mathrm{B}\sum _{\mathrm{secondary\; agonists}}{\mathrm{b}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{z}}+\mathrm{C}\sum _{\mathrm{min\; or\; agonists}}{\mathrm{c}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{z}}\\ & +\mathrm{D}\sum _{\mathrm{passive\; structures}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{z}}+\mathrm{E}\sum _{\mathrm{antagonists}}{\mathrm{M}}_{\mathrm{i}}^{\mathrm{z}}-{\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{y}}{\mathrm{F}}_{\mathrm{meidal}}^{\mathrm{x}}-{\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{y}}{\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{x}}+{\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{x}}{\mathrm{F}}_{\mathrm{medial}}^{\mathrm{y}}+{\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{x}}{\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{y}}\end{array}$$ (3)

$$\begin{array}{ll}{\mathrm{F}}_{\mathrm{external}}^{\mathrm{x}}& =\mathrm{A}\sum _{\mathrm{primary\; agonists}}{\mathrm{a}}_{\mathrm{i}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{x}}+\mathrm{B}\sum _{\mathrm{secondary\; agonists}}{\mathrm{b}}_{\mathrm{i}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{x}}+\mathrm{C}\sum _{\mathrm{min\; or\; agonists}}{\mathrm{c}}_{\mathrm{i}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{x}}\\ & +\mathrm{D}\sum _{\mathrm{passive\; structures}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{x}}+\mathrm{E}\sum _{\mathrm{antagonists}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{x}}+{\mathrm{F}}_{\mathrm{medial}}^{\mathrm{x}}+{\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{x}}\end{array}$$ (4)

$$\begin{array}{ll}{\mathrm{F}}_{\mathrm{external}}^{\mathrm{y}}& =\mathrm{A}\sum _{\mathrm{primary\; agonists}}{\mathrm{a}}_{\mathrm{i}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{y}}+\mathrm{B}\sum _{\mathrm{secondary\; agonists}}{\mathrm{b}}_{\mathrm{i}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{y}}+\mathrm{C}\sum _{\mathrm{min\; or\; agonists}}{\mathrm{c}}_{\mathrm{i}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{y}}\\ & +\mathrm{D}\sum _{\mathrm{passive\; structures}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{y}}+\mathrm{E}\sum _{\mathrm{antagonists}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{y}}+{\mathrm{F}}_{\mathrm{medial}}^{\mathrm{y}}+{\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{y}}\end{array}$$ (5)

$$\begin{array}{ll}{\mathrm{F}}_{\mathrm{external}}^{\mathrm{z}}& =\mathrm{A}\sum _{\mathrm{primary\; agonists}}{\mathrm{a}}_{\mathrm{i}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{z}}+\mathrm{B}\sum _{\mathrm{secondary\; agonists}}{\mathrm{b}}_{\mathrm{i}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{z}}+\mathrm{C}\sum _{\mathrm{min\; or\; agonists}}{\mathrm{c}}_{\mathrm{i}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{z}}\\ & +\mathrm{D}\sum _{\mathrm{passive\; structures}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{z}}+\mathrm{E}\sum _{\mathrm{antagonists}}{\mathrm{F}}_{\mathrm{i}}^{\mathrm{z}}+{\mathrm{F}}_{\mathrm{medial}}^{\mathrm{z}}+{\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{z}}\end{array}$$ (6)

$$\left(1­\mathrm{ml}\_\mathrm{ratio}\right){\mathrm{F}}_{\mathrm{medial}}^{\mathrm{x}}=\mathrm{ml}\_\mathrm{ratio}{\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{x}}$$ (7)

$$\left(1­\mathrm{ml}\_\mathrm{ratio}\right){\mathrm{F}}_{\mathrm{medial}}^{\mathrm{y}}=\mathrm{ml}\_\mathrm{ratio}{\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{y}}$$ (8)

$$\left(1­\mathrm{ml}\_\mathrm{ratio}\right){\mathrm{F}}_{\mathrm{medial}}^{\mathrm{z}}=\mathrm{ml}\_\mathrm{ratio}{\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{z}}$$ (9)

Table 1 lists the definitions of all variables. The nine equations were used to calculate the values of nine unknown variables (six contact force components, ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{x}}$, ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{y}}$, ${\mathrm{F}}_{\mathrm{medial}}^{\mathrm{z}}$, ${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{x}}$, ${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{y}}$, and ${\mathrm{F}}_{\mathrm{lateral}}^{\mathrm{z}}$, and three muscle group activation levels, A, B, and C). The unknown variables were calculated at 100 instances during the stance phase of level walking (every 1% of stance). Variables in the equations that were known, or calculated by other means, included the external moments and forces, and internal moments and forces from muscles and passive structures. Muscle force magnitudes, assuming maximum activation, were calculated using a SIMM (Software for Interactive Musculoskeletal Modeling, Santa Rosa, CA) musculoskeletal model of the lower limb. The model was modified from that reported by Hurwitz et al. (2003) and Delp et al. (1990) to allow input of knee joint motions for all six degrees of freedom. Software custom-written using Matlab v6.5 (The Mathworks, Natick, MA) was used to calculate the muscle moments about the knee joint, create muscle functional agonist groups, and solve the equilibrium equations. The muscles included in the model are listed in Table 2.

Table 2.

Muscles included in the model and example muscle group assignments for 21% stance of the patient analyzed. Agonist muscle groups A, B, and C represent muscles that are primary, secondary, and minor agonists, respectively, depending on their moment contribution about each axis of the coordinate system. At 21% stance the external moments were 2.60, -3.72, and -0.31 % body weight times height for moments about the x, y, and z axis, respectively (Figure 2). The muscle moments were calculated with custom-written Matlab software from the maximum muscle force obtained from the SIMM musculoskeletal model.

Muscles	Group at 21% stance	Moment about x1	Moment about y1
Semimembranosus	antagonist	-1.99	1.28
Semitendinosus	antagonist	-1.11	0.45
Biceps fermoris (long head)	C	-1.26	-2.27
Biceps femoris (short head)	C	-0.49	-1.31
Sartorius	antagonist	-0.12	0.76
Gracilis	antagonist	-0.17	0.36
Tensor fasciae latae	B	0.19	-0.93
Rectus femoris	A	5.60	-0.23
Vastus lateralis	A	4.39	-0.18
Vastus intermedialis	A	3.58	-0.15
Vastus medialis	A	3.25	-0.13
Popliteus	B	-0.46	-0.90
Plantaris	antagonist	-0.13	0.01
Lateral gastrocnemius	B	-0.98	-1.03
Medial gastrocnemius	B	-1.75	2.25

¹Internal muscle moment with units % body weight times height.

Muscles were categorized into four groups: three agonist groups, and one antagonist group, based on their function at each instance during stance. Muscle groups were determined by comparing the muscle moment components to the external moment components calculated using gait analysis. Muscles were considered agonists if their largest moment component about the x, y, or z axis served to balance the corresponding external moment. After the agonists were identified, they were divided into three groups based on the moments they imposed about all three axes of the coordinate system. Muscles were assigned to the antagonist group if the largest moment component was antagonistic when compared to the external moments. As an example, muscle groupings corresponding to 21% stance (the first peak external knee flexion moment, Figure 2) are listed in Table 2.

Figure 2.

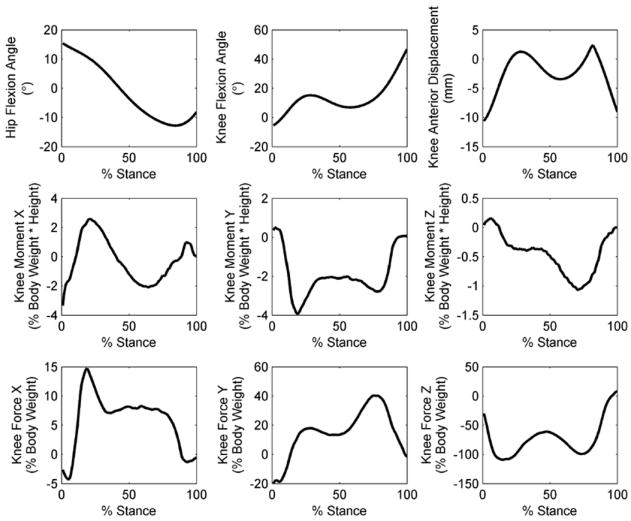
Kinematics and external moments and forces during 100 instances of the stance phase of level walking for a patient with a TKR (Wimmer and Andriacchi, 1997).

Each muscle in the three agonist groups was assigned an individual muscle relative activation (a_i, b_i, and c_i). This relative value was parametrically varied and the equilibrium equations solved at each value. The relative activation levels scaled the contribution of muscles within the same agonist group. To take into account the overall action of each group of agonist muscles, group muscle activation levels (A, B, and C), solved for with the equilibrium equations, also scaled the contribution of muscles within the same agonist group. Muscle activation level was defined as the product of the group activation level and relative activation level. Solutions were considered not valid if the product of the group and relative activation levels for any muscle was less than 0.0 (indicating an unphysiological role reversal or “pushing” rather than “pulling”) or greater than 1.0 (indicating muscle activation above the maximum physiological level).

The variable D, equal to zero or one, allowed for the omission or inclusion of the force and moment contribution from passive structures. The activation level of the antagonist muscles (E) was also a variable that could be parametrically varied. The variable “ml_ratio” defined the relationship between the contact forces on the medial and lateral aspects of the tibial plateau such that zero indicated only lateral force transfer and one indicated only medial force transfer. The ratio could also be parametrically varied and change temporally throughout the stance phase.

The parametric model was used to calculate knee contact forces for a TKR patient who had previously undergone gait analysis (Figure 2). AP displacement of the tibia (defining ${\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{y}}$ and ${\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{y}}$) was calculated following Wimmer and Andriacchi (1997). Variables ${\mathrm{ma}}_{\mathrm{medial}}^{\mathrm{x}}$ and ${\mathrm{ma}}_{\mathrm{lateral}}^{\mathrm{x}}$ were set to the center of each side of the tibial plateau. Relative muscle activation levels a_i, b_i, and c_i were varied between 0.1, 0.5, and 1.0. Variable “ml_ratio” was fixed throughout stance and set to 0.7 for the current analysis, indicating that 70% of the total contact force was transferred on the medial side. For the results reported in this study, the value of the moment contribution from the passive structures was equal to the difference between the external moment about the z-axis and the combined sum of the agonists muscle moment about the z-axis. Antagonist muscles were not included for the current analysis (E was set to zero). Results were compared to those from a previously published knee model (Wimmer and Andriacchi, 1997) for the same subject and the same walking trial.

RESULTS

A solution space of contact forces, averaging 6828 solutions for every 1% of stance, was calculated (Figure 3A). The solution space was a result of parametric variation of the relative muscle activation levels. The peak normal force occurred at 21% of stance; the average of the solution space was -3.3 body weights at this point, with a range of 0.38 body weights. The maximum range of normal forces was 0.5 body weights at 67% of stance. The maximum range of the resultant total force was 0.85 body weights at 76% stance.

Figure 3.

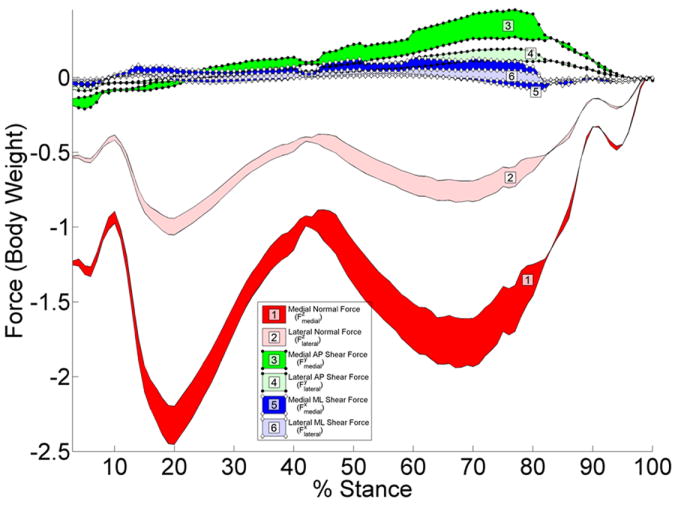
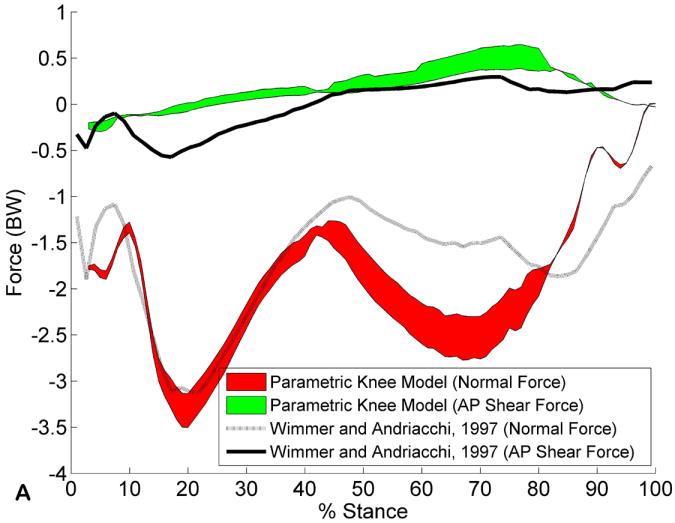
A. Three-dimensional contact forces (shaded regions) for 100 instances during the stance phase of level walking for the kinematics and external moments shown in Figure 2. Seventy percent of the total contact force was transferred through the medial tibial plateau, and 30% of the total contact force was transferred laterally. B. Comparison between the parametric model (results from the medial and lateral side are summed) and the results reported by Wimmer et al. (Wimmer and Andriacchi, 1997).

The results of the parametric model were similar to those reported by Wimmer and Andriacchi (1997) for the same subject and same walking trial (Figure 3B). Both the normal force (z-direction) and AP shear force (y-direction) were within ~0.5 body weight during the first half of the stance phase, but the normal force calculated by Wimmer and Andriacchi was less than that calculated with the current model during the second half of stance.

DISCUSSION

We have developed parametric methods for calculating three-dimensional knee joint contact forces through the medial and lateral aspects of the tibial plateau. This approach allows the physiological inclusion of all muscles crossing the knee joint. The calculated peak contact forces fit within the range reported in a review of previous numerical approaches (-1.7 to -4.9 body weights) (Komistek et al., 2005). The resulting solution space was reasonably small and the patterning compared well to that reported by Wimmer and Andriacchi (1997). While the peak force was very similar for both models (-3.12 previously versus -3.06 to -3.42 body weights for the current model), differences in force magnitude were present during mid- and terminal stance.

The previous model of Wimmer et al. calculated contact forces by grouping muscles into quadriceps, hamstrings and gastrocnemii, and balancing sagittal and frontal plane equilibrium equations while neglecting the transverse plane. This may account for the difference between the contact forces of the current and previous model during the second half of stance, as the z-axis external moment reached a peak value during that time (Figure 2). Muscles are not strategically aligned to counteract a transverse moment (typically a function of the cruciate ligaments); therefore the inclusion of this plane may be essential in determining accurate contact forces for TKR patients.

The medio-lateral force ratio was within the range of previously reported values (Johnson et al., 1980; Hsu et al., 1990; Schipplein and Andriacchi, 1991; Hurwitz et al., 1998; Shelburne et al., 2006), and for simplicity, was constant throughout stance although the ratio can vary with time in the model. For example, the ratio could follow the change in external knee adduction moment as recent studies with telemetric knee joints found a correlation between the medial contact force and the external knee adduction moment (Chaudhari et al. 2006; Zhao et al. 2007b).

Another simplification was that muscle activity for the antagonist group was set to “zero”. Despite this, the model allowed for co-contraction because muscles were not forced to act as agonists in all planes. This is exemplified during the first half of stance by the inclusion of the biceps femoris muscles because of their agonist contribution to the frontal and transverse planes, even though they act as antagonists in the sagittal plane.

The model could be modified to include more patient specific attributes by scaling the SIMM model to patient-specific anatomy and using patient specific electromyography to refine muscle group assignment. Further, the use of patient-specific knee contact kinematics will result in the correct assignment of in vivo muscle force lever arms to balance the external moments.

This parametric approach, newly applied to the knee, has many potential biomechanical and clinical applications that are not all possible with previous optimization and reduction approaches. For example the effect of the absence of soft tissue structures and/or the injury of muscle structures can be easily studied. Detailed systematic studies of antagonist muscle activity, contact paths, and medio-lateral force ratio variation are possible. Finally, by using in vivo input data, the parametric model can be used to determine more accurate contact and muscle force inputs for knee joint simulators and computational models, including the contact and muscle forces during a variety of activities of daily living.