HIGH-THROUGHPUT CELL AND PARTICLE CHARACTERIZATION USING ISO-DIELECTRIC SEPARATION

Abstract

Separations can be broadly categorized as preparative, where the objective is to extract purified quantities of a sample from a complex mixture, or analytic, where the goal is to determine and quantify the contents of the original mixture. Here we demonstrate the application of a new microfluidic separation method, iso-dielectric separation (IDS), to a range of analytic separations involving cells and particles spanning several orders of magnitude in volume and electrical conductivity. In IDS, cells are dielectrophoretically concentrated to the region along an electrical conductivity gradient where their polarizability vanishes; by measuring this position – the iso-dielectric point (IDP) – as operating conditions such as the frequency and voltage of the applied electric field are varied, we are able to sort cells or particles with distinct IDPs while simultaneously characterizing their electrical properties. We apply this technique to measure the electrical properties of polystyrene microspheres, viable and non-viable cells of the budding yeast Saccharomyces cerevisiae, and murine pro B cells, including how these electrical properties vary with the electrical conductivity of the surrounding solvent.

INTRODUCTION

Electrical properties, such as conductivity and permittivity, offer both insight into the composition and structure of cells and particles, as well as provide an intrinsic handle upon which separations can be based. Over the past several decades, dielectrophoresis (DEP)¹, electrorotation^2,3 and impedance spectroscopy^4,5 have emerged as effective techniques for characterizing the charge, conductivity, and permittivity of cells over a broad range of conditions. Simultaneously, related techniques – in particular, dielectrophoresis - have also proven effective as mechanisms for cell sorting^6,7. Still, for electrical separations to be most effective requires a more extensive understanding and characterization of cell properties. This improved understanding – a mapping of genetic and phenotypic information to the electrical properties of individual or groups of cells - could lead to new applications; however it requires techniques for measuring cell properties that are high throughput, adaptable to a wide range of cell types, and capable of rapidly exploring a large parameter space of environmental conditions. Despite the need for such measurements and the fundamental connection between cell characterization and cell sorting, to date, previous technology has focused on either cell separation or on cell characterization, with exceptionally few attempts to combine these two functionalities to create an analytic cell separation method.

We have recently developed a new method, called iso-dielectric separation (IDS), capable of performing preparative separations of cells and particles based upon their electrical properties over a range of frequencies and medium conductivities⁸. An analogy can be drawn between IDS and iso-electric focusing (IEF), a widely used analytic separation method for sorting and characterizing mixtures of biomolecules. In IEF, molecules with a pH-dependent charge are focused by an electric field in a pH gradient to equilibrium – the iso-electric point, where the net charge vanishes. In IDS, dielectrophoresis – the translational force on a polarizable body in a spatially non-uniform electric field⁹ - is used to drive cells and particles in an electrical conductivity gradient to the iso-dielectric point, or IDP, where the net polarization charge vanishes. We have previously demonstrated the efficacy of IDS for separating mixtures of synthetic polystyrene beads according to surface conductance, as well as biological cells according to a phenotypic marker (i.e. viable and non-viable cells of S. cerevisaie)⁸. In the present work, we focus on the use of IDS as an analytical tool for characterizing the electrical properties of cells and particles, including functionalized and non-functionalized polystyrene beads, viable and heat treated yeast, and mammalian white blood cells.

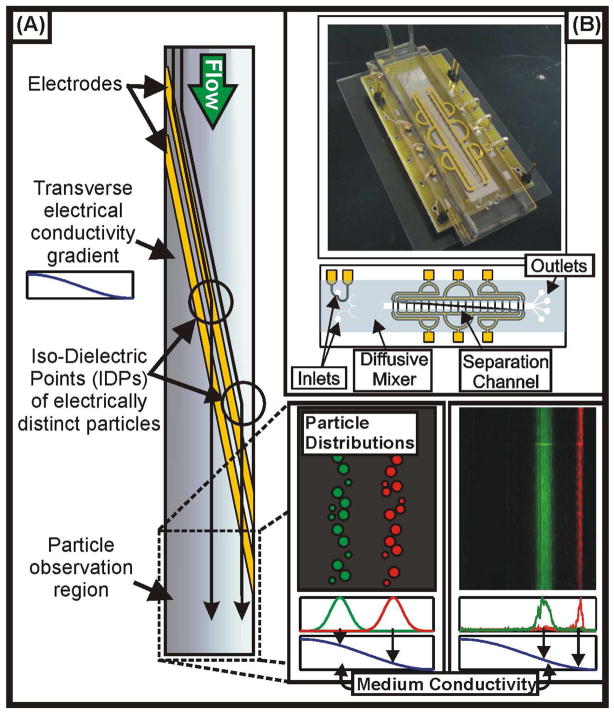
Figure 1 illustrates the concept of IDS. The device consists of a microfluidic channel into which we load a high conductivity solution, containing the suspension of cells or particles, and a low conductivity solution, free of particles. These solutions pass through a diffusive mixer, which establishes a smoothly varying conductivity profile at the entrance to a separation channel. The separation channel contains electrodes arranged across the bottom surface at a shallow angle with respect to the direction of flow in the channel. Because the particles are initially suspended in a high-conductivity solution, in which they exhibit negative polarizability, the non-uniform electric field created by the electrodes deflects the particles across the width of the channel, in the direction of decreasing medium conductivity. As the medium conductivity surrounding the particle decreases, so too does the particle’s polarization. This continues until the imposed drag force, acting along the axis of the channel, overwhelms the dielectrophoretic force created by the electrode barrier, allowing the particles to flow downstream unobstructed. Here, the particles may either be imaged (if the objective is to record their positions for the purpose of characterization), collected from one of a number of outlets (four in our architecture, though more could easily be added), or both. In this work, we are focused primarily on demonstrating the ability to characterize particles and thus imaged them at the outlet. Because the position along the width of the channel that a particle exits the device can be related back to the conductivity of the medium, the spatial distribution of particles at the outlet of the device encodes information about those particles’ electrical properties. In its use of a variable medium conductivity, IDS is superficially similar to a technique developed by Markx et al.¹⁰; however, while this previous approach leveraged a temporally applied “gradient” and was not extended to particle measurement, the conductivity gradient in our work is applied spatially (and is therefore a true gradient), and we focus in the current work on extending IDS as a tool for measuring cellular properties.

Figure 1.

Concept of the IDS device. (A) Cells and particles flow through a channel with electrodes across the diagonal and a conductivity gradient across the width (decreasing from left to right in the figure). The electrodes dielectrophoretically deflect cells or particles across the conductivity gradient until they reach their iso-dielectric point (IDP), where they pass over the electrode barrier. Finally, they flow to an observation region, where the cells and particles are imaged to determine their spatial distributions, and to outlets, where fractionated samples may be collected. (B) Photograph (top) and schematic (bottom) showing the packaging and layout of the device, respectively. The conductivity gradient is created by loading the two inlets with different conductivity solutions and then passing them through a diffusive mixer prior to the separation channel.

One feature of using IDS for measuring particle properties is its insensitivity to particle volume. Because the dielectrophoretic force is volumetric, most methods that use DEP are very sensitive to cell size. It is more difficult to specifically measure the electrical properties of cells, which manifest themselves as the effective conductivity and permittivity of the cell, embedded in the dimensionless Clausius-Mossotti factor, K(ω):

$$\underset{\_}{K}(\omega )=\frac{{\underset{\_}{\sigma }}_p-{\underset{\_}{\sigma }}_m}{{\underset{\_}{\sigma }}_p+2{\underset{\_}{\sigma }}_m}$$ (1)

Here, σ_p is the complex (frequency dependent) conductivity of the particle, given by σ_p ≡ σ_p + iωε_p. When Re{K} = 0, the particle is no longer polarized by the applied field, and the translational force vanishes. Importantly, the location of this iso-dielectric point in the conductivity gradient is determined only by the conductivity and permittivity of the cell and the surrounding medium, independent of the cell volume or other parameters. As a result, by observing convergence of cells to this point in the gradient, we obtain a more specific measurement of a cell’s electrical properties than is typically possible using dielectrophoresis.

A second feature of IDS is that it operates in a continuous flow manner, enabling the rapid characterization of >10⁴ cells per minute, including both the mean and variance of properties across a population. This is in contrast to techniques such as electrorotation², from which one must obtain detailed spectra for individual cells somewhat laboriously, or bulk impedance measurements¹¹, which only provide electrical properties averaged over large populations. While microfluidic impedance spectroscopy techniques have recently been developed to achieve high-throughput measurements of a broad range of the dielectric spectra of cells⁵, these methods consider only a single media conductivity at a time, whereas IDS enables rapid measurements of electrical properties subjected to variable medium conditions. Because particles with sizes of ~1 – 10 μm typically reach diffusive equilibrium on a timescale of ~1–100 ms (a²/D) while residence time in the separation channel is typically ~10 s, particles can be treated as instantaneously adjusting to variations in the external medium. This allows us to simultaneously map out the frequency and conductivity dependence of Re{K} by varying the conditions (i.e. applied voltage, frequency, and flowrate) of the separation. Examples of cells and particles for which electrical properties depend sensitively on the external environment are pervasive, including any particle or cell for which the outermost layer supports fixed charge and/or is porous. In these (nearly ubiquitous) cases, the ability to measure the dependence of polarizability on frequency and medium conductivity in a way that is essentially simultaneous complements existing characterization methods⁵ that focus on high-bandwidth measurements of electrical properties across varying frequencies. The combined advantages of insensitivity to variations in non-specific parameters (e.g. volume, density, etc.), high-throughput measurements of population averages and variation, and the ability to consider a range of frequencies and medium conductivities in a single experiment make IDS a promising tool for particle characterization and separation, and an effective complement to existing techniques well suited to obtaining high-resolution spectra of cells and particles at single conductivities.

THEORY

Interpreting the results of a separation to obtain quantitative information about the cells or particles being analyzed requires quantitative understanding of how the device operates. In general, the characteristics of a separation are determined by the contributions of both specific and non-specific forces acting on the particles. Here, a specific force refers to any force which depends upon the property of the particle being targeted for separation. Since IDS separates particles according to their effective electrical conductivity, dielectrophoresis represents the specific force within the system, whereas all other forces (hydrodynamic, gravitational, etc.) comprise non-specific forces, and thus interfere with the purity of the separation and undermine the potential for analysis. In our prior publication on using IDS for separation⁸, we developed models to design devices capable of creating electric fields in conductivity gradients while mitigating electrohydrodynamic instabilities, as required for IDS. In this section, we develop accompanying models for the much more challenging task of quantitatively correlating particle position in the device to that particle’s electrical properties in the face of specific and non-specific forces that can potentially arise in IDS.

Mass transport

Because the DEP force depends on the conductivity throughout the device’s separation channel, specifying the forces acting on particles requires the analysis of mass transport in the system. We have described previously⁸ the normalized steady-state conductivity profile σ̃_m obtained throughout the separation channel. Taking Eq. 1 from reference (8) and setting z = (ℓ/w)x (or, in terms of dimensionless coordinates, z̃ = x̃), we can obtain an expression for the conductivity in the frame of a particle as it is being deflected along the electrodes:

$${\stackrel{\sim }{\sigma }}_m(\stackrel{\sim }{x})=\frac{1}{2}+\sum _{n=1}^{\infty }{a}_{n}cos(n\pi \stackrel{\sim }{x})exp\left[-\frac{{(n\pi )}^2}{\text{Pe}}\stackrel{\sim }{x}\right]$$ (2)

This expression provides a means for mapping the position of a particle along the channel width (x) to the medium conductivity at which it reaches its threshold polarizability (σ_m). To extend this analysis to determining the electrical properties of the cells, we must relate this medium conductivity to the threshold polarizability, K, at which particles pass through the DEP barrier.

Force Balance

The threshold polarizability of a particle is determined from the balance between drag and dielectrophoretic forces. The force on a particle in a shallow channel, subject to an imposed external force and Poiseuille flow is given by¹²:

$${\mathbf{F}}_{\mathit{DEP}}=6\pi \mu a\left[{\xi }_1{\mathbf{u}}_{\mathbf{p}}-{\xi }_2{\mathbf{U}}_0\right]$$ (3)

where F_DEP denotes the DEP force, u_p denotes the particle velocity, and U₀ denotes the average velocity of the imposed Poiseuille flow. The parameters ζ₁ and ζ₂ are dimensionless corrections for the Stokes drag coefficient, necessitated by the nonuniform fluid velocity and the presence of the channel floor and ceiling. Integrating u_p with respect to time determines the trajectory of a particle subject to drag and DEP forces (Figure 2A, left). Because the particle polarizability and thus the DEP force vary with the conductivity, as particles approach their iso-dielectric points, F_DEP ≈ 0 and the particles pass through the DEP barrier. This will occur when the polarizability reaches a threshold value, Re{K} = K₀, such that the particle is no longer deflected along the axis of the electrodes. This corresponds to the condition that:

$$U_{\mathit{DEP}}^{max}=[{\xi }_{2}sin\theta ]U_0$$ (4)

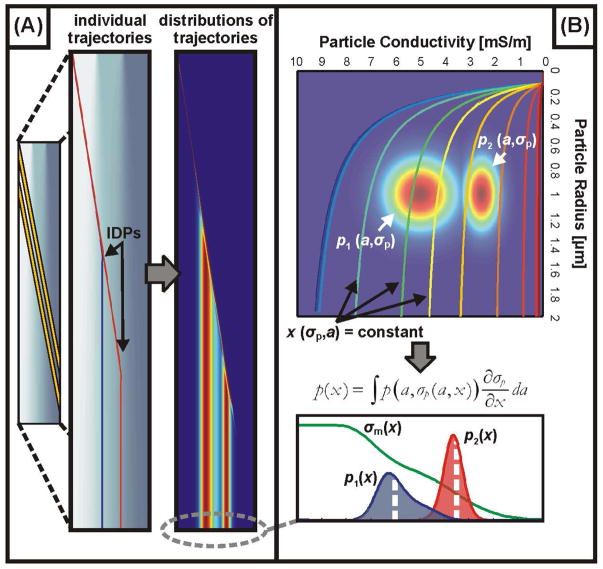
Figure 2.

Modeling and interpreting the distribution of particle trajectories through the device. (A) Simulations to determine individual particles’ trajectories (left) and distributions of these trajectories (right) for suspensions containing particles with a distribution of sizes (a) and conductivities (σ_p). (B) Relating the distribution of physical properties (size and conductivity, in this case), to the spatial distribution of particles at the outlet (p(x)) by integrating the property distributions (appropriately weighted) over contours of constant outlet positions. By fitting spatial distributions from this model to the observed distributions, we are able to infer how certain physical properties are distributed across the suspension.

Here, the angle θ denotes the inclination of the electrodes with respect to the direction of flow, and we have defined the dielectrophoretic “velocity”, U_DEP, of a particle of radius a in a fluid of viscosity μ as (6πμa)⁻¹ F_DEP, which has a maximum magnitude of $U_{\mathit{DEP}}^{max}$. To calculate U_DEP we use the conformal mapping solutions available for the coplanar electrode geometry¹³ to calculate the electric field, combined with custom scripts for efficiently calculating the multipolar DEP force¹⁴. The use of conformal mapping in determining the electric field assumes that the medium conductivity can be treated as locally homogeneous. This assumption is motivated by the disparate length scales characterizing variation in the conductivity (which varies over the width of the channel, w = 2 mm) and the electric field (which varies over the width and spacing of the electrodes, ~ 60 μm). Given the electric field, the dipole contribution to the DEP velocity is determined from:

$${\mathbf{U}}_{\mathit{DEP}}=\frac{a^2{\epsilon }_m}{3\mu }K(\omega )\nabla (\mathbf{E}·\mathbf{E})$$ (5)

To make this calculation consistent with our models for mass transport (in which we neglect any variation along the depth of the channel), we evaluate the DEP force one particle radius below the channel ceiling, where we define the dimensionless field intensity gradient for a channel of height H as $\stackrel{\sim }{\mathbf{G}}(a/H)\equiv V_{\mathit{rms}}^{-2}{H}^3\nabla (\mathbf{E}·\mathbf{E})$. This simplification is motivated by the strong levitational force exerted on the particles, and is also invoked in obtaining a more convenient expression for the dimensionless drag coefficient, ζ₂, from Eq. 4:

$${\xi }_2\simeq 8.22\frac{a}{H}\left[1-0.039\frac{a}{H}\right]\approx 8.22\frac{a}{H}$$ (6)

This dimensionless correction for the drag on a particle levitated to the channel ceiling in Poiseuille flow is valid for 0 < a/H < ½; for the common case where a/H ≪ 1, this may be linearized to further simplify analysis.

Equations 4–6 allow us to determine K₀, the threshold polarizability at which particles flow past the DEP barrier:

$$K_0(\omega )=49.32\frac{\mu H^{2}sin(\theta )U_0}{a{\epsilon }_m{V}_0^2\stackrel{\sim }{G}(a/H)}$$ (7)

In the limit of small particles (a/H → 0), G̃ reduces to a constant (≈ −0.2), and Eq. 7 reduces to:

$$K_0(\omega )/-250\frac{\mu H^{2}sin(\theta )U_0}{a{\epsilon }_m{V}_0^2}$$ (8)

We use Eq. 8 to calculate the threshold polarizability that determines where particles pass through the electrode barrier. By equating K₀ from Eq. 8 with Re{K} as given by Eq. 1 and calculating the medium conductivity from Eq. 2 and the observed locations of the particles, we are able to relate the threshold polarizability of a particle to its electrical properties, embodied by the effective (frequency dependent) particle conductivity, σ_p. This effective conductivity may then be interpreted in terms of the thickness, conductivity and permittivity of the different layers comprising a particle.

Particle and cell heterogeneity

Since the size and electrical properties of each particle in a suspension are not identical, the threshold polarizability (Eq. 8) and the medium conductivity at which it is reached will typically vary, giving rise to a spatial distribution of particles as they flow to the outlet of the device. By observing this distribution (denoted as p(x), where x is the position along the width of the channel), it is possible to study how the particle’s properties are distributed. Although the number of parameters contributing to the effective conductivity of a particle is typically large (consisting of, for example, the size, conductivity, and permittivity of each layer), for simple particles, or particles in which different layers can be isolated by performing measurements over a particular frequency range, we can use IDS to rapidly measure the variance of the properties of large numbers of cells or particles (>10⁴ per minute).

We consider a suspension of particles whose IDP is determined by the combination of N properties (in addition to the device’s operating conditions), which we denote as {q_i}, (i = 1… N). The properties of the particles in the suspension are thus described by the joint probability distribution function p(q₁, q₂, … q_N). We wish to relate the distribution of the N particle properties to p(x), the spatial distribution of particles at the outlet of the device. Given a measurement of the spatial distribution, we may then determine property distributions which are consistent with our observations.

To determine how p(x) is related to p(q₁, q₂, … q_N), we express one of the N parameters (q_N, for example) as a function of the remaining N-1 parameters and the outlet position, x, and calculate the following integral

$$p(x)=\int p(q_1,q_2,\dots q_N(q_1,q_2,\dots q_{N-1},x))\frac{\partial q_N}{\partial x}d{q}_{1}d{q}_2\dots d{q}_{N-1}$$ (9)

For the simplest case of a single parameter, q₁, with distribution p₁(q₁), the distributions are related by $p(x)=p_1\{q_1(x)\}\frac{d{q}_1}{dx}$. Figure 2 illustrates this transformation from distributions of physical properties (two in this case – particle radius and conductivity) to distributions of positions. The trajectories of individual particles (Figure 2A, right) are determined by both the physical properties of the cell (through Eq. 1) as well as the operating conditions of the device (through Eq. 2 and 8), and can be summarized by the IDP – the position of the particle at the device outlet. Although the electrical properties of a particle uniquely determine that particle’s IDP for a given set of operating conditions, the position at the outlet does not uniquely determine the properties of the particle; as an example, for a suspension containing particles with variable sizes (a) and conductivities (σ_p), there will exist a family of sizes and conductivities which produce the same IDP (the curves labeled x(σ_p,a) = constant in Figure 2B). Eq. 9 amounts to integrating the probability distribution p(a, σ_p) over these contours, inversely weighted according to how sensitive the IDP is to variations in particle conductivity (for this particular case). The result is distributions p(x) which match the property distributions for the appropriate set of operating conditions (Figure 2B, bottom).

Although the mapping of one parameter (the IDP) to several (size, conductivity, etc.) is inherently underspecified, in practice, it is often possible to eliminate all but the dominant source of variation, or to use orthogonal methods to determine the variation in one or more of the relevant properties (e.g. particle size). In all of our calculations, we assume that the properties are distributed narrowly enough that the physical properties all follow a normal distribution, although it would be straightforward to use more realistic one-sided distribution functions. Under this assumption, the task of determining the distribution of physical properties is reduced to finding their mean and variance.

Influence of non-specific forces

The primary non-specific forces that can interfere with particle separation and characterization in IDS arise from electrohydrodynamics (EHD)^15–18 and particle interactions¹⁹ in the system. Based on previous modeling and observations of EHD in our system⁸, we have found that for particles with diameter over 1 μm and conductivities and voltages of 0.1 S/m and 20 V_pp, thermally induced EHD produces a force of magnitude ~10% that of DEP. Accordingly, for similar or less stringent operating conditions (e.g. larger particles, lower conductivities, or lower voltages) EHD should not appreciably influence device performance.

Non-specific forces arising from electric or hydrodynamic interactions between particles can be avoided by operating at sufficiently low particle concentrations. This is further aided by the separation mechanism in IDS, which minimizes the disturbance caused by particles to the medium. For example, while the DEP force acting on a particle is linearly proportional to the real part of the particle’s CM factor, K, dipole interactions between two electrically similar particles vary as approximately K². Thus, as particles approach their IDPs (K → 0), interparticle forces decay more rapidly than the DEP force arising from the external field. By operating within the constraints imposed by these non-specific forces, it is possible to accurately neglect these contributions to the particle trajectories.

MATERIALS AND METHODS

Device Fabrication, Packaging and Preparation

We patterned planar electrodes on 6″ Pyrex wafers using e-beam evaporation of 2000-Å Au/100-Å Ti and a standard liftoff process. The electrode spacing and line width are 15 μm and 60 μm, respectively. For the microfluidic channels, we use PDMS replica molding from an SU-8 patterned silicon master (SU-8 2015, Microchem, Newton MA) to create channels with a width of 2 mm and a height of from 17 μm, achieving ~5% uniformity in film thickness over the area of the wafer. Prior to plasma bonding the PDMS mold to the diced Pyrex chip, we bore holes for the inlet and outlet ports using 0.025 OD × 0.017 ID steel pins (NE-1300-01, type 304 WD, New England Small Tube, Litchfield, NH). We fasten the device to a custom made printed circuit board, where we make electrical connections to interface with a function generator (33220A, Agilent, Palo Alto, CA). We use an oscilloscope (Tektronix, Richardson, TX) to monitor the voltage delivered to the pins of the PCB. To make fluidic connections between the device and a syringe pump (KD Scientific 200, Holliston, MA), we use Tygon tubing (ID 0.02″, OD 0.06″, VWR, Brisbane, CA) press fit into the PDMS.

Cell culture and bead preparation

We cultured the budding yeast Saccharomyces cerevisiae at 30 °C for two days in a medium comprised of 1% Yeast extract, 2% peptone and 2% glucose. After harvesting the cells, we centrifuged and resuspended them in deionized water. Cells to be heat treated were transferred to a glass vial and placed on a hot plate set to 90°C for ~20 minutes. Live/dead staining using Syto 9 (S-34854, Invitrogen, Carlsbad, CA) and propidium iodide (P1304MP, Invitrogen, Carlsbad, CA) confirmed that 100% of cells were non-viable after heat treatment, whereas typically >95% of the untreated cells remained viable. After staining, cells were washed three times in a solution of deionized water, 0.1% BSA, and PBS mixed to the desired conductivity.

For experiments involving polystyrene beads, three different types were used: green fluorescent carboxylate-modified (09719, Polysciences, Inc. Warrington, PA, 1.646 ± 0.069 μm true diameter), red fluorescent carboxylate-modified (F8825, Molecular Probes Eugene, OR, 2.0 μm true diameter, ~1% CV estimated by manufacturer), and green fluorescent (FS04F/6845, Bangs Laboratories, Inc. Fishers IN, 1.90 ± 0.22 μm true diameter).

For experiments with mammalian cells we use BA/F3 mouse pro B cells provided by Susan Lindquist (Whitehead Institute, Cambridge, MA). The cell line was transfected and cultered as described in²⁰. To assess the viability of mammalian cells after passing through the device, we collected samples from the device (operating at 6 Vpp and 10 MHz and a flowrate of 4 μl/min) and stained with Syto 9 and propidium iodide before manually counting viable and non-viable cells. Using this simple assay, we found no significant difference in viability before and after the cells were passed through the device with viability >85% in both cases. The lack of adverse effects on cell viability is consistent with the brief residence time of the cells in the device (~16 s under these operating conditions) and operation in a frequency range in which the transmembrane voltage is small.

Fluorescence Microscopy and Data Acquisition

Imaging is performed using an upright Zeiss Axioplan 2M microscope (Zeiss, Thornwood, NY) coupled to a LaVision Imager 3 QE CCD Digital Camera (LaVision GmbH, Goettingen, Germany) using FITC and Cy3 filters. We record videos of particle separations under 5 × magnification at the outlet of the device. To represent the trajectories of ensembles of particles over time in a 2D image, we process the videos using a first-order difference filter. We apply a uniform threshold, so that each particle receives identical weighting in the composite image, and average the video over the total number of frames to produce the final image.

Analysis of Results

After determining the one dimensional cell or particle distributions at the outlet of the device, we calculate the IDP (defined as the mean of the distribution) from $x_{\mathit{IDP}}={\int }_0^{w}xp(x)dx$. Substituting x_IDP into Eq. 2 for the conductivity along the axis of the electrodes gives σ_m, the local medium conductivity at the particle IDP. Using Eq. 8, we predict the value of Re[K(ω)] at which the particles pass through the electrode barrier. Combining this result with the local medium conductivity, we may calculate the conductivity or permittivity of different layers of the particle or cell by using an appropriate model for the particle we are considering.

RESULTS

Particle Separation and characterization

We use IDS and the model described above to separate and characterize particles covering a broad range of sizes (~1 – 10 um) and conductivities (~10⁻³ – 1 S/m). Our technique enables us to rapidly measure both the frequency and conductivity dependence of the electrical properties for large numbers (~10⁴–10⁵) of particles and cells. As our first demonstration of this capability, we determine the surface conductance, K_s, of functionalized and non-functionalized polystyrene beads at varying medium conductivities. These beads offer a widely studied example of particles whose electrical properties vary depending upon their interactions with the external solution. From this, we proceed to study biological cells both with and without a cell wall (the budding yeast S. cerevisiae and the BA/F3 murine pro B cell line, respectively). The charged, porous structure of the yeast cell wall presents a second example of system in which electrical properties are directly dependent upon the external medium.

Polystyrene Beads

The ability to control both the surface-to-volume ratio and surface chemistry of polystyrene (PS) beads has made them an attractive tool for chemical sensing and concentration (21,22), as well as more general characterization of microfluidic and dielectrophoretic devices ^23,24. Despite this wide use, the surface properties of these particles are often difficult to characterize, and the physical basis for these properties remains an area of active research²⁵. In the context of AC electrical measurements, DEP and electrorotation have been used to determine the surface conductance of PS and latex beads^2,26; however, the throughput of these measurements – typically performed in non-continuous flow devices or laboriously on single particles – is prohibitive for applications in which one wishes to quantify changes in surface conductance associated with chemical modification to the surface of a large number of (potentially heterogeneous) particles.

The electrical conductivity of a PS bead is given by σ_p = σ_bulk +2K_s/a, where σ_bulk denotes the bulk conductivity of polystyrene, a is the particle radius, and K_s is the surface conductance². Following others, we assume σ_bulk ≈ 0, such that the surface conductance and particle size are the sole determinants of the particle’s conductivity. A simple model for the surface conductance assumes that K_s is proportional to the net charge of the particle divided by the thickness of the layer over which counterions balance this charge: K_s ∞ ρ_s/δ²⁷. In considerably more detail, Mangelsdorf and White proposed that K_s is composed of contributions from both the stagnant (Stern) layer as well as the diffuse layer surrounding the particle²⁸, and others have shown that describing a particle’s total surface conductance as the sum of two terms, one increasing with and one independent of the external medium conductivity are consistent with experimental results²⁹. This suggests that at very low medium conductivity, where the diffuse layer becomes relatively thick, the surface conductance is determined primarily from the stagnant layer conductance. Accordingly, K_s is expected to be independent of the medium conductivity for low values of σ_m, and increase with the medium conductivity at higher values of σ_m, as the contribution of the diffuse layer conductance becomes more significant.

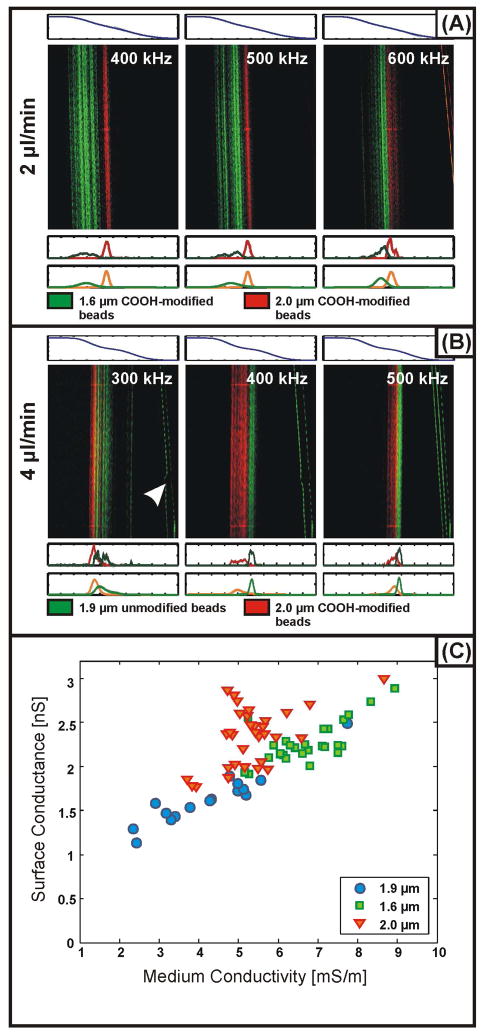
We have used IDS to simultaneously separate and characterize the surface conductance of PS beads with different sizes and surface chemistries. Representative particle distributions from these experiments are presented in Figure 3A&B. We can use these distributions to solve for K_s by substituting the expression for the beads’ effective conductivity into Eq. 1 and equating the result with the threshold polarizability given by Eq. 8. For the green carboxylate-modified beads, red carboxylate-modified beads and unmodified green beads, we find average values for K_s of 2.27 ± 0.23 nS, 2.34 ± 0.33 nS, and 1.64 ± 0.30 nS, respectively. We may also match individual measurements of the beads’ surface conductance with the medium conductivity at which they localized under particular conditions to study how the surface conductance depends on the medium conductivity. Our measurements show an increase in surface conductance from ~1–3 nS with increasing medium conductivity (Figure 3C) over the range 2 – 10 mS/m. Previous studies of surface conductance, performed using electrorotation, report values of K_s independent of the medium conductivity for σ_m from 0.2 – 1.6 mS/m, with values ranging from 0.2 – 2.1 nS². This may be attributable to the Stern layer conductance in the model of Mangelsdorf and White. Additionally, although they do not report specific results, the authors of this study observe the onset of a dependence upon the medium conductivity at higher conductivities, consistent with our observations. In obtaining our results, measurement of the non-functionalized beads was complicated by the larger CV of these beads (11% as provided from the vendor) and their tendency to form aggregates, possibly due to their lower surface charge. In our analysis, we have excluded this subpopulation which does not pass through the electrode barrier (Figure 3B); as a result, the numbers we report for non-functionalized beads may vary significantly from those that would be determined from a population average while enabling the discrimination of subpopulations (e.g. particle aggregates) from a nominally homogeneous, monodisperse suspension.

Figure 3.

(A) Measured distributions of red (2.0-μm diameter) and green (1.6-μm diameter) carboxylate-modified polystyrene beads. (B) Measured distributions of red (2.0-μm diameter) carboxylate-modified and green (1.9-μm diameter) unmodified polystyrene beads. Along with each fluorescence micrograph in both A and B, the conductivity (above, predicted from Eq. 2 with a high conductivity of 10 mS/m and a low conductivity of ~0 S/m) is plotted, as well as the one-dimensional measured (below, top) and modeled (below, bottom) particle distributions. The arrow in the leftmost panel in B indicates particle aggregates which do not pass through the electrode barrier. (C) Values for the surface conductance (K_s) of the three types of polystyrene beads as a function of medium conductivity extracted from measurements using IDS.

Because IDS measures the properties of many particles at once, we can extract information about particle properties from the shapes of the particle distributions measured at the outlet. Using Eq. 9 with the variable parameters taken to be particle radius (a) and surface conductance (K_s), we fit our model to the measured distributions. For the carboxylate-modified beads, approximate CV’s obtained from the vendors are 4.2% for the 1.6 μm beads and 1% for the 2.0 μm beads. For the non-functionalized 1.9 μm beads, since we exclude the fraction of the population which does not pass over the electrodes, we fit the distributions by allowing the CVs for both particle size and surface conductance to vary. Following this procedure, we obtain CVs of 11.4 ± 5.4% and 5.8 ± 3.9% for the K_s values of green and red carboxylate-modified beads, respectively. For the non-functionalized beads, best fits are obtained for a 1–2% variation in size with a 7.5% variation in surface conductance. Plots of measured and fitted particle distributions are presented in Figure 3A&B. These results suggest that the surface properties of these particles are approximately as homogeneous as their distributions in size. The larger variation in surface conductance for particles with smaller diameters may be attributable to the increased sensitivity of K_s to variations in the number of charged groups on the particle surface as the total number of these groups decreases.

Yeast Cells

The budding yeast Saccharomyces cerevisiae has been the focus of fundamental and applied research, from genetics and bioinformatics to antifungal drug development. Each of these applications seek to map the phenotype of particular cells to either their genotype or to the environmental conditions to which they have been subjected, an analysis that requires the ability to perform quantitative measurements on the cells. Accordingly, a common approach over the past several decades has been to study the dielectric spectra of mutant or environmentally perturbed yeast^30–32.

While others have used electrorotation or bulk impedance measurements to characterize the spectra of individual cells or population averages across frequency^2,3, IDS offers the ability to measure property distributions over a continuous range of medium conductivities spanning several orders of magnitude on a large number of cells. To investigate the possibility of using IDS to separate and characterize yeast with environmentally altered phenotype, we apply the technique to the study of viable and non-viable cells with emphasis on the electrical properties of the cell envelope; this measurement is particularly well suited to IDS, since, as with the polystyrene beads, the electrical properties of the porous, charged cell wall have been shown to depend sensitively on the conductivity of the external medium³³. Since the equilibration of mobile carriers within the wall occurs over a timescale on the order of the charge relaxation time (~0.1 μs under typical conditions), whereas the medium conductivity surrounding a cell evolves over the course of the convective timescale (~1–10 s), the electrical properties of the cell wall during the separation should be pseudosteady, changing essentially instantaneously with the medium conductivity.

Viable Yeast Cells

To determine the electrical properties of viable yeast cells, we use the parameters given in Table 1. Assuming literature values for some of the cell layers (cytoplasmic conductivity and permittivity, cell wall thickness and permittivity, and cell membrane thickness and conductivity), as well as using direct measurements of the cell radius obtained using a Coulter counter, constrains the fitting problem and allows us to focus on the characteristics of the cell envelope. With the exception of the cytoplasmic conductivity, measurements of which vary wildly through the literature (from 0.2 – 1.2 S/m), property values are taken from³¹. For the cytoplasmic conductivity, we use an approximate median value from the literature of 0.5 S/m. Because of the difficulty associated with determining the cytoplasmic conductivity, we also performed fitting for values of 0.25 S/m and 1.0 S/m. In both cases, the extracted cell wall conductivities changed by less than 10% from the results obtained using 0.5 S/m, confirming that the conditions for this measurement are not strongly dependent on the cell’s interior properties.

Table 1.

Parameters used in and determined from fitting the distributions of yeast at the outlet of the IDS device. Parameters labeled with ‘*’ are taken from (31).

	Membrane	Cell Wall	Cytoplasm
Viable Cells	2.5 × 10−7S/m*	~0.12 σm	0.5 S/m
	10ε0	60ε0*	50ε0*
	8 nm*	0.25 μm*	2.0 μm
Heat Treated Cells	1.6 × 10−4S/m*	~0.43 σm	0.05 S/m (= σhigh)
	10ε0	60ε0*	50ε0*
	8 nm*	0.25 μm*	2.0 μm

A common model for the conductivity of a charged, porous material such as the yeast cell wall, is of the form³³:

$${\sigma }_w\approx c_f^w{u}^w{\left[1+{(2{\sigma }_m/c_f^w{u}^0)}^2\right]}^{1/2}$$ (10)

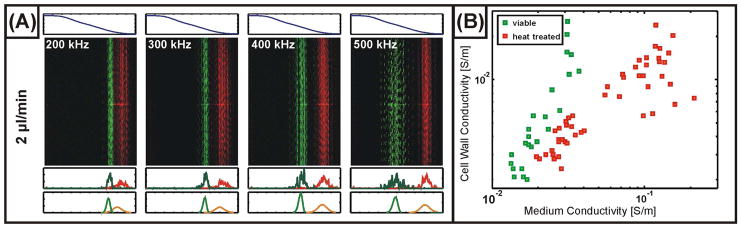
At sufficiently low medium conductivities, the wall conductivity is determined by the concentration of fixed charges ( $c_f^w$) and the mobility of counterions in the cell wall (u^w). At high medium conductivities, σ_w varies linearly with σ_m, with a slope depending upon the porosity of the cell wall, as parameterized by the mobility of ions inside the cell wall relative to their mobility in the bulk solvent (u⁰). We have characterized multiple cell cultures in conductivity gradients spanning both high (σ_h = 0.33 S/m, corresponding to the cells’ growth medium) and low (σ_h = 0.05 S/m) values. Figure 4A depicts representative distributions observed for viable and heat-treated yeast cells at the lower conductivity range. Comparison of the values of σ_w extracted from these measurements to Eq. 10 suggests that at media conductivities as low as ~0.02 S/m, the concentration of fixed charge in the wall is much less than the concentration of ions in the electrolyte (Figure 4B), as suggested by the approximately linear increase in σ_w with σ_m. Additionally, interpreting the slope of the curve (Δ σ_w/Δ σ_m) as relating the mobility of ions in the bulk solution to ions in the porous wall suggests an effective porosity for the cell wall of roughly 6%. This agrees with measurements presented elsewhere in the literature, for example the value of ~5% measured via impedance analysis reported in³⁰.

Figure 4.

(A) Measured distributions of viable (green) and non-viable (heat-treated) yeast cells. Along with each fluorescence micrograph, the conductivity (above, predicted from Eq. 2 with a high conductivity of 50 mS/m and a low conductivity of 10 mS/m) is plotted as well as 1-D measured and modeled (below, with fits determined using the parameters from Table 1) particle distributions. (B) Values for the yeast cell wall conductivity as a function of medium conductivity determined for viable (green) and heat-treated (red) cells obtained using IDS and the parameters from Table 1.

Heat Treated Yeast Cells

Heating the cell suspension to 90 °C for ~20 minutes renders the cells non-viable and is accompanied by several drastic changes in cell structure. It is believed, for example, that heat treatment permeabilizes the cell membrane, increasing membrane conductance as well as allowing the internal contents of the cell to equilibrate with the external medium³¹. In addition, it is expected that extreme heat treatment may alter the structure and composition of the cell wall through denaturation. To investigate this, we use IDS to characterize heat-treated cells from multiple cultures following the same procedure as for viable cells. Our results suggest that the cell wall conductivity is more nearly proportional to the medium conductivity (Figure 4B, from which we obtain σ_w ~ 0.43 σ_m). Since we generally cannot decouple the influence between the conductivity and thickness of the cell wall, this observation may also be attributable to the decreases in the cell wall thickness from heat treatment. It is also worth noting that in our analysis, we take the internal conductivity of the permeabilized cells to be equal to the high conductivity used in establishing the gradient (50 mS/m); this assumes that the internal conductivity does not equilibrate with its surroundings over times on the order of a few seconds. Since the validity of this assumption depends upon the porosity of the permeabilized cell membrane, we have also considered a model in which the internal conductivity equals the medium conductivity at all times (not shown). This leads to a similar conclusion (σ_w ~ 0.5 σ_m), but with an increase in the scatter of the data.

Mammalian Cells

Finally, to demonstrate the feasibility of characterizing the electrical properties of larger, more physiologically sensitive cells, we use IDS to determine the membrane and cytoplasmic electrical properties of mammalian (BA/F3) cells. Mammalian cells are commonly modeled as a relatively conductive core, representing a lumped model for the cells’ cytoplasm and internal structure, surrounding by a thin (~5 nm) primarily insulating membrane³⁴. Despite the simplicity of these models, they have provided an indicator of phenotype in screens for apoptotic cells^35,36, multidrug resistance reversal³⁷, or tumor cells³⁸. One of the primary obstacles in the electrical characterization of mammalian cells is the inability of these cells to maintain ion homeostasis in a medium with low ionic strength^39,40; in any effort to characterize the electrical response of a cell, it is thus essential to control for the aspects of the electrical response which are inextricably connected to the measurement technique. Our approach largely circumvents this challenge by keeping cells suspended in a high-conductivity solution (e.g. cell culture media) until seconds before the measurement is performed. Since we do not expect ion leakage over such a short time scale to be appreciable, cell characterization using IDS has the potential to reveal unperturbed cytoplasm and membrane properties.

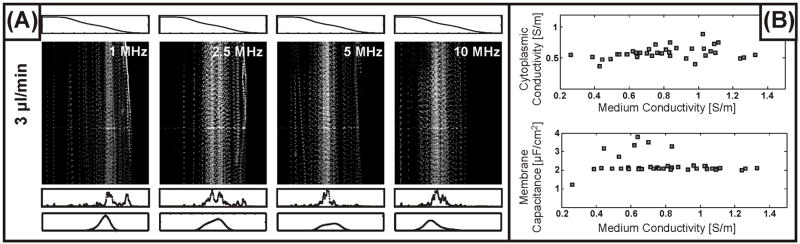
Figure 5 displays representative results for distributions of BA/F3 cells along with theoretical distributions generated from fitting the cytoplasmic conductivity and membrane capacitance using the model for device operation. Using a two-shell model for a mammalian cell suggests values of 0.58 S/m and 2.3 μF/cm² for the cytoplasmic conductivity and membrane capacitance, respectively, both in agreement with values reported elsewhere for white blood cells⁴¹. Importantly, we find that these parameters do not vary appreciably with the conductivity of the medium into which the cells localize (Figure 5B). This suggests that the cells maintain ion homeostasis for the duration of the measurement, enabling us to observe the unperturbed electrical properties of the cells. We also note that the typical peak width observed for these cells exceeds those measured for other particle and cell types. This may be attributed in part to the lower voltages used in these experiments as compared to those for yeast (3–5 V zero-to-peak amplitude as compared to 8–10 V for yeast). Thus despite the larger size of these cells, they do not converge as fully to equilibrium (K ~ 0), and thus exhibit a greater sensitivity to variations in cell size. In addition, we expect the electrical properties of the cells to be distributed over a finite range. Combining the different sources of variance, we estimate from the peak width a CV of ~10% for the cytoplasm and membrane electrical properties.

Figure 5.

(A) Measured distributions of BA/F3 cells in a conductivity gradient ranging from 1.5 S/m (corresponding to the growth medium of the cells) to an osmotically balanced sucrose solution that we treat as ~0 S/m. Beneath each image we plot the 1-D measured and modeled particle distributions, from which we obtain a cytoplasmic conductivity of 0.58 S/m and a membrane capacitance of 2.3 μF/cm². (B) Values for the cytoplasmic conductivity and membrane capacitance of BA/F3 cells determined from fitting to the particle distributions. The independence of both of these properties on the medium conductivity suggests that the exposure of the cells to low conductivity solutions is sufficiently short to avoid substantial disturbances of the cells’ ion homeostasis.

DISCUSSION

Analytic separation techniques can be broadly categorized as one of two types: those in which characterization may be coupled to downstream separation (e.g. impedance cytometry), and those in which the method of isolating particles in time or space is the fundamental mechanism of their characterization (e.g. iso-electric focusing, electrophoresis). While this latter category is well represented by molecular separation methods, there are exceptionally few analytic methods of this type for separating and analyzing cells. By using dielectrophoresis to both interrogate the electrical properties of cells as well as physically effect their separation, IDS fits into the category of analytic techniques that intrinsically also separate. The relative benefits of each of this approach to characterization depends on the application at hand; the rate at which measurements may be taken using IDS, for example, is constrained by the speed of separation - residence time of a cell in the device. For our architecture, this means that different conditions can be probed no faster than one every ~10s. In contrast, measurements of a single cell’s impedance at 512 frequencies in ~1 ms using impedance cytometry has been reported⁴². However, IDS offers the ability to characterize particles over two dimensions – frequency and conductivity – without the need to change the sample. This is advantageous in cases, such as those considered here of yeast and charged colloidal particles, where the dependence of electrical properties on the surrounding medium offers insight into the physical structure of a cell or particle’s surface. The ability to rapidly measure the interfacial electrical properties of particles for which these properties are inextricable from the external medium represents an advance over traditional approaches, and is enabled by the rapid equilibration of small particles with their immediate environment. Combining this ability with the ability to obtain full spatial distributions of the sample through the device in seconds allows for high throughput and high content characterization.

A second class of measurements for which IDS is well suited and which we have begun to explore here are those in which the cells being characterized may be perturbed from their native state by the environmental conditions. For example, although it is often advantageous to measure the electrical properties of mammalian cells in low medium conductivities, the stress that this places on the cell leads to changes in its electrical properties, as its ability to maintain ion homeostasis is compromised. Using IDS, it is possible to limit the exposure of cells to environmental stresses (such as low conductivities) to a few seconds, enabling measurements of the native properties of the cells under non-native conditions.

Although some of the experiments presented here have used fluorescent labels to better track subpopulations of cells in mixtures (e.g. viable and non-viable yeast), this is not a fundamental requirement of the technique. For example, results shown in figure 5 for the BA/F3 cell line were obtained by using the constitutive DsRed expression engineered into this cell line in place of cell staining. Furthermore, we have performed experiments (not shown) in which bright field imaging has been used in place of fluorescence to track particle distributions. This imaging approach appears to be robust for particles ~5 μm in diameter (e.g. yeast); however, we have not attempted this for particles substantially smaller than this, and for which it may prove difficult.

Regarding device design, the principle behind IDS is not specific to one particular architecture and thus allows for a broad range of implementations. Our design was guided by the objective of creating a device compatible with particles covering a broad range of sizes and conductivities, but different electrode dimensions and geometries may be better suited for applications targeting a specific type of cell or particle. Relevant considerations may include not only the force the electrodes are capable of imparting on a particle, but also factors such as the total power and power density dissipated in a particular design, as well as the ease of fabrication. As an example of the possible tradeoffs, assuming coplanar electrodes operated at a fixed voltage, the highest holding force is produced by using an electrode spacing much less than the channel height, regardless of the specific channel height used. However, too small of a gap will lead to excessive Joule heating and electrothermal convection, especially when higher conductivity buffers are used. A second example is the choice between coplanar electrodes and electrodes arranged parallel to each other on the top and bottom of the channel. While the parallel geometry leads to higher throughput in many (though not all) cases, it requires a more difficult fabrication process. Accordingly, the constraints and requirements of any specific application should be used to inform the device design.

We have demonstrated the feasibility of using IDS to better understand the electrical properties of cells and particles, especially regarding their dependence on the conductivity of the surrounding medium. Still, we believe that this approach to particle characterization and separation holds additional advantages for applications more advanced than those demonstrated here. The ability to combine characterization with separation could be used, for example, to screen cells according to their response to an environmental stressor, such as osmotic or thermal shock, or exposure to alkylating agents. With IDS, it would be possible to select cells of any level of resistance or susceptibility, provided that the stress response altered the electrical phenotype of the cell. Furthermore, the wide applicability of IDS which we have demonstrated here – characterizing cells and particles spanning several orders of magnitude in both volume and conductivity – suggests that its use is not limited to one type of cell, but could be applied to assays involving either prokaryotic or eukaryotic cells.