Improving performance of content-based image retrieval schemes in searching for similar breast mass regions: an assessment

Abstract

This study aims to assess three methods commonly used in content-based image retrieval (CBIR) schemes and investigate the approaches to improve scheme performance. A reference database involving 3000 regions of interest (ROIs) was established. Among them, 400 ROIs were randomly selected to form a testing dataset. Three methods, namely mutual information, Pearson’s correlation and a multi-feature-based k-nearest neighbor (KNN) algorithm, were applied to search for the 15 ‘the most similar’ reference ROIs to each testing ROI. The clinical relevance and visual similarity of searching results were evaluated using the areas under receiver operating characteristic (ROC) curves (A_Z) and average mean square difference (MSD) of the mass boundary spiculation level ratings between testing and selected ROIs, respectively. The results showed that the A_Z values were 0.893 ± 0.009, 0.606 ± 0.021 and 0.699 ± 0.026 for the use of KNN, mutual information and Pearson’s correlation, respectively. The A_Z values increased to 0.724 ± 0.017 and 0.787 ± 0.016 for mutual information and Pearson’s correlation when using ROIs with the size adaptively adjusted based on actual mass size. The corresponding MSD values were 2.107 ± 0.718, 2.301 ± 0.733 and 2.298 ± 0.743. The study demonstrates that due to the diversity of medical images, CBIR schemes using multiple image features and mass size-based ROIs can achieve significantly improved performance.

1. Introduction

As the advances of digital imaging technologies in the application of medical imaging, the development of content-based image retrieval (CBIR) schemes to automatically search for clinically relevant and visually similar reference images has been attracting wide research interest in medical imaging areas (El-Naga et al 2004, Muller et al 2004, Muller et al 2005). In digital mammography, several research groups have developed and tested new ‘visual aid’ tools based on different CBIR schemes in an attempt to improve the performance of computer-aided detection and diagnosis (CAD) schemes in detecting breast masses and classifying their likelihood of being malignant as well as to increase radiologists’ confidence in and reliance on CAD-cued (prompted) mass detection and classification results (Giger et al 2002, Alto et al 2005, Muramatsu et al 2005, Tao et al 2007, Zheng et al 2007a). In each of these CBIR-based CAD schemes, a large number of verified images or regions of interest (ROIs) with wide range variation of image characteristics are selected and assembled into a reference database (or library). Once a suspicious breast mass is either automatically detected by the CAD scheme or visually identified by the observer (radiologist) and manually queried, a CBIR scheme searches through the reference database for a set of the most ‘similar’ ROIs and computes detection and/or classification score (the likelihood of being a true-positive and/or a malignant mass). The CAD-generated score and a set of CBIR scheme selected ‘the most similar’ reference images are displayed on the screen of CAD workstation. Previous pilot observer performance studies have demonstrated that using this ‘visual aid’ concept and system could improve radiologists’ performance in classifying between the malignant and benign breast masses (Giger et al 2002) as well as increase radiologists’ confidence in their decision making of interpreting mammograms (Zheng et al 2007b).

Two typical types of CBIR methods have been developed and tested in CAD schemes of digital mammography. One uses the pixel value-based template matching methods (Tourassi et al 2003, Filev et al 2005) and the other uses the multi-image feature-based k-nearest neighbor (KNN) algorithm (Tao et al 2007, Zheng et al 2007a). In using the pixel value-based template matching method, a large number of similarity measures (indices) that are based on information theory and a spatial relationship of pixel value distributions have been tested. For example, one group extracted a reference dataset involving 1465 ROIs with a fixed size (512 × 512 pixels) from a publicly available image database (DDSM, Digital Database for Screening Mammography, University of South Florida). Among them, 809 ROIs depict verified masses and 656 ROIs were randomly extracted from the screening negative mammograms. The researchers developed and applied a mutual information-based template matching method to search for and retrieve ‘the most similar’ ROIs and classify between positive and negative ROIs (Tourassi et al 2003). Another group evaluated and compared the effectiveness of 12 different similarity measures to match 318 pairs of breast masses depicted on serial mammograms. Although this study did not directly search for similar ROIs from a large reference database, all of these 12 similarity measurement methods can be directly applied in the CBIR schemes. The study reported that Pearson’s correlation was one of three measures that provided significantly higher matching accuracy (p < 0.05) than other nine measures (including mutual information) (Filev et al 2005). In using a multi-feature-based KNN similarity searching method, each suspicious mass region is first segmented and a set of image features is computed. Then, each ROI is converted as one point located in a multidimensional feature space domain. The KNN searches for the points that have the smallest distance to the testing point representing the queried suspicious mass region (Zheng et al 2006). However, the advantages and limitations of these two types of CBIR-based similarity searching methods have not been evaluated and compared in previous studies. In particular, the clinical relevance and visual similarity of the searching results have not been separately evaluated and compared.

In this study, we conducted a set of experiments to evaluate and compare three commonly used CBIR methods, namely mutual information, Pearson’s correlation and multi-feature k-nearest neighbor (KNN) algorithm, based on a common testing dataset and an image reference database. Although pixel value-based template matching methods were often applied to the fixed-size ROIs without segmentation of actual masses (e.g. boundary contours) (Tourassi et al 2003), we also investigated and compared the performance difference of these template matching methods when applying to both the fixed-size ROIs and the ROIs with adaptively adjusted sizes based on the estimation of actual mass sizes. The detailed description of our reference image database, experimental procedures and results are presented here.

2. Materials and methods

2.1. Two indices to assess the performance of CBIR schemes

Since the reference images (or ROIs) selected by CBIR schemes should be evaluated by both clinical relevance and visual similarity, we selected and used two indices to separately evaluate the performance of CBIR schemes in this study. First, we applied the standard receiver operating characteristic (ROC) analytic method (Obuchowski 2005) to assess the clinical relevance of the results generated by the CBIR scheme. The area under ROC curve (A_Z value) is used as an index to assess the CBIR scheme performance in clinical relevance. Second, although visual similarity is important for radiologists to accept CAD-cued results based on any CBIR schemes, it is a subjective concept. Thus, visual similarity is very difficult to be quantitatively evaluated due to the large inter-observer variability (Muramatsu et al 2007, Zheng et al 2007c). In our previous observer preference study, we found that human eyes were very sensitive to the difference of mass boundary (margin) spiculation levels in determining the visual similarity of selected suspicious masses (reference ROIs). As a result, reducing the difference of mass boundary spiculation level ratings between the queried (testing) and reference mass regions significantly improves the visual similarity of the CBIR scheme selected similar ROIs (p < 0.01) (Zheng et al 2006). Based on this result, we selected and used the average mean square difference and standard error of mass boundary spiculation level ratings between the queried ROI and the selected reference ROIs as a measurement index to quantitatively assess and compare the visual similarity of the reference ROIs selected by the CBIR schemes.

2.2. A reference image database

In our research group, we have built a large and diverse image database of mammograms. The original digitized mammograms were generated using several film digitizers with the pixel size of 50 μm × 50 μm and 12 bit gray level resolution. To create a reference database used in CBIR-based CAD studies, our computer program first sub-sampled the images by the factor of 2 (increasing the pixel size to 100 μm × 100 μm) and then extracted all selected ROIs with a fixed size of 512 × 512 pixels. Each selected ROI includes either a verified true-positive mass or a CAD-cued false-positive mass. The center of each suspicious mass is also located in the center of the extracted ROI. Using the ROI center pixel as a mass region growth seed, the previously developed multi-layer topographic region growth algorithm (Zheng et al 1995) used in our CAD scheme was applied to segment the mass region (define its boundary contour). For each true-positive mass, the automated segmentation result (its boundary contour) was visually examined. If the noticeable segmentation error was identified, the mass boundary contour was manually corrected (re-drawn). For all false-positive mass regions, CAD-generated boundary contours were accepted without any modification.

Based on mass segmentation results, we first used a computer scheme to compute 14 morphological and intensity distribution features. Besides three whole breast area-based (global) features, namely (1) average pixel value in breast area, (2) average and (3) standard deviation of local pixel value fluctuation in the breast area, other 11 region-based local features were computed based on a region of interest (ROI) that is a rectangular frame covering the segmented mass area plus the extension of 25 pixels in all four directions. These 11 ROI-based features are (1) region conspicuity, (2) normalized mean radial length of the region, (3) standard deviation of radial length, (4) skew of radial length, (5) shape factor ratio of the region, (6) standard deviation of the pixel value inside the mass region, (7) standard deviation of gradient of boundary pixels, (8) skew of gradient of boundary pixels, (9) standard deviation of the pixel value in the surrounding background, (10) average local pixel value fluctuation in the surrounding background and (11) normalized central position shift between the region center pixel and the pixel with minimum digital value inside the region. The detailed definitions and computing methods of these 14 image features have been reported in our previous study (Zheng et al 2006). Second, in our previous study we have also asked three radiologists to visually rate the mass boundary spiculation level around the segmented mass boundary contour in a subset of our reference database. The boundary spiculation level is rated using a scale of 1–9 (where 1 represents totally circumscribed boundary with no visual spiculation such as those typically seen in depicted lymph nodes). As the rating scale increases, the degree of visually depicted margins spiculation level also increases (e.g. 9 represents highly spiculated mass regions) (Zheng et al 2007c). The 14 computed image features and the subjectively rated boundary spiculation level (if rated) have been saved in a feature data file with all extracted ROIs in our reference database.

From our latest available reference image database involving ROIs of suspicious breast masses, we selected a subset of ROIs as a common reference database used in this study. The first prerequisite of selecting this database is that in order to avoid the inter-observer variability in subjective rating mass boundary spiculation levels (Zheng et al 2007c), we selected only the reference ROIs in which the suspicious mass boundary spiculation levels have been rated by one experienced radiologist. As a result, we selected 3000 ROIs to form the reference database in this study. Among these 3000 ROIs, 1500 are true-positive regions that depict one mass each. Based on the biopsy and pathology verification reports, 1290 true-positive ROIs are associated with malignant masses and 210 depict benign masses. These 1500 mass regions were extracted from 784 positive mammography examinations (cases). In detail, 1290 malignant mass regions were extracted from 675 cases in which 615 masses are visible in two views and 60 are visible only in one view, while the 210 benign mass regions were extracted from 109 cases in which 101 masses are visible in two views and 8 are visible only in one view. When applying our CAD scheme to extract these mass regions, 288 of the 1500 selected mass regions (19.2%) showed noticeable error and their boundary contours were thus manually corrected. The diverse characteristic distributions of these mass regions have been previously reported (Zheng et al 2000, 2004). In brief, the size of the 1290 malignant mass regions ranged from 0.1 cm² to 12.4 cm² (with an average and a median size of 1.5 cm² and 1.1 cm², respectively). In previous studies approximately one half of these masses had been rated subjectively as ‘subtle’ to ‘very subtle’ by radiologists. The rest of the 1500 ROIs are negative regions. Each contains a CAD-cued false-positive mass region. To extract these 1500 CAD-cued false-positive regions, we applied our CAD scheme (Gur et al 2004) to the database with 1200 cases (including 784 positive cases). After sorting all CAD-cued false-positive regions based on CAD-generated detection scores, we selected 1500 negative regions in this reference database.

2.3. Three CBIR methods

The first CBIR method compared in this study uses a multi-feature-based k-nearest-neighbor (KNN) algorithm to search for the similar breast masses depicted on the reference database. The KNN algorithm has been previously optimized and reported (Zheng et al 2006). In brief, the similarity is measured by the difference in feature values, f_r (x), between a queried ROI (y_q) and a reference ROIs (x_i) in a multi-dimensional (n = 14) feature space:

$$d(y_q,x_i)=\sqrt{\sum _{r=1}^n{(f_r(y_q)‐f_r(x_i))}^2}.$$

All feature values have been previously normalized to be distributed between 0 and 1. The smaller the difference (‘distance’), the higher the degree of the computed ‘similarity’ between any two compared regions. The first K-regions that have the smallest distance are selected as the K ‘most similar’ reference regions (K = 15). A distance weight was defined as 1

$$w_i=\frac{1}{d{(y_q,x_i)}^2}.$$

The detection score of likely being a true-positive mass and the classification score of the mass being malignant are computed as

$$P_{\text{TP}}=\frac{{\sum }_{i=1}^N{w}_i^{\text{TP}}}{{\sum }_{i=1}^N{w}_i^{\text{TP}}+{\sum }_{j=1}^M{w}_j^{FP}},N+M=K,$$

where in computing the detection score N is the number of positive ROIs (including both malignant and benign mass regions) and M is the number of negative ROIs in a set of K ‘most similar’ ROIs; while in computing the classification score, N is the number of ROIs depicting malignant masses only and M is the number of non-cancer ROIs (including both benign and negative regions). To improve the visual similarity of the selection results, we also implemented two boundary conditions on size and circularity difference between a queried region and a reference region in the KNN algorithm. As a result, the KNN algorithm was restricted to selecting ‘similar’ regions each with a reasonably comparable size and an overall shape (Zheng et al 2006).

Although a large number of pixel value (or information-theoretic similarity measure)-based CBIR methods have been tested in searching for similar breast masses, in this study we selected and compared two most popular methods that generated the ‘best’ (or optimal) retrieval and detection results reported in previous studies (Filev et al 2005, Tourassi et al 2007a). The first one is a mutual information-based CBIR method. The mutual information of two compared ROIs, X (the queried ROI) and Y (the reference ROI), is computed as

$$MI=\sum _x\sum _{y}P(X,Y){log}_2\frac{P(X,Y)}{P(X)P(Y)},$$

where P(X, Y) is the joint probability density function (PDF) of the two ROIs and P(X) and P(Y) are the marginal PDFs. We used a histogram approach to compute the PDFs. In this approach, the joint PDF is estimated by computing the fraction of pixels in a particular pixel value bin in the 2D histogram divided by the total number of pixels inside the ROI (Maes et al 1997). Before computing these PDFs, normalization of a local histogram is applied to pre-process each paired ROIs in an attempt to reduce image noise and compensate the irregular variation or shift of the pixel value distributions. After computing the mean (μ) and the standard deviation (σ) of the pixel value distributions for each ROI, the computer program divides the interval [μ − 2σ, μ + 2σ] into 128 pixel value bins. All pixels with values falling outside the interval range are assigned to the nearest ending bin during histogram calculation. After computing mutual information between the queried ROI and each of the reference ROIs, the computer program selects 15 ‘similar reference ROIs’ that have the ‘largest’ MI values. Assuming in these K selected similar ROIs, there are N true-positive ROIs and M false-positive ROIs. Thus, the MI-based detection (or classification) score is computed as

$$P_{\text{TP}}=\frac{{\sum }_{i=1}^{N}M{I}_i^{\text{TP}}}{{\sum }_{i=1}^{N}M{I}_i^{\text{TP}}+{\sum }_{j=1}^{M}M{I}_j^{\text{FP}}}.$$

The second pixel value template matching-based CBIR is a spatial relationship-based method that uses Pearson’s correlation (r). For two compared ROIs, X and Y, PC is computed as

$$r=\frac{{\sum }_{i,j}(X(i,j)‐{\mu }_X)\times (Y(i,j)‐{\mu }_Y)}{\sqrt{{\sum }_{i,j}{(X(i,j)‐{\mu }_X)}^2}\times \sqrt{{\sum }_{i,j}{(Y(i,j)‐{\mu }_Y)}^2}},$$

where μ_X and μ_Y are the mean of all pixel values in the ROI of X and Y, respectively. The same image pixel value normalization used in computing mutual information is also applied in computing Pearson’s correlation. The larger r value indicates the increase of similarity between two compared ROIs (X and Y). After selecting K = 15 ‘most similar’ reference ROIs (including N true-positive ROIs and M false-positive ROIs), the detection (or classification) score is computed as

$$P_{\text{TP}}=\frac{{\sum }_{i=1}^N{r}_i^{\text{TP}}}{{\sum }_{i=1}^N{r}_i^{\text{TP}}+{\sum }_{j=1}^M{r}_j^{\text{FP}}}.$$

Since in both mutual information and Pearson’s correlation computation, the pixel shift between two compared ROIs may affect the computation results (MI and r values) (Filev et al 2005), we applied and tested two methods to compute both mutual information and Pearson’s correlation. One was based on one matching result in which the centers of two matched ROIs are registered (overlapped) and one used an iterative method to search for the ‘best’ matching between two ROIs. Specifically, in the iterative method the computer program fixes the center position of the queried ROI and shifts the center position of each reference ROI within a 3 × 3 frame. Using this shifting iteration, nine MI or r values are computed for each pair of compared ROIs. The maximum value is then used to represent the ‘best’ (or optimal) matching between two ROIs. The size of this shifting frame is empirically selected based on the consideration between the reduction of matching error and the tolerance of increasing computation time (or power).

2.4. Performance evaluation

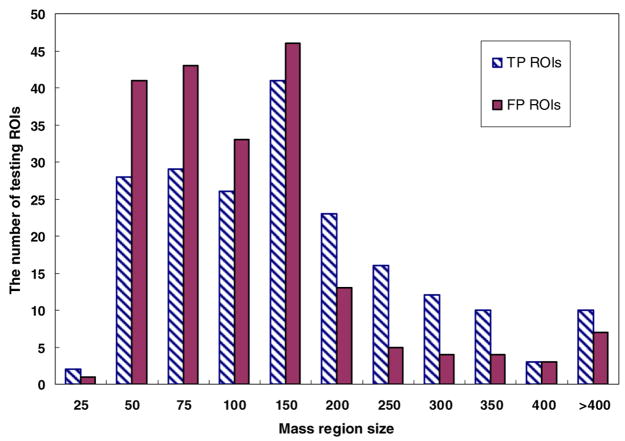
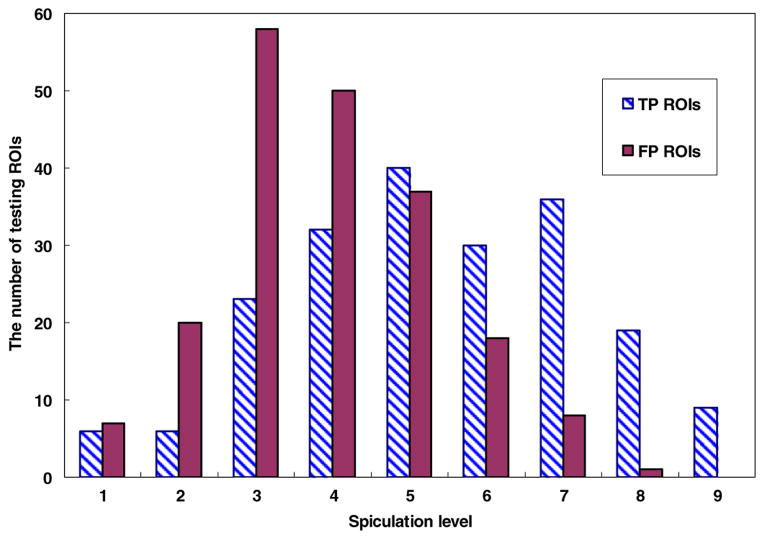
From the reference database that involves 3000 ROIs, we also randomly selected a testing subset that contains 400 ROIs with the same distribution of ROI categories. Specifically, among these 400 testing ROIs, 200 are positive ROIs (including 172 malignant masses and 28 benign masses) and 200 are negative ROIs depicted CAD-cued false-positive masses. Figures 1 and 2 show the diverse distribution of the segmented mass region size and the rated mass boundary spiculation levels of these 400 testing ROIs, respectively. For each testing ROI, each of three CBIR schemes searches through the remaining reference database with 2999 ROIs (excluding itself) for similar ROIs to this testing ROI. This searching method is similar to a commonly used ‘leave-one-case-out’ method, but it only applies to the 400 testing ROIs. As a result, three sets of K = 15 similar reference ROIs and three corresponding detection scores obtained from three tested CBIR methods were generated for each testing ROI.

Figure 1.

Histogram distribution of the segmented mass region size (mm²) of the testing dataset with 200 true-positive (TP) mass regions and 200 CAD-cued false-positive (FP) regions.

Figure 2.

Histogram distribution of the mass boundary spiculation level of the testing dataset with 200 true-positive (TP) mass regions and 200 CAD-cued false-positive (FP) regions.

We then took two steps to evaluate and compare the performance of three CBIR methods and schemes. First, based on detection scores of true-positive and false-positive ROIs, we applied a ROC data fitting and analysis program (ROCFIT; Metz 1998) to compute the ROC curve including the area under the ROC curve (A_Z value) and its standard deviation as well as the statistically significant difference (p value) between two ROC curves. The A_Z value is used as an index to assess the performance of the CBIR scheme in selecting clinically relevant reference ROIs. We compared the difference of three A_Z values generated based on the searching results of three CBIR schemes. The same performance procedure was applied to the classification scores generated by three CBIR schemes. Second, for each set of 15 selected similar reference ROIs, we computed the mean square difference of mass boundary spiculation level ratings between the testing ROI (SL_t) and each of reference ROIs (SL_k), $\mathrm{\Delta }SL=\frac{1}{15}\times \sqrt{{\sum }_{k=1}^{15}{(S{L}_k‐S{L}_t)}^2}$. We then computed the average mean square difference and standard error of all 400 testing ROIs ( $\overline{\mu }={\sum }_{i=1}^{400}\mathrm{\Delta }S{L}_i/400$, and ${\sigma }_{SL}=\sqrt{{\sum }_{i=1}^{400}{(\mathrm{\Delta }S{L}_i‐\overline{\mu })}^2/400}$) and used them as indices to assess and compare the visual similarity of searching results of three CBIR schemes.

Although using pixel value-based CBIR schemes typically does not need to accurately segment mass regions and some of previous studies used the ROIs with fixed size (e.g. 512 × 512 pixels; Tourassi et al 2003, 2007a), we also investigated and compared the performance difference when applying mutual information- and Pearson’s correlation-based CBIR schemes to both the ROIs with the fixed size and the ROIs with adaptively adjusted sizes based on the segmentation of actual mass sizes in this study. For this purpose, based on the previously segmented mass size or boundary contour in each reference ROI, we defined a new rectangular frame (window) that covers the segmented mass area plus the extension of 25 pixels in all four directions. Thus, each selected reference suspicious mass has two ROIs: one is the same as all other ROIs (512 × 512 pixels) and one is different based on the actual mass size. When applying mutual information and Pearson’s correlation methods to search for the similar reference ROIs based on the actual mass sizes, the computer schemes are limited only to compare and match ROIs in which the mass size difference between the testing mass (A_t) and the reference mass (A_r) meets the following condition as used in our KNN-based CBIR scheme ( $\frac{|A_t‐A_r|}{A_t}\le \frac{1}{3}$). Once this condition is met, the testing ROI frame is mapped to each of compared reference ROIs, which means that a sub-region that has the same size of the testing mass region and centered at the original center of the reference ROI is extracted. Thus, in computing the matching score of two ROIs, two new sub-regions with the same size are extracted from the original testing and a selected reference ROI for comparison. The mutual information and Pearson’s correlation are computed based on these two new sub-regions that are typically smaller than the original ROIs depending on the actual mass size segmented from the testing ROI. In this approach, the mutual information and Pearson’s correlation are not computed between the testing ROIs and the reference ROIs in which the mass sizes are substantially different.

3. Results

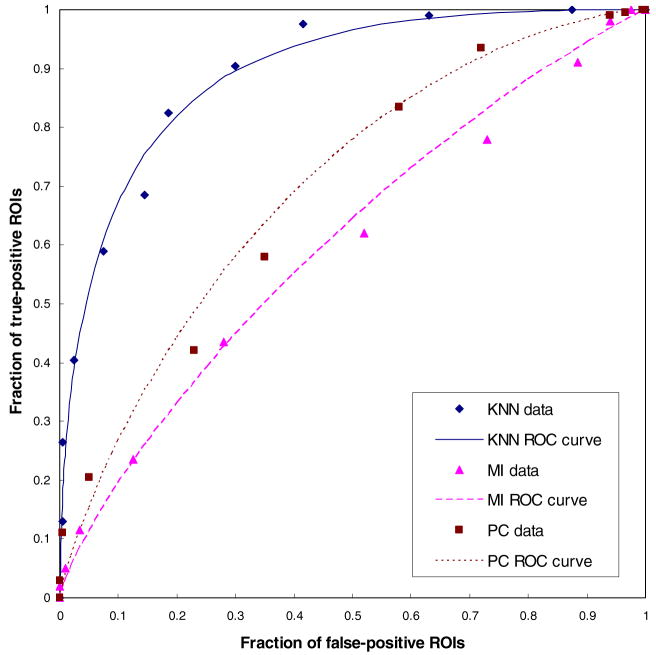
The A_Z value for detecting between 200 true-positive mass ROIs and 200 CAD-cued false-positive mass ROIs was 0.893 ± 0.009 when using the multi-feature-based KNN classifier. When applying mutual information and Pearson’s correlation searching methods to match the testing and reference ROIs with the fixed size (512 × 512 pixels), the computed A_Z values were 0.606 ± 0.021 and 0.699 ± 0.026, respectively. Figure 3 demonstrates the comparison of three sets of performance data and the fitted ROC curves. In classification between 172 ROIs associated with malignant masses and 228 either benign or negative ROIs, the A_Z values were 0.869 ± 0.011, 0.642 ± 0.021 and 0.704 ± 0.019 for KNN-, mutual information- and Pearson’s correlation-based CBIR schemes, respectively. The results indicate that (1) due to the complex and diverse distribution of breast masses and normal tissues, using multiple image features to search for similar reference ROIs yields significantly higher performance (p < 0.01) than using a single template matching-based measure, (2) the KNN-based scheme achieves higher performance in mass detection than in classification of malignant masses and (3) the mutual information- and Pearson’s correlation-based CBIR schemes achieve improved performance in classification of malignant masses. In this study, the mutual information-based scheme achieved significant performance improvement (p < 0.01), while the performance improved using Pearson’s correlation based scheme was not statistically significant (p = 0.821).

Figure 3.

Comparison of three sets of performance data and ROC curves. The areas under ROC curves are 0.893 ± 0.009, 0.606 ± 0.0205 and 699 ± 0.026 for three CBIR schemes based on multi-feature KNN, mutual information (MI) and Pearson’s correlation (PC) methods using the fixed ROIs with 512 × 512 pixels, respectively.

However, when applying the mutual information and Pearson’s correlation methods to the ROIs with adaptively adjusted sizes based on the actual mass sizes and only search for the similar ROIs with the comparable mass sizes, the A_Z value using mutual information was significantly increased from 0.606 ± 0.021 to 0.742 ± 0.017 (p < 0.01), while the A_Z value using Pearson’s correlation was also significantly increased from 0.699 ± 0.026 to 0.787 ± 0.016 (p < 0.01). The results suggest that eliminating the portion of un-related normal breast tissue background with lager pixel value variation or fluctuation significantly improves these pixel value-based searching results. In addition, compared to the commonly used matching method that simply registers the center of two comparing ROIs, using the iterative matching method with a 3 × 3 frame to search for the ‘best’ matching between two ROIs did not generate significant performance differences measured by A_Z values for both detection and classification tasks when applied to both mutual information- and Pearson’s correlation-based CBIR schemes.

The average mean square differences and standard errors of mass boundary spiculation level ratings between the testing ROI and the selected reference ROIs were 2.107 ± 0.718, 2.342 ± 0.812 and 2.298 ± 0.784 for using multi-feature KNN-, mutual information- and Pearson’s correlation-based CBIR schemes, respectively. When applied to the adaptively adjusted size ROIs, the average mean square differences and standard errors of mass boundary spiculation level ratings using mutual information- and Pearson’s correlation-based CBIR schemes were slightly improved to 2.301 ± 0.733 and 2.297 ± 0.743, respectively. Tables 1 and 2 show the correlation coefficients and p-values of the average mean square difference between each pair of three CBIR schemes. The results indicate that using the multi-feature-based KNN scheme yields the smaller average mean square difference and standard error in mass boundary spiculation level ratings between the testing ROI and the selected similar reference ROIs than using mutual information and Pearson’s correlation searching methods in which there is no statistically significant difference in measurement of this index.

Table 1.

The correlation coefficients of the mean square differences of mass boundary spiculation levels using three CBIR schemes.

	Multi-feature KNN	Mutual information
Mutual information	0.648
Pearson’s correlation	0.677	0.765

Table 2.

The P values computed using the paired t-test for the mean square differences of mass boundary spiculation levels using three CBIR schemes.

	Multi-feature KNN	Mutual information
Mutual information	<0.001
Pearson’s correlation	<0.001	0.933

4. Discussion

The development of CBIR schemes has been attracting wide research interest in medical imaging areas. It aims to provide radiologists the ‘visual aid’ tools to assist their decision making and improve diagnostic performance. Although CBIR schemes can be applied to a variety of medical imaging application areas (Muller et al 2004), the most of current CBIR studies focus on searching for and retrieving the similar suspicious breast masses (Muramatsu et al 2005, Tao et al 2007, Zheng et al 2007a) and micro-calcification clusters (El-Naga et al 2004) depicted on mammograms mainly due to the availability of large and diverse reference image databases of mammograms. The previous studies used two typical types of CBIR schemes. One is the multi-image feature-based KNN algorithm and one is the pixel value (or information-theoretic-based template) matching method. In general, the accuracy of computed image features relies on the accuracy of mass segmentation. Our previous study has shown that the automated mass segmentation error substantially reduced the performance of the CAD scheme in classifying the suspicious mass regions (Zheng et al 2008). Due to the lack of a reliable (or robust) algorithm for segmenting subtle masses surrounded and overlapped by complex (e.g. heterogeneously dense) breast tissues in mammograms, many of previous studies used the semi-automated method with manual correction to segment a fraction of identified mass regions with fuzzy boundary to reduce overall mass segmentation error and thus improve accuracy of computed image features (Zheng et al 2006, Tao et al 2007). Instead of using multiple image features, the information-theoretic-based template matching methods use the relationship of pixel value distributions between two compared ROIs to generate a single measure (e.g. mutual information and Pearson’s correlation) to determine the similarity of compared ROIs. Although some studies avoid mass segmentation and apply template-matching schemes to the ROIs with fixed size (i.e. 512 × 512 pixels (Tourassi et al 2003)), the performance of these schemes may be affected by the selection of ROI size and the number of histogram bins (Filev et al 2005). However, the performance of these CBIR methods (including both clinical relevance and visual similarity) has not been assessed and compared in previous studies. In this study, we evaluated and compared the performance of three commonly used CBIR schemes in searching for and retrieving ROIs depicted with ‘similar’ breast masses using a common image database. This includes the comparison of two performance indices that separately relate to the clinical relevance and visual similarity.

This study shows that the CBIR scheme using multiple image features computed from the ‘accurately’ segmented masses yields significantly higher performance than the schemes using a single measurement, which includes both higher A_Z value of ROC curve and smaller average mean square difference and standard error of mass boundary spiculation levels. We believe that this is because KNN has more flexibility to be trained to identify a set of effective features to better distinguish the subtle masses with diverse tissue background, while the pixel value-based methods can only be used ‘as is’ and as a result they can be more affected by or sensitive to the image ‘noise’ (e.g. orientation of mass regions and fluctuation of breast tissue background). Our finding that using Pearson’s correlation-based CBIR scheme achieves higher performance than using the mutual information-based scheme is consistent with a previous study reported by another research group (Filev et al 2005). However, the overall lower performance of using the mutual information-based CBIR scheme to search for the similar breast masses is surprising and different from other previous studies (Tourassi et al 2003, 2007a). We believe that such performance difference is probably generated by using different types of reference databases with varying difficult levels (Nishikawa et al 1994). Unlike the most of previous studies in which the sizes of the reference databases were much smaller and the negative ROIs were randomly extracted from negative mammograms, our reference database has bigger size and each of 1500 selected negative ROIs involved in our reference database depicts a CAD-cued false-positive mass region. Specifically, when applying the CAD scheme previously developed in our laboratory, which has comparable mass detection performance to the two leading commercialized CAD schemes (Gur et al 2004), to each of these negative ROIs, a suspicious but negative breast tissue area is automatically segmented and cued as a suspicious mass (a CAD-cued false-positive mass). As a result, distinction between positive ROIs and negative ROIs in our reference database is much more difficult. In order to achieve better performance to discard the difficult negative ROIs including CAD-cued false-positive mass regions, the CBIR scheme requires more effective and non-redundant features. We also believe that our reference database is more clinically useful or relevant because the ultimate goal of developing any CBIR schemes is to optimally assist radiologists better distinguish between subtle true-positive masses and difficult false-positive (highly suspicious but later proven as negative) regions.

This study suggests that accurate segmentation of mass regions is important not only for computing morphological image features but also for applying template matching-based CBIR schemes (including mutual information and Pearson’s correlation). Our experimental results show that by adaptively adjusting the size of comparing ROIs based on the actual mass size, we reduce the image noise and diverse breast tissue information that is unrelated to the targeted and compared breast masses. As a result, the performance of mutual information- and Pearson’s correlation-based CBIR schemes is significantly improved as compared to applying the schemes to the ROIs with fixed sizes. In addition, this study indicates that although slightly shifting the center registration points between two matching ROIs can change the computed mutual information and Pearson’s correlation values, the overall CBIR scheme performance measured by the A_Z value of the ROC curve remains comparable. This is likely due to the increase of the computed mutual information or Pearson’s correlation values in both positive- and negative-matched ROIs. As a result, our study suggests that one can avoid shifting the center registration points in computing mutual information and Pearson’s correlation when applying CBIR schemes to search for the similar ROIs. This can significantly improve computational efficiency of mutual information- or Pearson’s correlation-based CBIR schemes, which is an important issue that has attracted extensive research interest (Tourassi et al 2007b).

In summary, this assessment study compared the performance of three types of CBIR schemes using a common testing database and investigated several approaches that aim to improve scheme performance. The results demonstrate that due to the diversity of medical images, CBIR schemes using multiple image features and the ROIs based on actual mass size achieved significantly improved performance. Despite the encouraging progress that has been made and reported in recent research effort to develop CBIR schemes for medical images, in particular for mammograms, more research and development work is needed to identify optimal image features or measures and improve CBIR scheme performance in both clinical relevance and visual similarity in the future studies before any CBIR scheme can be confidently accepted by radiologists and routinely used in the clinical practice.