Designing the Optical Interface of a Transcutaneous Optical Telemetry Link

Abstract

Optical telemetry has long been an option for transcutaneous data transfer and has been used in various types of implanted systems. This telemetry modality and the efficiency of these optical links are becoming ever more important as higher bandwidth sources such as cortical recording arrays are being implemented in implanted systems. The design of the transmitter-skin-receiver interface (the “optical interface”) is paramount to the operation of a transcutaneous optical telemetry link. This interface functions to achieve sufficient receiver signal power for data communication. This paper describes a mathematical analysis and supporting data that quantitatively describes the relationship between the primary interface design parameters. These parameters include the thickness of the skin through which the light is transmitted, the size of the integration area of the optics, the degree of transmitter-receiver misalignment, the efficiency of the optics system, and the emitter power. The particular combination of these parameters chosen for the hardware device will determine the receiver signal power and, therefore, the data quality for the link. This paper demonstrates some of the tradeoffs involved in the selection of these design parameters and provides suggestions for link design. This analysis may also be useful for transcutaneous optical powering systems.

I. INTRODUCTION

CORTICAL interfacing is a rapidly advancing field that is showing great promise for the rehabilitation of the mobility impaired, among other applications. Recent work has shown that real-time control of computer cursors or robotic arms is possible by the actuation of recorded neural signals [1]–[4]. Currently, implantable cortical interfacing systems (such as the Cyberkinetics Neurotechnology, Inc. BrainGate system) utilize percutaneous connectors to transmit the large amounts of neural waveform data from the implanted array to external signal processors. The practical integration of cortical interfacing into clinically relevant systems (such as motor neural prostheses [5]) will ultimately require a data transmission system that eliminates the wires and connectors which cross the skin. Optical telemetry may provide the best solution for achieving such a telemetry system, due to the large bandwidths possible and the relative noise immunity associated with optical communication.

Optical transmission has been shown to be an effective modality for transcutaneous data transfer for several implanted device systems and has been used for many applications including neuromuscular stimulation systems [6], implanted cardiac assist devices [7]–[9], bladder stimulators [10], laboratory animal monitoring systems [11], neural recording systems [12], [13] and generic communication systems [14], [15]. While transmitter and receiver design for these systems is quite similar to fiber-optic or free air infrared links, the transmission medium is fundamentally different (skin).

When light is transmitted through skin, it is absorbed and scattered. This results in a non-uniform power distribution on the receiving surface of the skin. The receiver must be designed to collect enough of this light to reconstruct an error-free data stream. This paper describes a detailed analysis of the transmitter-skin-receiver interface (the “optical interface”) and demonstrates how this analysis can be used to design an optical telemetry link. It will be shown that the optical interface can be designed to optimize certain system-level design constraints/specifications, including power consumption, implant location, susceptibility to transmitter-receiver misalignment, and external device size.

To perform this analysis, knowledge of the pattern of light transmission that results on the receiving surface of the skin is required. Brief descriptions of distribution shape for rat skin [11] and porcine skin [14] have been published previously but are not sufficient for quantitative analysis. For this study, light transmission profiles were empirically measured for porcine skin samples of various thicknesses. Porcine skin was determined to be a sufficient model of human skin since the optical properties of each are similar; the absorption coefficient µ_a for each has been shown to be approximately 0.05 mm⁻¹, and the transport scattering coefficient µ_s has been shown to be approximately 1.6–2.3 mm⁻¹ and approximately 2.8⁻¹ mm for human and porcine skin, respectively [16], [17]. The samples were illuminated from the hypodermal surface by a narrow-band emitter. Since the emitter used is a power-efficient communications grade emitter, this analysis is considered to be particularly relevant.

These empirically measured profiles were used to determine the quantitative tradeoffs between the optical interface design parameters. This quantitative analysis of the optical interface will allow for an optimized optical link design that is guided by an a priori assessment of these parameters.

II. EXPERIMENTAL METHODS

A. Tissue Preparation

Dermal samples of approximately 5 cm × 5 cm in size and of various natural thicknesses were removed from the hide of five Yorkshire-cross farm pigs within 12 hr post-mortem. The samples were cleaned with saline and waxed and/or shaved to remove the hair. All samples were composed of epidermal and dermal layers (combined thickness of approximately 2 mm) and hypodermal/adipose layers of varying thickness (0 mm to approximately 9.5mmthick). The total sample thickness was measured by laying the sample flat on a horizontal surface (without any tension or compression) and taken to be the gap distance between the surface and a plate lowered towards the sample until it just touched the skin surface.

B. Measurement Technique

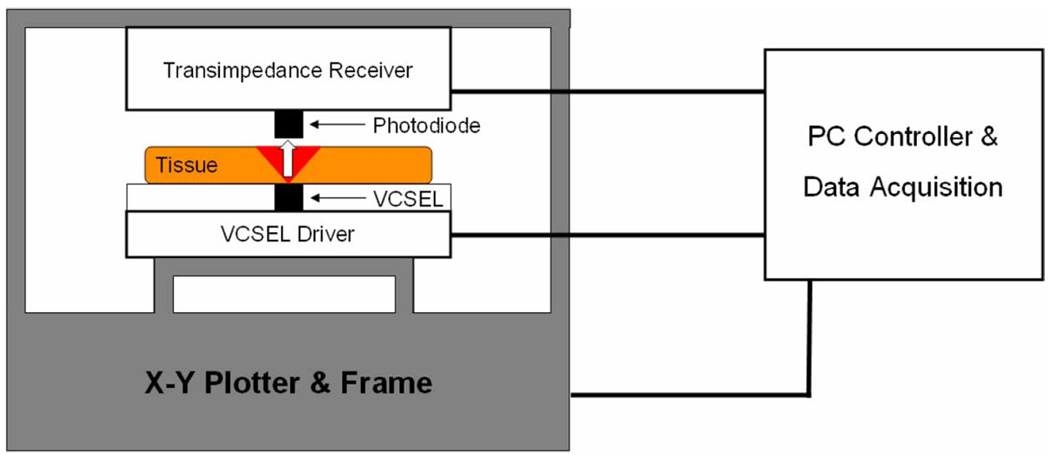
The distribution of the transmitted optical power on the epidermal face of the tissue was measured by moving a single small-area (~0.01 mm ²) PIN photodiode over the tissue surface (1 mm separation between photodiode and tissue surface) using the experimental setup shown in Fig. 1. A 850-nm narrowband (spectral bandwidth of 0.65 nm) communications emitter in a TO-46 can [Advanced Optical Components HFE 4093-342—a communications grade vertical cavity surface emitting laser, (VCSEL)] was used to transmit light through the skin. It was placed in direct contact with the skin’s hypodermal surface. For details on wavelength selection for the VCSEL, see the “Optical Interface Theory” section below. The VCSEL was driven with a simple FET current source, and the output power of the emitter was adjusted to ensure that the detector was operating in its linear region for all measurements. The position of the photodiode was manipulated using a computer controlled x–y plotter in conjunction with a data acquisition system. A measurement of transmitted optical power was performed at each of a grid of points on the surface of each skin sample (with a grid resolution of 0.6–1.2 mm depending on the thickness of the sample). A single stage anti-aliased transimpedance amplifier and the PIN photodiode (Hamamatsu G8522-03) operating in a photoconductive configuration comprised the receiving transducer. Each measured power distribution was made relative to the total power transmitted from the VCSEL and divided by the active area of the photodiode. This resulted in a discrete, empirical representation of the relative power flux distribution for each tissue sample. The total VCSEL optical power was empirically measured using the same setup to measure the output at the TO-46 window with a 0.025-mm grid resolution. The power measurements were spatially integrated to determine the total transmitter power. All measurements were recorded with a DC emitter output but also apply for higher frequencies relevant to data transfer because of the rapid transport of light through tissue. All measurements were performed within 24 hr post-mortem.

Fig. 1.

Experimental setup for the power distribution measurements. Transmitter, receiver, tissue, and the x–y plotter that manipulated the relative positions of the transmitter and receiver are shown.

C. Data Analysis

Statistical regression models were fit to each of the variables measured for the power distributions: the empirically measured total transmittance for each sample T_tot and the empirically measured full width at half of the maximum (FWHM) for each sample. These regression models allow for the estimation of these variables for values of tissue thickness that were not measured experimentally. For the T_tot data, an examination of data showed exponential trends between thickness and total transmittance. This suggested a two-parameter exponential model of the form

$$Y=a_1*a_2^{\ell }+\epsilon$$ (1)

which was fit to the data [18], where the parameter Y represents T_tot l represents the sample thickness, ε represents random error due to population and experimental variation, and a₁ and a₂ are the regression parameters.

For the FWHM data, we considered a variety of linear mixed models [19], [20] that allowed us to introduce the different sources of variation of the data. By model selection procedures with likelihood ratio tests (LRT) [21], we found the “best” model to establish the minimum order and number of error terms needed for accurate representation of the data. The final model with the form

$$Y=a_1+a_2\ell +a_3{\ell }^2+\epsilon$$ (2)

was fit to the data, demonstrating a parametric relationship between FWHM (variable Y) and the thickness, i.e., l, of the sample. As above, the parameter represents random error due to population and experimental variation. Maximum likelihood methods [21] were applied to fit the model.

A least-squares Gaussian model was fit to the power flux distribution of each sample, providing a convenient approximation of the distribution shape. This fit allows these distributions to be simulated for any thickness of interest simply and without using complex photon propagation models such as Monte-Carlo simulation techniques [22], [23]. The recreation of these distributions is necessary for the analysis of the optical interface design parameters, which is described in greater detail in the “Optical Interface” section of this paper. The Gaussian model was of the form

$$\mathit{\text{Jrx}}\lambda (r,\theta )=\frac{A}{\sigma \sqrt{2\pi }}{\mathrm{e}}^{-r^2/(2{\sigma }^2)}$$ (3)

and was fit to each of the experimentally measured power distributions. Only one spatial dimension r is considered since the distributions are radially symmetric for all angles θ.

Using the same model fitting procedure described above for the T_tot and FWHM data, an exponential and quadratic random coefficient model were selected to represent the Gaussian model parameters A and σ, respectively. The curves fit to this data allow for the recreation of any optical power distribution for a desired thickness.

III. OPTICAL INTERFACE THEORY

A generic optical telemetry link can be represented as having three essential components: a transmitter, a receiver, and an optical interface. The optical interface, as defined here, consists of the emitter, the transmission medium, the optics and the receiving photodiode. A transcutaneous optical telemetry link (TOTL) is very similar to a fiber optic or free-air optical telemetry link; the only essential difference is the nature of the optical interface. For a TOTL, the transmission medium is biological tissue instead of an optical fiber or air. The fundamental telemetry link design parameters (the emitter power, the skin thickness, the misalignment tolerance of the transmitter and receiver, and the area over which the optics integrate the transmitted light) all interact through the optical interface design, and the tradeoffs between them are made clear by an understanding of this interface. Knowledge of these tradeoffs allows for the design of an optical interface that is optimized for the requirements of the system of which the link is a part.

The design of the optical interface (the emitter, photodiode, optics and tissue selection) can be approached as achieving a signal-to-noise ratio (SNR) that is sufficient for adequate link operation. The receiver hardware being used will dictate the SNR required. For example, commercial optical receivers will often list the minimum signal photocurrent needed for low bit-error rate operation at a given data rate (assuming receiver noise is the dominant noise source and that a particular data encoding scheme is used). Custom receivers would likely be designed for a certain input range and would have to be characterized to determine the signal levels required. The optical interface can be designed to ensure that this SNR is achieved at the receiver input, and the parameters pertaining to its design can be optimized relative to the system level constraints (e.g., minimizing the total amount of power dissipated, allowing for certain implant locations/tissue thicknesses, tolerating a certain amount of lateral transmitter-receiver misalignment, or minimizing the size of the external optics used). The parameters that can be manipulated to optimize the design of this interface include the emitter wavelength, the emitter power, the tissue type and thickness, the lens type, and the misalignment that the link will be designed to tolerate.

Generically, the SNR at the input of the receiver SNR_i is defined by

$${\text{SNR}}_i=\frac{I_S}{I_N}=\frac{P_{S}R}{I_{N_{\text{elec}}+P_{N_{\text{amb}}}R}}$$ (4)

where I_s (A) and I_N (A) are the currents resulting from incident signal optical power and the input noise current, respectively.P_s is the received signal optical power (W), R is the photodiode responsivity (A/W),I_Nelec is the input referred current noise for the receiver, and P_Namb(W) is the incident optical power due to interfering light sources (such as ambient light).

The signal power is P_Sdefined by

$$P_S={\displaystyle {\int }_{A_T}{P}_{\mathit{\text{Tx}}}{J}_{\mathit{\text{Rx}}\lambda \eta \lambda }\mathit{\text{dA}}}$$ (5)

where P_Tx (W) is the optical power of the transmitted pulse,J_Rxλ (cm⁻²) is a function representing the spatial optical power distribution on the receiving surface of the skin at wavelength λ,η_λ is an efficiency factor (η_λ ≤1) accounting for inefficiencies in optics/optical filters at wavelength λ, andA_T represents the tissue area over which the receiver optics integrate the signal.

J_Rxλis a function of the two spatial dimensions over which the receiving optics integrate the signal light (i.e., the two dimensions of the skin surface under the receiver), and it represents the flux distribution of exiting photons on the epidermal surface of the skin. For the purpose of discussion, these two dimensions will be referred to as the “interface plane.”J_Rxλ is specific to a particular tissue type and varies with wavelength, tissue thickness, and the optical properties of that tissue. It is this distribution that was empirically measured for the porcine skin samples for this paper. One of these distributions (for a 4-mm-thick sample) can be seen in Fig. 2. The optical power flux is made relative to the optical power input by the transmitting emitter.

Fig. 2.

Typical optical power flux distribution J_Rxλ(data for 4-mm sample shown). The surface protruding from the center is the flux distribution of the VCSEL on a 1/500th scale.

A_Tis the surface under the receiving optics (in the interface plane), over which the transmitted power is integrated by the optics and focused onto the receiving photodiode. The dimensions of A_T are the dimensions of the area over which the receiver lens integrates the transmitted light (in the interface plane). The exact location of the integration area represented by A_T is dependent on the axial alignment of the transmitter and receiver; when the transmitter and receiver are perfectly aligned, J_Rxλ and A_T are concentric, and when they are not aligned, the center of A_Tis shifted from that of J_Rxλin the interface plane.

The emitter wavelength λ is an important design parameter and should be chosen to maximize power transfer across the skin (minimize absorption and scatter). Skin is an optically turbid media (both scatters and absorbs light). The wavelengths in the range of ~800–1300 nm represent a region where photon absorption and scattering are minimal for dermal tissue, creating a region which is optimal for efficient optical power transfer across the skin [16], [17], [24]. Many commercially available emitters and photodiodes are optimized for operation in this range, as this is the same wavelength range used for many fiber optic and free-air applications. A wavelength of 850 nm was selected for this work because it was within this wavelength range and because the most power efficient commercially available emitters are available at this wavelength.

The efficiency factor η_λis affected by several factors and can be quite significant. These factors include any transmission inefficiencies in the lens, filter and photodiode window, photons lost due to the acceptance angle of the imaging system, and the failure to collect photons with certain paths due to the optics system configuration. Photon loss due to these factors can be quite significant.

The factors that contribute to the input noise currentI_N are I_Nelec, which is the input referred current noise for the receiver, and P_Namb, which is the optical power incident on the photodiode that is due to light sources other than the link emitter.I_Nelec is a function of the receiver electronics. The presence, nature, and intensity of interfering light sources that contribute to P_Namb can vary greatly depending on environmental conditions. Common interfering light sources include daylight and fluorescent lights.

These various design parameters can all be manipulated to achieve the required SNR_i; it is the system-level design constraints that will dictate the way in which they are configured.

IV. RESULTS

A. Transmitted Optical Power Distribution

Fig. 2 shows a typical optical power flux distribution for a sample that is approximately 4 mm thick. The transmitted power is concentrated in the center of the distribution, directly over the emitter. Light that is emitted into the skin is scattered, resulting in a radially symmetric distribution that is spread over the surface of the skin. Overlaid on the same plot in Fig. 2 is the power flux from the VSCEL emitter as measured at the TO-46 glass window (note that the VCSEL distribution is actually plotted on a scale 1/500th that of the skin distribution for clarity of detail). The VCSEL energy is very highly concentrated within a circular area of 0.8 mm diameter and is ring-shaped due to a wire bond in the center of the VCSEL die.

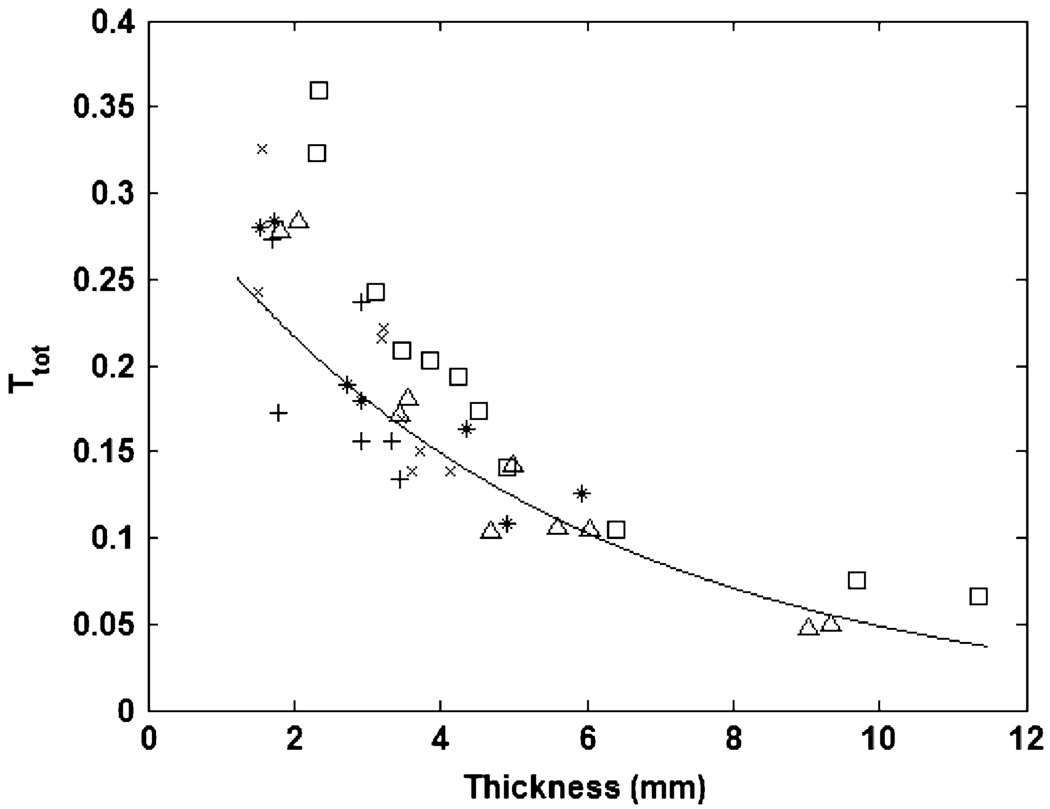
Fig. 3 shows the total transmitted fraction of light T_TOT for each measured sample (as calculated by numerical integration of the volume under the empirically measured flux distribution) with each sample’s thickness. Each marker type in Fig. 3 represents samples from one of the five animals in the study. The exponential curve fit allows for the estimation of T_TOT for values of tissue thickness that were not measured experimentally (transmittance estimates for very large thicknesses should be used with caution, as the accuracy of the estimate will decrease with thicknesses beyond the fitted range). Table I shows the exponential model fit parameters.

Fig. 3.

Total transmittance with tissue thickness. Each marker type represents samples from one of the five animals in the study.

Table I.

MODEL FIT PARAMETERS

Y	a1	a2	a3	${\sigma }_{\epsilon }^2$
Ttot	0.315	0.830	--	0.00211
FWHM	0.991	1.801	−0.052	0.533
FWHMlinear	2.08	1.27	--	0.671
A	1.808	0.719	--	0.0600
σ	0.0304	0.0259	−0.00041	0.000055
σlinear	0.0408	0.0212	--	0.00812

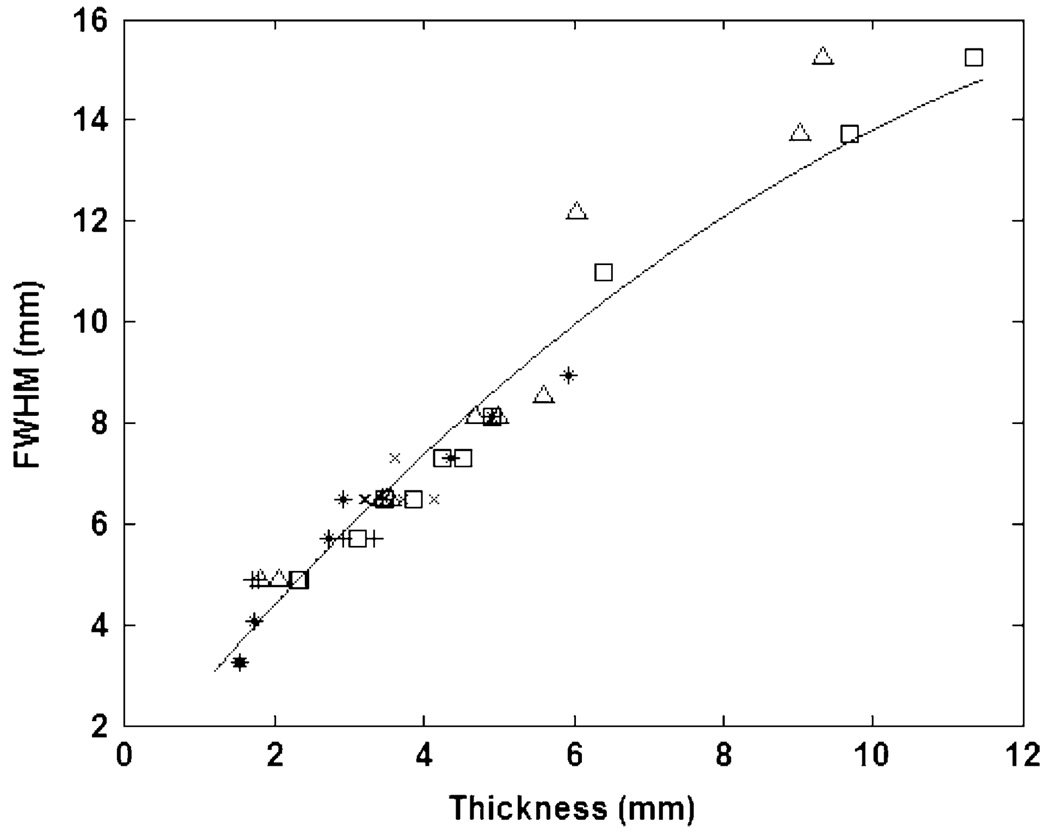
Fig. 4 shows the FWHM value for each sample with sample thickness. Each marker type in Fig. 4 represents samples from one of the five animals in the study. This plot demonstrates the increasing relative width of the distributions with an increase in thickness. In general, the height of the distributions decreases, and the relative width increases with an increase in tissue thickness. This results from an increase in photon absorption and scattering due to the additional hypodermal and adipose tissue present in the thicker samples. LRT showed that a simple quadratic regression model with independent and identically distributed (iid) errors was this simplest evaluated model that was sufficient to describe the data (P=1.1e–5 versus linear regression with iid errors, and P=0.53 versus quadratic random coefficients model with two error sources). As with the previous analysis, this curve fit allows for the estimation of FWHM for values of tissue thickness that were not measured experimentally. For estimates of FWHM at very large thicknesses, a linear model may be more appropriate. Table I shows the fit parameters for both models.

Fig. 4.

FWHM with tissue thickness. Each marker type represents samples from one of the five animals in the study.

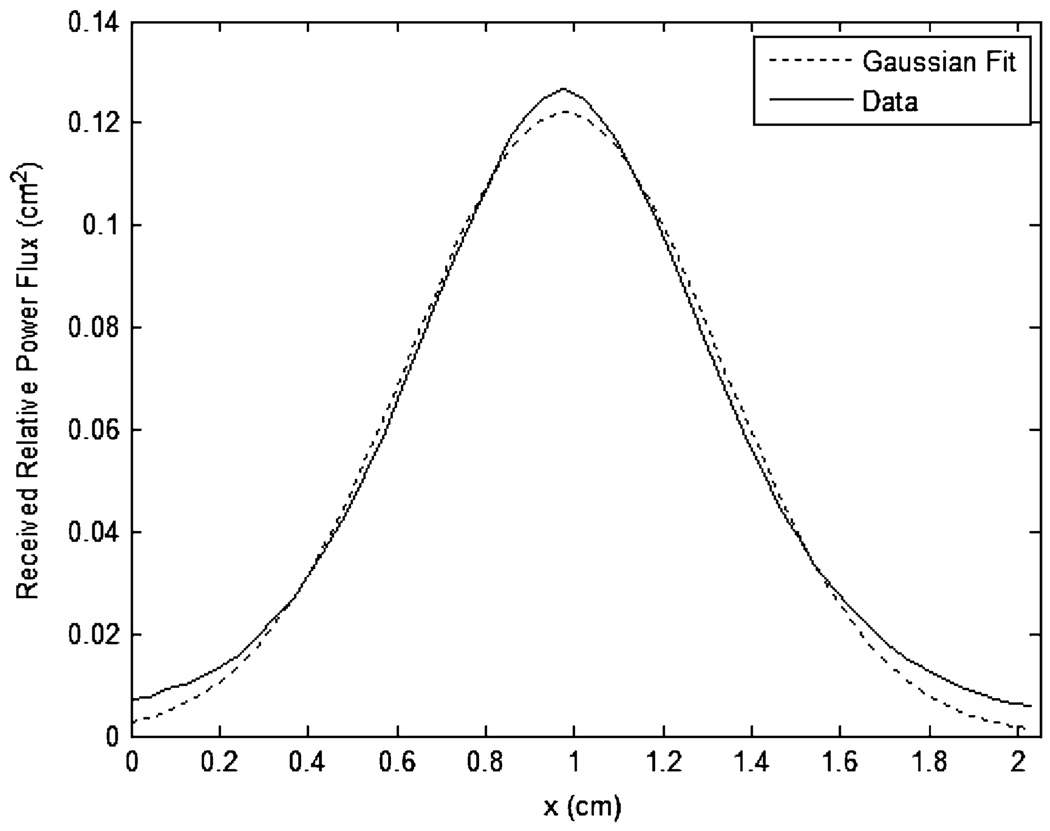
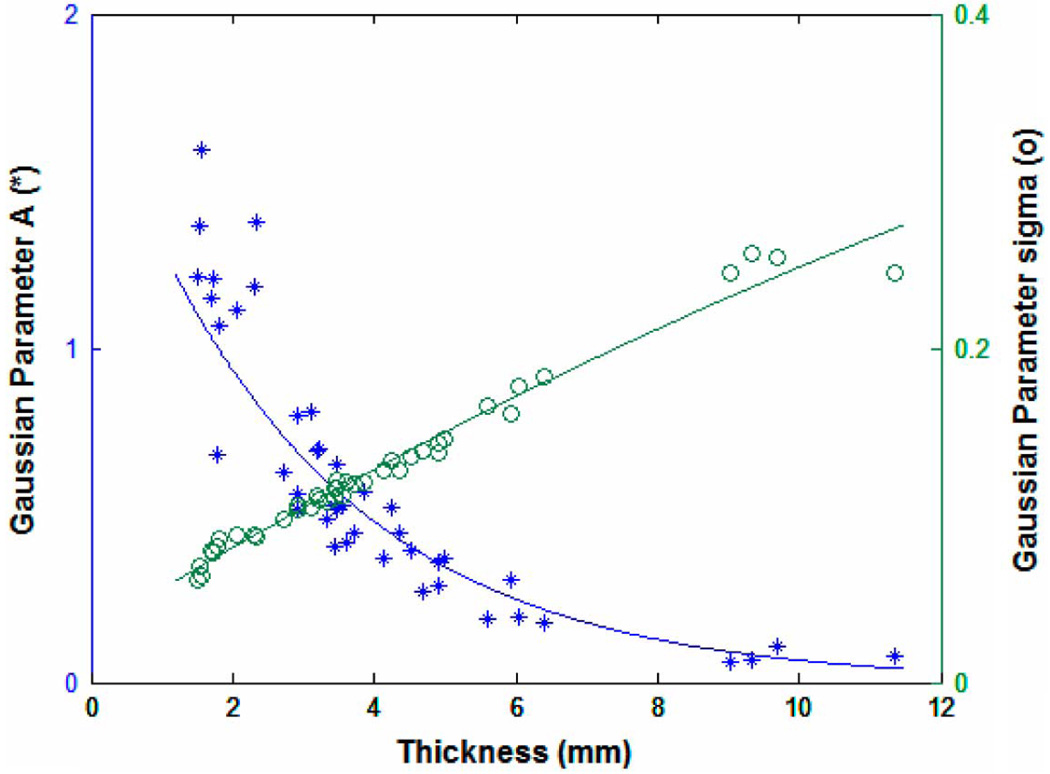
Fig. 5 shows a typical least-squares Gaussian model fit to an experimentally measured distribution for a sample of thickness 3.5 mm. The Gaussian fit provides a sufficient approximation of the distribution shape; the typical mean-squared error is less than 0.5% of the total transmittance, which is well within the variance of the experimentally measured total transmittance. Goodness of fit does not trend with sample thickness for the sample thickness range analyzed. Fig. 6 shows the Gaussian model parameters A and σ, as calculated for each sample, with sample thickness. An exponential and quadratic random coefficient model were selected to represent the Gaussian model parameters A and σ, respectively. These models allow for the recreation of any optical power distribution for a desired thickness. Table I shows the model fit parameters. It is of note that the correlation of σ and l is 0.987 and that the contribution of the second-order coefficient is statistically significant (p=0.0185) but quite small, suggesting that a linear approximation of σ may also be suitable. For estimates of σ at very large thicknesses, the linear model may be more appropriate. Table I shows the fit parameters for both models.

Fig. 5.

Typical Gaussian curve fit to experimentally measured distribution (the data shown is for a sample of thickness 3.5 mm).

Fig. 6.

Gaussian model fit parameters A and σ with sample thickness.

B. Optical Interface

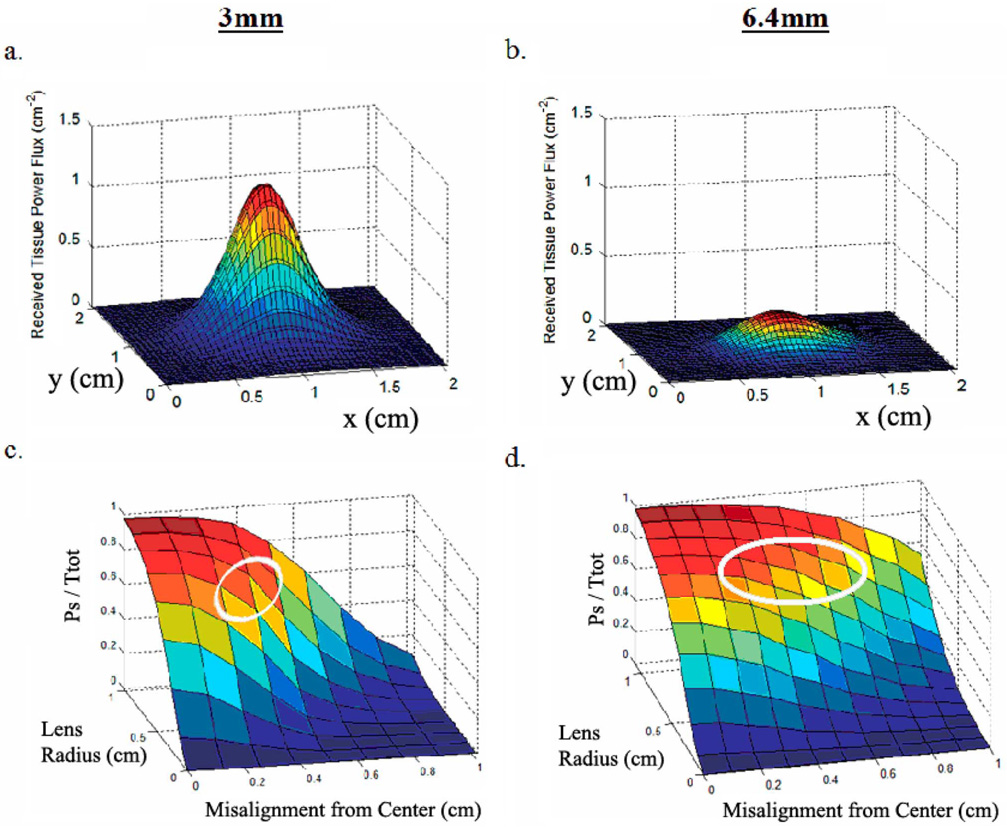
Fig. 7(a) and (b) shows the optical power flux distribution for light transmitted through two skin samples, with a total thickness of approximately 3 mm and 6.4 mm, respectively. Fig. 7(c) and (d) shows the data from Fig. 7(a) and (b) but processed to show the total fraction of transmitted optical power that is collected by a perfectly efficient optics system with various lens radii and for various transmitter-receiver misalignments. Each point in Fig. 7(c) and (d) was calculated by integrating the distributions shown in Fig. 7(a) and (b), respectively, over a circular region of radius 0 mm to 11 mm misaligned from the center of the distribution by 0 mm to 10 mm. These plots demonstrate the effect of lens diameter and misalignment on the fraction of total transmitted power collected by the optics system. Since the plots are normalized, it is useful to know the total transmittance for each sample: approximately 0.20 and 0.11 for the 3 mm and 6.4 mm sample, respectively.

Fig. 7.

(a) Power flux distribution for a 3-mm sample. (b) Power flux distribution for a 6.4-mm sample. (c) Effect of misalignment and lens size on fraction of collected light for a 3-mm sample. (d) Effect of misalignment and lens size on fraction of collected light for a 6.4-mm sample.

These figures show that an increase in lens radius increases the total power collected by the receiver. For each of these two sample thicknesses, a lens radius greater than ~10 mm did not result in significant power collection gains. Fig. 7(c) and (d) shows that an increased transmitter-receiver misalignment results in less total power collected by the receiver. Due to increased scatter and a wider power flux distribution on the epidermal surface of the 6.4-mm sample, Fig. 7(d) shows a less severe decrease in collected power fraction for a given misalignment than for the 3-mm sample curve.

V. DISCUSSION

A. Transmitted Optical Power Distribution

The T_tot data in Fig. 3 clearly shows a significant decreasing trend in the total transmittance with an increase in tissue thickness. Not surprisingly, an increased amount of light-scattering hypodermis and adipose tissue reduces the total amount of transmitted through tissue. This has strong implications for the implant location chosen for the data or power link since skin thickness will vary with anatomical location. For tissue thicknesses of 1.5 mm–11 mm, the total transmittance ranges from approximately 27% to approximately 5% of the total emitter power. These values are consistent with previously published ranges for T_tot through human skin [25], [26]. This data provides a quantitative means of evaluating the inherent tradeoff between skin thickness and power efficiency. The exponential model fit allows for the calculation of T_tot for thicknesses that were not measured in this study. For example, the total transmittance at a skin thickness of 2 cm is estimated to be approximately 0.0085. Traditional implant locations, such as the abdomen and chest, tend to have fatty deposits of up to several centimeters in thickness and, therefore, may be unfavorable for implantation of an optical device because of large power absorption. Choosing an implant location with a very thin dermal covering provides a very significant power advantage.

Fig. 4 demonstrates a near-linear relationship between skin thickness and the spread of the power distribution. This has strong implications for the type of optics required for collecting such diffusely distributed light and the effects of receiver-transmitter misalignment. Wider power distributions would require a larger optics integration area to collect sufficient fractions of the transmitted power since it is not concentrated in a small spatial area. Similarly, the relative amount of light lost by a misaligned transmitter/receiver pair will be less for a wider distribution of light. The parametric model fit to this data allows for the estimation of signal power spread for thicknesses not evaluated in this study.

The Gaussian model provided a reasonably good fit to the flux distributions. This model is a very convenient means of representing these distributions since it only requires two parameters and can be easily recreated using commercial mathematical analysis software. The reconstruction of a distribution at a given tissue thickness allows one to quantitatively assess the effects of the optics integration area and transmitter-receiver misalignment on the amount of power that is being collected by the receiver. The ability to quantitatively assess the tradeoffs between these design parameters can be quite powerful when designing a transcutaneous data or power link.

B. Optical Interface

Proper design of the optical interface is integral to achieving an SNR that is sufficient for device operation. The SNR can be maximized by maximizing the signal current and minimizing the noise. With respect to achieving sufficient signal current, Fig. 7(c) and (d) quantitatively and powerfully demonstrates the tradeoffs between the various design parameters affecting the optical interface (the emitter power, the lens integration area, the misalignment tolerance, and the tissue thickness). These plots effectively represent solutions to the equation for P_sdescribed above (i.e., various operating points for the link). The system-level design constraints (implant location requirements, power constraints, misalignment constraints, and external device size constraints) will ultimately determine the point in this parameter space at which one chooses to operate. For example, a link that is optimized for minimal link power consumption while maintaining a reasonable lens size and misalignment tolerance would likely operate in the parameter space outlined in white in Fig. 7(c) and (d). This region represents the range of operating points for which signal power is very high, yet the lens size is still moderately small, and the misalignment tolerance is still reasonably large. Further increasing the lens size beyond the range outlined by this region, or further constraining the misalignment tolerance, would only provide modest signal power gains. Operating with a lens that is smaller than that depicted by the outlined region will result in large signal power penalties per unit lens radius. Likewise, requiring misalignment tolerances beyond those enclosed by the outlined region will also result in substantial signal power penalties, although it should be noted that this penalty becomes less severe with an increase in tissue thickness, as shown by the reduced misalignment slope from Fig. 7(c) to (d) (it should be noted that a larger lens integration area also results in a greater misalignment tolerance due to the wider collection area). This increased device misalignment tolerance with skin thickness occurs because of the wider distribution of optical power on the skin. On the other hand, a system for which transmitter power is not a major design constraint can be realized with a small lens and/or a large lens misalignment tolerance.

Proper transmitter and receiver design, while outside of the scope of this paper, is also integral to achieving a low noise, high sensitivity, and overall low power system. SNR can be degraded due to electrical noise at both the transmitter and (especially) the receiver. Additionally, low power operation is dependent on a receiver that is designed for the proper input range. The interested reader is directed to books and articles published on optical receiver and transmitter design as it pertains to fiber optics and free air optical links for information on design technique. High-quality off-the-shelf transmitter and receiver parts are also commercially available.

This analysis may also be relevant to transcutaneous power transfer.

VI. CONCLUSION

We have measured the distribution of optical power flux through porcine skin samples ranging from 2 mm to 11.5 mm in thickness. Two descriptive measures of these distributions (T_tot and FWHM) were modeled using regression models. Analysis of these measures quantitatively showed the changes in flux distribution shape with tissue thickness. Additionally, the power flux distributions were modeled using a simple, two-parameter Gaussian model which allows for the convenient reconstruction of the flux distributions and subsequent analysis of optics collection area and misalignment effects. These distributions were then used to demonstrate the effect that the fundamental optical interface design parameters (lens integration area, misalignment tolerance, emitter power, and tissue thickness) have on the amount of power collected by the receiver. It should be reinforced here that the optical interface is designed with the receiving and transmitting circuitry elements in mind (i.e., the power output of the transmitter and the optical interface design should reflect the power levels required by the particular receiver design chosen). The analysis presented herein allows for the design of a transcutaneous optical telemetry link (or potentially an optical power transmission system) that is optimized to certain system-level design constraints: implant location requirements, power constraints, misalignment constraints, and external device-size constraints.

Biographies

D. Michael Ackermann, Jr. received the B.S. degree in biomedical engineering from Vanderbilt University, Nashville, TN, in 2004 and the M.S. degree in biomedical engineering from Case Western Reserve University (CWRU), Cleveland, OH. He is currently pursuing the Ph.D. degree in biomedical engineering at CWRU.

His research interests include implantable device design and neuromodulation techniques for the activation and inactivation of neural tissue.

Brian Smith received the B.Sc. (Honors) degree in electronic and electrical engineering from the University of Lancaster, LAncaster, U.K., in 1979.

He has held a number of senior engineering positions in academic research, contract engineering, medical device development, and start-up ventures. He presently holds a position with the Biomedical Engineering Department, Case Western Reserve University, Cleveland, OH, as an Engineering Manager for the Cleveland FES Center. His current responsibilities include the development of a new generation of stimulation and sensing devices that can be networked together as a flexible and scalable system to meet the technical needs of a broad range of neuroprosthetic applications.

Xiao-FengWang received the M.S. degree in applied mathematics from Huazhong University of Science and Technology, Hubei, China, and the Ph.D. degree in statistics from Case Western Reserve University (CWRU), Cleveland, OH.

He is Assistant Staff of biostatistics with the Department of Quantitative Health Sciences at the Cleveland Clinic and Assistant Professor of Medicine and Biostatistics at the CWRU School of Medicine. His main specialties are in nonparametric statistics, data mining, and neuroinformatics. Dr. Wang is an Elect Member of the International Statistical Institute.

Kevin L. Kilgore received the B.S. degree in biomedical engineering from the University of Iowa, Iowa City, in 1983 and the M.S. and Ph.D. degrees in biomedical engineering from Case Western Reserve University, Cleveland, OH, in 1987 and 1991.

Since 1991, he has been Clinical Research Director for the Cleveland FES Center. His research interests are in the clinical applications of functional electrical stimulation to hand and arm function and in the application of electrical currents to the control of unwanted neural activity.

P. Hunter Peckham received the undergraduate degree in mechanical engineering from Clarkson College of Technology (now Clarkson University), Potsdam, NY, and the M.S. and Ph.D. degrees in biomedical engineering from Case Western Reserve University (CWRU), Cleveland, OH.

He is currently the Donnell Institute Professor of biomedical engineering and orthopaedics at CWRU; a Senior Career Research Scientist with the Department of Veterans Affairs; Director of the VA Center of Excellence in Functional Electrical Stimulation; and the Director of Orthopaedic Research at MetroHealth Medical Center. The major area of his research is in rehabilitation engineering and neural prostheses. His research effort focuses on functional restoration of the paralyzed extremities in individuals with spinal cord injury. He and his collaborators have developed implantable neural prostheses that utilize electrical stimulation to control neuromuscular activation. They have implemented procedures to provide control of grasp-release in individuals with tetraplegia. This function enables individuals with central nervous system disability to regain the ability to perform essential activities of daily living. His present efforts concern the integration of technological rehabilitation and surgical approaches to restore functional capabilities. He is currently working on an advanced neuroprosthesis that employs implantable sensors for internal control and regulation of movement.