Comparing the optimal signal conditions for recording cubic and quadratic distortion product otoacoustic emissions

Abstract

Odd- and even-order distortion products (DPs), evoked by two primary tones (f₁,f₂,f₁<f₂), represent different aspects of cochlear nonlinearity. The cubic and quadratic difference tones (CDT 2f₁−f₂ and QDT f₂−f₁) are prominent representatives of the odd and even DPs. Distortion product otoacoustic emissions (DPOAEs) were measured within a primary level (L₁,L₂) space over a wide range of f₂∕f₁ ratios to compare the optimal signal conditions for these DPs. For CDT, the primary level difference decreased as L₁ increased with a rate proportional to the f₂∕f₁ ratio. Moreover, the optimal ratio increased with L₁. A set of two formulas is proposed to describe the optimal signal conditions. However, for a given level of a primary, increasing the other tone level could maximize the QDT amplitude. The frequency ratio at the maximal QDT was about 1.3 and quite constant across different primary levels. A notch was found in the QDT amplitude at the f₂∕f₁ ratio of about 1.22–1.25. These opposite behaviors suggest that the optimal recording conditions are different for CDT and QDT due to the different aspects in the cochlear nonlinearity. Optimizing the DPOAE recordings could improve the reliability in clinical or research practices.

INTRODUCTION

Our inner ears are nonlinear acoustic transducers where distortions are normal by-products of the conversion of sound into bioelectrical signals. The source of distortion is thought to be within the transduction process of outer hair cells (OHCs), since these cells respond to changes in membrane voltage with mechanical motion in either the cell body (Liberman et al., 2002) or the hair bundles (Kennedy et al., 2005). The OHC transduction shows a saturating nonlinearity and the resulting motile responses provide a mechanical feedback that can enhance hearing sensitivity and frequency selectivity. When stimulated by two tones (f₁,f₂,f₂>f₁), the inner ear can produce a family of distortion products (DPs) in various combinations of the primary frequencies, mf₁±nf₂. Depending on the sum of integers m and n, the DPs can be classified into two categories, odd- and even-order DPs. They reflect different aspects of the nonlinear transducer characteristics of OHCs in the overlapped region of traveling waves initiated by two pure tones. Odd-order DPs are relatively large at low primary levels, and representing the transducer gain of hair cells. In contrast, even-order DPs are only measurable at moderately high stimulus levels, and thus may reflect the saturation or compression of hair cell transducers. These DPs in mechanical vibrations of hair cells can propagate out of the inner ear and are measurable in the ear canal as faint sounds or distortion product otoacoustic emissions (DPOAEs). Therefore, DPOAEs provide a noninvasive tool to assess the functional status of the inner ear OHCs.

Given the possibility that DPOAEs can be used to evaluate the transducer characteristics of OHCs, the current clinical application is, however, limited to hearing screening (Lonsbury-Martin and Martin, 2003) where normal or abnormal hearing is judged by the presence or absence of emissions. Quantitative utilities, such as hearing threshold estimates, cochlear efferent function evaluation, and input∕output growth functions, are restricted to mostly research settings. One reason for the limited use of DPOAEs is the large variability in measurements. Among other factors (Garner, 2008), such as hearing sensitivity, middle ear transmission, and inner ear reflections, a source of the variability can be attributed to less optimized signal conditions of the primary tones (Johnson et al., 2006; Mills et al., 2007) that cannot evoke the largest DPOAEs. Since DP levels are correlated with the nonlinear characteristics of cochlear transduction (Lukashkin and Russell, 1999; Fahey et al., 2000; Bian et al., 2002; Bian, 2004), maximizing DPOAE magnitudes can improve the signal-to-noise ratio (SNR) so that more accurate estimates of cochlear function are possible. Therefore, there is a need for standardizing (Mills et al., 2007) or individualizing (Neely et al., 2005) the measurement procedures. Optimizing the recording conditions for DPOAEs is still an ongoing research effort.

The signal conditions for recording DPOAEs include the f₂∕f₁ frequency ratio and the levels of two primary tones (L₁ and L₂). The f₂ is usually predetermined for evaluating the cochlear function at a specific frequency of interest, because the overlapped region of the two-tone excitation patterns on cochlear partition is very close to the f₂ place. The frequency f₁ can be determined by selecting an appropriate f₂∕f₁ ratio. In current clinical practice, a value of 1.22 is commonly adopted for f₂∕f₁ ratio regardless of frequency and level. However, the optimal ratio can range from 1.2 to 1.3 with increase in primary levels and f₂ (Moulin, 2000; Johnson et al., 2006). Thus, for a certain f₂, selecting the frequency ratio is tied with the choice of primary levels. Currently, the decision on signal levels is an independent process and often a simple strategy of L₁ being 5–10 dB greater than L₂ is used. However, studies on DPOAE amplitude within a complete L₁×L₂ parameter space indicate that the primary level difference (ΔL=L₁−L₂) is also level dependent with greater deviations towards lower levels (e.g., Whitehead et al., 1995). The optimal L₁ as a linear deviation from L₂ is refined with an empirical formula (Kummer et al., 2000) given the observation that ΔL diminishes at 65 dB SPL. This primary level optimization allows a more accurate measurement of DPOAE amplitudes at low stimulus levels for estimating hearing sensitivity (Kummer et al., 1998). Another relation between the optimal L₁ and L₂ is proposed by Johnson et al. (2006) which takes f₂ into account. However, none of the approaches considers the inter-relation between the primary levels and the f₂∕f₁ ratio. The interaction between frequency ratio and primary levels on DPOAEs can be deduced from the fact that all these factors influence the amount of overlap between two excitation patterns in the cochlea and in turn determine the exact two-tone input to the nonlinear transduction of OHCs.

To date, all parametric studies on optimizing DPOAE recordings focus on the most prominent DP component, cubic difference tone (CDT, 2f₁−f₂). An obvious reason for CDT as the choice of DPOAE measure for research and application is simply its large size and SNR. Another reason is that at low signal levels CDT reflects the response growth or gain of OHC transducer and is parallel to hearing sensitivity and frequency selectivity of the inner ear (Brown et al., 1993; Gorga et al., 2003). However, CDT only represents the odd nonlinearity in cochlear transduction; thus, the estimation of hair cell function could not be complete without measuring the even-order DPs. The largest even-order DP is quadratic difference tone (QDT, f₂−f₁) which has not been considered clinically useful until recently. One reason for the lack of research and application is due to its low amplitude (Brown, 1993) and poor SNR. However, auditory nerve fiber responses in kittens show robust QDT that can be larger than CDT (Tubach et al., 1996). Neural QDT varies nonmonotonically with primary levels or frequencies and its behavior is different from CDT (Kim, 1980). Large QDT also presents in electrical responses in inner hair cells (Nuttall and Dolan, 1993), indicating that the source of QDT is presynaptic and possibly the OHCs. Indeed, QDT is the largest DP component found in the trans-membrane current that drives OHC somatic motility (Takahashi and Santos-Sacchi, 1999). Acoustic QDT can be associated with the saturating portions of OHC transduction, and its amplitude variation reflects the operating point (OP) shift of hair cells (Frank and Kössl, 1996). Studies in gerbils show that the QDT is enhanced or modulated by a low-frequency bias tone and the modulation patterns could be used to derive a cochlear transducer function (F_Tr) (Bian, 2004, 2006). This finding poses a possible clinical application in evaluating cochlear function or diagnosing inner ear disorders. Since the cochlear F_Tr can be quantified from low-frequency modulation of CDT in humans (Bian and Scherrer, 2007), combining this measure with QDT could provide a more comprehensive picture of cochlear function. Towards this goal, it is necessary to explore the optimal signal conditions for recording QDT, because the ideal conditions for CDT may not be applicable to QDT, especially, in humans. Therefore, the purpose of the present study is to compare the optimal conditions for CDT and QDT to provide guidelines for research and clinical practice.

METHODS

Subjects

Sixteen healthy subjects with age ranging from 23 to 40 years (mean 26.3) were recruited from the students at Arizona State University (ASU). They had no history of hearing disorders. Normal outer and middle ear functions were confirmed with an otoscopic examination. A DP-gram was measured with an 8-point∕oct procedure from 1 to 8 kHz (ILO92, Otodynamics Ltd., Herts, UK). Subjects with CDT amplitudes greater than 10 dB SPL in the frequency range between 1 and 4 kHz were selected for the study. Subjects with deep notches or spectral fine structures in this region were excluded to reduce interference of DPOAEs generated from reflections at the best frequency place (Knight and Kemp, 2001; Shera, 2004). To avoid possible influence and interference, the subjects were also screened to rule out spontaneous otoacoustic emissions in the testing ear. Subjects were seated comfortably in a sound-proofed booth and instructed to be as quiet as possible during the test to reduce noises. The recruiting protocol and experimental procedures were approved by the Institutional Review Board of ASU.

Stimulus presentation

Two primary tones were generated and controlled with a personal computer using software implemented in LABVIEW (National Instruments, NI, Austin, TX). Durations of the primary tones were 1 s with a 5-ms cos²-shaped rise and fall ramp, respectively. The signals were delivered separately to two earphones (ER-2A, Etymōtic Research, Inc., Elk Grove Village, IL) through a 24-bit dynamic signal acquisition and generation card (PXI-4461, NI) and acoustically mixed in the ear canal to stimulate the inner ear. The ear-canal acoustic response was then recorded by a calibrated probe microphone (ER-10B+). The recorded signal was amplified 20 dB by the built-in preamplifier of the ER-10B+ and digitized at a rate of 131.072 kS∕s (PXI-4461). Prior to each test, the fit of ER-10B+ probe was checked and adjusted to ensure a flat ear-canal frequency response up to 5 kHz to a frequency-sweeping tone at a constant level. This can avoid the interference from standing waves in the ear canal and acoustic leaks around the probe.

Data were collected over a range of f₂∕f₁ ratios using a “chess-grid” protocol, namely, the L₁ and L₂ were swept independently from 75 to 54 dB SPL in 3-dB steps to create an 8×8 grid of data sets for each f₂∕f₁ ratio. Lower signal levels were not used due to a concern of poor SNR for QDT. The primary levels were automatically adjusted and calibrated at the beginning of each decrement. To ensure the completion of experiments within 90 min, the frequency of f₂ was fixed at 4 kHz in the study. Based on the coverage of f₂∕f₁ ratio, the study was carried out in two phases. In phase 1, the f₂∕f₁ ratio was varied from 1.2 to 1.8 at a step size of 0.1 to explore the behaviors of CDT and QDT when f₁ and f₂ were separated further apart. It was initially thought that there could be a mechanical “(second) filter” just below the frequency of f₂ in the cochlea (Allen and Fahey, 1993; Brown et al., 1993), so that the QDT could be “amplified” if the f₂∕f₁ ratio was large enough to bring the QDT frequency into the filter bandwidth. In phase 2, conventional frequency ratios from 1.15 to 1.36 with a step size of 0.035 were used to reveal the optimal signal conditions for both DPOAE components. Ratios lower than 1.1 were not used to keep the QDT above 500 Hz, since the noise floor below this frequency was higher (>−10 dB SPL). Eight subjects participated in each phase.

Data collection and analysis

At each two-tone condition, the stimuli were repeated eight times and the recorded acoustic signal was averaged in the time domain to reduce random noise. Noisy data due to body movements were discarded with an artifact rejection routine which examined the noise floor from 300 to 800 Hz. The rejection threshold was adjustable depending on the noise condition of each subject to optimize the speed of data collection. Data were analyzed offline in MATLAB (Mathworks Inc., Natick, MA) using custom-written programs. The waveform of ear-canal acoustic signal was passed through a Hanning window and converted into the frequency domain via a fast Fourier transform (FFT). Then, the spectral magnitudes at the frequencies of 2f₁−f₂ and f₂−f₁ were extracted to result in the value of a single grid in the L₁×L₂ level space for CDT and QDT, respectively.

To examine the combined effects of primary levels and frequency ratio, the data were merged into an 8×8 grid of CDT or QDT amplitude-ratio functions with a specific L₁ and L₂ combination for each grid. Thus, the DPOAE amplitude could be examined in each dimension by fixing L₁, L₂, or f₂∕f₁ ratio, respectively. For the optimal signal conditions, relations between the two primary levels under different frequency ratios or the optimal ratios as functions of the primary levels were inspected. As the influence of L₁ on DPOAE amplitudes was stronger than L₂, the relations among these signal variables were expressed as functions of L₁. To reveal possible underlying rules, these relations were fit with appropriate linear or nonlinear functions. The curve fittings were usually performed on the averaged data and the parameters were validated by predicting the optimal conditions for each individual.

RESULTS

In this study, three signal variables, L₁, L₂, and f₂∕f₁ ratio, were varied simultaneously, creating an extra complexity in observing the behaviors of DPOAEs. It would be convenient to reduce the data into a two- or three-dimensional space by keeping one variable constant. For the optimal signal conditions, the data analysis focused on the relations between these variables. Data reported were mostly from phase 2, where common f₂∕f₁ ratios from 1.15 to 1.36 were used. Phase 1 data were reported in the section regarding the ratio effects.

Level effects

L₂ fixed

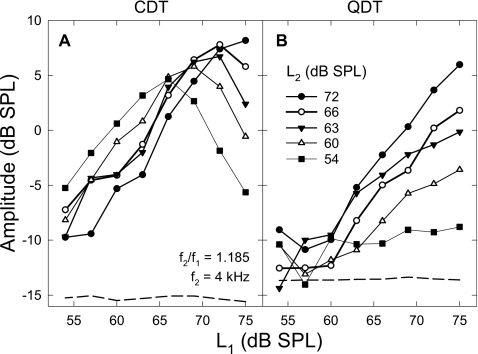
For different f₂∕f₁ ratios, the DPOAE magnitudes behaved similarly, but with different overall sizes. It would be reasonable to select a ratio that produced larger DPOAEs to show effects of L₁ when L₂ was fixed at different values. At the f₂∕f₁ ratio of 1.185, amplitudes of CDT and QDT averaged across eight ears showed different growth patterns (Fig. 1) with L₁. The CDT amplitude showed an initial increase and a rollover as L₁ was raised over L₂ [panel (A)]. The level of f₁ where the CDT reached the peak depended on the fixed level of f₂, usually when L₁ was 3–10 dB greater than L₂. As the fixed L₂ decreased, the peaks of CDT amplitudes showed a small shift towards lower values of L₁, indicating a larger level difference. In other words, for lower levels of f₂ a much larger L₁ was needed to produce a peak CDT magnitude. Moreover, the peak CDT values decreased slightly (<5–10 dB) when L₂ was lowered for about 20 dB. Therefore, these CDT amplitude functions were largely overlapped when L₁ was below 65 dB SPL. The growth rates of CDT amplitudes were about 1 dB∕dB, suggesting that the CDT increased proportionally with L₁ until the peak values were reached.

Figure 1.

DPOAE amplitudes as functions of L₁ under different L₂ settings. (A) CDT magnitudes rise with L₁ and roll over at different L₁ values. (B) QDT amplitudes increase with L₁ in different growth rates depending on the L₂ settings. Dashed lines indicate the averaged noise floor of DPOAE measures. Data reflect an average across eight subjects.

In contrast, the growths of QDT amplitudes showed no obvious signs of peaks and rollovers [Fig. 1B]. On average, the amplitudes of QDT were smaller than the CDT, especially, when L₁ was less than 60 dB SPL. At these lower f₁ levels, the QDT was usually within 5 dB from the noise floor (around −12–−13 dB SPL). Then, the QDT amplitude started to grow when L₁ exceeded 60 dB SPL. The rate of growth and the maximal QDT level seemed to be proportional to the fixed level of f₂. The slope of QDT growth function could reach about 1 dB∕dB when L₂ was set at 72 dB SPL and progressively decrease with L₂. QDT magnitudes usually reached their highest values when L₁ was maximal (75 dB SPL). The largest QDT level could be greater than 6 dB SPL when both L₁ and L₂ were at the highest level. There was also a slight compression of the QDT growth functions when L₁ was above 70 dB SPL.

L₁ fixed

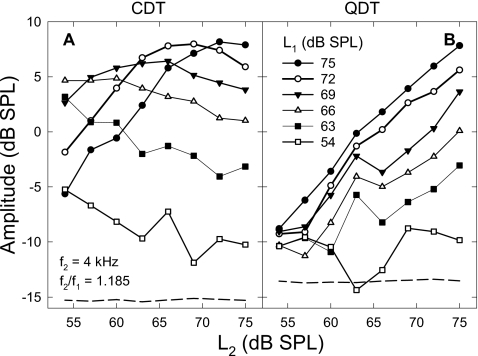
When L₁ was fixed at different levels, the averaged CDT magnitude showed a range of different patterns as L₂ increased [Fig. 2A]. The patterns and overall value of CDT amplitudes were predominated by the fixed levels of f₁. As L₁ was gradually set to lower values, the CDT amplitudes showed three types of patterns with increasing L₂: (1) a compressive growth; (2) a slower initial growth with a rollover; and (3) a gradual decrease. The overall CDT magnitudes also decreased with reductions in L₁. The progression of these CDT patterns reflected a dramatic shift of the CDT peak towards lower L₂ along with a significant reduction in overall sizes. This indicated that CDT amplitudes could reach a higher value when L₁ was set higher and the CDT growth only occurred when L₂ was lower than L₁. Consistent with the growth curves in Fig. 1A, the CDT peaked if L₂ reached 3–10 dB below the fixed L₁. When L₂ was greater than these levels or L₁, only a gradual decrease of CDT magnitude could be observed [Fig. 2A].

Figure 2.

DPOAE amplitudes as functions of L₂ under different L₁ settings. (A) CDT magnitudes show different patterns depending on the L₁ settings. The CDT peak decreases with L₁ and shifts to lower L₂ values as L₁ reduces. At lower L₁ settings, only a decrease in CDT level can be observed. (B) QDT amplitudes increase with L₂ in different growth rates depending on the L₁ settings. Note: a notch can be observed at moderate to low levels of the f₁. Dashed lines indicate the averaged noise floor of DPOAE measures. Data reflect an average across eight subjects.

In comparison, the QDT amplitude showed a less variable growth pattern with the increase of L₂. When L₁ was fixed above 70 dB SPL, the QDT amplitude grew quite linearly with L₂. As L₁ was lowered, the growth functions of QDT became nonmonotonic with the presence of a notch around the f₂ levels of 63 to 67 dB SPL. There seemed to be a slight shift of the notch towards lower values of L₂. The QDT magnitude grew at a 1 dB∕dB rate before the notch (lower L₂), which was consistent with the linear growths at high f₁ levels. If L₁ was very low (<55 dB SPL), the QDT level was flattened within about 5 dB from the noise floor (−13 dB SPL). Thus, QDT magnitudes were influenced by both L₁ and L₂.

Both L₁ and L₂ varied

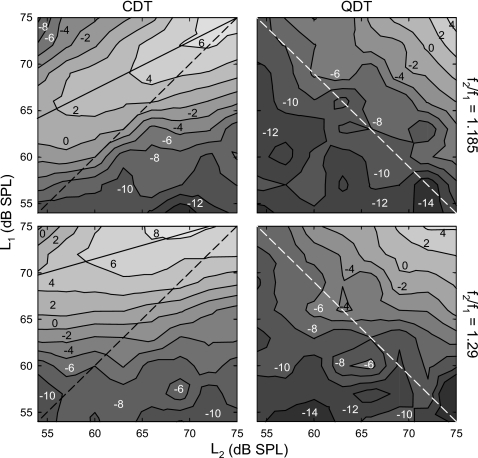
The combined effects of L₁ and L₂ on the averaged CDT and QDT amplitudes were evaluated with contour plots in the L₁×L₂ level spaces (Fig. 3). From the DPOAE contours, the optimal signal levels that produced the highest DPOAEs could be evident. The CDT amplitude contour (left panels) showed a confined ridge spanning from the upper right corner towards the moderate values of L₁ and the minimal L₂. The tips of contour lines on the ridge, where both L₁ and L₂ were minimal to evoke a certain level of CDT, reflected the optimal primary levels for CDT. The relation between the optimal L₁ and L₂ (solid line) indicated that L₁ was preferred to be greater than L₂. This ΔL became progressively larger at lower primary levels with reference to the dashed line depicting L₁=L₂. At the L₂ of about 75 dB SPL, the optimal L₁ was roughly the same as L₂, i.e., no level difference. Comparing the contours from two different f₂∕f₁ ratios (1.185 and 1.29), the optimal ΔL became larger for the higher frequency ratio (lower left panel). In addition, the CDT magnitude was largely dominated by L₁ and the influence of L₂ was weak at higher ratios as indicated by the nearly horizontal contour lines.

Figure 3.

Contour plots of DPOAE amplitudes in L₁×L₂ spaces of two f₂∕f₁ ratios. Left: CDT magnitude shows a ridge spanning from the upper right corner (75,75) to moderate L₁ and low L₂. Solid lines indicate the optimal primary levels that yield the maximal CDT magnitude. Diagonal dashed lines indicate the condition L₁=L₂. Distances between the two lines represent the optimal level difference (ΔL=L₁−L₂). Note: ΔL is greater for higher f₂∕f₁ ratio (lower panel). Right: QDT magnitude contour lines are parallel to the diagonal dashed line representing L₁+L₂=129 dB SPL. For each fixed L₁ or L₂, maximizing the other primary level would optimize the QDT amplitude. Note: the slope of the contour for the larger ratio (lower panel) is shallower than the smaller ratio (top). Data reflect an average across eight subjects at an f₂ of 4 kHz.

Although the maximal QDT magnitudes were also located at the upper-right corners of the QDT contour maps (Fig. 3, right panels), paths of the isoamplitude lines were quite different from the CDT. These parallel contour lines stepped down towards lower L₁ and L₂ with no obvious ridges formed. The direction of the contour lines followed the diagonal line from the highest L₁ to the highest L₂ (dashed line), meaning that a relatively large QDT could be obtained by keeping one of the primary levels high. Thus, the QDT amplitude seemed to be proportional to L₁+L₂, i.e., higher QDT magnitudes correlated with larger sums of the primary levels. If one of the primary levels was fixed, raising the other could increase the QDT accordingly. This diagonal direction of contour lines was unaffected by varying the f₂∕f₁ ratio. However, the contour gradient at the higher f₂∕f₁ ratio (lower right panel) was shallower than the lower ratio (top right), indicating that larger QDT magnitudes could be observed at lower primary levels.

Effects of the f₂∕f₁ ratio

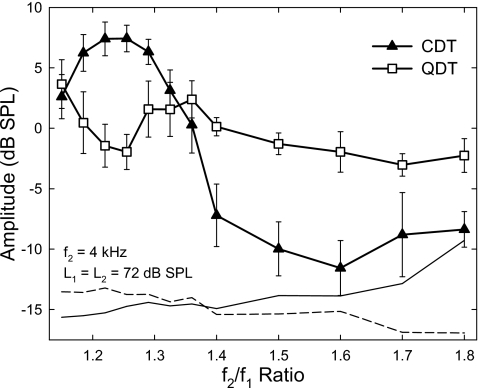
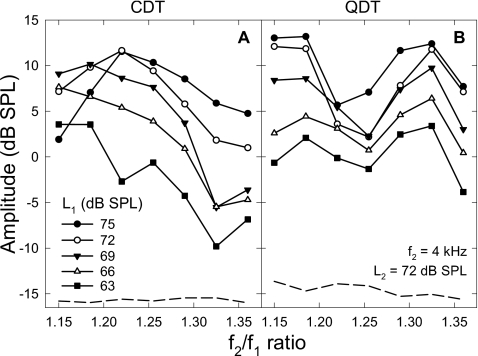
Since different ranges of f₂∕f₁ ratios were adopted in phase 1 and phase 2 experiments, results from both phases were pooled together to evaluate the effects of a widely changed frequency ratio. Both CDT and QDT magnitudes showed a variability which was influenced by the amplitude and frequency of the emissions. The standard error (SE) of emission amplitudes was less than 2 dB when the emission magnitude was greater than −5 dB SPL or the frequency was above 1 kHz. The SE could increase up to 5 dB if the emission frequency and amplitude were below 500 Hz and −5 dB SPL, respectively. Despite the variability, the averaged DPOAE magnitudes showed different patterns as the f₂∕f₁ ratio was increased from 1.15 to 1.8 (Fig. 4). As shown in this example (L₁=L₂=72 dB SPL), the CDT amplitude increased with the f₂∕f₁ ratio starting from the lowest value of 1.15 and reached a maximum of nearly 8 dB SPL at the ratios of 1.22 to 1.25. Then, the CDT magnitude decreased quickly as the ratio further increased and dropped below −5 dB SPL for the ratios above 1.4. The QDT magnitude, however, showed an opposite change when the f₂∕f₁ ratios were below 1.4, i.e., it produced a notch with a minimum of −2 dB SPL at the ratio of about 1.25. With further increase in the ratio, QDT levels bounced back and reached a peak at 1.36. For f₂∕f₁ ratios greater than 1.4, both CDT and QDT magnitudes reduced continuously. Despite a slower reduction, the QDT amplitude showed no signs of a bandpass characteristic (“the second filter”) when the f₂∕f₁ ratio increased to 1.8, a ratio where the QDT frequency was equivalent to the CDT generated at the ratio of 1.36. From the CDT curve, a dramatic 10-dB increase in amplitude could be observed from the ratios of 1.4 to 1.32.

Figure 4.

DPOAE amplitudes as functions of f₂∕f₁ ratio. Each curve is a combination of the averaged results from the two experimental phases. For frequency ratios below 1.4, the CDT amplitude reaches a peak at about 1.25, where the QDT magnitude drops to a local minimum. For f₂∕f₁ ratios above 1.4, both CDT and QDT amplitudes decline to minimal values at the frequency ratios of 1.6 and 1.7. Error bars represent the standard errors of the data. Solid and dashed lines indicate the averaged noise floor in CDT and QDT measures, respectively. Each data point reflects an average across eight subjects.

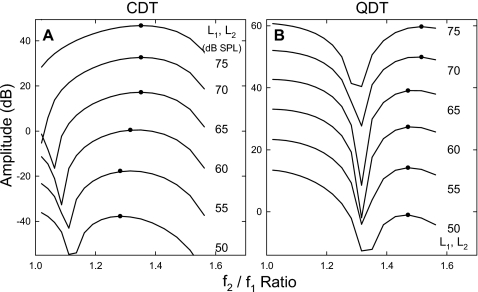
The opposite behaviors of CDT and QDT were also presented under the conditions of unequal primary levels. A series of averaged CDT and QDT amplitude-ratio functions was displayed to examine the influence of L₁ with L₂ held constant at 72 dB SPL (Fig. 5). It could be observed from panel (A) that the CDT amplitudes showed an asymmetrical bell shape as the frequency ratio varied. The peaks of CDT curves progressively shifted towards lower ratios when L₁ decreased, i.e., the optimal f₂∕f₁ ratio for CDT was smaller (<1.2) for lower f₁ levels (<66 dB SPL). For QDT magnitudes [panel (B)], a notch presented at about 1.22–1.25 for different levels of f₁. However, no clear trend of shifting of the notch could be observed. On either side of the notches, the QDT level peaked around the frequency ratios of 1.18 and 1.32, respectively. For levels of f₁ below 70 dB SPL, the patterns of QDT amplitude were more asymmetrical, with peaks at the ratio of 1.32 being higher.

Figure 5.

Effects of primary levels on DPOAE amplitude-ratio functions. (A) As L₁ decreases, the peak of CDT amplitude shifts to lower f₂∕f₁ ratios. (B) QDT magnitudes show a notch around the f₂∕f₁ ratios of 1.22–1.25. No obvious shift of the notches can be observed with varying L₁. Among the two possible optimal ratios (1.185 and 1.325), the larger one is selected as the optimal ratio for recording QDT so that the QDT frequency can be maintained above 500 Hz. Data reflect an average across eight subjects.

Optimal signal conditions

Primary level difference

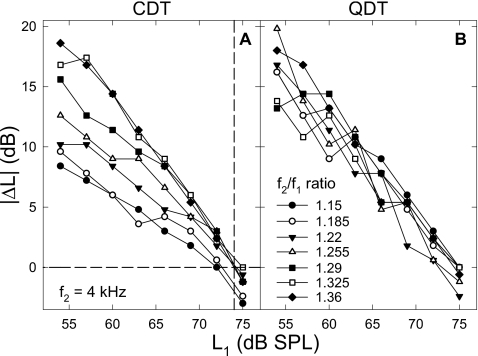
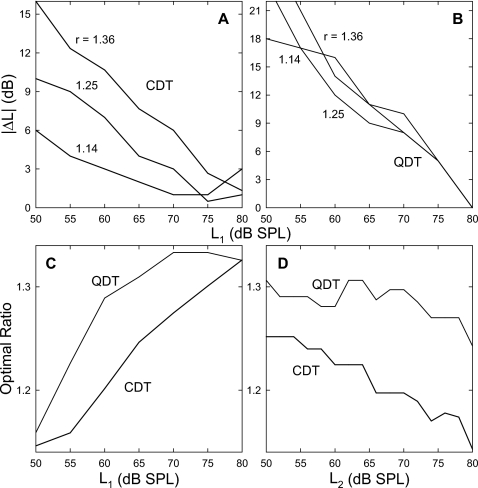
Inter-relations among the optimal signal conditions (L₁, L₂, and f₂∕f₁ ratio) were explored and quantified. As noted above, L₁ should be greater than L₂ to evoke a large CDT (Fig. 3 left) and the ΔL was greater at lower primary levels. The ΔL was further affected by the f₂∕f₁ ratio, i.e., larger for higher ratios, and the optimal ratio increased with the primary level [Fig. 5A]. These relations were depicted with a series of optimal ΔLs obtained at different frequency ratios plotted as functions of L₁ (Fig. 6). For CDT [panel (A)], these ΔLs decreased linearly with the L₁ and became 0 at the L₁ of about 74 dB SPL. The only obvious difference among these ΔL functions was their varying slopes that decreased with the f₂∕f₁ ratio. Thus, the ΔL functions could be fit with a cluster of straight lines passing through a single point (74, 0),

$$\Delta L=K\left(r\right)(L_1-74),$$ (1)

where K(r) is the slope of the ΔL functions. Note that the slope K is a function of the f₂∕f₁ ratio (r) and the values are listed in Table 1. As can be observed, the relation between the slopes and the ratios was approximately linear with a 0.96 correlation coefficient (r²). Therefore, the slope could be obtained from K(r)=a⋅r+b, where a=−2.09, b=1.91.

Figure 6.

Effect of L₁ on the optimal primary ΔL. For both CDT and QDT, the optimal ΔL declines with the increase in L₁. Different lines represent different f₂∕f₁ ratios in each panel. (A) The slope of ΔL decrease with L₁ varies depending on the f₂∕f₁ ratio. The maximal ΔL at the lowest L₁ is proportional to the frequency ratio and ΔL approaches zero around the L₁ of 74 dB SPL (dashed lines). (B) Similar trends can be observed in the ΔL for measuring QDT, but the effect of f₂∕f₁ ratio is minimal. Note: the absolute value of ΔL is used, i.e., ∣ΔL∣=L₁−L₂, because L₂ could be greater than L₁ for recording QDT. Data reflect an average of eight subjects.

Table 1.

Relation between the f₂∕f₁ ratio (r) and the slope K used for calculating the primary level difference (ΔL) in Eq. 1.

r	1.15	1.185	1.22	1.255	1.29	1.325	1.36
K	−0.52	−0.56	−0.64	−0.66	−0.78	−0.90	−0.93

For QDT, ΔL was also reduced as L₁ increased [Fig. 6B]. Unlike CDT, these ΔL functions for different f₂∕f₁ ratios were close to each other, indicating that the influence of the frequency ratio was weak. The slopes of these ΔL functions were approximately −1, meaning that the effect of primary levels was a linear decrease with increasing f₂∕f₁ ratio. Solving Eq. 1 with K=−1, there were two possible relations between the primary levels: one of the primaries L₁ or L₂=74 dB SPL, or L₁=L₂∕2+37, if both primaries were at moderate levels. However, the second solution was not the optimal condition, because for a given primary level the sum of L₁ and L₂ was not greater than when the other tone was held at the maximal value. It should be noted that L₂ could be greater than L₁ to evoke a large QDT.

Frequency ratio

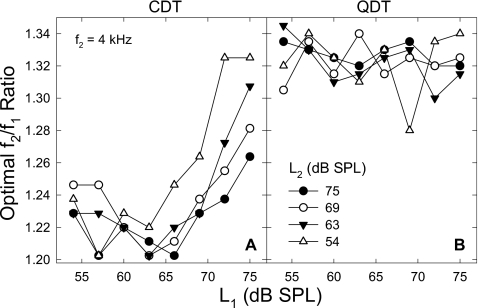
For CDT, the influence of primary levels on the optimal f₂∕f₁ ratio was mainly from L₁, since the ratio showed only a small reduction with L₂ (data not shown). At different L₂ levels, the optimal ratio as functions of L₁ demonstrated a series of “J”-shaped curves [Fig. 7A]. Generally, the optimal ratio declined slightly as L₁ increased to 60–65 dB SPL. With further increase in L₁, the ratio rose considerably. As L₂ was lowered, the optimal ratio change with L₁ showed three trends: (1) a steeper slope; (2) a higher maximal ratio; and (3) a shift of the minimum to lower L₁. For each fixed L₂, the ratio curve could be fit with a quadratic function,

$$r=r_0+s{(L_1-L_0)}^2,$$ (2)

where r₀ is the minimal f₂∕f₁ ratio (when L₁=L₀) and s is the slope of ratio growth. Values of the parameters obtained from curve fitting varied with L₂ (Table 2). For simplicity, linear functions were used to approximate the relations between the parameters and L₂,

$$\{\begin{array}{l}{r}_0=c_1{L}_2+d_1\\ s=c_2{L}_2+d_2\\ L_0=c_3{L}_2+d_3\end{array}\phantom{\}},$$ (3)

where c₁=−3.65×10⁻⁴, d₁=1.25, c₂=−1.65×10⁻⁵, d₂=1.42×10⁻³, c₃=0.19, and d₃=50.91.

Figure 7.

Influence of primary levels on optimal f₂∕f₁ ratio. (A) After an initial dip, the optimal frequency ratio increases nonlinearly with L₁. The rate of f₂∕f₁ growth and the maximal value are inversely related to L₂. The minimal ratios (>1.20) present at the L₁ of about 55–65 dB SPL. (B) The optimal f₂∕f₁ ratios for QDT vary between 1.3 and 1.34 with only a slight decrease with L₁. No influence from L₂ can be observed. Data reflect an average of eight subjects.

Table 2.

Relation between L₂ and the parameters in Eq. 2. r²: correlation coefficient of a linear regression between the parameter and the L₂.

L2 (dB SPL)	75	72	69	66	63	60	57	54	r2
r0	1.223	1.227	1.230	1.230	1.224	1.233	1.236	1.228	0.62
s(×10−4)	2.31	1.72	2.65	1.75	5.52	4.53	4.33	5.06	0.74
L0 (dB SPL)	65.44	64.96	63.9	61.61	63.98	62.20	61.91	61.15	0.37

There could be two optimal ratios for QDT as indicated by the two peaks of the QDT amplitude-ratio patterns [Figs. 45B]. Only the larger ratio was chosen to keep the QDT frequency above 500 Hz for a better SNR. For QDT, no systematic increase of the optimal f₂∕f₁ ratio was observed [Fig. 7B]. The ratios fluctuated between 1.30 and 1.34 regardless of L₂. Examined across different levels of L₂, the frequency ratios showed a slight decrease with increasing L₁. On average, the f₂∕f₁ ratios ranged from 1.32 to 1.33. Therefore, the influence of primary levels on the f₂∕f₁ ratio to record QDT was weak and a value slightly greater than 1.3 could be used as the optimal frequency ratio.

DISCUSSION

To explain the experimental results and explore the generating mechanisms of DPOAEs, a model combining the cochlear mechanics of traveling wave and the nonlinearity in hair cell transduction is used (Fig. 8). Simulated effects of manipulating the primary tones are compared with experimental data. Adding a traveling-wave component to the hair cell transducer model (Bian et al., 2002) is to determine the extent of two-tone interaction on the basilar membrane (BM) and the exact input levels to hair cell transduction.

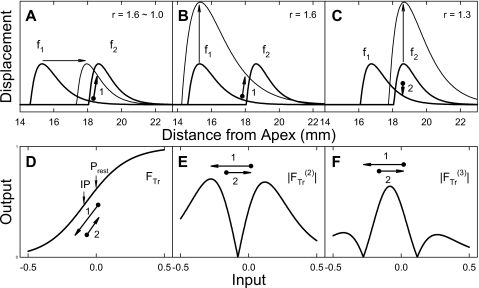
Figure 8.

A model of DPOAE generation. Top row: two tone interaction via traveling waves. (A) Sweeping f₁ to reduce the f₂∕f₁ ratio (r) while keeping primary levels constant (L₁=L₂). (B) Increasing L₁ while keeping the f₂∕f₁ ratio constant. The overlap of traveling wave envelopes increases as f₁ approaches f₂ or as L₁ increases. Influence of f₁ on f₂ or the effective L₁, as indicated by the crossing point of the envelopes, rises accordingly. The direction of the crossing point change (dot arrow) marks the direction of OP shift on the F_Tr (path 1). (C) Raising L₂ while keeping the frequency ratio constant. As L₂ increases, changes in the overlapped region and the effective L₁ are small. Actually, the influence of f₁ on f₂ is reduced. Relative to the f₂ peak, the direction of the crossing point change (dot arrow) is reversed (path 2). Bottom row: the hair cell transducer nonlinearity and DP generation. The direction and path of the OP shift resulting from traveling wave interactions are indicated by the numbered dot arrows. (D) A cochlear F_Tr marked with the resting position (P_rest) and inflection point (IP). (E) and (F) Absolute values of the second and third derivatives of the F_Tr, or $\mid F_{\mathrm{Tr}}^{\left(2\right)}\mid$ and $\mid F_{\mathrm{Tr}}^{\left(3\right)}\mid$, respectively. Following the OP paths, the differential behaviors of QDT and CDT can be observed from panels (E) and (F).

Interaction of traveling waves

A simplified gamma-tone envelope (Carney, 1993) can be used to describe the spread of excitation or displacement along the BM in response to a pure tone,

$$P_{\mathrm{TW}}\left(l\right)=n\cdot l\cdot e^{-nl},$$ (4)

where P_TW is the traveling wave envelope as a function of the BM location l in millimeters from the apex and n is a constant which is unique to the traveling wave peak location (l_P). Since the slope or derivative of the envelope at its peak is zero, i.e., $P_{\mathrm{TW}}^{\prime }=n(1-nl)e^{-nl}=0$, thus n=1∕l_P. Ideally, l_P is determined by the cochlear frequency map (Greenwood, 1990), where the characteristic frequency (f_CF) location from the apex is l_CF=(1∕α)log₁₀(f_CF∕A+k), where α=0.06 mm⁻¹, A=165 Hz, and k=1 for humans. With increasing stimulus level, two alterations in traveling wave properties are also implemented: a basal peak shift and an envelope widening. Since the maximal peak shift is about 1∕2 octave above the f_CF (Robles and Ruggero, 2001), the shift can be quantified as l_P=l_CF+(l_1.5CF−l_CF)L, where L is the signal level in pascals. Width of the traveling wave is defined as the distance between l_P and the apical zero crossing (l₀). Given a 35-mm-long BM, the width is a fraction (w) of the basal portion of the traveling wave (35−l_P). This yields to l₀=l_P−w(35−l_P)L^1∕2, where w=1∕3. Thus, the actual traveling wave envelope is calculated as

$$P_{TW}\left(l\right)=\{\begin{array}{c}n(l-l_0)e^{-n(l-l_0)}\\ 0,\text{if}l<l_0,\hfill \end{array}\phantom{\}}$$ (5)

where n=1∕(l_P−l₀) and the BM apical to l₀ does not respond.

Since DPs are generated from the overlapped region of two traveling wave envelopes initiated by the primary tones [Fig. 8A], only a portion of the f₁ envelope contributes to the two-tone interaction. The effective L₁, indicated by the crossing point of f₁ and f₂ envelopes, is critical in determining the contribution of f₁ and the influence of f₁ on f₂ (Lukashkin and Russell, 2001). Effects of f₁ with respect to a fixed f₂ were systematically examined by: (1) varying f₁ with equal primary levels; (2) varying L₁ with f₁ fixed; and (3) varying L₂ with a fixed f₂∕f₁ ratio [Figs. 8A, 8B, 8C]. As f₁ approaches f₂ [panel (A)], the overlapped region becomes larger and the effective L₁ at the crossing point climbs up. When both f₁ and f₂ are fixed, increasing L₁ enlarges the traveling wave overlap and the effective L₁ (panel B), similar to raising f₁. The manipulation of L₂, however, produces a limited effect, because the basal slope of f₁ envelope is shallow and expansion of apical portion of f₂ pattern is small [Fig. 8C]. All three situations produce more or less similar changes of the CDT, i.e., a limited or saturated increase in CDT amplitude, since the effective L₁ is limited by the f₂∕f₁ ratio of 1, or the fixed settings of L₂ and L₁. Increase in traveling wave overlap alone cannot explain the nonmonotonic changes in DPOAE magnitudes and differential behaviors of CDT and QDT (Figs. 12345). In essence, the optimal signal conditions are not solely dependent on traveling wave interactions. A second component in the model, the transducer nonlinearity, is thus necessary.

Interaction with the hair cell transducer

The nonlinearity of OHC transducer is characterized by a second-order Boltzmann function [Fig. 8D] relating cochlear responses to the BM displacement x (Bian et al., 2002),

$$F_{\mathrm{Tr}}=F_{\max }∕[1+e^{bx-c}(1+e^{dx-e})],$$ (6)

where F_max is a scaling factor determining the maximal output, (b,d) are slope constants, (c,e) are constants setting the resting position of the hair cell transducer. The main advantage of using the second-order Boltzmann function is its asymmetry. The inflection point (IP) on the F_Tr curve is located off zero input (resting point) and the slopes on two sides are different (Bian, 2004). These F_Tr asymmetries can be observed from the center notch or peak of the absolute values of its second and third derivatives (corresponding to the IP) and the sizes of sidelobes [panels (E) and (F)]. Note that there is a 180° phase difference between the sidelobes or side and center peak of the second and third derivatives, respectively. In addition to traveling wave interactions, the second and third derivatives of F_Tr largely dictate the behaviors of QDT and CDT.

Ratio effects

Influence of L₁ on the overlapped region is not only a modification of actual input to the cochlear transducer, but also a biasing of the OP of hair cells in that region due to a tilting of hair bundles or shrinking of cell bodies caused by the f₁ traveling wave. With the absence of f₁ or when f₁ is far away from f₂, the OP at the f₂ place usually is at the resting point [Fig. 8D]. When f₁ approaches f₂, or L₁ steps up, the BM may undergo a progressive baseline shift or an OP shift [Figs. 8A, 8B]. The direction of OP shift on F_Tr could be from the resting position towards the IP (path 1). When the influence of f₁ becomes very large, e.g., at a very small f₂∕f₁ ratio or an intense L₁, the OP could pass the IP and eventually approach the minima on the third derivative [panel (F)]. Therefore, the CDT magnitudes, as functions of f₂∕f₁ ratio [Figs. 45A] or L₁ [Fig. 1A], show a maximum and a rollover. Another evidence for the OP shift across the IP could be the notch presented on the QDT amplitude-ratio functions [Figs. 45B], which was also observed by Brown (1993). The simulated results of QDT and CDT (Fig. 9) well represent the scenarios of OP shifts on the second and third derivatives of F_Tr as the f₂∕f₁ ratio is reduced.

Figure 9.

Model simulation: effects of f₂∕f₁ ratio. (A) CDT magnitudes are maximized at the ratio between 1.2 and 1.3 and otherwise reduced. The peak CDT amplitude (dots) shifts to higher ratios with increase in primary levels (L₁=L₂). Note: a notch is presented at the f₂∕f₁ ratio of about 1.1. (B) QDT amplitudes are minimized at the frequency ratio of about 1.3 and maximized at higher (>1.4) or lower ratios. The maximal QDT magnitudes at the higher ratios are marked with dots.

A result of the simulation is that the CDT magnitudes reach a minimum and then increase when the f₂∕f₁ ratio is reduced below about 1.1 [Fig. 9A]. This notch could not be observed in the present study due to the limited frequency ratio selection (⩾1.15). However, the notch in CDT amplitude-ratio function has been reported in adults (Harris et al., 1989, Moulin, 2000; Londero et al., 2002) and neonates (Abdala, 1996; Lasky, 1997; Vento et al., 2004). Applying the above scenario and following path 1 of the OP shift, the CDT can reach a minimum and regain its magnitude when f₁ further approaches f₂ [Fig. 8F]. It has been suggested that when f₂∕f₁<1.1, reflection or place-fixed DPOAEs may become dominant (Stover et al., 1999; Knight and Kemp, 2001; Dhar et al., 2005) and cancel the nonlinearly generated DPs. However, the possibility that a nonlinear mechanism alone is capable of producing the notch cannot be ruled out (Lukashkin and Russell, 2001). Several investigators have measured the widths of CDT amplitude-ratio functions as the bandwidth of a “second cochlear filter” (Brown et al., 1993; Abdala, 1996; Vento et al., 2004) and found it narrower at lower primary levels. The simulated results [Fig. 9A] are consistent with these observations. Although the “second filter” is not evident by bringing the QDT frequency into the filter bandwidth (Fig. 4; Fahey et al., 2006), the shape of CDT amplitude-ratio function partly reflects the third derivative of cochlear F_Tr which is level dependent (Patuzzi and Moleirinho, 1998; Bian and Chertoff, 2001). Indeed, the sharpness of cochlear filter and the hair cell transducer gain may be intimately related.

Level effects

The effect of increasing L₁ is similar to reducing f₂∕f₁ ratio where the CDT amplitude first increases and then rolls over [Fig. 1A]. The nearly linear growth of CDT with L₁, which is also observed by others (Gaskill and Brown, 1990; Whitehead et al., 1995; Dreisbach and Siegel, 2005), may reflect the elevation of the effective L₁ at the overlap of traveling wave envelopes [Fig. 8B]. Since the apical slope of f₂ traveling wave envelope is very steep, the increase of effective L₁ follows the rise of the tail of f₁ envelope proportionally. When L₁ exceeds L₂, the traveling wave overlap reaches a maximum and the OP may shift (path 1) to the IP of F_Tr, thus producing a peak in CDT magnitude. Unlike the frequency ratio change, the CDT-L₁ functions rarely show a notch [Fig. 1A]. However, such a notch is frequently found in gerbils (Mills, 2002) and chinchillas (Rhode, 2007), because the frequency places of the primaries are closer in small rodents and L₁ is perhaps more effective in biasing OHCs at the f₂ place. At the lowest f₂∕f₁ ratio (1.15), a notch was indeed observed on the L₁ side of the L₁×L₂ space. It is worth noting that larger f₂∕f₁ ratios are used to evoke DPOAEs in rodents (Brown, 1987).

In contrast, increasing L₂ may result in an opposite OP shift, because the influence of f₁ on f₂ diminishes as L₂ rises due to unchanged effective L₁ [Fig. 8C]. The direction of OP shift is from a prebiased position in the negative pressures towards the resting position of hair cell F_Tr (path 2). Depending on the value of L₁, the initial OP shift could vary, thus resulting in variable patterns of CDT amplitude [Fig. 2A]. For high f₁ levels, the initial OP shift is large and the OP can pass through the IP as L₂ increases, causing CDT to rise and fall [Fig. 8E]. For lower L₁, the small initial shift may not even reach the IP, and CDT can only show a decrease as the OP returns to its resting point. These different patterns are indeed observed as increasing L₂ while holding L₁ at various levels [Fig. 2A; Hauser and Probst, 1991]. Notches of the QDT amplitude in Fig. 2B may also indicate the OP path. However, the OP shift on QDT is less influential than the primary levels. This can be evident from the QDT contours in humans (Fig. 3, right) and rabbits (Martin et al., 2003) that show diagonal contour lines indicating increasing influences from both primary levels. In contrast, the ridge on CDT contours implies that a specific influence of L₁ on L₂, i.e., a unique OP shift, can maximize the amplitude. From Figs. 8D, 8E, 8F, it can be noted that CDT at lower input level is related to the center peak of the third derivative and the IP. In contrast, QDT is associated with sidelobes of the second derivative that are maximal for high input levels or large OP shifts. Moreover, sidelobes of the second and third derivatives are both related to saturation regions of the F_Tr. Indeed, the direction of QDT contour line is consistent with the “passive” CDT evoked at high primary levels (Mills, 1997).

Optimal signal conditions

Descriptions of the optimal signal conditions derived from the simulation are comparable with the experimental results. For equal primary levels, the optimal frequency ratio for CDT increases with the signal level [Fig. 9A], which is consistent with the observations in the present study (Figs. 45) and works by others (e.g., Johnson et al., 2006). The level-dependent drift of the optimal ratio is probably due to narrower traveling wave envelopes at low levels so that the two tones need to be placed closer to produce an interaction. Unlike the CDT, the optimal ratio for QDT shows no obvious drift with the primary level [Figs. 5B, 9B]. One reason for this difference could be that the deep notch on the second derivative of F_Tr [Fig. 8E] could severely affect the QDT magnitude compared to variations in traveling wave overlap.

Another important signal parameter is ΔL, which shows two linear relations in both experimental and simulated results (Figs. 610). First, ΔL decreases linearly with L₁. Such a linear decrease is predictable from the differential growths of BM vibrations at the f₂ place in response to f₁ and f₂ (Kummer et al., 2000), i.e., linear growth of effective L₁ and compression of L₂. Additional sound pressure is required to compensate the insensitivity for f₁ at the f₂ location until about 70–75 dB SPL, where tuning at the f₂ place is broadened. Second, for CDT, the slope of ΔL decrease is proportional to the f₂∕f₁ ratio [Figs. 6A, 10A]. Again, it becomes clear that the tuning property at the f₂ place determines that a smaller ΔL is required for a more closely placed f₁ to produce a certain level of interaction [Figs. 8A, 8B, 8C]. These linear trends allow the derivation of Eq. 1 to calculate the ultimate ΔL for a given frequency ratio. Other formulas (Whitehead et al., 1995; Kummer et al., 2000) are also developed in a similar way. A formula by Johnson et al. (2006), incorporates the f₂ and can be applied to different frequencies. Our formula in Eq. 1, however, includes the f₂∕f₁ ratio and is flexible for situations where the ratio is predetermined.

Figure 10.

Model simulation: optimal signal conditions. (A), (B) Influence of L₁ on primary ΔL. For both CDT and QDT, the ΔL decreases with L₁. For CDT, the slope of the ΔL decrease is proportional to the f₂∕f₁ ratio; however, such an effect is minimal for QDT. (C), (D) Effects of the primary levels on the optimal frequency ratio. For both CDT and QDT, the ratio increases with L₁ and slightly reduces with L₂. These level effects are smaller for QDT. Note the optimal frequency ratio is higher for QDT than CDT.

In practice, f₂ and L₂ are usually preselected to assess cochlear functions at a particular frequency location. The decisions to be made are to find f₁ by selecting an appropriate f₂∕f₁ ratio and to determine L₁. From the experimental data and model simulation, it is known that the optimal f₂∕f₁ ratio is nonlinearly dependent on the primary level [Figs. 710C, 10D]. For CDT, the optimal ratio stays low for lower values of L₁ and grows quickly at higher levels. The quadratic fit of the optimal ratio function coincides with the formula of Johnson et al. (2006), in which a squared L₂ is used. The effect of L₂ on the optimal frequency ratio is a slight decrease [Fig. 10D]. Moving f₁ closer could produce more two tone interactions if L₂ is substantial, whereas moving f₁ away could avoid suppressing f₂ if L₂ is weak. For QDT, the simulated optimal ratios (about 1.3) are generally comparable with the data for L₁>65 dB SPL [Figs. 7B, 10D], even though the measured ratios show no obvious change with the primary levels.

For CDT, the complex interactions among frequency ratio and primary levels could be determined from the abstracted relations between a collective pairs of variables. Therefore, two of the relations are formulated using ΔL and optimal ratio [Eqs. 1, 2]. Since these relations coexist, the optimal conditions should satisfy both equations. Therefore, a set of two formulas is proposed for obtaining the optimal signal conditions for CDT,

$$\{\begin{array}{l}[1-(a\cdot r+b)]L_1=L_2-74(a\cdot r+b)\\ r=r_0+s{(L_1-L_0)}^2\end{array}\phantom{\}},$$ (7)

where r₀=c₁L₂+d₁, s=c₂L₂+d₂, and L₀=c₃L₂+d₃. Solving both equations together, the optimal f₁ and L₁ could be determined. These formulas with parameters obtained from the data predict the optimal conditions for each subject in the study. Using f₂∕f₁ ratio as an example, the prediction accuracy is as high as 95% with an average of 73%. From Eq. 7, the calculated values of L₁ and f₂∕f₁ are well comparable with results in humans (Kummer et al., 2000; Johnson et al., 2006) and rodents (Pibal et al., 2002; Michaelis et al., 2004). Parameters used in the formulas still need to be tested and refined by large-scaled studies with wider stimulus ranges.

SUMMARY AND CONCLUSION

Amplitudes of CDT and QDT were measured within a finite L₁×L₂ space across a wide range of f₂∕f₁ ratios. For CDT, three relations are found among the optimal signal conditions: (1) L₁ should always be greater than L₂, until about 74 dB SPL where the level difference diminishes; (2) the rate of primary ΔL decrease is proportional to the f₂∕f₁ ratio; and (3) the optimal frequency ratio increases with L₁ in a nonlinear fashion. A set of two formulas is proposed to quantify the optimal signal conditions, namely, f₁ and L₁ for a given L₂. For QDT, different relations are observed: (1) maximizing one of the primary levels can optimize the QDT amplitude; (2) the ΔL decreases with the signal level, but independent of the f₂∕f₁ ratio; and (3) the optimal frequency ratio was constant at just over 1.3. An important finding is the QDT notch around the optimal ratio for CDT (1.22–1.25). Therefore, the optimal signal conditions for CDT cannot be applied to QDT. If applied cautiously to avoid system distortions, maximizing the signal level could allow for recording of robust QDT and CDT that may persistent after cochlear damages (Avan et al., 2003). The present results are consistent with the notion that DPOAEs mainly originate from the OHC nonlinearity in the overlapped region of the traveling waves. Optimizing DPOAE recordings could improve the measurement reliability and repeatability, thus allowing for more accurate estimates of cochlear function and a wider range of clinical utilities.