Abstract
Sound systems and speech technologies can benefit greatly from a deeper understanding of how the auditory system, and particularly the auditory cortex, is able to parse complex acoustic scenes into meaningful auditory objects and streams under adverse conditions. In the current work, a biologically plausible model of this process is presented, where the role of cortical mechanisms in organizing complex auditory scenes is explored. The model consists of two stages: (i) a feature analysis stage that maps the acoustic input into a multidimensional cortical representation and (ii) an integrative stage that recursively builds up expectations of how streams evolve over time and reconciles its predictions with the incoming sensory input by sorting it into different clusters. This approach yields a robust computational scheme for speaker separation under conditions of speech or music interference. The model can also emulate the archetypal streaming percepts of tonal stimuli that have long been tested in human subjects. The implications of this model are discussed with respect to the physiological correlates of streaming in the cortex as well as the role of attention and other top-down influences in guiding sound organization.
INTRODUCTION
In our daily lives, we are constantly challenged to attend to specific sound sources in the midst of competing background chatter—a phenomenon usually referred to as the cocktail party problem (Cherry, 1953). Whether at a real cocktail party, walking down a busy street, or having a conversation in a crowded coffee shop, we are constantly exposed to cluttered information emanating from multiple sources in our environment that we have to organize into meaningful percepts (Bregman, 1990). This challenge is not confined to humans. Animals too, including other mammals, birds, and fish, have to overcome similar challenges in order to navigate their complex auditory scenes, avoid predators, mate, and locate their newborns (Aubin and Jouventin, 1998; Fay, 1998; Hulse et al., 1997; Izumi, 2001).
Despite the seemingly effortless and intuitive nature of this faculty and its importance in understanding auditory perception as a whole, we still know very little about the principles that govern stream segregation in the brain, or about the neural underpinnings underlying this perceptual feat. How does the auditory system parse acoustic scenes as interferences appear sporadically over time? How does it decide which parts of the acoustic signal belong together as one coherent sound object? Tackling these questions is key to understanding the bases of active listening in the brain as well as the development of efficient and robust mathematical models which can match up to the biological performance of auditory scene analysis tasks.
To solve this problem, the auditory system must successfully accomplish the following tasks: (a) extract relevant cues from the acoustic mixture (in both monaural and binaural pathways), (b) organize the available sensory information into perceptual streams, (c) efficiently manage the biological constraints and computational resources of the system to perform this task in real time, and (d) dynamically adapt the processing parameters to successfully keep up with continuously changing environmental conditions.
Due to the significance of this question in both perceptual and engineering sciences, interest in tackling the phenomenon of auditory scene analysis has prompted multidisciplinary efforts spanning the engineering, psychology, and neuroscience communities. On one end of the spectrum, numerous studies have attempted strict engineering approaches such as the successful application of blind source separation techniques (Bell and Sejnowski, 1995; Jang and Lee, 2004; Roweis, 2000), statistical speech models (Ellis and Weiss, 2006; Kristjansson et al., 2006; Varga and Moore, 1990), and other machine learning algorithms. Despite their undeniable success, these algorithms often violate fundamental aspects of the manner humans and animals perform this task. They are generally constrained by their own mathematical formulations (e.g., assumptions of statistical independence), are mostly applicable and effective in multisensor configurations, and∕or require prior knowledge and training on the speech material or task at hand. On the other end of the spectrum are the psychoacoustic studies that have focused on the factors influencing stream segregation, and, in particular, the grouping cues that govern the simultaneous and sequential integration of sound patterns into objects emanating from a same environmental event (Bregman, 1990; Moore and Gockel, 2002). These efforts have triggered a lot of interest in constructing biologically inspired systems that can perform intelligent processing of complex sound mixtures. Models developed in this spirit offer mathematical frameworks for stream segregation based on separation at the auditory periphery (Beauvois and Meddis, 1996; Hartman and Jonhson, 1991; McCabe and Denham, 1997), or extending to more central processes such as neural and oscillatory networks (von der Malsburg and Schneider, 1986; Wang and Brown, 1999), adaptive resonance theory (Grossberg et al., 2004), statistical model estimation (Nix and Hohmann, 2007), and sound-based models (Ellis and Weiss, 2006). Despite demonstrations often restricted to relatively simple and abstract stimuli (e.g., tones and noise sequences), these implementations contributed heavily and in different ways to our current thinking of the neurobiology of scene analysis.
The present work attempts at bridging the gap between these two directions. Like the former, it provides a tractable computational framework to segregate complex signals (speech and music); but like the latter approaches, it does so in the spirit of biological plausibility. The fundamental aim of this model is to demonstrate how specific auditory cortical mechanisms can contribute to the formation of perceptual streams.1 The model operates on single (monaural) inputs. It is “behaviorally” realistic, requiring no prior training on specific sounds (voices, languages, or other databases), no assumptions of statistical independence or multiple microphones, and can segregate sounds ranging from the simple (tones and noise) to the complex (speech and music). The architecture of the model consists of two main components: (i) a feature analysis stage that explicitly represents known perceptual features in a multidimensional space, such as tonotopic frequency, harmonicity (pitch), and spectral shape and dynamics (timbre) and (ii) an integrative and clustering stage that reconciles incoming perceptual features with expectations derived from a recursive estimation of the state of the streams present in the environment. Sensory information is hence assigned to the perceptual clusters that match them best.
This paper begins with a detailed description of the model in Sec. 2. In Sec. 3, we present simulations of the performance of the model under different auditory scene configurations. We also test the contribution of the different cortical mechanisms modeled in the current study to the process of stream segregation. Finally, we end with a summary of the different aspects of the model, then a discussion of the interaction between the cortical circuitry and higher-level attentional signals, and the possible role and mechanisms of dynamic change in the auditory cortex in perceptual stream formation.
THE COMPUTATIONAL AUDITORY MODEL
The computational scheme presented here is principally based on functional models of the primary auditory cortex (A1). This work is motivated by a growing body of evidence strongly suggesting a role of the auditory cortex in processes of auditory stream formation and sound organization [see Nelken (2004) for a review]. Specifically, the present model abstracts and incorporates three critical properties of A1 physiology. (i) Multidimensional feature representation: Auditory cortical neurons are selectively sensitive to a host of acoustic features (sometimes in an ordered manner manifested as “response maps”) such as the tonotopic axis, tuning bandwidth and asymmetry maps, thresholds, fast temporal AM and FM modulations, and interaural cues (Middlebrooks et al., 1980; Schreiner, 1998). This varied sensitivity implies that sounds with different perceptual attributes may activate different neural populations, enabling them to potentially be perceived as segregated sources. (ii) Multiscale dynamics: A1 responses exhibit temporal dynamics (Kowalski et al., 1996; Miller et al., 2002) that are commensurate with time scales of stream formation and auditory grouping as well as speech syllabic rates and intonation contours, musical melodies, and many other sensory percepts (Carlyon and Shamma, 2003; Elhilali et al., 2003; Miller and Taylor, 1948; Viemeister, 1979). Furthermore, numerous studies have corroborated the involvement of the auditory cortex in the temporal organization of acoustic sequences (Colombo et al., 1996; Jerison and Neff, 1953; Kelly et al., 1996; Rauschecker, 2005). (iii) Rapidly adapting receptive fields: Physiological and imaging studies suggest that cortical receptive fields are rapidly modulated by auditory experience, behavioral context, attentional and cognitive state, expectations and memories, as well as the statistics of the stimulus (Fritz et al., 2005; Hughes et al., 2001). These findings support a view of auditory perception and scene analysis as a dynamic process mediated by an adaptive cortex that optimizes its representation of incoming sounds according to the objectives of the auditory task.
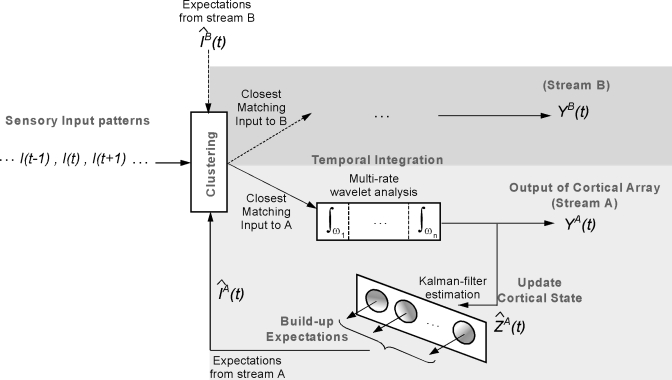
These three cortical response properties provide the key ingredients of the present model, as described in detail below and schematized in Fig. 1. While not strictly biophysical in detail, all elements of the model are nevertheless abstracted from known auditory physiological processes, perceptual phenomena, and anatomical structures.
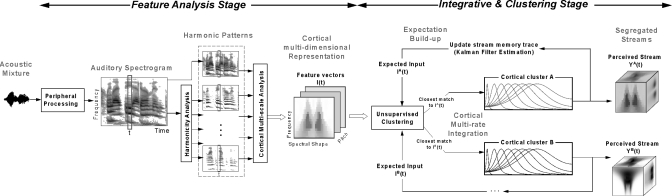
Figure 1.
Schematic of a model for auditory scene analysis. The computational model consists of two stages: a feature analysis stage, which maps the acoustic waveform into a multidimensional cortical representation, and an integrative and clustering stage, which segregates the cortical patterns into corresponding streams. The gray captions within each stage emphasize the principle outputs of the different modules. In the feature analysis stage, additional dimensions are added to the representation at each module, evolving from a 1D acoustic waveform (time) to a 2D auditory spectrogram (time-frequency) to a three-dimensional harmonicity mapping (time-frequency-pitch frequency) to a 4D multiscale cortical representation (time-frequency-pitch frequency-spectral shape). The integrative and clustering stage of the model is initiated by a clustering module which determines the stream that matches best the incoming feature vectors I(t). These vectors are then integrated by multirate cortical dynamics, which recursively update an estimate of the state of streams A and B via a Kalman-filter-based process. The cortical cluster use their current states to make a prediction of the expected inputs at time t+1: IA(t+1) and IB(t+1). The perceived streams are always available online as they evolve and take their final stable form.
The feature analysis and representation stage
The initial feature analysis stage projects the input sound onto a multidimensional perceptual space, allowing a natural segregation of the acoustic waveform along multiple dimensions, whereby different sound features occupy different areas of this space. This stage parallels the feature selectivity in neurons along the auditory pathway up to the auditory cortex, whereby a host of cells is tuned or best driven by different attributes of the acoustic signal along several dimensions (tonotopic frequency, spectral shape, etc). Our working hypothesis is that these feature maps are, in fact, a mechanism which permits the brain to “see” elements of each sound object distinctly represented, with minimal interference from the other sources, hence getting an uncontaminated “look” at features of each stream. By having a rich enough representation, different sound objects occupy different regions of the feature space, hence the emergence of “clean looks” of each individual stream. In our model, this operation is performed by mapping the sound mixture onto a succession of instantaneous clean looks based on primitive acoustic features such as onsets, harmonic relationships, or spectral shapes and bandwidths. It is important to note that these looks or patterns are extracted on an instant-by-instant basis, yielding a sequence of unlabeled feature vectors at any given instant. Only in the subsequent clustering stage of the model are they assigned to their corresponding “streams” and integrated over time.
In the current version of the model, the initial analysis stage consists of the following operations. (i) A frequency analysis that captures early auditory processing in the cochlea and midbrain nuclei (Shamma, 1998; Wang and Shamma, 1994). It transforms the acoustic stimulus to an auditory time-frequency spectrographic representation with enhanced onsets and (to a lesser extent) offsets. (ii) A harmonicity analysis which groups harmonically related components into different channels in a process consistent with the perception of pitch (Goldstein, 1973; Oxenham et al., 2004; Wightman, 1973). (iii) A multiscale spectral analysis of the auditory spectrogram, as presumed to occur in primary auditory cortex (Schreiner, 1998). It is implemented by an instantaneous affine wavelet transformation of the spectral slices of the auditory spectrogram. All parameters of these processes are consistent with physiological data in animals (Langner, 1992; Miller et al., 2002; Schreiner and Urbas, 1988) and psychoacoustical data in human subjects (Eddins and Bero, 2007; Green, 1986; Supin et al., 1999; Viemeister, 1979). In the current implementation of the model, we have left out several acoustic features that are known to aid stream segregation such as fast AM and FM modulations as well as spatial cues. They can be readily incorporated into the model by creating additional representational axes. Next, we elaborate on the implementation of each one of these operations.
Peripheral auditory processing
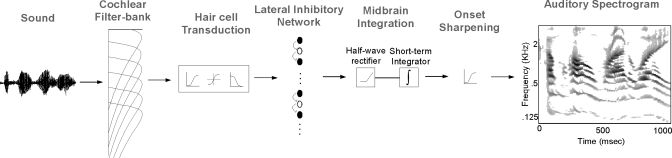
The initial stage of the model starts with a transformation of the signal from a pressure time waveform to a spatiotemporal activation pattern. It captures the basic processing taking place at the level of the auditory periphery (Pickles, 1988), including cochlear filtering, hair-cell transduction, and auditory-nerve and cochlear-nucleus spectrotemporal sharpening. Briefly, it consists of a cochlear-filter bank of 128 constant-Q highly asymmetric bandpass filters (Q=4) equally spaced on a logarithmic frequency axis x with center frequencies spanning a range of 5.3 octaves (i.e., with a resolution of 24 channels per octave). Next, a hair-cell stage transduces the cochlear-filter outputs into auditory-nerve patterns via a three-step process consisting of high-pass filtering, a nonlinear compression, and low-pass leakage, effectively limiting the temporal fluctuations below 5 kHz. Finally, a lateral inhibitory network performs a sharpening of the filter-bank frequency selectivity mimicking the role of cochlear-nucleus neurons (Sacks and Blackburn, 1991; Shamma, 1998). It is modeled as a first difference operation across the frequency channels, followed by a half-wave rectifier, and then a short-term integrator. Extensive details of the biophysical grounds, computational implementation, and perceptual relevance of this model can be found in Wang and Shamma (1994) and Yang et al. (1992).
We complement the model above with an additional onset sharpening stage to emphasize the presence of transient events in this spectrographic representation. We apply a high-pass filter (filter cutoff about 400 Hz) to the output of each frequency channel to boost the transient energy in the signal. By accentuating the representation of onsets in the spectrogram, we are reinforcing the likelihood of synchronous frequency channels to emerge as a congruent spectral segment, hence biasing them to be labeled as originating from a common source (Bregman, 1990). It is worth noting that this stage does not explicitly extract common onsets across frequency channels. Rather, the sharpening process is performed on each individual channel independently by way of contrast enhancement. An indirect consequence of this stage is that sound elements starting at the same time will emerge with an enhanced representation, increasing the likelihood of grouping them together.
Given a discrete-time signal s(t); t=0,1,…,n, the operations above compute a time-frequency activity pattern P(t,x) that represents a noise-robust (Wang and Shamma, 1994) equivalent of an acoustic spectrum, called a sharpened-onset auditory spectrogram (see Fig. 2). It not only encodes the instantaneous power in each frequency band but also captures the temporal dynamics of the spectral components falling within the bandwidth of each band, giving rise to fast “envelope modulations” of the signal. In addition, it exhibits an enhanced representation of onset cues across the entire spectrum.
Figure 2.
Peripheral auditory processing. The schematic depicts the stages of early auditory processing starting from cochlear filtering, followed by hair-cell transduction, spectral and temporal sharpening, and onset enhancement. The output of this process is an onset-enhanced time-frequency auditory spectrogram.
Harmonic analysis
Grouping of sound elements is facilitated if they bear a harmonic relationship to each other, making them easily segregated from elements with different fundamental frequencies (Moore et al., 1986). Hence, we add an explicit periodicity pitch axis to the time-frequency spectrogram P(t,x). We use a pitch extraction algorithm based on a template matching model, similar to that proposed by Goldstein (1973) and Shamma and Klein (2000).
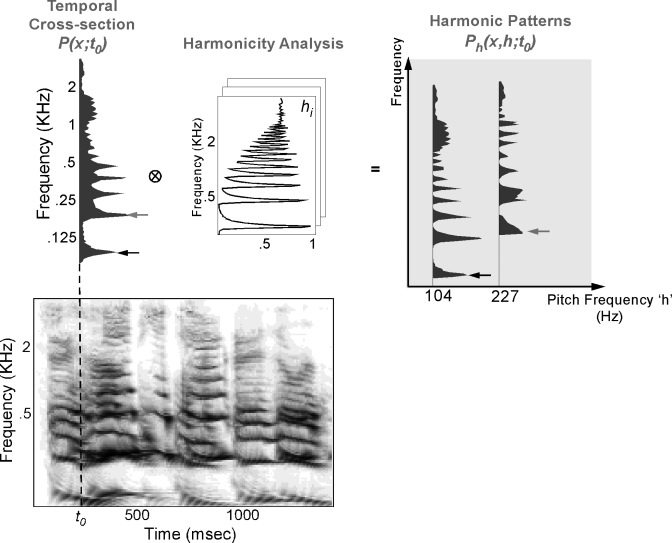
The algorithm begins by generating an array of harmonic templates at different fundamental frequencies (F0’s) following the procedure in Shamma and Klein (2000). Next, a template matching procedure is applied, essentially similar in spirit to numerous pitch matching techniques present in literature (Cohen et al., 1995; Duifhuis et al., 1982). This stage starts by comparing the input spectrum P(x;t0) at every time instant t0 with the entire array of templates using a point-by-point multiplication of the spectra (of the signal and each template for all F0 values). Based on the match between the input spectrum and the harmonic templates, we build a distribution of pitch values across the F0 (or harmonicity) axis, where the pitch strength at a given fundamental frequency F0 is based on the goodness of match (Euclidean distance) between the spectrum and the corresponding template (Fig. 3). Hence, the one-dimensional (1D) spectrum P(x;t0) yields a two-dimensional (2D) pattern Ph(x,h;t0) indexed by tonotopic frequency x (covering a range of 5.3 octave) and fundamental frequency h (covering the pitch range from 70 to 300 Hz). Additionally, we append to the pitch axis a copy of the full original spectrum P(x;t0). This serves to present evidence of the energy in the signal in the absence of any salient harmonicity cues. For instance, a fricative (such as [s]) would produce an aperiodic hissing that lacks any salient pitch estimate and, hence, is only captured by its full original profile P(x;t0).
Figure 3.
Harmonicity analysis stage. The auditory spectrogram is further analyzed to extract any harmonically related spectral channels. The lower left panel in the figure depicts a mixture of male and female utterances shown in the lower panel. At time instant t0, a temporal cross section of the spectrogram P(x;to) is extracted and processed through a template matching model. The output of this template matching is shown in the top rightmost panel and reveals that the cross section P(x;to) yields a good match with a harmonic template at 104 Hz and another one at 227 Hz, corresponding to the male and female voices, respectively, at that time instant.
While many pitch extraction algorithms have been successfully applied in sound segregation schemes, we particularly chose the template matching technique for two main reasons. First, the template model is assumption-free as to the nature∕number of pitches present in the signal and allows us to extract harmonic structures at any given time instant, without performing a pitch tracking over time or without an explicit representation of pitch. Second, models of template matching have been argued to be plausible biological mechanisms for periodicity pitch (Cohen et al., 1995). Work by Shamma and Klein (2000) suggested a biologically inspired model for the formation of harmonic templates in the early stages of the auditory system based on the phase-locking properties of cochlear filters. Their model explains how harmonic templates can emerge in the peripheral auditory system from a simple coincidence detection network operating across cochlear channels.
Though quite successful in yielding proper pitch estimates of various spectral patterns, the template matching method has been criticized for its lack of robustness and particularly for introducing additional estimates at octave or subharmonic intervals of the fundamental frequency. These additional estimates are not a real concern for our current scene analysis model. As shall be discussed later in the description of our algorithm, the sound segregation is performed based on a best match to the estimate of the sound source, irrespective of the presence of redundant information about a source.
Cortical processing
Following this peripheral stage, the model proceeds to a finer analysis of the time-frequency patterns Ph(x,t,h), mimicking processing of central auditory stages (particularly the primary auditory cortex). This analysis is strongly inspired by extensive physiological and psychophysical experiments carried over the past two decades. Our current understanding of cortical processing reveals that cortical units exhibit a wide variety of receptive field profiles (Kowalski et al., 1996; Miller et al., 2002; Elhilali et al., 2007). These response fields, also called spectrotemporal receptive fields (STRFs), represent a time-frequency transfer function of each neuron, hence capturing the specific sound features that selectively drive the cell best. Functionally, such rich variety implies that each STRF acts as a selective filter specific to a range of spectral resolutions (or scales) and tuned to a limited range of temporal modulations (or rates), covering the broad span of psychoacoustically observed modulation sensitivities in humans and animals (Eddins and Bero, 2007; Green, 1986; Viemeister, 1979). In the current model, we break down this analysis into a spectral mapping and a temporal analysis. The spectral shape analysis is considered to be part of the feature analysis stage of the model, as it further maps the sound patterns into a spectral shape axis (organized from narrow to broad spectral features). On the other hand, the temporal cortical analysis spans two primary ranges: slow (<30 Hz) and fast (>30 Hz). The slow dynamics refer to the typical range of phase-locking rates in the cortical responses and are correlated with a host of perceptual phenomena as we review below. In the model, these dynamics come into play in the next integrative and clustering stage. Fast dynamics arise from the selective sensitivity and encoding of rapid rates of AM and FM stimulus modulations in cortical and precortical responses (>30 Hz) (Chi et al., 2005; Langner, 1992). This feature is not included in the current version of the model.
Spectral shape analysis. Based on the premise that spectral shape is an effective physical correlate of the percept of timbre, we perform a spectral analysis of each spectral pattern extracted in the earlier stages. This multiscale analysis is performed by a wavelet decomposition, where each cross section from the auditory spectrogram Ph(x,t,h) (at a given time instant t and harmonic profile h) is processed via a bank of analysis filters SΩ≜{GS(x,Ω)}:
| (1) |
where ∗x is convolution with respect to the tonotopic axis x. The filter GS(⋅) is a complex-valued spectral “impulse response,” implemented as a Gabor-like mother wavelet that is parametrized by its most sensitive spectral modulation (Ω), spanning the range [1∕8,1∕4,1∕2,1,2,4,8] cycles∕octave, and defined as
| (2) |
where gs(⋅) and form a Hilbert transform pair. By defining the filters as complex valued, we are efficiently conjoining arrays of filters with the same magnitude responses and varying phase responses. This same analysis can be reformulated in real space R by unwrapping the functions gs(⋅) along all possible phases between 0 and 2π. Further details on the filter design can be found in Chi et al. (2005) and Wang and Shamma (1995).
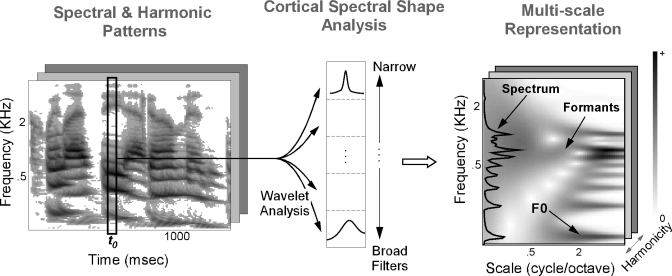
This spectral decomposition offers an insight into the timbre components of each of the acoustic features extracted so far (Fig. 4). The local and global spectral shapes in the acoustic patterns are captured via a bank of spectral modulation filters tuned at different scales (1∕8–8 cycles∕octave). On the one hand, the coarsest modulation scales capture the general trend in the spectrum, hence highlighting its broad spectral attributes, such as speech formants. On the other hand, the high-order scale coefficients describe the denser spectral patterns corresponding to features with higher spectral density, such as harmonic peaks. Unlike the cepstral analysis commonly used in speech recognition systems (O’Shaughnessy, 2000), the multiscale model operates locally along the tonotopic frequency axis.
Figure 4.
Cortical spectral shape analysis. Each spectral slice is further analyzed via a multiresolution wavelet analysis. The multiscale mapping highlights various features of the original spectrum, namely, the fundamental frequency F0 and its harmonic partials as well as its formant peaks (particularly the second and third formant frequencies F2 and F3).
The integrative and clustering stage
The second integrative and clustering stage induces stream segregation by reconciling incoming sensory information with gradually formed expectations (Fig. 1). The model builds on the cortical representation described in Sec. 2A3 as an infrastructure to map the incoming signal into a multidimensional space where features arising from different sound sources distribute into areas of activity with minimal overlap. It effectively allows the system to capture clean looks of the different streams present in the environment by mapping the cluttered sound mixtures onto a multitude of perceptually relevant dimensions. Using these activation patterns, the next critical stage of the model is to integrate these incoming looks and set up computational rules to cluster them by labeling them according to the different streams present in the scene. These rules (or schemas) come into play to govern how sound elements are assigned to their corresponding perceptual objects and integrated to form coherent segregated streams.
This integration process postulates that clusters of A1 neurons with typical multiscale dynamics of 2–30 Hz (Miller et al., 2002) integrate their sensory inputs to maintain a form of a working memory representation. This memory trace is used to build expectations of how a stream evolves over time and makes predictions about what is expected at the next time instant. By reconciling these expectations with the actual incoming sensory cues, the system is able to assign incoming features to the perceptual group that matches them best (Nix and Hohmann, 2007). Specifically, the integrative stage consists of different cortical clusters (two clusters in the current model), both governed by a recursive Markovian process which (i) integrates the input of each cortical array with dynamics typical of time constants of A1, (ii) uses a Kalman-filter-based estimation to track the evolution of each array∕stream over time, and (iii) utilizes the recent auditory experience to infer what each cluster expects to “hear” next. The computation of these different operations is detailed next and schematized in Fig. 5.
Figure 5.
Architecture of the feature integration and clustering processes. The schematic illustrates the various stages involved in segregated the acoustic patterns represented in the feature analysis stage. The incoming sensory inputs I(t) are compared to predicted patterns and . The features which are most consistent with are “passed through” the stream A branch into a cortical integrative array. This neural cluster plays a dual role: it accumulates the information and outputs a representation of stream A (YA(t)) and it uses the available information (I(t),Y(t)) to update the current memory trace of stream A via a Kalman-filter estimation. This information is in turn used to build an expectation about the next input , hence closing the feedback loop. The upper (yellow) panel indicates that a similar process takes place over a second cortical cluster (B), which tracks the evolution of another stream in the environment.
Temporal dynamics and integration. The integrative stage of the model is initiated by a temporal analysis which integrates sensory information over time in a process mimicking functional cortical models. Specifically, A1 neurons exhibit selectivity to various temporal dynamics present in the acoustic input. The temporal features of sound vary over multiple time scales ranging from sharp transitions to very slowly evolving patterns. The encoding of these temporal dynamics (at least at the level of primary auditory cortex) appears to be achieved through richly diverse networks of neurons whose STRFs vary from rapidly decaying responses to more sluggish types. The collection of all such neurons extends over a broad span of psychophysically observed temporal modulation sensitivities in both humans and animals, covering the range 2–30 Hz (Dau et al., 1996; Drullman, 1995; Green, 1986; Viemeister, 1979).
Mathematically, we capture this temporal analysis via a wavelet decomposition through a bank of complex-valued filters Rω≜{GT(t,ω)}:
| (3) |
where ∗t is convolution with respect to the time axis t. The filter GT(⋅) is based on a gamma function parametrized by the temporal modulation (ω) which take the values [2,4,8,16,32] Hz and is defined as
| (4) |
The use of complex valued instead of real filters is motivated by the same efficient implementation as described for the spectral filters GS(⋅). Further details about the design and temporal filtering procedure can be found in Chi et al. (2005).
Inference and clustering. Apropos of the clustering stage, we focus on inference schemas to regulate the pattern segregation process. Inference principles are generic rules that effectively bias the system to parse the acoustic scene based on its recent acoustic experiences and contextual expectations (Barlow, 1994; Humphrey, 1992). Specifically, the model uses its recent experience with sources in the environment to infer what it expects to hear at the next time instant. If that expectation is matched with physical acoustic cues, then the cues are assigned to that corresponding sound object. If not, they are flagged as a different perceptual object. These processes capture the dynamic nature of auditory scene analysis, whereby information about a specific object builds up and accumulates over time to segregate it from competing information generated by other streams in the environment. In addition, they are applicable to all domains of sounds covering speech, music, environmental sounds, etc. They are generally supplemented by additional cognitive mechanisms that involve even higher-level processes such as linguistic knowledge, sound familiarity, as well as attentive and memory-based schemas [see Bregman (1990) and references therein]. These latter effects are outside the scope of the current model and shall not be discussed in the present study.
Mathematically, we implement the inference-based processes by reformulating the cortical temporal analysis to allow each perceptual stream to be temporally tracked by a different family of neurons R+ representing an array of rate-selective units (Rω) so that R+={Rω}, where ω∊[2–30] Hz. The superscript “+” refers to the different perceptual objects being represented in the model, the number of which needs to be fixed ahead of time. In the current version of the model, we limit that number to two sources, i.e., implementing two neural populations R1 and R2. These neural arrays capture the dynamics of two streams, phenomenologically representing foreground and background streams. Computationally, the segregation model now proceeds as a three-step feedback-loop system involving the following.
-
1.
Estimation process: Each rate-selective array R+ acts as a system of memory units whose internal states capture the recent history of the acoustic object it represents. By updating these internal states over time, we can track the temporal evolution of the streams and maintain a working memory representation of the object at the level of the cortical network R. This operation is carried out by formulating the temporal analysis in Eq. 3 as an autoregressive moving average (ARMA) model (Oppenheim and Shafer, 1999; Proakis and Manolakis, 1992), which can be easily mapped into state-space form by introducing a latent variable representing the internal state (or explicit memory register).
-
2.
Prediction process: The memory units for each sound stream are used to build an expectation of what the stream family R+ expects to hear in the next time instant (t0+1) given the auditory experience acquired up to time t0. The states of this dynamic system are recursively predicted using a Kalman filter (Chui and Chen, 1999; Welch and Bishop, 2001).
-
3.
Clustering process: The predicted and actual I(t0+1) incoming cues are compared in order to assign the input patterns to their corresponding clusters based on the best match between the actual and predicted features. This implementation of a best-match clustering uses a simple Euclidean distance measure to contrast the incoming features with the predicted states from stage 2 and assign the clusters (or streams) based on the smallest distance to the cluster centroids.
The specific implementation of each stage is detailed in the Appendix0. A schematic describing the interaction between the three processes described above is given in Fig. 5.
RESULTS
To demonstrate the effectiveness of the model, we first test some of the classic paradigms widely used in perceptual studies of scene analysis (Bregman, 1990) so as to explain the role played by the different modules of the model in sound segregation. We then show simulations of the model using natural speech-on-music, speech-on-speech, and vocoded speech mixtures. All tone and speech simulations employ the same model configuration without changes or tuning of parameters across different stimuli. Finally, we test the contribution of the different model components to its performance and establish the relationship between cortical mechanisms and the process of stream segregation.
Organization of tone sequences
Stream segregation is strongly influenced by the rhythm and frequency separation between sound tokens. One of the simplest and most compelling demonstrations of auditory streaming involves sequences of alternating tones presented at different rates and frequency separations. It consists of two alternating tones; a high “A” note and a low “B” note. Such sequence is usually perceived as one stream when it is played at slow rates (<2 Hz) or with small frequency separations (approximately <1∕6 octave) (van Noorden, 1975). However, at larger separations and higher rates, the sequence perceptually splits into two simultaneous auditory streams.
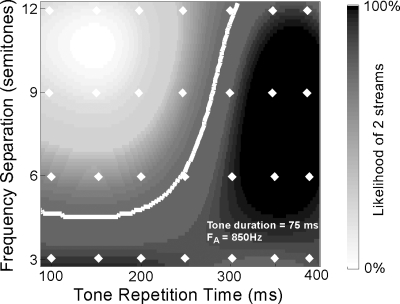
We explore the model’s ability to mimic human perception as we vary these two critical parameters (frequency separation between the two notes ΔFAB and tone repetition time ΔT). The simulation consisted of 10 s long sequences of alternating two tones. The low note was fixed at 850 Hz, and the frequency separation between the high and low notes was varied over the range [3, 6, 9, 12] semitones. Each tone in the sequence was 75 ms long and the separation onset to onset between tones A and B was varied systematically over [100,150,200,300,400] ms. The simulation was repeated 25 times for each sequence without changing the parameters of the model. Due to the inherent variability in the noise terms of the Kalman-filter prediction, the outcome of the simulation can vary if the clustering process is not strongly biased to segregate one way or another. Each simulation can yield either a “two-stream” outcome (i.e., each note sequence segregating into a separate cluster) or a “one-stream” outcome (i.e., both notes labeled as belonging to one cluster). We tallied the simulation outcomes across all 25 repetitions and computed the average predicted likelihood of perceiving two streams for all ΔF and ΔT values. Figure 6 depicts the average segregation results across trials. The simulations show that sequences are more likely to segregate if the frequency separation is above four semitones repeating at a rate of about 3 Hz or more. Note that the “perceptual segregation boundary” (shown as a white contour representing a threshold value of 25% in Fig. 6) qualitatively replicates the shape of this boundary measured in human subjects (van Noorden, 1975). The exact location of this boundary, however, can be readily shifted downward or sideways to match human or animal performance. For instance, by sharpening further the bandwidth of the frequency analysis, we can shift the boundary downward, thus increasing the likelihood of perceiving two streams at smaller ΔFAB’s. Similarly, by increasing sensitivity to faster temporal modulations, we can shift the boundary to the left, thus enabling the model to track the alternating tones hence decreasing the likelihood of perceiving two separate streams (as shall be shown in detail in a later section of the results).
Figure 6.
Induction of streaming with alternating two tone sequences. The model’s segregation of alternating two-tone sequences is tested with different stimulus parameters and averaged across 25 repetitions. The frequency separation and tone repetition time values tested are shown with the white diamond-shaped points. The surface shown in the figure is an interpolation of the results from these points using a cubic 2D interpolation. The white contour represents a contour of 25% to indicate a potential coherence boundary. The low tone in the sequence was fixed at 850 Hz, while the high note was placed3, 6, 9, 12 semitones higher. Each tone was 75 ms long.
In our simulations of the alternating tone sequences, the emergence of the different streams occurs rather rapidly, sometimes within one or two presentations of each tone. In many circumstances, it is reported that buildup of streaming can range from a few hundreds of milliseconds to several seconds (Anstis and Saida, 1985; Bregman, 1978). To reproduce these time scales, it is necessary to incorporate more biological realism to the cortical processing stage via simple adaptation processes or synaptic depression mechanisms known to operate at the level of thalamocortical projections [see Elhilali et al. (2004) for details]. Habituation of A1 responses over time has been postulated as a possible neural mechanism responsible for the observed perceptual buildup of streaming (Micheyl et al., 2005).
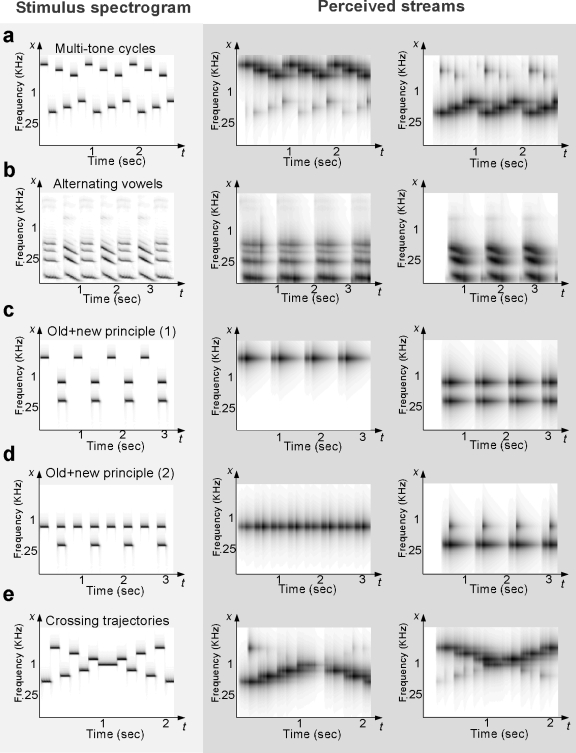
The role of frequency separation in scene analysis can be further demonstrated by a sequence of alternating multitone cycles [Fig. 7a] which consists of interleaved high (H1, H2, H3) and low (L1, L2, L3) notes, constructing a sequence H1, L1, H2, L2, H3, L3,… (Bregman and Ahad, 1990). The high frequencies were fixed at 2500, 2000, and 1600 Hz and the low frequencies were 350, 430, and 550 Hz. When the tones are played at a fast repetition rate (e.g., 4–5 Hz), the sequence is perceived as two segregated streams of high and low melodies, as depicted in the gray panels of Fig. 7a. The model’s account of this percept originates in the distribution of receptive field bandwidths (along the multiscale spectral analysis axis) which range from the very narrow (<1∕10 octave) to the broad (>2 octaves) with an average bandwidth of about 1∕6 octave. Humans are most sensitive to patterns with peak spacings of this order (Eddins and Bero, 2007; Green, 1986). Consequently, when the alternating tones are closely spaced, only a minority of receptive fields can resolve them into two streams. On other hand, when tones are well separated, two classes of receptive fields are differentially activated by each tone hence easily segregating them into two clusters. Similarly, the dependence of streaming on tone presentation rates reflects the dominant neuronal dynamics of the auditory cortex, as represented by the multiple time constants governing the cortical integration in the model. At very slow rates, integrators cannot sustain their memory (and hence, their expectations) for sufficiently long times to influence the input, hence biasing the system to label it as a single stream. At faster rates (commensurate with cortical time constants), expectations are fed back, causing spectrally resolved incoming tones to cluster into two streams.
Figure 7.
Model simulations of “classic” auditory scene analysis demonstrations. The left column of panels shows the acoustic stimuli fed to the model. The middle and right columns depict the results of the stream segregation process, which are defined as the time-frequency marginal obtained by integrating the time-frequency activity across the entire neural population (scale and rate filters) representing each cluster. (a) Multitone cycles: The stimulus consists of alternating a high sequence of 2500, 2000, and 1600 Hz notes and a low sequence of 350, 430, and 550 Hz (Bregman and Ahad, 1990). The frequency separation between the two sequences induces a perceptual split into two streams (middle and right panels). (b) Alternating vowels: Two natural ∕e∕ and ∕ə∕ vowels are presented in an alternating sequence at a rate of roughly 2 Hz. The vowels are produced by a male speaker with an average pitch of 110 Hz. Timbre differences (or different spectral shapes) cause the vowel outputs to segregate into separate streams. (c) Old+new principle (1): An alternating sequence of a high A note (1800 Hz) and BC complex (650 and 300 Hz) is presented to the model. The tone complex BC is strongly glued together by virtue of common onset cues, and hence segregates from the A sequence which activates a separate frequency region. (d) Old+new principle (2): The same design as in simulation (c) is tested again with a new note A frequency at 650 Hz. Since tones A and B activated the same frequency channel, they are now grouped as a perceptual stream separate from stream C (gray panels), following the continuity principle. (e) Crossing trajectories: A rising sequence (from 400 to 1600 Hz in seven equal log-frequency steps) is interleaved with a falling sequence of similar note values in reverse (Bregman and Ahad, 1990).
Timbre-based segregation
Stream segregation in general can be induced between sound sequences that differ sufficiently along any feature dimension in the cortical representation, including different distributions along the spectral analysis axis (timbre), harmonicity axis (pitch), and other axes not included in the current model such as location cues and fast modulation rates (Grimault et al., 2002; Shinn-Cunningham, 2005). Figure 7b illustrates the streaming of the two alternating natural vowels ∕e∕ and ∕ə∕, each repeating roughly twice per second (i.e., about 2 Hz). Although they have the same pitch (110 Hz) and occupy roughly the same frequency region, the vowels are perceived as two segregated streams because their cortical representations are sufficiently distinct along the multiscale spectral analysis axis. A detailed discussion of the sequential organization of vowels (similar to those tested here) as well as other speech sounds can be found in Bregman (1990), Chap. 6.
Old-plus-new heuristic
Implicit in the notion of a stream is a sequence of sounds that share consistent or smoothly varying properties. To this effect, sounds with drastically different features violate expectations built up over time for the ongoing streams and are hence assigned to new streams. This is consistent with the well-known old-plus-new principle, stating that “If part of a sound can be interpreted as being a continuation of an earlier sound, then it should be” (Bregman, 1990). Figures 7c, 7d offer a simple illustration of this principle. In Fig. 7c, an alternating sequence of A tones and a two-tone complex (B and C) are perceived as two separate streams (Bregman and Pinker, 1978) because tones B and C are strongly grouped by this common onset and are sufficiently separated from the A tone in frequency (1800 Hz versus 650 and 300 Hz). When tones A and B are equal in frequency [Fig. 7d], a continuity is created that combines these tones into a single stream and breaks the previous grouping of B and C (Bregman and Pinker, 1978). Instead, tone C is now perceived as the “new” evidence, against the “old” continuing stream of the A and B tones.
Another striking illustration of this “continuation” principle is the crossing trajectories paradigm depicted in Fig. 7e (Tougas and Bregman, 1985). When rising and falling tone sequences are interleaved, subjects are unable to follow the patterns of notes in each sequence. Instead, they report hearing a bouncing percept of two streams, as depicted in the gray panels of Fig. 7e, presumably caused by the expectations of two separate (high and low) streams built up prior to the crossing point, and which are maintained (by continuity) after it.
Segregation of speech sounds
Parsing complex sound mixtures of speech and∕or music exploits the same principles described for tone sequences. In both, basic acoustic features are used to extract “clean” looks from the mixture, which are then parsed into separate streams based on their consistency with built-up expectations. In the earlier tone sequence examples, clean features were readily available since the tones were sequentially presented. With speech mixtures, clean looks of one speaker or another are principally derived when components from one speaker (i) share a common onset and hence are enhanced together, (ii) are harmonically related and differ in pitch from the other speaker, and (iii) appear in the gaps within the simultaneous speech of another speaker, hence providing opportunities to sneak clean looks of one of the speakers.
We tested the model’s effectiveness in segregating randomly selected and mixed pairs of speech utterances from the TIMIT speech database. Given that our approach does not allow any language-based grammars or speaker-specific information to shape the segregation process, we are in effect testing the ability of the model to track and segregate a given voice based on consistent timbre properties or smooth evolution of its harmonics. To evaluate the results of the model, we compared how closely the segregated streams matched the original unmixed signals as quantified by the correlation coefficient between the original and segregated cortical representations. This measure computes a direct linear correlation at zero lag between the two vectors representing the cortical tensors of clusters A and B. Other suitable metrics that yield comparable results include the signal-to-noise ratio (SNR) (between the energy in the original spectrogram and the difference between the original and segregated spectrograms) or the improvement in intelligibility measured by the spectrotemporal intelligibility index (Elhilali et al., 2003). These measures yielded qualitatively equivalent results to those obtained from the correlation coefficient. Samples of reconstructed segregated sentences can be heard at http:∕∕www.isr.umd.edu∕∼mounya∕CPP∕speech_simulations.htm. They were synthesized by inverting the streamed multidimensional representations using a convex-projection algorithm (Chi et al., 2005).
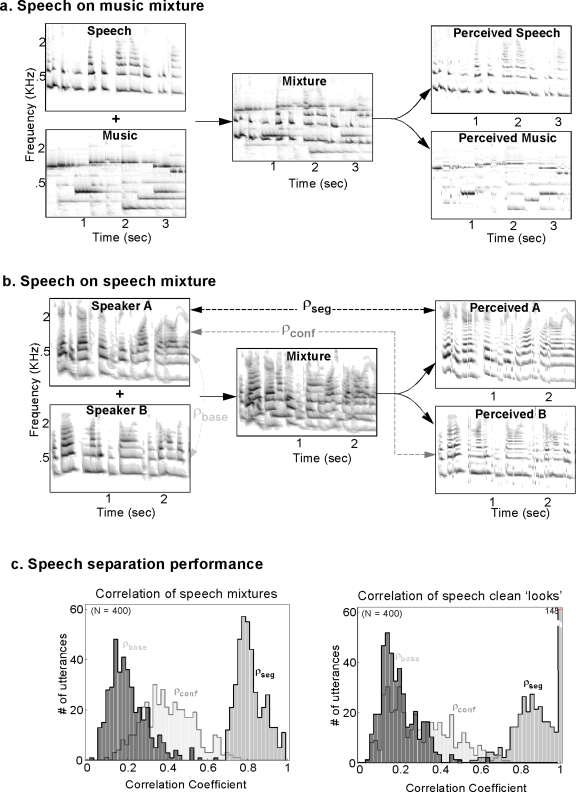
Examples of segregating speech from music and mixtures of two simultaneous speakers are shown in Figs. 8a, 8b, respectively. In both cases, the segregated spectrograms resemble the original versions and differ substantially from the mixed signal. We quantified the apparent improvement in the case of the speech-on-speech-mixtures by computing the correlation coefficients from 400 speech mixtures from both genders, as shown in Fig. 8c. For each pairwise mixture, we computed the similarity between (i) the original and segregated samples (ρseg, segregation correlations), (ii) the two original samples (ρbase, baseline correlations), and (iii) the segregated samples against the original competing signal (ρconf, confusion correlations). The histograms demonstrate that segregation occurs with an accuracy of ρseg=0.81, which is substantially higher than the “confusability” baseline, indicated by ρconf=0.4 and ρbase=0.2, hence demonstrating the efficacy of the segregation of the speech signals into different streams.
Figure 8.
Model performance with real speech mixtures. (a) Speech-on-music mixtures: Left panels depict spectrograms of a male utterance and a piano melody. The mixture of these two waveforms is shown in the middle. Model outputs segregate the two sources into two streams that resemble the original clean spectrograms (derived as time-frequency marginals similar to Fig. 7). (b) Speech-on-speech mixtures: Male and female speech are mixed and fed into the model, which segregates them into two streams. To evaluate performance, correlation coefficients (ρ) are computed as indicators of the match between the original and recovered spectrograms: ρseg measures the similarity between the original and streamed speech of the same speaker. ρbase measures the (baseline) similarity between the two original speakers. ρconf measures the confusions between an original speaker and the other competing speaker. (c) Speech segregation performance is evaluated by the distribution of the three correlation coefficients. Left panel illustrates that the average values of ρseg=0.81 are well above those of ρconf=0.4 and ρbase=0.2, indicating that the segregated streams match the originals reasonably well, but that some interference remains. Right panel illustrates results from the model bypassing the harmonic analysis stage (see text for details). The improved separation between the distributions demonstrates the remarkable effectiveness of the integrative and clustering stage of the model when harmonic interference is completely removed (distribution means ρseg=0.9, ρconf=0.3, and ρbase=0.2).
Finally, to assess more clearly the role of the integrative stage in sorting and clustering its inputs, we sought to remove the errors introduced by imperfect harmonic analysis of the mixed inputs and hence test the performance of the remaining stages in model. To do so, we assumed a “perfect” harmonic analysis module that can fully separate each frame of mixed speakers into its two original unmixed frames. Specifically, we simply bypassed the harmonic analysis by supplying the original unmixed (unlabeled, onset enhanced, and multiscale analyzed) pairs of spectral cross sections of the speech signals and determined the performance of the integrative stage in sorting and clustering the patterns into two streams. As expected, the resulting segregation [indicated by the correlation coefficients in Fig. 8c, right panel] is slightly better: ρseg=0.9, ρconf=0.3, and ρbase=0.2. This improvement is due to the cleaner separation between the overlapping harmonic complexes and unvoiced speech phonemes that cannot be segregated by the harmonic analysis module (as simulated in the section above), which ultimately causes a feedthrough between the target and competing streams, hence increasing the confusion correlation ρconf. Consequently, the quality of the reconstructed segregated speech in this case is noticeably better than the quality obtained from the segregation of the “true” mixtures.
Segregation of mixtures of vocoded speech
We extend the testing of the model by exploring conditions that would not normally induce streaming, hence mimicking human failure at segregating certain sound mixtures. We used simulations of cochlear-implant processing to explore the model’s performance of impoverished speech-on-speech mixtures. It is well known that hearing-impaired listeners experience great difficult perceiving speech in noisy conditions (Festen and Plomp, 1990; Peters et al., 1998). Recent work by Qin and Oxenham (2003) explored this phenomenon using implant simulations and showed that fluctuating masker backgrounds (including concurrent speakers) greatly degrade normal-hearing listeners’ ability to segregate and perceive vocoded speech. We used a similar procedure as in the Qin and Oxenham (2003) study to simulate a vocoder channel. Specifically, each speech utterance (taken from the TIMIT database) was filtered into 24 contiguous frequency bands, equally spaced on an equivalent rectangular bandwidth (ERB) scale between 80 and 6000 Hz. The envelope output of each band was used to modulate narrow-band noise carriers, hence creating a vocoded speech signal with minimal spectral cues and no temporal fine-structure information [see Qin and Oxenham (2003) for details].
We simulated the effect of implant processing on 25 male utterances, each contaminated by a randomly chosen sentence spoken by a female speaker and added at 0 dB SNR. The sentences were processed through the vocoder described above and presented to the model. We quantified the model’s performance in a similar fashion, as described in Fig. 8, by calculating a ρseg, ρconf, and ρbase for each pair of sentences. Our results show that a 24-channel simulation yields average values of ρseg=0.63, ρconf=0.58, and ρbase=0.2, indicating a worse segregation performance (lower ρseg value) and an increased confusion with the concurrent utterance (higher ρconf). Just like in Qin and Oxenham (2003), the impoverished spectral resolution in the implant simulation as well as lack of temporal fine structure and pitch cues is largely responsible for the poor segregation between concurrent utterances at the level of the cortical representation. This in turn affects the subsequent integration and clustering stage where features from different sources are confused as belonging to the same cluster, and hence the poor model segregation mimicking listeners’ experiences in these conditions.
Testing the model’s components
The model’s aim is to demonstrate how specific auditory cortical mechanisms contribute to the process of scene analysis and formation of perceptual streams. The processes of particular interest here are the multiscale analysis, the cortical dynamics, and the adaptive nature of cortical processing. In order to explore the role of the first two components in perception of complex auditory scenes and demonstrate their contribution to the model’s performance, we modified the structure of the model for testing purposes, as shall be shown next. The third component (namely, the expectation process) is hard to modify or omit since it constitutes the core of the integration and clustering operation. The additional transformations in the model (e.g., harmonicity analysis, onset enhancement, etc.) clearly contribute to solving the stream segregation problem (as shown by the vocoded speech simulation, for instance). In this section, we solely focus on the contribution of the first two cortical mechanisms to sound segregation.
Multiscale analysis
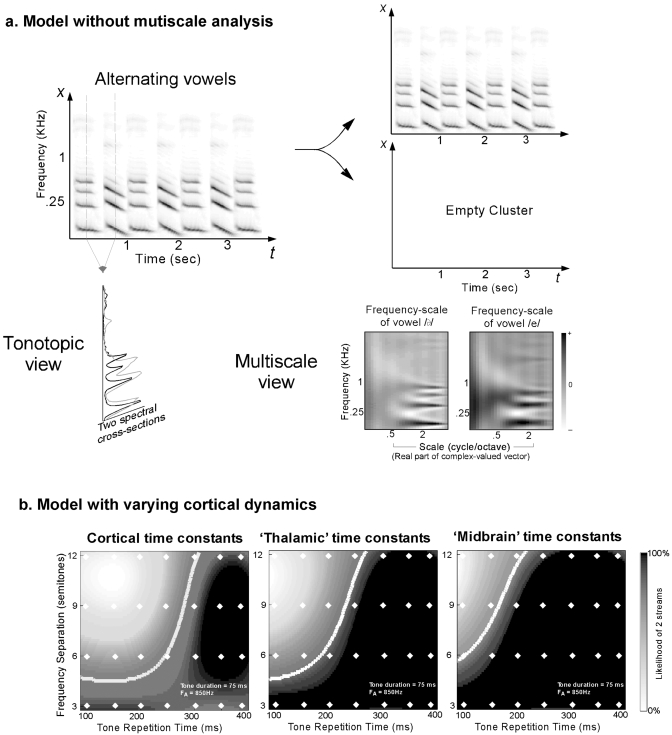
We remove the multiscale analysis stage and basically perform the clustering operation directly on the harmonic patterns extracted from the auditory spectrogram (Ph(x,t,h)). The goal of this exercise is to explore how the model’s performance would deteriorate in the absence of the spectral pattern analysis. The other stages of the model remained unchanged, with the exception that, now, the integrative and clustering stage takes—as input—a time-frequency-pitch representation as opposed to a four-dimensional (4D) tensor. In the biological system, this modification of the model would be equivalent to bypassing the spectral analysis performed at the level of auditory cortex and confining the system to a spectral decomposition performed in precortical nuclei.
We argued earlier that the contribution of the cortical spectral analysis is to map different spectral patterns into different regions of the multiscale axis. For instance, vowels with different spectral profiles will excite different filters and hence segregate along this axis, even though they might occupy the same frequency region and share a common harmonic structure. In the absence of this spectral analysis, the model has to rely on the segregation resulting from the cochlear analysis as well as the harmonicity mapping, making it blind to any difference in timbre structure between different streams. We test this model stripped of its multiscale analysis on the alternating vowel example shown in Fig. 7b. Figure 9a shows the results of this incomplete model. As expected, the vowels ∕e∕ and ∕ə∕ produced by the same speaker share a common pitch of about 110 Hz and occupy roughly the same spectral region. Therefore, the model has no evidence to segregate them and to group them into one stream. Using the tonotopic axis alone, the two vowels overlap greatly [lower left panel of Fig. 9a]. In contrast, the multiscale analysis reveals the different timbre structures arising from the two vowels [lower right panels of Fig. 9a]. This simulation clearly demonstrates an example of the role of multiscale spectral analysis in discerning timbres of complex sounds and strengthens the claim that the topographic organization of mammalian auditory cortex with neurons of different spectral resolutions and sensitivities (orthogonal to its tonotopic organization) does indeed underlie the system’s ability to distinguish between natural sounds of distinct timbres (e.g., speech) (Sutter, 2005).
Figure 9.
Model performance after modification of parameters. (a) Omitting the multiscale analysis: The model (without the scale analysis) is simulated using alternating vowels ∕e∕ and ∕ə∕ [shown in Fig. 7b]. A time-frequency spectrogram is presented to the incomplete model and leads to the entire stream being grouped as one cluster (shown above) and an empty second cluster. The two top rightmost panels depict the time-frequency marginals reflecting the energy in each cluster. Below: A tonotopic view of the two vowels (obtained from two cross sections of the spectrogram at different time instances) reveals a great overlap in the spectral region occupied by both phonemes. The right panels show a multiscale view of both phonemes and reveal the different timbre structures that emerge from the multiple scale filters. (b) Varying the cortical dynamics: The three panels show results of segregation of alternating two tones with varying dynamic ranges for the cortical filters. The white contours are all boundaries reflecting a 25% threshold of streaming. The leftmost panel is a replica of Fig. 6.
Cortical dynamic
We stipulate in the current model that cortical time constants play a role in the process of auditory scene organization by facilitating the tracking of sound streams over the course of few to tens of hertz. To test this hypothesis, we modified the range of cortical time constants implemented in the model by adjusting the parameters of the temporal filters (shown in Fig. 1 as cortical clusters A and B). The full architecture of the model remains unchanged, except that now the integrative and clustering stage operates according to three possible modes: (1) a normal cortical mode with five filters spread over the range 2(1,2,3,4,5) Hz (exactly the same simulation as in Sec. 3A), (2) thalamiclike dynamics where we also use five filters distributed over the range 2(4,4.5,5,5.5,6) Hz (Miller et al., 2002), and (3) midbrainlike dynamics with five filters spanning the range 2(5,5.5,6,6.5,7) Hz (Miller et al., 2002). In all three cases, we fixed the number of temporal filters to 5 in order to maintain a fair comparison between all three modes of operation. We only varied the dynamic range of the filters’ tuning.
We tested the model under all three conditions on the classic alternating two-tone sequence with varying frequency separation ΔF and tone repetition time ΔT (similar to that described in Sec. 3A). As expected, the boundary (representing a threshold value of 25%) shifts to the left indicating that the model becomes sensitive to faster repetition rates and is able to track streams repeating at faster rates, hence following the tones in both frequency channels and grouping them as one stream [Fig. 9b]. The leftmost panel is an identical replica of Fig. 6 and is shown to contrast the changing boundary as a result of the change in the dynamics of the model. As the simulations show, the model’s ability to track streams of separate tonal frequencies is dictated by the clock which paces the cortical integrative stage, which can be made faster or slower. The segregation boundary [shown in Fig. 8b] is in agreement with human behavioral data only for the “cortical-like” time constants (leftmost panel), hence corroborating our claim of the involvement of cortical-like integrative processes in the organization of auditory scenes and formation of perceptual streams.
DISCUSSION
In summary, we have demonstrated that a computational model of cortical auditory processing consisting of a multidimensional feature representation stage followed by an integrative clustering stage can successfully tackle aspects of the “cocktail party problem” and provide an account of the perceptual process of stream formation in auditory scene analysis. The model directly tested the premise that cortical mechanisms play a fundamental role in organizing sound features into auditory objects by (1) mapping the acoustic scene into a multidimensional feature space and (2) using the spectral and temporal context to direct sensory information into corresponding perceptual streams. Key to this organizational role are the multiple time scales typically observed in cortical responses, as well as an internal representation of recent memory that allows the smooth evolution of streams over time.
A powerful aspect of our formulation is its real-time capability because the model forms auditory streams as it receives its input data, requiring no prior training on a specific speech corpus or early exposure to a set of voices, sound categories, and patterns. As shown in Sec. 3, such an adaptive cortical scheme can successfully simulate stimulus configurations typically tested in auditory scene analysis studies. Furthermore, it makes use of a variety of instantaneous and sequential grouping mechanisms that are postulated to play a pivotal role in streaming, thus demonstrating that these principles can be effectively generalized to parse complex stimuli such as real speech mixtures.
The current implementation of the model can be readily extended to include other perceptual features known to play a role in sound separation. For instance, the spatial location of sound sources influences their streaming (Wittkop and Hohmann, 2003). Adding this perceptual attribute to the model entails augmenting the cortical multidimensional representation with a spatial dimension whose responses are computed from midbrainlike processing of binaural cues, e.g., extraction of interaural-time and interaural-level differences in the medial superior olive (MSO) and lateral superior olive (LSO), or of monaural spectral cues to estimate elevation (Colburn et al., 2006). Other perceptual attributes important for streaming that can be added to the model include loudness (Bregman, 1990) and rapid temporal modulations (Grimault et al., 2002).
Role of cortical mechanisms in stream segregation
The overarching motivation of the present work is to explore the significance of the auditory image that emerges at the level of A1 and its implications for the process of stream segregation and scene analysis. Each physiological mechanism incorporated in the model is ascribed a particular functional role and can potentially guide our understanding of the brain function in general and biological auditory scene analysis, in particular.
Multiscale cortical representation
The organization of the auditory pathway up to the auditory cortex indicates that different auditory features are extracted from the incoming sounds at various stages and probably organized into auditory objects at the cortical level (Nelken, 2004). This rich image which emerges at the level of A1 effectively projects the acoustic waveform into a higher dimensional perceptual space in a mapping reminiscent of operations taking place in classification and regression techniques such as support vector machines and kernel-based classifiers (Cristianini and Shawe-Taylor, 2000; Herbrich, 2001). Specifically, one can draw an analogy between this cortical representation and kernel-induced feature spaces, where input vectors are projected onto a higher-dimensional feature space, hence increasing the computational power of the classifier and improving the segregation between the different classes. In a similar fashion, the cortical mapping used in the current model attempts to enhance discrimination between the different auditory objects in the scene by allowing them to occupy nonoverlapping parts of the perceptual space.
A complementary view of this cortical representation can be thought of in terms of a sparse coding strategy employed by the auditory system. The rich span of neuronal selectivities in the primary auditory cortex may underlie a sparse distributed representation of natural scenes, allowing the system to optimally and robustly encode the complex sensory information in acoustic environments with multiple sources and sound objects (Klein et al., 2003; Olshausen and Field, 2004; Denham et al., 2007). Evidence from auditory cortical physiology is consistent with this view (Woolley et al., 2005) and suggests that the correspondence between cortical tuning and spectrotemporal features in natural sounds constitutes a mapping that effectively enhances discriminability among different sounds. The feature analysis stage described in the current model builds on this principle by outlining an extensive perceptual representation with filters that are selectively driven by particular sound features.
An important contribution of the model presented here is to formalize a framework that allows us to better understand this image which emerges at the level of A1. A final word of caution, however, is that including or excluding one of these dimensions does not always affect the representation of that feature alone because the different representational dimensions do not necessarily interact linearly. Consequently, leaving out one axis at any stage might also affect the separability of sound elements along other axes, especially with “complex” or “naturalistic” sounds such as speech.
Cortical dynamics
Information in sound occurs on multiple time scales with different temporal features having distinct acoustic manifestations, neural instantiations, and perceptual roles. At the level of the central auditory system (particularly the primary auditory cortex), numerous physiological investigations have shown that cortical responses appear to be particularly tuned to relatively slow rates of the order of few to tens of hertz. The sluggishness of cortical responses has been postulated to correspond very closely to important information components in speech and music. In speech, slow temporal modulations reflect movements and shape of the vocal tract, and consequently the sequence of syllabic segments in the speech stream. In music, they reflect the dynamics of bowing and fingering, the timbre of the instruments, and the rhythm and succession of notes. Overall, the analysis windows at the level of the cortex constitute the “clock” that paces the process of feature integration over time. In this respect, the appropriate choice of time constants for this process is crucial for achieving the desired performance. Our work emphasizes that the choice of cortical time constants is not arbitrary for the process of stream segregation. Rather, it builds on the compatibility between cortical windows and information in natural sounds and argues for a tight correspondence between cortical encoding and the processes of auditory scene analysis. The present model is grounded in this view and actually relies on the choice of cortical dynamics to regulate the tempo of the feature integration. As discussed in the results shown in Fig. 8b, one can certainly bias the performance of the model to “speed up” or “slow down” the process by choosing a different range of time constants or alternatively weighting the different temporal filters differently. However, the choice of the range of temporal parameters remains critical to obtain a correct behavior of the model as well as regulating the predictive stage as shall be discussed next.
Expectation processes
In addition to the appropriate choice of the representational space, the model relies strongly on a sound classification methodology for assigning the feature vectors to their corresponding classes. Unlike batch techniques, real-time segregation of these features requires continuous monitoring of the input and tracking of the different objects in the scene. Our present implementation accomplishes this process via an ongoing accumulation of expectations of each object. These expectations can be thought of as a matched filter that permits into the cluster only sensory patterns that are broadly consistent with recent history of that class. The principle of a matched filter has been presented as a reasonable hypothesis to explain observed plastic changes of cortical receptive fields (Fritz et al., 2007). The physiological plausibility of this mechanism rests on the existence of feedback projections that mediate the adaptive representation of biological information under continuously changing behavioral contexts and environments.
Adaptive signal processing techniques such as Kalman filtering have been successfully implemented to model many forms of dynamic neural adaptation and plasticity in hippocampal and motor circuits (Eden et al., 2004; Srinivasan et al., 2006; Wu et al., 2006). In the current model, we rely on the recursive nature of the Kalman filter to continuously estimate the state of each sound stream. The choice of a linear technique such as Kalman filtering (as opposed to other statistical filtering approaches such as particle filtering) is motivated by a long history of linear systems theory in characterizing receptive fields in physiological studies. The cortical STRFs (referred to through this paper) are linear approximations to a neuron’s selectivity to different features. We therefore used the same linear formulation as the basis of the Kalman-filter model.
Architecture of the model
Overall, our work stresses that computational schemes that can capture the essence of these three processes (multiscale representation, cortical dynamics, and expectancies) would be able to perform robustly in problems of sound segregation. It also ascribes specific roles to these neural phenomena in the overall strategy of sound organization in the auditory system. While not all stages may be necessary for the process of sound segregation for any particular acoustic scene, putting all of them together is what allows the model to perform with any sound mixture without prior knowledge of the sound class.
For instance, segregation of the tone sequences shown in Figs. 67 can easily be achieved without the harmonicity analysis nor any particular enhancement of the onset cues. They do, however, rely greatly on the frequency analysis performed at both the peripheral level and the spectral shape analysis at the cortical level. Similarly, the harmonicity analysis contributes to the formation of different speaker streams in two ways: to help segregate simultaneous (overlapped) speech segments and to attend to one harmonic spectrum over another. Both of these stem from the unique association of harmonics with pitch through the postulated harmonic templates (Fig. 3). To understand these assertions, consider first how the model streams two alternating (nonoverlapping) different spectra from two speakers. Just as with the two alternating tones, the two distinct harmonic spectra will be assigned to different clusters. In this case, harmonicity does not afford any added advantage to the formation of the streams. When the two harmonic spectra overlap, harmonicity (through the templates) helps breakup the combined spectrum into the two distinct harmonic spectra, which can then be again assigned to the appropriate clusters. Without harmonicity, the complex combined spectrum is treated as a new different spectrum and assigned to a new cluster. The association of harmonicity with pitch (through the templates) also facilitates attending to one harmonic stream over another by “focusing” on the pitch of the speaker, which in turn may enhance the representation and streaming of that speaker from the mixture. Without pitch, attending to a specific speaker would have to depend on other attributes such as their timbre, accent, or location. Finally, it is conceivable that other (less commonly encountered) spectral “regularities” beyond harmonicity can also be utilized in this streaming process provided they have the same type of anchor (e.g., pitch or templates) (Roberts and Bregman, 1991).
Neural correlates of streaming and attention
The present model is based on the premise that streaming is reflected in the response properties of neurons in the primary auditory cortex. This hypothesis is corroborated by a growing body of evidence from experiments that explore the neural bases of auditory stream segregation. For example, studies by Fishman et al. (2001) and Micheyl et al. (2005) have identified a possible correlate of stream segregation in the primary auditory cortex (A1) of awake monkeys presented with repeating ABAB tone sequences. Qualitatively similar results have been obtained in bats by Kanwal et al. (2003) and in birds by Bee et al. (2004). Recent results using awake ferrets trained on auditory scene analysis tasks reveal changes in the spectrotemporal tuning of cortical receptive fields in a direction that promotes streaming and facilitates the formation of two segregated objects (Yin et al., 2007).
The question remains, however, as to where and how exactly in the model does the adaptive nature of the STRFs emerge and serve functionally to promote streaming? We propose that the buildup of the clusters over time and the subsequent feedback that changes (or controls) the input stream into the integrative stage is the model’s explanation for the experimentally observed rapid STRF changes during streaming. Specifically, if we were to imagine recording from a cortical cell represented by one of the integrators in Fig. 1 in the quiescent state (i.e., without feedback), we would observe responses with spectral and temporal selectivity that mimics the STRFs typically seen in A1 (Miller et al., 2002). During streaming, the top-down feedback would alter the input into this cell (at the junction labeled “unsupervised clustering” in Fig. 1), effectively changing the selectivity of the cell or its STRF. Such a change would enhance the inputs that match the cell’s cluster and suppress those that do not (i.e., belong to the competing stream), in agreement with experimental observations (Yin et al., 2007).
This view of the relationship between streaming and rapid STRF plasticity makes several specific predictions that need to be explored in the future. For instance, STRF changes in the model essentially represent the neural correlate of the so-called “buildup” of streaming. This means that STRF plasticity must occur rather rapidly, within one or a few seconds of the initiation of streaming, at a rate commensurate with the dynamics of the buildup of the clusters in the model. So far, STRF adaptation has been detected only over relatively long epochs (minutes) due to the need to collect enough spikes to estimate them. New experimental techniques are therefore needed to estimate the STRFs rapidly, in particular, during the perceptual buildup of the streams.
Another key prediction of the model concerns the role of attention and its neural correlates in streaming. At first glance, the model appears to segregate streams rather automatically without “supervision,” suggesting perhaps a minimal or no role for attention in the buildup of this percept. However, an alternative hypothesis is that the top-down “feedback loop” in the model is enabled only when the listener’s attention is engaged. Clearly, without feedback, clustering ceases and no streams can form. Attention, we postulate, engages the feedback loop and enables streaming. We further postulate that “selective attention” to one stream or another can modulate the gain in the appropriate feedback loop, and hence favor the formation and perception of one (e.g., the foreground stream) over the other (the background). Although still conjectural, this view is consistent with several physiological and psychoacoustic data. One is the experimental finding that STRF plasticity is not observed in the absence of attentive behavior (Fritz et al., 2005), implying that streaming would not occur without top-down feedback activated by behavior (and presumably attention). Another is the modulation by attention of the mismatch negativity (MMN) component of the auditory evoked response, which is often interpreted as a potential neural index of streaming (Sussman et al., 2007). A second source of evidence for the critical role of attention is psychoacoustic studies, demonstrating that switching of attention to an ongoing acoustic stimulus is always associated with a perceptual buildup of its streams as if it had been initially “unstreamed” (Carlyon et al., 2001). Furthermore, attention has been shown to modulate streaming, e.g., as in the ability to switch at will between hearing certain tone sequences as one or two streams (Sussman et al., 2007) or the interaction between stimulus parameters and listener’s attentional control in delimiting the “fission boundary” and the “coherence boundary” in the perception of alternating tones (Bregman, 1990; van Noorden, 1975).
We should note, however, that the exact role of attention in streaming remains debatable with some evidence suggesting that sound organization can occur in the absence of attention. Such streaming is thought to be driven by “intrinsic” neural processes, manifested by oddball effects [generally arising from novel and unexpected stimuli (Näätänen, 1992)] and the persistence of the MMN component even when subjects display no overt attention to the sound (Sussman, 2005; Ulanovsky et al., 2003). This preattentive component of streaming is usually termed “primitive” stream segregation (Bregman, 1990). In our model, such primitive stream segregation implies that the top-down feedback must continue to operate in the absence of attention and that, therefore, STRFs should display adaptation during passive listening to sound reflecting the buildup of streams. This hypothesis remains physiologically untested.
ACKNOWLEDGMENTS
This research is supported by a CRCNS NIH Grant No. RO1 AG02757301, Southwest Research Institute, and Advanced Acoustic Concepts under a STTR from AFOSR.
APPENDIX: FEATURE INTEGRATION AND CLUSTERING
The clustering of sound features into different classes (two in the current model) proceeds through a three-step feedback loop which involves an estimation, prediction, and clustering stage. Each of these steps is mathematically implemented as follows.
Estimation
To make the dynamics of each filter more mathematically tractable and allow the tracking of its evolution over time, we reformulate Eq. 3 as a nth order ARMA difference equation (Oppenheim and Shafer, 1999; Proakis and Manolakis, 1992):
| (A1) |
where {ai} and {bi} are scalar coefficients corresponding to impulse response gt(t,ω) and whose values are determined by applying the Steiglitz–McBride algorithm (Ljung, 1999). This latter is a commonly used technique in filter design and parametric modeling of systems, which allows the computation of the ARMA coefficients for a prescribed time domain impulse response.
Next, we reduce this difference equation into a first-order vector equation following so-called state-space methods (Durbin, 2001; Pollock, 1999). Widely used in control theory, these methods are well suited for defining recursive time-series systems and compactly describing multi-input multi-output models in vectorial form. Thus, we introduce a latent variable called Z(t) which captures the internal state of the system at discrete times t, and hence operates as a memory register for the stream being represented. We follow standard techniques for converting difference equations into state-space forms (Bay, 1999; Pollock, 1999), yielding the new model formulation:
| (A2a) |
| (A2b) |
where , and A, B, and C are three fixed-coefficient matrices derived from filter parameters {ai} and {bi} following the standard techniques used in difference equation to state-space conversions [see Pollock (1999) for a step-by-step procedure description]. Note that we chose to define the state-space model as an output-input relationship (and not the other way around) by deriving the observation equation A2a as a function of the input I(t) [not the output Y(t)] because our ultimate goal is to use this model to make predictions about expected inputs for a given stream. Additionally, we introduced noise terms [ν(t) and η(t)] to both equalities in Eq. A2. This allows us to formulate a statistical model of the temporal analysis of each temporal unit , which permits a stochastic estimation of the state-vector Z, and hence a nondeterministic prediction of the expected input . The perturbation terms ν(t) and η(t) are two Gaussian-noise processes drawn from zero mean multivariate distributions with covariances P and Q, respectively.
Therefore, the underlying dynamical system [captured in Eq. A2] is now a Markovchain model where the state estimate at the next time increment Z(t+1) is a function of the current state Z(t) combined with the input-output variables (I(t),Y(t)). Note that we have as many such systems as we have rate-selective units ({Rω}) representing the neural array R+ (i.e., each array R+ encompasses five dynamical systems operating at rates of 2,4,32 Hz). Hence, the overall model is effectively a family of hidden Markov models evolving over successive discrete-time instants, which collectively capture the temporal evolution of a given stream.
Given the present formulation, we define an optimal solution for updating the latent variables Z in a way that enables both recursive tracking and prediction of future states. We opt for a Kalman-filter estimation (Chui and Chen, 1999; Haykin, 1996) because of its various advantages: (1) it is a computationally tractable and well defined mathematical solution to such estimation problem, (2) is optimal in the least mean square sense, and (3) is an online recursive technique where the current state estimate is computed only from the previous state (i.e., using recent history of the stream). Henceforth, the state variable Z is now updated as a Kalman filter-based evaluation (Haykin, 1996; Pollock, 1999), where the estimate of Z at time t is given by
| (A3) |
where is the new predicted state at time t, is a priori estimate of Z conditioned on all prior information up to time t−1, KG is the Kalman gain (Haykin, 1996), and Π(t) is the estimate error covariance matrix between the actual and estimated Z. The starting conditions Z(0) and Π(0) are initialized to small random values.
One of the advantages of using a multirate analysis for the temporal tracking is the fact that each neural array R+ encompasses a wide range of temporal dynamics. To this effect, it is important to note that the vector Z(t) reflects more than the state of the system at exactly time instant t. Rather, it captures the past history of the system over a time window governed by the filter dynamics determined by the transition matrices A, B, and C. This memory can go as far back as 500 ms in the case of the slow filters operating at ω=2 Hz.
Prediction
So far in the model, the input-output pair (I(t),Y(t)) is used to update the current estimate of the latent variable Z(t). The next stage involves using this triplet (I(t),Y(t),Z(t)) to make an inference about the next expected input . To proceed with this prediction, we take advantage of known temporal regularities likely to exist in sound patterns arising from the same source (i.e., no abrupt spectral transitions from one time instant to the next) (Becker, 1993; Foldiak, 1991; Griffiths et al., 2001). We model this temporal uniformity by assuming a locally smooth evolution of the cortical representation for each time step; i.e., the estimated cortical state equals the current state Y(t). Based on this assumption, the model can make a prediction about the next input vector following the system’s equation A2. This prediction represents the acoustic patterns that the cortical unit is expecting to hear based on its recent history in order to maintain a smooth temporal evolution. Given that each stream is represented by an entire array of cortical neurons , we sum across the predictions of all ω-units within the array to obtain two expected inputs and from the two streams R1 and R2 represented in the model.
Clustering
The final stage is the most crucial step to segregating incoming sound patterns I(t) into their corresponding perceptual streams. This procedure is performed based on a simple clustering rule that contrasts each input pattern with its closest match from the predictions of the arrays R1 and R2. Only the pattern that closely matches the predictions or is used as the next input I(t+1) for that stream following the clustering “closest match” rule:
| (A4) |
Footnotes
Throughout this paper, we use the term “stream” to refer to the clustered sound elements corresponding to the cognitive representation of a physical acoustic source. The term stream is occasionally used interchangeably with the term auditory object.
References
- Anstis, S., and Saida, S. (1985). “Adaptation to auditory streaming of frequency-modulated tones,” J. Exp. Psychol. Hum. Percept. Perform. 10.1037//0096-1523.11.3.257 11, 257–271. [DOI] [Google Scholar]
- Aubin, T., and Jouventin, P. (1998). “Cocktail-part effect in king penguin colonies,” Proc. R. Soc. London, Ser. B 10.1098/rspb.1998.0486 265, 1665–1673. [DOI] [Google Scholar]
- Barlow, H. (1994). Large-Scale Neuronal Theories of the Brain (MIT Press, Cambridge, MA: ), pp. 1–22. [Google Scholar]
- Bay, J. S. (1999). Fundamentals of Linear State Space Systems (McGraw-Hill, Boston: ). [Google Scholar]
- Beauvois, M. W., and Meddis, R. (1996). “Computer simulation of auditory stream segregation in alternating-tone sequences,” J. Acoust. Soc. Am. 10.1121/1.415414 99, 2270–2280. [DOI] [PubMed] [Google Scholar]
- Becker, S. (1993). Advances in Neural Information Processing Systems (Morgan Kaufmann, San Mateo, CA: ), Vol. 5, pp. 361–368. [Google Scholar]
- Bee, M. A., and Klump, G. M. (2004). “Primitive auditory stream segregation: A neurophysiological study in the songbird forebrain,” J. Neurophysiol. 92, 1088–1104. [DOI] [PubMed] [Google Scholar]
- Bell, A. J., and Sejnowski, T. J. (1995). “An information maximization approach to blind source separation and blind deconvolution,” Neural Comput. 10.1162/neco.1995.7.6.1129 7, 1129–1159. [DOI] [PubMed] [Google Scholar]
- Bregman, A. S. (1978). “Auditory streaming is cumulative,” J. Exp. Psychol. Hum. Percept. Perform. 10.1037//0096-1523.4.3.380 4, 380–387. [DOI] [PubMed] [Google Scholar]
- Bregman, A. S. (1990). Auditory Scene Analysis: The Perceptual Organization of Sound (MIT Press, Cambridge, MA: ). [Google Scholar]
- Bregman, A. S., and Ahad, P. A. (1990). “Demonstrations of auditory scene analysis: The perceptual organization of sound,” Compact Disk, Department of Psychology, McGill University, Montreal, Canada.
- Bregman, A. S., and Pinker, S. (1978). “Auditory streaming and the building of timbre,” Can. J. Psychol. 10.1037/h0081664 32, 19–31. [DOI] [PubMed] [Google Scholar]
- Carlyon, R. P., Cusack, R., Foxton, J. M., and Robertson, I. H. (2001). “Effects of attention and unilateral neglect on auditory stream segregation,” J. Exp. Psychol. Hum. Percept. Perform. 10.1037//0096-1523.27.1.115 27, 115–127. [DOI] [PubMed] [Google Scholar]
- Carlyon, R., and Shamma, S. (2003). “An account of monaural phase sensitivity,” J. Acoust. Soc. Am. 10.1121/1.1577557 114, 333–348. [DOI] [PubMed] [Google Scholar]
- Cherry, E. C. (1953). “Some experiments on the recognition of speech, with one and two ears,” J. Acoust. Soc. Am. 10.1121/1.1907229 25, 975–979. [DOI] [Google Scholar]
- Chi, T., Ru, P., and Shamma, S. A. (2005). “Multiresolution spectrotemporal analysis of complex sounds,” J. Acoust. Soc. Am. 10.1121/1.1945807 118, 887–906. [DOI] [PubMed] [Google Scholar]
- Chui, C. K., and Chen, G. (1999). Kalman Filtering With Real Time Applications (Springer-Verlag, New York: ). [Google Scholar]
- Cohen, M. A., Grossberg, S., and Wyse, L. L. (1995). “A spectral network model of pitch perception,” J. Acoust. Soc. Am. 10.1121/1.413512 98, 862–879. [DOI] [PubMed] [Google Scholar]
- Colburn, S., Shinn-Cunningham, B., Jr, G. K., and Durlach, N. (2006). “The perceptual consequences of binaural hearing,” Int. J. Audiol. 45, 34–44. [DOI] [PubMed] [Google Scholar]
- Colombo, M., Rodman, H. R., and Gross, C. G. (1996). “The effects of superior temporal cortex lesions on the processing and retention of auditory information in monkeys (cebus apella),” J. Neurosci. 16, 4501–4517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cristianini, N., and Shawe-Taylor, J. (2000). Introduction to Support Vector Machines and Other Kernel-Based Learning Methods (Cambridge University Press, Cambridge, UK: ). [Google Scholar]
- Dau, T., Püschel, D., and Kohlrausch, A. (1996). “A quantitative model of the effective signal processing in the auditory system,” J. Acoust. Soc. Am. 10.1121/1.414959 99, 3615–3622. [DOI] [PubMed] [Google Scholar]
- Denham, S., Coath, M., and Balaguer-Ballester, E. (2007). “Sparse time-frequency representations in auditory processing,” 19th International Congress on Acoustics, Madrid.
- Drullman, R. (1995). “Temporal envelope and fine structure cues for speech intelligibility,” J. Acoust. Soc. Am. 10.1121/1.413112 97, 585–592. [DOI] [PubMed] [Google Scholar]
- Duifhuis, H., Willems, L. F., and Sluyter, R. J. (1982). “Measurement of pitch in speech: An implementation of Goldstein’s theory of pitch perception,” J. Acoust. Soc. Am. 10.1121/1.387811 71, 1568–1580. [DOI] [PubMed] [Google Scholar]
- Durbin, J. (2001). Time Series Analysis by State-Space Methods, 3rd ed. (Oxford University Press, New York, NY: ). [Google Scholar]
- Eddins, D. A., and Bero, E. M. (2007). “Spectral modulation detection as a function of modulation frequency, carrier bandwidth, and carrier frequency region,” J. Acoust. Soc. Am. 10.1121/1.2382347 121, 363–372. [DOI] [PubMed] [Google Scholar]
- Eden, U. T., Frank, L. M., Barbieri, R., Solo, V., and Brown, E. N. (2004). “Dynamic analysis of neural encoding by point process adaptive filtering,” Neural Comput. 16, 971–998. [DOI] [PubMed] [Google Scholar]
- Elhilali, M., Chi, T., and Shamma, S. A. (2003). “A spectro-temporal modulation index (STMI) for assessment of speech intelligibility,” Speech Commun. 10.1016/S0167-6393(02)00134-6 41, 331–348. [DOI] [Google Scholar]
- Elhilali, M., Fritz, J. B., Chi, T., and Shamma, S. A. (2007). “Auditory cortical receptive fields: Stable entities with plastic abilities,” J. Neurosci. 27, 10372–10382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elhilali, M., Fritz, J. B., Klein, D. J., Simon, J. Z., and Shamma, S. A. (2004). “Dynamics of precise spike timing in primary auditory cortex,” J. Neurosci. 10.1523/JNEUROSCI.3825-03.2004 24, 1159–1172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis, D. P. W., and Weiss, R. J. (2006). “Model-based monaural source separation using a vector-quantized phase-vocoder representation,” Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, IEEE ICASSP’06, Vol. 5, pp. 957–960.
- Fay, R. R. (1998). “Auditory stream segregation in goldfish (carassius auratus),” Hear. Res. 10.1016/S0378-5955(98)00058-6 120, 69–76. [DOI] [PubMed] [Google Scholar]
- Festen, J. M., and Plomp, R. (1990). “Effects of fluctuating noise and interfering speech on the speech-reception threshold for impaired and normal hearing,” J. Acoust. Soc. Am. 10.1121/1.400247 88, 1725–1736. [DOI] [PubMed] [Google Scholar]
- Fishman, Y. I., Reser, D. H., Arezzo, J. C., and Steinschneider, M. (2001). “Neural correlates of auditory stream segregation in primary auditory cortex of the awake monkey,” Hear. Res. 10.1016/S0378-5955(00)00224-0 151, 167–187. [DOI] [PubMed] [Google Scholar]
- Foldiak, P. (1991). “Learning invariance from transformation sequences,” Neural Comput. 3, 194–200. [DOI] [PubMed] [Google Scholar]
- Fritz, J. B., Elhilali, M., David, S., and Shamma, S. A. (2007). “Does attention play a role in dynamic receptive field adaptation to changing acoustic salience in a1,” Hear. Res. 229, 186–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritz, J. B., Elhilali, M., and Shamma, S. A. (2005). “Differential receptive field plasticity to salient cues in primary auditory cortex during two-tone frequency discrimination,” J. Neurosci. 25, 7623–7635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein, J. L. (1973). “An optimum processor theory for the central formation of the pitch of complex tones,” J. Acoust. Soc. Am. 10.1121/1.1914448 54, 1496–1516. [DOI] [PubMed] [Google Scholar]
- Green, D. M. (1986). Auditory Frequency Selectivity, NATO ASI Series, Series A: Life Sciences (Plenum, New York, NY: ), pp. 351–359. [Google Scholar]
- Griffiths, T. D., Uppenkamp, S., Johnsrude, I., Josephs, O., and Patterson, R. D. (2001). “Encoding of the temporal regularity of sound in the human brainstem,” Nat. Neurosci. 10.1038/88459 4, 633–637. [DOI] [PubMed] [Google Scholar]
- Grimault, N., Bacon, S. P., and Micheyl, C. (2002). “Auditory stream segregation on the basis of amplitude-modulation rate,” J. Acoust. Soc. Am. 10.1121/1.1452740 111, 1340–1348. [DOI] [PubMed] [Google Scholar]
- Grossberg, S., Govindarajan, K. K., Wyse, L. L., and Cohen, M. A. (2004). “Artstream: A neural network model of auditory scene analysis and source segregation,” Neural Networks 17, 511–536. [DOI] [PubMed] [Google Scholar]
- Hartman, W. M., and Jonhson, D. (1991). “Stream segregation and peripheral channelling,” Music Percept. 9, 155–184. [Google Scholar]
- Haykin, S. (1996). Adaptive Filter Theory (Prentice-Hall, Upper Saddle River, NJ: ). [Google Scholar]
- Herbrich, R. (2001). Learning Kernel Classifiers: Theory and Algorithms (MIT Press, Cambridge, MA: ). [Google Scholar]
- Hughes, H. C., Darcey, T. M., Barkan, H. I., Williamson, P. D., Roberts, D. W., and Aslin, C. H. (2001). “Responses of human auditory association cortex to the omission of an expected acoustic event,” Neuroimage 13, 1073–1089. [DOI] [PubMed] [Google Scholar]
- Hulse, S. H., MacDougall-Shackleton, S. A., and Wisniewski, A. B. (1997). “Auditory scene analysis by songbirds: Stream segregation of birdsong by European starlings (sturnus vulgaris),” J. Comp. Psychol. 10.1037//0735-7036.111.1.3 111, 3–13. [DOI] [PubMed] [Google Scholar]
- Humphrey, N. (1992). A History of the Mind (Simon and Schuster, New York, NY: ). [Google Scholar]
- Izumi, A. (2001). “Relative pitch perception in Japanese monkeys (macaca fuscata),” J. Comp. Psychol. 115, 127–131. [DOI] [PubMed] [Google Scholar]
- Jang, G., and Lee, T. (2004). “A maximum likelihood approach to single-channel source separation,” J. Mach. Learn. Res. 4, 1365–1392. [Google Scholar]
- Jerison, H. J., and Neff, W. D. (1953). “Effect of cortical ablation in the monkey on discrimination of auditory patterns,” Fed. Proc. 12, 73–74. [Google Scholar]
- Kanwal, J. A., Medvedev, A., and Micheyl, C. (2003). “Neurodynamics for auditory stream segregation: Tracking sounds in the mustached bat’s natural environment,” Network Comput. Neural Syst. 14, 413–435. [PubMed] [Google Scholar]
- Kelly, J. B., Rooney, B. J., and Phillips, D. P. (1996). “Effects of bilateral auditory cortical lesions on gap-detection thresholds in the ferret (mustela putorius),” Behav. Neurosci. 10.1037//0735-7044.110.3.542 110, 542–550. [DOI] [PubMed] [Google Scholar]
- Klein, D. J., König, P., and Körding, K. P. (2003). “Sparse spectrotemporal coding of sounds,” EURASIP J. Appl. Signal Process. 7, 659–667. [Google Scholar]
- Kowalski, N., Depireux, D. A., and Shamma, S. A. (1996). “Analysis of dynamic spectra in ferret primary auditory cortex. I. Characteristics of single-unit responses to moving ripple spectra,” J. Neurophysiol. 76, 3503–3523. [DOI] [PubMed] [Google Scholar]
- Kristjansson, T., Hershey, J., Olsen, P., Rennie, S., and Gopinath, R. (2006). “Super-human multi-talker speech recognition: The ibm 2006 speech separation challenge system,” Proceedings of the International Conference of Spoken Language Processing, ICSLP’06.
- Langner, G. (1992). “Periodicity coding in the auditory system,” Hear. Res. 10.1016/0378-5955(92)90015-F 6, 115–142. [DOI] [PubMed] [Google Scholar]
- Ljung, L. (1999). System Identification: Theory for the User, 2nd ed. (Prentice-Hall, Upper Saddle River, NJ: ). [Google Scholar]
- McCabe, S. L., and Denham, M. J. (1997). “A model of auditory streaming,” J. Acoust. Soc. Am. 10.1121/1.418176 101, 1611–1621. [DOI] [Google Scholar]
- Micheyl, C., Tian, B., Carlyon, R. P., and Rauschecker, J. P. (2005). “Perceptual organization of tone sequences in the auditory cortex of awake macaques,” Neuron 10.1016/j.neuron.2005.08.039 48, 139–148. [DOI] [PubMed] [Google Scholar]
- Middlebrooks, J. C., Dykes, R. W., and Merzenich, M. M. (1980). “Binaural response-specific band in primary auditory cortex (ai) of the cat: Topographical organization orthogonal to isofrequency contours,” Brain Res. 181, 31–49. [DOI] [PubMed] [Google Scholar]
- Miller, L. M., Escabi, M. A., Read, H. L., and Schreiner, C. E. (2002). “Spectrotemporal receptive fields in the lemniscal auditory thalamus and cortex,” J. Neurophysiol. 87, 516–527. [DOI] [PubMed] [Google Scholar]
- Miller, G. A., and Taylor, W. G. (1948). “The perception of repeated bursts of noise,” J. Acoust. Soc. Am. 10.1121/1.1906360 20, 171–182. [DOI] [Google Scholar]
- Moore, B. C. J., Glasberg, B. R., and Peters, R. W. (1986). “Thresholds for hearing mistuned partials as separate tones in harmonic complexes,” J. Acoust. Soc. Am. 10.1121/1.394043 80, 479–483. [DOI] [PubMed] [Google Scholar]
- Moore, B., and Gockel, H. (2002). “Factors influencing sequential stream segregation,” Acta. Acust. Acust. 88, 320–332. [Google Scholar]
- Näätänen, R. (1992). Attention and Brain Function (Lawrence Erlbaum Associates, Hillsdale, NJ: ). [Google Scholar]
- Nelken, I. (2004). “Processing of complex stimuli and natural scenes in the auditory cortex,” Curr. Opin. Neurobiol. 14, 474–480. [DOI] [PubMed] [Google Scholar]
- Nix, J., and Hohmann, V. (2007). “Combined estimation of spectral envelopes and sound source direction of concurrent voices by multidimensional statistical filtering,” IEEE Trans. Audio, Speech, Lang. Process. 15, 995–1008. [Google Scholar]
- Olshausen, B. A., and Field, D. J. (2004). “Sparse coding of sensory inputs,” Curr. Opin. Neurobiol. 10.1016/j.conb.2004.07.007 14, 481–487. [DOI] [PubMed] [Google Scholar]
- Oppenheim, A., and Shafer, R. (1999). Discrete Time Signal Processing, 2nd ed. (Prentice-Hall, Upper Saddle River, NJ: ). [Google Scholar]
- O’Shaughnessy, D. (2000). Speech Communications: Human and Machine, 2nd ed. (Institute of Electrical and Electronics Engineers, New York, NY: ). [Google Scholar]
- Oxenham, A. J., Bernstein, J. G., and Penagos, H. (2004). “Correct tonotopic representation is necessary for complex pitch perception,” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0306958101 101, 1421–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters, R. W., Moore, B. C., and Baer, T. (1998). “Speech reception thresholds in noise with and without spectral and temporal dips for hearing-impaired and normally hearing people,” J. Acoust. Soc. Am. 103, 577–587. [DOI] [PubMed] [Google Scholar]
- Pickles, J. O. (1988). An Introduction to the Physiology of Hearing (Academic, St Louis, MO: ). [Google Scholar]
- Pollock, D. S. G. (1999). A Handbook of Time-Series Analysis, Signal Processing and Dynamics (Academic, Cambridge, UK: ). [Google Scholar]
- Proakis, J. G., and Manolakis, D. G. (1992). Digital Signal Processing (McMillan, New York, NY: ). [Google Scholar]
- Qin, M. K., and Oxenham, A. J. (2003). “Effects of simulated cochlear-implant processing on speech reception in fluctuating maskers,” J. Acoust. Soc. Am. 10.1121/1.1579009 114, 446–454. [DOI] [PubMed] [Google Scholar]
- Rauschecker, J. P. (2005). “Neural encoding and retrieval of sound sequences,” Ann. N.Y. Acad. Sci. 1060, 125–135. [DOI] [PubMed] [Google Scholar]
- Roberts, B., and Bregman, A. S. (1991). “Effects of the pattern of spectral spacing on the perceptual fusion of harmonics,” J. Acoust. Soc. Am. 10.1121/1.401779 90, 3050–3060. [DOI] [Google Scholar]
- Roweis, S. (2000). “One microphone source separation,” Neural Information Processing Systems (NIPS’00), Vol. 13, pp. 793–799.
- Sacks, M., and Blackburn, C. (1991). Neurophysiology of Hearing: The Central Auditory System, 15th ed. (Raven, New York, NY: ). [Google Scholar]
- Schreiner, C. (1998). “Spatial distribution of responses to simple and complex sounds in the primary auditory cortex,” Audiol. Neuro-Otol. 10.1159/000013785 3, 104–122. [DOI] [PubMed] [Google Scholar]
- Schreiner, C. E., and Urbas, J. V. (1988). “Representation of amplitude modulation in the auditory cortex of the cat. II. Comparison between cortical fields,” Hear. Res. 10.1016/0378-5955(88)90146-3 32, 49–64. [DOI] [PubMed] [Google Scholar]
- Shamma, S. A. (1998). Methods of Neuronal Modeling, 2nd ed. (MIT Press, Cambridge, MA: ), pp. 411–460. [Google Scholar]
- Shamma, S. A., and Klein, D. J. (2000). “The case of the missing pitch templates: How harmonic templates emerge in the early auditory system,” J. Acoust. Soc. Am. 10.1121/1.428649 107, 2631–2644. [DOI] [PubMed] [Google Scholar]
- Shinn-Cunningham, B. G. (2005). “Influences of spatial cues on grouping and understanding sound,” Proceedings of the Forum Acusticum.
- Srinivasan, L., Eden, U. T., Willsky, A. S., and Brown, E. N. (2006). “A state-space analysis for reconstruction of goal-directed movements using neural signals,” Neural Comput. 18, 2465–2494. [DOI] [PubMed] [Google Scholar]
- Supin, A. Y., Popov, V. V., Milekhina, O. N., and Tarakanov, M. B. (1999). “Ripple depth and density resolution of rippled noise,” J. Acoust. Soc. Am. 10.1121/1.428105 106, 2800–2804. [DOI] [PubMed] [Google Scholar]
- Sussman, E. S. (2005). “Integration and segregation in auditory scene analysis,” J. Acoust. Soc. Am. 10.1121/1.1854312 117, 1285–1298. [DOI] [PubMed] [Google Scholar]
- Sussman, E. S., Horvath, J., Winkler, I., and Orr, M. (2007). “The role of attention in the formation of auditory streams,” Percept. Psychophys. 69, 136–152. [DOI] [PubMed] [Google Scholar]
- Sutter, M. L. (2005). “Spectral processing in the auditory cortex,” Int. Rev. Neurobiol. 70, 253–298. [DOI] [PubMed] [Google Scholar]
- Tougas, Y., and Bregman, A. S. (1985). “The crossing of auditory streams,” J. Exp. Psychol. Hum. Percept. Perform. 11, 788–798. [Google Scholar]
- Ulanovsky, N., Las, L., and Nelken, I. (2003). “Processing of low-probability sounds in cortical neurons,” Nat. Neurosci. 10.1038/nn1032 6, 391–398. [DOI] [PubMed] [Google Scholar]
- van Noorden, L. P. (1975). “Temporal coherence in the perception of tone sequences,” Ph.D. thesis, Eindhoven University of Technology. [Google Scholar]
- Varga, A. P., and Moore, R. K. (1990). “Hidden Markov model decomposition of speech and noise,” Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, IEEE ICASSP’90, Vol. 2, pp. 845–848.
- Viemeister, N. F. (1979). “Temporal modulation transfer functions based upon modulation thresholds,” J. Acoust. Soc. Am. 10.1121/1.383531 66, 1364–1380. [DOI] [PubMed] [Google Scholar]
- von der Malsburg, C., and Schneider, W. (1986). “A neural cocktail-party processor,” Biol. Cybern. 10.1007/BF00337113 54, 29–40. [DOI] [PubMed] [Google Scholar]
- Wang, D. L., and Brown, G. J. (1999). “Separation of speech from interfering sounds based on oscillatory correlation,” IEEE Trans. Neural Netw. 10.1109/72.761727 10, 684–697. [DOI] [PubMed] [Google Scholar]
- Wang, K., and Shamma, S. A. (1994). “Self-normalization and noise-robustness in early auditory representations,” IEEE Trans. Speech Audio Process. 10.1109/89.294356 2, 421–435. [DOI] [Google Scholar]
- Wang, K., and Shamma, S. A. (1995). “Spectral shape analysis in the central auditory system,” IEEE Trans. Speech Audio Process. 10.1109/89.466657 3, 382–395. [DOI] [Google Scholar]
- Welch, G., and Bishop, G. (2001). “An introduction to the Kalman filter,” ACM SIGGRAPH.
- Wightman, F. (1973). “A pattern transformation model of pitch,” J. Acoust. Soc. Am. 10.1121/1.1913591 54, 397–406. [DOI] [PubMed] [Google Scholar]
- Wittkop, T., and Hohmann, V. (2003). “Strategy-selective noise reduction for binaural digital hearing aids,” Speech Commun. 10.1016/S0167-6393(02)00062-6 39, 111–138. [DOI] [Google Scholar]
- Woolley, S. M., Fremouw, T. E., Hsu, A., and Theunissen, F. E. (2005). “Tuning for spectro-temporal modulations as a mechanism for auditory discrimination of natural sounds,” Nat. Neurosci. 8, 1371–1379. [DOI] [PubMed] [Google Scholar]
- Wu, W., Gao, Y., Bienenstock, E., Donoghue, J. P., and Black, M. J. (2006). “Bayesian population decoding of motor cortical activity using a Kalman filter,” Neural Comput. 18, 80–118. [DOI] [PubMed] [Google Scholar]
- Yang, X., Wang, K., and Shamma, S. A. (1992). “Auditory representations of acoustic signals,” IEEE Trans. Inf. Theory 10.1109/18.119739 38, 824–839. [DOI] [Google Scholar]
- Yin, P., Ma, L., Elhilali, M., Fritz, J. B., and Shamma, S. A. (2007). Hearing: From Basic Research to Applications (Springer Verlag, New York, NY: ). [Google Scholar]