Scanning probe recognition microscopy investigation of tissue scaffold properties

Abstract

Scanning probe recognition microscopy is a new scanning probe microscopy technique which enables selective scanning along individual nanofibers within a tissue scaffold. Statistically significant data for multiple properties can be collected by repetitively fine-scanning an identical region of interest. The results of a scanning probe recognition microscopy investigation of the surface roughness and elasticity of a series of tissue scaffolds are presented. Deconvolution and statistical methods were developed and used for data accuracy along curved nanofiber surfaces. Nanofiber features were also independently analyzed using transmission electron microscopy, with results that supported the scanning probe recognition microscopy-based analysis.

Introduction

Tissue scaffold engineering is an active and successful research field (Atala 2005; Hu and Athanasiou 2006; Xu et al 2006). However, much fundamental understanding is still needed to design scaffolds with the most appropriate mechanical, topographical and chemical properties for particular cells or cell classes. For actin-based cells, cell motility towards and adhesion to tissue scaffolds results from the extension of cell protrusions due to actin polymerization. Motility and adhesion are triggered through a complex interaction of receptors at the leading edge of the protrusion with the external environment ahead, as well as with the cell internal environment behind. Features of the cell internal environment have been recently reported (Svitkina et al 1996, 1997, 2003; Svitkina and Borisy 1999; Bear et al 2002; Vignjevic et al 2003; Biyasheva et al 2004). The signalling cascades that trigger narrow filopodia and broad lamellipodia extension through assembly of actin filaments into defined structures have been partly identified. High resolution electron microscopy has identified a strongly cross-linked actin polymerization with filopodia extension versus a widely-branched actin polymerization for lamellipodia extension. However, the combination of environmental factors that trigger the formation and continuance of actin polymerization of either extension type are still in need of elucidation. This is difficult because more than one environmental factor is known to stimulate leading edge formation. Cell sensing of surface roughness (haptotaxis) (Lampin et al 1997; Deligianni et al 2001; Gaudet et al 2003), elasticity (durotaxis) (Pelham and Wang 1997; Lo et al 2000; Engler, Bacakova et al 2004; Engler, Richert et al 2004; Micoulet et al 2005; Discher et al 2005; Guo et al 2006; Gupta et al 2006), and surface chemistry (chemotaxis) (Murray 2003; Arnold et al 2004; Stevens and George 2005) are all known to trigger cell motility through actin-based extension of filopodia and lamellipodia towards conditions which promote adhesion.

In the studies cited above, the surface roughness, elasticity and surface chemistry were all investigated separately for widely varying cell types that demonstrated the maximal response to each type of environmental trigger. There is a need to acquire the information for all pertinent environmental triggers that induce leading edge formation over the same location, and then to assemble them into a composite picture more truly representative of a cell’s perception of its environment.

Leading edge formation corresponds to a 10’s of nanometers sensing area at the cell’s extending tip. The environmental triggers should therefore be assessed on a comparable scale. Atomic force microscopy is an investigative tool with nanometer-scale resolution which may be used to investigate minimally conductive biological surfaces (Braga and Ricci 2003). In the present studies, we use atomic force microscopy operated in a new mode, Scanning Probe Recognition Microscopy, to investigate the environmental triggers for cell response to a series of tissue scaffolds fabricated from electrospun carbon nanofibers. Scanning Probe Recognition Microscopy is a new scanning probe microscopy technique which allows us to adaptively follow along individual nanofibers within a tissue scaffold. Statistically significant data for multiple properties can be collected and combined by repetitively fine-scanning over a region of interest. Using Scanning Probe Recognition Microscopy, we have investigated the surface roughness and elasticity of a series of three tissue scaffolds provided as a blind test. The tissue scaffolds were random nanofiber meshes, with differences that resulted from different electrospinning conditions.

Materials and methods

Tissue scaffold samples

Three samples of tissue scaffolds fabricated from electrospun (Taylor 1969; Dzenis 2004) carbon nanofibers were obtained from the Donaldson Company. These will be referred to as samples A, B, and C. The nanofibers were electrospun using an adapted electrospinning probe procedure described in the reference by (Chung et al 2004). No further information about the tissue scaffolds samples was provided.

Nanoscope IIIa Special SPRM Modification

The scanning probe microscopy (SPM) experiments were performed using a Veeco Instruments Nanoscope IIIa operated in atomic force microscopy contact mode in ambient air (Binnig et al 1986; Bonnell 2001; Braga and Ricci 2003; Andrea and Paolo 2005). The system has a special modification developed by our research group in partnership with Veeco Instruments. The SPM system itself is given the ability to auto-track on regions of interest through incorporation of recognition – based tip control, described as scanning probe recognition microscopy (SPRM). The recognition capability is realized using algorithms and techniques from computer vision, pattern recognition and signal processing fields. Adaptive learning and prediction are also implemented to make detection and recognition procedures quicker and more reliable. The integration of recognition makes the SPRM system more powerful and flexible in investigating specific properties of samples.

Other instrumental parameters include the use of a J scanner with a maximum 125 × 125 square micron x-y scan range and silicon nitride tips with a nominal 20 nm tip radius of curvature. Transmission electron microscopy (TEM) with selected area electron diffraction (SAED) was performed using a JEOL 100CXII TEM. Scanning electron microscopy (SEM) was performed using a Hitachi S-4700II field emission SEM.

Experimental results

Atomic force microscope (AFM) images of tissue scaffold samples A, B, and C are shown in Figures 1a–1c. Scanning electron microscope (SEM) images, shown in Figures 1d–1f, were also used to ensure that the AFM results were representative over larger scaffold areas. The general appearance of the nanofibers was similar for samples A, B, and C. Tissue scaffold samples A, B, and C were then analyzed using Scanning Probe Recognition Microscopy for the more specific environmental triggers surface roughness and elasticity.

Figure 1.

AFM and SEM images of electrospun carbon nanofiber tissue scaffolds. (a–c) AFM images of Sample A, B and C. The scan area of each image is 5 square microns and the z-height projection is 1500 nanometers. (d–f) SEM images of Sample A, B and C. The scan area of each image is 20 square microns.

Surface roughness

The surface roughness of the substrate has been shown to influence cell attachment. It is therefore important to obtain this information accurately and efficiently along tissue scaffold nanofibers. In the majority of studies, the surface roughness is the Root Mean Square (RMS) of height values in a region of interest as defined in equation (1).

$$RMS=\sqrt{\frac{\sum _{i=1}^N{(Z_i-Z_{ave})}^2}{N}}$$ (1)

For AFM-based measurements, N is the number of total pixilated data points in this region; Z_i is the height value at each pixel and $Z_{ave}=\frac{1}{N}\sum _{i=1}^N{Z}_i$ is the average value of all height values.

In conventional atomic force microscopy, the surface roughness information is acquired through manual application of a rectangular region of interest box (Digital Instruments 2003). The surface roughness within the box is then calculated. There are several problems with the conventional approach to surface roughness investigation when the sample is a tissue scaffold nanofiber. The shape of the region of interest (ROI) may not be rectangular, necessitating the application of several small ROI boxes which follow the curvature of the nanofiber. Only a single value is provided for each time of operation. Therefore, in order to get surface roughness along a nanofiber, this operation would need to be repeated many times.

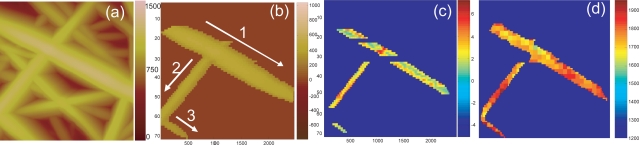
In the SPRM system, a recognition-based scan plan can be generated to auto-focus tip motion along an individual nanofiber (Fan et al 2005). The result of SPRM auto-track imaging versus traditional AFM raster imaging is shown by comparison of Figure 2(b) with Figure 2(a). Also, adaptive scanning enables SPRM to fol low along an individual nanofiber even when it crosses another nanofiber as shown in Figure 2b. Therefore, the whole nanofiber, or the whole nanofiber mesh becomes the region of interest.

Figure 2.

SPRM analysis of sample C (a) AFM images; (b) auto-tracking scan along three individual nanofibers; (c) surface roughness map. Note that the apparent width of the nanofiber is reduced from (b) as a result of the erosion operation; (d) elasticity map.

Using data obtained by SPRM along individual nanofibers, the surface roughness was calculated on each pixel based on a local neighborhood region. The shape and size of the local neighborhood region can be adjusted by the user, which makes the system adaptable for different samples. We chose a rectangular box around each pixel as the local neighborhood region, with a box size of 219.76 nm (close to the nanofiber diameter). Multiple sets of overlapping surface roughness information were generated, with the provision that any box that extended outside the nanofiber boundaries was automatically truncated. A surface roughness map along individual nanofibers was then generated.

Figure 2c shows a typical surface roughness map for sample C. Similar maps, not shown, were generated for samples A and B. In addition to the surface roughness maps, histograms showing the distribution of the surface roughness analyzed over several nanofibers were calculated for samples A, B and C. This is the first time that statistically meaningful information has been extracted along individual nanofibers using an automatic procedure that maintains uniformity of experimental conditions.

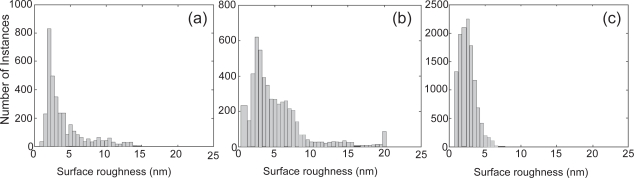
The histograms of the surface roughness for samples A, B and C are shown in Figure 3. From the histograms, the mode, the mean value, the range, and the variance of the surface roughness were investigated for several nanofibers for each tissue scaffold sample. The distribution was also approximately analyzed. Table 1 shows the results from the statistical analysis of surface roughness.

Figure 3.

Histograms of surface roughness (a) Sample A; (b) Sample B; (c) Sample C.

Table 1.

Surface roughness statistical analysis

Sample	Data points	Mode (nm)	Mean (nm)	Range (nm)	Variance (nm2)
A	3482	2.0	4.17	0.8 ∼ 19.7	9.1
B	5063	2.5	5.10	0.4 ∼ 20.0	15.5
C	12205	2.5	2.53	0.7 ∼ 7.4	1.2

The mode values were close for all three samples. The mean values might indicate a progression between the samples: Sample C (least) < Sample A < Sample B (greatest). However, the surface roughness distributions of samples A and B were wide spread with prominent tails and irregular values while the surface roughness distribution for sample C was narrow, peaked and smoothly connected. Analysis of the surface roughness distribution therefore indicated that sample C was different from samples A and B. The corresponding range and variance values further indicated that samples A and B were similar to each other but different from Sample C.

The histogram analysis shows the possibilities for misinterpretation of data using conventional AFM methods. The surface roughness mode values for the three samples were all very close. An individually applied ROI box would be most likely to return the mode value. However, the variances and distributions differed substantially between the samples. This was the true difference between the surface roughness of the samples, and it specifically indicated that sample C was different from samples A and B.

Elasticity

Atomic force microscopy can be used to measure elastic properties by collecting force curves over points on the surface of the sample. A single force curve records the force felt by the tip as it approaches and is then drawn away from the sample (Cappella and Dietler 1999; Butt et al 2005). It is more useful to collect arrays of force curves across the sample surface at regular intervals and this is known as force volume imaging (Hoh et al 1997). A force volume data set can be used to generate a 3-D map of interaction forces between the sample and tip.

The force curves in the force volume data set record the cantilever deflection (d) versus the height of the sample surface (Z). Rather than using the sample surface position (Z), it is more useful to use the distance (D) which is the relative separation between the tip and the sample surface, and this is known as a force-distance curve. A force-distance curve (FD) is defined as the cantilever deflection versus the absolute distance (D) between the tip and sample surface (D = Z – d). The Force Integration to Equal Limits (FIEL) (A-Hassan et al 1998) mapping method can be used to produce a robust measurement of relative elasticity. This method has the advantage of being independent of the tip-sample contact point, and of not requiring calibration of the AFM cantilever’s spring force constant. Using the Hertz model (Hertz 1881), which has been widely applied to AFM data, if the tip of an AFM is approximated by a sphere, then the force on the cantilever (F) can be defined from the indentation (δ), elastic modulus (E), Poisson ratio (v) and radius of the probe sphere

$$F_c=\frac{4E\sqrt{R}}{3(1-v)}{\delta }^{3/2}$$ (2)

To compare the elastic properties at two different positions, a pair of FD curves is collected at positions P1 and P2 using the relative trigger mode (Digital Instruments 2003–2). At these points, the force F₁ equals force F₂. The work done by the cantilever at each position is the area under a force-distance curve, and is given by

$$\text{w}={\int }_0^{{\delta }_t}\text{Force}.\hspace{0.17em}\hspace{0.17em}d\delta =\frac{8}{15}\frac{\sqrt{\text{R}}}{\pi \text{k}}{\delta }_t^{5/2}$$ (3)

Therefore, the relationship between the elasticity and the force-distance curve at two different data positions is

$$\frac{w_1}{w_2}={\left(\frac{k_1}{k_2}\right)}^{2/3}$$ (4)

where $k=\frac{1-v}{\pi E}$ is inversely proportional to E, the elastic constant which represents the local elasticity of the sample. The area under the FD curve can be calculated and used to represent the inverse relative elasticity of the tissue scaffolding. Similar to Reference (A-Hassan et al 1998), this area value was used to compare the three samples.

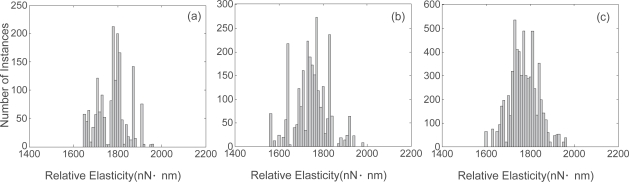
Each force curve in all three samples was triggered to exhibit the same maximum relative deflection of 45 nm. The area map of sample C, generated using the FIEL method, is shown in Figure 2d. Area maps for samples A and B, not shown, were also generated using the same method. The histograms for samples A, B and C are shown in Figure 4. As before, the mode, the mean value, the range, and the variance were investigated for each tissue scaffold sample, and the distribution was approximately analyzed. Table 2 shows the results from the statistical analysis of the elasticity.

Figure 4.

Elasticity histograms for (a) Sample A; (b) Sample B; (c) Sample C.

Table 2.

Elasticity/area map statistical analysis

Sample	Data points	Mode (nm2)	Mean (nm2)	Range (nm2)	Variance (nm4)
A	1739	1780.0	1777.8	1953.6 ∼ 1961.4	4463.3
B	2757	1770.0	1747.5	1563.7 ∼ 1979.2	5760.5
C	6325	1730.0	1770.7	1602.5 ∼ 1961.4	4144.3

The distribution of sample C was almost a normal distribution, while samples A and sample B had a symmetric but irregular distribution at both sides.

Two points were identified from the histogram analysis. The first was that samples A and B had similar distributions, but sample C had a different distribution even though the mode and mean of all three were close. The second was that sample B had the widest range, the largest variance and the most irregular distribution.

Curvature and deconvolution

Our properties measurements by SPRM techniques were along individual nanofibers, ie, along non-planar substrates. Two additional aspects considered in our analyses will now be discussed.

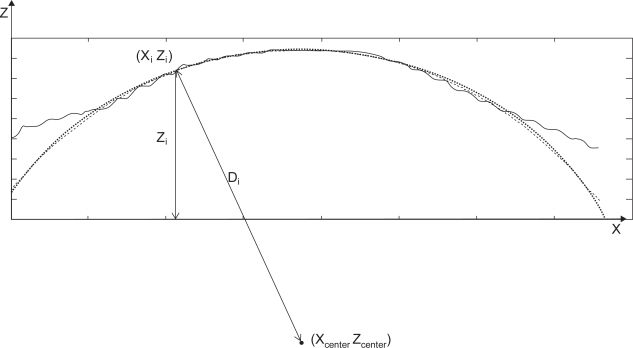
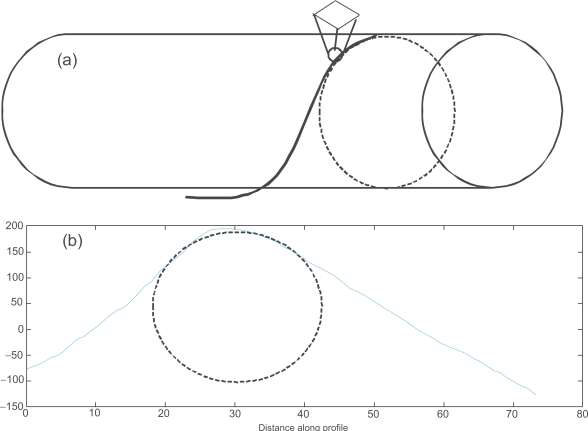
Height data, Z, is used to calculate the surface roughness. This is acceptable for samples whose surfaces are relatively flat because then the variation in height data will reflect the variation in their surface roughness. This assumption is no longer appropriate for tissue scaffolds because the nanofibers have a cylindrical shape. Therefore, the variation of the height data, Z, includes not only its surface roughness variation, but also the variation caused by the shape. In Scanning Probe Recognition Microscopy, distance data, D, instead of height data, Z, was used to determine the real roughness of the sample surface. The Kảsa circle fit method (Kasa 1976) was implemented to get the center (X_center, Z_center) of the most fitted circle as shown in Figure 5. Then the distance D_i

$$D_i=\sqrt{{(Z_i-Z_{center})}^2+{(X_i-X_{center})}^2}$$ (2)

between each point on the surface and the center was evaluated and used to calculate the surface roughness maps and histograms.

Figure 5.

Circle fit based on Kảsa method.

Only the center part of the height data was used to find the best fit circle. The boundary regions are unreliable due to tip-shape dilation effects. Dilation, or broadening of the image, is a result of the side of the tip coming into contact with the curved side of the nanofiber (Keller 1991; Villarrubia 1994). When an SPRM scan is focused on an individual nanofiber, both the edge and center data is acquired. However, only the center part of the nanofiber provides reliable data because of the tip convolution effect (Villarrubia 1997; Udpa et al 2006). The ideal AFM would have an infinitely sharp tip to reach as much of the surface as possible and an infinitely sharp impulse response in its feedback system to instantly adjust the height of the tip as it is scanned over the surface. In reality, the tip has a pyramidal or conical shape with some finite end radius so that it is durable enough to withstand the surface interaction forces. The effects of the tip shape cannot be avoided and these result in characteristic tip-dilation artifacts, as shown in Figure 6. In the present work, we restricted our properties evaluations to regions of reliable data through the use of an erosion operation (Gonzalez and Woods 2002). This is an important consideration when analyzing tissue scaffold nanofiber geometries (instead of planar substrates) using AFM-based methods.

Figure 6.

(a) Characteristic tip-dilation artifacts; (b) The cross section of a real AFM nano fiber image and the best fit circle.

Nanofiber diameter by transmission electron microscopy

TEM images of several nanofibers were taken to provide independent verification of nanofiber diameter, and from this, an estimate of the severity of tip-dilation artifacts present in the AFM images. Representative TEM images are shown in Figures 7a–7c. The nanofiber diameter measurements within the TEM images were taken using Scion Image software (http://www.scioncorp.com). Scion Image was used to obtain a conversion factor relating pixels to nanometers using the scale bar in the lower right corner of the TEM images. Scion Image uses this conversion factor to measure lines drawn in the program’s image editor in units of physical length. For each TEM image, three measurements of the nanofiber diameter were taken at distinct points along the length of the nanofiber. Care was taken to identify fluctuations in diameter that would be reflected in the mean and variance of the measurements.

Figure 7.

TEM images of (a) Sample A; (b) Sample B; (c) Sample C, with corresponding selective area electron diffraction (SAED) images shown (d–f).

Nanofiber diameter measurements within the AFM images were taken using the Nanoscope software. The software can be used to take a series of cross sections of the image orthogonal to the longitudinal axis of the nanofiber being measured. These cross sections are returned to the user as 1-dimensional signals representing height versus distance parallel to the cross section. The software can then be used to position markers at various points along the signal, allowing the user to measure the distance between them. As in the TEM images, three measurements were taken at a variety of points along the length of the chief nanofiber in each image. Variations in diameter were not as apparent in the AFM images, so care was taken to space the measurements evenly along the length of the nanofiber.

The discrepancy between the diameters measured using the TEM images and the diameters measured using the AFM images are given in Table 3. Based on these measurements, a dilation factor of over 100% was estimated for AFM measurements of all three samples. These results are demonstrative of the severity of tip dilation effects in AFM techniques. As previously discussed, an erosion operation was applied to both the surface roughness and elasticity data to restrict the properties analysis to the most reliable data.

Table 3.

Nanofiber diameter measurements using TEM and AFM images

Image	Section 1 (nm)	Section 2 (nm)	Section 3 (nm)	Mean (nm)	Standard deviation (nm)
TEM a1	120	100	130	116.6667	12.47219
TEM a2	110	120	150	126.6667	16.99673
TEM a3	109.86	99.78	105.74	105.1267	4.137933
TEM b1	117.67	117.02	106.88	113.8567	4.94038
TEM b4	111.3	77.52	97.52	95.44667	13.86834
TEM b9	65.91	111.96	98.03	91.96667	19.28252
TEM b12	110.01	94.34	91.89	98.74667	8.026939
TEM c3	69.14	82.53	84.76	78.81	6.898063
TEM c4	390	380	350	373.3333	16.99673
TEM c5	390	380	350	373.3333	16.99673
TEM c7	312.96	313.21	309.12	311.7633	1.871903
TEM c8	351.19	348.64	329.44	343.09	9.707986
TEM c9	345.83	325.06	327.96	332.95	9.184164
TEM c11	345.71	346.33	345.36	345.8	0.401082
TEM c14	415.95	388.83	345.04	383.2733	29.21432
TEM c16	377.23	369.2	337.71	361.38	17.05524
AFM A	647	589.91	494.77	577.2267	62.79142
AFM B	781.25	722.66	742.19	748.7	24.35819
AFM C	761.72	800.78	644.53	735.6767	66.39381
Average Dilation of A		509.5275%
Average Dilation of B		739.6577%
Average Dilation of C		220.8495%

Nanofiber properties by transmission electron microscopy with selected area electron diffraction

Typical TEM images of samples A, B, and C with corresponding selective area electron diffraction (SAED) images are shown in Figures 7d and 7e. Samples A and B both showed a dark contrast outer layer surrounding a light contrast inner core, possibly hollow, while sample C was solid throughout. Diffraction images for samples A and B showed prominent rings typical of disordered structures while diffraction images for sample C showed spots typical of an ordered (crystalline) structure. These results indicated that the atomic arrangement of sample C nanofibers was substantially different from sample A and B nanofibers.

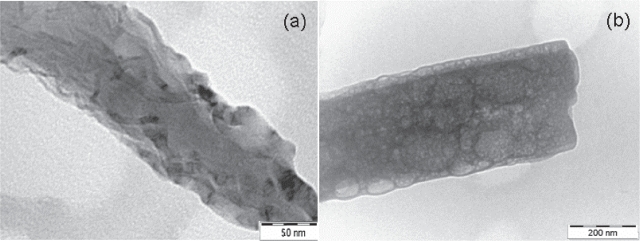
Close-up TEM images of samples B and C are shown in Figure 8. These images are consistent with the normal and narrow surface roughness distribution of sample C as well as the wide variance and irregular surface roughness distribution of sample B. Therefore the TEM results were consistent with the results obtained by SPRM which consistently indicated (1) that sample C was different from both samples A and B, and (2) that samples A and B, while similar, had differences with sample B having the more extreme values.

Figure 8.

Close up images (a) Sample B; (b) Sample C.

Conclusions

Using SPRM, we have performed first investigations of tissue scaffold properties directly along individual nanofibers. We have investigated surface roughness and elasticity properties that have been shown to influence cell attachment. This is the first time that statistically meaningful information has been extracted along individual nanofibers using an automatic procedure that maintains uniformity of experimental conditions.

The SPRM approach provided a wealth of data. Statistical methods based on histograms were developed to analyze the surface roughness and elasticity properties of the tissue scaffold nanofibers. The mode, mean range variance and distribution of surface roughness and elasticity were analyzed for tissue scaffold samples A, B and C. Sample C consistently showed properties that differed from samples A and B. The most prominent differences were observed in the surface roughness and elasticity distributions rather than in the individual mode values.

TEM with electron diffraction analysis confirmed that both the structure and surface properties of sample C differed from those of samples A and B. The electron microscopy results were consistent with the results of the histogram analyses using SPRM generated data, including the large property variances and wide irregular distributions observed for sample B as well as for the small variances and narrow smooth distributions observed for sample C.

SPRM has the obvious advantage of saving operation time by scanning only regions of interest and ignoring other parts of the sample. This is especially useful for investigations of tissue scaffold properties, as a scaffold is composed of many individual nanofibers. SPRM also enabled us to discriminate and use only the most reliable data from each nanofiber for the properties evaluations. Tissue scaffold nanofibers are curved surfaces while the conventional analyses are designed for flat surfaces. In the present work, a Kasa circle fit method is used to acquire the true surface roughness on a curved surface. An erosion operation was applied as the inverse operation to reverse the tip-shape dilation artifacts observable in AFM Section measurements and confirmed by independent TEM measurements of nanofiber diameter. In ongoing work, the hand-applied erosion operation will be replaced by automated erosion determined by mathematical morphology methods (Udpa et al 2006; Villarrubia 1997).

Any property that can be investigated by scanning probe microscopy can be investigated by Scanning Probe Recognition Microscopy auto-tracking of a region of interest. Work is ongoing to develop SPRM-based surface chemistry investigations, as this is known to be an important property for cell motility and adhesion (Ahmed et al 2006). Further work will develop data fusion methods that combine surface roughness, elasticity and surface chemistry information into a composite picture more truly representative of a cell’s perception its environment.