A Point Process Approach to Assess Dynamic Baroreflex Gain

Abstract

Evaluation of arterial baroreflex in cardiovascular control is an important topic in cardiology and clinical medicine. In this paper, we present a point process approach to estimate the dynamic baroreflex gain in a closed-loop model of the cardiovascular system. Specifically, the inverse Gaussian probability distribution is used to model the heartbeat interval, whereas the instantaneous mean is modulated by a bivariate autoregressive model that contains the previous R-R intervals and systolic blood pressure (SBP) measures. The instantaneous baroreflex gain is estimated in the feedback loop with a point process filter, while the RR→SBP feedforward frequency response gain can be estimated by a Kalman filter. The proposed estimation approach provides a quantitative assessment of interacting heartbeat dynamics and hemodynamics. We validate our approach with real physiological signals and evaluate the proposed model with established goodness-of-fit tests.

1. Introduction

Sudden changes in arterial blood pressure (ABP) induce a baroreceptor-cardiac reflex (baroreflex) that evokes an inverse change in heart rate (HR). Hence, a measure of baroreflex gain is essential in characterizing cardiovascular control and explaining both heartbeat dynamics and hemodynamics [1,2]. Since the cardiovascular system has a closed-loop interactions between many variables including R-R interval and ABP, research efforts have been devoted to estimating the baroreflex gain with a closed-loop system identification approach, which yields a more accurate assessment compared to open-loop approaches [3].

In our previous work [4-8], we have successfully applied probabilistic point process models for estimating instantaneous measures of HR, HR variability (HRV), as well as respiratory sinus arrhythmia (RSA). The point process framework enabled us to estimate these physiological indices in a dynamic fashion with a fine timescale. This paper expands on the point process approach to model the heartbeat interval, allowing for a dynamical assessment of the baroreflex gain in the feedback loop. In the meanwhile, we also model the feedforward cardiovascular loop and use a Kalman filter to track the parameters for estimating the RR→SBP frequency response. We demonstrate our proposed method with some physiological recordings and present some discussions in cardiovascular control.

2. Heartbeat interval point process model

Given a set of R-wave events ${\left\{u_j\right\}}_{j=1}^J$ detected from the electrocardiogram (ECG), let RR_j=u_j− u_j−1 > 0 denote the j^th R-R interval. By treating the R-waves as discrete events, we may develop a probabilistic point process model in the continuous-time domain. Assuming history dependence, the waiting time t − u_t (as a continuous random variable) until the next R-wave event can be modeled by an inverse Gaussian model [4]:

$$p\left(t\right)={\left(\frac{\theta }{2\pi t^3}\right)}^{\frac{1}{2}}\text{exp}\left(-\frac{\theta {\left(t-u_t-{\mu }_t\right)}^2}{2{\mu }_t^2\left(t-u_t\right)}\right)\left(t>u_t\right),$$

where u_t denotes the previous R-wave event occurred before time t, θ > 0 denotes the shape parameter, and μ_t ≡ μ_RR (t) denotes the instantaneous R-R mean that can be modeled by a time-varying linear predictive model:

$${\mu }_t=a_0\left(t\right)+\text{∑}_{i=1}^p{a}_i\left(t\right)R{R}_{t-i}+\text{∑}_{j=1}^p{b}_j\left(t\right)SB{P}_{t-j}$$ (1)

where the first two terms represent a linear autoregressive (AR) model of the past R-R intervals, and SBP_t−j denotes the previous j^th SBP value prior to time t.

2.1. Instantaneous indices of HR and HRV

Heart rate is defined as the reciprocal of the R-R intervals. For RR measured in seconds, r = c(t−u_t)⁻¹ (where c = 60 s/min) is a physiological measurement in beats per minute (bpm). By the change-of-variables formula, the HR probability $p\left(r\right)=p\left(c{\left(t-u_t\right)}^{-1}\right)$ is given by $p\left(r\right)=\left|\frac{dt}{dr}\right|p\left(t\right)$, and the mean and the standard deviation of heart rate r can be derived [4,5]

$${\mu }_{HR}={\stackrel{‵}{\mu }}^{-1}+{\stackrel{\sim }{\theta }}^{-1},{\sigma }_{HR}=\sqrt{\left(2\stackrel{‵}{\mu }+\stackrel{\sim }{\theta }\right)/\stackrel{‵}{\mu }{\stackrel{\sim }{\theta }}^2,}$$ (2)

where μ̀ = c⁻¹ μ_RR and θ͂ = c⁻¹θ. Essentially, the instantaneous indices of HR and HRV are characterized by the mean μ_HR and standard deviation σ_HR, respectively.

It is known from the point process theory that the conditional intensity function (CIF) λ(t) is related to the inter-event probability p(t) by a one-to-one transformation [9]: $\lambda \left(t\right)=\frac{p\left(t\right)}{1-{\int }_{u_t}^{t}p\left(\tau \right)d\tau }$. The estimated CIF can be used to evaluate the goodness-of-fit of the probabilistic model for the heartbeat dynamics. In addition, the quantity λ(t)Δ yields approximately the probability of observing a beat during the [t,t+Δ] interval.

2.2. Adaptive point process filtering

Let $\xi =\left[{\left\{a_i\right\}}_{i=0}^p,{\left\{b_j\right\}}_{j=1}^p,\theta \right]$ denote the vector that contains all unknown parameters in the probabilistic model, we can recursively estimate them via adaptive point process filtering [5]:

$$\begin{array}{c}{\xi }_{k|k-1}={\xi }_{k-1|k-1}\\ P_{k|k-1}=P_{k-1|k-1}+W\\ {\xi }_{k|k}={\xi }_{k|k-1}+P_{k|k-1}\left(\nabla \text{log}{\lambda }_k\right)\left[n_k-{\lambda }_k\Delta \right]\\ P_{k|k}={\left[P_{k|k-1}^{-1}+\nabla {\lambda }_k\nabla {\lambda }_k^T\frac{\Delta }{{\lambda }_k}-{\nabla }^2\text{log}{\lambda }_k\left[n_k-{\lambda }_k\Delta \right]\right]}^{-1}\end{array}$$

where P and W denote the parameter and noise covariance matrices, respectively; Δ =5 ms denotes the time bin size; $\Delta {\lambda }_k=\frac{\partial {\lambda }_k}{\partial {\xi }_k}$ and ${\Delta }^2{\lambda }_k=\frac{{\partial }^2{\lambda }_k}{\partial {\xi }_k\partial {\xi }_k^T}$ denotes the first- and second-order partial derivatives of the CIF w.r.t. ξ at time t = kΔ, respectively. The indicator variable n_k = 1 if a heart beat occurs in time ((k−1)Δ, kΔ] and 0 otherwise.

2.3. Closed-loop cardiovascular control

Baroreflex gain (SBP→RR loop)

First, we aim to model and assess the SBP→RR feedback loop, which is directly related to heart rate baroreflex. Among many methods, baroreflex gain has been estimated based on the coherence between heart rate and blood pressure [10]; alternatively, it has been estimated by a closed-loop bivariate AR model [3]. However, all of these approaches are batch-based with the assumption that the signals are stationary or locally stationary (within a moving window). Consequently, these approaches cannot fully capture the dynamic (non-stationary) nature of the physiological signals due to the drastic cardiovascular control compensatory changes. In contrast, our point process approach offers a way to estimate the instantaneous barorefex gain and to assess the heartbeat dynamics with a fine timescale.

Specifically, in light of (1) we can compute the frequency response for the baroreflex (SBP→RR loop)

$$H_{12}\left(f\right)=\frac{{{\sum }_{j=1}^q{b}_j\left(k\right)z^{-j}|}_{z=e^{j2\pi f_2}}}{1-{{\sum }_{i=1}^p{a}_i\left(k\right)z^{-i}|}_{z=e^{j2\pi f_2}}},$$ (3)

where f₁ and f₂ denote the rate for the R-R and SBP intervals, respectively; here we assume f₁ ≈ f₂ ≡ f. With the estimated time-varying AR coefficients a_i (k) and b_j (k) at time t = kΔ, we may evaluate the dynamic baroreflex gain (amplitude) and autospectrum in the frequency domain at different ranges (VLF, 0.01-0.05 Hz; LF, 0.05-0.15 Hz; HF, 0.15-0.5 Hz). The baroreflex gain, characterized by H₁₂ (f), represents the effect of SBP on heart beat, mediated by the neural autonomic reflex.

Modeling RR→SBP feedforward loop

Simultaneous to baroreflex assessment, we aim to model the RR→SBP feedforward loop, which enables us to study quantitatively the hemodynamics and to evaluate the impact of heartbeat on the arterial blood pressure. Similarly, SBP is modeled by a bivariate AR model:

$${\text{SBP}}_k=c_0+\text{∑}_{i=1}^p{c}_i\left(k\right){\text{SBP}}_{k-i}+\text{∑}_{i=1}^p{d}_j\left(k\right){\mu }_{RR}\left(k-i\right),$$

where μ_RR (k−i) represents the estimated instantaneous R-R mean value at the time when SBP-events occur. The coefficients ${\left\{c_i\right\}}_{i=0}^p$ and ${\left\{d_i\right\}}_{i=1}^p$ will be dynamically tracked by a Kalman filter [11]. Unlike the point process filter, the update occurs only at the time of SBP-events. Similarly, we can also estimate the frequency response of the RR→SBP cardiovascular loop:

$$H_{21}\left(f\right)=\frac{{{\sum }_{i=1}^p{d}_j\left(k\right)z^{-j}|}_{z=e^{j2\pi f}}}{1-{{\sum }_{i=1}^p{c}_i\left(k\right)z^{-i}|}_{z=e^{j2\pi f}}}$$ (4)

where f denotes the sampling rate (beat/sample) for SBP-SBP intervals. Likewise, we can estimate the dynamic gain and phase of H₂₁ (f) at each single SBP-event.

2.2. Goodness-of-fit tests

The goodness-of-fit of the probabilistic model is based on the Kolmogorov-Smirnov (KS) test [9]. Given a point process specified by J discrete events: 0 < u₁ < ··· < u_j < T, compute $z_j={\int }_{u_{j-1}}^{u_j}\lambda \left(\tau \right)d\tau$. If the model is correct, then the variables v_j = 1−exp(−z_j) are independent, uniformly distributed within the range [0, 1], and g_j = Φ⁻¹(v_j) (where Φ(‵) denotes the cumulative density function (cdf) of the standard Gaussian distribution) are independent standard Gaussian random variables. To compute the KS test, the v_j s are sorted from the smallest to largest value, and plotted against the cdf of the uniform density defined as $\frac{j-0.5}{J}$. Ideally, the points should lie on the 45° line, and the 95% confidence interval lines are $y=x\pm \frac{1.36}{{\left(J-1\right)}^{1/2}}$. The KS distance, defined as the maximum distance between the KS plot and the 45° line, is used to measure the lack-of-fit between the model and the data. We also compute the autocorrelation function of g_js: $\text{ACF}\left(m\right)=\frac{1}{J-m}{\sum }_{j=1}^{J-m}{g}_j{g}_{j+m}$. If the g_js are independent, ACF (m) shall be small (around 0 and within the 95% confidence interval $\frac{1.96}{{(J-1)}^{1/2}}$) for all values of m.

3. Experimental Results

The first heartbeat data set, which was retrieved from Phyisonet (http://www.physionet.org/) [12], consists of multi-parameters including ECG traces, arterial pressure recorded from patients in critical care units (from MGH/MF Waveform Database). Due to space limit, we randomly selected segments of recordings from one subject who had artifact-free calibrated R-R series and arterial pressure measurements. Figure 1 illustrates the signals as well as their power spectra and coherence (magnitude and phase). As seen from the figure, the R-R and SBP signals appear more coherent in the VLF and LF ranges.

Figure 1.

1st column: A snapshot of ECG and ABP signals (systolic and diastolic pressures are measured at the time of ventricular contraction and relaxation, respectively). 2nd column: 20-min recordings of R-R and SBP time series. 3rd column: Parametric AR(8) autospectra. 4th column: Coherence magnitude and phase

The initial parameters are estimated from the first 2-min recordings of the R-R and SBP beat series. Parameters ${\left\{a_i\right\}}_{i=0}^p,{\left\{b_i\right\}}_{i=1}^p$, and ${\left\{c_i\right\}}_{i=0}^p,{\left\{d_i\right\}}_{i=1}^p$ are estimated by a bivariate AR model assuming a closed-loop system [3], whereas the shape parameter is estimated by θ = μ³/σ² from the R-R series. Order selection of the bivariate AR was selected based on the Akaike information criterion (AIC). Order p=8 was used in the current experiment.

For the selected subject, we estimate the instantaneous HR and HRV statistics (Fig. 2), the dynamic baroreflex gain and phase, as well as the mean gains of the frequency responses in both feedback and feedforward loops (Fig. 3). To evaluate the model fit, we examine the resultant KS plot and autocorrelation plot (Fig. 4). The fact that the curves fall almost within the 95% confidence bounds indicates a good fit of the model to the heartbeat events. As a comparison, we also conducted an experiment that does not consider SBP in the point process model and repeated the KS test. The KS distance was found to be 0.092. Therefore, the inclusion of SBP as covariate helps improve the model fit for the data. This result is not surprising considering that in the closed-loop cardiovasular system, heartbeat and blood pressure/volume are directly (or indirectly through other factors) influenced by each other. In addition, the correlation coefficients between the mean baroreflex gain (LF) and μ_RR (t) and μ_HR (t) are 0.837 and -0.843, respectively, suggesting that in this case fast dynamic changes of the baroreflex gain reflect reverse changes in HR.

Figure 2.

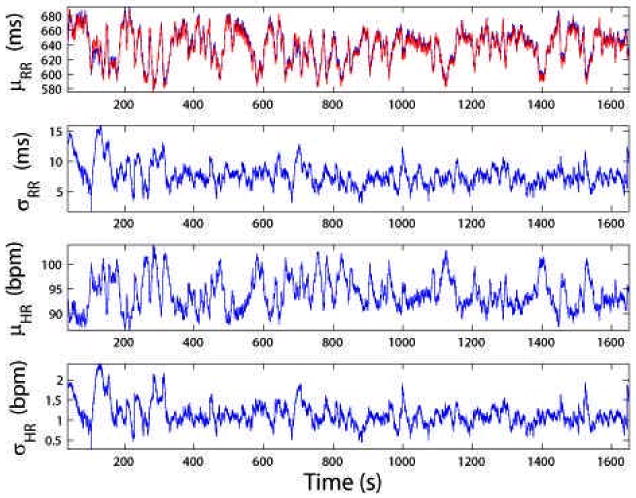
From top to bottom: instantaneous estimates of μ_RR (superimposed by red trace of R-R time series), σ_RR, μ_HR and σ_HR statistics (MGH/MF database subject 007)

Figure 3.

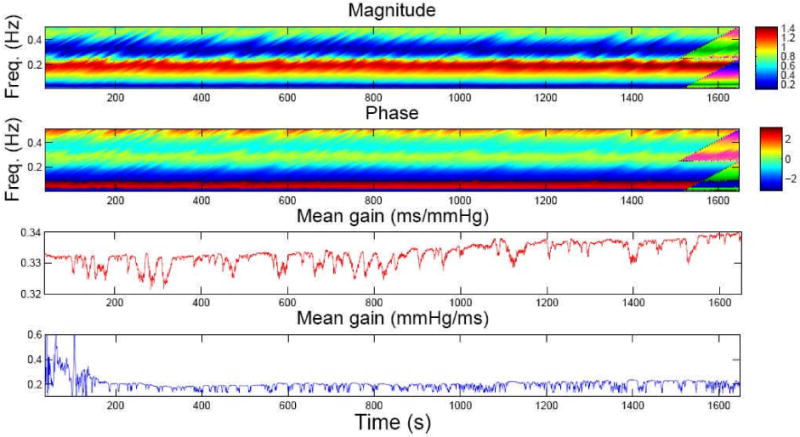
Top two panels: Image visualization of dynamic baroreflex gain and phase (within 0.01-0.5 Hz). Bottom two panels: tracking the mean baroreflex gain (red) and the mean gain of RR→SBP frequency response (blue)

Figure 4.

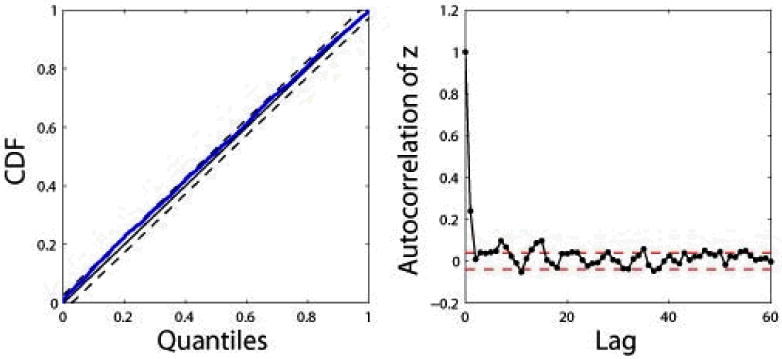
KS plot (KS dist. 0.052) and autocorrelation plot (dashed lines indicate the 95% confidence bounds)

Next, we analyzed a previously studied heartbeat data set (details of the “tilt-table” protocol were given in [4]). For demonstration purpose, in Fig. 5 we plot eight epochs of R-R and SBP recordings when a subject underwent a few cycles of “rest” and “tilt” posture conditions. The instantaneous HR, HRV, and baroreflex gain indices are estimated from the complete time courses (Fig. 5) and then divided into two groups (rest vs. tilt) for statistical comparison. Furthermore, a rank-sum test was applied to evaluate the null hypothesis that the medians of the rest and tilt conditions are equal. The null hypothesis is tested with 95% confidence (P<0.05). As a comparison, the open-loop baroreflex gain (denoted as $\left|H_{12}^{\text{open}}\left(f\right)\right|$) was also computed for each epoch with a standard batch spectral estimation method [10]. As seen in Table 1, the open-loop method tends to overestimate the baroreflex gain (in both LF and HF). Similar results were also found in other subjects (not shown here).

Figure 5.

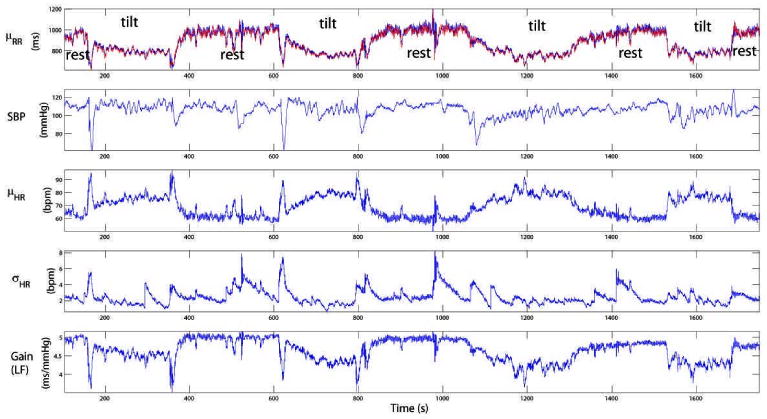
Dynamic tracking of the baroreflex gain in a rest-tilt study

Table I. Comparison of statistical indices between the rest and tilt conditions (in one subject). The baroreflex gains (ms/mmHg) listed here are computed within the LF range.

	RR (ms)	SBP (mmHg)	HRV (bpm)	|H12 (f)|	$\left|H_{12}^{\text{open}}(f)\right|$
rest	965±47	108.9±4.7	2.70±0.87	4.91±0.12	12.8 ±1.5
tilt	773±36	105.2±6.4	1.96±0.56	4.37±0.19	5.9±0.9
P-value	< le-8	< le-8	<le-8	<le-8	0.02

4. Conclusion

We propose a point process framework to capture the transient dynamics of HR and HRV, and to model the dynamic nature of the baroreflex frequency response in a non-stationary environment.

Our results confirm that the closed-loop identification approach is a more appropriate framework for modeling cardiovascular control dynamics, and that the open-loop approach leads to overestimation of the baroreflex gain. In addition, the instantaneous estimation of baroreflex frequency response produces a dynamic assessment at a fine timescale. Currently, our model is restricted in using only the SBP events. A possible inclusion of the diastolic events, or even the continuous ABP traces, will be the subject of our future investigation. Consideration of continuous-time ABP as covariate could reveal a more accurate description of the complex dependency between heartbeat dynamics and hemodynamics.

To conclude, statistical modeling of the feedforward and feedback loops in cardiovascular control could shed important insights into a large majority of cardiovascular diseases and disorders (e.g., hypertension and congestive heart failure) related to systemic hemodynamic dysfunction. Furthermore, the instantaneous point process indices of HR, HRV, and baroreflex gain can provide a potential real-time noninvasive assessment for ambulatory monitoring in clinical practice.