Abstract
Cardiac resynchronization therapy (CRT) is a promising therapy for heart failure patients with a conduction disturbance, such as left bundle branch block. The aim of CRT is to resynchronize contraction between and within ventricles. However, about 30% of patients do not respond to this therapy. Therefore, a better understanding is needed for the relation between electrical and mechanical activation. In this paper, we focus on to what extent animal experiments and mathematical models can help in order to understand the pathophysiology of asynchrony to further improve CRT.
Keywords: Biventricular pacing, CHF, LBBB, Dyssynchrony
1. Introduction
A proper, almost synchronous, sequence of activation is important for optimal cardiac pump function. The physiological activation of the ventricles is altered in the presence of a conduction disturbance, such as left bundle branch block (LBBB), and during conventional right ventricular (RV) pacing. In both conditions the electrical activation and contraction moves from RV to left ventricle (LV) and within the LV from septum to free wall. During the last decade it has been recognized that this kind of asynchrony is a risk factor for development of heart failure (Sweeney and Prinzen, 2006). Meanwhile also cardiac resynchronization therapy (CRT) has evolved. In this therapy electrical activation and contraction of the ventricles are resynchronized by (almost) simultaneous stimulation of both ventricles (“biventricular (BiV) pacing”). CRT is currently recommended for patients with heart failure (NYHA class II–IV) and wide QRS complex. In practice, this relates to patients with LBBB or with a RV pacemaker. Clinical CRT trials have demonstrated that patients’ cardiac pump function (Auricchio et al., 1999) and quality of life improve, and that hospitalization for heart failure and mortality decreases (McAlister et al., 2007). Currently, on a yearly basis tens of thousands of CRT devices are implanted worldwide. A clear positive response to CRT is observed in about 70% of the patients (McAlister et al., 2007). This number implies that about 30% of patients receive insufficient therapy and/or unjustified pacemaker implantation. Moreover, the variable degree of benefit between the “responders” raises the question whether CRT is always applied in the optimal fashion. Therefore, there is a need for better understanding the role of asynchrony and resynchronization on pump function and heart failure. Several excellent reviews have recently appeared about clinical aspects of CRT (Bax et al., 2005; Kass, 2005; McAlister et al., 2007). The goal of the present article is to review to what extent animal experiments and mathematical models can help to understand the pathophysiology of asynchrony and can be used to further improve CRT. To this purpose we will discuss the following issues:
The effect of asynchronous electrical activation on cardiac regional and global pump function, especially during LBBB. In patients this relation is hard to investigate, because comorbidity may confound the role of LBBB. This topic will be discussed using data from the canine LBBB model (Section 2.1). Furthermore, studies in mathematical models (Section 3.2) allow better understanding of the cellular mechanisms of mechanical dyssynchrony (Prinzen et al., 1999), which are incompletely understood (Coppola et al., 2007). Moreover, computational models were used to establish the role of mechanical interaction between the RV and LV (Section 3.1), an interaction, which has been proposed to be important for optimal application of CRT (Bleasdale et al., 2004).
The role of longer lasting LBBB on cardiac structure and function is not known, nor to what extent CRT restores cardiac function to “pre-LBBB” levels. This is due to the fact that it is usually not known when LBBB started and because comorbidity in LBBB patients is considerable. In Section 2.2 data will be discussed on the long-term effects of isolated LBBB and of CRT in canine LBBB hearts.
The abnormal mechanical loading of the myocardium in asynchronous ventricles may elicit mechano-electrical feedback, thereby influencing ventricular repolarization (Costard-Jackle et al., 1989), potentially leading to pro-arrhythmogenic effects of CRT (Medina-Ravell et al., 2003). Data from animal experiments will be discussed in order to evaluate this topic (Section 2.3).
The optimal site and timing of stimulation in CRT are still debated. Insight in this field from computer models will be discussed in Section 3.3.
In part 4 a synthesis is provided, relating all studies to potential clinical implications and discussing the strengths and weaknesses of the models used.
2. Animal experiments in LBBB hearts
The detrimental effect of ventricular pacing on cardiac function—as compared with a physiologically activated heart—has been well documented (reviewed in Prinzen and Peschar, 2002; Sweeney and Prinzen, 2006). However, the case of LBBB is less well characterized, because usually LBBB has a silent onset. Moreover, LBBB frequently coincides with other cardiovascular complications, thus obscuring the influence of LBBB on cardiac function. Therefore, the recent development of an animal model of LBBB is an important contribution to this field. LBBB was created by radiofrequency ablation of the proximal part of the left bundle branch in the canine heart (Verbeek et al., 2003; Vernooy et al., 2007).
The sequence of electrical activation is similar in RV pacing and LBBB (Verbeek et al., 2003). Therefore, in this article data from RV pacing will be mentioned if corresponding data from LBBB are unavailable.
2.1. Electro-mechanics
Fig. 1 shows bulls-eye plots of electrical activation and mechanical function before inducing LBBB, during LBBB and during BiV pacing in the canine LBBB model. In the normal heart electrical endocardial activation of the LV is virtually synchronous (within 10 ms; 2nd row of Fig. 1). This coincides with QRS duration of ∼60 ms (upper row of Fig. 1). During LBBB the shape of the QRS complex changes, QRS width increases to ∼120 ms (1st row) and electrical activation of the LV lateral wall is delayed (second row). BiV pacing (using an AV-delay shorter than intrinsic AV conduction and simultaneous stimulation of the RV apex and LV lateral wall) causes narrowing of the QRS complex from ∼120 to 105 ms and more synchronous endocardial LV activation than during LBBB, albeit with a slightly later activation in the posterior than in the anterior wall (Vernooy et al., 2007).
Fig. 1.
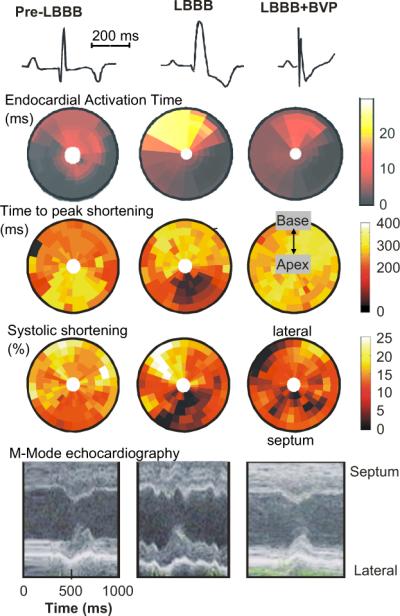
Electro-mechanics in the canine LBBB model. Examples of ECG (first row), endocardial electrical activation (2nd row), time to peak shortening (3rd row), percent systolic shortening (4th row) and endocardial wall motion (5th row), as observed before (left panels) and after inducing LBBB (middle panels) and during biventricular pacing (BVP) in the LBBB model (right panels). Timing of peak shortening is the time between the R wave and minimum circumferential strain. The % systolic shortening is the difference in circumferential strain between begin and end ejection. In the bulls-eye plots the lower half depicts the interventricular septum and the upper half the LV lateral wall; outer rings represent the base and inner rings the apex. Data are derived from (Vernooy et al., 2007). For each row the scale holds for each panel.
In Fig. 2 midwall circumferential strains, as derived from MRI tagging measurements, are depicted (Vernooy et al., 2007). Before LBBB the shape of strain vs. time is similar around the LV wall, with almost a linear shortening in all regions during the ejection phase. The 3rd row of Fig. 1 shows that in the normal heart the timing of peak shortening (time from Q-wave on ECG or pacing artifact until the first peak of shortening) is almost simultaneous. The percent systolic shortening (4th row in Fig. 1) ranges between 10−15% in the septum and 15−20% in the LV free wall. On M-mode echocardiograms (5th row), inward endocardial wall motion peaks almost simultaneously in the septum and lateral wall, resulting in a septum–posterior wall motion delay of about 60 ms (Vernooy et al., 2007).
Fig. 2.
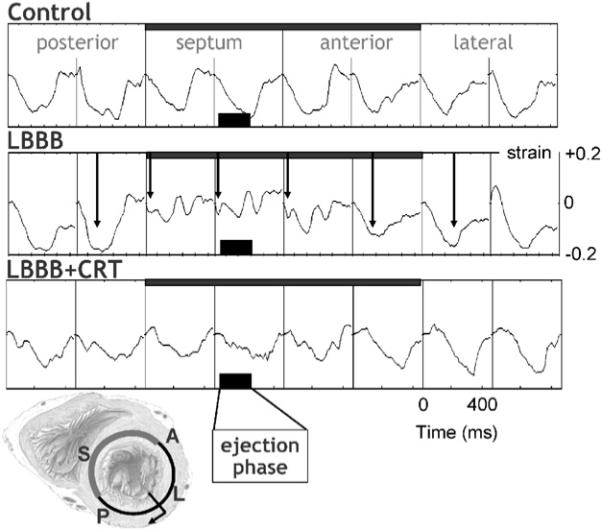
Typical example of myocardial circumferential strain tracings in eight regions along the circumference in a mid-basal short-axis LV slice. Strain was referenced to end-diastole. Arrows in the middle row indicate the time of peak shortening. Data are derived from Vernooy et al. (2007). Scales mentioned in one panel also hold for the other panels. The short axis section of the heart in the lower left corner illustrates the position of the eight regions of which the strains are derived from. P = posterior, S = septum, A = anterior.
The asynchronous electrical activation during LBBB also leads to asynchronous and dyscoordinate contraction, as evidenced by the strain and endocardial wall motion patterns. In the septum, being activated earliest, shortening also starts early (middle column in Fig. 1), resulting in a small and very early peak of shortening (middle row in Fig. 2). After this early peak in shortening, no further shortening occurs during systole, often even systolic stretch occurs, followed by premature relaxation (Fig. 2). In contrast, in late-activated regions in the LV anterior and lateral wall the fibers are subjected to early systolic pre-stretch (Fig. 2). This stretch is followed by doubling of net systolic shortening and by delayed relaxation. Therefore, during asynchronous activation local contraction patterns do not only differ in their onset, but also, and more importantly, in their pattern. Consequently, the dyssynchrony with regards to peak shortening is considerably larger (approximately 300 ms, middle panel of the 3rd row of Fig. 1) than the electrical asynchrony. A qualitatively similar difference between electrical and mechanical asynchrony has been observed in the normally activated heart, albeit that absolute time differences are obviously smaller (Ashikaga et al., 2007).
The described contraction patterns also imply that opposing regions of the ventricular wall are out of phase and that energy generated by one region is dissipated in opposite regions. This explains that observed efficiency of metabolic to mechanical energy conversion is lower during RV pacing than during atrial pacing (Baller et al., 1988).
The local differences in wall motion and deformation, as mentioned above, reflect regional differences in myocardial work. This was demonstrated by construction of local fiber stress–fiber strain diagrams and calculation of local external and total mechanical work (Prinzen et al., 1999; Vernooy et al., 2005). In early activated regions (as in the septum of the LBBB heart) shortening occurs at low pressure, whereas these areas are transiently being stretched at higher ventricular pressures. As a consequence the stress–strain loops have a figure-eight like shape with a low net area, indicating the absence of external work. In regions remote from the pacing site (or in the lateral wall in case of LBBB), the loops are wide and external work can be up to twice that during synchronous ventricular activation. Total myocardial work (sum of external work and potential energy) is reduced by 50% in early activated regions and is increased by 50% in late-activated regions, as compared with atrial pacing (Prinzen et al., 1999; Vernooy et al., 2005).
In accordance with the regional differences in mechanical work in the LBBB heart, differences in regional blood flow are also observed. During LBBB septal blood flow is ∼30% lower than before LBBB, whereas it is ∼30% higher in the lateral wall (Vernooy et al., 2005). Reduced septal perfusion and oxygen consumption have also been observed in patients with LBBB (Lindner et al., 2005). Various observations, such as close correlation between local myocardial oxygen consumption, work and blood flow as well as the absence of hibernation in canine hearts with chronic LBBB, suggest that the depressed septal perfusion is a physiological consequence of the lower demand. It can, however, not be excluded that at higher heart rate the asynchronous contraction pattern may also impede myocardial perfusion (reviewed in Prinzen and Peschar, 2002).
BiV pacing in the LBBB heart causes an almost normalization of the time course of strain (right panels in Fig. 1 and lower row in Fig. 2). Peak shortening time becomes more synchronous and systolic shortening is more uniformly distributed during BiV pacing than during LBBB, albeit that some differences remain. Most notably, during BiV pacing some regions in the septum and LV lateral wall show a low systolic shortening, presumably because these are close to the site of pacing. Briefly upon starting BiV pacing, the distribution of myocardial blood flow is normalized and this is maintained throughout 8 weeks of BiV pacing (Vernooy et al., 2007). This quick normalization of blood flow is a further indication that, as discussed above, myocardial blood flow in asynchronous hearts follows regional energy demands.
Given the highly abnormal and dyscoordinate contraction patterns observed during LBBB, it is not surprising to see that LBBB significantly impairs cardiac pump function. Immediately upon inducing LBBB in the canine heart, indices of systolic and diastolic function, such as the maximal rate of rise of LV pressure (LV dP/dtmax, to 78 ± 5% of pre-LBBB) and maximal rate of fall of LV pressure (LV dP/dtmin) are decreased (Vernooy et al., 2007). These changes are comparable with those during ventricular pacing (reviewed in Prinzen and Peschar, 2002). LV dP/dtmax is dependent on preload, but because LBBB hardly influences LV end diastolic pressure (Table 1) the decrease in LV dP/dtmax can be regarded as a strong indication that LBBB reduces LV contractility.
Table 1.
Canine hemodynamic data for LBBB and CRT
| Pre-LBBB | Acute LBBB | 8 weeks LBBB | Acute BVP | 8 weeks LBBB + 8 weeks BVP | |
|---|---|---|---|---|---|
| Heart rate (bpm) | 89±9 | 95±9 | 82±11 | 90±12 | 92±10 |
| QRS duration (ms) | 69±8 | 119±9a | 123±11a | 108±8a,b | 102±9a,b |
| LV SP (mmHg) | 105±4 | 100±5 | 111±4 | 116±3 | 101±4 |
| LV EDP (mmHg) | 8±3 | 6±2 | 7±4 | 8±5 | 6±3 |
| LV dP/dtmax (mmHg/s) | 2263±671 | 1777±373a | 1798±490a | 2003±580a,b | 2160±509b |
| LV dP/dtmin (mmHg/s) | 2360±296 | 1988±412a | 1616±274a | 1871±270a,b | 2021±342c |
| RV SP | 27±5 | 33±7 | 25±7 | 30±7 | 27±4 |
| RV EDP | 4±2 | 4±2 | 4±2 | 6±2 | 4±1 |
| RV dP/dtmax | 458±138 | 527±227 | 408±176 | 487±236 | 556±227 |
| RV dP/dtmin | 334±159 | 309±153 | 264±113 | 313±118 | 309±134 |
LV dP/dtmax: maximal rate of increase in left ventricular (LV) pressure; LV SP: LV systolic pressure; LV EDP: LV end-diastolic pressure. Values are presented as mean ± SD.
p<0.05 compared to pre-LBBB.
p<0.05 compared to 8 weeks’ LBBB.
p<0.05 vs. acute BVP.
Interestingly, LBBB did not reduce RV function parameters, RV dP/dtmax even tended to increase. Upon starting BiV pacing, LV dP/dtmax immediately increased to 86 ± 5% of pre-LBBB followed by a slight further improvement to 89 ± 5% of pre-LBBB values after 8 weeks of BiV pacing. Therefore, the data from this animal study indicate that BiV pacing clearly improves cardiac pump function in the LBBB heart, but does not return it completely to normal values, presumably because the physiological sequence of activation and contraction cannot be completely restored (Wyman et al., 2002).
2.2. Chronic effects: structural remodeling
While the previous paragraph describes the considerable acute electro-mechanical consequences of LBBB, long-term adaptations of the heart to LBBB may be at least as important. These adaptations to LBBB and ventricular pacing have many characteristics in common with, for example, pressure and volume overload and myocardial infarction.
First of all, changes in regional mechanics (stretch, systolic shortening, and mechanical work) seem to have an important impact on regional growth. This was initially demonstrated in dogs with chronic LV pacing (Van Oosterhout et al., 1998), where echocardiographically observed growth corresponded with changes in local myocyte size, thus demonstrating that heterogeneous cellular hypertrophy is an important consequence of asynchronous activation.
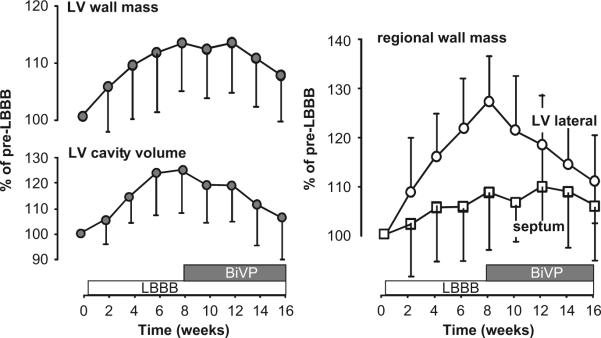
Asymmetric hypertrophy also applies to the situation of LBBB (Vernooy et al., 2005). Within 2 months of experimental LBBB, hypertrophy is observed specifically in the late activated LV lateral wall (Fig. 3, right panel), the region where mechanical work is increased (Fig. 1). There, local wall mass increases by ∼30%, whereas mass of the septum hardly changes. Similar to the normalization of regional workload after initiation of BiV pacing, regional differences in hypertrophy also disappear within 2 months of BiV pacing (Fig. 3, right panel). In addition to the changes in local muscle mass, total LV mass (by ∼17%) and LV cavity size (by ∼30%) increased within two months of LBBB (Fig. 3, left panels). Within 2 months of BiV pacing, LV cavity size returns to pre-LBBB levels, whereas LV mass decreases, but still remains somewhat elevated. The relative decrease in LV cavity size upon BiV pacing in the canine LBBB model ( 20%) is similar to that observed in patients receiving CRT (Yu et al., 2002).
Fig. 3.
Time course of LV wall mass and cavity volume (left, global structural remodeling) and septal and LV free wall mass (regional structural remodeling, right) during 8 weeks of LBBB followed by 8 weeks of biventricular pacing in the canine heart. Data are derived from Vernooy et al. (2007). Mean values and SD are presented.
2.3. Mechano-electrical feedback
In addition to the structural changes, electrophysiological changes have also been found in the chronically asynchronous heart. Spragg and coworkers showed that after 4 weeks of LBBB, action potential duration (APD) and refractory period are reduced in the late activated lateral wall (Spragg et al., 2005). Somewhat different, but equally interesting data were reported recently by (Jeyaraj et al., 2007). This group showed that 4 weeks of LV pacing in dogs prolonged APD in the earliest and latest activated regions, but shortened in regions with intermediate activation time. In addition to the abovementioned changes in APD, also conduction velocity is reduced in the late activated regions (Spragg et al., 2005). Moreover, normal differences in conduction velocity between endocardium and epicardium are reversed in the late activated lateral LV wall (Spragg et al., 2005). While the total expression of connexin43 is unaltered in LBBB hearts, its subcellular location was redistributed in late-activated myocardium from intercalated discs to lateral myocyte membranes.
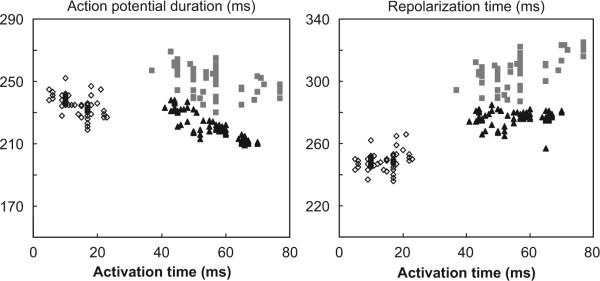
In many cases electrical remodeling leads to arrhythmogenesis. However, arrhythmias are rare in LBBB hearts (Spragg et al., 2005; Vernooy and Prinzen, unpublished data). This may be explained by examining the relation of local APD with local activation time (AT, Fig. 4).
Fig. 4.
Action potential duration (left) and repolarization time (right) as a function of activation time of a canine heart during normal ventricular conduction (open diamonds), 1 h (grey squares) and 4 months after inducing LBBB (black triangles). Each data point represents measurement at one of 64 electrodes at the LV endocardium.
This relation was obtained with use of a 64-electrode array (“basket electrode”) positioned along the LV endocardium in a canine heart before LBBB as well as after 1 h and 4 months of LBBB. Each data point is derived from one of the 64 electrodes. Before LBBB, APD is inversely related to AT (open symbols, left panel). As a consequence, the dispersion of repolarization time is small (∼20 ms, right panel). After 1 h of LBBB the relation between AT and APD is shifted upward and considerably less clear (grey symbols in left panel) and leads to an increase in dispersion of repolarization to ∼40 ms (right panel). However, 4 months later the AT–APD relation shows that the latest activated regions again have the shortest APD (left panel, black symbols) and that the dispersion of repolarization is similar to the pre-LBBB situation. These observations confirm the observations of Spragg and colleagues that, during chronic LBBB APD shortens in late activated regions (Spragg et al., 2005) and also shows that this APD shortening in late activated regions compensates, at least partly, for the delay in activation, resulting in virtually unchanged dispersion in repolarization despite asynchronous activation. Our data are also in agreement with the data from Costard-Jäckle and Franz in the paced rabbit heart, showing disturbance of the AT–APD relation after a short period of pacing (Costard-Jackle et al., 1989).
The mechanism by which this electrical remodeling takes place is not yet completely resolved. However, it is striking that APD is altered in the latest activated region, the region, which also undergoes early systolic stretch. Since it is hard to imagine that cells on their own can sense the sequence of electrical activation, plausible triggers for such electrical remodeling are the abnormal mechanical loading sensed by the cells or, potentially, local cardiac nerves. Jejeray et al provide, indeed, some evidence that changes in APD during long lasting asynchronous activation are related to the abnormal strains (Jeyaraj et al., 2007). Therefore, the intriguing paradigm emerges that abnormal electro-mechanical activation leads to mechano-electrical feedback. In the non-failing LBBB heart, as discussed here, this feedback appears to be functional in that it prevents dispersion of repolarization to increase in an asynchronous heart. This physiological adaptation may be lost in failing hearts, because failing asynchronous hearts are susceptible to arrhythmias. This aberration could be explained by more pronounced molecular remodeling in failing than in non-failing LBBB hearts (Spragg et al., 2003).
3. Mathematical simulation of LBBB and resynchronization
Animal experiments are very useful for solving some of the questions on effects of a derangement (like LBBB) and a therapy (like CRT). However, such experiments have the drawback that within the same individual, only a limited number of parameters can be easily manipulated and/or measured and that the biological variation (in time and between individuals) can obscure effects.
Mathematical models lack these disadvantages and can, therefore, be very effective. For clinical application, predictive mechanistic models (Kerckhoffs et al., 2006; McCulloch, 2004) will become more feasible because of growing computer power, development of efficient algorithms, and availability of more data on molecular and cellular mechanisms.
Below, data from various computational models are discussed in the light of the topics (a) and (d), mentioned in Section 1.
3.1. Ventricular interaction
3.1.1. The TriSeg/CircAdapt model
To better understand the influence of timing of ventricular mechanical activation on global ventricular pump function, we used a mathematical model consisting of the CircAdapt model, extended with the TriSeg module, which incorporates mechanical interaction of the three ventricular wall segments.
The CircAdapt model of the heart and circulation is a lumped-parameter model of the whole circulation, (Arts et al., 2005) meaning that the continuous distribution of pressures and flows in the circulation is represented by pressure and flow values at a few representative locations. It differs from other lumped-parameter models in that the number of independent parameters is reduced enormously (from several dozens to 12) by incorporating adaptation of ventricular and vascular geometry to mechanical load so that stresses and strains in walls of heart and blood vessels are normalized to a tissue-specific physiological standard level. Resulting time courses of flows and pressures in the simulated circulation appear physiological during various hemodynamic conditions (Arts et al., 2005).
The CircAdapt model is configured as a network, consisting of a few types of modules, i.e. contractile chambers, compliant blood vessels, valves with inertia, and flow resistances (Fig. 5A). The atria and ventricles are chambers, described by the one-fiber model, defining sarcomere length in the wall as a function of cavity volume. With a realistic model of sarcomere mechanics, incorporating Hill's and Starling's relations, sarcomere length renders fiber stress and the velocity of sarcomere shortening. Using the stress-related equation of the one-fiber model, cavity pressure is described as a function of myofiber stress and the ratio of cavity volume to wall volume. For blood vessels, the same one-fiber model is used, relating blood pressure and cross-section of lumen and wall to stress and strain in the fibers of the wall material.
Fig. 5.
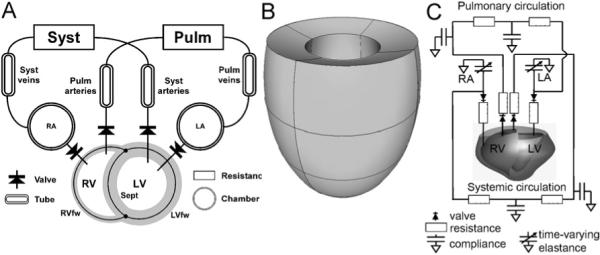
Three kinds of computational models. (A) The TriSeg/CircAdapt model. Three thick-walled spherical segments, i.e. the LV free wall segment (LVfw), the RV free wall segment (RVfw), and the septal wall segment (Sept) are coupled mechanically at the midwall junction, thus forming a left (LV) and a right (RV) ventricular cavity. Cardiac valves connect the atria to the ventricles (chamber module) and the ventricles to the systemic (Syst) and pulmonary (Pulm) circulations, containing tube and resistance modules. (B) Finite element model of the left ventricle, approximated by an ellipsoid (Kerckhoffs et al., 2003). (C) Hybrid finite element model of LV/RV and lumped parameter systems-model with a realistic geometry of a canine heart (Kerckhoffs et al., 2007b).
The TriSeg module describes ventricular mechanics and consists of two ventricular cavities separated by a shared septal wall and enclosed by an LV and an RV free wall (Fig. 5A). The wall segments are modeled as thick-walled spherical segments that are coupled mechanically at a common midwall junction (Lumens et al., 2008). In the TriSeg module, ventricular geometry is described initially by known LV and RV cavity volumes and estimates of size and curvature of the septum. The latter two geometric parameters are solved by stating equilibrium of forces in the junction of the wall segments. From the geometry of the walls, sarcomere length is calculated, serving as basis for calculation of myofiber stress using the empirical model of sarcomere mechanics mentioned above. Transmural pressure differences and tensions of the wall segments are derived from myofiber stress, while using curvature and thickness of the wall. Finally, pressures in the LV and RV cavities are calculated from the pressure differences across the walls (Lumens et al., 2008).
Size and thickness of the ventricular wall segments, atrial walls, and blood vessels were adapted to accommodate baseline canine loading conditions.
3.1.2. Simulation of ventricular interaction
Simulations were performed in the Control condition, where mechanical activation of the RV free wall, the septum and the LV free wall was simultaneous. Subsequently, LBBB was simulated by a delay (30 ms, “LV30,30”) of septal and LV free wall activation time with respect to that of the RV, thus simulating activation of the ventricles from the right bundle branch alone in combination with a synchronous LV (RV–LV asynchrony, intra-LV synchrony). Furthermore, “LV30,60” and “LV30,90” simulations were performed, using a septal delay of 30 ms in combination with a LV free wall delay of 60 and 90 ms, respectively (RV–LV asynchrony in combination with intra-LV asynchrony). Under all conditions, cardiac output, heart rate, and mean arterial pressure were kept constant, because we assumed that in the organism in the chronic situation homeostatic mechanisms keep these variables approximately constant.
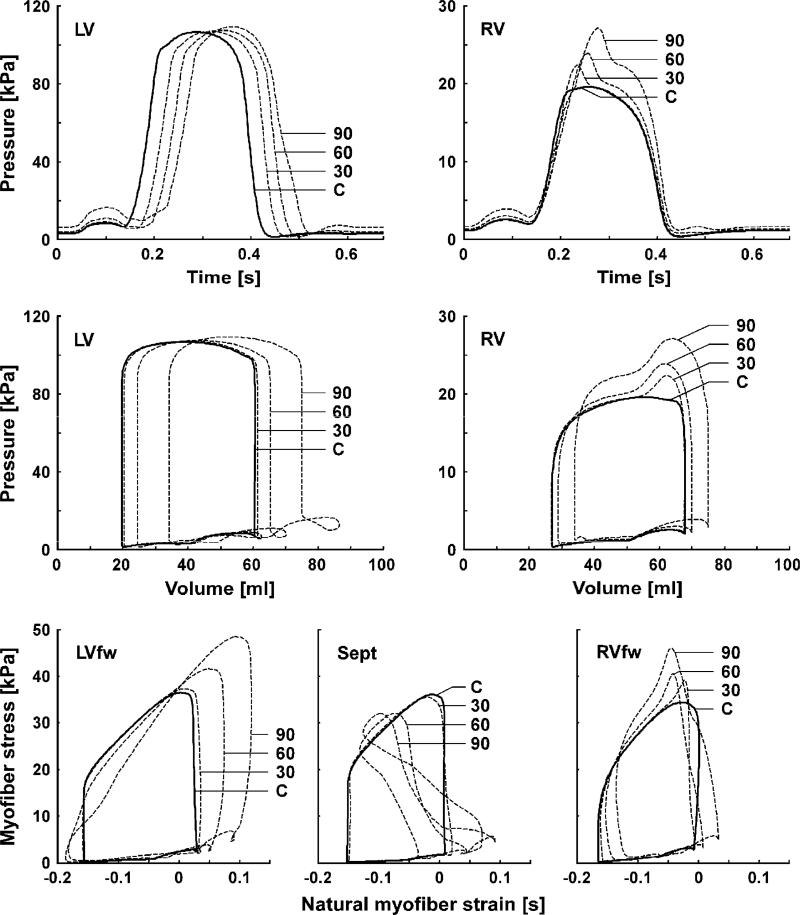
The top row of Fig. 6 shows simulated time courses of LV and RV pressures. Delaying the activation of the LV by 30 ms caused a delay in LV pressure rise by 18 ms (Table 2).
Fig. 6.
Left (LV) and right (RV) ventricular hemodynamics and myofiber mechanics as simulated with the TriSeg model in control (solid lines) and simulations with delayed activation of the LV (dashed lines). Top row: time courses of LV and RV pressures. Second row: LV and RV pressure–volume loops. Bottom row: predicted myofiber stress–strain loops of the LV free wall (LVfw), septal wall (Sept), and RV free wall (RVfw). Abbreviations C, 30, 60 and 90 indicate simulated results in control, and with delay of LV free wall activation by 30, 60 and 90 ms, respectively.
Table 2.
Derived interventricular asynchrony and maximum rates of pressure rise and decay in the TriSeg model
| Simulation | τRV–τLVa (ms) | dP/dtmaxb (mmHg/s) |
dP/dtminb (mmHg/s) |
||
|---|---|---|---|---|---|
| LV | RV | LV | RV | ||
| Control | −7 | 2116 | 369 | −2646 | −386 |
| LV30,30 | −25 | 1934 | 379 | −2656 | −383 |
| LV30,60 | −42 | 1897 | 259 | −2414 | −401 |
| LV30,90 | −60 | 1726 | 258 | − 1787 | −494 |
Simulations concern completely synchronous contraction (Control) and a delay of septal activation with 30 ms in combination with a delay in LV free wall activation with 30, 60 and 90 ms, with respect to the RV (LV30,30, LV30,60 and LV30,90, respectively).
τRV–τLV represents the timing difference between the upslopes of LV and RV pressure curves. A negative timing difference indicates an earlier RV than LV pressure rise.
dP/dtmax and dP/dtmin represent maximum rates of ventricular pressure rise and decay, respectively.
Amplitude of LV pressure remained unchanged because mean arterial pressure was fixed. However, peak systolic RV pressure increased. Table 2 also indicates that LV dP/dtmin and LV dP/dtmax hardly changed by a 30 ms delay of the entire LV activation (LV30,30). With further delay of LV free wall activation (LV30,60 and LV30,90), LV and RV dP/dtmax decreased considerably, similar to findings in the canine LBBB model (Table 1). Furthermore, with increasing delay of LV free wall activation, LV dP/dtmin decreased, while that of RV dP/dtmin increased (Table 2).
Simulation results of LV and RV pressure–volume loops are shown in the second row of Fig. 6. Switching from the Control to the LV30,30 simulation hardly affected LV and RV global LV pump function. However, in the LV30,60 and LV30,90 simulations (intra-LV asynchrony) LV and RV pressure–volume loops shifted towards higher volumes. Moreover, the LV pressure–volume loops showed an increase of mitral regurgitation as indicated by an increasing volume overshoot at end-diastole. In LV30,30, the RV pressure–volume loop showed an increase in RV pump work due to increase of RV systolic pressure. With further delay of LV free wall activation RV pump work increased further (up to 20% at LV30,90) while the RV dilated.
The bottom row of Fig. 6 shows simulated myofiber stress–strain loops for each wall segment. In LV30,30, contractile tissue function hardly changes as compared to Control. However, with further delay of the LV free wall the model predicts: (1) an increase (up to 50% in LV30,90) of contractile work density and peak myofiber stress in the late activated LV free wall, (2) a decreased contractile work in the septum down to a negative value in LV30,90, and (3) little change (less than 12%) of contractile work in the RV free wall, though the shape of the stress–strain loop changed. These changes in myofiber stress–strain loops within the LV wall are similar to those experimentally observed during ventricular pacing (Prinzen et al., 1999).
Therefore, the TriSeg model allows novel insight in possible mechanisms of disturbed pump function in LBBB hearts. First of all, intra-LV asynchrony appears to affect LV pump function more than interventricular asynchrony. Moreover, the model shows that LBBB increases RV mechanical performance. Clearly, changes in pump function of one ventricle influence the pump function of the other ventricle due to their mechanical interaction. Finally, even in this simple model, delayed LV free wall activation directly increases mitral regurgitation, which is also observed in patients with LBBB.
3.2. Mechanisms of mechanical dyssynchrony
3.2.1. Finite element model of LV electromechanics
Finite element models are used to solve partial differential equations at a multitude of locations in complex geometries. Many models have been published that use the finite element method to solve a multitude of biophysical problems in the ventricles (Kroon et al., 2007; ten Tusscher and Panfilov, 2006; Wall et al., 2006).
By solving for equations related to impulse conduction in the cardiac geometry, this method can be used to investigate normal and abnormal activation of the ventricles, including ventricular pacing. To this purpose Kerckhoffs et al. (2003, 2005) designed a thick-walled truncated prolate ellipsoid model with a realistic myofiber orientation (Fig. 5B). For the timing of depolarization tdep within the wall the eikonal-diffusion equation was solved for the gradient of tdep:
Parameter cf (0.67 m/s) represents the velocity of the depolarization wave along the myofiber direction. Constant k0 (2.1 × 10−4 m2 s−1) determines the influence of wave-front curvature on wave velocity. Tensor M takes into account anisotropy of the tissue. This relatively simple equation saves much computation time (it was solved in less than an hour for more than 20,000 degrees of freedom on a 225 MHz single processor).
Active stress was initiated at pre-computed timing of depolarization. When coupled to a model that solves for divergence of 3D stress σ in the cardiac geometry:
Regional strains and passive and active stresses (σp and σa, resp.) in the cardiac walls were predicted as a result of a variety of activation sequences, with cavity pressures as an important boundary condition. The nonlinear anisotropic constitutive equations for 3D passive stress were derived from a strain-energy function, whereas the equations for active stress—generated by the myofibers—were modeled dependent on time, sarcomere length, calcium concentration, and shortening velocity.
3.2.2. Simulation of mechanical dyssynchrony
Possible causes of the complicated regional contraction patterns, as observed in animal experiments (see Section 2.1) are the local differences in myocardial fiber length (preload) or fiber stress (afterload). In studies using two isolated papillary muscles in series asynchronous stimulation of the two muscle causes a downward shift in the force–velocity relation in the earlier activated muscle and an upward shift in the later activated one (Tyberg et al., 1969). Also, in vivo, a linear relation was found between stretch during the isovolumic contraction phase and regional systolic fiber shortening during ventricular pacing (Van Oosterhout et al., 1998). Also a close correlation exists between the time of local electrical activation and the degree of systolic fiber shortening (Delhaas et al., 1993). These findings support an important role for effective local preload as the cause of the regional differences in contraction pattern during asynchronous activation. However, Coppola et al. (2007) also found evidence that the increased systolic shortening in late activated regions may be due to decreased afterload.
In order to understand in more detail how electrical asynchrony leads to mechanical abnormalities, the finite element model of the LV, mentioned above, was used (Fig. 5B). Aim of the study was to investigate to what extent global and regional mechanical function of the heart during ventricular pacing could be obtained with relatively simple structural (fiber orientation), mechanical (force-length and force-shortening velocity relations) and impulse conduction properties (eikonal-diffusion equation, well-known conduction velocities) (Kerckhoffs et al., 2005). Simulations of a normal (sinus rhythm) heartbeat and of pacing at the RV apex were performed. Simulation results of RV apex pacing on local depolarization time and systolic midwall circumferential strain were compared with those measured in dogs, using an epicardial sock electrode and MRI tagging, respectively.
The same methods for data analysis were used for simulation and experiment. For example, temporal midwall circumferential strain was computed from the MR tagging data as well as from the model. Because measured epicardial activation times were related to measured midwall strains, the same was done in the model. The model agreed qualitatively with the experimental data on a global and regional scale: RV pacing decreased systolic pressure and ejection fraction relative to natural sinus rhythm; shortening during ejection and stroke work declined in early depolarized regions and increased in late depolarized regions. Moreover, midwall circumferential ejection strain depended linearly on depolarization time and the slope and intercept of this relation in mathematical model closely approximated those in the animal experiment (Kerckhoffs et al., 2005). Therefore, this data suggest that the main features of the abnormal global and local mechanical behavior during RV apex, and presumably other kinds of asynchronous activation, can be understood from the timing differences in electrical activation in combination with well-known properties of excitation–contraction coupling (force-length and force-shortening velocity relations).
3.3. Influence of sequential pacing in CRT response
3.3.1. Modeling heart failure
To gain insight in the effects of sequential pacing in a clinically relevant model, we developed 3D numerical models of the failing and non-failing canine ventricles coupled to a lumped-parameter systems model of the systemic and pulmonary circulations (Kerckhoffs et al., 2007a) (see Fig. 5C). Both the failing and non-failing heart model have been published before (Kerckhoffs et al., 2007b). Here, we will recapitulate on the major characteristics of these models.
3.3.1.1. Circulation
The systemic and pulmonary circulations for the non-failing and failing heart were each modeled with two lumped windkessel compartments in series, one compartment for arterial and capillary blood and one for venous blood. The atria were represented with time-varying elastance models, and were activated 120 ms before the ventricles.
3.3.1.2. Heart geometry and myofiber orientation
The non-failing and failing heart had an LV cavity to wall volume ratio of 0.27 and 0.57, respectively. The normal geometry has been used before (Kerckhoffs et al., 2007b), while the dilated ones were created by inflating both ventricles to the desired cavity to wall volume ratio, and defining that state as the undeformed one. The same realistic myofiber architecture was included in both geometries, since the myofiber distribution in normal and dilated hearts is not significantly different (Helm et al., 2006).
3.3.1.3. Mechanical material properties
In the failing hearts, passive properties of cardiac tissue were the same as in the normal heart. The active properties of the failing non-infarcted tissue were scaled from human data (Pieske et al., 1996), in which peak myofiber stress was 27% lower than in healthy tissue, and relaxation prolonged by 17%.
3.3.1.4. Pericardium
The pericardium plays an important role in direct ventricular interaction, and as suggested by (Bleasdale et al., 2004), direct ventricular interaction plays an important role during LV pacing of failing hearts. The effect of the pericardium was modeled by a pericardial pressure that acted on the ventricular epicardium, and was added to the atrial cavity pressures. Pericardial pressure was exponentially dependent on the total volume encompassed by the pericardium (Freeman and Little, 1986), hence included ventricular and atrial wall volumes, ventricular and atrial cavity volumes, and pericardial fluid volume. The difference in the pericardial pressure–volume relation between normal and dilated hearts was also included in the analysis (Freeman and Lewinter, 1984).
3.3.1.5. Electrophysiology
In this model the transmembrane potential v was simulated using the phenomenological spatially distributed modified FitzHugh–Nagumo equations for impulse conduction
where w = , repolarization variable, which is solved as a function of space and time. The parameters a, b, c1, c2 determine the shape of the action potential. Diffusion tensor D takes into account anisotropy of the tissue. Depolarization time—which served as input to the mechanics model—was defined as the time when the transmembrane potential was half way between resting and maximum potential. This mono-domain model is more computational intensive than the eikonal-diffusion equation (see Section 3.2), but still more efficient to solve than a more biophysically detailed bidomain/ionic model.
The cardiac anatomic model was discretized into 48 tricubic Hermite elements, with 1968 degrees of freedom. The model was solved with a modified Newton iteration scheme. Integration was performed with 3 × 3 × 3 Gaussian quadrature points. Convergence was reached when the maximal value of the residuals was lower than 10−5. The system of linear equations was solved with SuperLU, a direct solver optimized for sparse matrices. The hybrid model was solved with the Continuity 6.3 package (http://www.continuity.ucsd.edu). All simulations were solved in parallel using 12 nodes on a 105 node Dell™ Rocks Linux cluster with 3.2 GHz 64 bit Xeon® processors and 2 GB of RAM. Maximum RAM needed per simulation was about 120 MB.
3.3.2. Effects of sequential pacing
In failing and non-failing hearts five different activation sequences were simulated: LBBB, single-site pacing at the left ventricular free wall (LVp), and BiV sequential pacing with various stimulation delays (VVD = −40, 0, and 40 ms) between pacing at the RV apex (RVA) and the LV lateral free wall. VVD was defined as LV activation time minus RV activation time; hence the RV was stimulated first at a positive VVD. Regional mechanical parameters of spatial mean and standard deviation of ejection (SDE) strain were obtained in steady state for both ventricles as well as the fraction of tissue (FTS) stretched during ejection and the location of this tissue. Also the CURE index (Helm et al., 2007) of mechanical non-uniformity for LV midwall ejection strain was calculated, which ranges from zero (asynchronous) to one (synchronous). The VVD, resulting in optimal LV global function (VVGF), was obtained by calculating the optimum of a 4th order polynomial fit through the results of LV dP/dtmax, EF, and stroke work from the five simulations. Also, the VVD, resulting in optimal regional function (VVRF), was calculated for left ventricular SDE, FTS, and CURE as a function of VVD.
Compared with LBBB, BiV pacing improved LV dP/dtmax, ejection fraction and stroke work up to 10%, 3%, and 8% in the non-failing heart, and up to 16%, 4%, and 6% in the failing hearts (Table 3). VVD at which optima for LV dP/dtmax and ejection fraction occurred (VVGF) were ∼25 ms more negative ( = LV earlier) for failing than for non-failing hearts, but the VVGF for stroke work was not different between failing and non-failing hearts (Table 4).
Table 3.
Global function from hybrid cardiovascular model
| Non-failing heart |
Failing heart |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RAp | LBBB | VVD40 | VVD0 | VVD-40 | LVp | LBBB | VVD40 | VVD0 | VVD-40 | LVp | ||
| QRS width (ms) | - | 86 | 73 | 66 | 97 | 107 | 126 | 106 | 84 | 124 | 139 | |
| dP/dtmax (mmHg/s) | LV | 1630 | 1440 | 1491 | 1564 | 1577 | 1479 | 635 | 671 | 699 | 715 | 713 |
| RV | 463 | 406 | 410.3 | 418.7 | 378.4 | 314 | 236 | 233.7 | 237.0 | 233.7 | 217 | |
| SP (mmHg) | LV | 101.0 | 97.4 | 99.67 | 100.9 | 101.1 | 100.2 | 88.4 | 89.44 | 89.99 | 89.96 | 89.7 |
| RV | 27.7 | 26.2 | 26.56 | 26.86 | 26.24 | 25.1 | 24.6 | 24.50 | 24.48 | 24.43 | 24.0 | |
| EF (%) | LV | 43.8 | 42.3 | 43.3 | 43.5 | 43.3 | 43.1 | 22.0 | 22.6 | 22.8 | 22.8 | 22.4 |
| RV | 51.5 | 50.4 | 51.3 | 51.4 | 51.1 | 50.7 | 40.4 | 40.8 | 41.0 | 40.6 | 39.9 | |
| SW (mmHgml) | LV | 1662 | 1523 | 1619 | 1642 | 1639 | 1619 | 1314 | 1371 | 1396 | 1392 | 1361 |
| RV | 370 | 324 | 348.1 | 351.2 | 336.3 | 325 | 324 | 325.4 | 327.1 | 321.8 | 308 | |
| EDV (ml) | LV | 45.0 | 44.2 | 45.00 | 44.92 | 44.84 | 44.8 | 83.0 | 82.79 | 82.60 | 82.41 | 82.3 |
| RV | 37.8 | 37.2 | 37.77 | 37.80 | 37.85 | 37.9 | 45.9 | 46.02 | 46.12 | 46.26 | 46.5 | |
| EDP (mmHg) | LV | 13.9 | 14.5 | 13.86 | 13.79 | 13.69 | 13.8 | 15.7 | 15.43 | 15.32 | 15.17 | 15.2 |
| RV | 7.44 | 8.03 | 7.406 | 7.396 | 7.401 | 7.46 | 6.98 | 6.934 | 6.929 | 6.959 | 7.02 | |
dP/dtmax: maximum pressure increase; EDP: end-diastolic pressure; EDV: end-diastolic pressure; EF: ejection fraction; LVp: LV pacing; Rap: synchronous stimulation; SP: systolic pressure; SW: stroke work; VVD-40, VVD0, and VVD40: biventricular pacing, 40ms LV before RV, simultaneously, and 40 ms RV before LV, respectively.
Table 4.
Estimated optimal VV-delay for global function (optimalVVDglob, ms), based on LV dP/dtmax, EF, and SW and optimal VV-delay for regional function (optimalVVDreg, ms) based on LV SDE, FTS and CURE
| Non-failing heart | Failing heart | |
|---|---|---|
| OptimalVVDglob | ||
| dP/dtmax | −26 | −56 |
| EF | 4.5 | −21 |
| SW | −15 | −15 |
| Mean (±SD) | −12±15 | −31±22 |
| OptimalVVDreg | ||
| SDE | −20 | −39 |
| FTS | 3.8 | −33 |
| CURE | −26 | −45 |
| Mean (±SD) | −14.1±15.8 | −39.0±6.0 |
Simulations performed in non-failing and failing heart.
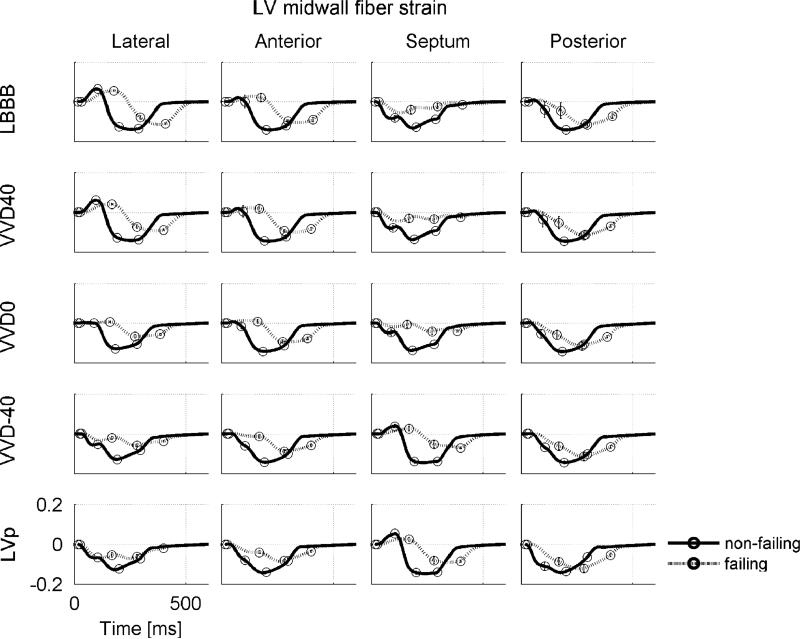
Fig. 7 shows the effects of VVD on fiber strains in the normal and failing heart. In the failing LBBB heart septal wall regions that shortened early during isovolumic contraction were stretched during ejection (Fig. 7, upper row). In the non-failing LBBB heart this did not seem to occur: early activated septal fibers shortened further during ejection. A similar strain pattern is observed during LVp in the LV lateral wall, indicating that this behavior is related to early activated regions in general. The difference in this behavior between failing and non-failing myocardium may be explained by the Frank-Starling mechanism which is intact in the non-failing myocardium, but reduced in the failing myocardium. Accordingly, when late activated regions become activated, attempting to stretch the already contracted early activated regions, early activated failing myocardium cannot generate enough active force and thus is stretched during ejection.
Fig. 7.
Fiber strain during a cardiac cycle in the LV midwall at the equator for all simulations. Cardiac phase transitions are indicated by circles, starting at end-diastole (which is also the state strain is referenced to). LBBB = left bundle branch block; VV-40, VV0 and VV40 = biventricular pacing with a RV–LV pacing interval of −40, 0 ms, and 40 respectively; LVp single site pacing at LV lateral wall. Scales mentioned in one panel also hold for the other panels.
In the non-failing heart, LV ejection strain was about equally non-uniform during LBBB and during LVp, and most uniform during VVD0 (Figs. 7 and 8A). RV ejection strain was most non-uniform during LVp (Fig. 8A). In the failing heart, both LV and RV ejection strain were most non-uniform during LBBB, and most uniform during VVD-40. In the paced non-failing heart, few fibers were stretched during ejection, but in the failing heart FTS was 20.3% in the LV with LBBB (Fig. 8B). All pacing conditions lowered FTS, VVD-40 being optimal for both the LV and RV. Most systolic stretching occurred near the pacing sites (Fig. 8D). CURE was consistently lowest for LBBB. Highest CURE values were reached for VVD0 in the non-failing heart and for VVD-40 in the failing heart (Fig. 8C). Accordingly, mean VVRF was ∼20 ms more negative in the failing than in the non-failing hearts (Table 4).
Fig. 8.
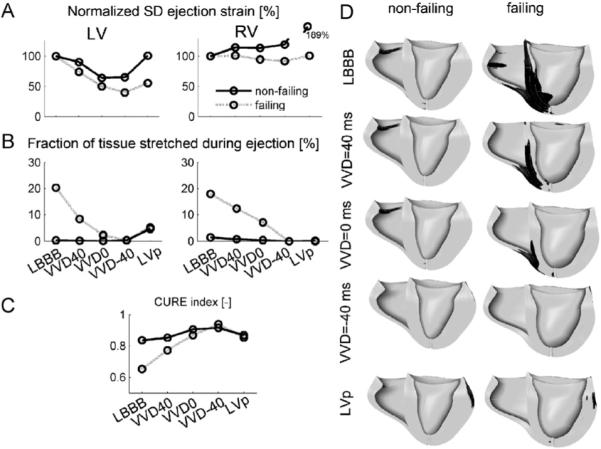
(A)–(C): Measures of regional mechanical dispersion in the hybrid model during various simulated pacing modes in the failing and non-failing heart. (A) Standard deviation of RV and LV ejection strain, normalized to LBBB, (B) fraction of tissue stretched during the ejection phase, (C) CURE index, and (D) regions in the ventricles that are stretched (black) during ejection. Abbreviations as in Fig. 7. Scales mentioned in one panel also hold for the other panels.
This data indicate the influence of VV delay on global and regional contraction. The different optimal VV delays calculated in failing and non-failing hearts may be explained by the different heart sizes, prolonged relaxation, or a combination of both, and at least in part, why VV delays appear quite different between patients. The preference for LV pre-excitation in failing hearts is in agreement with invasive hemodynamic measurements during LV pacing in non-failing dog hearts and in CRT candidates (Verbeek et al., 2006).
4. Concluding remarks
4.1. Critiques on the animal and computational models
For proper interpretation of the abovementioned findings in animal and computational models, these models need to be compared with data obtained in patients.
Table 5 compares data from various measurements in patients and in dogs with LBBB. The data show that, in general, absolute values of asynchrony indices are larger in the LBBB patients than in the canine LBBB model, but that the relative increase during LBBB as compared to controls is similar. The difference in absolute values can be attributed at least partly by the fact that patients had heart failure on top of LBBB, whereas the dogs did not.
Table 5.
Comparison between canine LBBB animal model and LBBB patients
| LBBB patients | LBBB dogs | ||
|---|---|---|---|
| QRS duration | LBBB | 169±16ms | 123±4ms |
| Controls | 80−100ms | 69±3ms | |
| Inter-ventricular asynchrony (RV–LV pressure difference) | LBBB | −50±17ms | −32±7ms |
| Controls | −5±10ms | −6±9ms | |
| Intra-ventricular asynchrony (Electrical mapping, ms) | LBBB | 61±15ms | 26±6ms |
| Controls | NA | 5±2ms | |
| Time to first peak systolic shortening septum to LV lateral wall delay (MR tagging) | LBBB | 351±92ms | 173±21ms |
| Controls | NA | −27±15ms | |
| Septal to posterior wall motion delay (SPWMD) | LBBB | 192±92ms | 221±13ms |
| Controls | NA | 64±9ms | |
| Echocardiography (% of controls) | |||
| Hypertrophy | 142 (%) | 117 (%)±15 (%) | |
| LV EDV/wall mass ratio | 114 (%) | 110 (%)±12 (%) | |
| Sep/lat wall mass ratio | 98 (%)−90 (%) | 84±2% | |
| Myocardial blood flow (% of mean LV) | Using PET | Using microspheres | |
| Septum | 93% | 83±16% | |
| Lateral wall | 113% | 118±12% | |
Comparing the changes in cardiac function parameters due to LBBB in canine hearts (Table 1) and due to delayed LV activation in the Triseg model (Table 2) with normal hearts shows remarkable, even quantitative similarities. In the hybrid model in the non-failing mode (Table 3) LV dP/dtmax was lower, but the relative decrease upon simulation of LBBB was similar to that in the canine hearts and TriSeg model. Also the increases in functional parameters (increase in LV dP/dtmax, stroke work) upon starting CRT are similar in the canine LBBB and the computational models.
These observations, in combination with the similarities in strains in canine hearts and finite element model (Section 3.2) strengthen the idea that the animal and computational models allow studying many basic aspects of asynchrony and CRT, at least in a qualitative way.
As compared to the finite element models, the TriSeg/CircAdapt model greatly reduces the number of parameters, needed to describe the cardiovascular system, by adapting the size of its constituents to mechanical load. As a consequence the model solves almost in real-time. The TriSeg model describes mean mechanics of each wall segment; no dispersion is present within a wall segment. The model also assumes that mechanical activation exactly mimics electrical activation and that duration of sarcomere activation is the same in all segments. These simplifications of the TriSeg model are both its strength and weakness. If higher spatial resolution is required, the use of finite element models is recommended.
Finite element models of cardiac electromechanics, as mentioned in Section 3.3—of which computation time can take about 30 min per heartbeat—are well suited to investigate regional cardiac function and the influence of regional alterations in electrophysiology (activation sequence) and mechanics (ischemia, scarring) on global cardiac function. Joining the CircAdapt and finite element models in one model using clinically measured input may, in the future, result in a powerful tool for predicting outcome of CRT tailored to the patient.
4.2. Conclusions
Animal and computer models are of great importance in understanding the events and consequences of asynchrony and resynchronization. Studies in experimental animals show the considerable effects of asynchronous activation on myocardial mechanics. This also holds for LBBB, the most relevant pathology for CRT. These mechanical effects are sufficient to elicit various adaptation processes, such as structural and electrical remodeling.
Mathematical models of various kinds showed that the abnormal, complex contraction patterns in asynchronous hearts can be understood from simple well-known electrical and mechanical properties of the myocardium. Detailed animal measurements and dedicated computer simulations demonstrate that LBBB not only affects LV function, but also that of the RV, albeit sometimes in an opposite way. These findings may stimulate studies in patients, specifically oriented to these as of yet unknown topics.
Funding sources
Studies at UCSD and Maastricht University have been supported in part by Medtronic Inc, Minneapolis, MN. Further support was provided by the National Biomedical Computation Resource (NIH grant P41 RR08605) (to A.D.M), the National Science Foundation (grants BES-0096492 and BES-0506252) (to A.D.M), UC Discovery Grant ITL06−10159 (to A.D.M.), and NIH grant HL32583 (to J.H.O.). Part of this investigation was conducted in a facility constructed with support from Research Facilities Improvement Program grant number C06 RR-017588−01 from the National Center for Research Resources, National Institutes of Health. K.V. was supported in part by a AGIKO grant of the Netherlands Organization for Research Zon-MW.
Footnotes
Editor's note
Please see also related communications in this issue by Ravelli et al. (2008) and Li et al. (2008).
Disclosures
Andrew McCulloch and Jeffrey Omens are co-founders of and consultants to Insilicomed Inc., a licensee of UCSD-owned software used in this research. Insilicomed was not involved in this research. Frits Prinzen is consultant to Medtronic Inc. (Minneapolis) and Boston Scientific Corp. (St. Paul).
References
- Arts T, Delhaas T, Bovendeerd P, Verbeek X, Prinzen FW. Adaptation to mechanical load determines shape and properties of heart and circulation: the CircAdapt model. Am. J. Physiol. Heart Circ. Physiol. 2005;288:H1943–H1954. doi: 10.1152/ajpheart.00444.2004. [DOI] [PubMed] [Google Scholar]
- Ashikaga H, Coppola B, Hopenfeld B, Leifer E, McVeigh E, Omens J. Transmural dispersion of myofiber mechanics. Implications for electrical heterogeneity in vivo. J. Am. Coll. Cardiol. 2007;49:909–916. doi: 10.1016/j.jacc.2006.07.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auricchio A, Stellbrink C, Block M, Sack S, Vogt J, Bakker P, Klein H, Kramer A, Ding J, Salo R, Tockman B, Pochet T, Spinelli J. Effect of pacing chamber and atrioventricular delay on acute systolic function of paced patients with congestive heart failure. The Pacing Therapies for Congestive Heart Failure Study Group. The Guidant Congestive Heart Failure Research Group. Circulation. 1999;99:2993–3001. doi: 10.1161/01.cir.99.23.2993. [DOI] [PubMed] [Google Scholar]
- Baller D, Wolpers H-G, Zipfel J, Bretschneider H-J, Hellige G. Comparison of the effects of right atrial, right ventricular apex and atrioventricular sequential pacing on myocardial oxygen consumption and cardiac efficiency: a laboratory investigation. PACE. 1988;11:394–403. doi: 10.1111/j.1540-8159.1988.tb05998.x. [DOI] [PubMed] [Google Scholar]
- Bax JJ, Abraham T, Barold SS, Breithardt OA, Fung JW, Garrigue S, Gorcsan J, 3rd, Hayes DL, Kass DA, Knuuti J, Leclercq C, Linde C, Mark DB, Monaghan MJ, Nihoyannopoulos P, Schalij MJ, Stellbrink C, Yu CM. Cardiac resynchronization therapy: part 1—issues before device implantation. J. Am. Coll. Cardiol. 2005;46:2153–2167. doi: 10.1016/j.jacc.2005.09.019. [DOI] [PubMed] [Google Scholar]
- Bleasdale RA, Turner MS, Mumford CE, Steendijk P, Paul V, Tyberg JV, Morris-Thurgood JA, Frenneaux MP. Left ventricular pacing minimizes diastolic ventricular interaction, allowing improved preload-dependent systolic performance. Circulation. 2004;110:2395–2400. doi: 10.1161/01.CIR.0000145169.82004.CF. [DOI] [PubMed] [Google Scholar]
- Coppola BA, Covell JW, McCulloch AD, Omens JH. Asynchrony of ventricular activation affects magnitude and timing of fiber stretch in late-activated regions of the canine heart. Am. J. Physiol. 2007;293:H754–H761. doi: 10.1152/ajpheart.01225.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costard-Jackle A, Goetsch B, Antz M, Franz MR. Slow and long-lasting modulation of myocardial repolarization produced by ectopic activation in isolated rabbit hearts. Evidence for cardiac “memory”. Circulation. 1989;80:1412–1420. doi: 10.1161/01.cir.80.5.1412. [DOI] [PubMed] [Google Scholar]
- Delhaas T, Arts T, Prinzen FW, Reneman RS. Relation between regional electrical activation time and subepicardial fiber strain in the canine left ventricle. Eur. J. Physiol. (Pfluegers Arch.) 1993;423:78–87. doi: 10.1007/BF00374964. [DOI] [PubMed] [Google Scholar]
- Freeman GL, Lewinter MM. Pericardial adaptations during chronic dilation in dogs. Circ. Res. 1984;54:294–300. doi: 10.1161/01.res.54.3.294. [DOI] [PubMed] [Google Scholar]
- Freeman GL, Little WC. Comparison of in situ and in vitro studies of pericardial pressure–volume relation in dogs. Am. J. Physiol. 1986;251:H421–H427. doi: 10.1152/ajpheart.1986.251.2.H421. [DOI] [PubMed] [Google Scholar]
- Helm PA, Younes L, Beg MF, Ennis DB, Leclercq C, Faris OP, McVeigh ER, Kass DA, Miller MI, Winslow RL. Evidence of structural remodeling in the dyssynchronous failing heart. Circ. Res. 2006;98:125–132. doi: 10.1161/01.RES.0000199396.30688.eb. [DOI] [PubMed] [Google Scholar]
- Helm RH, Byrne M, Helm PA, Daya SK, Osman NF, Tunin R, Halperin HR, Berger RD, Kass DA, Lardo AC. Three-dimensional mapping of optimal left ventricular pacing site for cardiac resynchronization. Circulation. 2007;115:953–961. doi: 10.1161/CIRCULATIONAHA.106.643718. [DOI] [PubMed] [Google Scholar]
- Jeyaraj D, Wilson LD, Zhong J, Flask C, Saffitz JE, Deschenes I, Yu X, Rosenbaum DS. Mechanoelectrical feedback as novel mechanism of cardiac electrical remodeling. Circulation. 2007;115:3145–3155. doi: 10.1161/CIRCULATIONAHA.107.688317. [DOI] [PubMed] [Google Scholar]
- Kass DA. Cardiac resynchronization therapy. J. Cardiovasc. Electrophysiol. 2005;16(Suppl 1):S35–S41. doi: 10.1111/j.1540-8167.2005.50136.x. [DOI] [PubMed] [Google Scholar]
- Kerckhoffs RC, Bovendeerd PH, Kotte JC, Prinzen FW, Smits K, Arts T. Homogeneity of cardiac contraction despite physiological asynchrony of depolarization: a model study. Ann. Biomed. Eng. 2003;31:536–547. doi: 10.1114/1.1566447. [DOI] [PubMed] [Google Scholar]
- Kerckhoffs RC, Faris OP, Bovendeerd PH, Prinzen FW, Smits K, McVeigh ER, Arts T. Electromechanics of paced left ventricle simulated by straightforward mathematical model: comparison with experiments. Am. J. Physiol. Heart Circ. Physiol. 2005;289:H1889–H1897. doi: 10.1152/ajpheart.00340.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerckhoffs RC, Healy SN, Usyk TP, McCulloch AD. Computational modeling of cardiac electromechanics. Proc. IEEE. 2006;94:769–783. [Google Scholar]
- Kerckhoffs RC, McCulloch AD, Omens JH, Mulligan LJ. Effect of Pacing Site and Infarct Location on Regional Mechanics and Global Hemodynamics in a Model Based Study of Heart Failure. Lecture Notes in Computer Science. 2007a;4466:350–360. [Google Scholar]
- Kerckhoffs RC, Neal ML, Gu Q, Bassingthwaighte JB, Omens JH, McCulloch AD. Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Ann. Biomed. Eng. 2007b;35:1–18. doi: 10.1007/s10439-006-9212-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroon W, Delhaas T, Arts T, Bovendeerd P. Constitutive Modeling of Cardiac Tissue Growth. Lecture Notes in Computer Science. 2007;4466:340–349. [Google Scholar]
- Lindner O, Vogt J, Kammeier A, Wielepp P, Holzinger J, Baller D, Lamp B, Hansky B, Korfer R, Horstkotte D, Burchert W. Effect of cardiac resynchronization therapy on global and regional oxygen consumption and myocardial blood flow in patients with non-ischaemic and ischaemic cardiomyopathy. Eur. Heart J. 2005;26:70–76. doi: 10.1093/eurheartj/ehi046. [DOI] [PubMed] [Google Scholar]
- Weihui Li, Viatcheslav Gurev, McCulloch Andrew D, Trayanova Natalia A. The role of mechanoelectric feedback in vulnerability to electric shock Prog. Biophys. Mol. Biol. 2008;97:461–478. doi: 10.1016/j.pbiomolbio.2008.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lumens J, Delhaas T, Kirn B, Arts T. Modeling ventricular interaction: a multiscale approach from sarcomere mechanics to cardiovascular system hemodynamics. Pac. Symp. Biocomput. 2008;13:378–389. [PubMed] [Google Scholar]
- McAlister FA, Ezekowitz J, Hooton N, Vandermeer B, Spooner C, Dryden DM, Page RL, Hlatky MA, Rowe BH. Cardiac resynchronization therapy for patients with left ventricular systolic dysfunction: a systematic review. JAMA. 2007;297:2502–2514. doi: 10.1001/jama.297.22.2502. [DOI] [PubMed] [Google Scholar]
- McCulloch AD. Functionally and structurally integrated computational modeling of ventricular physiology. Jpn. J. Physiol. 2004;54:531–539. doi: 10.2170/jjphysiol.54.531. [DOI] [PubMed] [Google Scholar]
- Medina-Ravell VA, Lankipalli RS, Yan GX, Antzelevitch C, Medina-Malpica NA, Medina-Malpica OA, Droogan C, Kowey PR. Effect of epicardial or biventricular pacing to prolong QT interval and increase transmural dispersion of repolarization: does resynchronization therapy pose a risk for patients predisposed to long QT or torsade de pointes? Circulation. 2003;107:740–746. doi: 10.1161/01.cir.0000048126.07819.37. [DOI] [PubMed] [Google Scholar]
- Pieske B, Sutterlin M, Schmidt-Schweda S, Minami K, Meyer M, Olschewski M, Holubarsch C, Just H, Hasenfuss G. Diminished post-rest potentiation of contractile force in human dilated cardiomyopathy. Functional evidence for alterations in intracellular Ca2+ handling. J. Clin. Invest. 1996;98:764–776. doi: 10.1172/JCI118849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitzalis MV, Iacoviello M, Romito R, Massari F, Rizzon B, Luzzi G, Guida P, Andriani A, Mastropasqua F, Rizzon P. Cardiac resynchronization therapy tailored by echocardiographic evaluation of ventricular asynchrony. J. Am. Coll. Cardiol. 2002;40:1615–1622. doi: 10.1016/s0735-1097(02)02337-9. [DOI] [PubMed] [Google Scholar]
- Prinzen FW, Peschar M. Relation between the pacing induced sequence of activation and left ventricular pump function in animals. PACE. 2002;25:484–498. doi: 10.1046/j.1460-9592.2002.00484.x. [DOI] [PubMed] [Google Scholar]
- Prinzen FW, Cheriex EM, Delhaas T, Van Oosterhout MFM, Arts T, Wellens HJJ, Reneman RS. Asymmetric thickness of the left ventricular wall resulting from asynchronous electrical activation. A study in patients with left bundle branch block and in dogs with ventricular pacing. Am. Heart J. 1995;130:1045–1053. doi: 10.1016/0002-8703(95)90207-4. [DOI] [PubMed] [Google Scholar]
- Prinzen FW, Hunter WC, Wyman BT, McVeigh ER. Mapping of regional myocardial strain and work during ventricular pacing: experimental study using magnetic resonance imaging tagging. J. Am. Coll. Cardiol. 1999;33:1735–1742. doi: 10.1016/s0735-1097(99)00068-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flavia Ravelli, Michela Masè, Marcello Disertori. Mechanical modulation of atrial flutter cycle length. Prog. Biophys. Mol. Biol. 2008;97:417–434. doi: 10.1016/j.pbiomolbio.2008.02.018. [DOI] [PubMed] [Google Scholar]
- Spragg DD, Leclercq C, Loghmani M, Faris OP, Tunin RS, DiSilvestre D, McVeigh ER, Tomaselli GF, Kass DA. Regional alterations in protein expression in the dyssynchronous failing heart. Circulation. 2003;108:929–932. doi: 10.1161/01.CIR.0000088782.99568.CA. [DOI] [PubMed] [Google Scholar]
- Spragg DD, Akar FG, Helm RH, Tunin RS, Tomaselli GF, Kass DA. Abnormal conduction and repolarization in late-activated myocardium of dyssynchronously contracting hearts. Cardiovasc. Res. 2005;67:77–86. doi: 10.1016/j.cardiores.2005.03.008. [DOI] [PubMed] [Google Scholar]
- Sweeney MO, Prinzen FW. A new paradigm for physiologic ventricular pacing. J. Am. Coll. Cardiol. 2006;47:282–288. doi: 10.1016/j.jacc.2005.09.029. [DOI] [PubMed] [Google Scholar]
- ten Tusscher KHWJ, Panfilov AV. Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. 2006;291:H1088–H1100. doi: 10.1152/ajpheart.00109.2006. [DOI] [PubMed] [Google Scholar]
- Tyberg JV, Parmley WW, Sonnenblick EH. In-vitro studies of myocardial asynchrony and regional hypoxia. Circ. Res. 1969;25:569–579. doi: 10.1161/01.res.25.5.569. [DOI] [PubMed] [Google Scholar]
- Van Oosterhout MFM, Prinzen FW, Arts T, Schreuder JJ, Vanagt WYR, Cleutjens JPM, Reneman RS. Asynchronous electrical activation induces inhomogeneous hypertrophy of the left ventricular wall. Circulation. 1998;98:588–595. doi: 10.1161/01.cir.98.6.588. [DOI] [PubMed] [Google Scholar]
- Vassallo JA, Cassidy DM, Marchlinski FE, Buxton AE, Waxman HL, Doherty JU, Josephson ME. Endocardial activation of left bundle branch block. Circulation. 1984;69:914–923. doi: 10.1161/01.cir.69.5.914. [DOI] [PubMed] [Google Scholar]
- Verbeek X, Vernooy K, Peschar M, Cornelussen R, van der Nagel T, van Hunnik A, Prinzen F. Intra-ventricular resynchronization for optimal left ventricular function during pacing in experimental left bundle branch block. J. Am. Coll. Cardiol. 2003;42:558–567. doi: 10.1016/s0735-1097(03)00641-7. [DOI] [PubMed] [Google Scholar]
- Verbeek XAAM, Auricchio A, Yu Y, Ding J, Pochet T, Vernooy K, Kramer A, Spinelli J, Prinzen FW. Tailoring cardiac resynchronization therapy using interventricular asynchrony. Validation of a simple model. Am. J. Physiol. 2006;290:H968–H977. doi: 10.1152/ajpheart.00641.2005. [DOI] [PubMed] [Google Scholar]
- Vernooy K, Verbeek XAAM, Peschar M, Crijns HJGM, Arts T, Cornelussen RNM, Prinzen FW. Left bundle branch block induces ventricular remodeling and functional septal hypoperfusion. Eur. Heart J. 2005;26:91–98. doi: 10.1093/eurheartj/ehi008. [DOI] [PubMed] [Google Scholar]
- Vernooy K, Cornelussen RNM, Verbeek XAAM, Vanagt WYR, Van Hunnik A, Kuiper M, Arts T, Crijns HJGM, Prinzen FW. Cardiac resynchronization therapy restores dyssynchronopathy in canine LBBB hearts. Eur. Heart J. 2007;28:2148–2155. doi: 10.1093/eurheartj/ehm207. [DOI] [PubMed] [Google Scholar]
- Wall ST, Walker JC, Healy KE, Ratcliffe MB, Guccione JM. Theoretical impact of the injection of material into the myocardium: a finite element model simulation. Circulation. 2006;114:2627–2635. doi: 10.1161/CIRCULATIONAHA.106.657270. [DOI] [PubMed] [Google Scholar]
- Wyman BT, Hunter WC, Prinzen FW, Farris OP, McVeigh ER. Effects of single- and biventricular pacing on temporal and spatial dynamics of ventricular contraction. Am. J. Physiol. 2002;282:H372–H379. doi: 10.1152/ajpheart.2002.282.1.H372. [DOI] [PubMed] [Google Scholar]
- Yu CM, Chau E, Sanderson JE, Fan K, Tang MO, Fung WH, Lin H, Kong SL, Lam YM, Hill MR, Lau CP. Tissue doppler echocardiographic evidence of reverse remodeling and improved synchronicity by simultaneously delaying regional contraction after biventricular pacing therapy in heart failure. Circulation. 2002;105:438–445. doi: 10.1161/hc0402.102623. [DOI] [PubMed] [Google Scholar]
- Zwanenburg JJ, Gotte MJ, Kuijer JP, Heethaar RM, van Rossum AC, Marcus JT. Timing of cardiac contraction in humans mapped by high-temporal-resolution MRI tagging: early onset and late peak of shortening in lateral wall. Am. J. Physiol. 2004;286:H1872–H1880. doi: 10.1152/ajpheart.01047.2003. [DOI] [PubMed] [Google Scholar]