Modeling of Glycerol-3-Phosphate Transporter Suggests a Potential ‘Tilt’ Mechanism involved in its Function

Abstract

Many major facilitator superfamily (MFS) transporters have similar 12-transmembrane α-helical topologies with two six-helix halves connected by a long loop. In humans, these transporters participate in key physiological processes and are also, as in the case of members of the organic anion transporter (OAT) family, of pharmaceutical interest. Recently, crystal structures of two bacterial representatives of the MFS family — the glycerol-3-phosphate transporter (GlpT) and lac-permease (LacY) — have been solved and, because of assumptions regarding the high structural conservation of this family, there is hope that the results can be applied to mammalian transporters as well. Based on crystallography, it has been suggested that a major conformational “switching” mechanism accounts for ligand transport by MFS proteins. This conformational switch would then allow periodic changes in the overall transporter configuration, resulting in its cyclic opening to the periplasm or cytoplasm. Following this lead, we have modeled a possible “switch” mechanism in GlpT, using the concept of rotation of protein domains as in the DynDom program¹⁷ and membranephilic constraints predicted by the MAPAS program.²³ We found that the minima of energies of intersubunit interactions support two alternate positions consistent with their transport properties. Thus, for GlpT, a “tilt” of 9°–10° rotation had the most favorable energetics of electrostatic interaction between the two halves of the transporter; moreover, this confirmation was sufficient to suggest transport of the ligand across the membrane. We conducted steered molecular dynamics simulations of the GlpT-ligand system to explore how glycerol-3-phosphate would be handled by the “tilted” structure, and obtained results generally consistent with experimental mutagenesis data. While biochemical data remain most consistent with a single-site alternating access model, our results raise the possibility that, while the “rocker switch” may apply to certain MFS transporters, intermediate “tilted” states may exist under certain circumstances or as transitional structures. While wet lab experimental confirmation is required, our results suggest that transport mechanisms in this transporter family should probably not be assumed to be conserved simply based on standard structural homology considerations. Furthermore, steered molecular dynamics elucidating energetic interactions of ligands with amino acid residues in an appropriately modeled transporter may have predictive value in understanding the impact of mutations and/or polymorphisms on transporter function.

1. Introduction

Small molecules, including drugs, are transported and/or excreted by transporter proteins in the cell membrane. A certain class of these transporters, known as the major facilitator superfamily (MFS), is highly represented in the human genome, and its members play an important role in mediating the interface between the internal composition of the cell and the external environment. Understanding how they function is of considerable medical and pharmacological value. So far, only bacterial transporters of this family have been crystallized, revealing their static three-dimensional (3D) structures; computational modeling based on fundamental physical principles is required to understand their functional properties. The conservation of structure among bacterial and human transporters suggests that understanding the mechanism of transport in bacterial transporters will shed light on human transporters. Using a theoretical approach, including molecular modeling and simulation, we have evaluated mechanisms of function of a representative of the MFS family — glycerol-3-phosphate transporter. Existing hypotheses suggest that MFS transporters function using a “rocker switch” mechanism with consecutive openings of the transporters toward the cytoplasm or periplasm. Our results suggest that, while the full rocker switch model may apply to certain transporters, it is possible that intermediate “tilted” states may exist under certain circumstances or as transitional structures. The approaches we use may aid in drug design and in the prediction of how genetic variation affects drug response.

Many transmembrane transporters, so-called “secondary active membrane transporters”, utilize a solute gradient to transport compounds.^1–4 The largest family of these transporters is the major facilitator superfamily (MFS).^1,5–7 MFS proteins have around 400–600 amino acids, and have a similar 12-transmembrane α-helical topology with two six-helix halves connected by a long loop. Crystallographic structures of two representatives of the MFS family have been recently solved.^1,2 The crystal structures of these transporters are open to the cytoplasm and closed to the periplasm. Because of this, the explanation for transport by these transporters may not be straightforward.

Both groups that solved these structures suggested that there is some type of conformational alteration necessary for proper functioning of these transporters. This alteration is presumed to enable periodic changes in the overall transporter configuration that would result in its cyclic opening to the periplasm or the cytoplasm. Biochemical data support a single-site alternating access model, and one of the proposed scenarios is that this occurs via a “rocker switch” of one of the two homologous subdomains of GlpT or LacY relative to the other. Such a profound “switch” would allow the transporter to exist in two major conformations with its opened channel facing either the cytoplasm or the periplasm. It has been hypothesized that one of the driving forces for such a switch in GlpT is inorganic phosphate (Pi) pulling together two arginines (Arg45 and Arg269) from different subdomains.^8,9

Structural¹ and biochemical data for GlpT^8–12 support the hypothesis that the glycerol-3-phosphate transporter (GlpT) operates by allowing alternating access to a single binding site. For LacY, a 60° total rotation of one subunit relative to the other (30° each) has been proposed based on the results of cross-linking experiments.^2–4 For GlpT, it has been suggested that ∼ 6° rotation of each domain generates a structure that can “fit” into that of another MFS protein, OxlT, as determined at 6.5 Å by cryoelectronic microscopy, with a conformation open to the periplasm.^13,14 Lemieux et al.^8,9 state that approximately 10° rotation of each domain is sufficient to close the pore on the cytosolic side of the molecule and open the pore on the periplasmic side. It was also proposed that the final position is at ∼ 16° of rotation of each GlpT subunit relative to the other; the supporting data for this hypothesis were the “fitting” of the rotated subdomains of the previously solved GlpT structure into the relatively low-resolution structure of another MFS protein, OxlT.^13,14 Implicit in these proposals is the notion that the “rocker switch” mechanism of transport applies to all of these transporters.

Our computational rotation experiments were based on the comprehensive studies of Hayward and colleagues,^15,16 who have demonstrated that a significant number of proteins have two or (in some cases) more stable conformations that can be clearly defined by the rigid-body rotation of one part of the protein molecule versus another with specified axes of rotation. The database of domain movements calculated with the DynDom program¹⁷ has been created on the basis of the proteins with two different conformations listed in the Protein Data Bank (PDB). We explored the interaction energy profiles for several proteins by rotating one of the domains versus another using the rotational axes proposed by DynDom. In all cases, we observed the minimums of energy at the end points of rotation. This finding is also supported by several studies.^18–20

Using this approach, we performed an analysis of subdomain rotation energetics and further ligand transport (using steered molecular dynamics) in the context of experimental mutational data. The two subdomains of the GlpT molecule were disconnected at the linker region. Then, the “left” and “right” subdomains of this molecule were rotated at increments of 0.5° in alternative directions. At each step, both subdomains were copied, and the copies were subjected to steepest descent minimization for 100 iterations to avoid possible side chain close contacts that would result in unrealistic values of interaction energies. We then calculated energies of interaction between these “left” and “right” copies. Energies were calculated using the binding free energy cycle with a linearized Poisson–Boltzmann equation including Coulombic and van der Waals contributions (see Sec. 2). After determining the energy minima from these rotations, we constructed models of the relative configurations of hemidomains of the transporters. We then conducted steered molecular dynamics simulations in a water box with constant pressure (see Sec. 2) of anion transport through the configurations of the transporter. The results suggest that “tilted” conformations of GlpT can exist, at least under certain circumstances, as intermediates in the transport of the ligand from the periplasm to the cytoplasm. Based on steered molecular dynamics analyses, the constructed models of the configurations of GlpT can be utilized for prediction of the impact of possible mutations on transporter function.

2. Methods

2.1. Modeling of most favorable energetic state by rotation

The protein conformers for initial studies of energy profiles during the rigid-body rotations were extracted from the DynDom database.¹⁷ These proteins were disconnected in the hinge regions and one domain rotated versus another using the DynDom proposed axes. The rotations were done at increments of 1° with 100 iterations of steepest descent minimization after each step of rotation to avoid possible side chain intersection.

For study of GlpT, we utilized the crystal structure (PDB ID lpw4).¹ Using the Insight II Biopolymer module (Accelrys, 2006), we broke the C-N bond between the residues in the linker region between the two six-helix subdomains of the transporters. Then, both subdomains were rotated around axes positioned parallel to the membrane (passing through the center of coordinates of each six-helix subdomain and perpendicular to the side projection of the transporter, as shown in Fig. 2). The rotations were done at increments of 0.5° with 100 iterations of steepest descent minimization after each step of rotation to avoid possible side chain interactions that occur in a rigid model. At each step, we measured the binding free energy of interaction between the “left” and “right” domains of molecules with the Gemstone option²¹ of the program APBS,²² and van der Waals energies using the InsightII program (Accelrys, 2006).

Fig. 2.

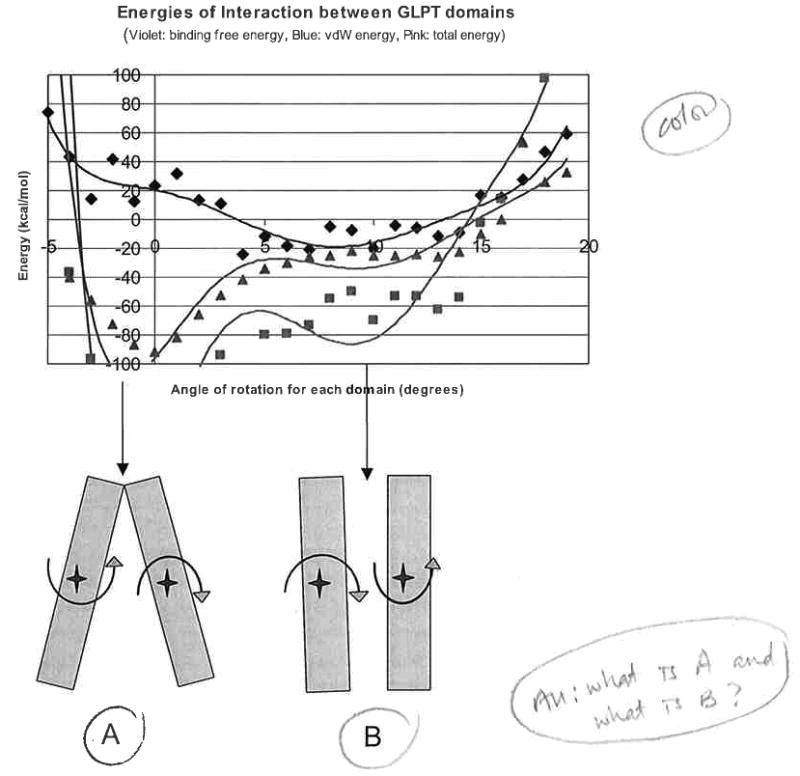
The lower part of the figure shows sketches of the “open to periplasm” and “open to periplasm and cytoplasm” configuration. The upper part of the figure shows corresponding profiles of energies of interaction between the domains of GlpT.

Binding free energy was calculated using the binding free energy cycle:

$$\Delta {\Delta }_{\text{bind}}G={\Delta }_{4}G-{\Delta }_{1}G-{\Delta }_{2}G,$$

where Δ₄G is the free energy of transfer of the complex from the homogeneous dielectric environment to an inhomogeneous dielectric environment with different internal and external dielectric constants; and Δ₁G and Δ₂G are free energies of transfer of the “left” and “right” subdomains of the transporter, respectively, from the homogeneous dielectric environment to an inhomogeneous dielectric environment with different internal and external dielectric constants.

Coulombic contributions to the binding free energy for a two-component complex of “left” and “right” halves of the transporter (mol1 and mol2) were calculated, with cutoff 100 Å, with the following equation:

$$\Delta {\Delta }_{\text{Coul}}G={\Delta }_{\text{Coul}}{G}_{\text{complex}}-{\Delta }_{\text{Coul}}{G}_{\text{mol}1}-{\Delta }_{\text{Coul}}{G}_{\text{mol}2}.$$

The total binding free energies were calculated as:

$$\Delta {\Delta }_{\text{tbind}}G=\Delta {\Delta }_{\text{bind}}G+\Delta {\Delta }_{\text{Coul}}G.$$

The total energies of interaction were calculated with the addition of the van der Waals term Δ_vdW of intermolecular interaction between the protein and the transported anion.

For transport simulations, the “reversed” configurations of transporters were situated at the selected minimum-energy rotational positions (10° rotation for GlpT). Then, the model was “repaired” by reinstalling a linker C-N bond, and the linker configuration was reconstructed using the fragment library method with the Homology module of the Insight II program (Accelrys, 2006). Homology modeling was used only for “repair” of the 12-residue linker region of the molecule (GlpT). The rest of the molecules were used as these are presented in the PDB coordinate files; just both six-helix domains were rotated as rigid bodies. The entire “tilted” structure of GlpT, in preparation for further steered molecular dynamics simulations, underwent 10000 iterations of steepest descent minimization with the program Discover (Accelrys, 2006).

The validity of the predicted second minimum energy rotational conformer of GlpT was examined with the program MAPAS,²⁴ which predicts membrane-contacting surfaces of proteins.

2.2. Steered molecular dynamics (MD) simulation

The purpose of these simulations was not to study physical properties of the membrane-inserted GlpT, which is by itself a very important task. Our goals were more practical — to show that with 10° tilt of each domain (total tilt, 20°) the GlpT transporter can transport its anion ligands, and to show that this simplified system can be used to predict possible effects of mutation to the ligands' transport.

We conducted 10-ps MD simulation in water box at a constant pressure of 1 atm, and periodic boundary conditions at 300°K with preliminary equilibration 2 ps, step 1 fs. This temperature was selected to ensure a proper sampling of the transporter's side chain conformational space, i.e. to ensure that the side chains would be able to move enough to avoid artificial obstacles to the ligand movement from the rigid side chains. Simulation of anion movement through the transporters was performed using the program Discover (Accelrys, 2006), with a small steering force applied to the ligands initially situated 10 Å “above” the periplasm entrance to the transporter and directed from the extracellular part of the partially reversed models (or the periplasm) toward the cytoplasm. The applied force was so small that it did not create any distortions in the covalent bond length of either the compound or amino acids of the transporter. After the end of the dynamic run, we calculated the energies along the transport trace between the ligand and the protein at each 10-fs step of the molecular dynamics simulation using the program APBS²¹ with the Gemstone option,²² and van der Waals energies using the InsightII program (Accelrys, 2006). We used the same concept of free energy cycles for these calculations as we described above for rotational modeling. The complex contained two molecules: the first, the entire GlpT protein; and the second, the Glp molecule.

3. Results and Discussion

It has been shown in several examples that there exists a potential barrier between the open and closed domain conformations for a number of proteins,^18–20 and that one conformation of the protein can be transformed to the other by rigid-body rotation of one of the structural domains. One possible conclusion that could be drawn on the basis of such results is that the existence of two energy minimums and an energy barrier between two protein conformations having different interdomain rotation angles is a more general property. This may thus be used for the possible prediction of a second rotated conformation of a protein molecule.

We randomly selected from the DynDom database a set of proteins having two possible rigid domain rotational positions. Then, we disconnected them in the hinge region into two separate molecules and rotated one of them versus another around the axes proposed in the database at increments of 1° with short minimizations on each step to avoid artificial side chain close contacts. At each step, we measured the energies of interaction between the two domains.

Figure 1 shows that for three examined proteins, there exist minima of electrostatic and total energies around the endpoints proposed in DynDom. For 5′-nucleotidase [Fig. 1(a)], clear minima exist around 0° and 98° (when the rotation angle between domains proposed by DynDom is 96.7°). The additional minimum existing around 40° may indicate a possible intermediate conformation that can also exist in this protein, but is still not crystallized. For cytidylate kinase [Fig. 1(b)], the energy minima are located around 2° and 33°, which is quite close to the rotational angle of 31.8° calculated with DynDom. For exopolyphosphatase [Fig. 1(c)], we see the energy minima around 0° and 10°–11° (the DynDom-calculated rotational angle is 11.5°). It is likely that more precise flexible docking or steered molecular dynamics theoretical experiments can bring an even more closer correspondence of energy minima with the DynDom-predicted domain rotations. We are in the process of more comprehensively modeling the proteins presented in DynDom; for now, most of the calculated cases support the above-mentioned examples.

Fig. 1.

Two possible conformers of selected proteins (right) and profiles of interdomain interaction energy during rotation from one endpoint to another based on the conformations presented in DynDom (left). (a) For 5′-nucleotidase, two minima exist around 0° and 98° (the rotation angle proposed by DynDom is 96.7°). (b) For cytidylate kinase, two energy minima are located around 2° and 33° (the rotation angle proposed by DynDom is 31.8°). (c) For exopolyphosphatase, two energy minima are located around 0° and 10°–11° (the rotation angle proposed by DynDom is 11.5°).

Our goal was to use the finding that proteins having two defined conformational states usually have two different energy minima corresponding to these conformations for possible prediction of the second conformational state of proteins on the basis of energy profiles.

We studied the transmembrane protein GlpT in detail. It is worth noting that, in the case of transmembrane proteins, the possible domain rotation is even more defined than in the case of other proteins. Dimensions of the membrane are the natural boundaries of possible conformational changes, so, for example, the open and closed conformations of GlpT must have membrane-contacting surfaces. Our program MAPAS²³ can predict the transmembrane protein's membrane-contacting surfaces. We used this program to determine whether the predicted second minimum energy conformation of this transmembrane protein is supported by the fact that the predicted membrane-contacting residues are in contact with the membrane.

We have modeled the conformation of GlpT, in which the position of one six-helix subdomain of the protein molecule is rotated relative to the other while the conformation of each 6 helix subdomain remains rigid. It is important to emphasize the parsimony of this model, as only one change is required: rotation of each subdomain of the transporter. Below, we refer to the crystal conformation of GlpT where the transporter's channel is open toward the cytoplasm and closed toward the periplasm as “initial”, whereas the hypothetical conformation of GlpT where the transporter's channel is open to the periplasm (defined on the basis of interdomain energy calculations) is referred to as “reversed”.

3.1. Interdomain interactions

Figure 2 shows the binding energy profiles for concerted rotation of the GlpT sub-domains and provides a schematic representation of subdomain configuration at their minimum states of total energy of interdomain interaction. It is apparent that van der Waals energies of interaction remain negative for a wide range of angles, having minima at around 0° (initial crystal structure opened to cytoplasm) for both molecules. Van der Waals energies grow (above zero) for rotational angles less than −3° to −4° and above 15° for both proteins. These van der Waals energies define the general boundaries of possible rotations. We have to note that, because of the type of theoretical experiment that we conducted (rotations of the protein domains from the initial position followed by short minimization at each step to avoid possible side chain close, contacts), values of vdW energies at each point may vary to some extent on the conditions of minimization in local regions of the transporter. At the same time, values of electrostatic energies of interdomain interactions are quite robust. Electrostatic energies define more precisely the positions of possible “stops” for the “tilting”-to-“full switching” mechanisms of these transporters. The left minima of total energy (Fig. 2) are close to the 0° rotation point and, in this region, the final configuration of the molecule is defined by the sum of electrostatic and van der Waals energies. The right minima of electrostatic energies for GlpT are 8° to 10° (rotational angles of each domain), consistent with the hypothesis of Lemieux et al.,^8,9 which in turn is based on the correspondence to the low-level structure of another transporter MFS protein, OxlT. It was not postulated whether this can be either a transitioned intermediate or possibly a final position of the transporter, i.e. that under certain circumstances this degree of tilting may be sufficient for effective transport of the ligand from the periplasm to the cytoplasm.

Total energy profiles have minima mostly close to the positions of the minima of electrostatic energies (Fig. 2). The plots presented in Fig. 2 correspond to a selected run of “rotation simulation”. We obtained similar profiles in a number of such simulations.

Figure 3 shows the vertical cross-section of two superimposed GlpT 3D images: the initial structure (given as black-dotted surface), and the structure with both domains tilted 10° (given as orange solid surface and ball-and-stick molecular representation) along with the Glp molecule near the entrance to the tilt-opened pore. One can see that the pore is opened by the transporter's tilt to make Glp transport possible.

Fig. 3.

Vertical cross-section of two superimposed GlpT 3D images: the initial structure (given as black-dotted surface), and the structure with both domains tilted 10° (given as orange solid surface and ball-and-stick molecular representation) along with the Glp molecule near the entrance to the opened-by-tilt pore. One can see that, whilst completely closed in the initial structure, the pore is opened with the transporter's tilt to make Glp transport possible.

3.2. Reversed structure and reasons for rotation

Figure 4 shows the ribbon models of the “initial” crystal structure (magenta) and the 20° “reversed” (brown) model of GlpT. Colored dark blue parts of the ribbon diagrams for the initial and reversed conformations of GlpT are clearly predicted to be in contact with the membrane surface. Moreover, the coefficient of membrane asymmetry (MAS) — one of two main parameters for predicting the membrane-contacting surface — is about 50% higher for the reversed conformation. Lower parts of the molecule were not elucidated by the MAPAS program, probably because these regions contain a combination of the membrane-contacting and cytoplasmic parts of the molecule; in this case, MAPAS needs additional information regarding the studied molecules for a more comprehensive analysis, which is beyond the scope of this article. The membrane-contact analysis supports our concept that the reversed conformation of GlpT may exist and would remain in contact with the membrane after the proposed rotation.

Fig. 4.

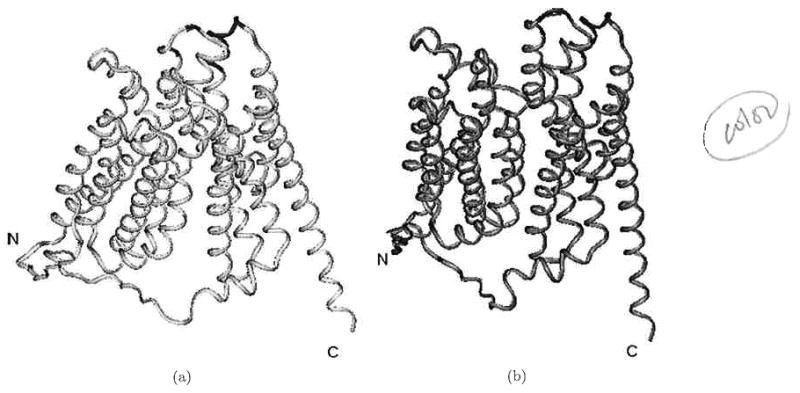
(a) Ribbon diagrams of the original structure and (b) the reversed 10° structure model of GlpT.

Upon partial reversal of the structure of GlpT, the key arginines that are located on the inner surface of the opening of the molecule can participate in general binding of Pi to GlpT. The shortest distance between these residues is about 10.8 Å. We are thus able to elaborate at the molecular level on the general speculation of Lemieux et al.^8,9 and suggest that, after negative Pi binding to arginines 45 and 269 of the initial structure of GlpT opened to the cytoplasm, a “tilt” can occur, and then a subsequent position of the “tilted” GlpT has these arginine side chains located somewhat further from each other. This distance no longer supports a hydrogen bond-constrained position of Pi and could represent a transitional structure that leads to release of Pi into the periplasm through the opening of GlpT, although there may be in vitro conditions in which full translocation occurs. The next step is binding of the negative glycerol-3-phosphate (Glp) from the periplasm to the same site (defined by the two arginines). Glp, having larger dimensions than Pi, adapts to this binding by pushing both subunits in the opposite direction, eventually supporting a reversal. Then, in the recovered initial position (open to the cytoplasm), Glp does not have a productive geometrical fit with the site of arginines 45 and 269 and is thus pushed out of GlpT to the cytoplasm. Figure 4 shows initial configurations of these transporters consistent with the first minimum of total energy (and crystal structure) and configurations consistent with the second minimum of total energies of GlpT. Again, we emphasize that this theoretical data need not be considered inconsistent with the occurrence of a full rocker switch under wet lab conditions, where many other factors operate, and this position may represent a potential transitional structure.

3.3. Transport of anions by GlpT

With a dynamic model consistent with crystallographic data and energetic considerations in hand, we conducted accelerated steered molecular dynamics (energy sampling) simulations to explore how Glp may be continuously transported by the “tilted” GlpT transporter. First, to determine whether the tilted structures (10° rotation of each subdomain) represent potential physiologically relevant states of GlpT, we positioned the compound known to be transported by GlpT, glycerol-3-phosphate (Glp), near the partially open entrance to the transporter from the periplasm and conducted molecular dynamics simulations simultaneous with low energy restraints directing the compound through the channel (in this kind of simulation, side chains move in a manner consistent with the simulation temperature of 300°K; see Sec. 2). Figure 5 demonstrates snapshots of one such run of Glp transport in the 10° rotated position of GlpT.

Fig. 5.

Snapshots of Glp transport through the 9°-rotated GlpT (violet ribbon) pore.

Figure 6 shows sketches of the “open to the cytoplasm” and “partially open to the periplasm and cytoplasm (tilted)” configurations of GlpT. Although, with our modeling, we are unable to determine the precise mechanism of translocation of the ligand (and assume single-site alternating access), intriguingly, the 9°–10° tilted GlpT has potential openings to both the cytoplasm and the periplasm. In order for transport of Glp to occur against the membrane potential gradient, GlpT would seem to have to require or generate additional force that ensures the final movement of the ligand from the binding site inside the transporter to the cytoplasm. Such a jump can be caused by the tilt conformation of the transporter itself when it becomes closed to the periplasm and opens widely to the cytoplasm. So, it seems conceivable that the mechanism has some overlap with traditional alternating access models as well as channels an idea that is supported in the literature.^1–4

Fig. 6.

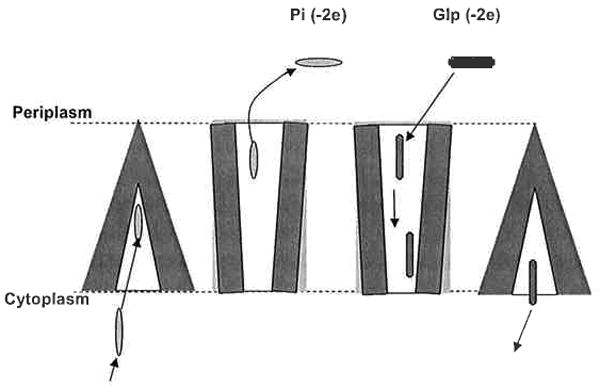
Possible steps of Glp and Pi transport by GlpT via a “tilt” mechanism with the following steps: (1) Inorganic phosphate (Pi) enters the transporter. (2) A “tilt” occurs. (3) Pi leaves the transporter supported by a lower concentration of Pi in the periplasm and because affinity of Glp to GlpT is greater than the affinity of Pi. (4) Glp moves through the transporter. (5) Glp binds to the minimal energy binding site near the cytoplasmic exit of the transporter. (6) GlpT switches back, causing the translocation of Glp to the cytoplasm. The transporter closes to the periplasm and opens the site for Pi binding and next “tilt”.

As depicted in Fig. 6, possible steps of Glp and Pi transport by GlpT via a “tilt” mechanism are as follows: (1) inorganic phosphate (Pi) enters into the transporter; (2) “tilt” occurs; (3) Pi leaves the transporter supported by a lower concentration of Pi in the periplasm and because the affinity of Glp for GlpT is greater than the affinity of Pi; (4) Glp moves through the transporter; (5) Glp binds to the minimal energy binding site near the cytoplasmic exit of the transporter; and (6) GlpT tilts back, causing a translocation of Glp to the cytoplasm. The transporter closes to the periplasm and opens to the site for Pi binding, and thereby allows for occurrence of the next “tilt”. However, we do not exclude the possibility that a rocker switch operates under in vivo conditions, as we expect to be true for LacY. In that case, the tilt could represent intermediate states for GlpT transport that may or may not be present in LacY; alternatively, the tilted states may primarily be present in an artificial system, such as a single protein in an artificial lipid bilayer.

Figure 7 shows the binding free energies and total energies of interaction between the Glp molecule and wild-type (wt) (blue diamonds) and mutated (red diamonds) GlpT for a run of SMD (similar profiles were obtained for repeated runs) during transport of Glp from the periplasm to cytoplasm by the “tilted” GlpT. The plots demonstrate that the binding free energy of protein–ligand interactions for wt GlpT consistently diminishes during transport toward the point around 30 Å (here and later, we define binding free energy as the sum of solvation and Coulombic energies of interactions, and total energy as the sum of binding free energy and van der Waals interaction energies). The van der Waals (vdW) energy fluctuates around zero as Glp passes through the entire transporter. This is consistent with the shape of the transporter in the partially reversed state that is open to both sides of the membrane.

Fig. 7.

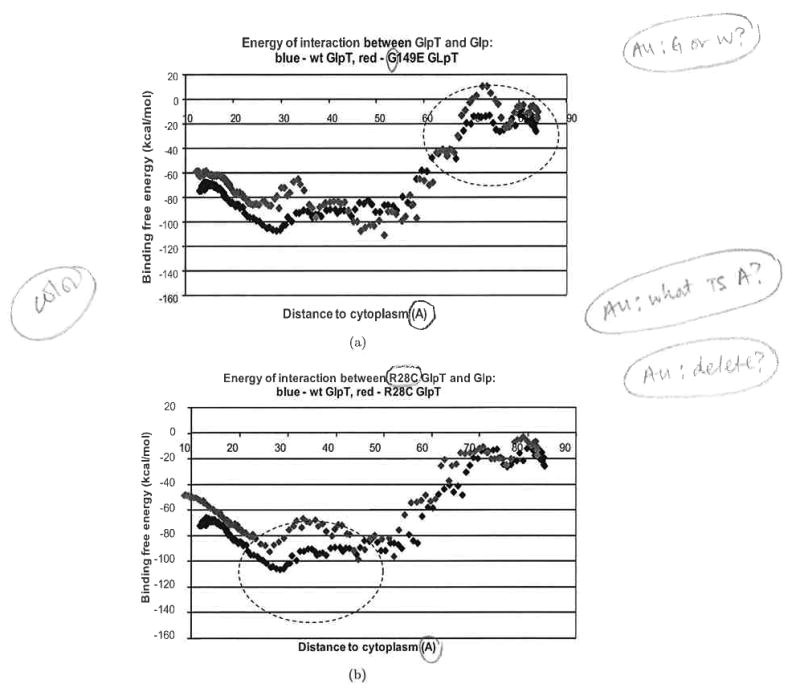
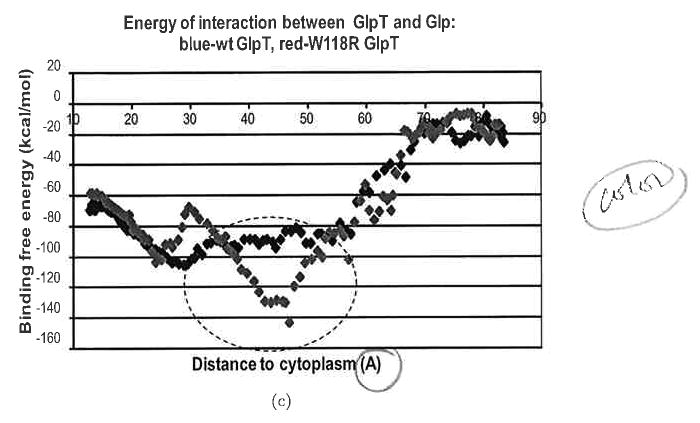
Profiles of binding free energy for wild-type (wt) (blue diamonds) and mutant (red diamonds) GlpT during Glp transport from the periplasm to the cytoplasm in the 10° rotated GlpT. (a) W149E mutant of GlpT; (b) R28G mutant of GlpT; (c) W118R mutant of GlpT. The Glp molecule movement is from right to left. Entrance of the Glp to the transporter is around the point 75 Å, where as the exit from the transporter to the cytoplasm is around the point 15 Å.

3.4. Impact of GlpT mutations on transport is predicted by modeling

An important test of this model was to determine whether it is consistent with experimental data on transport after various key amino acid mutations have been introduced. Fortunately, considerable mutational experimental data exist for this well-studied transporter.^9,24,25 E. coli GlpT has 28% sequence identity and 46% positive residue correspondence to human GlpT, and is a clear structural homolog of human GlpT. This fact made it possible to impose mutation sites defined in the human GlpT (which, interestingly, can lead to glycogen storage disease) upon the 3D structure of E. coli GlpT. We chose three mutations in the E. coli GlpT corresponding to R28C, W118R, and G149E (human transporter G16p-based numbering) that were shown to completely abolish uptake of Glp by G16p^14,24,25 in order to determine whether the energy profile of ligand interactions with the transporter by molecular dynamics simulation in the “tilting” structure could predict the impact of these mutations on the transporter function.

Figures 7 clearly indicates that, in all three cases, significant changes in the binding free energies and total energies of transporter–ligand interactions create specific energy profiles that are not favorable to passage of the ligand through the transporter. The mutation G149E inserting the negative residue occurs at a site on the interior of the pore of the transporter close to the periplasm [Fig. 8(a)]. Figure 7(a) shows that this mutation significantly increases the binding free energy of transporter–ligand interaction. This mutation causes the appearance of the free energy barrier around 20 kcal/mol at the entrance to the transporter from the extracellular side. The mutation R28C [Fig. 8(b)] deletes a positive residue in the transporter pore. One can see a clear maximum of binding free energy around than 20 kcal/mol that appears due to this mutation [Fig. 7(b)]. The third mutation W118R [Fig. 8(c)] is particularly interesting because the positive residue introduced into the transporter pore would seem, at first glance, to support increased transport of the negative ligand. In fact, molecular dynamics simulation indicates that this mutation creates a deep minimum of binding free energy in the transporter's channel [Fig. 7(c)]; most likely, this mutation creates a situation where the ligand cannot move out of this minimum.

Fig. 8.

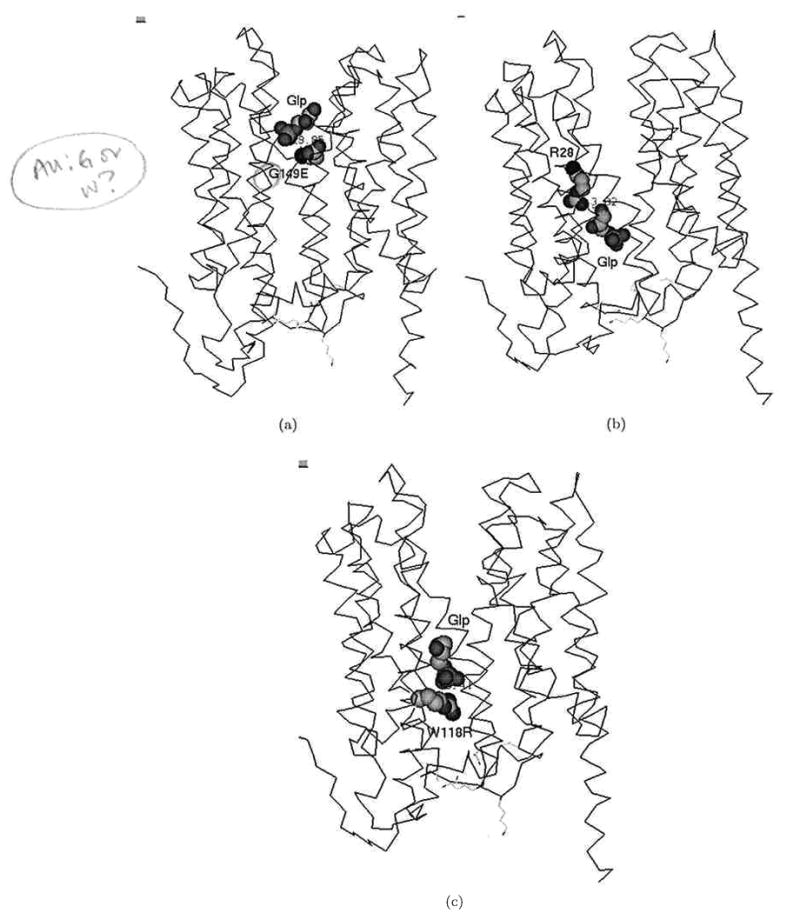
Snapshots of Glp transport in GlpT. Positions of Glp (a) near the mutated residue G149E, (b) near the residue R28 (which further mutated to Cys), and (c) near the mutated residue W118R.

Table 1 shows that our theoretical predictions of the possible disruption of normal function of the human GlpT equivalent transporter correspond well with the experimental data for transporter dysfunction.²⁵ We show that all three transporter dysfunction mutations can be predicted on the basis of our SMD simulations. Moreover, we propose four additional mutations that can also prevent normal function of GlpT, although they are yet to be experimentally tested.

Table 1.

Prediction of possible impact of mutations of microsomal glucose 6-phosphate transporter on the basis of our theoretical calculations with Glp transport in GlpT.

Mutation in human transporter	Predicted activity (%)	Experimentally validated15
wt	100	Yes
R28C	0	Yes
W118R	0	Yes
G149E	0	Yes
K29Xa	0	Not tested
K64Xa	0	Not tested
R134Xa	0	Not tested
R240Xa	0	Not tested

^aX: egative or neutral residue.

4. Conclusion

In summary, we have shown that profiles of binding free energy of Glp moving through the “tilted” GlpT transporter, created by considering the energetic relationships between the two six-helix subdomains of GlpT in the context of different rotations, can be used for prediction of possible effects of mutation on Glp transport (Table 1). Our results suggest that the full “rocker switch” model for solute carrier (SLC) transporters introduced by Lemieux et al.^8,9 may not apply to all members of this large family of genes that is involved in vital transport functions and drug handling. We show here that a simple “tilt” model with rotation of an SLC transporter's six-helix subdomains to 9°–10° creates an opening sufficient for anion transport without the need for a “rocker switch”. Alternatively, the tilt may exist as an intermediate in transport or may mainly be present under artificial conditions. Thus, the data need not be viewed as inconsistent with the rocker-switch mechanism or in a single-site alternating access model that seems completely with current biochemical data. What we suggest here is the theoretical possibility of both transporter and channel-like properties that require further wet lab experimental exploration.

The model that we propose should be applicable to other SLC family members, although it is possible that other types of models will explain the mechanism of transport for different SLC subfamilies. This awaits further structural studies and modeling. Experimental confirmation or refutation of the “tilt” model may require a combination of crystallization in other ligand-bound states, studies of the dynamics of movement of ligands through the transporters as well as movement of transporter amino acid residues during transport, and mutational analysis. In fact, our model suggests new types of mutational studies of residues in helices of SLC family members that might otherwise not have been considered to be mechanistically critical for transport. Given that SLC proteins transport many common drugs and toxins, polymorphisms in these residues may influence drug handling and susceptibility to toxicity.

Biography

Igor F. Tsigelny, Ph.D., is a project scientist at the University of California, San Diego, USA. His group develops methods and programs in the fields of protein structure prediction, molecular modeling of various diseases, bioinformatics, and computer-based drug design.

Jerry Greenberg received his Ph.D. in Chemistry from the University of California, San Diego, USA. His thesis work consisted of using and developing chemical potential models to simulate aqueous solution and silicate melt equilibria. He worked as a staff scientist at the San Diego Supercomputer Center, where he developed molecular visualization codes, worked on parallelization of chemistry programs, and most recently collaborated on a project to develop a web services-based framework for accessing scientific codes running on the grid.

Valentina Kouznetsova received her Ph.D. in Information Theory and Cybernetics from the Institute of Physics and Mechanics of the Ukrainian Academy of Sciences, Ukraine. Her work is devoted to the development of new methods of data and image processing, molecular modeling, and simulations. She works as an assistant project scientist at the University of California, San Diego, USA.

Sanjay K. Nigam, M. D., is a Professor of Pediatrics, Medicine, and Cellular and Molecular Medicine at the University of California, San Diego, USA. He is also appointed in the Division of Bioinformatics. His group studies the basis of drug and metabolite handling by organic anion transporters.