Modeling the Pediatric Paradox: Birth Weight by Gestational Age

Abstract

The “pediatric paradox“ of African versus European American infant mortality is often observed with respect to birth weight, but rarely to gestational age, even though the two measures are biologically related. This paper models the pediatric paradox by birth weight and gestational age simultaneously, using Covariate Density Defined mixture of logistic regressions (CDDmlr) fitted to 1985–1988 New York State births. The model controls for unobserved heterogeneity and isolates the pediatric paradox in the “compromised” subpopulation. The paradox is not limited to low birth weights and/or short gestational ages, but surrounds the normal birth range. Nevertheless, the pediatric paradox is only observed in the marginal distribution of birth weight and not the marginal distribution of gestational age. These results are consistent with the hypothesis that higher fetal losses in the “compromised” subpopulation may be responsible for the pediatric paradox and that African versus European American infant mortality differentials are underestimated.

INTRODUCTION

The term “pediatric paradox” was originally invoked to describe the common observation that African American births experience better birth weight specific survivorship than European American births among births weighing less than 3000 grams (Buehler et al. 1987; Gage et al. 2004b; Johnson 1987; North and MacDonald 1977; Platt et al. 2004a; Sappenfield et al. 1987; Wilcox and Russell 1990). This finding is considered counter intuitive given the common assumptions: a) that aggressive medical intervention is likely to be most effective among low birth weight births, and b) that African American births are less likely to have access to these medical services (Wilcox and Russell 1990). An example is the recent development of surfactant treatment for respiratory distress syndrome (RDS). This treatment has proven to reduce infant mortality due to RDS and is more effective among low birth weight European American births than among low birth weight African American births. It has been argued that this might nullify or even reverse the all cause mortality advantage of lower birth weight African American infants, that is, eliminate the pediatric paradox (Frisbie et al. 2004). However, post surfactant treatment birth cohorts still clearly display the pediatric paradox at birth weights below about 3000 grams when all causes of death are considered (Platt et al. 2004a). Thus the paradox remains and becomes increasingly counter intuitive as new medical interventions, which favor the European American birth cohort, like surfactant treatment, are developed.

Although the pediatric paradox was originally defined in terms of African versus European American infant mortality, it can be applied to most comparisons of stressed versus unstressed populations. Examples of such comparisons are: European American birth cohorts with Hispanic Americans (Frisbie et al. 1996), or with Asian Americans (Yip et al. 1991), as well as with a variety of environmentally “stressed” versus “non-stressed” birth cohorts (births to smokers versus non-smokers, twin births versus singleton births, low versus high altitude births, first born versus higher parity births, and births to low versus high social class mothers) (Buekens and Wilcox 1993). The ubiquity of the pediatric paradox at the lower birth weights (<3000 grams or so) between stressed versus non-stressed populations suggests that the mechanism may be similar in all of the birth weight pediatric paradoxes. On the other hand, population comparisons of gestational age specific infant mortality are rarely associated with a pediatric paradox, despite the close theoretical and empirical relationship between gestational age and weight at live birth. An analysis of the pediatric paradox by birth weight and gestational age is needed to explain the full extent of the pediatric paradox, and why the paradox is apparent from the marginal distribution of birth weight but not from the marginal distribution of gestational age.

Covariate Density Defined mixtures of logistic regression (CDDmlr), a statistical method that controls for unobserved heterogeneity, has been shown to isolate the African/European birth weight pediatric paradox to a specific latent subpopulation of the birth cohort. This subpopulation is usually interpreted as representing births compromised during fetal development. Based on these results it has been hypothesized that the pediatric paradox may be driven by fetal loss selecting on heterogeneity in the birth cohort (Gage 2002a; Gage et al. 2004b). Recently a birth weight by gestational age specific version of the CDDmlr model has been developed and the birth weight by gestational age density and mortality surfaces described for the New York State 1985–88 birth cohort (Fang et al. 2007). The aim of the present analysis is to extend the results presented in Fang et al. (2007) to a statistical comparison of the African versus European American birth weight by gestational age densities and mortality surfaces for the same New York State 1985–88 birth cohort. In particular the analysis maps the African/European American pediatric paradox in birth weight by gestational age space. It differs from previous studies of the pediatric paradox based on conventional methods in that a) studies of the pediatric paradox usually condition on birth weight alone, b) birth weight and gestational age are modeled on a continuous scale, rather than as binned data, c) the method controls for unobserved heterogeneity in infant mortality, d) the birth weight by gestational age regions where mortality differs significantly between African and European Americans are identified, and e) analyses are carried out separately by sex. The results presented below indicate a) that as with analyses using only birth weight (Gage et al. 2004b), the pediatric paradox can be attributed to the “compromised” subpopulation of births, and b) that the birth weight by gestational age region where African American mortality is lower than European American mortality is not restricted to low birth weight and pre-term births, but is more extensive, particularly in males. These findings are consistent with the hypothesis that differential fetal loss may drive the pediatric paradox.

METHODS

The data used in this analysis consists of African and European American female and male birth cohorts from the linked birth/death files of New York State, 1985–1988. These data are used instead of more recent birth cohorts, because the higher death rates improve the resulting estimates, while the overall sample sizes are still of manageable size. Further, the New York State data during this period are relatively accurate and consistently collected. Birth weight is reported in grams and gestational age in fractional weeks to the nearest day. Multiple births, births without matching parental racial identification, and births missing birth weight or gestational age were eliminated from the analysis. The characteristics of these birth cohorts are summarized in Table 1.

Table 1.

Descriptive Statistics for the Sample Populations

Birth Cohort	# Births	Missing Data (%)			Mean		# Deaths	CDR
		w	g	overall	w	g
Af. Am. F.	54,968	0.1	2.1	2.2	3119	39.1	690	12.6
Af. Am. M.	57,449	0.2	2.0	2.2	3240	39.1	848	14.8
Eu. Am. F.	255,516	0.2	2.0	2.2	3375	40.0	1294	5.1
Eu. Am. M.	270,189	0.2	2.1	2.2	3507	39.9	1734	6.4

Source: Table 1 in Fang et al. 2007, p. 477

Af. = African, Eu. = European, Am. = American, F. = Females, M. = Males

w = Birth weight (gram)

g = Gestational age (week)

CDR = Crude death rate (deaths per 1000 births)

The model employed is a multivariate extension of the model (Covariate Density Defined mixture of logistic regressions, CDDmlr) proposed by Gage and his colleagues (2002; 2004b). It differs substantially from the standard finite mixtures of logistic regressions (McLachlan and Peel 2000; Wang 1994) and the generalized growth mixture regression models of Muthen (2004).

The multivariate CDDmlr (Fang et al. 2007) is defined in terms of the joint density of the covariate vector (X), which comprises birth weight (x_w) and gestational age (x_g), and the occurrence of death (y):

$$L(\beta ,\theta )=f(y,X;\beta ,\theta )=f_2(y|X;\beta ,\theta )\times f_1(X;\theta )$$ (1)

where θ and β are the determining parameters for the covariate density function f₁ (X;θ) and the conditional mortality function f₂(y|X;β,θ), respectively.

The birth weight by gestational age density f₁(X;θ) for the two-subpopulation case where each subpopulation is a Gaussian distribution is given by:

$$f_1(X;{\pi }_p,{\mu }_p,{\sum }_p,{\mu }_s,{\sum }_s)={\pi }_p\times N(X,{\mu }_p,{\sum }_p)+(1-{\pi }_p)\times N(X;{\mu }_s,{\sum }_s)$$ (2)

with π_p as the mixing proportion, defined as the proportion of births belonging to the bivariate Gaussian density accounting for the larger proportion of the birth cohort. The mixing proportion, π_p, has been transformed as η = logit(π_p). The larger subpopulation is called the primary (p) subpopulation, while the remaining subpopulation is referred to as the secondary (s) subpopulation. For i = s and p, N(X;µ_i,∑_i) is a bivariate Gaussian density function with mean vector µ_i = [µ_iw, µ_ig]^t and variance-covariance matrix ${\sum }_i=\left[\begin{array}{cc}\hfill {{\sigma }_{\mathit{\text{iw}}}}^2\hfill & \hfill {\rho }_i{\sigma }_{\mathit{\text{iw}}}{\sigma }_{\mathit{\text{ig}}}\hfill \\ \hfill {\rho }_i{\sigma }_{\mathit{\text{iw}}}{\sigma }_{\mathit{\text{ig}}}\hfill & \hfill {{\sigma }_{\mathit{\text{ig}}}}^2\hfill \end{array}\right]$. The ρ_i terms represent the correlation between gestational age and birth weight for their respective subpopulations.

The conditional mortality function f₂ (y|X; β,θ) with two subpopulations is:

$$\begin{array}{c}{f}_2(y|X;{\beta }^{(p)},{\beta }^{(s)},\theta ))\hfill \\ \hfill =q(X;\theta )\times P(y|X;{\beta }^{(p)})+(1-q(X;\theta ))\times P(y|X;{\beta }^{(s)})\end{array}$$ (3)

where q(X;θ) is the probability that an infant of covariate vector X belongs to subpopulation p. The birth weight by gestational age density f₁(X;θ) (Equation 2) determines that:

$$q(X;{\pi }_p,{\mu }_p,{\sum }_p,{\mu }_s,{\sum }_s)=\frac{{\pi }_p\times N(X;{\mu }_p,{\sum }_p)}{{\pi }_p\times N(X;{\mu }_p,{\sum }_p)+(1-{\pi }_p)\times N(X;{\mu }_s,{\sum }_s)}$$ (4)

And for i = s and p,

$$P(y|X;{\beta }^{(i)})=P(y|X;a_i,B_i,C_i)=e^{y\times (a_i+B_i^{t}X+X^t{C}_{i}X)/(1+e^{a_i+B_i^{t}X+X^t{C}_{i}X})}$$ (5)

where B_i = [b_iw,b_ig]^t and $C_i=\left[\begin{array}{cc}\hfill c_{\mathit{\text{iw}}}\hfill & \hfill \frac{1}{2}{\mathit{\text{cv}}}_i\hfill \\ \hfill \frac{1}{2}{\mathit{\text{cv}}}_i\hfill & \hfill c_{\mathit{\text{ig}}}\hfill \end{array}\right]$. The interaction term between birth weight and gestational age (cv_i) represents the combined impact of birth weight and gestational age on the mortality of the i subpopulation, over and above the independent effects of birth weight and gestational age.

Alternative specifications for the birth weight by gestational age density and component specific mortality are possible within the context of CDDmlr. The bivariate Gaussian density is assumed here given that the sum of two Gaussians is an extremely good fit to either birth weight or gestational age (Fryer et al. 1984; Gage and Therriault 1998; Gage 2000) and because the sum of two Gaussians fit these data, as well, or better than several biologically plausible alternatives in the univariate case (Gage 2002b). The quadratic specification of component specific mortality is assumed because this is commonly found to be the parsimonious model for birth weight specific infant mortality in the homogeneous case (Fryer et al. 1984; Solis et al 2000). All together there are 23 unique parameters, 11 defining the covariate mixture submodel f₁(X;θ), and 12 defining the conditional mortality submodel f₂(y|X; β,θ) (Fang et al. 2007).

The model (Equation 1) is fitted to individual level data by the method of maximum likelihood. In particular, we use the ms() function in Splus to minimize the negative log likelihood. Standard hierarchical methods and bias adjusted confidence intervals are used to evaluate the significance of each parameter and identify the parsimonious model. The hierarchical methods use the standard likelihood ratio criterion. Bias-adjusted confidence intervals are obtained by bootstrap methods (Davison and Hinkley 1997). For additional statistical details, proof of identification and properties of the model see Gage et al. (2004a).

RESULTS

The Distribution of Births by Birth Weight and Gestational Age

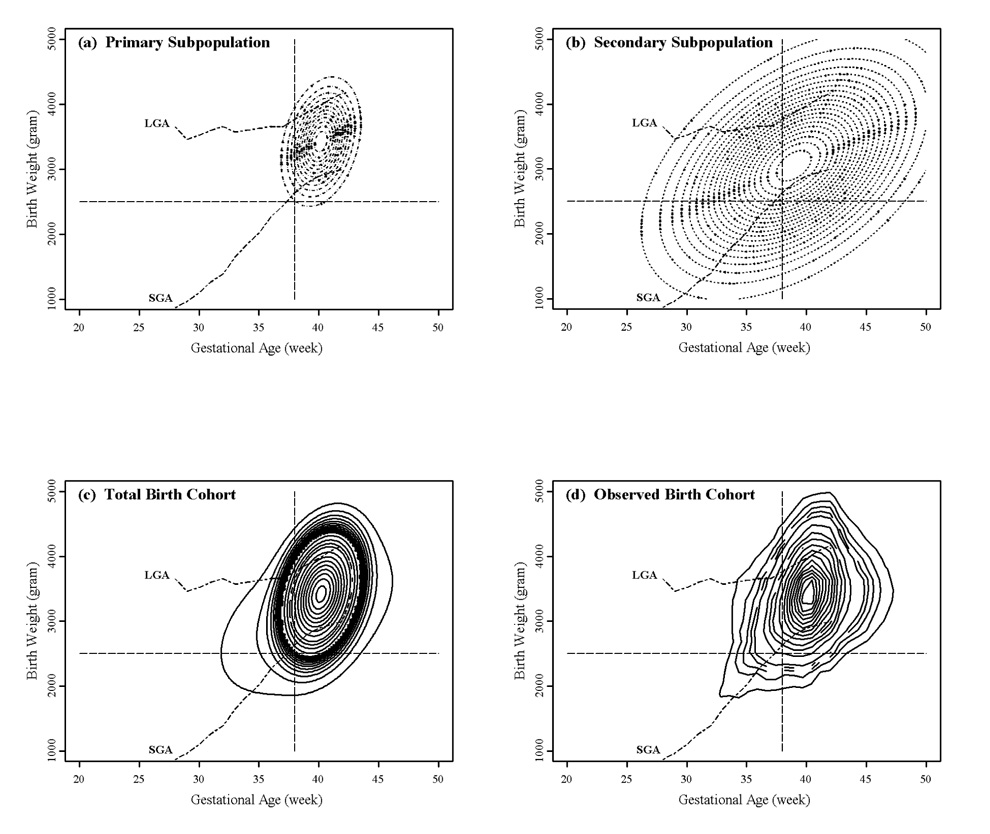
The birth weight by gestational age distributions of the two subpopulations are “hill-shaped” surfaces represented by contour plots in Figure 1. The full mixture submodel is parsimonious in all four cases (Fang et al. 2007). The primary subpopulation accounts for 83 to 88 percent of births in these analyses (Table 2) and is largely confined to the normal birth weight by gestational age range (Figure 1(a)). The secondary subpopulation is more widely distributed (Figure 1(b), Table 2). Given that the majority of births traditionally classified as “compromised” births are accounted for by the secondary subpopulation, it is reasonable to conclude that this subpopulation includes the infants compromised in some way during fetal development, while the primary subpopulation represents infants that underwent normal fetal development (Fang et al. 2007; Gage 2003). The total modeled birth weight by gestational age density is presented in Figure 1(c). It is similar to the non-parametric smooth of the empirical distribution (Figure 1(d)).

Figure 1.

Contour plots of model-estimated (a–c) and observed (d) birth weight by gestational age distributions: European American females. SGA (small for gestational age) and LGA (large for gestational age) represent the 10^th and 90^th percentiles of birth weight conditioned on gestational age at live births based on observed data, respectively. The cross-hair lines are the traditional cutoffs for low birth weight (<2500 grams) and pre-term (<37 completed weeks) infants.

Table 2.

Parameter Estimates and Bias-adjusted 95% Confidence Intervals for the Mixture Submodel f₁(X;θ)

Parameter	Af. Am. F.	Af. Am. M.	Eu. Am. F.	Eu. Am. M.
πp	0.83 (0.82, 0.84)	0.84 (0.84, 0.85)	0.88 (0.87, 0.88)	0.87 (0.87, 0.88)
µpw	3219 (3214, 3225)	3345 (3339, 3350)	3423 (3420, 3425)	3566 (3564, 3568)
µpg	39.75 (39.73, 39.76)	39.68 (39.66, 39.70)	40.19 (40.18, 40.20)	40.08 (40.08, 40.09)
σpw	450 (445, 455)	462 (458, 466)	441 (439, 443)	466 (464, 467)
σpg	1.71 (1.67, 1.74)	1.77 (1.75, 1.79)	1.47 (1.46, 1.48)	1.52 (1.50, 1.53)
ρp	0.25 (0.24, 0.26)	0.26 (0.24, 0.27)	0.29 (0.28, 0.29)	0.33 (0.31, 0.32)
πs	0.17 (0.16, 0.18)	0.16 (0.15, 0.16)	0.12 (0.12, 0.13)	0.13 (0.12, 0.13)
µsw	2653 (2621, 2682)	2691 (2657, 2718)	3048 (3035, 3062)	3112 (3096, 3128)
µsg	36.35 (36.13, 36.59)	36.06 (35.84, 36.23)	38.95 (38.87, 39.03)	38.62 (38.55, 38.71)
σsw	952 (929, 971)	985 (967, 1008)	837 (824, 853)	872 (858, 884)
σsg	5.36 (5.26, 5.48)	5.51 (5.41, 5.61)	5.17 (5.07, 5.27)	5.22 (5.11, 5.31)
ρs	0.49 (0.47, 0.51)	0.50 (0.48, 0.52)	0.47 (0.46, 0.48)	0.50 (0.49, 0.51)

Source: Table 4 in Fang et al. 2007, p. 480

Af. = African, Eu. = European, Am. = American, F. = Females, M. = Male

for i = p (primary) and s (secondary) subpopulations, π_i, µ_iw, µ_ig, σ_iw, σ_ig, and ρ_i are the proportion, the mean birth weight, the mean gestational age, the standard deviation of birth weight, the standard deviation of gestational age, and the correlation between birth weight and gestational age respectively. Birth weight is in grams. Gestational age is in weeks.

Statistically significant differences occur between the races and sexes in the subpopulation means, while significant racial variation also occurs in the mixing proportions (Table 2). Compared to European Americans, African American births of the same sex have significantly lower mean birth weights (approximately 210 and 410 gram in the s and p subpopulation, respectively) and shorter mean gestational ages (approximately 3 and 18 days in the s and p subpopulation, respectively). Females versus males of both races tend to have lower mean birth weight (approximately 135 and 50 gram in the s and p subpopulation, respectively), but longer mean gestational age (approximately 14 hours and 2 days in the s and p subpopulation, respectively) in both subpopulations, although the differences in gestational age are not statistically significant. On the other hand, the proportion of secondary births is significantly higher in African American births, compared with European American births of the same sex. Thus a larger proportion of African American births may be “compromised”.

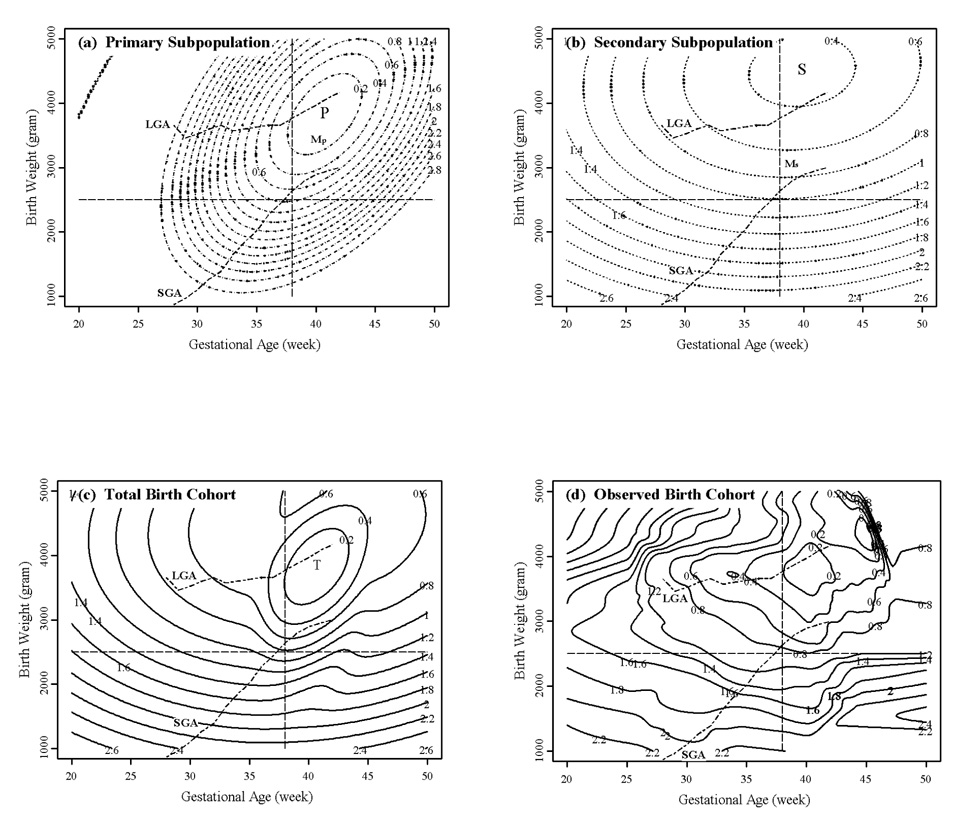
The Birth Weight by Gestational Age Mortality Surface

The primary and secondary mortality surfaces resemble “valleys” (Figure 2) with minimum mortality occurring in the normal birth weight by gestational age range. The full mortality submodel is usually not parsimonious (Table 3). In most cases the interaction terms (birth weight by gestational age) are not significant, while in a few cases, the squared terms of the polynomial are not significant. Since the linear terms are all negative, the few cases of insignificant squared terms indicate that mortality does not always increase at higher levels of birth weight and gestational age. For all but African American males, the birth weight by gestational age specific secondary mortality surface is significantly lower than the primary mortality surface except in the normal birth weight by gestational age range where secondary exceeds primary mortality (Fang et al. 2007). Among African American males, the secondary mortality surface is always lower than primary specific mortality surface. On the other hand, total secondary mortality is approximately an order of magnitude higher than total primary mortality in all populations examined (Table 4). Though the secondary subpopulation accounts for less than 17% of the total births of African and European Americans (Table 2), more than 60% of the infant deaths are attributed to this subpopulation (Table 4). The lower birth weight and gestational age specific mortality but higher over all mortality among secondary births compared to primary births is an example of Simpson’s paradox (Simpson 1951) and is due to the higher proportion of secondary births that occur at unfavorably low and high birth weights and gestational ages.

Figure 2.

Contour plots of model-estimated (a–c) and observed (d) birth weight by gestational age specific mortality (deaths per 1000 births) using a log10 scale: European American females. A value of 3 indicates 100 percent mortality. The location of minimal mortality of the primary and secondary subpopulation is designated by “P” (Fig. 2a) and “S” (Fig. 2(b)), respectively. The mean of the primary and the secondary distribution is marked by “Mp” (Fig. 2(a)) and “Ms” (Fig. 2(b)), respectively. The global minimum of the total birth cohort is designated by “T” (Fig. 2(c)).

Table 3.

Parameters Estimates and Bias-adjusted 95% Confidence Intervals for the Conditional Mortality Submodel f₂(y|X; β,θ)

Parameter	Af. Am. F.	Af. Am. M.	Eu. Am. F.	Eu. Am. M.
ap	66.4 (1.3, 124.2)	76.1 (39.0, 106.3)	57.4 (−3.5, 114.5) &	25.7 (−31.2, 83.9) &
bpw (× 10−3)	0.3 (−6.4, 7.9) &	−5.5 (−10.9, −0.5)	0.8 (−5.5, 7.7) &	−1.7 (−6.7, 3.0) &
cpw (× 10−7)	9.7 (4.7, 14.0)	9.4 (5.8, 12.3)	12.8 (9.8, 15.1)	9.5 (6.3, 12.5)
bpg	−3.6 (−6.2, −0.6)	−3.6 (−5.1, −1.7)	−3.2 (−6.0, −0.4)	−1.3 (−4.2, 1.5) &
cpg (× 10−2)	5.2 (1.6, 8.5)	4.6 (2.1, 6.7)	5.2 (1.7, 8.6)	2.2 (−1.5, 6.0) &,+
cνp (× 10−4)	−1.9 (−3.8, −0.1)	−0.4 (−1.9, 1.3) &,+	−2.6 (−4.3, −1.0)	−1.5 (−2.8, −0.0) +
as	9.2 (6.6, 11.7)	9.2 (6.0, 13.2)	9.1 (7.6, 10.6)	8.7 (7.4, 10.1)
bsw (× 10−3)	−3.8 (−4.7, −3.1)	−3.2 (−4.0, −2.5)	−3.0 (−3.4, −2.7)	−3.5 (−4.0, −3.1)
csw (× 10−7)	6.6 (5.2, 7.9)	6.9 (5.5, 8.0)	3.9 (3.2, 4.5)	4.0 (3.3, 4.7)
bsg	−0.4 (−0.6, −0.3)	−0.4 (−0.7, −0.2)	−0.4 (−0.5, −0.3)	−0.3 (−0.4, −0.3)
csg (× 10−3)	6.6 (4.0, 8.9)	6.3 (3.1, 10.1)	5.9 (4.5, 7.3)	4.1 (2.6, 5.6)
cνs (× 10−5)	−2.3 (−4.5, 0.4) &	−5.3 (−7.7, −2.5)	−1.1 (−2.4, 0.2) &,+	0.1 (−1.3, 1.7) &,+

source: Table 5 in Fang et al. 2007, p. 481

Af. = African, Eu. = European, Am. = American, F. = Females, M. = Males

for i = p (primary) and s (secondary) subpopulations, a_i, b_iw, c_iw, b_ig, c_ig, and cν_i are the constant, the linear term on birth weight, the square term on birth weight, the linear term on gestational age, the square term on gestational age, and the interaction term on birth weight and gestational age respectively. Birth weight is in grams. Gestational is in weeks.

^&not significantly different from zero based on the bias-adjusted 95% confidence interval

⁺not significantly different from zero based on the standard hierarchical method

Table 4.

Model-based Mortality

Birth Cohort	Primary Subpopulation		Secondary Subpopulation		Total Birth Cohort
	DRa	% to Total DR	DRa	% to Total DR	Total DRa
Af. Am. F.	5.5	37.8	43.2	62.6	12.0
Af. Am. M.	6.7	40.1	54.6	60.4	14.1
Eu. Am. F.	2.1	39.1	23.5	61.1	4.8
Eu. Am. M.	2.6	38.4	29.5	61.5	6.0

Af. = African, Eu. = European, Am. = American, F. = Females, M. = Males

DR = death rate (deaths per 1000 births)

^afrom Table 3 in Fang et al. 2007, p. 479

The model-estimated total mortality surface (Figure 2(c)) is similar to the kernel smoothed empirical mortality surface (Figure 2(d)) particularly in those birth weight by gestational age regions where significant numbers of births occur. The total mortality surface (Figure 2(c) and 2(d)) is not a simple “valley”. In fact multiple birth weight by gestational age mortality minima are common, particularly in African Americans (Fang et al. 2007). The global minimum mortality always occurs within the normal birth weight gestational age range and it is due to the primary subpopulation. On the other hand, the local minima occur at normal birth weights but low and/or high gestational ages and they are due to the relatively lower mortality of the secondary subpopulation compared to the primary subpopulation in those regions.

The Birth Weight by Gestational Age Pediatric Paradox

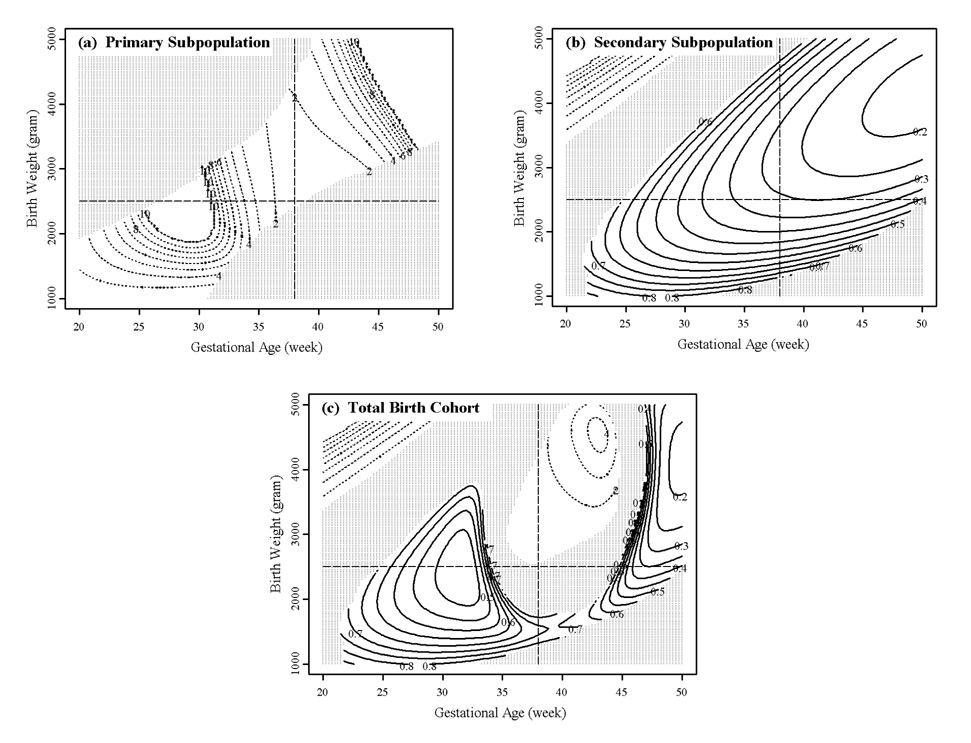
Comparisons of African versus European mortality surfaces by sex indicate that the pediatric paradox is due principally to the secondary subpopulation. The results are presented for males in Figure 3. Primary mortality is generally higher among African American births compared to European Americans of the same sex and significantly higher in the normal birth weight by gestational age range where most primary births occur (Figure 3(a)). Similarly, secondary mortality is lower among African American male births throughout the region where most secondary births occur (Figure 3(b)). The total mortality surface (combined primary and secondary mortality) indicates that within the normal birth weight by gestational age range, African American mortality is higher, but outside the normal birth weight by gestational age range, African American mortality is lower (Figure 3(c)). Among males, African American mortality is significantly lower in the low birth weight, pre-term range, but also significantly lower in a ring surrounding the normal birth weight by gestational age range. The results for females are not as extreme, that is, African American mortality is only lower in the low birth weight and pre-term regions. Nevertheless, the results for males indicate that the pediatric paradox is not limited to low birth weights as is generally reported.

Figure 3.

Contour plots of birth weight by gestational age mortality ratios of African versus European American males. The solid-line () contour intervals represent the birth weight by gestational age ranges where African American males have significantly lower mortalities. The dotted-line () contour intervals represent the birth weight by gestational age ranges where European American males have significantly lower mortalities. The shaded areas () represent areas where differences are not statistically significant.

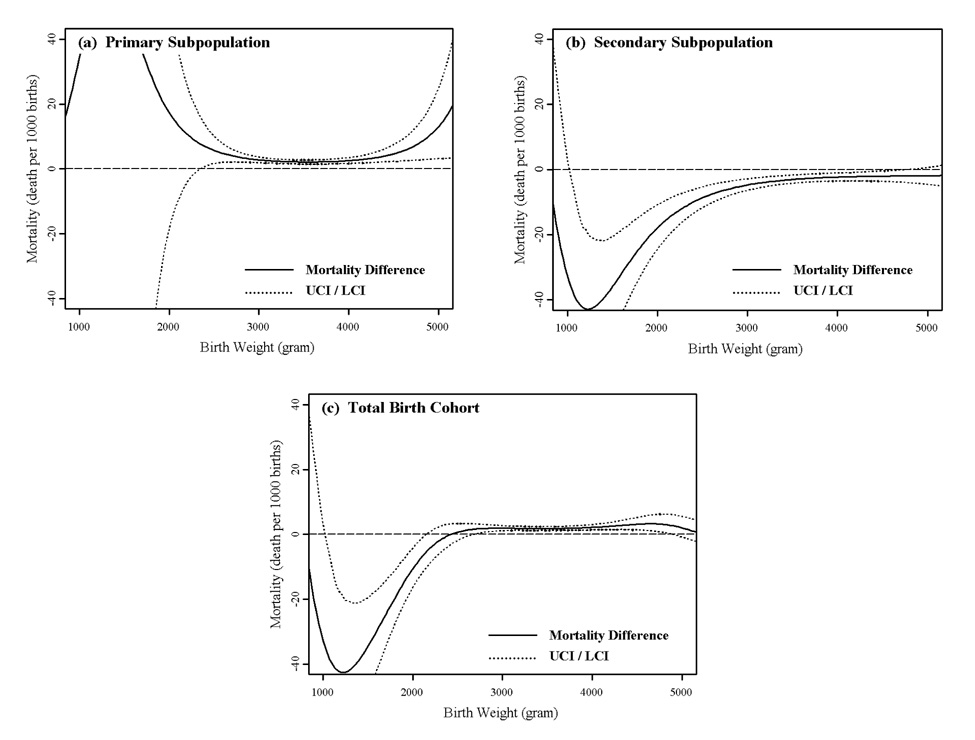
Viewed from the marginal distribution of birth weight of the fitted models (Figure 4), African American primary mortality is significantly higher than European American primary mortality in the normal birth weight range (Figure 4(a)). African American secondary mortality is significantly lower over most of the range but particularly at the lower birth weights (Figure 4(b)). The result is the standard African-European American “pediatric paradox”, with significantly lower African American mortality at low birth weights and significantly higher African American mortality over the normal birth weight range (Figure 4(c)). All of these results confirm that the pediatric paradox is due principally to the secondary subpopulation.

Figure 4.

Marginal view of birth weight specific infant mortality differences (deaths per 1000 births) between European and African American males. The horizontal dashed line represents no mortality difference. Values > 0 indicate higher African American mortality and values < 0 indicate lower African American mortality compared to European American infant mortality.

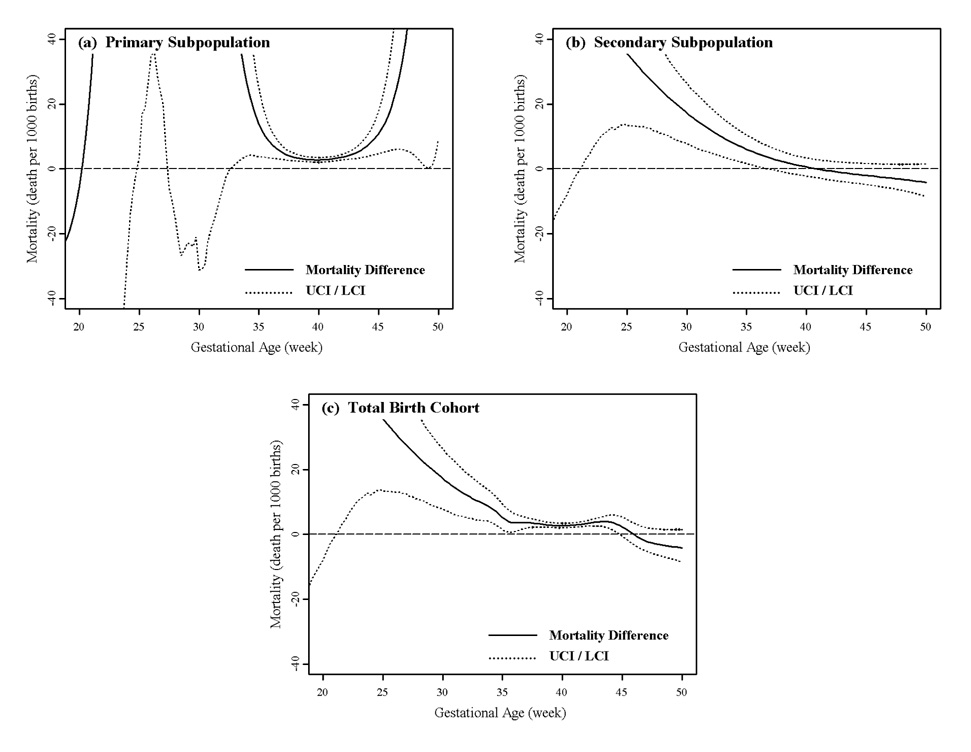
On the other hand, the “pediatric paradox” is not visible at all from the marginal distribution of gestational age of the fitted models. African American primary and secondary mortality are generally higher, and never significantly lower than corresponding European American mortality (Figure 5(a) and (b)). As a result, African American mortality is significantly higher than European American mortality except at the very highest and lowest gestational ages (Figure 5(c)). African American mortality is never significantly lower than European American mortality at any gestational age. Thus a pediatric paradox, that is lower African American specific mortality, is visible from the marginal distribution of birth weight but not from the marginal distribution of gestational age.

Figure 5.

Marginal view of gestational age specific infant mortality differences (deaths per 1000 births) between European and African American males. The horizontal dashed line represents no mortality difference. Values > 0 indicate higher African American mortality and values < 0 indicate lower African American mortality compared to European American infant mortality.

DISCUSSION

Over the last several decades, most analyses of infant mortality have employed birth weight and gestational age and not simply birth weight or gestational age (Battaglia and Lubchenco 1967; Cassady and Strange 1987; Lubchenco and Koops 1987; Lubchenco et al. 1972). However, the use of gestational age based on mother’s last reported menstrual period (LMP) in any analysis of birth outcomes has limitations, including considerable estimation error (Kramer et al. 1988; Mustafa and David 2001; Platt et al. 2001; Savitz et al. 2002), and a relatively large amount of missing data which are correlated with infant death (David 1980; Fang et al. 2007; Gould et al. 2002). In this regard, one advantage of the CDDmlr method for studying birth outcomes is that births with abnormally short and long gestational ages given birth weight (that is births with likely miss-estimated gestational ages) are accounted for by the secondary (compromised) subpopulation. Consequently, analyses of primary births should be relatively free of estimation error in gestational age.

Despite the problems associated with measurement of gestational age, many studies using LMP estimates suggest that birth weight conditioned on gestational age provides more information than birth weight alone (Battaglia and Lubchenco 1967; Cassady and Strange 1987; Lubchenco and Koops 1987; Lubchenco et al. 1972). The results presented in this paper are a case in point. The extent of the “pediatric paradox” can not be fully assessed using birth weight alone. The marginal view from birth weight suggests that the pediatric paradox is restricted only to low birth weight infants, while the marginal view from gestational age obscures the pediatric paradox entirely. Both birth weight and gestational age are necessary to show that the “pediatric paradox” can occur at “normal” birth weights, as well as, at the lower birth weights. Both birth weight and gestational age are also necessary to show that the “pediatric paradox” occurs at each gestational age for some range of birth weights.

The birth weight by gestational age distribution and mortality surfaces presented above have been discussed in detail previously by Fang et al. (2007) and are consistent with other applications of parametric mixture modeling (Fryer et al. 1984; Gage 2000; Gage 2003; Gage and Therriault 1998), and CDDmlr methods (Gage 2002; Gage et al. 2004b) to birth outcomes. In all cases, the results support the interpretation, that the primary subpopulation represents births that underwent “normal” fetal development and the secondary subpopulation accounts for those births “compromised” by some shock or stress during fetal development, resulting in low birth weight, pre-term, post-term (>42 completed weeks), intrauterine growth retarded, or small for gestational age births, as well as, some births in the normal birth weight by gestational age range. It remains to be determined if the secondary births in the normal birth weight by gestational age range are simply miss-classified normal births or births that are “compromised” in ways that do not lead to abnormal birth weight and gestational age. However, clinicians have argued that there are “compromised” births in the normal birth weight range, and that these births are understudied simply because they can not be easily identified using standard indicators, that is, low birth weight and short gestational age etc (Cassady and Strange 1987; Godfrey and Barker 2000). CDDmlr can probabilistically identify these births and statistically study their characteristics. Additional analyses with CDDmlr could resolve this issue, but are beyond the scope of the present analysis.

The results are also consistent with the hypothesis that some of the observed birth weight and gestational age specific dynamics of infant mortality is due to fetal loss selecting on heterogeneity in the birth cohort. In particular, the results show that at least outside of the normal birth weight by gestational age range birth weight by gestational age specific secondary mortality tends to be lower than primary mortality, although total secondary mortality is considerably higher than primary mortality, an example of Simpson’s paradox (Simpson 1951). The fetal loss hypothesis argues that during fetal development the secondary subpopulation (as the “compromised” subpopulation) experiences greater stressors and undergoes relatively greater fetal loss, so that by the time of live birth, secondary births tend to be more highly selected and more robust than their birth weight and gestational age specific peers in the primary subpopulation who were not stressed (Gage 2002; Gage et al. 2004b).

Given these results and interpretations, the “pediatric paradox” can be reasonably attributed to greater stress on the disadvantaged population. First, mortality in the African American cohort is higher in the primary subpopulation than among European Americans. Thus African American births undergoing “normal” fetal development have higher mortality postpartum than European American births. This is consistent with the idea that the African American population is under greater stress. Second, a larger percentage of African American births are “compromised” during fetal development, that is African American births are more heterogeneous. This can also be interpreted as greater stress on the fetal development of African American births. Finally, the lower mortality of the African American cohort of “compromised” births might be due to higher African American fetal losses. In particular, higher fetal losses might lead to greater selection, on “compromised” African American births compared to “compromised” European American births resulting in lower mortality at birth among “compromised” African American births. Over all births, the higher mortality at normal birth weights, and the lower mortality at lower birth weights of the disadvantaged population are both attributable to greater stressors operating on the disadvantaged population, resolving the paradox.

Empirical estimates of fetal loss rates are very difficult to obtain. Nevertheless, there is independent evidence indicating that fetal loss is higher among African than European Americans (Kallan 1993), including the New York State birth cohorts examined here (Buck et al. 1995). Other empirical analyses also suggest that the pediatric paradox is driven by fetal loss. In particular, Platt et al. (2004b) find that when a) fetal deaths and live births are included in the birth cohort, as opposed to the normal practice of studying only live births, and b) when age is defined as time since conception, as opposed to the normal practice of defining age as time since live birth, then the pediatric paradox disappears. This method has been questioned, largely for treating fetuses and infants of the same age, (age since conception), as equivalent (Klebanoff and Schoendorf 2004; Wilcox and Weinberg 2004). Nevertheless, the fact that the pediatric paradox disappears when observed fetal deaths (some proportion of total fetal loss) are included along with live births also suggests that the pediatric paradox maybe due to fetal loss selecting on a heterogeneous birth cohort, as suggested by Gage (2002) and Gage et al. (2004b). In addition, Powers et al. (2006) in their analysis of variation in racial disparities over the first year of life conclude that this variation is consistent with heterogeneity in the birth cohort and implicate differential fetal loss as a possible explanation

If the fetal loss interpretation of the pediatric paradox is correct, then racial disparities in infant mortality using simple comparisons of infant mortality rates are under estimates of the true racial disparity (Gage et al. 2004b; Wilcox and Russell 1986). In particular, higher fetal loss among African American births reduces infant deaths (traditionally computed on live births) more than among European Americans. Comparisons of racial disparities should control for this difference in fetal loss. The results presented above suggest that there are two important aspects to racial disparities in birth outcomes. The first aspect is higher infant mortality among “normal” African American births. A second aspect is the greater proportion of “compromised” births (greater heterogeneity) in African American birth cohorts. A comprehensive assessment of racial disparity should include both aspects of disparity.

While the interpretation above resolves the paradox of the “pediatric paradox”, the exogenous stressors causing differential heterogeneity and the determinants driving fetal loss and selection remain to be identified. The effects of exogenous stressors on birth outcomes and infant mortality can be further explored using extensions of CDD mixtures of logistic regressions. This methodology accounts for heterogeneity by distinguishing between primary and secondary subpopulations of births and treats these subpopulations as separate regression analyses. Covariates representing exogenous factors (e.g. maternal age, parity, education etc.) may be incorporated into the analysis on either or both subpopulations and may condition the birth weight by gestational age densities (i.e. as stressors acting indirectly on infant mortality through birth weight and gestational age) or the birth weight by gestational age mortality surfaces (i.e. as direct effects on infant mortality). The method of CDD mixtures of logistic regressions can identify characteristics of the understudied, “compromised” births found in the normal birth weight by gestational age range. Further, since CDD mixtures of logistic regressions treats the two subpopulations as separate regressions, the exogenous stressors influencing the low secondary mortality (the pediatric paradox) and the exogenous factors causing excess primary African American infant mortality can both be examined as statistically separate effects. Conventional methods of analysis cannot correct for “unmeasured” heterogeneity, often depend upon arbitrary classification systems, such as, low birth weight, pre-term, IUGR and SGA, can not identify “compromised” births in the normal birth weight by gestational age range, and do not allow covariates to affect “normal” and “compromised” births differently. Consequently, further applications of the CDD mixtures of logistic regressions methodology to birth outcomes and mortality would greatly improve our understanding of racial and ethnic disparities in neonatal and infant mortality.

CONCLUSIONS

This paper presents a model of the African American versus European pediatric paradox using Covariate Density Defined mixtures of logistic regressions, incorporating birth weight and gestational age as continuous variables, and controlling for otherwise unobserved heterogeneity. The results suggest:

1. that the “pediatric paradox” is not limited to the lower birth weights and shorter gestational age births. It can occur at all birth weight by gestational ages out side of the normal range, particularly in males.

2. that the “pediatric paradox” is due to the secondary, that is, “compromised”, subpopulation, and may be driven by fetal loss.

3. that excess African American infant mortality is due to the larger size of its secondary subpopulation and to higher mortality in its primary, that is, “normal”, subpopulation. The role of the both of these factors is understudied since conventional analyses have concentrated on the effects of low birth weight and conventional methods do not control for heterogeneity in the birth cohort.

4. that as a result of the subpopulation structure (heterogeneity), the African American/European American infant mortality differential may be significantly underestimated. and

5. that Covariate Density Defined mixtures of logistic regressions can be used to control for unobserved heterogeneity and to identify the indirect (through birth weight / gestational age) and the direct effects of other exogenous covariates on infant mortality.