Time to Send the Preemie Home? Additional Maturity at Discharge and Subsequent Health Care Costs and Outcomes

Abstract

Objective

To determine whether longer stays of premature infants allowing for increased physical maturity result in subsequent postdischarge cost savings that help counterbalance increased inpatient costs.

Data Sources

One thousand four hundred and two premature infants born in the Northern California Kaiser Permanente Medical Care Program between 1998 and 2002.

Study Design/Methods

Using multivariate matching with a time-dependent propensity score we matched 701 “Early” babies to 701 “Late” babies (developmentally similar at the time the earlier baby was sent home but who were discharged on average 3 days later) and assessed subsequent costs and clinical outcomes.

Principal Findings

Late babies accrued inpatient costs after the Early baby was already home, yet costs after discharge through 6 months were virtually identical across groups, as were clinical outcomes. Overall, after the Early baby went home, the Late–Early cost difference was $5,016 (p<.0001). A sensitivity analysis suggests our conclusions would not easily be altered by failure to match on some unmeasured covariate.

Conclusions

In a large integrated health care system, if a baby is ready for discharge (as defined by the typical criteria), staying longer increased inpatient costs but did not reduce postdischarge costs nor improve postdischarge clinical outcomes.

The expression “you can't rush mother nature” is certainly true when considering the discharge of infants from the neonatal intensive care unit (NICU). An infant born 2 or 3 months premature may often spend an equivalent time or more in the NICU maturing until additional physiologic functioning makes discharge feasible. The costs associated with prematurity are staggering. The Institute of Medicine (IOM) estimates that annual medical costs associated with preterm birth in the United States was $16.9 billion or $33,200 per infant born premature (IOM 2007). The average inpatient costs in the first year of life for premature infants <28 weeks gestation is approximately $181,000, and even infants with gestational age (GA) between 28 and 31 weeks have inpatient costs of $85,000 (IOM 2007).

Defining exactly when a baby may finally be discharged entails a complicated algorithm at most hospitals, but certain requirements must be met before most neonatologists would be comfortable sending the premature baby home (American Academy of Pediatrics 1998). Despite a general consensus, there is considerable variation in the decision as to when to discharge infants, and consequently, there may be considerable variation in the costs experienced by the health care system caring for these patients (Brooten et al. 1986; Casiro et al. 1993).

After the child is free of obvious physical supports such as the need for mechanical ventilation or intravenous fluids and medications, physiologic competencies usually recognized as necessary before discharge include the following (Schmidt and Levine 1990; Medoff-Cooper 1994; American Academy of Pediatrics 1998; Raddish and Merritt 1998): (1) Maintenance of body temperature fully clothed in an open crib at room temperature. (2) Coordinated sucking, swallowing, and breathing while taking an adequate volume of feeding. (3) Sustained pattern of weight gain. (4) Demonstration of maturity and stability in cardiorespiratory function through avoiding apnea and bradycardia episodes for a specified period of time (say, at a minimum, 2–5 days). Often, stimulants such as caffeine are necessary to prevent these episodes. (5) Another dimension, not absolutely required but highly desired, is to be free of the need for supplemental oxygen before discharge, although some patients with chronic lung conditions may require oxygen at home. Finally, aside from the child's physiologic status, the family's ability to care for the fragile premature infant must be evaluated and demonstrated.

In this study we ask a simple question. When a premature baby stays a few days longer in the hospital, does the accompanying increased physiologic maturity reduce expenditures after discharge? Do a few days matter? This question is by no means trivial. As NICUs have rules and styles of practice that govern discharge, thousands of dollars per admission depend on whether these infants go home a few days earlier or later (Rogowski et al. 2001).

To answer this question, we collected daily physiologic data for 1,402 premature babies near discharge, and matched half the 1,402 babies (701 “Early” babies), to the other half of the babies, 701 “Late” babies, who looked very similar on the day each Early baby went home, but who actually were discharged between 2 and 7 days later (in terms of postmenstrual age [PMA]). We chose 2–7 days because this represents a period of discretion on the part of neonatologists that has economic significance. This is a form of “risk set matching,” which means that when a baby is discharged from the hospital, the baby is paired with another baby who might have been discharged (who was “at risk of discharge”) but who was not discharged (Li, Propert, and Rosenbaum 2001; Lu 2005). The matching was optimal in the sense that it minimized the total covariate distance between babies in the same pair among all possible pairings of the 1,402 babies (“optimal nonbipartite matching” [Derigs 1988]).

The matching controlled numerous maturity and risk factors relevant to discharge, including a daily time-dependent propensity score for discharge (Li, Propert, and Rosenbaum 2001; Lu 2005). So, in the end, we have 701 pairs of two babies who looked similar on the day (the PMA) that the earlier baby was discharged, although one baby stayed in the hospital a few more days. Were the extra days of benefit to the baby who received them? Or did they add to costs without benefit to the baby? We will ask, in various ways: (1) Are 6-month total costs comparable between the Early and Late babies? and (2) Are 6-month clinical outcomes similar or not?

Methods

Study Population

The Infant Functional Status (IFS) Study examined premature births at the Northern California Kaiser Permanente Medical Care Program (KPMCP), which is a managed care organization with integrated information services whose perinatal outcomes have been described in a number of previous reports (Escobar et al. 1995, 2005; Escobar 1999; Joffe et al. 1999; Newman et al. 1999; Smith et al. 2004; Escobar, Clark, and Greene 2006). Eligible infants for the IFS study were born at one of five KPMCP hospitals between 1998 and 2002. To create our cohort, all infants surviving to discharge who were born at a GA of 32 weeks or less were included in the cohort, plus a random sample of infants with a GA of 33 or 34 weeks. Infants were excluded for major congenital anomalies; mechanical ventilation at home after discharge; placement of a ventriculo-peritoneal shunt or other major surgery that necessitated transfer of the infant to a hospital outside KPMCP (e.g., for cardiac surgery); or loss to follow-up within 1 year of discharge from the NICU. Overall, 2,144 infants were initially screened for the study; 670 infants met one of the exclusion criteria, and an additional 42 infants had incomplete medical records from their NICU admission. Thus, the final IFS cohort included 1,402 infants with 246 having a GA of 28 weeks or below.

This project was approved by the Institutional Review Board of The Children's Hospital of Philadelphia, The University of Pennsylvania, and the Northern California KPMCP.

Data Collection

Electronic Data

We estimated inpatient and outpatient costs based on daily resource consumption from the health system perspective. For inpatients, we had access to all coded diagnoses, as well as resource information on a daily basis. This included physician and nurse staffing, pharmacy, radiology, laboratory medicine, and level of care information. For outpatients, we obtained information on all office visits, pharmacy costs, outpatient home care expenditures, emergency department encounters, and subsequent hospital admissions.

We utilized resource estimates from KPMCP. We estimated a base cost for hospital procedures, radiologic tests, and outpatient visits using 2001 Medicare data (Centers for Medicare and Medicaid Services 2002b); pharmacy resources using the 2001 Red Book of wholesale drug prices for pharmacy resources (2001); personnel costs using the Bureau of Labor Statistics (2002b); laboratory costs using 2001 Medicare data (Centers for Medicare and Medicaid Services 2002a); and room costs from prior literature (Kotagal et al. 1997; Chalom, Raphaely, and Costarino 1999; Rogowski 1999). All base costs were adjusted to 2001 dollars using inflation data from the Bureau of Labor Statistics (2002a).

In-Patient Chart Abstraction

Starting from age 31 weeks PMA (or later if born after 31 weeks) we recorded daily variables utilized to determine discharge status. This included data from the NICU flow sheet common to each KPMCP NICU. Information on physiologic maturity included respirator and incubator settings, body temperature, notations of apnea and bradycardia, use of caffeine or methylxanthines (stimulants to help avoid apnea and bradycardia), weight, feeding method, and requirements for intravenous fluids.

Defining Outcomes

Defining Costs

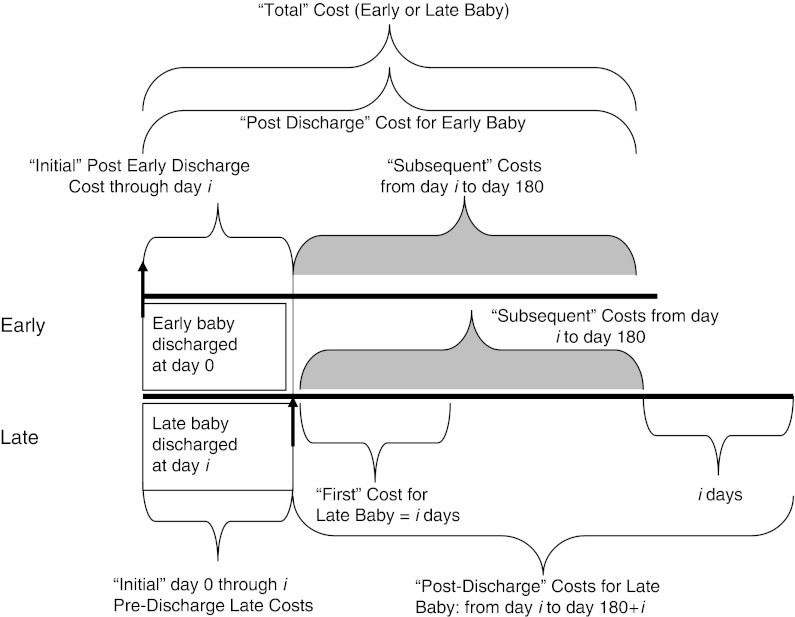
We define five types of costs described in Figure 1, comparing the matched late-versus-early pairs. “Total Cost” (TC) reflects 180 days worth of resource consumption starting from the Early baby discharge. The Early baby is represented in Figure 1, and time from Early baby discharge to 180 days defines the TC time interval. TC is divided into two periods. The “Initial” cost (IC) period is the time, typically a few days, from the Early baby discharge to the Late baby discharge in a matched pair. The “Subsequent” cost variable tracks the time period after the Late baby is discharged until 180 days from discharge of the Early baby in the matched pair. Using TC produces a fair comparison between early and late babies in terms of PMA because both babies were of the same age at the time the Early baby went home; that is, in terms of PMA, it is the same 180 days for both babies. However, we expected and found that the first few days after discharge were often associated with elevated costs for both early and late babies, as readmissions may be a significant problem whenever Early or Late babies first go home. To shed light on this, we also construct 180-day “post discharge” (PD) costs defined to start at each baby's own discharge, for both the earlier and later baby, and extending 180 days. Of course, during PD, both babies have been discharged, but the late baby is slightly older in terms of PMA, so the comparison is not entirely equitable, as an older baby would be expected to have lower cost simply by virtue of being older. To further explore the period right after discharge, we also define what we call the “First” cost, which is the cost in the Late baby starting from discharge and extending for the same number of days (i days in Figure 1) after discharge as defined by the IC time period in the Early baby. This “First” cost compares the first period after discharge for both early and late babies for the same number of days for babies of different ages. Finally, there were five deaths among the 1,402 babies. We count the deaths in our data set as infinite costs, so mortality is never rewarded as being efficient.

Figure 1.

Defining Costs for the “Early” Versus “Late” Baby

Initial cost starts to accrue for both the Early and Late baby when the Early baby goes home. Note that the “Initial” time period is i days for both Late and Early babies, and the “Subsequent” time period is 180−i days in both Late and Early babies as well. “Total” cost is defined as initial cost plus Subsequent cost for both the Early and Late baby. “Postdischarge” cost would be collected for 180 days for the Early baby (Initial plus Subsequent) and 180 days for the Late baby (Subsequent plus i more days). The “First” cost is the initial i days after discharge in the Late baby and will be compared with the Early baby “Initial” cost (also i days). Where noted, “First” cost represents i days after discharge for both the Early and Late baby).

Defining Nonfinancial Outcomes after Discharge

Outcomes after discharge ranged from well baby care to death. We converted the variety of outcomes after discharge into “coherence rank” scores (Rosenbaum 1994), which assign higher scores to babies with worse outcomes, lower scores to babies with better outcomes. Because health outcomes are multidimensional, when two babies are compared, it may be possible to say that one baby had a uniformly worse outcome than the other, or it may be that the two babies are hard to compare, because in some ways one baby had worse outcomes and in other ways it was the other baby who had worse outcomes. The coherence rank compares each of the 1,402 babies to all the others, ranking the babies using the uniform or unambiguous comparisons. The score viewed death as the worst outcome overriding everything else, days in the ICU and total hospitalized days co-equals for the second and third most serious, then number of visits to the emergency department, and finally, least importantly, sick visits to a physician. In terms of these outcomes, a score for baby i was constructed as follows: baby i was compared with every other baby j, scoring 1 if baby i had worse outcomes than baby j, a −1 if i had better outcomes than j, and a 0 if baby i was worse in some respects and better in others; then these were summed over all comparison babies j. As there were 1,402 babies, there would be 1,401 outcome comparisons for a given baby. Rather than letting the scores range from −1,401 to 1,401, we divided by 1,401 and multiplied by 100 to get a percent, so 100 percent corresponds with 1,401 for the worst outcome among the 1,402 matched babies.

The Nonbipartite Matching Algorithm

Using optimal nonbipartite matching (Derigs 1988), the 1,402 babies were divided into 701 pairs of two babies to minimize the total distance within pairs. In addition to a caliper on the time-dependent propensity score (Silber et al. 2001), the matching used a Mahalanobis distance on key covariates listed below, including the current values of the time-dependent milestones, and an added penalty to force separation of PMA by at least 2 days. Lu (2005) has made Derigs's Fortran code for optimal nonbipartite matching available through the statistical programming language R. Further details can be found elsewhere (Rosenbaum and Silber in press).

Consider 701 possible pairs of two babies with one baby discharged earlier (the “Early” baby), with a lower PMA, than the other baby (the “Late” baby). On the day or PMA that the Early baby was discharged, we examined the covariates for the Late baby, even though this was not the discharge day for the Late baby, and we calculated a distance, defined below, that measured how similar the two babies were on the day the Early baby was discharged. We wanted to find pairs of babies such that on the day the Early baby was discharged, the baby typically had achieved the functional milestones and had maintained them for several days. On the same PMA that the Early baby went home, the Late baby had also achieved these milestones and had maintained them for several days, but did not go home.

We calculated a time-dependent propensity score (Li, Propert, and Rosenbaum 2001; Lu 2005) as the fitted hazard from Cox's proportional hazards model (Kalbfleish and Prentice 1980) predicting discharge from time-dependent covariates; it was a key element in the matching. The model included two types of time varying covariates, namely daily maturity scores and current weight (0 if <1,700 g, 1 if between 1,700 and 1,799 g, and 2 if ≥1,800 g), and the following fixed covariates: GA at birth (Tyson et al. 1996), birth weight, infant race (white versus nonwhite), sex, history of necrotizing enterocolotis, retinopathy of prematurity ≥stage 2, bronchopulmonary dysplasia (Smith et al. 2004), and maternal income, age, marital status, and number of other children (0, 1, and >1 coded as 2). SNAP-II score (Richardson et al. 2001) was in the Mahalanobis distance (a multivariate version of a difference in covariate value in units of the standard deviations [Rubin 1980]), while other variables were utilized in both the propensity score and Mahalanobis distance. An important feature of the matching algorithm was the attempt to match not only on physical maturity on discharge but also on how long the level of physical maturity had been achieved. We did this using a smoothed version of each time-varying covariate, specifically an exponentially weighted average of past values of the covariate (Cox 1961), which gives greatest weight to the current value, substantial weight to yesterday's value, reduced weight to the value a day before that, and so on. A score of 1 indicated the baby had never achieved the milestone, while a score of 0 indicated that the baby had never been observed with the milestone unachieved, and the smoothed score declined from 1 to 0 as more days passed after the first day the baby had achieved and maintained the milestone. The longer the baby had achieved a level of maturity, the lower the exponentially smoothed score. The maturity variables were days off incubator, days off gavage feeding, days without apnea, days without bradycardia, days since last methylxanthine exposure, days off oxygen, and a combined exponential smoothing variable for all six smoothed dimensions. The distance function attempted to match Early and Late babies on these maturity variables, on the day the Early baby went home (i.e., the PMA that the Early baby had on discharge).

Statistical Tests

For individual outcomes, we report medians and 95 percent nonparametric confidence intervals for the median, whereas tests comparing outcomes in matched pairs used Wilcoxon's signed rank test, the associated confidence interval, and the associated Hodges-Lehmann point estimate (Hollander and Wolfe 1999). We also report results that adjusted for the five individual NICUs using a rank statistic (Rosenbaum 1988, 2002, p. 100), or using multiple regression (Rubin 1979) with m-estimation as implemented in SAS version 9 (SAS Institute Inc., Cary, NC) with Huber weights (Huber 1981). The rank statistic is Wilcoxon's signed rank test compared with a permutation distribution in which the numbers of early and late babies at each NICU are identical to the observed frequencies (Rosenbaum 1988); it is the matched pair version of the general method of removing bias in a permutation distribution by conditioning on a sufficient statistic for the propensity score (Rosenbaum 1984).1 The regression method regresses matched pair differences in outcomes on matched pair differences in covariates (Rubin 1979). The m-estimation results were almost exactly the same as the ranking statistic adjustments so are not reported.

In measuring balance on covariates, we used two standard informal measures: DIFFAVE (Rosenbaum and Rubin 1985; Silber et al. 2001), defined to be the difference in covariate means divided by the standard deviation, and the significance level from Wilcoxon's rank sum test, which compares the balance obtained by matching on covariates to the balance expected in a completely randomized experiment. For estimating odds ratios from paired data we used either the McNemar test for a 2 × 2 contingency table, or a generalized McNemar test or Symmetry test for a K×K table (Bishop, Fienberg, and Holland 1975); for binary regression utilizing matched pairs, we used conditional logistic regression (Breslow and Day 1980).

Results

Quality of the Matches

Table 1 asks whether the matching was effective, that is, whether the matched babies were indeed comparable on the day one baby went home and the other stayed in the hospital. In Table 1 some variables describe the baby and others describe the mother. In column 2 we display the 701 Early babies with characteristics noted on the day of their own discharge. In column 3 we display the matched 701 “Late” babies at the same PMA as the PMA of their Early baby matched mate when that Early baby was discharged. We aimed to have close matches here, so that we can compare the two groups, one discharged earlier than the other, but both looking physiologically similar at the PMA when the Early baby went home. To assess whether these groups were similar, we report the “DIFFAVE” results in column 5. Note that there are no significant differences between any variables described in columns 2 and 3 (no significant p-values in column 5, and no important differences in units of standard deviations). Hence, the Late baby group looked very similar to the Early group at the PMA that the Early group had when the Early group went home.

Table 1.

Matching Results for 701 Early and 701 Matched Late Babies

(1) Variable Name	(2) Early Baby Discharge	(3) Late Baby at Early Baby Discharge	(4) Late Baby at Late Baby Discharge	(5) DIFFAVE (3)–(2) (SD)	(6) DIFFAVE (4)–(2) (SD)
Postmenstrual days	247.4	247.4	250.9	0	0.29*****
Gestational age (weeks) at birth	31.1	31.1	31.2	0.03	0.03
Weight at birth (g)	1,669	1,686	1,686	0.03	0.03
SNAP-II 20–59	0.15	0.13	0.13	−0.05	−0.05
SNAP-II 10–19	0.18	0.20	0.20	0.04	0.04
SNAP-II 0–9	0.67	0.67	0.67	0.01	0.01
Male sex	0.51	0.52	0.52	0.01	0.01
Propensity to discharge	0.67	0.64	1.33	−0.03	0.75*****
Apnea smoothed score	0.04	0.05	0.03	0.08	−0.16
Brady smoothed score	0.06	0.07	0.04	0.09	−0.15
Methyl smoothed score	0.04	0.03	0.02	−0.08	−0.17
Oxygen smoothed score	0.11	0.11	0.07	0.01	−0.15*
Gavage smoothed score	0.22	0.23	0.10	0.01	−0.65*****
Incubator smoothed score	0.15	0.15	0.08	−0.01	−0.34*****
Combined maturity score	0.62	0.63	0.34	0.02	−0.70*****
Weight on day specified	2,153	2,148	2,231	−0.01	0.22*****
Weight <1,700 g	0.02	0.03	0.01	0.06	−0.09
1,700 ≤ weight <1,800	0.06	0.06	0.02	−0.03	−0.17****
Weight ≥1,800 g	0.92	0.91	0.97	−0.01	0.19*****
Broncho-pulmonary dysplasia	0.09	0.11	0.11	0.06	0.06
Necrotizing enterocolitis	0.01	0.01	0.01	−0.04	−0.04
Retinopathy stage ≥2	0.06	0.06	0.06	−0.01	−0.01
Intraventricular hemorrhage ≥3	0.02	0.01	0.01	−0.05	−0.05
Maternal age (years)	29.9	30.3	30.3	0.08	0.08
Marital status single	0.24	0.24	0.24	0	0
Other children=0	0.40	0.37	0.37	−0.07	−0.07
Other children=1	0.34	0.37	0.37	0.07	0.07
Other children ≥2	0.26	0.26	0.26	0.01	0.01
Income ($)	59,517	59,460	59,460	0	0
White race	0.47	0.48	0.48	0.02	0.02
Black	0.10	0.09	0.09	−0.02	−0.02
Asian	0.20	0.23	0.23	0.08	0.08
Hispanic	0.22	0.18	0.18	−0.09	−0.09

Note that each match compares an earlier discharged infant to a similar infant discharged between 2 and 7 days later (using postmenstrual age as the time scale).

^*p<.05.

^**p<.01.

^***p<.005.

^****p<.001.

^*****p<.0001.

Column 4 describes what the Late group looked like when the Late group went home and column 6 describes the difference between columns 4 and 2. Of course, staying longer, the late babies were more mature on the day of their own discharge, and column (6) shows this in many ways. Here, the Late group was different in that they did not go home and instead stayed significantly longer (250.9–247.4 or approximately 3 days on average). Furthermore, the time from birth to discharge was 31 and 34 days for the Early and Late babies, respectively (results not shown). At their own day of discharge, the Late babies were older (by 3 days), had a higher propensity score hazard for discharge than when the Early babies went home (p<.0001), had a longer time interval without oxygen (a lower smoothed score) (p<.05), a longer time off gavage feeds (p<.0001), a longer time off the incubator (p<.0001), a greater combined maturity score (p<.0001), higher weight on discharge (p<.0001), a lower percent of babies discharged between 1,700 and 1,799 g, and a higher percent of patients with weight ≥1,800 g at discharge (p<.0001).

In short, the matching algorithm achieved what was desired. Late babies were comparable to Early babies when the Early baby went home, but the Late baby went home about 3 days later and were more mature on a number of dimensions.

The Day of the Week and the Discharge Rate

Why did the late baby stay longer in the hospital? There was a decreased rate of discharge on the weekend (observed number=157/day, expected=200.2/day) and an increased rate on Monday and Friday surrounding the weekend (observed=243.5/day, expected=200.2/day) (p<.0001). Hence, the maturity may not be the only factor influencing discharge—the day of the week that infants obtain maturity plays a role in determining whether such a baby may go home sooner or later.

The NICU and the Discharge Rate

There were five hospitals in our data set, all had level IIIC NICUs, all had pediatric and GYN residents, and one had residents in the NICU. There were no differences in formal discharge requirements at these institutions. There was significant variability in the rate of Early discharge between NICUs, with one NICU with as many as 65 percent of its discharges in the Early group and another NICU with as few as 37 percent (this was the NICU that utilized residents). These differences were highly significant (p<.0001 using the generalized McNemar's test), suggesting that hospital style may play a role in discharge decisions, beyond day of the week. We also constructed a conditional logistic regression model that utilized the 701 pairs of patients, and we included a variable for day of the week and distance from patient to hospital (by ZIP code centroid) and again found significant differences in the odds of being in the Early group by NICU (results not shown).

Cost and Clinical Outcomes

Table 2 displays the cost and clinical outcome results comparing Early and Late matched sets. TCs were higher in those who stayed longer in the hospital. The Late group had higher TCs than the Early group, with a typical difference of $5,016 (95 percent CI $4,714, $5,235). The difference in TC was due to differences in IC (when the Early baby is already home and the Late baby is still in the hospital). ICs in the Early matched babies were small (typically $0) compared to the hospital costs in the Late matched babies (typically near $4,387 or about $1,462/hospital day). Costs subsequent to the initial period were very similar for Early and Late babies, the typical difference being about $17 for the Late–Early match. PD costs (180 days after discharge for both Early and Late) were also almost identical, with a typical difference of $12. First Costs (the costs just after discharge) for both the Late and Early babies, displayed no indication of a difference between groups. Adjusting for the individual NICU did not change the results.

Table 2.

Results for Cost and Coherence Outcomes

Variable Name	Total Cost ($, Median)	Cost Initial ($, Median)	Cost Subsequent ($, Median)	Cost 180 Days Postdischarge (Median)	Cost First (Median)	Coherence Postdischarge (Median)	Coherence First (Median)
Late	5,011	4,387	332	335	0	2.6	−27.6
95% CI	(4,821, 5,823)	(4,346, 4,474)	(307, 351)	(313, 357)	(0,0)	(−11.3, 13.1)	(−27.7, −27.7)
Early	326	0	307	326	0	2.6	−27.6
95% CI	(299, 347)	(0, 0)	(281, 331)	(299, 347)	(0, 0)	(−11.3, 2.6)	(−27.7, −27.7)
Late–Early	5,016	4,940	17	12	0	4.2	0
95% CI	(4,714, 5,235)	(4,485, 5,103)	(−20, 56)	(−26, 52)	(−5.43, 8.69)	(−2.1, 11.0)	(0,0)
p-value	.0001	.0001	.38	.54	.71	.21	.96
Late–Early (adjusted by NICU)	4,957	4,644	8	0.9	0	7.5	0
95% CI	(4,575, 5,227)	(4,454, 5,103)	(−36,53)	(−44,48)	(0,0)	(−6.3,12.6)	(0,0)
p-value	<.0001	<.0001	.71	.96	.24	.79	.09

All results refer to cost and outcome definitions as defined in Figure 1

We describe the median differences based on the Hodges-Lehmann estimate, with 95% confidence intervals (CIs) for the median (note: the five deaths in the sample were assigned infinite cost, so medians, not means, were reported). Results are displayed for both unadjusted for specific NICU and adjusted. Coherence scores were displayed similarly. Note that coherence values are reported as medians: 100 × median/1,401, for 95% CI (a,b): (100 × a/1,401,100 × b/1,401). As can be seen, the difference between the Late and Early baby total costs typically was about $5,000 accrued over about 3 days inside the hospital. However, after discharge the subsequent costs were almost identical, as were the 180-day postdischarge costs and the first costs. When looking at outcomes after discharge, there was no significant difference between Early or Late babies. There were three deaths in the Early group and two in the Late group.

For clinical outcomes we also found no significant difference and no clinically meaningful difference between Late and Early babies. For the Late–Early matched set examining differences in outcomes PD, the typical Late baby had outcomes that ranked slightly, but not significantly, worse than the Early babies (4.3 percent worse, p=.21), so there is no sign early discharge did any harm. When examining the “First” clinical outcomes for both groups, i.e., those outcomes that occurred immediately after the discharge from the initial NICU stay, again there was no difference in median coherence scores (percent difference in ranks=0, p=.96). Again, adjusting for individual NICU did not alter our findings.

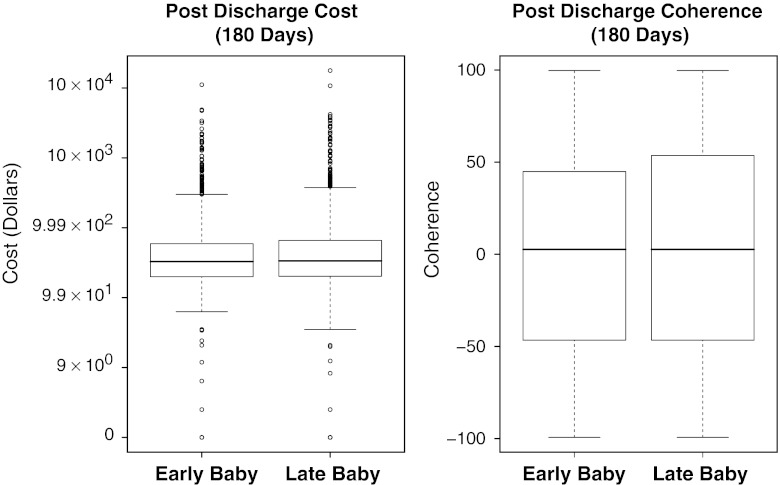
A summary of the 180-day PD results for Early as compared with Late costs and clinical outcomes (coherence scores) is displayed in Figure 2. For costs and clinical coherence, the distribution of outcomes is almost identical when comparing the Early and Late babies.

Figure 2.

Boxplots of Cost and Outcome Results by Matched Sets. PD, Postdischarge

Displayed above are cost and outcome results for the time period discharge plus 180 days (PD). For cost we use cost plus $1 and plot on the log₁₀ scale. Not depicted in the cost figure are the three early deaths and two late deaths, all outliers on this graph, but contributing to the medians and the interquartile ranges. For outcomes we display the associated coherence scores normalized as described in Table 2 (including the five deaths). Note that the PD costs and outcomes are almost identical between the Early and Late babies.

Sensitivity Analyses on Costs

Could it be that we failed to match on some crucial covariate that was not recorded, and this covariate hides a substantial reduction in postdischarge costs in infants staying longer? We conducted a sensitivity analysis to addresses this possibility (Rosenbaum 1987, 1991, 2002; Rosenbaum and Silber in press). The tests we constructed were equivalence tests, so they interchange the familiar null and alternative hypotheses (Berger and Hsu 1996). The first null hypothesis we tested was whether there is actually a difference in postdischarge costs ≥|$500|, so rejecting this hypothesis of inequivalent costs provides strong evidence that the difference in costs are equivalent (defining equivalent as being <|$500|). The sensitivity analysis showed that if there were no bias from unobserved covariates, there would be overwhelming evidence (p<.00001) that the postdischarge difference in cost is <$500. If an unobserved covariate might double the odds of discharging later, and might have a very strong relationship with postdischarge costs, the maximum possible p-value for testing equivalency for |$500| is .0071, so such an unobserved covariate could not mislead us to think that the difference in postdischarge costs is <|$500| when this is not so. An unobserved covariate that tripled the odds of later discharge could conceivably mask a $500 difference in cost, but even one that increased the odds of later discharge by sixfold could not mask a difference in cost of |$2,500| (p<.002), still roughly only one-half the dollar amount needed to recover the cost of delayed discharge in our study. Here, $2,500 is about half the cost of a delayed discharge.

Discussion

Using risk set matching, we found that early discharge saved money, and the hospital costs saved in the hospital were not counterbalanced by subsequent savings derived from babies being more mature at discharge. Of course babies should not be discharged before the point when they develop physiological maturity, and of course there may be extraneous factors besides those noted in our model that prevent discharge in particular cases. For example, babies cannot be discharged if the parents are not ready to receive them. Our study should not be construed as providing evidence that all infants can be discharged at an earlier time in their development. Yet we believe we can reassure caregivers and parents that once the baby has achieved the requirements for discharge, staying longer (for no other reason than to become more mature) does not save money after discharge or improve postdischarge outcomes.

We understand that important yet undocumented features of the infant may force caregivers to delay discharge. However, for there to be a $2,500 difference in PD costs that is hidden by a failure to adjust for an undocumented characteristic of the infant, that characteristic would need to be a near perfect predictor of PD costs and six times more common among babies discharged later.

One potentially interesting finding concerning style of practice was that babies were less likely to be discharged on the weekend. It may not be easy to change this pattern because weekend services may be more costly and not realistically available for some infants and cross-covering physicians on weekends can be reluctant to discharge patients they do not know well. Similarly, we found that style of practice at hospitals influenced the odds of being discharged earlier or later. Future research could identify infants with similar daily maturity scores (as we developed in this analysis) and directly ask physicians why they did, or did not, discharge their patients.

Generalizability of results is always a concern. To gain a better idea as to similarities in practice style between the NICUs in our study hospitals and other facilities throughout the United States, it is interesting to compare the mean length of stay (LOS) from birth to discharge for babies <1,500 g. In our study we observed these babies had a mean LOS of 55.5 days (SD=25.2) as compared with 47 days (using the Vermont Oxford Network) (Horbar, Plsek, and Leahy 2003; Rogowski 2003) and 53.5 days using data from Intermountain Healthcare Health plans (IOM 2007). Hence, LOS in our study was in line with other published reports.

In summary, keeping infants a few additional days after the usual discharge criteria solely for the purpose of gaining additional maturity is unlikely to be associated with cost savings from the perspective of an integrated health care system. It also appears that hospitals, even inside a single integrated health care delivery system, show considerable variability in the algorithms used to discharge premature infants. Because the costs for delaying discharge in these premature infants appear considerable, and the apparent benefits to longer stays do not appear to compensate or counterbalance these increased NICU costs, we would conclude that more uniformity in the algorithms for discharge based on the physiologic maturation of the premature infant may be a reasonable goal for the future.

Supporting Information

Additional supporting information may be found in the online version of this article:

Appendix SA1: Author Matrix.

Please note: Wiley-Blackwell is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.