The predicted structure of the headpiece of the Huntingtin protein and its implications on Huntingtin aggregation

Abstract

We have performed Simulated Tempering (ST) molecular dynamics simulations to study the thermodynamics of the headpiece of the Huntingtin protein (N17^Htt). With converged sampling, we found this peptide is highly helical, as previously proposed. Interestingly, this peptide is also found to adopt two different and seemingly stable states. The region from residue 4 (L) to residue 9 (K) has a strong helicity from our simulations, which is supported by experimental studies. However, contrary to what was initially proposed, we have found simulations predict the most populated state as a two helix bundle rather than that of a single straight helix, though a significant percentage of structures do still adopt a single linear helix. The fact that Huntingtin aggregation is nucleation dependent infers the importance of a critical transition. It has been shown that N17^Htt is involved in this rate-limiting step. In this study, we propose two possible mechanisms for this nucleating event stemming from the transition between two helix bundle state and single helix state for N17 ^Htt, and the experimentally observed interactions between the N17^Htt and polyQ domains. More strikingly, an extensive hydrophobic surface area is found to be exposed to solvent in the dominant monomeric state of N17^Htt. We propose the most fundamental role played by N17^Htt would be initializing the dimerization and pulling the polyQ chains into adequate spatial proximity for the nucleation event to proceed.

Introduction

Huntington's disease is a neurodegenerative disorder associated with protein misfolding. Specifically, it is caused by a tri-nucleotide repeat expansion for polyGln in the first exon of the Huntingtin protein on chromosome 4 ^{1; 2}). The pathological range for Huntington's disease is 37-122 repeats, which form high molecular weight protein aggregates. ^{3; 4}

Typical of the amyloid proteins, polyGln tends to have high aggregation propensity and relatively unstable intermediates. This presents many experimental difficulties when using experimental methods to determine structural properties and has lead to a diversity of opinions about the exact structure and aggregation process. A thorough understanding of these details may prove essential in combating Huntington's disease.

Biophysical evidence does indicate monomeric polyGln to be unstructured. ^{5; 6; 7} However, most of the in vivo and in vitro experimental results so far concerning the aggregation of poly-glutamine indicate a nucleation-dependent polymerization.⁸ This would necessitate a random coil to β-sheet transition within an individual monomer. Understanding the thermodynamics involved in the crucial early stages may help in understanding the mechanistic details of the nucleation event and the fibril elongation process.

Though much attention has been given to the polyGln repeat tract due to its clinical implications ⁹, recent studies have identified the N-terminal 17 residues of Htt-exon1 (N17^Htt) as a cis-acting amyloid switch of polyGln aggreagation^{10; 11}. They have shown N17^Htt to promote rapid polyGln aggregation through interactions with both the N17^Htt and the polyGln tracts within Htt. The hydrophobic residues of N17^Htt are shown essential for polyGln aggregation, which is thought to be the result of the hydrophobic face of an amphipathic helix. Removal of these residues by Alanine point mutation, or the insertion of two Proline “helix-breaker” residues in the same manner, was shown to completely halt aggregation.^{10; 11} In a similar manner, aggregation was observed after the Alanine substitution of the polar residues, but on a much shorter time-scale. Aggregation results were quantified by a filter trap assay which probed for the S-tag, and binding specific interactions were obtained using crosslink studies. Here we aim to gain structural insight and a better thermodynamic understanding of the system in a way which compliments and extends these experimental results.

Results

Convergence of the sampling

Convergence of the weights

As shown in Table 1, weights obtained from ST simulations starting from different initial configurations are converged. Free energy difference between neighboring temperatures (g_i+1 / β_i+1 − g_i / β_i) is always less than 0.2 KJ/mol, smaller than a KT. As discussed before, converged weights will produce uniform sampling in ST. In Fig. 2 (a) and (b), the amount of sampling at each temperature obtained from a series of 2000 4ns simulations is displayed. The sampling is biased to the high temperatures at the beginning, indicating the weights are not converged. After about 24000ns, simulations tend to spend mostly equal time exploring each temperature. We also note that due to the asynchronous nature of FAH (i.e. different nodes have different CPU speed) the order of the trajectories show n in Fig 2 is only an estimate.

Table 1.

Convergence of the weights is shown for representative temperatures Δg = g_j – g_i obtained from distributed computing simulations starting from a helical structure (third column) and a coil structure (fourth column) at different temperature pairs. Differences between free energy differences Δf_ji = gj/β_j –g_i/β_i obtained from simulations starting from a helical structure and a coil structure are displayed in the 5th column. KT at temperature i is shown in the sixth column. Δf_ji(Helical)-Δf_ji(coil)(KJ/mol) is much smaller than KT (KJ/mol) at all temperature pairs.

Ti	Tj	Δgji(Helical)	Δgji(Coil)	Δfji(Helical)-Δfji(coil)	KTi
285	288	417.00	417.00	0.00	2.37
292	296	523.15	523.17	-0.03	2.43
300	304	491.06	491.07	-0.03	2.49
308	312	461.67	461.67	-0.01	2.56
317	322	537.33	537.33	-0.01	2.63
327	332	499.48	499.47	0.01	2.72
337	342	465.25	465.24	0.02	2.80
347	352	434.22	434.20	0.03	2.88
357	362	405.97	405.97	0.01	2.97
367	372	380.23	380.23	-0.01	3.05
377	383	426.71	426.70	0.03	3.13
388	393	333.10	333.09	0.03	3.22
399	405	372.81	372.81	0.01	3.32
411	418	404.06	404.05	0.05	3.41
425	432	372.94	372.93	0.04	3.53
439	447	393.28	393.27	0.03	3.65
454	461	318.26	318.24	0.07	3.77
468	476	337.18	337.15	0.11	3.89
483	490	274.05	274.04	0.05	4.01
497	506	327.18	327.16	0.10	4.13
516	524	266.13	266.10	0.13	4.29
532	540	247.04	247.01	0.14	4.42
548	556	229.77	229.74	0.12	4.55
565	574	239.30	239.28	0.10	4.69
583	592	221.54	221.52	0.12	4.84

Fig 2.

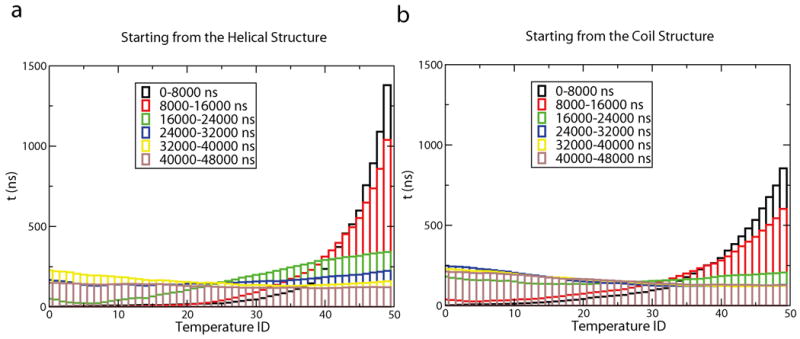
(a). Amount of time the ST simulations starting from a helical structure spent at each of the 50 temperatures. (b). The same as (a) except that data is collected from simulations starting from a coil structure.

Convergence of the helical properties

The helix melting curves demonstrate that simulations starting from the helical and unfolded states converge excellently as shown in Fig 4. The system has a significant fraction of the helical content at low temperatures, e.g. at the room temperature (300K), the average helical content is about 36%. The average helical properties as a function of time at 300K are also plotted in Fig. 3. The simulations starting from different configurations reach the convergence at the timescale of about 20ns. The average number of helical segments is around 1.5, indicating that this peptide tends not to form one single straight helix, but to bend into multiple helix segments. Similar behaviors are also been observed for another 22 residue helical peptide.¹²

Fig 4.

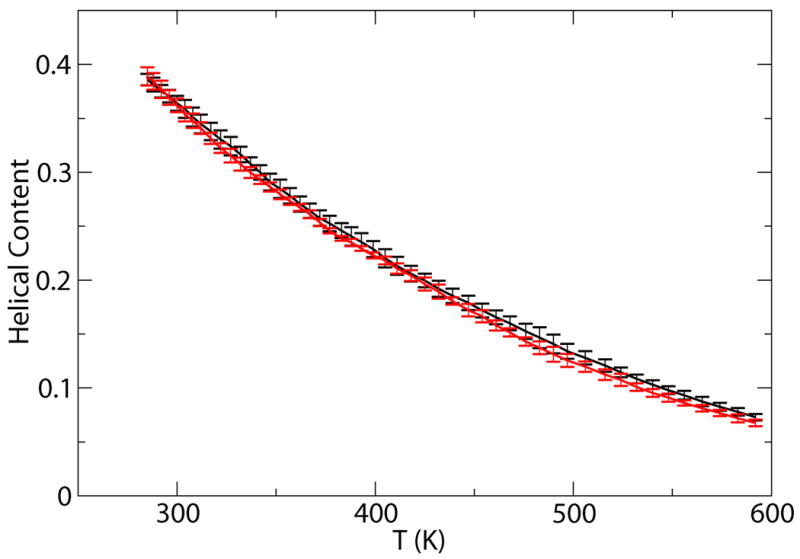
Helical content as a function of temperature obtained from ST simulations starting from the helical structure (black) and those from the coil structure (red). Error bars are calculated by block averaging over the configurations later than 32ns.

Fig 3.

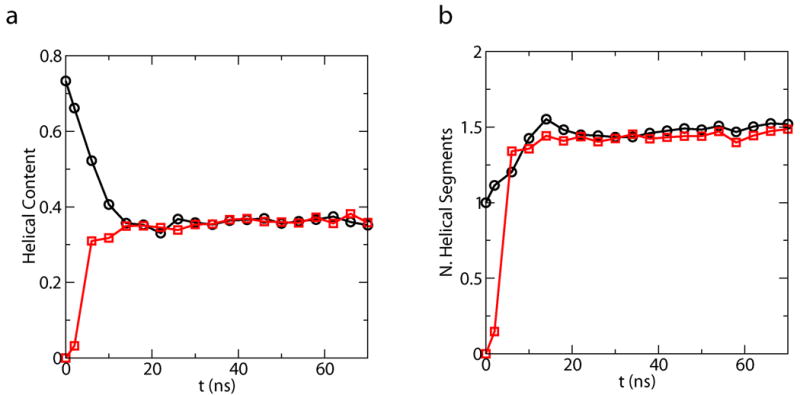
Convergence of the average helical properties as a function of time at 300K. Helix properties at each conformation is defined according to classical LR counting theory. Plots obtained from simulations starting from the helix structure (black, circle) and the coil structure (red, square) are displayed for (a). average helical content. (b). average number of helical segments.

Secondary Structure

The finding of multiple helix segments is clearly shown in the secondary structure analysis. The secondary structure as calculated using DSSP¹³ is shown by residue in Figure 5. The probability spike in turn propensity involving residues Lys₉-Ala₁₀-Phe₁₁ shows a clear division between the C- and N-terminal helices. (Fig 5) Though alpha helix is clearly the dominant feature, it is interesting to note the increased presence of 3₁₀ helix in the C-terminal region. The presence of both helix geometries implies a higher degree of flexibility in the N-terminal region. We believe this might facilitate the observed N17^Htt-PolyQ domain interactions and have possible implications in the aggregation mechanism.

Fig 5.

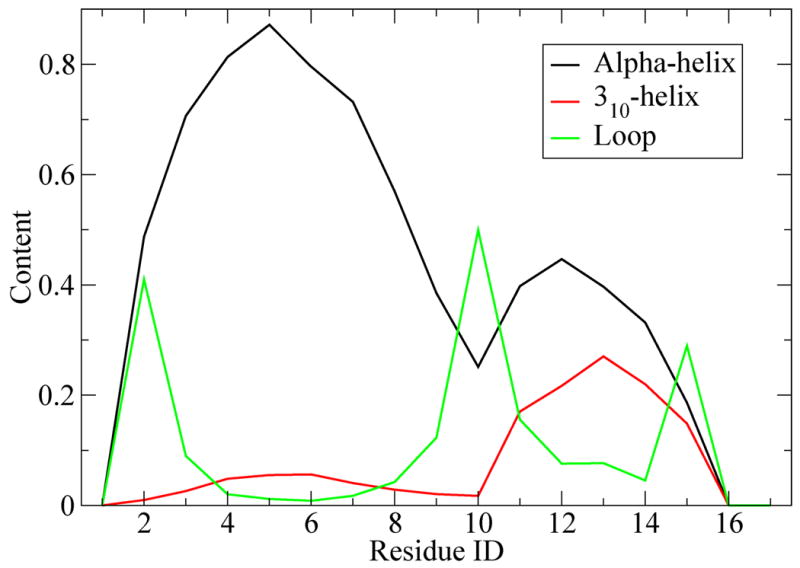
Alpha helix (black), 3₁₀-helix (red) and loop (green) content by residue at 300K. There is a higher propensity for alpha for the first 10 n-terminal residues, followed by a sharp peak in loop content and a second area of high probability for alpha helix content at the C-terminus. This indicates a tendency for a 2-helix bundle, and can be visualized in figure 7.

Lastly it is interesting to note the helix content diminishes with increasing temperature (as shown in Fig 6), while loop and turn content increases, with the exception of the loop-spike, which remains somewhat independent of temperature. Since we also observe the number of helical segments to diminish and the two-helix bundle percentage to decrease both in magnitude and with respect to the single linear helix, it is likely some of the loop content is attributable to the disordered state.

Fig 6.

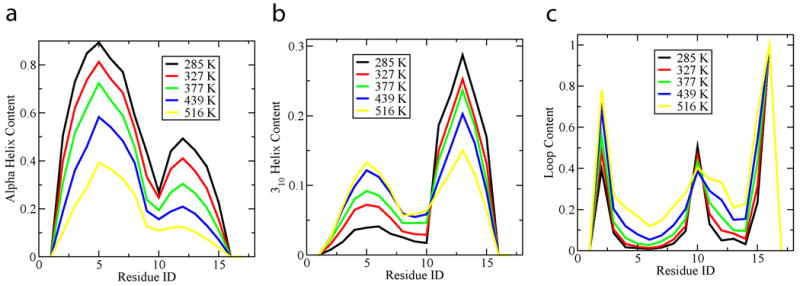
(a). Alpha helix content by residue over a series of temperatures. There is a trend over all residues for helical content to decrease with increased temperature. (b) 3₁₀-helix content by residue over a series of temperatures. (c). Loop content by residue for a series of temperatures. It is interesting to note the dramatically increased fraction of loop in the two helical stretches, but the relatively low temperature dependence of residue 10.

Structural Clusters

Visualizing the structural ensemble via a set of k-means clusters showed a strong agreement with the numerical findings, and gave additional insight into the driving forces and possible implications of the study. Two helical segments, separated by Ala₁₀ as predicted was the dominant feature in over 70% of the structures at low (biological) temperatures (300K) as shown in Fig. 8. The two helices appeared to be stabilized by a large hydrophobic face on one side, and a grouping of charged residues on the opposing face. Of the ten clusters, five fit into this category, including cluster 9, the single largest cluster. With ∼35% of the population at 300K, and an rmsd of ∼3 Å with respect to the centroid structure, cluster 9 contained twice the population of the others while also retaining the tightest rmsd, suggesting a free energy minimum for the monomeric state. Similar results were obtained using 5 or 20 clusters (data not shown).

Fig 8.

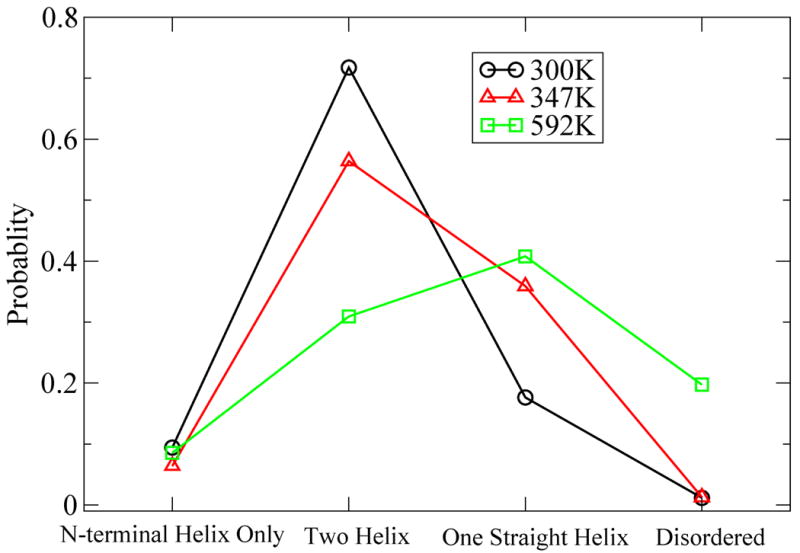
Probability for different states of the system: N-terminal helix only, two-helix, one straight helix and disordered state. N-terminal helix state contains a N-terminal helix, but the C-terminal part of the peptide is disordered. Two-helix state with a two-helix bundle is the most populated state. Plots for three temperatures are shown: 300K (Black circle), 347K (Red triangle), and 592K (Green square).

The remaining clusters fell into one of three additional categories: N-terminal helix only, disordered, and linearly oriented helix/helices. The N-terminal helix as seen in these structures was significantly formed in all clusters excluding the disordered state. The C-terminal helix, which had an increased tendency to occupy the more narrow 3/10 helix than the corresponding N-terminal residues, was only seen disordered in cluster 10. (See Fig. 7) Of the linearly oriented helix groups, cluster 8 shows something very similar to our initially hypothesized “native-state”, and was shown to be the second largest cluster at room temperature, but with a much higher (∼5 Å) rmsd than cluster 9. The two other linearly oriented helix clusters show the single helix bending (cluster 5) and then breaking at the high turn propensity Ala₁₀ residue.

Fig 7.

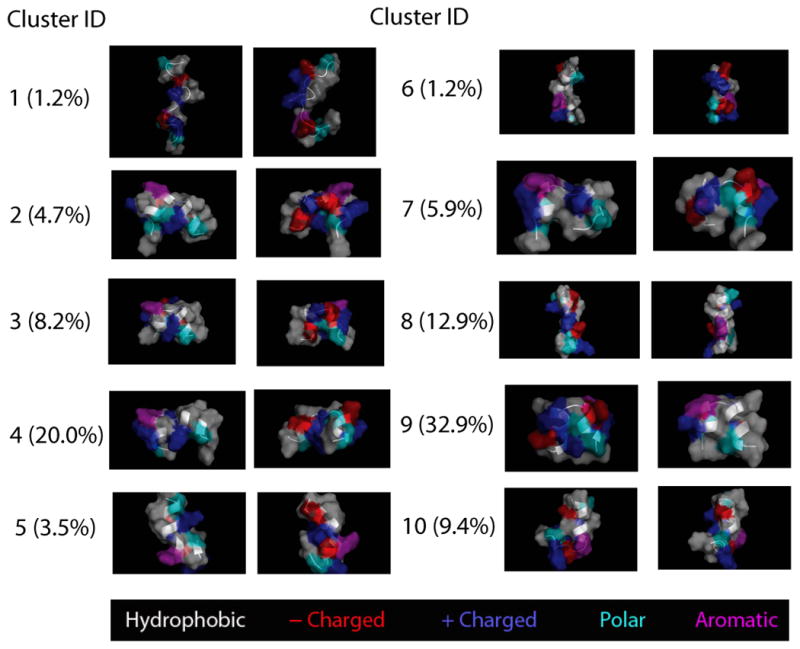
Structures closest to cluster center and the population at 300K for each of the 10 clusters are shown. The most populated cluster (cluster 9) is a two-helix bundle structure.

At high temperatures (592K) the population of the disordered cluster was observed to increase ∼10 fold (17%) placing it among the three most populated clusters. (For the lower temperatures it had the lowest total population of any cluster with 0.15%.) The two helix bundles retained ∼30% of the structural ensemble, however the single linear helices became the most populated state with ∼40%, including the single most populated state at high temperature (592K). (See Fig 8)

There appears to be two dominant factors governing the structural configuration of the system. Some insight can be gained from looking at notable differences between the two-helix clusters. In some cases the charge groups are in very close proximity with an optimal alternating pattern (cluster 2). However, the hydrophobic face is then split apart by Lys₆. Likewise, the set of structures possessing the hydrophobic region in a single unbroken face show the charged residues split into two separate groups. In the cluster with a disordered second helix (cluster 10), the charged residues line the inside of a C-terminal J-like turn, which may prove energetically favorable when considering the addition of the polyQ tail.

Discussion

We have found from our ST simulations that N17^Htt forms two primary states: a single extended helix and a two-helix bundle of which the c-terminal helix exhibits some degree of flexibility. Both states display a large hydrophobic face opposite a region of alternating charge in amphipathic fashion. Tam et. al^{10; 11} have previously predicted N17^Htt to form an amphipathic alpha helix as a result of experimental data and a sequence comparison search. We have found the system can adopt multiple stable thermodynamic states, of which the dominant state at relevant temperatures is a two-helix bundle. This two-helix bundle state initially seems inconsistent with experimental findings, but in fact it agrees well with experimental data. With respect to the experimental mutation studies, insertion of two Proline “helix-breaker” residues within residues L₄-K₉ was shown to completely halt aggregation, indicating that this region is highly helical. In our computational study, those same residues are found to adhere almost exclusively to this regime, showing near 90% helicity at 300K mid stretch. Since the two helical regions are separated by Ala₁₀, our proposed two-helix structure is not in contrast to the experimental findings.

Our structures agree very well with the main notion that N17^Htt is amphipathic. While the polar residues and the hydrophobic face are the driving factors for the two-helix conformation, they appear to compete for the precise configuration the two helices will adopt with relation to one another. Although in some structural clusters we see the most prominent feature as a salt-bridge network, in the structure characterized as the ensemble's free energy minimum, the two helices create a large uninterrupted hydrophobic face. Such a conformation would favor hydrophobic packing through dimerization to reduce its surface area. This also adheres to Tam et. al's previous work^{10; 11} in which they found the hydrophobic residues as a prerequisite for aggregation, and the polar residues to significantly control the rate and extent of aggregation.

It has been shown that Htt aggregation is nucleation dependent.¹⁴ This infers the existence of a critical transition, which has been hypothesized to be monomeric beta formation in the polyQ tail. It has also been shown that the rate limiting step in the aggregation pathway involves N17^{Htt 10; 11}. Our simulation results provide two possible mechanisms for such a nucleation event.

It is shown that N17^Htt has binding interactions with both itself and the polyQ domains. It is energetically favorable for N17^Htt to dimerize in such a way as to pack the two hydrophobic faces together, simultaneously exposing the charged residues to solvent while minimizing non-polar surface area. In order for intra-chain N17^Htt-polyQ binding interactions to exist, a turn is required to have been formed by N17^Htt or PolyQ. A hydrogen bonding network between the charged residues of N17^Htt and the polar polyQ side chains would contribute to these binding interactions by creating a beta-like strand. Moreover, the correct formation of this beta-like strand might be crucial for the nucleation event. Both mechanisms we propose are based on the formation of a beta-strand structure, which we feel is the key role N17^Htt plays in Htt aggregation kinetics. However, they differ in whether N17^Htt or PolyQ makes the turn for the initial beta-strand.

In the first mechanism, the turn connecting two-helix bundle in N17^Htt will naturally serve as the turn. We have observed a degree of flexibility in the C-terminal helix orientation and conformation, (alpha-helix, 3-10-helix, disordered, etc.) The correct C-terminal helix orientation could help to facilitate the polyQ repeat domain interactions with N17_Htt by allowing the chain to more easily wrap back on itself and keeping both domains in close proximity. (See Fig. 9 (b))

Fig 9.

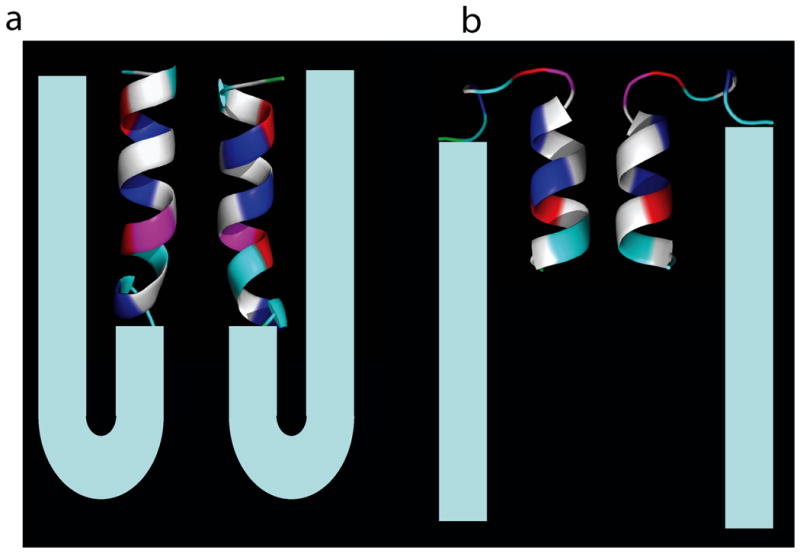
Cartoons showing the N17^Htt-PolQ structures in two proposed mechanisms described in the text. Two representative cluster centroid structures are shown with faces paired to minimize exposed hydrophobic surface area. Each shows a model polyQ tail (cyan) which satisfies the observed N17^Htt – polyQ domain interactions. (a). N17^Htt adopts the single straight helix conformation and has the charged residues in a surface geometry which would compliment the polyQ tail's β-strand configuration. (b). N17^Htt adopts a two-helix bundle conformation. The increased flexibility in the C-terminus of the two-helix bundle creates the turn necessary for polyQ – N17^Htt interactions.

In the second mechanism, the polyQ chain makes the turn and N17^Htt adopts a single helix conformation in the aggregates. In this case, there would be an additional step. An initial transition is needed for N17^Htt from its dominant two-helix bundle state into the single helix state. Subsequently, the polyQ tail forms the turn for the beta-strand like configuration. This has the potential of being a rare event, and also of being able to propagate similar events in a nucleating fashion due to the lengthened scaffold of charged residues it presents. In addition, this mechanism puts more emphasis on the polar residue layout, and less on a covalent tether between the two domains. This could prove insightful due to an observed increase in aggregation kinetics with the addition of unbound N17^Htt to polyGln^{10; 11}.

A general topology coinciding with these two structures was proposed by Tam et al^{10; 11}. Moreover, the concept of N17^Htt as a scaffold fits in nicely with the current hypotheses regarding Htt fibril structure and rate-limiting nucleation events. The end-to-end length of the N17^Htt polar region corresponds roughly to one turn of the current model for β-sheet elongation, excluding the turn residues. Wetzel et. al. performed a series of experimental point mutation studies in which induced β-turns interspersed by 9-10 glutamine residues showed aggregation potential nearly as efficient as polyGln₄₅^{15; 16}. In contrast, peptides containing 7-8 glutamines between β-turns aggregated much less readily, indicating periodic β turns staggered every 9-10 glutamines in the aggregate form. In addition, we have found previous computational studies of polyGln to indicate a repeating β-turn topology of similar length¹⁷. We feel these matching dimensions strongly support the N17^Htt role as a molecular scaffold.

There are several current ideas representing the rate-limiting nucleation step. Since it is generally accepted that monomeric polyglutamine exists as a random coil, a globular to β-sheet transition is required. There are currently two acknowledged possibilities capable of explaining the free-energetic pathway for this transition^{8; 18}, both of which would benefit from the idea of N17^Htt acting as a molecular scaffold.

Chen et al.⁸ propose the single chain critical nucleus to be a “compact β-sheet” of roughly four turns and of very high β content. Such a structure would be a local free energy minimum or meta-stable state, having each of the four segments stabilized through hydrogen bonds with the neighboring intra-chain segment. The problem arising in reaching such a conformation is that initially there are no existing β-segments for an un-coiled stretch to interact with. N17^Htt would facilitate this process by presenting a constant stretch of accessible polar residues for hydrogen bonding by an uncoiled region of glutamines.

Crick et al.¹⁸ point out the possibility of the critical nucleus existing as a free energy maximum in the case of a single structure, or a heterogeneous mix of high energy structures. In this case the stability would come only after fibrillar addition through interchain interactions. This is similar to the first transition, but differs by existing as a local free energy maximum needing inter-chain interactions to adopt its configuration permanently. Pre-fibril, two or more of these events might be required simultaneously and in close spatial proximity to induce fibril formation. N17^Htt would again present a constant source of polar residues, reducing or eliminating the need for simultaneous globule to rod-like transitions by acting as a source of interchain interactions. In addition, any hydrophobic induced dimerization caused by N17^Htt can be imagined to be quite beneficial with this type of transition as well, due to its dependence on the proximity of other chains.

System and Methods

Simulated Tempering (ST)

Computer simulation, such as Molecular Dynamics, is a powerful technique to explore the conformation space. However, those simulations are often trapped in local free energy minima when applied to complex protein systems.¹⁹ Generalized ensemble sampling methods such as simulated tempering ^{20; 21} and parallel tempering (or replica exchange method)^{19; 22} were developed to overcome this trapping problem by inducing a random walk in temperature space. In ST, configurations are sampled from a mixed canonical ensemble in which the canonical ensembles with different temperatures are weighted differently as defined by a generalized Hamiltonian:

$${\Xi }_n(X,p)={\beta }_{n}H(X,p)-g_n$$ (1)

Where β_n =1/(k_BT_n), H(X, p) is the Hamiltonian for the canonical ensemble at temperature T_n, and the a priori determined constant g_n is the weight for the temperature T_n.

ST works as follows: one single simulation starts from a particular temperature and an attempt is made periodically to change the configuration to another temperature according to a well defined transition probability. The transition probability is shown below,

$$P_{i\to j}=\text{min}\{1,e^{-({\beta }_j-{\beta }_i)U^i(X)+(g_j-g_i)}\}$$ (2)

where Uⁱ(x) is the potential energy sampled from the canonical ensembles at T_i. A set of weights need to be pre-determined to calculate these transition probabilities. Without proper weighing, ST simulations will be constrained to a subset of the temperature space and become inefficient. ^{21; 23} It was shown that weights leading the system to perform a random walk in temperature space equal the unit-less free energies at different temperatures.

It is not an easy task to determine these free energy weights enabling system to perform a random walk in the temperature space. A recent proposed efficient method for determining initial weights allowing the system based on short trial simulations is adopted in this study.²³ These weights are updated throughout the production simulation by an adaptive weighting method using adaptive WHAM in a distributed computing environment.²⁴ The initial weights are calculated based on the property that the “free energy” weights leading to uniform sampling must yield the same acceptance ratios for both forward and backward transitions from T_i to T_j as shown below.

$$<P_{i\to j}>=<P_{j\to i}>$$ (3)

where

$$<P_{i\to j}>=\underset{-\infty }{\overset{\infty }{\int }}{P}_{i\to j}P(U_i)d{U}_i;<P_{j\to i}>=\underset{-\infty }{\overset{\infty }{\int }}{P}_{j\to i}P(U_j)d{U}_j$$ (4)

Where P (U_i) is the potential energy distribution function (PEDF) at Ti. PEDFs for each temperature are estimated from the short trial MD simulations by assuming the distributions are Gaussian. By solving Eq. 3, we can obtain a set of near “free energy” weights.

Simulation Details

In this study we examined the 17 N-terminal residue headpiece (N17^Htt) of the Huntingtin protein. The AMBER2003²⁵ force field was used with a version of the GROMACS molecular dynamics simulation package^{26; 27} modified to include an ST algorithm and the FAH²⁴ infrastructure (http://folding.stanford.edu). Two initial configurations are used: a helix structure with a helical content of 73.3% and a random coil structure with no helical content. (See Fig. 1) Each system is solvated in a 42 □ cubic box using 2335 TIP3P water molecules.²⁸ 1 Na⁺ and 2 Cl⁻ counter ions were included to neutralize the charged peptide. The simulation systems were minimized using a steepest descent algorithm, followed by a 100ps MD simulation applying a position restraint potential to the peptide heavy atoms. All simulations were conducted using constant NVT with a Nose-Hoover thermostat²⁹ having a coupling constant of 0.02ps^-1. Long-range electrostatic interactions were treated using the reaction field method with a dielectric constant of 80. 9 □ cutoffs were imposed on non-bonded interactions. Neighbor lists were updated every 10 steps. A 2fs time step was used and covalent bonds involving hydrogen atoms were constrained with the LINCS algorithm.³⁰

Fig 1.

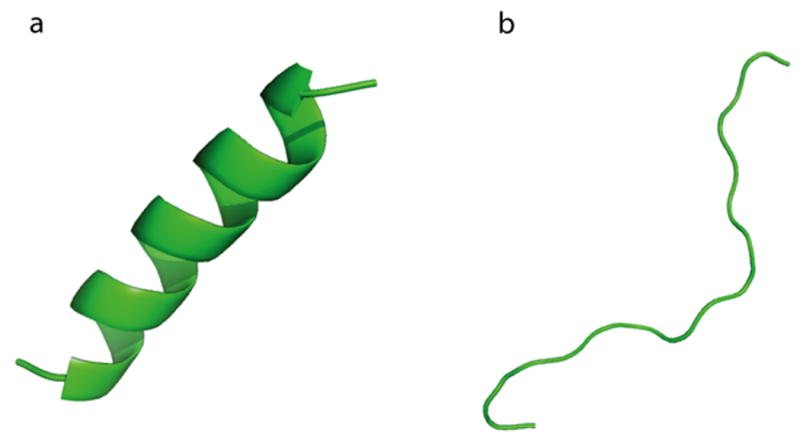
The two initial configurations used for simulations of the N17 headpiece: (a). A helical structure and (b). A random-coil structure.

1000 simulations from each initial configuration were performed on a distributed computing environment using ST enhanced sampling method. The total simulation time was aggregated to more than 40μs. A roughly exponentially distributed temperature list covering a range from 285 to 592K was used. 20 simulations started from each of 50 temperatures, each with a different set of initial velocities. In ST, swap of temperatures were attempted every 2ps. The initial weights were computed using the data obtained from 50 4ns trial simulations. Subsequently, the weights were updated approximately every 400ns by an adaptive weighing scheme.³¹

Lifson-Roig helix-coil theory

Helical properties were computed using the Lifson-Roig helix-coil counting theory.³² In this model, a residue is considered to be helical if φ = −60 ± x and ψ = −47 ± x degrees. x is set to 40 degrees, which is shown to give the best agreement with the melting temperature.¹² In LR model, a helical segment is defined as three or more consecutive helical residues. Each segment has a length of n − 2, where n is the total number of consecutive helical residues. Thus, the maximum helical length of our 17 residue peptide system is 15. The helical content is defined as

$$N_c=\frac{\text{∑}_{h=1}^{N_s}{N}_h}{N_{\text{max}}}$$ (5)

Where N_c is the helical content, N_s is the number of helical segments, N_h is the length of segment h, and N_max is the maximum possible helical length.

Clustering

We use a variation of the K-mean clustering, also named as K-medoids clustering. The algorithm works as follows: All conformations are placed in one of K clusters. A conformation from each cluster nearest its center of mass is assigned as its centroid. All other conformations are reassigned to the cluster representing the centroid to which it is nearest. Centroids are then updated to the conformation nearest the cluster center of mass taking into account the new assignments. This updating procedure may be continued for some predetermined number of iterations or until the answer converges.