Timescales of inference in visual adaptation

Abstract

Adaptation is a hallmark of sensory function. Adapting optimally requires matching the dynamics of adaptation to those of changes in the stimulus distribution. Here we show that the dynamics of adaptation in the responses of mouse retinal ganglion cells depend on stimulus history. We hypothesized that the accumulation of evidence for a change in the stimulus distribution controls the dynamics of adaptation, and developed a model for adaptation as an ongoing inference problem. Guided by novel predictions of this model, we found that the dynamics of adaptation depend on the discriminability of the change in stimulus distribution and that the retina exploits information contained in properties of the stimulus beyond the mean and variance to adapt more quickly when possible.

Introduction

Adaptation—a stimulus or activity-driven change in a system's input-output relation—is a nearly universal feature of neural systems. Sensory systems have a particularly acute need for adaptive coding. For example, the photon flux reaching a glacier climber's retina from sunlit snow can be 1,000 times greater than that from deep shadow in the same scene (Alasdair Turner, personal communication), while the retinal output has a dynamic range of ∼100. Without adaptive coding, the retinal output would either saturate or fail to distinguish different intensity levels within everyday scenes.

Adaptation maintains efficient coding as stimuli change by matching a cell's input-output relation to the distribution of stimuli encountered (Laughlin, 1981; Brenner et al., 2000; Fairhall et al., 2001; Gaudry and Reinagel, 2007). Adaptive coding, however, is not without drawbacks, as it can create ambiguities in decoding (Fairhall et al., 2001; Lundstrom and Fairhall, 2006) and add noise to neural responses (Dunn and Rieke, 2006). Thus, to be effective, the dynamics of adaptation should reflect a balance between adapting rapidly to avoid saturation and adapting slowly to avoid erroneous gain changes in the absence of real changes in the input statistics. This tradeoff suggests that we consider adaptation as a statistical inference problem, where the dynamics of adaptation depend on how rapidly evidence accumulates for a change in the stimulus ensemble (DeWeese and Zador, 1998; Kording et al., 2007). The ease or difficulty of detecting changes in the stimulus ensemble depends in turn on both how much the stimulus changes and prior knowledge about the ensemble inferred from the stimulus history.

Because changes in the world happen on many timescales, we might expect adaptation to exhibit a similar diversity of timescales. Indeed, luminance and temporal contrast adaptation in the retina occur on timescales ranging from a fraction of a second to many seconds or minutes (e.g. Smirnakis et al., 1997; Baccus and Meister, 2002; Kim and Rieke, 2001; Zaghloul et al., 2005; Manookin and Demb, 2006; Brown and Masland, 2001; Chander and Chichilnisky, 2001; Enroth-Cugell and Shapley, 1973; Yeh et al., 1996; Dowling, 1987). It is unclear how these processes together control adaptation in the retinal output. Most past work characterizes adaptation as an exponential process with one or two time constants (e.g. references above). A few studies describe adaptation as a linear process with a wide range of time scales, producing, e.g., a power-law dependence of response on time (Thorson and Biederman-Thorson, 1974; Fairhall et al., 2001; Drew and Abbott, 2006; Lundstrom et al., 2008). It has also been suggested that the parameters of the adaptation process could be adjustable depending on stimulus history (DeWeese and Zador, 1998). No studies have directly distinguished between these possible scenarios.

Here we show that the dynamics of adaptation in the synaptic input to retinal ganglion cells (RGCs) depend on stimulus history. The form of this dependence is inconsistent with linear models of adaptation. Instead, the observed adaptation dynamics require a process with adjustable parameters. We construct an inference model in which prior history and the detectability of changes in the stimulus ensemble govern the dynamics of adaptation, and test novel predictions that this model makes about how the dynamics of adaptation depend on stimulus statistics.

Results

Adaptation following a change in stimulus luminance or contrast often has two components. Linear or linear-nonlinear cascade models have identified a rapid component of adaptation that occurs within the duration of the system's impulse response (typically 100-200 ms; Enroth-Cugell and Shapley, 1973; Baccus and Meister, 2002; Fairhall et al., 2001; Baccus and Meister, 2002). In addition, many systems exhibit a slower change in the mean or root-mean-square (r.m.s.) response (e.g. Fairhall et al., 2001; Smirnakis et al., 1997; Baccus and Meister, 2002; Kim and Rieke, 2001). Here we focus on the dynamics of the slow component of adaptation.

Contrast and luminance adaptation exhibit multiple timescales

Dynamics of adaptation to temporal contrast

To determine if the dynamics of contrast adaptation depend on stimulus history, we measured responses to a periodic switch between low and high contrast stimuli. As described below, the dynamics of adaptation following an increase in contrast depended on the stimulus switching period.

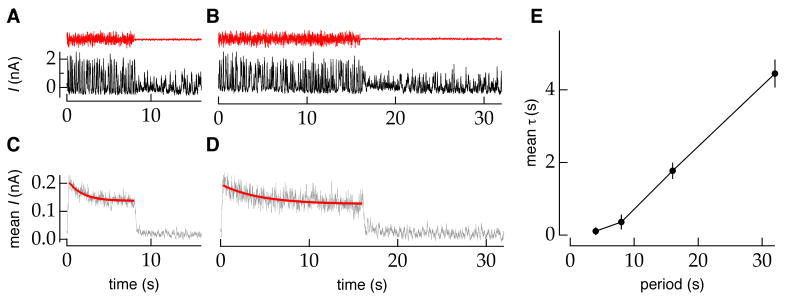
Figures 1A and 1B show the inhibitory postsynaptic currents in an OFF-transient RGC elicited by a single cycle of a stimulus that switched between low and high contrast with period of 16 s (Figure 1A) or 32 s (Figure 1B). When averaged across trials with different instantiations of the random contrast stimulus, both the mean (Figures 1C and 1D) and r.m.s synaptic input (Supplemental Figure S1) decreased over the course of several seconds following the increase in contrast. The slow relaxation of the mean and r.m.s. current following an increase in contrast indicates a change in the gain with which light inputs are converted to RGC synaptic inputs – i.e. variations in the light input shortly after the step produce larger responses than those several seconds later. This slow adaptation caused the mean response to decline to 64 ± 6% (mean±sem, n=41) of its initial peak.

Figure 1.

The time course of adaptation following an increase in temporal contrast depends on the period between contrast switches. A,B, Inhibitory synaptic current to an OFF-transient RGC (holding potential 10mV) in response to a single switch in stimulus contrast (6%-36%, mean ∼400 R*/rod/s; red). The switching period was 16 s in A and 32 s in B. C,D, Mean synaptic currents from approximately 100 trials as in A and B. Exponential fits to the response following an increase in contrast are shown in red. E, Population-averaged (n≈10 for each period) time constant (mean±sem) of the exponential fit to the response following an increase in contrast (6-36%) for all RGC types (ON, OFF-sustained, OFF-transient and ON-OFF) as a function of stimulus switching period.

The trajectories of the mean responses in Figures 1C and 1D following an increase in contrast appear different; this suggests that the dynamics of adaptation depended on stimulus switching period. To quantify this dependence, we fit the mean input current with an exponential, $I(t)=A{e}^{\stackrel{-(t-\Delta )}{}/\underset{\tau }{}}+c$, where τ is the effective adaptation time constant, c is an offset and Δ allows for the delay in the cell's response (red lines in Figures 1C and 1D). Response delay was typically 250–500 ms under the conditions tested. For cells in which the input currents were non-rectified, the r.m.s. current was fit with the same function. The exponential amplitude A and baseline c did not change significantly as a function of the switching period (not shown).

Figure 1E shows the population average time constant as a function of period. The average effective time constant of adaptation scales approximately linearly across a broad range of switching periods (∼8-32s). The observed scaling fails for short periods but extends to the longest period (T=32s) that we could measure reliably. A similar relationship was observed when comparing the time constant of an exponential fit to only the first 8s of 8, 16, and 32s periods (not shown). Thus the effect is not simply the result of fitting an exponential to a non-exponential response over varying time windows. These results indicate that a fixed first-order process does not govern the dynamics of contrast adaptation in mouse retina. Instead, the adapting machinery has access to multiple timescales.

Dynamics of adaptation to luminance

To test the generality of multiple-timescale dynamics of adaptation, we measured responses to periodic changes in mean light intensity (luminance). As for contrast adaptation, the dynamics of adaptation following an increase in luminance depended on the stimulus switching period.

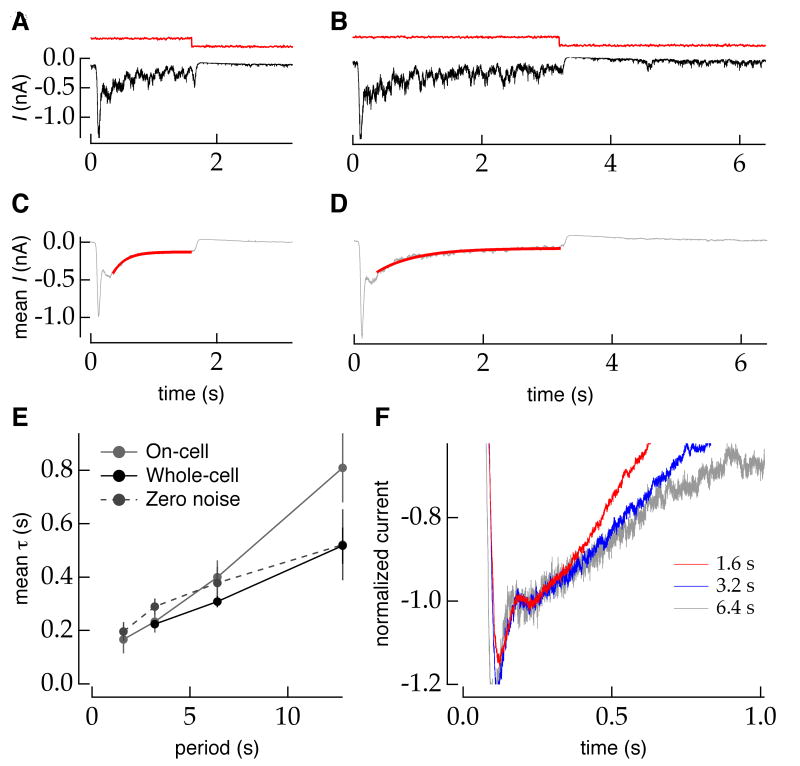
Figures 2A and 2B show responses to a single presentation of a periodic luminance step lasting 3.2 or 6.4 s. Figures 2C and 2D show average responses to many repetitions of the luminance step with different instantiations of the random additive noise. The mean synaptic current following a change in luminance shows an initial rapid transient component followed by a slower second component. The r.m.s. current had a similar trajectory, indicating an adaptive change in response properties (Supplemental Figure S1). The first component of the mean response is predicted by the (biphasic) linear impulse response function of the cell (not shown) and is thus unrelated to adaptation; the kinetics of this component did not depend on the switching period. We therefore focused on the slow component of the response. During this part of the response, the mean current declined to 38 ± 5% (mean±sem, n=34) of its amplitude at the end of the first component.

Figure 2.

The time course of adaptation following an increase in luminance depends on the period between luminance switches. A,B, Excitatory synaptic current to an ON RGC (holding potential -60mV; black) in response to a single switch in stimulus luminance (∼40-80 R*/rod/s with 6% contrast superimposed; red). The switching period was 3.2 s in A and 6.4 s in B. C,D, Mean synaptic input currents from approximately 50 trials as in A and B. The mean current shows a stereotyped component followed by a slow adaptation component. The exponential fit to the slower of these two components is shown in red. E, Population-average (n≈10 for each period) time constant (mean±sem) of adaptation in synaptic input currents to ON RGCs (black) recorded in whole-cell configuration or spike rate of ON RGCs (grey) recorded from different cells in the on-cell configuration as a function of stimulus switching period. F, The normalized mean responses to different switching periods diverge following the stereotyped component of the step response (shown for an ON RGC).

The exponential fits in Figure 2C and 2D (red traces) begin after the first component—i.e. at a fixed time after the luminance step. The responses are plotted on equal time axes but the second component of the responses appears different, suggesting that the timescale of adaptation is different for the two switching periods. Indeed, the exponential time constant of the fit to the slow component of luminance adaptation in the RGC input currents scaled approximately linearly with stimulus-switching period across the range of switching periods probed (Figure 2E, black). In a separate population of ON RGCs, we measured the mean spike rate to the same switching stimulus. As with the synaptic input currents, the time constant of an exponential fit to the change in rate following an increase in luminance scaled across the range of switching periods probed (Figure 2E, grey). This range began at shorter periods than for contrast adaptation and persisted to the longest period we were able to measure (T=40s in a few cells; not shown). This rescaling was not a peculiarity of the exponential fits, as the time to 80% recovery (including the stereotyped component) showed a similar dependence on switching period (Supplemental Figure S2). Results were very similar with and without a small amount of noise added to the luminance step (Supplementary Figure S3). Thus luminance adaptation, like temporal contrast adaptation, has access to multiple timescales.

A dependence on stimulus history predicts that the trajectory of adaptation following a change in the stimulus ensemble should diverge for different switching periods. Previous studies have not tested this prediction directly, at least in part because the trajectories following a change in temporal contrast are noisy and difficult to compare directly. To compare the trajectories of the responses to different switching periods, we aligned the normalized mean currents for different switching periods at the end of the first, stereotyped component following the luminance increase (Figure 2F). The trajectories diverge from this common starting point. Thus the time constant of luminance adaptation itself adapts to the timescale of changes in the stimulus.

An inference model for adaptation dynamics

We hypothesized that the dynamics of adaptation are governed by the accumulation of evidence for a change in the stimulus ensemble. To formalize this idea, we constructed a model that estimates the stimulus ensemble's parameters (e.g. mean, variance) by combining information about the current stimulus with accumulated knowledge from previous stimulus samples. Unlike related models (e.g. DeWeese and Zador, 1998), we do not impose a prior belief on the dynamics of changes in the stimulus ensemble, as doing so imposes a timescale on the dynamics of adaptation predicted by the model. Instead, that timescale emerges from the ease or difficulty in detecting changes in the stimulus ensemble.

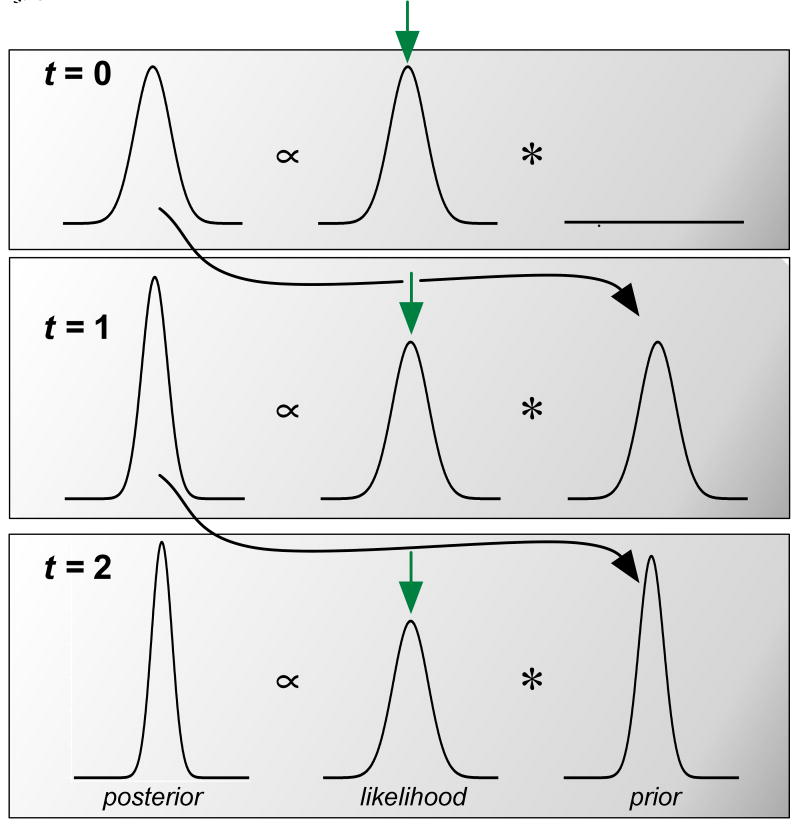
At each time step, the model estimates the distribution of possible stimulus ensemble parameters given the stimulus history, $P\left({\phi }_t{|\stackrel{\rightharpoonup }{s}}_{j\le t}\right)$, where φ_t is the vector of stimulus parameters at time t and ${\stackrel{\rightharpoonup }{s}}_{j\le t}$ is the vector of stimulus samples up to, and including, time t. This a posteriori distribution is estimated recursively by approximating Bayes' rule (Figure 3; see Experimental Procedures for details). The estimate of the current vector of stimulus parameters φ̂_t is the peak of the a posteriori distribution, the most likely parameter value given the stimulus and the distribution of estimated parameters in the previous time step. Because we varied only a single stimulus parameter (e.g. mean or variance) in the experiments and simulations here, we consider φ̂_t as a scalar corresponding to the changing stimulus parameter.

Figure 3.

Operation of the inference model. The model is schematized for estimating the mean of the stimulus distribution (shown by the green arrow in all panels) with a Gaussian likelihood and Gaussian prior distribution. At the first time step (t=0), the average stimulus value produces an average likelihood function indicated by the green arrow. Multiplied by a large variance prior, the first posterior distribution is shown on the left after appropriate normalization. At the following time step (t=1), the previous time step's posterior distribution is substituted for the current prior and the Bayesian calculation is repeated. In this example, the stimulus ensemble is constant; thus the posterior at time t=1 is more peaked around the stimulus mean than in the previous time step. Similarly, at time t=2, the posterior becomes further peaked around the stimulus mean. At each time step the model chooses the maximum a posteriori value as its current estimate of the stimulus ensemble's parameters.

Comparing the model with experiment requires an assumption about how adaptation works (e.g. whether it is multiplicative or subtractive). The changes in r.m.s. current following a change in stimulus luminance or contrast (Supplemental Figure S1) indicate that at least part of the slow component of adaptation reflects a change in sensitivity of the RGC synaptic inputs. Thus we use the model estimate as a multiplicative gain term, ${\widehat{\phi }}_t^{-1}$. Internal noise will enforce that φ̂_t is greater than 0 even if the stimulus luminance or contrast is 0. This definition of gain means that the model normalizes the stimulus by the estimated stimulus standard deviation or mean. Normalization by the estimated mean insures, e.g., encoding of contrast or reflectance in a scene independent of changes in the illuminating light source (Shapley and Enroth-Cugell, 1984). Normalization by the estimated standard deviation means that the response range does not depend on the magnitude of stimulus variations, an effective strategy for maximizing information transfer given a fixed output range (Cover and Thomas, 1991; Brenner et al., 2000). This normalization is also consistent with models of contrast adaptation later in the visual system (e.g. Bonin et al., 2005; Carandini and Heeger, 1994). A model based on a subtractive mechanism could also account for the measured dynamics of adaptation. The key aspect of the model is not how the parameter estimate produces adaptation, but rather the ease or difficulty in inferring changes in stimulus properties.

We use the inference model in three ways below. First, we show that it captures the qualitative features of the contrast and luminance adaptation experiments of Figures 1 and 2. Second, we fit the model's free parameters to experimental data to make a quantitative comparison between the model and experiment for luminance adaptation. Finally, we explore how the discriminability of changes in the stimulus distribution affects the dynamics of adaptation.

Dependence of adaptation dynamics on temporal period of the stimulus

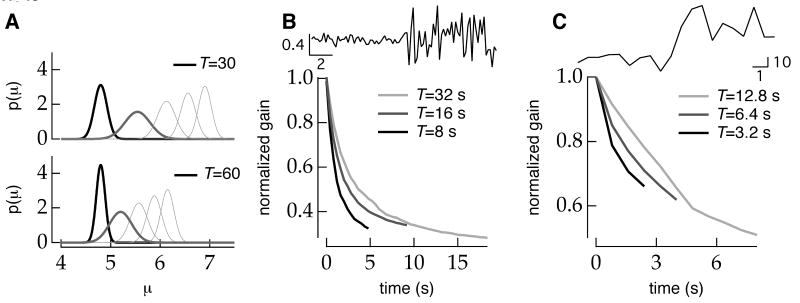
The time course of gain change in the model is determined by how rapidly a change in the stimulus parameters can affect a change in the distribution of possible parameter values. This in turn is determined by the distribution of possible stimulus parameters prior to the change in stimulus and by the magnitude of the change in stimulus values. The dependence on stimulus switching period enters the model through the prior distribution—the longer the model spends in a steady state stimulus ensemble, the more peaked the prior distribution becomes around the steady state estimate φ̂_∞ and the more evidence is required to overcome this prior (Figure 4A).

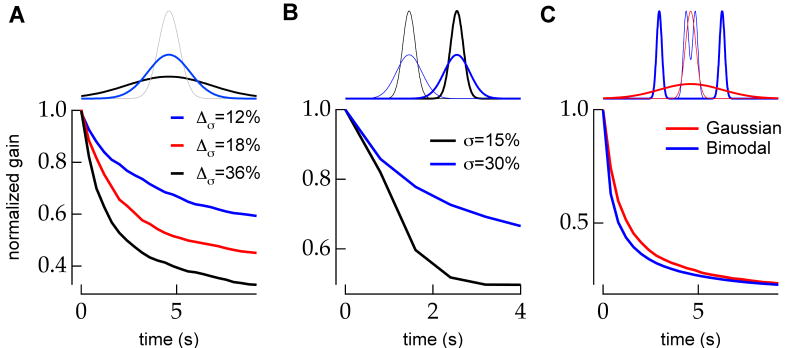
Figure 4.

The inference model captures the observed dependence of time course of adaptation on stimulus switching period. A, Immediately preceding a periodic increase in luminance from 4.8 to 9.6 (arbitrary units), the model's a priori distribution of stimulus contrasts is more peaked during long switching periods (T=60; black, bottom) than during shorter switching periods (T=30; black, top). The width of the a priori distribution reflects the uncertainty about the current stimulus parameter. When the a priori distribution is narrower, more evidence is required to shift this distribution towards the new luminance following a change in the stimulus ensemble. Thus the expected first a posteriori distribution (dark gray) after observing a sample from the new stimulus ensemble is shifted farther towards the new stimulus mean during short periods (top) than long periods (bottom). Light gray traces show the expected a posteriori distribution at equally spaced time points to t=15. Normalized average model output (gain) following a periodic increase in contrast (B) or luminance (C) shows qualitative agreement with observed data (Figures 1-2). The rate of adaptation decreases with increasing switching period. Simulation results are the average of 100 trials.

The time course of the change in model gain following a periodic increase in stimulus contrast (Figure 4B) or luminance (Figure 4C) increased with the switching period for a range of stimulus periods. Thus the model could capture the basic dependence of adaptation dynamics on switching period for both contrast and luminance changes.

Fitting model parameters

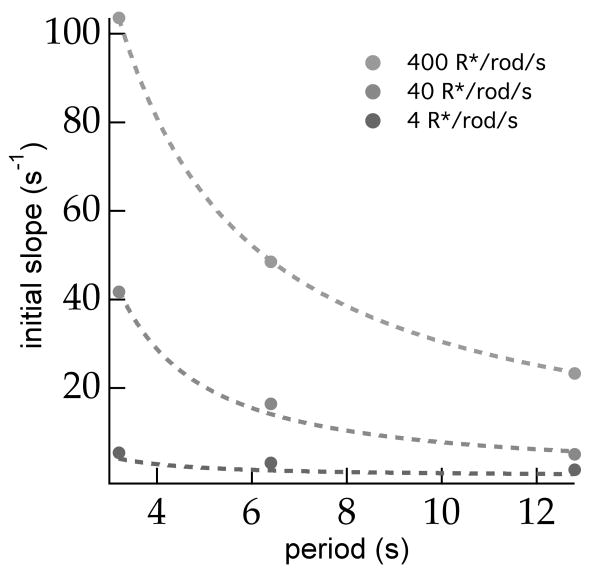
The dynamics of adaptation in the model depends on two parameters: (1) the time step for accumulating independent samples, corresponding to the integration time of the adapting mechanism, and (2) the noise in the signal controlling adaptation, which we will express as an effective stimulus contrast noise. For luminance steps, the model is analytically solvable for Gaussian stimuli and a Gaussian initial prior (see Experimental Procedures), which simplifies fitting the model to the data. To reduce sensitivity to non-exponential gain trajectories, we fit the slopes of the initial experimental gain trajectories. We decreased the integration time by a factor of two between 40 and 400 R*/rod/s to account for the speeding of rod-mediated responses with background light (Dunn et al., 2006). For a range of effective noise and integration time (approximately 12-20% contrast and approximately 0.7-0.8s at 40 R*/rod/s respectively), the model predictions agree closely with experiment across light levels (Figure 5).

Figure 5.

Quantitative model predictions. For Gaussian stimuli, the inference model can be solved analytically for periodic switching stimuli (see Experimental Procedures). Model predictions were insensitive to the initial prior mean and standard deviation for standard deviations much larger than the stimulus standard deviation. Fixing the initial prior standard deviation at approx. 10 times the stimulus standard deviation, we fit the initial slope of the adaptation transient predicted by the inference model for periodic luminance steps (dashed lines) to the observed initial slope of adaptation in the synaptic input currents to ON RGCs (circles; see Supplemental Figure S4). Free parameters in the fit were effective stimulus noise contrast at each luminance level and integration time of the adapting mechanism. In correspondence with previous results, we decrease the integration time by 50% between 40 and 400 R*/rod/s. Fitted parameters were: λ ≅ 0.92, τ ≅ 0.80s, σ₄ ≅ .73, σ₄₀ ≅ 4.73, and σ₄₀₀ ≅ 47.32, where effective noise is given in arbitrary model stimulus units and λ is the scale factor that relates physical stimulus units (R*/rod/s) to arbitrary model units.

Effect of discriminability of the luminance or contrast step

The timescale of adaptation in the model is determined by the rate of accumulation of evidence for a new stimulus ensemble. Thus, the adaptation time course should depend on the ease or difficulty of discriminating a change in stimulus parameters. Specifically, the time required to adapt to a change should be shorter for larger changes in parameter (assuming constant noise), and increase with increasing background noise. Indeed, the model gain changed more quickly for larger contrast steps (Figure 6A). Similarly, adaptation slowed with increasing noise added to a periodic switch in luminance (Figure 6B). These results predict that the dynamics of adaptation depend on the discriminability of a change in stimulus parameters.

Figure 6.

The time course of model adaptation depends on the discriminability of the change in stimulus ensemble. A, The rate of model adaptation following a periodic change in contrast increases as the size of the contrast step increases. Stimulus distributions for a 12% (blue) and 36% (black) contrast step from starting contrast (gray) are shown above. B, The rate of model adaptation following an increase in stimulus luminance decreases as the signal to noise ratio of the step relative the added noise (i.e. contrast) decreases. Stimulus distributions for 30% (blue) and 15% (black) contrast at the low mean are shown above. Thin lines show the starting (low luminance) distributions. C (top), Following an increase in variance of a Gaussian distribution, many random samples from the high contrast distribution (thick red) are nearly equally likely in the low contrast (thin red) and high contrast distributions. Only rarely will a random sample from the high contrast distribution be highly unlikely in the low contrast distribution. In this case, it is difficult for an observer to infer that the contrast of the distribution has changed. The same contrast change in a bimodal distribution is easily detectable, however. If the width of the peaks is small relative to the change in their separation, as shown, random samples from the high contrast distribution (thick blue) are unlikely in the previous low contrast distribution (thin blue), and thus, a contrast change is easy to detect. C (bottom), The rate of model adaptation following a matched increase in stimulus contrast is greater for a bimodal stimulus ensemble than for a Gaussian ensemble. The model used a Gaussian likelihood function in both conditions. All traces are the average of 100 simulated trials.

Stimulus distribution

The form of a stimulus distribution can affect estimation of a change in stimulus parameters and so might affect adaptation dynamics (DeWeese and Zador, 1998). For example, it is more difficult to detect an increase in the contrast of a Gaussian distribution than a bimodal distribution. Following an increase in the contrast of a Gaussian stimulus, many stimulus samples will be similarly likely in the old and new distributions (Figure 6C, top, red). However, for a bimodal distribution with two peaks that are narrow relative to their change in position during a change in contrast, previously likely stimulus samples are very unlikely in the new distribution and vice versa (Figure 6C, top, blue). Thus, in principle, an adapting mechanism could more rapidly acquire evidence that the stimulus ensemble had changed when encountering stimuli from a bimodal distribution than a Gaussian distribution. Consistent with this expectation, the model adapted more quickly to a step in contrast of a bimodal distribution than to an equivalent contrast step of a Gaussian distribution (Figure 6C, bottom).

Testing model predictions

The complex relationships between stimulus history and the dynamics of adaptation predicted by the model are not suggested directly by previous experiments. Thus we tested the inference model's predictions experimentally.

Effect of discriminability of the contrast or luminance step

The inference model predicts that adaptation to a small change in stimulus contrast will be slower than adaptation to a large change in stimulus contrast (Figure 6A). Indeed, for cells in which we could reliably fit the mean response to both the small and large contrast steps (e.g. Figure 7A), the time constant for adaptation to the small contrast step was longer than that for the large contrast step (Figure 7B). Thus the time course of adaptation following a contrast step depends on both the size of the contrast step and the duration of the previous state (Figure 1). The inference model, using parameters from fits to luminance adaptation (see Experimental Procedures), predicted the direction, but not the magnitude of the change in time constants.

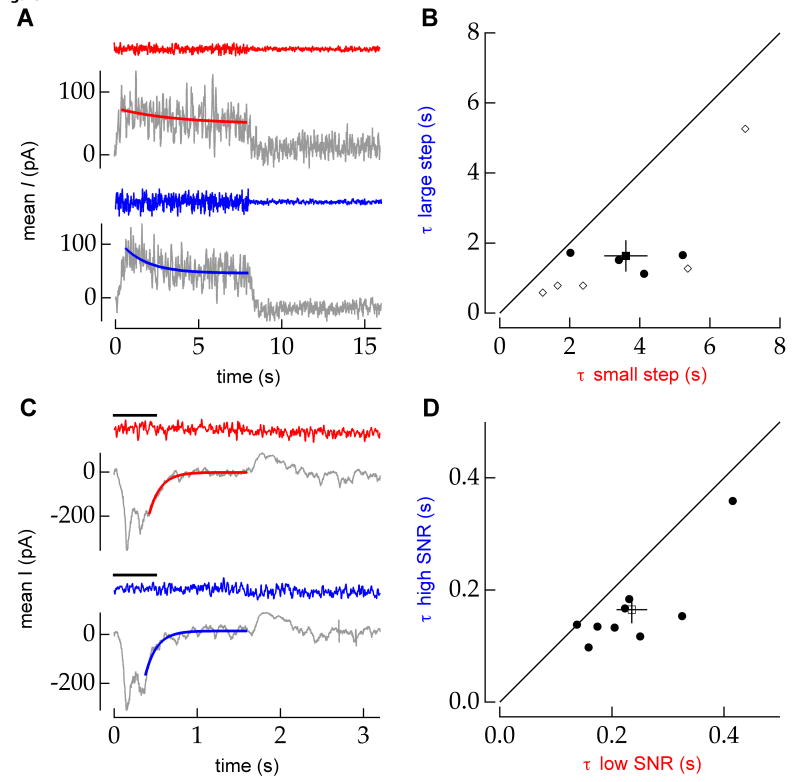
Figure 7.

The time course of adaptation following an increase in stimulus contrast or luminance depends on the size of the contrast step or the signal to noise ratio of the luminance step. A, The time constant of an exponential fit to the mean inhibitory synaptic input current to an OFF RGC in response to a periodic (T=16s) 12-24% contrast switch (red) is larger than that (blue) for a 12-36% contrast switch. Example stimuli are shown above each trace on equal vertical scales. B, In a population of ON, OFF-transient, OFF-sustained, and ON-OFF RGCs (n=9), the timescale of adaptation to a periodic contrast step is longer when the contrast step is smaller (3.6 ± 0.6 vs. 1.6 ± 0.4 s, mean±sem; p = 0.002, paired t-test). Solid line denotes equality. Filled circles (open diamonds) denote cells comparing a 12-24% (12-17%) vs. 12-36% contrast step. The filled square marks the population average. Error bars denote standard error in the mean. C, The fitted time constant of the mean excitatory input to an ON RGC in response to a periodic (T=3.2 s) luminance step (∼40-80 R*/rod/s) when the stimulus variance was high (red) is longer than the time constant when the variance was low (blue). Stimulus variance is evaluated in the 500 ms (black bar) following the increase in luminance. Example stimuli are shown above each trace on equal vertical scales. The standard deviation of the samples in the red (low SNR) trace is approximately 1.5× the standard deviation of the blue (high SNR) trace in the 500ms immediately following the luminance step (∼18.4 vs. ∼11.2 R*/rod/s) D, In a population of ON, OFF-transient, and OFF-sustained RGCs (n=9), the timescale of adaptation to a periodic luminance step with low SNR is slower than adaptation to a luminance step with high SNR (0.24 ± 0.03 vs. 0.16 ± 0.02 s, mean±sem; p = 0.003, paired t-test). Solid line marks equality. Filled circles represent individual cells. The open square marks the population average.

To test the effect of discriminability on the time course of luminance adaptation, we asked whether the dynamics of adaptation were correlated with trial-to-trial stimulus variations. We sorted the responses to a luminance step with constant added noise according to the stimulus variance in the 500 ms immediately following the luminance step. Trials in which the stimulus variance was, by chance, low provide lower noise and hence greater discriminability for the luminance step than trials in which the stimulus variance was high. The 500 ms window was chosen to include the stereotyped component and approximately one time constant of the slow adaptive component of the response. Adaptation was slower for the high stimulus variance trials than the low variance trials (Figure 7C and D). Similar results were obtained for window sizes between 350 ms and 500 ms. As above, the inference model, with stimulus variances equal to the high and low experimental conditions, predicted the direction but not the magnitude of this change. Thus the time course of adaptation following a luminance step depends both on the discriminability of the step and the duration of the previous state (Figure 2).

Dependence on stimulus distribution

While the early visual system adapts to contrast, it does not appear to adapt to changes in higher-order moments of the stimulus distribution such as kurtosis (Bonin et al., 2006). However, model results (Figure 6C) suggest that these higher-order moments (e.g. those that distinguish Gaussian and bimodal distributions) could affect the dynamics of adaptation to changes in lower-order moments such as contrast. The experiments described below indicate that this is the case.

We first measured adaptation to a stimulus that switched periodically between a binary and a temporally quantized (“stair-stepped”) Gaussian distribution (Figure 8A). The distributions were matched in mean and variance but differed in higher statistical moments. Neither the mean nor the r.m.s. synaptic input changed during switches in the distribution, as illustrated in Figure 8B (top) for the ON RGC shown in Figure 8A. To combine results across cells, we measured the ratio of the mean synaptic current at the beginning and end of each stimulus condition. We excluded the first 500 ms following a switch in stimulus distribution to account for response delay introduced by retinal transduction and circuitry (approximately 350 ms under the experimental conditions) and any linear filtering effects such as those in Figure 2. The resulting ratio of mean currents was not significantly different from one for either condition (Figure 8B, bottom).

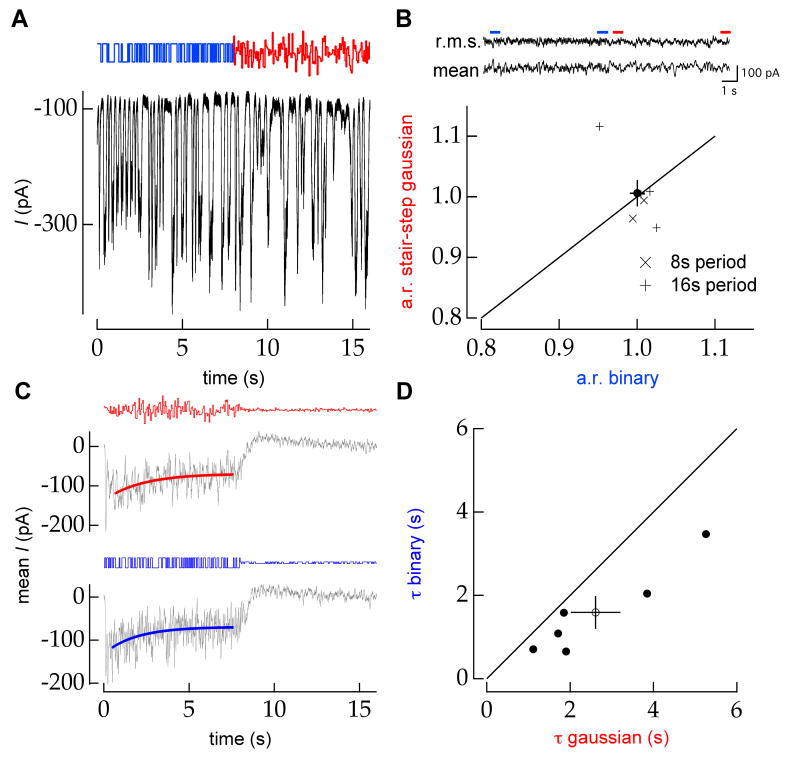
Figure 8.

Higher-order moments of the stimulus distribution affect the time course of adaptation to changes in stimulus contrast. A, Example record (black trace) of the excitatory synaptic input current to an ON RGC in response to a periodic (T=16s) switch in stimulus distribution from binary to Gaussian (mean and variance held constant) (top). B, The mean and r.m.s. synaptic input current during ∼50 periods like that shown (C) (top). Although there may be a change in the structure of the response distribution, there is no obvious adaptation. Adaptation ratio (a.r.) for each condition was defined as the ratio of mean synaptic current in the second and last 500ms of each condition (indicated by red and blue bars). Combining results of measurements from T=8s and T=16s periods, the adaptation ratio for stair-step Gaussian and binary conditions are not significantly different from 1 (bottom; 1.01 ± 0.02 vs. 1.00 ± 0.01 (mean±sem); p=0.91 and p=0.99, respectively). The black circle shows the population mean. Error bars show standard error of the mean. C, The time constant of an exponential fit (red) to the mean excitatory input to an ON RGC to a periodic 6-36% contrast step in a stair-step Gaussian distribution (top) is longer than the time constant of the exponential fit (blue) to the mean response to a periodic 6-36% contrast step in a binary distribution (bottom). Stimuli were updated at either 11 or 19Hz and results were averaged across all trials. Example stimuli for the Gaussian (red) and binary (blue) conditions are shown above each trace on equal vertical scales. D, Across a population of ON RGCs (n=6), the timescale of adaptation is longer for periodic contrast steps in a stair-step Gaussian distribution than for similar contrast steps in a binary distribution (2.6 ± 0.6 vs. 1.6 ± 0.4 s mean±sem; p = 0.015, paired t-test). The solid line marks equality. Each filled circle represents one cell and the open circle marks the population mean.

Although a change in stimulus distribution did not induce adaptation, the inference model predicts that adaptation to a contrast step will be faster for binary stimuli than for Gaussian stimuli (Figure 6C). Consistent with this prediction, inputs to ON RGCs adapted more quickly to periodically switching binary stimuli than to Gaussian stimuli (Figure 8C and 8D). Thus, although the retina did not appear to adapt to higher-order stimulus moments, these higher moments did affect the time course of adaptation to lower-order moments. Unlike the other experiments described above, which give similar results for both ON and OFF cell types, this dependence of adaptation time course on higher order moments appears to be restricted to synaptic input to ON RGCs.

Discussion

The investigations of the timescales of luminance and contrast adaptation reported here lead to three main conclusions: (1) adaptation to luminance and contrast in the mammalian retina occurs on many timescales, with the observed timescale depending on the past history of the stimulus; (2) the timescale of both luminance and contrast adaptation depends on the discriminability of the change in stimulus parameters; and (3) statistical properties of the stimulus beyond the mean and variance can affect the time course of adaptation to contrast even when the retina does not adapt directly to these properties. These results support a model in which the dynamics of adaptation are governed by the rate at which evidence accumulates in favor of a change in stimulus parameters.

Functional form of adaptation

Several functional models could produce multiple time constants of adaptation. Previous studies have described the trajectory of adaptation with a multiple exponential (e.g. Kim and Rieke, 2001) or a power-law (e.g. Thorson and Biederman-Thorson, 1974; Fairhall et al., 2001; Lundstrom et al., 2008) dependence of gain on time. Although these models may be implemented by highly nonlinear systems, their functional output depends linearly on the stimulus (Drew and Abbott, 2006; Lundstrom et al., 2008). History dependence in these models arises from long timescales (or low frequencies) in the linear response. For this class of models, the responses to contrast steps of different sizes or luminance steps with different amounts of noise should change in amplitude but not in timescale. Contrary to this prediction, we observed that the timescale of adaptation decreased when the size of the contrast step increased and when the signal to noise ratio of a luminance step increased (Figure 7). This result is inconsistent with a linear model of adaptation dynamics. Instead, our data requires a model with tunable dynamics, such as a single exponential process with a tunable timescale or a combination of exponential processes whose relative contributions are adjusted nonlinearly according to stimulus history.

Mechanism of tunable adaptation

Adaptation to luminance (Dunn et al., 2006; Dunn et al., 2007) and contrast (Kim and Rieke, 2001; Rieke, 2001; Kim and Rieke, 2003; Baccus and Meister, 2002; Zaghloul et al., 2005) occur at multiple sites in the retinal circuitry, and these different locations may have distinct temporal properties. Tuning of the timescale of adaptation could occur if the stimulus properties alter the relative contributions of these different sites. Consistent with this idea, the dominant site of luminance adaptation depends on light level (Dunn et al., 2006; Dunn et al., 2007). Similar stimulus-dependent shifts in the dominant site of adaptation could produce a reweighting of mechanisms with different timescales, providing a potential explanation for the dependence of the dynamics of contrast and luminance adaptation on switching period (Figures 1 and 2) and on discriminability (Figure 7).

The history dependence of the timescale of adaptation could also be achieved by a single mechanism with a tunable time scale. Such tunable timescales could be produced by mechanisms such as multiple sodium channel inactivation states with distinct recovery rate constants (Toib et al., 1998; Gilboa et al., 2005) leading to stimulus-duration dependent timescales. Indeed, although faster than the timescales reported above, the existence of multiple, possibly tunable timescales in the retina is suggested by responses to the offset of temporal patterns that occur with a timing that depends on the stimulus frequency (Schwartz et al., 2007).

The excitatory input to ON RGCs and inhibitory input to OFF RGCs likely share common retinal circuitry through the ON cone bipolar cell and the AII amacrine cell (Murphy and Rieke, 2008; Manookin et al., 2008). Excitatory input to ON RGCs and inhibitory input to OFF RGCs showed similar adaptation dynamics, suggesting this common circuitry exhibits mechanisms of tunable adaptation. The difference in sensitivity of the dynamics of adaptation to stimulus distribution between ON and OFF cells (Figure 8) suggests that this sensitivity is provided by mechanisms in circuitry these cell types do not share, such as the ON cone bipolar terminal.

Adaptation as estimation

Adaptation is an inherently risky process. Adapting mechanisms must operate rapidly to avoid saturation of neural responses by rapid changes in stimulus ensemble, such as those produced by visual saccades. But neural responses are noisy on these short time scales, raising the possibility that adaptation could be invoked unnecessarily. Balancing the tradeoff of adapting quickly and adapting with certainty suggests that we consider adaptation as an estimation process, where the dynamics of adaptation are governed by the acquisition of evidence for a change in the parameters of the stimulus ensemble.

We formalized the hypothesis that adaptation involves estimation of stimulus parameters by constructing a model that estimates the stimulus parameter (e.g. mean or variance) given the current stimulus and accumulated knowledge of stimulus history. This model could account qualitatively for the history dependence of the dynamics of adaptation to both luminance and contrast. In the case of luminance adaptation, parameters of the inference model could be fit to data, providing quantitative agreement between the model and experiment. The model also made three novel predictions: (1) adaptation should speed up with larger contrast steps; (2) adaptation should speed up with less noise during luminance steps; and (3) the dynamics of adaptation should depend on higher statistical moments of the stimulus distribution that influence the discriminability of changes in the stimulus ensemble, even if these properties of the stimulus do not themselves produce adaptation. All three model predictions held experimentally.

The most surprising of these model predictions was the role of higher-order statistical moments. Consistent with past work, we did not find evidence of retinal adaptation when the stimulus switched from a Gaussian to a binary distribution – i.e. when we changed the stimulus kurtosis and higher moments (Figure 8). However, the timescale of adaptation to an equal contrast step differed for stimuli from the two distributions. Natural stimuli, which are highly non-Gaussian (Ruderman and Bialek, 1994), may thus contain information that allows the retina to adapt more quickly compared to Gaussian stimuli.

Limitations of the inference model

The inference model underestimated the magnitude of the change in time constant with changes in the discriminability of the step (Figures 6 and 7). There are several reasons why the model may have failed to generalize from the data used to set its free parameters. One key assumption in the model is that adaptation is determined by the most likely value of the stimulus mean or contrast; this assumption effectively implies an equal weighting of the costs of adapting erroneously and failing to adapt. In reality these costs may be weighted differently. For example, slower adaptation may be an acceptable (and unavoidable) cost of avoiding erroneous adaptation. Such an effect would increase the effective noise in the model and thus require a greater increase in step discriminability to produce a given speeding of adaptation. Indeed, the inference model matches the ratio of time constants of adaptation in the experiment described in Figure 7C-D if the difference in stimulus noise between the low and high noise conditions is increased by 40%.

Functional importance of adjustable adaptation

Sensory transduction and signal processing mechanisms are, in many instances, well matched to the task of optimizing sensory performance. Adapting optimally requires striking a balance between adapting quickly to maintain efficient coding and adapting slowly to avoid introducing fluctuations in gain due to noise in the neural responses. This balance depends on how the statistics of the input signals change. The experiments and analysis described here indicate that the retina adapts more rapidly when sufficient evidence is available to outweigh the risk of adapting. A similar tuning of the dynamics of adaptation to the ease or difficulty of detecting changes in the stimulus distribution may help other sensory systems maintain efficient coding in an ever-changing sensory world.

Experimental Procedures

Tissue

Retinas were isolated from dark adapted C57BL/6 mice (Harlan; Indianapolis, IN) following procedures approved by the Administrative Panel on Laboratory Animal Care at the University of Washington. Eyes were hemisected, the vitreous humor was removed, and the eye cups were stored at 32° C in bicarbonate-buffered Ames medium (Sigma-Aldrich; St. Louis, MO) equilibrated with 5% CO₂/95% O₂. For recording, a section of retina was separated from the pigmented epithelium, placed in the recording chamber photoreceptors down on a nylon mesh and held in place with nylon fibers. All manipulations were performed under infrared (>850 nm) illumination. During recording the retina was superfused with Ames medium warmed to 30–33° C.

Electrophysiology

Whole-cell voltage clamp recordings were made using glass patch electrodes as previously described (Murphy and Rieke, 2006). Electrodes were filled with an internal solution containing (in mM) 105 CsCH₃SO₃, 10 TEA-Cl, 20 HEPES, 10 EGTA, 5 Mg-ATP, 0.5 Tris-GTP, and 2 QX-314 (pH ∼7.3 with CsOH, ∼280 mOsm). Series resistance was typically 10-20 MΩ and was compensated approximately 75% in all recordings. Excitatory and inhibitory synaptic input currents were isolated by voltage-clamping the cell at -60 mV (the calculated chloride reversal potential) and +10 mV (the approximate cation reversal potential). Signals were low-pass filtered at 3 kHz, amplified with an AxoPatch 200B amplifier (Molecular Devices; Sunnyvale, CA) and digitized at 10 kHz (HEKA; Port Washington, NY). Liquid junction potentials (∼-10 mV) have not been corrected.

Cell Identification

Recorded cells belonged to four visually and functionally identifiable groups. Cells from each group were identified visually from their soma size and shape and functionally by their characteristic spiking and synaptic input responses to a dim light step from darkness. ON, OFF-transient, and OFF-sustained RGCs were identified as previously described (Murphy and Rieke, 2006). ON-OFF ganglion cells were identified by large somas (∼20 μm in diameter, slightly smaller than ON RGCs), transient spiking responses at both the onset and offset of a dim light step in darkness, no sustained firing in darkness and transient excitatory and inhibitory currents at both light onset and offset. For dim light steps, excitatory currents were generally similar in magnitude but faster in kinetics than inhibitory currents. We filled several ON-OFF cells with fluorescent dye (0.1 mM Alexa-488; Molecular Probes). Confocal images showed that these cells had large, bistratified dendritic arbors approximately 200 μm in diameter.

Stimulus

Light from a blue light-emitting diode (LED; 470 nm peak emission) was focused on the retina by the microscope condensor to illuminate uniformly a circular area 630 μm in diameter centered on the recorded cell. The command signal to the LED was updated at 10 kHz. LED command signals were converted to rhodopsin isomerizations (R*)/rod/sec using the calibrated LED output, the LED spectrum and the rod spectral sensitivity.

Experiments studying contrast adaptation were performed at a mean light level of ∼400 R*/rod/sec. Experiments studying luminance adaptation were performed from a starting luminance of ∼40 R*/rod/sec, except where noted. We did not observe robust adaptation to stimulus contrast at ∼40 R*/rod/sec, consistent with other recent results (Beaudoin et al., 2008).

In the luminance adaptation experiments shown in the figures of the main text, we added a small amount of noise to the stimulus. It is unknown whether adaptation mechanisms in the retina respond to changes in contrast or changes in stimulus standard deviation. We chose to add noise of constant variance to the luminance step rather than maintaining constant stimulus contrast across the luminance step. Thus, there was thus a two-fold decrease in stimulus contrast at the luminance step, though this change in contrast was not responsible for the change in timescale (Supplemental Figure S3). Except when studying the effect of discriminability of the luminance step (Figure 7), the added noise corresponded to 6% contrast at the low luminance level. In control experiments, we did not find any evidence of contrast adaptation from a 6% to 3% contrast step (not shown), likely because these stimuli produce smaller fluctuations in retinal responses at the site of adaptation than cellular noise sources.

Band-limited Gaussian noise was generated by first generating white Gaussian noise in the frequency domain and filtering at either 50Hz, 60Hz or 100Hz with a 4-pole filter. Each frequency component was scaled such that the stimulus had the desired total power and the result transformed into the time domain to produce the final stimulus.

Binary stimuli were generated by sampling from a Bernoulli distribution at either 11 or 19Hz. The Bernoulli distribution was symmetric (offset = σ * μ) about the desired stimulus mean. Stimuli were constant during the ∼50 or ∼91 ms interval between samples. Temporally quantized Gaussian stimuli differed from binary stimuli only in that the samples were drawn from a Gaussian distribution.

The model was driven with Gaussian stimuli identical to those used in the experiments, except that no band-limiting filter was applied since the discrete time steps of the model represent independent stimulus samples. “Bimodal” stimuli were generated by drawing at each time step from one of two Gaussian distributions of fixed width σ′ and means μ′ = μ ± α according to a Bernoulli random variable. σ′ was chosen arbitrarily. The offset α to produce a desired final variance σ² was then given by $\alpha =\sqrt{{\sigma }^2-\sigma {\prime }^2}$. In all model simulations, σ′ = 0.03.

In all experiments, each trial used a new instantiation of the random stimulus.

Analysis

We measured adaptation from the RGC synaptic input or spiking responses to a set of random stimuli with periodic switches in the parameters of the distribution from which those stimuli were drawn. For a typical ∼1 hr recording, a cell's synaptic inputs provided a clearer measure of the dynamics of adaptation than its spike outputs, likely due to the relative sparseness of the spike response. ON RGCs had very little inhibitory input (Murphy and Rieke, 2006), while OFF and ON-OFF RGCs had noticeably larger inhibitory input than excitatory input. Therefore, we recorded excitatory inputs to ON RGCs and inhibitory inputs to OFF and ON-OFF RGCs.

The time course of adaptation following a change in stimulus ensemble (either low to high contrast or low to high luminance) was estimated from an exponential fit to the synaptic input current averaged across all trials. In a small number of cells, the input currents were not rectified (they showed equal deviations above and below their mean) and the mean current remained near zero during contrast switching experiments. In these cells we used the root mean square (r.m.s.) current to characterize adaptation. The mean or r.m.s. current was fit with the function $I(t)=A{e}^{\stackrel{-(t-\Delta )}{}/\underset{\tau }{}}+c$, where Δ denotes the response delay of the cell and τ gives the exponential time constant. We estimated Δ as the time to maximal response in a window ∼300 to 500 ms following the change in stimulus ensemble. The remaining parameters (A,τ,c) were fit using nonlinear least squares fitting (Matlab's nlinfit (Mathworks; Natick, MA) for Figure 1, SciPy's ODRPACK (Jones et al., 2001) for remaining figures).

The fitting procedure was initialized with parameter values estimated from the data: A was initialized to the normalized max current, τ to one quarter the switching period, and c to the mean current in the final 100ms of the high contrast or luminance segment. Proposed fitted parameters were confirmed by 10 random restarts, varying the parameters between 0 and twice their fitted value. We excluded cells from further analysis if the mean parameter estimates of successful fits from the random restarts differed from their initial estimates by more than 10%.

Modeling

To capture the dynamics of adaptation, we developed a simplified recursive Bayesian estimation model, closely related to the model of DeWeese and Zador (1998). The model chooses a gain at each discrete time step t based on estimates of the stimulus ensemble parameters, ${\stackrel{\rightharpoonup }{\phi }}_t$. In the experiments and simulations herein, only a single ensemble parameter is varied. Thus we consider ${\stackrel{\rightharpoonup }{\phi }}_t$ as a scalar, φ_t (here, either mean or standard deviation). Since the adapting mechanism has access only to the stimulus history, one ideal estimate of φ_t is the maximum value of the a posteriori distribution $P({\phi }_t|{\stackrel{\rightharpoonup }{s}}_{j\le t})$ —i.e. the probability of φ_t given the stimulus history ${\stackrel{\rightharpoonup }{s}}_{j\le t}$. The a posteriori distribution is computed from independent stimulus samples using Bayes' rule:

$$\begin{array}{c}P({\phi }_t|{\stackrel{\rightharpoonup }{s}}_{j\le t})=\frac{1}{\Omega }P({\stackrel{\rightharpoonup }{s}}_t|{\phi }_t,{\stackrel{\rightharpoonup }{s}}_{j<t})P({\phi }_t|{\stackrel{\rightharpoonup }{s}}_{j<t})\hfill \\ \propto P({\stackrel{\rightharpoonup }{s}}_t|{\phi }_t,{\stackrel{\rightharpoonup }{s}}_{j<t})P({\phi }_t|{\stackrel{\rightharpoonup }{s}}_{j<t})\hfill \\ =P({\stackrel{\rightharpoonup }{s}}_t|{\phi }_t)P({\phi }_t|{\stackrel{\rightharpoonup }{s}}_{j<t})\hfill \\ =P({\stackrel{\rightharpoonup }{s}}_t|{\phi }_t)\int d{\phi }_{t-1}P({\phi }_t|{\phi }_{t-1})P({\phi }_{t-1}|{\stackrel{\rightharpoonup }{s}}_{j<t}).\hfill \end{array}$$ (1)

where Ω is a normalizing constant $(P({\stackrel{\rightharpoonup }{s}}_t|{\stackrel{\rightharpoonup }{s}}_{j<t})),P({\phi }_t|{\stackrel{\rightharpoonup }{s}}_{j<t})$ is the a priori distribution and $P({\stackrel{\rightharpoonup }{s}}_t|{\phi }_t)$ is the likelihood of the observed stimulus sample (DeWeese and Zador, 1998).

This model assumes prior knowledge of the dynamics of the stimulus distribution, expressed in terms of the transition probability P(φ_t | φ_t−1). Since we wish to avoid imposing any particular dynamics, we instead simplify this model:

$$\begin{array}{c}P({\phi }_t|{\stackrel{\rightharpoonup }{s}}_{j\le t})\propto P({\stackrel{\rightharpoonup }{s}}_t|{\phi }_t,{\stackrel{\rightharpoonup }{s}}_{j<t})P({\phi }_t|{\stackrel{\rightharpoonup }{s}}_{j<t})\hfill \\ =P({\stackrel{\rightharpoonup }{s}}_t|{\phi }_t)P({\phi }_t|{\stackrel{\rightharpoonup }{s}}_{j<t})\hfill \\ \approx P({\stackrel{\rightharpoonup }{s}}_t|{\phi }_t)P({\phi }_t={\phi }_{t-1}|{\stackrel{\rightharpoonup }{s}}_{j<t})\hfill \end{array}$$ (2)

where in the last step we approximate the prior on the current parameter estimate, φ_t, with the best estimate of φ_t−1, $P({\phi }_{t-1}|{\stackrel{\rightharpoonup }{s}}_{j<t})$. This simplification is equivalent to assuming that the stimulus parameters are constant from one time step to the next—i.e., the transition probability P(Φ_t = φ_t | Φ_t−1 = φ_t−1) is zero except when φ_t = φ_t−1. Although no longer Bayes optimal, this simplified model captures the intuition that the estimator accumulates evidence for the current state of the world in its prior belief about φ.

Time units in the model could be converted to physical time by an appropriate scaling factor, τ, which describes the effective integration time of the adaptive mechanism. We assume that there is an additional scale factor, λ, relating our choice of physical stimulus units (R*/rod/s) to the arbitrarily chosen model stimulus units. The final model is then expressed as

$$P(\lambda {\phi }_u|\lambda {\stackrel{\rightharpoonup }{s}}_{j\le u})\cong P(\lambda {\stackrel{\rightharpoonup }{s}}_u|\lambda {\phi }_u)P({\phi }_u={\phi }_{u-1}|\lambda {\stackrel{\rightharpoonup }{s}}_{j<u})$$ (3)

where u = t / τ.

Fitting

In the case of Gaussian stimuli, starting with a Gaussian initial prior (mean μ_prior and standard deviation σ_prior), the expected mean and variance of the a posteriori distribution are easily calculated:

$$\begin{array}{l}M=E_{\stackrel{\rightharpoonup }{s}}[{\mu }_{\text{posterior}}]=\frac{{\mu }_{\text{stim}}{\sigma }_{\text{prior}}^2+{\mu }_{\text{prior}}{\sigma }_{\text{stim}}^2}{{\sigma }_{\text{prior}}^2+{\sigma }_{\text{stim}}^2}\hfill \\ \sum =E_{\stackrel{\rightharpoonup }{s}}[{\sigma }_{\text{posterior}}]=\sqrt{\frac{{\sigma }_{\text{prior}}^2{\sigma }_{\text{stim}}^2}{{\sigma }_{\text{prior}}^2+{\sigma }_{\text{stim}}^2}}\hfill \end{array}$$ (4)

for stimuli drawn from $\overrightarrow{S}$ with mean μ_stim and standard deviation σ_stim.

From these definitions, the expected mean (M) and standard deviation (Σ) of the posterior as a function of time in a constant stimulus ensemble can be solved for time t, using Mathematica's RSolve routine (Wolfram; Champaign, IL):

$$M_{t,{\mu }_{\text{prior}},{\sigma }_{\text{prior}}}=\frac{{\mu }_{\text{prior}}{\sigma }_{\text{prior}}^2+t{\mu }_{\text{stim}}{S}^2-{\mu }_{\text{stim}}{\sigma }_{\text{prior}}^2+{\mu }_{\text{prior}}{\sigma }_{\text{stim}}^2}{t{\sigma }_{\text{prior}}^2+{\sigma }_{\text{stim}}^2}$$ (5)

and

$${\sum }_{t,{\sigma }_{\text{prior}}}=\sqrt{\frac{{\sigma }_{\text{prior}}{\sigma }_{\text{stim}}^2}{{\sigma }_{\text{stim}}^2-{\sigma }_{\text{prior}}+{\sigma }_{\text{prior}}t}.}$$ (6)

Given these expressions, we calculated the trajectory of adaptation following an increase in luminance by calculating the posterior mean and standard deviation following one half-period of low luminance stimulation and using these as the starting prior mean and standard deviation for the high luminance condition. The results were largely insensitive to the initial prior mean and standard deviation so long as the initial standard deviation was significantly greater than the stimulus standard deviation.

The analytical solution above contains discontinuities in the gain trajectory following a change in luminance for some combinations of the model parameters. To fit the model to observed data, we therefore chose to fit the slope of the model trajectory at 500ms to the slope of the exponential fit to the observed data 500ms following the step. We expect the integration time of retinal mechanisms to decrease with increasing light level. Thus we allowed the integration time of the adapting mechanism to decrease by a factor of 2 between 40 and 400 R*/rod/s. We fit the free parameters (λ, ${\sigma }_{\text{stim}}^{\text{effective}}$, and τ) of the analytically solved model to luminance steps from 4-400 R*/rod/s (Figure 5, Supplemental Figure S4) using the FindFit constrained optimization method in Mathematica (Wolfram; Champaign, IL). The parameter constraints were $0.06\le \frac{{\sigma }_{\rho \in \{4,40,400\}}}{\lambda }\le 0.2\Lambda \lambda >0\Lambda \tau >0$ where σ_ρ is the effective noise for luminance steps starting at ρ R*/rod/s. Estimated values for λ and τ were unchanged when we used data from a single luminance value (e.g. only data for 40 R*/rod/s) to fit the model parameters.

Simulations

In all model simulations, the prior P(φ₀) was initialized to the uniform distribution over the domain of φ and the stimulus likelihood, $P({\stackrel{\rightharpoonup }{s}}_t|{\phi }_t)$, was given by a Gaussian distribution with fixed mean (in simulations of contrast adaptation) or fixed variance (in simulations of luminance adaptation). Noise and integration time parameters for all simulations were taken from the fitted parameters (Figure 5; see above). Because we do not assume the adapting mechanism to be the same for luminance and contrast adaptation, simulations of contrast adaptation should be regarded as qualitative rather than quantitative.

The effective noise at the site of the adapting mechanism(s) is determined by a combination of stimulus variance, filtering in retinal circuitry and internal noise sources. The noise parameter fit by the procedure described above is a measure of the standard deviation of independent samples presented at the site of adaptation. Therefore, to make quantitative predictions of experimental results (e.g. Figure 7), we had to estimate the contributions of each of these sources of variability. Filtering of the stimulus during generation produced independent samples at approximately 100Hz. We assume that photoreceptor integration time is of order 100ms, giving an approximate 3-fold reduction in stimulus variance post-photoreceptor. We further assume that the adapting mechanism summed approximately 8 such independent post-photoreceptor samples during its ∼800ms estimated integration time. The effective stimulus noise is therefore approximately $\frac{8}{3}{\sigma }_{\text{stim}}$. We assume that internal noise is independent and additive.