Testing the influenza–tuberculosis selective mortality hypothesis with Union Army data

Abstract

Using Cox regression, this paper shows a weak association between having tuberculosis and dying from influenza among Union Army veterans in late nineteenth-century America. It has been suggested elsewhere [Noymer, A. and M. Garenne (2000). The 1918 influenza epidemic’s effects on sex differentials in mortality in the United States. Population and Development Review 26(3), 565–581.] that the 1918 influenza pandemic accelerated the decline of tuberculosis, by killing many people with tuberculosis. The question remains whether individuals with tuberculosis were at greater risk of influenza death, or if the 1918/post-1918 phenomenon arose from the sheer number of deaths in the influenza pandemic. The present findings, from microdata, cautiously point toward an explanation of Noymer and Garenne’s selection effect in terms of age-overlap of the 1918 pandemic mortality and tuberculosis morbidity, a phenomenon I term “passive selection”. Another way to think of this is selection at the cohort, as opposed to individual, level.

Introduction

This paper uses data on Union Army veterans from the US Civil War to test whether, in the late nineteenth century and early twentieth century, having tuberculosis was a risk factor for death due to influenza. The question of influenza–tuberculosis selective mortality has been raised in the context of the 1918 influenza pandemic (Noymer & Garenne, 2000). This paper examines data from the period before the pandemic. However, the question of selective mortality for these two diseases need not have applied only during the pandemic. The present findings point to selective mortality in 1918 having been either a cohort (vs. individual) phenomenon, or alternately that the selection was peculiar to 1918.

Background

The concepts of early life influences on mortality and selective mortality intertwine. Early life influences include any exposure to, or influence on, an individual that affects later mortality outcomes. These exposures and influences may be biological or social or both. Early influences work also when the unit of analysis is the cohort, not the individual. It makes no sense to talk about the long-term impact of fatal outcomes at the level of the individual. However, a cohort experiencing an adverse mortality environment or event early in its lifetime may, through selective mortality, be more robust (less frail) after the event than before, with salutary effects on mortality. This is termed “cohort inversion” (Hobcraft, Menken, & Preston, 1982). The pioneers of the mathematical demography approach to selective mortality were Keyfitz and Littman (1979) and, especially, Vaupel, Manton, and Stallard (1979). The broader early influences literature is much older, with well-developed versions going back to Derrick (1927) and Kermack, McKendrick, and Mckinlay (1934) if not before.

Cohort vs. individual perspectives can have countervailing directions. Non-fatal adverse impacts on the individual generally are supposed to have adverse delayed effects on longevity, whereas cohort inversion implies positive delayed effects for cohorts. By pure aggregation, the direction of the effect of early life influences may also run in the same way for cohorts as for individuals (adverse leading to adverse, as long as we are dealing with non-fatal outcomes). Excepted from this is hormesis–viz., where mild infections impart lifelong immunity from reinfection (e.g. chickenpox, measles). However, post-infection lifelong immunity, as with measles, does not mean that the infection in question does not also have lasting adverse effects. For example, blindness can be a sequela of measles, especially in vitamin A deficient children.

Selective mortality in the 1918 influenza pandemic

In 2000, Noymer and Garenne proposed that there was selective mortality in the 1918 influenza pandemic (Noymer & Garenne, 2000). This hypothesis — that the 1918 influenza pandemic played a role in the decline of tuberculosis (TB) – is potentially relevant to mortality studies generally, due to the importance of TB as a cause of death, and due to the magnitude of the 1918 pandemic.

In the context of early life influences on later mortality, those findings implied that exposure to one disease, in this case tuberculosis, can enhance mortality risks to another disease, in this case influenza. Being a chronic disease, tuberculosis precedes influenza (an acute condition), by years in most cases, and is therefore an earlier life influence. This is the aggregation aspect: an adverse early impact (contracting TB) makes for adverse later effects (dying in the influenza pandemic). The cohort inversion aspect is that tuberculosis deaths plummeted in later years, because the normal “slow burn” of TB deaths was consumed all-at-once during the explosive influenza pandemic, and from the subsequent reduction in tuberculosis transmission.

The 1918 influenza pandemic

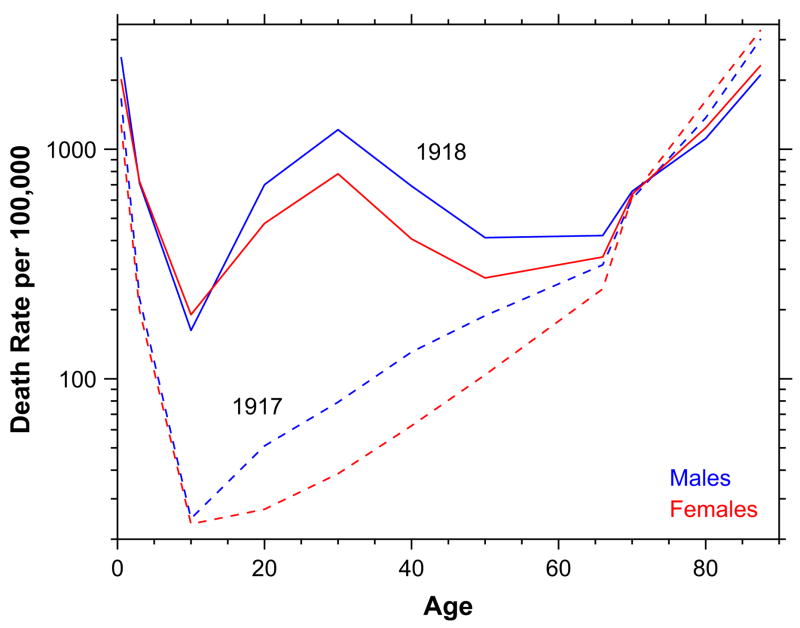
The 1918 influenza pandemic was the most deadly disease outbreak in the twentieth century, killing an estimated 40–100 million (Johnson & Mueller, 2002). The age–mortality profile of influenza deaths is typically U-shaped. Children and the elderly are the most susceptible to influenza mortality. Adults, at the base of the U, have the lowest mortality. Atypically, in 1918 the age–mortality profile was W-shaped. The typical U (1917) and atypical W (1918) age–mortality profiles for influenza and pneumonia (combined) are shown in Fig. 1.

Fig. 1.

Age mortality profile, influenza and pneumonia, 1917 and 1918, United States death registration area. Data from U.S. Department of Health, Education, and Welfare (1956).

Males had higher influenza and pneumonia death rates in 1918, particularly at the middle mode of the W. The male excess mortality remains a mystery, but does not appear to be an artifact of mobilization for the First World War, as it occurred in nonbelligerent countries. The influenza–tuberculosis selection effect could play a role in the maleness of the influenza mortality, as TB was more a male disease at the ages in question. The leading explanation for the W itself is that flu victims experienced an unchecked immune response that flooded their lungs with fluid. This is consistent with clinical histories from 1918, where doctors and nurses reported standing by helplessly while victims became cyanotic and died from lack of oxygen (Lichty, 1919). Adults, not the young or the elderly, have the strongest immune systems, and would have experienced this pulmonary complication most severely. This adult peak superimposed on the usual U-shape putatively accounts for the W. The 1918 virus itself was very unusual (see e.g. Kash et al., 2004; Kobasa et al., 2004; Stevens et al., 2006; Taubenberger et al., 2005; Tumpey et al., 2004, 2005).

The selection hypothesis

Selection theories lend themselves to formalization (see e.g. Hougaard, 1984; Manton & Stallard, 1984; Vaupel & Yashin, 1985; Vaupel et al., 1979). However, the tuberculosis/influenza selective mortality theory (hereinafter “the selection hypothesis”) may be neatly summarized as: who died, who survived, and did this change the ante- vs. post-epidemic population composition? The influenza–tuberculosis selection hypothesis for 1918 holds that those who died in the middle of the W in 1918 influenza were unhealthy to begin with. Not necessarily all of them, of course, but enough so that the remaining population, in 1919 and beyond, was healthier, on average, compared to the pre-pandemic state. “Unhealthy” is vague, and disproportionally tuberculous is more precise. According to the selection hypothesis, many 1918 influenza deaths were among people with tuberculosis, and the post-epidemic population was therefore healthier. Using data from Chicago, 1850–1925, Ferrie and Troesken (2008, p. 12) make a similar observation: “influenza and scarlet fever appear to have been killing off the weakest and most vulnerable parts of the population so that high death rates from these diseases actually reduced death rates from other causes”.

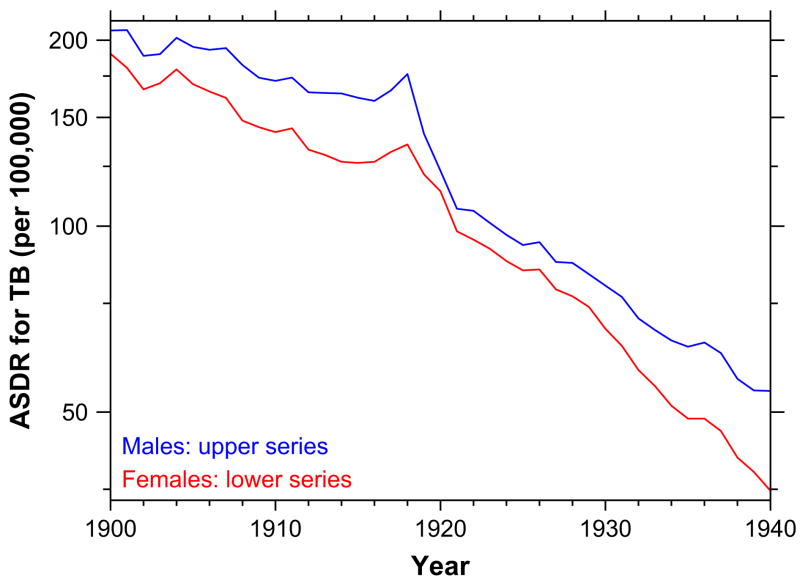
The hypothesis is supported by a variety of data, including age-specific changes tuberculosis death rates in 1919 and thereafter, as shown in Fig. 2. Of course, tuberculosis death rates were falling throughout the early twentieth century — but they fell most steeply after 1918. A thumbnail sketch of the age-specific aspects of the problem is that tuberculosis was, in this time period, typically a disease of adults rather than of children or the elderly, just like the 1918 influenza pandemic mortality, but unlike the usual seasonal influenza. And the lungs are the shared site of pathology of both diseases. Noymer and Garenne (2000) provide the particulars.

Fig. 2.

Age-standardized death rate, tuberculosis, 1900–1940, United States death registration area. Source: U.S. Department of Health, Education, and Welfare (1956).

It is worth noting that the selection hypothesis does not posit that the unusual virulence of the 1918 pandemic is due to the confluence of tuberculosis and influenza. After all, both high tuberculosis prevalence and winter flu epidemics were in effect throughout the early twentieth century (and before), and only the 1918 pandemic had the unusual W-shaped age–mortality profile. Tuberculosis was not a cause of the unusual virulence of the 1918 influenza. Rather, according to the selection hypothesis, changes in tuberculosis epidemiology were a consequence of the influenza pandemic.

Relevance to early life influences

Selection is relevant to the cohort approach to mortality, longevity and long-term health. According to frailty models, mortality selection of the frail increases within-cohort robustness over time. Theoretically, older (less frail) cohorts do better than would be expected were the early selection of the frail not taken into account. There is a black-box aspect to this state of affairs, because while death rates are observed, there are two free parameters in the theory — the baseline mortality rate and the frailty distribution, or the distribution of individual deviations from the baseline. These two free parameters combine to produce one observed phenomenon: death rates. The observed death rates identify a unique frailty distribution assuming a baseline mortality rate, or the observed death rates identify a unique baseline mortality rate assuming a frailty distribution, but one cannot simultaneously identify both the frailty distribution and the baseline mortality from observational data. Put another way, the observed death rates determine the baseline mortality against a counterfactual frailty distribution, or vice versa.

Recognizing this, research has moved in the direction of trying to open the black-box, through genetics (as in Weiss, 1990, or Yashin & Iachine, 1997), kinship analysis (e.g. Kerber, O’Brien, Smith, & Cawthon, 2001; Mineau, Smith, & Bean, 2002; Smith, Mineau, & Bean, 2002), analysis of biological (viz., laboratory) populations (cf. for example, Carey, 2003), and the study of early life influences (such as: Almond & Mazumder, 2005; Bengtsson & Lindström, 2000; Costa, 2000). By bringing in more information a priori, the challenge of understanding two phenomena (baseline mortality and frailty) from one (observed death rates) becomes easier.

The selection hypothesis (Noymer & Garenne, 2000) used the 1918 influenza pandemic as a natural experiment to show how exposure to a disease at a certain point in time can affect mortality from another cause at a later point in time. This is another way to open the black-box, and is, in effect, a way of looking at early life conditions, albeit loosening the restriction that the early conditions take place in utero or during development. The selection hypothesis takes a rather cohort-oriented level of analysis, as opposed to individual-oriented, though the selection phenomenon ostensibly operates down to the level of the individual.

Elaboration with microdata

Aggregate vs. microdata

The data used to establish and substantiate the selection hypothesis were mostly death rates for age groups, by sex (Noymer and Garenne, 2000). The changes in the aggregate mortality patterns are large, and the sex- and age-specific contours of the data are congruent with predictions of the selection hypothesis. Ultimately, however, it is desirable to analyze individual-level data.

Individual-level historical data sets rich in detail on mortality as well as pre-death illnesses are difficult to come by. However, one example is the Union Army data set, collected by the Center for Population Economics at the University of Chicago. Although most of the Union Army veterans died before 1918, these data provide a unique opportunity to investigate connections between tuberculosis and influenza in historical context. If the selection hypothesis in its strongest interpretation (cf. section “Active” and “passive” selection below) is correct, it should apply even in years other than 1918.

This paper tests and elaborates upon the selection hypothesis in two ways. First, microdata are analyzed whereas the original work dealt predominantly with ecological data. Second, the period analyzed encompasses all of the late nineteenth and early twentieth century morbidity and mortality experiences of the Union Army cohorts, illuminating whether or not the selection hypothesis held in pre-pandemic years.

“Active” and “passive” selection

The 1918 pandemic, due to its unusual severity, has certain advantages for use as a natural experiment. Nonetheless, looking at tuberculosis illness and influenza mortality in years before the pandemic can help define the selective effect more precisely. Two versions of the selection hypothesis can account for the observations of Noymer and Garenne (2000). The stronger form is individual-level enhancement of influenza mortality among the tuberculous (compared to the non-tuberculous). Call this “active selection”. If active selection is operating, having tuberculosis should predispose one to death from influenza in years other than the pandemic, unless active selection required specifically the 1918 influenza virus strain.

The weaker version of the selection effect is that the changes in tuberculosis mortality seen after 1918 are a result of what might be called “age–mortality overlap” between the influenza pandemic and the tuberculous sub-population. That is to say, the unusual 1918 influenza killed at non-elderly adult ages (i.e. in the W-shape, section Background), and tuberculosis was prevalent at those same ages, and simply by this fact, many of the tuberculous died. Call this “passive selection”. Another way to describe passive selection is that tuberculosis is a neutral factor with respect to death from influenza. Under this scenario, the effects seen in Noymer and Garenne (2000) stem from the sheer numbers of dead from influenza in 1918, not from any enhanced mortality at the individual level. Due to the age profile of the 1918 mortality, a large number of the tuberculous must have been among the dead. This occurs despite the fact that — assuming passive selection — tuberculosis is not a risk factor for influenza death. It is also natural to think of this as a cohort- vs. individual-level phenomenon (passive and active selection, respectively).

Microdata analysis can help adjudicate between active and passive selection. Passive selection predicts no effect in mircodata; active selection predicts tuberculosis as a risk factor for death to influenza, including in non-pandemic years. Suppose hypothetically that active selection (not specific to the 1918 viral strain) is the correct explanation for the effects seen in Noymer and Garenne (2000). Why then was the connection between tuberculosis morbidity and influenza mortality in the nineteenth and early twentieth centuries overlooked by contemporary observers? The 1918 pandemic was so quantitatively huge, with over half a million deaths in the United States (Johnson and Mueller, 2002). If tuberculosis has an enhancing effect on influenza mortality, the 1918 pandemic is clearly the most propitious place to look; the signal-to-noise ratio may be small in other years. Bozzoli, Deaton, and Quintana-Domeque (2007) examine scarring vs. selection and make the related point that these two countervailing forces may behave differently in different mortality environments. They write: “at very high levels of mortality, selection may dominate scarring, at which point further increases in mortality will result in increased adult heights in the surviving population.” Their outcome of interest is stature, but the point translates very well to the topics of this paper. In the 1918 flu pandemic — a very high mortality level, indeed — selection predominates, and we see a healthier (not taller) population afterward. In other periods, we may not see the selection, as scarring predominates.

Data

Data source

The data set is the “Union Army” data, collected at the University of Chicago’s Center for Population Economics under the direction of Robert W. Fogel. The data are described in detail on the Internet (Chicago Center for Population Economics, n.d.) and by Fogel and Wimmer (1992) and Fogel (1993, 2004a). The sample “consists of 35,747 white males mustered into the Union Army during the Civil War, for whom military, socioeconomic, and medical information from several sources throughout their lifetimes has been collected” (Chicago Center for Population Economics, n.d.). The sample frame is a cluster sample of 304 companies, about 100 men per company, plus replacements for deaths and discharges. The data are representative of the military age white male population of the Union states in the early 1860s. Representativeness was assessed by comparisons with, and record linkages to, the 1860 census (Costa, 1998; Fogel, 1993). Within each sampled company, every enlisted man (i.e. non-officer) is included; enlisted men promoted to brevet officer or officer are included, but men who began their military service as commissioned officers are not.

The Union Army data set includes records on health conditions of soldiers during the war and, through pension files, after the war. A number of scholars have exploited this aspect of the data to study the health of the Union Army veterans; Lee (1997, 2003, chap. 3) gives overviews. Lee (2005) looks at how wartime health affected later economic outcomes. Costa (1993, 2003) exploits the longitudinal nature of the data set to compare individual-level characteristics at enlistment with later-life mortality outcomes; she finds that early life infections had an adverse impact on later-life outcomes. Wilson (2003, chap. 6) examines respiratory disease in particular, and in addition to providing a thick quantitative description of the prevalence of respiratory conditions in the Union Army cohort, he finds a strong correlation between wartime respiratory illness and later-life respiratory illness. Like the present study, Birchenall (2006) uses Union Army data to look at tuberculosis, though his interest is illness during the war itself. Birchenall finds, inter alia, that stature predicts the risk of tuberculosis infection in the expected direction (i.e. taller individuals had less infection), with childhood nutrition being the putative causal link.

The Union Army data set provides an unequaled opportunity for historical demographic research. To investigate the selection hypothesis, using data from the late nineteenth century is second-best only to microdata from 1918, which, as noted, are unavailable. In the nineteenth century, tuberculosis prevalence and mortality were both high — 1 in 5 deaths in the United States in the nineteenth century were due to tuberculosis (Preston, Keyfitz, & Schoen, 1972). And influenza was ever-present. Additionally, as noted above, using pre-1918 data will allow us to test whether the selection hypothesis only works in the sui generis context of the 1918 influenza pandemic.

Data description

Wartime survivors are followed through the nineteenth and early twentieth century, until death in most cases. Pension information, visits to the doctor’s office (for those awarded medical pensions), and eventual cause of death are recorded for most records (Fogel, 1993). This study used 17,679 of the 35,570 records. Wartime deaths (N = 4980) were excluded due to the special circumstances of war being unusual. Moreover, to be included in the study, veterans had to have a known or imputable date of birth, and a known date of death. Date of birth, when missing per se, was imputed from stated age at pension application, the dates of which were recorded. Despite the record loss due to missing biographical dates, the usable data contain thousands of nineteenth-century records — and therefore well over 100,000 person-years of exposure — and is a unique resource in American demographic data.

Some descriptive statistics are presented in Table 1. These descriptive statistics are for the sample used in the regressions. The median body mass index (BMI) was 23.06 kg/m². It is not surprising, given the nineteenth-century setting, that even the 75th percentile of BMI was below today’s overweight threshold (25 kg/m²). The median number of tuberculosis cases per company was 1; 35% of companies had no recorded tuberculosis cases, while 37% of companies recorded two or more cases and 20% had three or more. One company from Ohio recorded 8 cases. Note that these are cases of active tuberculosis. The concept of latent tuberculosis did not even exist during the US Civil War, as the tuberculin skin test for latent infection came into use in the 1890s (Starr, 1982, p. 191). The key veterans in the regression sample who died of flu, but had tuberculosis morbidity, died on average at age 53.6, were 1.74 meters tall on average, had an average BMI of 20.4 and all of them possessed a pension record. The younger than average age of death, and lower than average BMI are not surprising, and nothing else about their descriptive statistics is especially notable.

Table 1.

Descriptive statistics. “p25” (“p75”) is the 25th (75th) percentile. “I” for indicator (dummy) variable. Indicator variables are naturally coded (0/1) so mean is interpretable as a proportion having the characteristic (etc.). Had TB indicates lifetime ever having tuberculosis, and is described in much greater detail in the text. Height is measured in meters. Short is 1.68 m (5 feet 6 inches) or shorter. Tall is 1.80 m (5 feel 11 inches) or taller. BMI is body mass index: (weight [kg]) ÷ (height [m], squared). TB in company is the number of recorded wartime tuberculosis cases in each company of approx. 100 soldiers; there are 304 companies. See also discussion in text.

Variable	N	Mean	SD	p25	Median	p75
Age at death	17,679	71.22	12.71	64.22	73.08	80.24
Year of birth	17,679	1838	7.724	1834	1840	1844
Age at enlistment	11,442	23.55	6.497	18.76	21.56	26.79
Had TB [I]	17,679	0.0653
Height (m)	17,653	1.72	0.0684	1.676	1.727	1.765
Short [I]	17,653	0.3097
Tall [I]	17,653	0.1302
BMI (kg/m2)	15,745	23.06	3.335	20.83	22.48	24.66
TB in company	17,679	1.474	1.557	0	1	2

Records lacking birth date, or pension information that permits inference of birth date, were dropped. There is a small (0.67 cm) difference in height between records in the regression sample and those omitted, with those in the regression sample being slightly taller. The magnitude of the average difference in height, two-thirds of a centimeter, is not very large, however. The mean age of death of the regression sample (71.22) does show that, conditional on surviving to military age, and then surviving the war, and having the necessary information to be included in the data set, the veterans could live quite long by contemporary standards. Those not in the regression sample, of course, have no age of death with which to compare. Some sample selectivity cannot be ruled out, however, given the long average lifetime of those in the sample.

The Arrears Act of 1879 expanded pension benefits, and the Disability Pension Act of 1890 codified pension benefits for all veterans with disabilities, not just those with medical problems that originated in the war (Kanjanapipatkul, 2003, chap. 9; Song, 2000). The longer a veteran lived, the more likely that he would have usable information. For example, by putting occupation on a pension application, a veteran would generate information on social status, but those who lived longer (ostensibly, with higher social status) are also more likely to have seen the liberalization of the pension law. Thus, there is a potential bias between social status and possessing usable information. There is, even more likely, a correlation between early mortality (whether correlated with socioeconomic status or not) and having usable information. These biases go toward the null hypothesis and thus do not tilt the data in favor of finding an effect. Early deaths are less likely to be on the pension rolls and hence in the data set. But it is just these deaths, when they are due to TB (an adult, non-elderly disease) causing risk for influenza, that would help reject the null.

Occupational information was known for 11,186 records in the regression sample (63%); for those records that contained occupational information, it was recoded into a simple three-tiered system. The top tier included the (original) occupational codes “farmer/agriculturalist” and “professionals and proprietors I/II”. The middle tier included “artisans” and “service, semi-skilled, and operative”. The low tier included “manual labor”, “unproductive”, and “farm/agricultural labor”. Highest-attained occupation was used; in the data set, 3584 (29%) were able to climb this three-tiered occupational category during the life course (of which 1309 men climbed one place in the ladder, and 2275 climbed two places). In the regression sample, 3954 men were in the top tier, or 35% of those with known occupation; 2202 (20%) were in the middle tier; and 5030 (45%) were in the low tier. These percentages are similar to the sample where birth date is not known: 34%, 24%, 42%, respectively. This, on the other hand, is not suggestive that the regression sample is selected toward higher social status.

In the regression sample, 1119 men are flagged specifically as “illiterate”, or were otherwise classified as not being able to read or write or both (or 7.6% of 14,774 veterans in the regression sample for whom literacy information is known using all possible sources of this information, such as record linkages to various censuses). In the data set as a whole, surprisingly, slightly less (6.7%) are flagged as illiterate; one would expect that the whole sample (i.e. including men with unknown birthdays) would have a higher illiteracy rate. This again indicates that the effects of sample selection may not be too large. Note that this applies only to the veterans for whom literacy information is known, one way or another — 37% of the 35,570 are missing any information on literacy. It is probably a safe bet that a fair number of this 37% were illiterate.

Tuberculosis and influenza classification

Tuberculosis morbidity is the key independent variable in the analysis, and it is worth explaining in more detail how it was measured. Tuberculosis is a textbook example of a chronic infectious disease, particularly in the pre-chemotherapeutic era. Symptomatic infection (viz., active pulmonary tuberculosis) could last years, until recovery or death, and even recovery could (and frequently did) lead to recrudescence.

The tuberculosis status of an individual is based on wartime military medical records and on post-war pension records. Given the nineteenth-century setting, I assume that no veteran who has tuberculosis is ever fully cured. Thus, the independent variable for tuberculosis in the regressions is an indicator variable representing ever having had the disease. The veterans’ wartime and pension medical records were searched (using the AWK computer language, Aho, Kernighan, & Weinberger, 1988) for any mention of tuberculosis disease.

Consider the types of possible misclassification. Of particular interest are veterans who had tuberculosis but were not recorded as such. This could happen if a sick veteran did not seek medical care, or if records were lost. It is certainly possible, indeed almost certain, that some veterans suffered from tuberculosis but no records of this survived. Conditional on having medical records, misdiagnosis is unlikely, because doctors in this time period were well acquainted with the signs and symptoms of pulmonary tuberculosis (the most prevalent form by far) and it is unlikely they would have recorded tuberculosis in the medical record of, e.g., an asthmatic but non-tuberculous veteran or failed to notice all but the most subtle cases. Tuberculosis includes a host of non-pulmonary symptoms, including weight loss, that would have assisted diagnosis. As already noted, active pulmonary tuberculosis is the relevant measure here — latency was not part of contemporary medical knowledge.

In terms of quality of diagnosis, conditional on a veteran visiting a doctor, false positives would likely have been rare. As noted, the signs and symptoms of tuberculosis were well known, and positive diagnosis would not have been made in the absence of these. Moreover, the medical records show that the Army and pension board physicians were on guard for malingerers. The same cannot be said for false negatives, as tuberculosis carried enormous stigma in the nineteenth century, and for this reason, it is plausible that, after the war, veterans would have tried to avoid diagnosis, perhaps by staying away from the doctor altogether. During the war, on the other hand, medical discharge for tuberculosis was possible.

Table 2 is an illustration of how tuberculosis was coded. As noted in the marginal total in the lower right hand corner, Table 2 is based on the whole Union Army data set. The regression sample is a subset of this table and is therefore similarly cross-classified. The columns of Table 2 represent what is observed in the data, and the rows represent how the data were coded. The left three columns tally veterans who had observed tuberculosis morbidity; the marginal total as noted in the bottom left is 923, or 2.6% of the whole sample. Of these 923, there was a recorded cause of death for 506 (left second-to-bottom marginal total). Reading the left three cells of the first row of the table: among the observed tuberculous for whom there is a cause of death, 165, or 32%, died of tuberculosis; 341 died of something else; and 417 of the observed tuberculous lack a recorded cause of death. Any record with observed tuberculosis was classified as such, so the left three cells of the second row of the table are all structural zeros (indicated as ⊘).

Table 2.

Tuberculosis morbidity and mortality classification. See text for discussion.

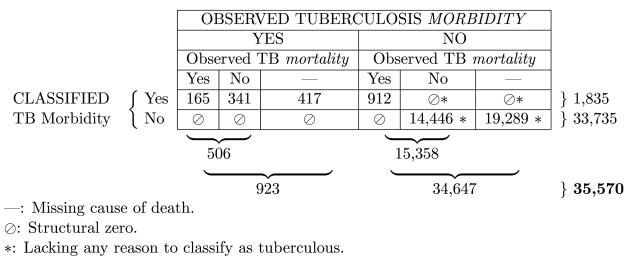
Moving on to the right three columns of Table 2, these 34,647 records (marginal total, bottom line, right) have no observed tuberculosis morbidity based on medical records. Ostensibly, then, these are non-tuberculous. However, in these six cells, it is necessary to classify with care, as it is possible to determine the tuberculous status of some. Of the 34,647 veterans with no observed tuberculosis morbidity, 19,289 are also missing cause of death (lower right cell). Cells marked with an asterisk (*) are designated as “lacking any reason to classify as tuberculous”, and are classified as not tuberculous. The 19,289 in the lower right cell are a good example of the use of the asterisk: presumably some of these men had tuberculosis, but it does not appear in their medical records (or they had no medical records whatsoever), and they are also missing cause of death, so there is not a lot to go by.

For 14,446 men (lower row, second cell from the right), there is a cause of death, but it is not tuberculosis (both proximate and contributory causes were checked); again, no evidence of tuberculous. However, 912 men died of tuberculosis who had no medical record of the disease while they were alive. All these men were classified as tuberculous because they must have had the disease if they died of it. The cell below 912 is thus a structural zero. The remaining two cells are structural zeros by default (⊘, *).

As Riley, (1999, p. 103) notes, “sickness creates fewer records than does death”. Overall, 912 tuberculous veterans are coded as such based on their death record alone; this is nearly half the total classified as tuberculous. Of these 912, some 27% (246) had known birth dates, while in the overall sample 36% have known birth dates. As one would expect, this indicates that when the only tuberculosis information is the death certificate information, the sample is skewed somewhat toward those with little information in general.

These 912 men had tuberculosis while they were alive and for whatever reason no record of it survived except the cause recorded on the death certificate. There is no doubt that if the proportion of such cases were smaller, it would instill greater confidence in the data. Specifically, if one only had information from the left three columns of Table 2, one would like to assume that the hypothetical total in that case (923) was a good estimate of the prevalence of tuberculosis. In fact it would be too low by half. However, not all the missed diagnoses should be attributed to poor data quality, per se. The pension program was not a mandatory medical-inspection program. Some veterans were not examined by a doctor or went to a private doctor outside the pension program. Given that their death certificate lists tuberculosis, it seems wasteful not to use this information.

Death due to influenza — the dependent variable — was coded using a similar procedure, in terms of searching the records, except only causes of death were searched. “Influenza” or “pneumonia” were the search terms.

Analysis

The analysis is a continuous time event history analysis, assessing tuberculosis morbidity as a risk factor for death due to influenza, restricted to adult (age 65 and under) deaths. The elderly are excluded. As noted previously, the reason for this is that, in the original setting of the 1918 pandemic, the influenza–tuberculosis selection hypothesis operated at the level of adult mortality. Thus there are no deaths from 1918; the US Civil War ended in 1865, making the Union Army veterans too old, by 1918, to be below age 65. Nonetheless, I wish to look at what happens at pre-elderly ages, as in the pandemic.

In the models, tuberculosis is not a time-varying covariate. I know if a veteran ever had tuberculosis, or if, as far as I can tell, he never had it. In reality, tuberculosis infection is time-varying — people are not born with pulmonary tuberculosis. But tuberculosis status was not treated as time-varying covariate because, foremost among other reasons, the date of recorded diagnosis is not a reliable estimate of date of infection.

The Cox models being estimated take the following form:

$$h(t\mid \mathbf{x})=h_0(t)exp({\mathit{\beta }}^{\prime }\mathbf{x}).$$ (1)

In Eq. (1), h(t) represents the hazard at time t; h₀(·) is a baseline hazard; β is a vector of coefficients to be estimated; and x is a vector of covariates. Kalbfleisch and Prentice (2002) discuss the details of Cox regression. Models were estimated using STATA software, version 10.1 (StataCorp LP, College Station, Texas). The regression results are in Tables 4 and 5, presented as hazard ratios (exponentiated coefficients).

Table 4.

Cox regression results, continued. See discussion in text.

	Hazard ratio of influenza death
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
TB morbidity	1.197	1.201	1.207	1.165	0.967	1.324	0.957	1.152
	(0.34)	(0.34)	(0.34)	(0.33)	(0.36)	(0.37)	(0.48)	(0.35)
	[0.53]	[0.52]	[0.51]	[0.59]	[0.93]	[0.32]	[0.93]	[0.64]
Height quintile		0.986	1.146	1.149	1.061	1.259	1.095	1.279
		(0.040)	(0.094)	(0.095)	(0.10)	(0.11)	(0.13)	(0.12)
		[0.73]	[0.097]	[0.092]	[0.54]	[0.011]	[0.44]	[0.0073]
Short			1.541	1.556	1.337	2.203	1.640	2.045
			(0.38)	(0.39)	(0.40)	(0.62)	(0.56)	(0.57)
			[0.080]	[0.075]	[0.33]	[0.0054]	[0.15]	[0.011]
Tall			0.673	0.667	0.801	0.597	0.821	0.573
			(0.16)	(0.16)	(0.22)	(0.15)	(0.31)	(0.15)
			[0.093]	[0.085]	[0.42]	[0.042]	[0.60]	[0.030]
TB in company				1.098	1.119	1.115	1.118
				(0.049)	(0.059)	(0.051)	(0.077)
				[0.037]	[0.032]	[0.018]	[0.11]
Illiterate					0.392
					(0.17)
					[0.032]
BMI						0.958		0.960
						(0.023)		(0.023)
						[0.067]		[0.091]
Company dummies	No	No	No	No	No	No	No	Yes
Occupation dummies	No	No	No	No	No	No	Yes	No
LL	−2301	−2301	−2298	−2295	−1434	−1851	−824.6	−1671
N	17,679	17,679	17,653	17,653	14,753	15,745	11,173	15,745
N fail	239	239	239	239	152	195	90	195
Fail time	62.22	62.22	62.22	62.22	62.99	62.96	63.61	62.96

Robust standard errors in parentheses.

p-Values in square brackets.

Table 5.

Cox regression results, continued. Heart disease regressions (see text).

	hazard ratio of heart disease death
	(1a)	(6a)	(8a)
TB morbidity	0.708	0.789	0.801
	(0.17)	(0.19)	(0.20)
	[0.15]	[0.33]	[0.38]
Height quintile		0.999	1.011
		(0.058)	(0.062)
		[0.99]	[0.86]
Short		0.952	0.931
		(0.16)	(0.17)
		[0.78]	[0.69]
Tall		1.128	1.183
		(0.17)	(0.18)
		[0.42]	[0.28]
BMI		1.051	1.050
		(0.013)	(0.013)
		[0.000044]	[0.00012]
TB in company		1.018
		(0.029)
		[0.54]
Company dummies	No	No	Yes
Occupation dummies	No	No	No
LL	−5931	−5090	−4898
N	17,679	15,745	15,745
N fail	618	536	536
fail time	62.22	62.96	62.96

Robust standard errors in parentheses.

p-Values in square brackets.

First, before the regression results, Table 3 presents a simple 2 × 2 layout. This shows that 1.21% of the tuberculous died of flu, while a roughly equal proportion (1.36%) the non-tuberculous died of flu. Running a logistic regression gives the same odds ratio as stated in the table, with |z| = 0.43, p = 0.67; not near significant. These tabular findings can be elaborated upon by a simple Cox regression of the effect of having tuberculosis on the hazard of influenza death (Table 4, column 1). The hazard ratio is higher than the analogous odds ratio from Table 3 because the Cox regression is a person-years of exposure framework, whereas Table 3 only looks at dichotomous outcomes and exposures. The data underlying both the tabulation of Table 3 and the estimation of Table 4, column 1 are exactly the same; only the mode of analysis is different. Here, in model 1 of Table 4, the result is in the expected direction of active selection (tuberculosis being a risk factor for influenza death, or a hazard ratio greater than one), although as with Table 3, it is not statistically significant. All the Cox models cluster on companies.

Table 3.

2 × 2 Table of tuberculosis morbidity vs. influenza mortality

Died of flu	Had tuberculosis
	No	Yes
No	16,299	1141
Yes	225	14
Percentage	1.36	1.21

Odds ratio = (16, 299 ×14) ÷ (1, 141 × 225) = 0.88.

In historical populations, ceteris paribus, height proxies for childhood nutrition and thus for social status. There is a genetic component of height, but over time and between groups, nutrition is key. There is a large literature on this subject — cf. Floud, Wachter, and Gregory (1990), Steckel (1994, chap. 9, 1995), and Floud (1998), among others. Fogel (2004b) offers a comprehensive account of the increases in both nutrition and height over time; some have argued that he gives short shrift to the metabolic advantages of decreased infectious disease burden (see e.g. Deaton, 2006). It remains uncontroversial, however, that better-fed populations — all things equal — are taller. Height is a useful control variable to include in the regressions.

For the Union Army data in particular, Haines (1998) and Wilson and Pope (2003, chap. 5) discuss height in great detail. The height of the veterans was measured at enlistment, and thus is unaffected by loss of stature at older ages. However, in the nineteenth-century peak adult height was often not reached until after age 18. Younger recruits tended to be about one inch (2.5 cm) shorter than older recruits, which is not a negligible difference. Height is therefore included as quintile of height-for-age in order to avoid any spurious correlation of height and age at enlistment. Table 4, column 2 shows that the hazard ratio of tuberculosis morbidity on influenza mortality is unaffected by inclusion of this control. Potential nonlinearities are captured by dummy variables for shortness (five feet six inches and below) and tallness (five feet 11 inches and above). Note that tallness is a priori expected to decrease the risk of being tuberculous, but not necessarily the risk of death due to influenza, conditional on being tuberculous. Tallness also ostensibly proxies for a veteran having more complete medical records, again working through socioeconomic status. The coefficient on height changes sign upon inclusion of the short and tall dummies, and it becomes protective (i.e. taller means less risk). This is more in-line with theoretical expectations, indicating that the dummies for short and tall are probably a useful addition to the model.

One way to try to capture non-recorded cases is to look at the number of cases of tuberculosis at the company level, as a proxy for unmeasured tuberculosis. There were on average 1.4 cases of tuberculosis per company during the war (about 100 men per company). Because tuberculosis is contagious, the more cases of tuberculosis in a company, the greater chance that an individual soldier would have contracted it. In this sense, tuberculosis in company is not a control variable, but an alternate measure of exposure to tuberculosis. Including the TB in company variable in the model (Table 4, column 4) does not affect the main hazard ratio of interest. However, the TB in company variable is, itself, a risk-enhancer. The magnitude of the effect is not especially large, but it is statistically significant (at least at the 10% threshold) in every model in which it is included.

Model 5 (Table 4, column 5) includes a dummy variable for illiteracy, a salient measure of educational attainment. Inclusion of the literacy dummy variable nudges the hazard ratio of interest (tuberculosis) away from the expected direction (under active selection), though as noted it was not significant to begin with. When BMI is included in the model, the hazard ratio of interest, tuberculosis, becomes larger in the direction of active selection, albeit still short of statistical significance (model 6: Table 4, column 6).

As with literacy and BMI, including occupational information diminishes sample size (model 7: Table 4, column 7). The coefficient of interest in this model again is nudged to the other side of the predicted effect (assuming active selection), and is not significant. All the models have relatively small numbers of influenza deaths, making statistical significance hard to attain, but this model, with only 90 deaths, is especially difficult to interpret.

Model 8 (Table 4, column 8) contains company fixed effects. Companies were organized by individual states (i.e. recruits from Massachusetts and Connecticut would not have served in the same company). So model 8 conditions on both shared wartime experiences of individual companies and on state of origin. The hazard ratio of interest in model 8 is slightly lower than that in model 6, but it still points toward active selection, though like all these models the sample size is too low to permit statistical significance.

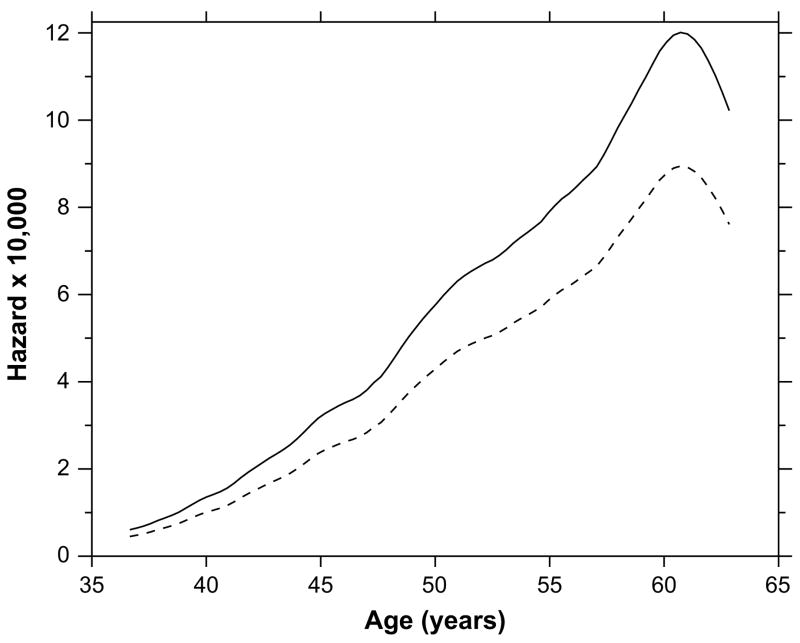
Fig. 3 shows the hazard function, taken from model 6 (Table 4, column 6), for the tuberculous (solid) and non-tuberculous(dashed). This is a smoothed empirical hazard, not a parametric functional form. It is interesting that the hazard peaks below age 65. During this time period it is well understood that tuberculosis was a disease of adulthood, not old age. The hazard in Fig. 3 is for death due to influenza, however, which is usually regarded as a disease for which hazard rates increase monotonically above about age 45.

Fig. 3.

Smoothed hazard graph from model 6 (Table 4). The solid curve represents the hazard of influenza death among the tuberculous, and the dashed curve among the non-tuberculous. See text for discussion.

Table 5 contains control regressions. Here “control” is not used in the sense of having variables in the right hand side of the regression equation. It is meant to test the idea that the tuberculous veterans may be, simply, sickly people who have increased hazards of dying from all diseases. Therefore, Table 5 shows the results of model 1, model 6, and model 8 from Table 4 but with death by heart disease as the outcome variable. The hazard ratios in Table 5 are smaller than their analogues in Table 4. The “simply sick veterans” alternate explanation of the results in Table 4 does not have much traction in light of the results in Table 5. If the tuberculous were simply sick and dropping like flies, one would expect them to die also of heart disease.

The results in Table 5 also help rule out the potential of a more specific inclusion bias of sick veterans. Most of the eligible veterans were on the pension rolls by about 1890. Prior to this time, those on the pension rolls were disproportionally ill. As touched upon above, the present interest is in adult mortality (below age 65) and so the time frame of interest includes some deaths before 1890. The potential inclusion bias here is that, due to the pension law, to be included in the sample in the period after the war but before about 1890 means that a veteran was disproportionally likely to be sick of some cause. Table 5 points away from this inclusion bias as a major problem.

Two other points are worth mentioning. The first is whether the models are affected by changing sample composition from model-to-model, as covariates are added. At the bottom of the regression tables, the row labeled fail time gives the mean age of death or censoring for all the veterans in the regression sample of each column. That is to say, it averages not just the times to influenza death, but also time to any other death. The biggest change is when occupation dummies are introduced (not surprisingly, the direction is toward longer life), but all things considered the mean time to failure is quite robust. For example, from model (5) to model (6), the change in average fail time is 0.03 year overall.

The second point is statistical power. Given the sample size, are these models likely to find a statistically significant effect, even if one exists? This is important because there are many non-significant coefficients, which would not be at all surprising if the sample size is too low. The power of models (1)–(8) is good by the standards of historical epidemiology, in the 85% range. This is assuming detection of a hazard ratio ≥ 2.0, with an alpha threshold of 10% in a one-sided test. For example, for model (6), the power is 86%; for a two-sided test it would be 76%.

Bryder (1996) argues that, historically, many tuberculosis deaths were classified on death certificates as pneumonia, due to the social stigma of tuberculosis. According to Bryder, pressure, implicit or otherwise, could be put on physicians not to list tuberculosis on the death certificate. A family history of tuberculosis was an impediment to obtaining life insurance (cf. Bryder, 1996, p. 261, as well as Beckett, 1923). If correct, the phenomenon Bryder describes would spuriously affect the results in the same direction as active selection, but only for cases where there was some evidence of tuberculosis morbidity apart from the cause of death.

Conclusion

In section “Active” and “passive” selection, I drew the distinction between active and passive selection, where both forms could potentially account for the effects seen in Noymer and Garenne (2000). Active selection would mean that the tuberculous in 1918 were at greater risk of influenza death. Passive selection would mean that the unusual (for influenza) age-mortality profile in 1918 accounts for so many tuberculous being caught in the net of fatal influenza, without any enhancement at the individual level.

In the present results, no statistically significant enhancement of influenza mortality was seen among Union Army veterans with tuberculosis morbidity. For an alternate measure of tuberculosis exposure — cases of tuberculosis in the same Army company — a statistically significant, though relatively small, positive effect of TB on influenza death was seen. Inclusion of controls such as body mass index (BMI) and company fixed effects did not produce overwhelming changes in the regression coefficients. The effects observed when the outcome is influenza death are greater than when the outcome is heart disease mortality. These results recall Jay Winter’s observation that “regression analysis is not the most subtle of tools in historical demography” (Winter, 2003, p. 139). The present results tentatively point toward passive selection being behind the effects seen in Noymer and Garenne (2000). Active selection, but specific to the 1918 flu strain, cannot be ruled out. The changes in tuberculosis mortality in the close wake of the 1918 influenza pandemic may not have been due to any specific enhancement of risk of influenza death among the tuberculous — but simply due to the tuberculous population being “in the wrong age group at the wrong time”.

An alternate way to test the tuberculosis–influenza selection hypothesis with microdata would be to collect data from developing countries today, where tuberculosis prevalence remains high (Dye, Scheele, Dolin, Pathania, & Raviglione, 1999) and where influenza is also a major problem (Viboud, Alonso, & Simonsen, 2006). Even so, the longitudinal nature of the Union Army data set makes it more appealing than any data that could be collected easily in a short time span. It is also worth bearing in mind that HIV complicates matters considerably today because, in addition to being a major cause of death, HIV is a risk-enhancer for many diseases. And modern clinical records from high-income nations (i.e. where microdata may be readily available) are not a good guide to the epidemiology of tuberculosis in the pre-chemotherapeutic era.

Whether active or passive selection is behind the results of Noymer and Garenne (2000), when demographers look at early life influences on later mortality, they should also think about which diseases a cohort has experienced, because prior exposure to an illness may affect outcomes to seemingly-unrelated illnesses years later, and this is more general than intrauterine or childhood deprivation effects that have been extensively studied in the early influences literature. The presence of one disease can affect the demography and epidemiology of another. Competing risks are sometimes dependent.