Abstract
In this study, we investigate whether an inverse modeling approach can be used to characterize vascular tissue behavior from experimental data of blood vessels subjected at various levels of internal pressure and axial stretch that mimics clinical data. In-vivo condition of blood vessel with either constant or variable axial response is considered. To compensate for the limitation of this data that does not provide axial force information, a new concept to constrain the ratio of axial to circumferential elastic moduli to a typical range is proposed. Vessel wall constitutive behavior was modeled with a transversely isotropic hyperelastic equation that accounts for dispersed collagen fibers, and both single-layer and bi-layer models were implemented for examination. The possibility of obtaining the fiber orientation in this approach was also evaluated. The characterized behavior was validated with an independent pipette-aspiration biaxial data on the same samples. It was found that homogenous assumption is an over-simplification. The constrained bi-layer model was in excellent agreement with both types of experimental data. Fiber angle is needed to be pre-defined to avoid covariance problem. Finally, our approach is relatively invariant to any particular axial response. Therefore, we believe that inverse modeling approach is suitable for in-vivo characterization.
1 Introduction
Finite element (FE) modeling is increasingly being used or contemplated as a tool for conducting in-vivo analysis of blood vessel and blood vessel tissue integrity in various (normal and abnormal) vascular conditions. For pre-surgical applications, FE modeling of blood vessel has been used to study and compare normal subjects and patients with hypertension2–5 or stenotic arteries.50 For surgical operations, FE stress-strain analysis has been used for estimating the tissue damage resulting from surgical clamping9, 17 and evaluating the procedure of balloon angioplasty in vivo.21 For post-surgical applications, FE simulations have been used to study and predict the outcomes of different types of vascular surgery, such as bypass graft surgery8 and surgical procedure of shunts.33 Such studies require tissue characterization in vivo conditions for the in-vivo FE modeling and analysis.
Bench-top testing of tissues in a laboratory setting may be inappropriate for in-vivo analysis because it requires tissue excision. In general, vascular tissue possesses different properties in vivo and in vitro.27 However, in-vivo vascular data typically consists of separate measurements of blood flow7,18,47 or pressure,46,51,57 diameter,22,46,51 and axial displacement.12,51,59 Unlike biaxial data,6,28,29,37,39 this data does not provide information about the axial force. This lack of axial force data requires that the analyst make assumption about the relationship between axial and circumferential behavior.
A recent and very relevant study proposed that the behavior of human arteries could be characterized directly from in-vivo data.40 This study was based on clinical ultrasound and pressure catheter-manometer data of a normotensive and a hypertensive subject.47 It was determined that the aorta of the hypertensive subject was less compliant than that of the normotensive subject.40 The basic assumptions operating in this study were that 1) the axial stretch and axial external force of blood vessels in vivo were constant, and 2) the in-vivo internal pressure was the only force-determining factor that induces blood vessel deformation. These assumptions were well-motivated and based on previous studies of in-vitro animal tissue testing.13,24,49,52,53,55,56 However, many recent in-vivo studies have called into question these assumptions, a possibility of which the authors were rightly aware.
For example, a number of clinical studies in human subjects have shown that there is a significant axial downward motion of the aortic root due to the motion of the heart during systole,3–5,26,31 with an average motion of 8.9 mm.26 The mechanical effects of this motion have been evaluated in a recent numerical model registered to magnetic resonance imaging (MRI) data.2–5 Specifically, when the boundary axial motion was increased from 4.3 mm to 7.3 mm, it was found that there was a significant increase of longitudinal stress in the aortic root, aortic arch, and supra-aortic vessels, in particular a increase of 32 % in longitudinal stress up to 290 kPa in the ascending aorta.4,5 In a similar study, it was found that the axial stress was increased by 50 % to 320 kPa when an 8.9 mm axial displacement was applied in addition to 120 mm Hg internal pressure in the ascending aorta. This was accompanied by a significant increase in axial stress in the thoracic aorta.2,3
Furthermore, in coronary cineangiograms, it was found that the right coronary arteries and left anterior descending coronary arteries, which are attached to the epicardial surface or penetrate the myocardial wall, have a mean total axial stretch of 5.4 % and 4.0 % respectively, corresponding to the motion of the heart.12 Similarly, by using biplane cineangiograms and intravascular ultrasounds, it was found that the right coronary arteries in human in vivo exhibit cyclic axial strains, and that they play a statistically significant role on wall thickness.59
In an in-vivo ultrasound study of the common carotid arteries in pigs, it was found that with a mean pulse pressure of 33 mm Hg, there was a mean systolodiastolic difference of 2.7 % and 5.1 % of axial strain and circumferential strain respectively in these arteries.51 Based on in-vivo observations, more recent studies have described the cyclic axial stretch and axial external force of blood vessel in human and animal in vivo as a common phenomenon, and they demonstrated the significant biochemical and biomechanical effect of this axial stretch and axial external force on blood vessel.11,42,54 In fact, the motion of the heart is not the sole cause of axial stretch and axial external forces on in-vivo blood vessels. There are at least a couple of other biomechanically relevant causes such as the movement of the joints23,34 and motion due to respiration.14
The aim of the present study is to investigate whether an inverse modeling approach can be used to characterize vascular tissue behavior from one set of experimental data that mimics in-vivo vascular data and then subsequently validate that behavior against a mechanically independent experimental dataset. The primary dataset is in the form of bench-top inflation data from blood vessels, subjected to various levels of axial stretch and known pressure. The validation data consists of the same tissue samples undergoing various levels of biaxial stretch that are simultaneously subjected to pipette aspiration. Unlike previous approaches that assumed a constant axial stretch and a constant axial force40 or that have assumed a constant ratio of circumferential to axial stress,40 we propose a new concept; that is, to constrain the ratio of the instantaneous axial to circumferential elastic moduli to be within a typical range. To be clear, we do not assign a value to that ratio, but rather during inverse analysis allow that ratio to fall within an upper and lower bound established from published values for cardiovascular tissues.15,41,58 To examine the homogeneous40 and the inhomogeneous17 tissue layer assumption to characterize tissue behavior in the approach, the constitutive behavior of the three-dimensional FE blood vessel is in the form of a poly-convex, hyperelastic, and transversely isotropic equation,15,16 and both single-layer40 and bi-layer17 models are implemented in the vessel. Also, the equation accounts for dispersed collagen fiber orientation,15,16 and the possibility of obtaining this orientation from the approach is evaluated. Though the data used in this study are both in vitro and axisymmetric, the methods are designed with both in-vivo and non-axisymmetric data in mind.
2 Methods
Below we present the constitutive equation employed in this study, which is based on a new invariant theory for biological tissues with a statistical dispersion of collagen fibers.15,16 However, as the emphasis of the present manuscript is on the validation of the vascular tissue characterization from clinical data, the constitutive equation will simply be stated without elaboration. Interested readers are referred to Einstein et al. (2005) and Freed et al. (2005). Next we describe the construction of a simple FE model of a section of blood vessel, and introduce our implementation of a single-layer model and a second model that decomposes the aortic wall into two principle layers, the media and the adventitia. Then we describe our inverse approach to tissue parameter characterization for the cases of 1) a single set of experimental inflation-testing pressure-diameter data with constant axial stretch, and 2) a four-sets experimental inflation-testing pressure-diameter data at four different levels of axial stretch.35 This inverse approach, which has been described elsewhere,15 is based on the successive response surface method (SRSM), an extension of the better-known response surface method (RSM). Interested readers are referred to Einstein et al. (2005). Following that we make clear the imposition of a constraint on the ratio of axial to circumferential elastic moduli and its justification. Finally, we explain the validation of the converged parameters by reconstructing the results in each study case to conventional biaxial data and then we compare the reconstructed tissue biaxial responses to the behavior of an independent pipette-aspiration biaxial experiment on the same samples.35
2.1 Constitutive equation
Briefly, in Lagrangian frame, the constitutive equation is written as
| (1) |
where S is the second Piola-Kirchhoff stress tensor, κ is the bulk modulus, and J is the determinant of the deformation gradient,
| (2) |
C is the right Cauchy-Green tensor, μ is the shear modulus, and DEV [•] is the Lagrangian deviatoric operator,
| (3) |
C̄ is the modified right Cauchy-Green tensor,
| (4) |
i is a summation component, n is the total number of fiber families, σi is the fiber stress, and λi is the fiber stretch,
| (5) |
Ki is the global anisotropic material stiffness,
| (6) |
where Q is a rotation matrix that rotates ki from the local Cartesian coordinate system (e1, e2, e3) to the global Cartesian coordinate system (eA, eB, eC) (Fig. 1). ki is the local anisotropic material stiffness, and can be approximated as
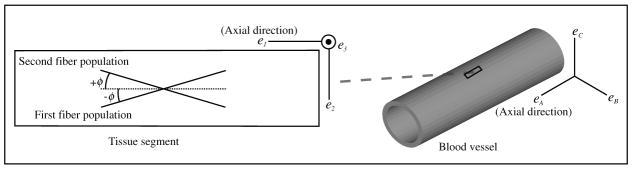
Fig. 1.
A schematic diagram of the distribution of the collagen fiber populations in blood vessel tissue. The tissue was assumed to be composed of two dispersed fiber populations, separated by an equal but opposite angle (∓φ) in eA or e1· eA is the global axial direction in blood vessels. eA is the local axial direction in each tissue segment. These fiber populations were assumed to be distributed only in e1–e2 plane in the tissues.
| (7) |
Ri is a rotation matrix that rotates one of the fiber populations from the original direction to e1. ςi and fi are the dispersion material parameters. ςi governs the amount of local in-plane dispersion, and f governs the extent of dispersion to the third dimension, φi is the fiber angle.
This formulation is general. In the present case of blood vessels possessing two principle fiber directions,20 we assumed that the tissues were composed of two (n = 2) identical (ς = ς1 ς2 and f = f1 = f2) dispersed collagen fiber populations, separated by an equal but opposite angle (∓φ) in axial direction (Fig. 1).
The stress-strain rule of each population (σi) is defined as15,16
| (8) |
where A and B are the fiber material parameters that govern the stiffness of the fiber populations.
In equation (1), the three terms on the right are respectively the volumetric, distortional isotropic, and distortional anisotropic deformation parts. The volumetric part is governed by κ of the material matrix. The distortional isotropic part is governed by μ of the material matrix. The distortional anisotropic part is governed by the dispersion material parameters φi, ςi, fi, and the fiber material parameters A and B. The κ value of blood vessel tissue was assumed to be the same as in water (2.2 gPa).19 The dispersion was assumed to be in plane (e1–e2) only (Fig. 1)20 and therefore, f was set to be 1. Thus, the equation had five free parameters: μ, φ, ς, A, and B. Note that while φ may be measured experimentally from histology,20 it is not possible to be measured in vivo up-to-date. For the purpose of this study, we have left it to be characterized. A separate study was conducted by fixing the fiber angle to literature value.20
2.2 FE model
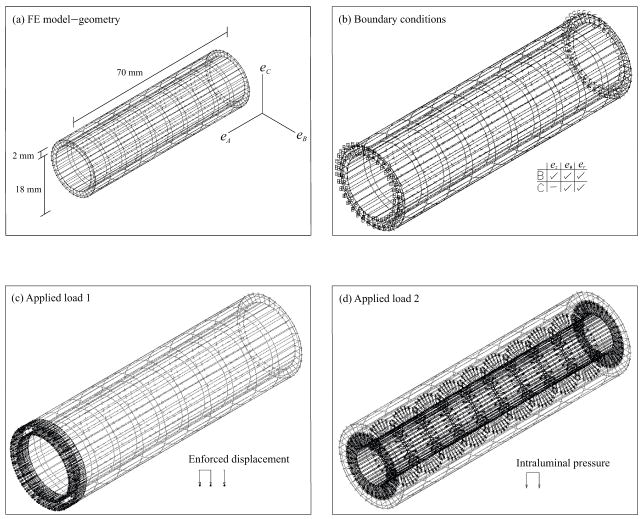
The FE model employed for parameter characterization, was an idealization of the experimental setup fully described by Ohashi et al. (2005). It consisted of a symmetrical cylinder that was 18 mm inner diameter (Fig. 2a), 70 mm in length, and with a wall thickness of 2 mm. These values corresponded to the mean geometric values of porcine thoracic aortas measured in the published experimental study.35
Fig. 2.
FE model setup. (a) The geometry of the blood vessel was symmetrical and was based on the mean values of porcine thoracic aortas.35 (b) The boundaries were free at one end and fixed in axial direction at the other end. (c) The enforced axial displacement was added at the free end. (d) The intraluminal pressure was applied inside against the wall.
The boundary conditions are fully illustrated in Fig. 2b. Both ends of the cylinder were assumed to dilate freely, with one end fixed in axial direction. In other words, the fixed end was free to move only in eθ and er in the cylindrical coordinate system (ez, eθ,er). The other end was free to dilate (Fig. 2b), and was extended as a result of an enforced axial displacement (Fig. 2c). For clarity, the axial stretch (λz) is defined as
| (9) |
where Δl is the enforced displacement, and lo is the initial length (70 mm).
To imitate the variable axial response of vessels in vivo, four independent simulations with different Δl were performed with λz equal to 1.0, 1.1, 1.2, and 1.3, respectively. To imitate the constant axial response, only one simulation of λz equal to 1.2 was performed. Simultaneously, the intraluminal pressure was applied from 0 to 200 mm Hg (26.6 kPa) in 20 mm Hg (2.66 kPa) increments (Fig. 2d). The circumferential stretch ratio (λθ) is defined as
| (10) |
where Δd is the increment of the outer diameter, and do is the initial outer diameter (20 mm).
The FE model was discretized with a total of 1800 mixed pressure-displacement brick elements, with an anisotropy of 8/1. Equation (1) was coded as a user-subroutine in ADINA.1 The well-noted numerical issues surrounding the implementation of incompressibility in a FE framework were handled with a two-field pressure/displacement interpolation.48
Finally, each axial stretch simulation was carried out with an assumption of one mechanically equivalent layer - essentially homogenizing the intima, media and adventitia.40 In addition, each simulation was repeated with an assumption of two dominant layers, the media and adventitia.17 In other words, the inner and the outer of the two layers were assigned individual sets of independent tissue parameters. The media-to-adventitia thickness ratio was approximated to be 2:1,17 with media layer on the lumenal side.
2.3 Tissue parameter characterization
Tissue parameters were characterized by performing an inverse analysis of the experimental inflation data. Briefly, in the SRSM, minimization proceeds by constructing a smooth approximation to functions in multi-dimensional space.32,36 The minimum of one set of experiments, or of one response surface, becomes the starting point for the next set of experiments. This cycle of forward solutions (i.e. FE simulations) at selected combinations of parameter values is followed by the minimization of the objective function with respect to the response surface. This is repeated until the prescribed tolerance in the residual is reached. In this method, the parameter space is condensed and possibly moved with each set of experiments, such that the sampling is conducted on a smaller and smaller region.43,44 This assures that, in the neighborhood of a minimum, the response surface captures finer and finer features of the system response. Conversely, the approximate nature of the response surface over a wider parameter space at the start of optimization assures that the method is relatively insensitive to local rather than global minima, and similarly relatively insensitive to experimental noise.43,44
In the present application, the “experiments” were the FE simulations of vessel inflation subjecting to axial stretch and the “targets” were the measured experimental inflation data.35 This data was generously provided by Dr. Toshiro Ohashi and his group from the Department of Bioengineering and Robotics at the Tohoku University, and has been reported elsewhere.35 The initial values are summarized in Table 1. Additionally, the weight of each experimental data point was scaled to be inversely proportional to its standard deviation. The objective and the design criteria were set to be 0.01. For each configuration, the parameters were characterized with one set of experimental inflation-testing pressure-diameter data corresponding to a single axial stretch value of 1.2, and subsequently with four sets of experimental inflation-testing pressure-diameter data corresponding to four levels of axial stretch. All calculations were conducted on a PC with two Intel dual core Xeon 3.6 gHz processors, running in LS-OPT45 in Red Hat Linux.
Table 1.
Initial values of the tissue parameter characterization.
| Single- / bi-layer ( ) | μ (in kPa) | φ (in rad.) | ς (in rad.) | A (in kPa) | B |
|---|---|---|---|---|---|
| Initial lower bound | 5.00 | 0.0001 / | 0.0001 | 0.10 | 0.10 |
| Initial upper bound | 50.00 | 1.5707 / | 1.5000 | 100.00 | 10.00 |
| Initial guess | 25.00 | 0.0100 / | 0.0100 | 50.00 | 5.00 |
In the separate study of fixing the fiber angle, only the bi-layer model was used, and the values of these angles in adventitia and media were set to be 15 degrees and 75 degrees respectively, which were about the reported mean values in coronary arteries.20 Only the multiple pressure-diameter data was adopted for this study case.
2.4 Constraint - ratio of axial to circumferential elastic moduli
Because in-vivo vascular data does not provide information about the axial force to characterize tissue axial properties, we introduce a constraint (α) on the ratio of axial to circumferential elastic moduli ( ) during tissue parameter characterization. α restricts Ez to be within a certain range from Eθ. This value is typically 0.80 ≤ α ≤ 2.05 in aorta.41 For example, α of porcine aortic root tissue was found to be between 1.2 ≤ α ≤ 1.6.15 In dog thoracic aortas, α was estimated to be 1.1 ≤ α ≤ 1.5.58
In this study, α was set to be 1.1 ≤ α ≤ 1.6. For simplicity, the the axial and circumferential elastic moduli (Ez and Eθ) are defined as
| (11) |
| (12) |
where m refers to the equivalent stretch in axial and circumferential direction. Thus, when m is 1.2, we designate Ez(1.2) and Eθ(1.2) to represent the elastic moduli when the blood vessel in ez and eθ are stretched to 1.2 (λz = λθ = 1.2). The constraint was added as a restrict condition in the process of the inverse characterization of the tissue parameters in LS-OPT.45 In order to evaluate the utility of this constraint, the inverse analysis with and without the constraint were both carried out. In the separate fixed-fiber study, the constraint was applied.
2.5 Validation
In a separate set of experiments, Dr. Toshiro Ohashi and his group carried out a series of biaxial tests with pipette aspiration on the same samples after the inflation testing.35 The experiments have been described elsewhere35 but, simply put, consisted of holding the tissue at various levels of biaxial stretch while simultaneously subjecting it to pipette aspiration with a rectangular cross-sectioned pipette. The data was reported as elastic moduli (Erz and Erθ) at these different levels of biaxial stretch, and as such they may be considered to be local estimations of incremental anisotropic moduli. Because this data was obtained as part of a mechanically different experiment, we used them to validate our reconstructed biaxial data from the converged tissue parameters in the inverse characterization. To reconstruct the conventional biaxial data, the axial and circumferential elastic moduli (Ez and Eθ) were obtained from equation (11) and equation (12) respectively.
Note that although both conventional and pipette-aspiration biaxial data are applicable for characterizing the highly nonlinear and anisotropic behavior in planar soft tissues, they are not exactly the same.35 In particular, Erz is a mixed value of Ez and Er, where Er is the elastic moduli in radial direction. Similarly, Erθ is a mixed value of Eθ and Er. It has been reported from experimental study that these two sets of data are close.35
Further note that in the pipette-aspiration biaxial tests, Erz and Erθ were measured when either the axial stretch or the circumferential stretch was held constant (λz = 1.0 or λθ = 1.0) while the other was being increased.35 In our study, Ez and Eθ were obtained when the tissues in both directions were stretched equivalently (λz = λθ). For validation purposes, the reaction force and stretch in axial direction was assumed to be independent of the applied force in circumferential direction, and vice versa. The assumption is valid for these tissue samples35 and vascular soft tissues in general.13,24,49,52,53,55,56
3 Results
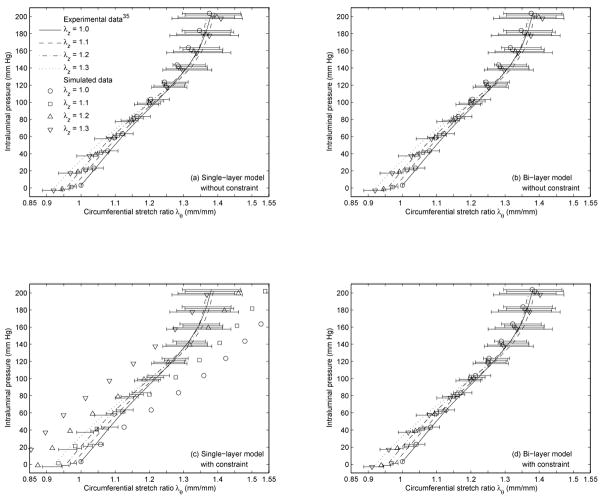
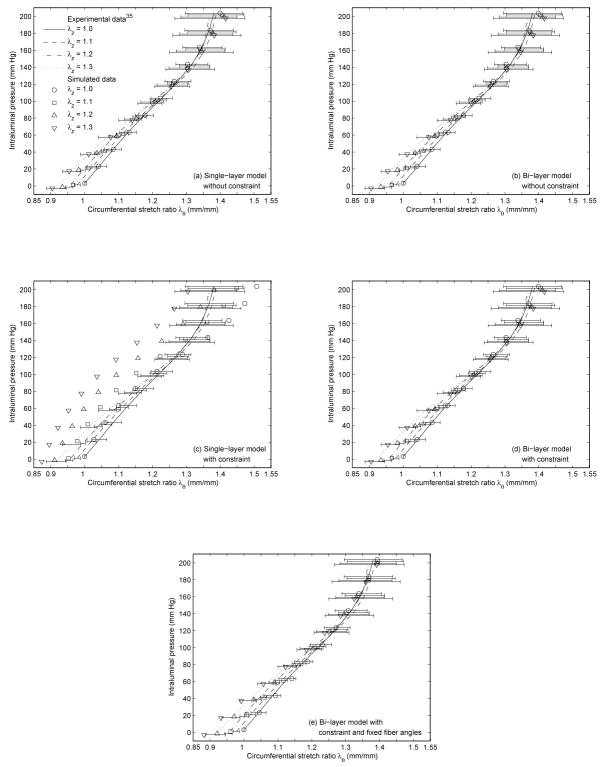
The converged tissue parameters of the single-layer and the bi-layer FE model with and without the constraint from the single and the multiple experimental inflation-testing pressure-diameter data35 are reported in Table 2 and Table 3 respectively. Note that the converged tissue parameters of the fixed fiber-angle bi-layer model with the constraint was reported as part of the results from the multiple experimental pressure-diameter data35 in Table 3. The corresponding CPU time and number of iterations in each study case are reported in Table 4 and Table 5, as are the initial and converged composite residuals. The experimental inflation-testing pressure-diameter data35 and the simulated pressure-diameter data based on the converged tissue parameters in Table 2 and Table 3 are shown in Fig. 3 and Fig. 4 respectively. Note that the converged tissue parameters (Table 2) implemented in Fig. 3 were based on one set of experimental pressure-diameter data with axial stretch equal to 1.235 (λz = 1.2), Separately, these parameters generated four datasets, corresponding to four levels of axial stretch (λz = 1.0, 1.1, 1.2, and 1.3).
Table 2.
Converged values of the tissue parameter characterization from experimental single-axial (λz = 1.2) inflation-testing pressure-diameter data.35
| Single- / bi-layer ( ) | μ (in kPa) | φ (in rad.) | ς (in rad.) | A (in kPa) | B |
|---|---|---|---|---|---|
| Without constraint | 7.92 / | 1.5656 / | 0.0010 / | 34.34 / | 1.96 / |
| With constraint | 8.96 / | 0.3374 / | 0.7835 / | 31.85 / | 4.56 / |
Table 3.
Converged values of the tissue parameter characterization from experimental multi-axial (λz = 1.0, 1.1, 1.2, and 1.3) inflation-testing pressure-diameter data.35
| Single- / bi-layer ( ) | μ (in kPa) | φ (in rad.) | ς (in rad.) | A (in kPa) | B |
|---|---|---|---|---|---|
| Without constraint | 8.36 / | 1.4036 / | 0.2397 / | 28.98 / | 2.26 / |
| With constraint | 23.03 / | 0.5472 / | 1.0293 / | 1.67 / | 9.31 / |
| With constraint and fixed fiber angles | - / | - / | - / | - / | - / |
Table 4.
CPU time, number of iterations, and initial and converged composite residual of the tissue parameter characterization from experimental single-axial (λz = 1.2) inflation-testing pressure-diameter data.35
| Single-/bi-layer | CPU time (in mins) | Number of iterations | Initial composite residual | Converged composite residual |
|---|---|---|---|---|
| Without constraint | 93 / 146 | 37 / 12 | 3.33 / 4.27 | 0.25 / 0.25 |
| With constraint | 119 / 656 | 10 / 31 | 3.33 / 4.27 | 1.51 / 0.27 |
Table 5.
CPU time, number of iterations, and initial and converged composite residual of the tissue parameter characterization from experimental multi-axial (λz = 1.0, 1.1, 1.2, and 1.3) inflation-testing pressure-diameter data.35
| Single-/bi-layer | CPU time (in mins) | Number of iterations | Initial composite residual | Converged composite residual |
|---|---|---|---|---|
| Without constraint | 148 / 565 | 15 / 10 | 7.42 / 7.88 | 0.52 / 0.51 |
| With constraint | 134 / 939 | 11 / 13 | 7.42 / 7.88 | 3.82 / 0.51 |
| With constraint and fixed fiber angles | - / 1466 | - / 43 | - / 4.19 | - / 0.44 |
Fig. 3.
Experimental inflation-testing pressure-diameter data35 and simulated pressure-diameter data. The simulated data was based on the converged tissue parameters in Table 2, corresponding to (a) the single-layer model without the constraint, (b) the bi-layer model without the constraint, (c) the single-layer model with the constraint, and (d) the bi-layer model with the constraint.
Fig. 4.
Experimental inflation-testing pressure-diameter data35 and simulated pressure-diameter data. The simulated data was based on the converged tissue parameters in Table 3, corresponding to (a) the single-layer model without the constraint, (b) the bi-layer model without the constraint, (c) the single-layer model with the constraint, (d) the bi-layer model with the constraint, and (e) the bi-layer model with the constraint and fixed fiber angles.
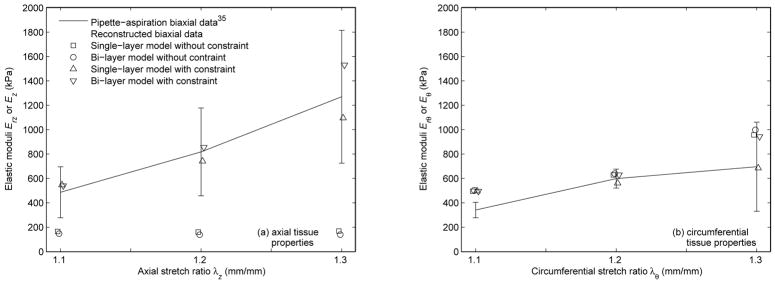
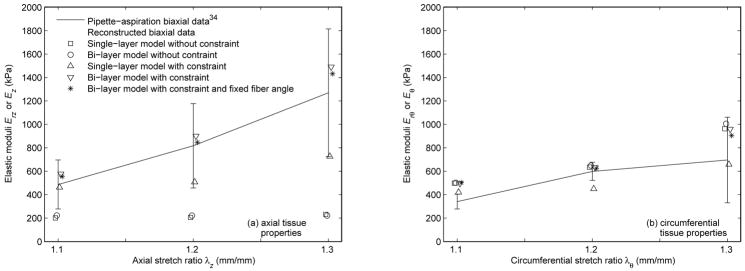
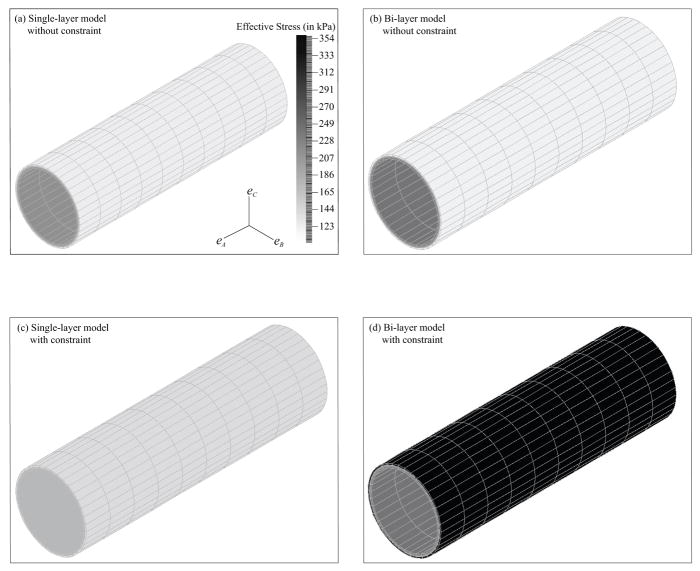
The reconstructed biaxial data based on the converged tissue parameters in Table 2 and Table 3 versus the measured moduli derived from the experimental pipette-aspiration biaxial data35 are shown in Fig. 5 and Fig. 6, respectively. The associated percent differences are reported in Table 6 and Table 7. The results in effective stress, which is an invariant stress quantity calculated from the principal stresses,10 are demonstrated in Fig. 7. Only the results of the FE model based on the converged tissue parameters in Table 3 with λz equal to 1.2 at a intraluminal pressure of 140 mm Hg are shown in Fig. 7. Note that the results of the fixed fiber-angle FE model in effective stress are not shown, as they are just like the results in Fig. 7d. To be more specific, their axial and circumferential stresses are reported in Table 10.
Fig. 5.
Reconstructed biaxial data based on the converged tissue parameters in Table 2 versus the experimental pipette-aspiration biaxial data35 in (a) axial direction and (b) circumferential direction.
Fig. 6.
Reconstructed biaxial data based on the converged tissue parameters in Table 3 versus the experimental pipette-aspiration biaxial data35 in (a) axial direction and (b) circumferential direction.
Table 6.
Percent differences associated with Fig. 5.
| Reconstructed biaxial data versus pipette-aspiration biaxial data (single-/bi-layer) | |||
|---|---|---|---|
| Axial % difference | λz = 1.1 | λz = 1.2 | λz = 1.3 |
| Without constraint | −66.12/−69.85 | −80.46/−83.09 | −86.75/−89.05 |
| With constraint | 12.36/10.97 | −9.29/4.57 | −13.73/20.48 |
| Circumferential % difference | λθ = 1.1 | λθ = 1.2 | λθ = 1.3 |
| Without constraint | 45.25/47.60 | 5.10/6.78 | 37.55/43.36 |
| With constraint | 45.83/45.31 | − 6.25/5.12 | − 1.55/35.51 |
Table 7.
Percent differences associated with Fig. 6.
| Reconstructed biaxial data versus pipette-aspiration biaxial data (single-/bi-layer) | |||
|---|---|---|---|
| Axial % difference | λz = 1.1 | λz = 1.2 | λz = 1.3 |
| Without constraint | −58.58 / −54.31 | −74.91 / −72.90 | −81.79 / −82.54 |
| With constraint | −4.88 / 18.68 | −37.84 / 10.13 | −42.81 / 17.36 |
| With constraint and fixed fiber angles | - / 13.96 | - / 3.62 | -/12.72 |
| Circumferential % difference | λθ = 1.1 | λθ = 1.2 | λθ = 1.3 |
| Without constraint | 46.25 / 47.23 | 6.05/8.36 | 38.38 / 44.45 |
| With constraint | 23.58 / 45.40 | −24.82/5.70 | − 5.41 / 37.89 |
| With constraint and fixed fiber angles | - / 47.45 | - / 4.28 | - / 30.00 |
Fig. 7.
Pictures of the FE model in effective stress based on the converged tissue parameters in Table 3 with λz equal to 1.2 at 140 mm Hg. They were (a) the single-layer model without the constraint, (b) the bi-layer model without the constraint, (c) the single-layer model with the constraint, and (d) the bi-layer model with the constraint.
4 Discussion
In the inverse parameter characterization, the longest CPU time among all study cases were 1466 mins on a standard PC, and the highest number of iterations to reach convergence was 43 (Table 4 and Table 5). These CPU time and number of iterations are acceptable,?,15 considering an inverse solution was sought with the number of experimental data points35 (Fig. 3) and the number of free parameters in the constitutive equation (Table 1). Indeed, the successive response surface method has the advantage over classical gradient descent methods that it is relatively insensitive to local minima and thus to experimental noise,15, 43, 44 while the constitutive equation has the advantage of capturing a broad range of passive tissue stress-strain behavior while remaining computationally efficient.15,16 It should be noted that the simulation time would be greatly reduced on a commodity distributed-memory cluster, since the successive response surface method is inherently parallel.15,45 In all of the cases examined, the composite residuals were able to converge quickly and to very small values except in the case of the constrained single-layer model (Table 4 and Table 5).
Overall, the constrained single-layer model performed poorly. For this case, the simulated pressure-diameter data from the converged tissue parameters (Table 2 and Table 3) failed to fit the experimental pressure-diameter data from inflation testing35 (Fig. 3c and Fig. 4c). This was reflected in the relatively high composite residual at convergence in the inverse analysis (Table 4 and Table 5). Furthermore, the fact that the converged fiber angle (φ) was about 45 degrees (Table 2 and Table 3) implies a great dependency of the axial reaction force and axial stretch to the circumferential applied force and vice versa,25 which contradicts the literature.13,24,49,52,53,55,56
When the constraint was not applied to the single-layer model, the simulated data was in good agreement with the inflation data35 (Fig. 3a and Fig. 4a); however, it failed to characterize the tissue axial properties in the independent pipette-aspiration biaxial experiments on the same samples35 (Fig. 5a, Fig. 6a, Table 6, and Table 7). Specifically, the characterized circumferential tissue properties in the reconstructed biaxial data from the converged parameters were close to the measured circumferential tissue properties in the pipette-aspiration biaxial data35 (Fig. 5b and Fig. 6b), and their % differences were relatively small (Table 6 and Table 7). However, the characterized axial tissue properties was not close to the measured axial tissue properties (Fig. 5a and Fig. 6a), and their % differences were relatively large (Table 6 and Table 7).
When the unconstrained single-layer model was replaced by the bi-layer model, the results were similar (Fig. 3b, Fig. 4b, Fig. 5, Fig. 6, Table 6, and Table 7). In addition, the small values of the converged fiber material parameter (A and B) in adventitia (Table 2 and Table 3) indicates a linear behavior, which is contradicted by the literature.20,30 These results reinforce the observation that clinical vascular data, or the experimental inflation data35 in our case, does not provide the axial force information, is therefore incomplete for characterizing the tissue properties without making appropriate assumption about the relationship between axial and circumferential behavior.
In contrast, when the constraint was added to the bi-layer model, the simulated data fitted well with the inflation data35 (Fig. 3d and Fig. 4d), and the reconstructed biaxial data accorded well with the pipette-aspiration biaxial data35 in both axial and circumferential directions (Fig. 5, Fig. 6, Table 6, and Table 7). To be more specific, this was the only study case where the characterized tissue behavior fell well within one standard deviation to the experimental data overall. Some increases from the pipette-aspiration biaxial data35 was expected, as it was noted that the elastic moduli (Erz and Erθ) from the pipette-aspiration biaxial data depends also on Er, which is smaller than Ez and Eθ from conventional biaxial data.35 The converged fiber material parameters (A and B) were not small, and the converged fiber angles (φ) were mostly oriented in axial and circumferential directions in adventitia and media respectively (Table 2 and Table 3), Both of these findings basically agree with histologic observations,20 with previous numerical studies,30 and with the results of published mechanical tests.13,24,49,52,53,55,56 Though, extreme fiber angles (φ ≈ 0 degree and φ ≈90 degrees) are outside the normal physiological range.20
To address with this concern, a separate study was conducted with the fiber angles fixed to the normal physiological values.20 It was found that the converged parameters between the free fiber-angle and the fixed fiber-angle cases were close (Table 3), and their simulated data (Fig. 4d and Fig. 4e) and reconstructed data (Fig 6) was similar. Furthermore, the characterized vessel behavior under pressure and axial force was about the same (Fig. 7d and Table 10) and very different from the rest (Fig. 7a–c). This indicates that inverse modeling approach from in-vivo vascular data, or experimental inflation data35 in our case, is not possible to obtain accurate fiber angles due to covariance of the tissue parameters. To avoid this problem, the only way is to assume the fiber angles to typical physiological values. There is a need in the future to develop a method for quantifying these values directly from in-vivo measurement.
Finally, to test whether our approach would be suitable for both constant axial stretch and variable axial stretch pressure-diameter data, two sets of inverse analyses were carried out. Firstly, all of the tissue parameters were characterized from inflation data of a single set of axial stretch experiments in which the axial stretch was held at 1.2.35 Secondly, all of the tissue parameters were simultaneously characterized from four sets of experimental data with λz equal to 1.0, 1.1, 1.2, and 1.3,35 respectively. Not only were the converged composite residuals similar between the two constrained bi-layer models (Table 4 and Table 5), but significantly the converged set of parameters for both sets of inverse analysis and for both layers (media and adventitia) were virtually identical (Table 2 and Table 3). Not to mention their simulated pressure-diameter data (Fig. 3d and Fig. 4d) and their reconstructed biaxial data (Fig. 5 and Fig. 6) with the calculated percent differences with respect to the experimental pipette-aspiration biaxial data (Table 6 and Table 7) were all about the same. These results demonstrated that our approach is relatively invariant to the axial response of blood vessels, regardless of the axial mechanical field to which they may or may not be subjected. This finding also recommends the approach to the analysis of in-vivo vascular clinical data with either constant or variable axial response.
In the present study, the inflation data and the independent pipette-aspiration biaxial data from the same samples35 was obtained in a controlled in-vitro setting. While it would be ideal to work with in-vivo data directly, acquiring human tissue samples for bench-top testing for validating the approach is difficult, and there is no such data available in literature up-to-date. In fact, it was noted that this was a problem to validate the results in the previous approach.40 Working with bench-top data enables us to gather independent data from the same subjects, and it is appropriate for a proof-of-concept study.
By using the in-vitro setting, we were able to demonstrate that the popular homogeneous tissue layer assumption40 is an over-simplification, and cannot comprehensively capture the highly nonlinear and anisotropic behavior of vascular soft tissues. This also implies the single-layer model, like in the previous approach,40 is not suitable for inverse modeling analysis. In fact, histology20 and FE modeling analysis30 have shown that the fibers are oriented very differently in the adventitia and media of arteries,20 and each of these tissue layers contributes significantly but differently to the tissue behavior.30
Furthermore, the aim of the present study is to investigate whether an inverse modeling approach can be used to characterize vascular tissue behavior from experimental data that mimics in-vivo vascular data. To account for scenarios where the axial response is either constant or variable in-vivo, we proposed a new concept of constraining the axial to circumferential ratio to typical physiological range from literature.15,41,58 We were able to demonstrate that the bi-layer model with the constraint was successful in capturing the highly nonlinear and anisotropic behavior of these vascular tissues from experimental pressure-diameter data.35 This indicates that the proposed constraint is effective in overcoming the limitation of using in-vivo data for characterizing the tissue behavior, when paired to an appropriate constitutive equation and inverse characterization scheme and under the assumption of at least two mechanical layers. Also in our investigation, we found that fiber orientation are required to be pre-defined to avoid covariance problem.
There are still a lot of research required to further develop the techniques of using inverse modeling analysis for in-vivo characterization. In fact, this and the previous studies40 are only the starting line. In the previous study, only the internal pressure and the change of blood vessel diameter were considered.40 In the present study, axial response of blood vessel is also put into consideration. However, blood vessel in vivo condition is much more complicated. For example, blood vessel geometry is more or less non-axisymmetric. And, there are other types of blood vessel deformation in vivo such as bending and torsion.14 In addition, there are perivascular (external) pressure and residual stresses. 40 Furthermore, blood vessels in vivo are surrounded by muscle, fat and connective tissues, which possibly takes up a considerable portion of pressure loaded on the vessel wall. Finally, the active and adoptive tissue mechanical properties in vivo are still under intensive research. Understanding and implementing these conditions to characterize in-vivo tissue behavior comprises our future work, and we very much look forward to working with willing clinical and research groups.
Table 8.
Axial and circumferential stresses of the FE model in Fig. 7d and the same model with fixed fiber angles.
| Bi-layer ( ) | Axial stress (in kPa) | Circumferential stres (in kPa) | ||
|---|---|---|---|---|
| Free fiber angles |
|
|
||
| Fixed fiber angles |
|
|
Acknowledgments
The authors would like to thank Dr. Ivan Vesely and the Heart Valve Research Laboratory at Childrens Hospital Los Angeles for their financial support and vision. Dr. Einstein’s contribution was supported by NIH-NHLBI1 -R01 HL077921-01A2.
References
- 1.Bathe KJ. ADINA System 8.3 Release Notes. Watertown: ADINA R & D, Inc.; 2005. [Google Scholar]
- 2.Beller CJ, Labrosse MR, Thubrikar MJ, Robicsek F. Finite element modeling of the thoracic aorta: including aortic root motion to evaluate the risk of aortic dissection. J Med Eng Technol. 2007;16:1–4. doi: 10.1080/03091900600687672. [DOI] [PubMed] [Google Scholar]
- 3.Beller CJ, Labrosse MR, Thubrikar MJ, Robicsek F. Role of aortic root motion in the pathogenesis of aortic dissection. Circulation. 2004;109:763–769. doi: 10.1161/01.CIR.0000112569.27151.F7. [DOI] [PubMed] [Google Scholar]
- 4.Beller CJ, Labrosse MR, Thubrikar MJ, Szabo G, Robicsek F, Hagl S. Increased aortic wall stress in aortic insufficiency: clinical data and computer model. Eur J Cardiothorac Surg. 2005;27:270–275. doi: 10.1016/j.ejcts.2004.11.011. [DOI] [PubMed] [Google Scholar]
- 5.Beller CJ, Labrosse MR, Thubrikar MJ, Szabo G, Robicsek F, Hagl S. Are there surgical implications to aortic root motion? J Heart Valve Dis. 2005;14:610–615. [PubMed] [Google Scholar]
- 6.Billiar KL, Sacks MS. A method to quantify the fiber kinematics of planar tissues under biaxial stretch. J Biomech. 1997;30:753–756. doi: 10.1016/s0021-9290(97)00019-5. [DOI] [PubMed] [Google Scholar]
- 7.Bogren HG, Buonocore MH. 4D magnetic resonance velocity mapping of blood flow patterns in the aorta in young vs. elderly normal subjects. J Magn Reson Imaging. 1999;10:861–869. doi: 10.1002/(sici)1522-2586(199911)10:5<861::aid-jmri35>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 8.Cacho F, Doblaré M, Holzapfel GA. A procedure to simulate coronary artery bypass graft surgery. Med Biol Eng Comput. 2007;45:819–827. doi: 10.1007/s11517-007-0201-2. [DOI] [PubMed] [Google Scholar]
- 9.Chen HY, Einstein DR, Chen K, Vesely I. Computational modeling of vascular clamping: a step toward simulating surgery. Conf Proc IEEE Eng Med Biol Soc. 2005;1:302–303. doi: 10.1109/IEMBS.2005.1616404. [DOI] [PubMed] [Google Scholar]
- 10.Cook RD, Malkus DS, Plesha ME, Witt RJ. Concepts and Applications of Finite Element Analysis. 4. New York: John Wiley & Sons, Inc; 2001. Basic elements; pp. 78–135. [Google Scholar]
- 11.Davis NP, Han HC, Wayman B, Vito R. Sustained axial loading lengthens arteries in organ culture. Ann Biomed Eng. 2005;33:867–877. doi: 10.1007/s10439-005-3488-x. [DOI] [PubMed] [Google Scholar]
- 12.Ding Z, Friedman MH. Dynamics of human coronary arterial motion and its potential role in coronary atherogenesis. J Biomech Eng. 2000;122:488–492. doi: 10.1115/1.1289989. [DOI] [PubMed] [Google Scholar]
- 13.Dobrin PB. Biaxial anisotropy of dog carotid artery: estimation of circumferential elastic modulus. J Biomech. 1986;19:351–358. doi: 10.1016/0021-9290(86)90011-4. [DOI] [PubMed] [Google Scholar]
- 14.Draney MT, Zarins CK, Taylor CA. Three-dimensional analysis of renal artery bending motion during respiration. J Endovasc Ther. 2005;12:380–386. doi: 10.1583/05-1530.1. [DOI] [PubMed] [Google Scholar]
- 15.Einstein DR, Freed AD, Stander D, Stander N, Fata B, Vesely I. Inverse parameter fitting of biological tissues: a response surface approach. Ann Biomed Eng. 2005;33:1819–1830. doi: 10.1007/s10439-005-8338-3. [DOI] [PubMed] [Google Scholar]
- 16.Freed AD, Einstein DR, Vesely I. Invariant formulation for dispersed transverse isotropy in aortic heart valves: an efficient means for modeling fiber splay. Biomech Model Mechanobiol. 2005;4:100–117. doi: 10.1007/s10237-005-0069-8. [DOI] [PubMed] [Google Scholar]
- 17.Gasser TC, Schulze-Bauer CA, Holzapfel GA. A three-dimensional finite element model for arterial clamping. J Biomech Eng. 2002;124:355–363. doi: 10.1115/1.1485284. [DOI] [PubMed] [Google Scholar]
- 18.Hassan T, Timofeev EV, Saito T, Shimizu H, Ezura M, Tominaga T, Takahashi A, Takayama K. Computational replicas: anatomic reconstructions of cerebral vessels as volume numerical grids at three-dimensional angiography. AJNR Am J Neuroradiol. 2004;25:1356–1365. [PMC free article] [PubMed] [Google Scholar]
- 19.Hayashi K. Mechanical properties of soft tissues and arterial walls. In: Holzapfel GA, Ogden RW, editors. Biomechanics of Soft Tissue in Cardiovascular Systems. New York: Springer Wien New York; 2004. pp. 15–64. [Google Scholar]
- 20.Holzapfel GA. Determination of material models for arterial walls from uniaxial extension tests and histological structure. J Theor Biol. 2006;238:290–302. doi: 10.1016/j.jtbi.2005.05.006. [DOI] [PubMed] [Google Scholar]
- 21.Holzapfel GA, Stadler M, Schulze-Bauer CA. A layer-specific three- dimensional model for the simulation of balloon angioplasty using magnetic resonance imaging and mechanical testing. Ann Biomed Eng. 2002;30:753–767. doi: 10.1114/1.1492812. [DOI] [PubMed] [Google Scholar]
- 22.Honda T, Yano K, Matsuoka H, Hamada M, Hiwada K. Evaluation of aortic distensibility in patients with essential hypertension by using cine magnetic resonance imaging. Angiology. 1994;45:207–212. doi: 10.1177/000331979404500305. [DOI] [PubMed] [Google Scholar]
- 23.Humphrey JD. Mechanics of the arterial wall: review and directions. Crit Rev Biomed Eng. 1995;23:1–162. [PubMed] [Google Scholar]
- 24.Humphrey JD, Kang T, Sakarda P, Anjanappa M. Computer-aided vascular experimentation: a new electromechanical test system. Ann Biomed Eng. 1993;21:33–43. doi: 10.1007/BF02368162. [DOI] [PubMed] [Google Scholar]
- 25.Kollár LP, Springer GA. Mechanics of Composite Structures. Cambridge: Cambridge University Press; 2003. p. 480. [Google Scholar]
- 26.Kozerke S, Scheidegger MB, Pedersen EM, Boesiger P. Heart motion adapted cine phase-contrast flow measurements through the aortic valve. Magn Reson Med. 1999;42:970–978. doi: 10.1002/(sici)1522-2594(199911)42:5<970::aid-mrm18>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- 27.L’Italien GJ, Chandrasekar NR, Lamuraglia GM, Pevec WC, Dhara S, Warnock DF, Abbott WM. Biaxial elastic properties of rat arteries in vivo: influence of vascular wall cells on anisotropy. Am J Physiol. 1994;267:574–579. doi: 10.1152/ajpheart.1994.267.2.H574. [DOI] [PubMed] [Google Scholar]
- 28.Lanir Y, Fung YC. Two-dimensional mechanical properties of rabbit skin. I. Experimental system. J Biomech. 1974;7:29–34. doi: 10.1016/0021-9290(74)90067-0. [DOI] [PubMed] [Google Scholar]
- 29.Lanir Y, Fung YC. Two-dimensional mechanical properties of rabbit skin. II. Experimental results. J Biomech. 1974;7:171–182. doi: 10.1016/0021-9290(74)90058-x. [DOI] [PubMed] [Google Scholar]
- 30.Lu X, Pandit A, Kassab GS. Biaxial incremental homeostatic elastic moduli of coronary artery: two-layer model. Am J Physiol Heart Circ Physiol. 2004;287:1663–1669. doi: 10.1152/ajpheart.00226.2004. [DOI] [PubMed] [Google Scholar]
- 31.Mercer JL. Movement of the aortic annulus. Br J Radiol. 1969;42:623–626. doi: 10.1259/0007-1285-42-500-623. [DOI] [PubMed] [Google Scholar]
- 32.Myers RH, Montgomery DC. Response Surface Methodology: Progress and Product Optimization Using Designed Experiments. New York: Wiley; 2002. [Google Scholar]
- 33.Migliavacca F, Pennati G, Di Martino E, Dubini G, Pietrabissa R. Pressure drops in a distensible model of end-to-side anastomosis in systemic- to-pulmonary shunts. Comput Methods Biomech Biomed Engin. 2002;5:243–248. doi: 10.1080/10255840290010689. [DOI] [PubMed] [Google Scholar]
- 34.Monos E, Raffai G, Contney SJ, Stekiel WJ, Cowley AW., Jr Axial stretching of extremity artery induces reversible hyperpolarization of smooth muscle cell membrane in vivo. Acta Physiol Hung. 2001;88:197–206. doi: 10.1556/APhysiol.88.2001.3-4.2. [DOI] [PubMed] [Google Scholar]
- 35.Ohashi T, Abe H, Matsumoto T, Sato M. Pipette aspiration technique for the measurement of nonlinear and anisotropic mechanical properties of blood vessel walls under biaxial stretch. J Biomech. 2005;38:2248–2256. doi: 10.1016/j.jbiomech.2004.09.019. [DOI] [PubMed] [Google Scholar]
- 36.Roux WJ, Stander N, Haftka RT. Response surface approximations for structural optimization. Int J Numer Methods Eng. 1998;42:517–534. [Google Scholar]
- 37.Sacks MS. Biaxial mechanical evaluation of planar biological materials. J Elast. 2000;61:199–246. [Google Scholar]
- 38.Sacks MS. Incorporation of experimentally-derived fiber orientation into a structural constitutive model for planar collagenous tissues. J Biomech Eng. 2003;125:280–287. doi: 10.1115/1.1544508. [DOI] [PubMed] [Google Scholar]
- 39.Sacks MS, Sun W. Multiaxial mechanical behavior of biological materials. Annu Rev Biomed Eng. 2003;5:251–284. doi: 10.1146/annurev.bioeng.5.011303.120714. [DOI] [PubMed] [Google Scholar]
- 40.Schulze-Bauer CA, Holzapfel GA. Determination of constitutive equations for human arteries from clinical data. J Biomech. 2003;36:165–169. doi: 10.1016/s0021-9290(02)00367-6. [DOI] [PubMed] [Google Scholar]
- 41.Silver FH. Biological Materials: Structure, Mechanical Properties, and Modeling of Soft Tissues. New York and London: New York University Press; 1987. Mechanical properties of connective tissues; pp. 164–195. [Google Scholar]
- 42.Sipkema P, van der Linden PJ, Yin FC. Effect of cyclic axial stretch of rat arteries on endothelial cytoskeletal morphology and vascular reactivity. J Biomech. 2003;36:653–659. doi: 10.1016/s0021-9290(02)00443-8. [DOI] [PubMed] [Google Scholar]
- 43.Stander N, Craig KJ. On the robustness of a simple domain reduction scheme for simulation-based optimization. Eng Comput. 2002;19:431–450. [Google Scholar]
- 44.Stander N, Craig KJ, Müllerschön H, Reichert R. Material identification in structural optimization using response surfaces. Struct Multidisc Optim. 2005;29:93–102. [Google Scholar]
- 45.Stander N, Roux W, Eggleston T, Craig K. LS-OPT User’s Manual: A Design Optimization and Probabilistic Analysis Tool for the Engineering Analyst. Livermore: LSTC; 2004. [Google Scholar]
- 46.Steele BN, Wan J, Ku JP, Hughes TJ, Taylor CA. In vivo validation of a one-dimensional finite-element method for predicting blood flow in cardiovascular bypass grafts. IEEE Trans Biomed Eng. 2003;50:649–656. doi: 10.1109/TBME.2003.812201. [DOI] [PubMed] [Google Scholar]
- 47.Stefanadis C, Stratos C, Vlachopoulos C, Marakas S, Boudoulas H, Kallikazaros I, Tsiamis E, Toutouzas K, Sioros L, Toutouzas P. Pressure-diameter relation of the human aorta. A new method of determination by the application of a special ultrasonic dimension catheter. Circulation. 1995;92:2210–2219. doi: 10.1161/01.cir.92.8.2210. [DOI] [PubMed] [Google Scholar]
- 48.Sussman T, Bathe KJ. A finite element formulation for nonlinear incompressible elastic and inelastic analysis. Comput Struct. 1987;26:357–409. [Google Scholar]
- 49.Takamizawa K, Hayashi K. Strain energy density function and uniform strain hypothesis for arterial mechanics. J Biomech. 1987;20:7–17. doi: 10.1016/0021-9290(87)90262-4. [DOI] [PubMed] [Google Scholar]
- 50.Tang D, Yang C, Kobayashi S, Ku DN. Steady flow and wall compression in stenotic arteries: a three-dimensional thick-wall models with fluid-wall interactions. J Biomech Eng. 2001;123:548–557. doi: 10.1115/1.1406036. [DOI] [PubMed] [Google Scholar]
- 51.Tozzi P, Hayoz D, Oedman C, Mallabiabarrena I, Von Segesser LK. Systolic axial artery length reduction: an overlooked phenomenon in vivo. Am J Physiol Heart Circ Physiol. 2001;280:2300–2305. doi: 10.1152/ajpheart.2001.280.5.H2300. [DOI] [PubMed] [Google Scholar]
- 52.Van Loon P. Length-force and volume-pressure relationships of arteries. Biorheology. 1977;14:181–201. [PubMed] [Google Scholar]
- 53.von Maltzahn WW, Warriyar RG, Keitzer WF. Experimental measurements of elastic properties of media and adventitia of bovine carotid arteries. J Biomech. 1984;17:839–847. doi: 10.1016/0021-9290(84)90142-8. [DOI] [PubMed] [Google Scholar]
- 54.Vorp DA, Severyn DA, Steed DL, Webster MW. A device for the application of cyclic twist and extension on perfused vascular segments. Am J Physiol. 1996;270:787–795. doi: 10.1152/ajpheart.1996.270.2.H787. [DOI] [PubMed] [Google Scholar]
- 55.Weizsäcker HW, Lambert H, Pascale K. Analysis of the passive mechanical properties of rat carotid arteries. J Biomech. 1983;16:703–715. doi: 10.1016/0021-9290(83)90080-5. [DOI] [PubMed] [Google Scholar]
- 56.Weizsäcker HW, Pinto JG. Isotropy and anisotropy of the arterial wall. J Biomech. 1988;21:477–487. doi: 10.1016/0021-9290(88)90240-0. [DOI] [PubMed] [Google Scholar]
- 57.Wikström J, Holmberg A, Johansson L, Löfberg AM, Smedby O, Karacagil S, Ahlström H. Gadolinium-enhanced magnetic resonance angiography, digital subtraction angiography and duplex of the iliac arteries compared with intra-arterial pressure gradient measurements. Eur J Vasc Endovasc Surg. 2000;19:516–523. doi: 10.1053/ejvs.1999.1083. [DOI] [PubMed] [Google Scholar]
- 58.Zhou J, Fung YC. The degree of nonlinearity and anisotropy of blood vessel elasticity. Proc Natl Acad Sci USA. 1997;94:14255–14260. doi: 10.1073/pnas.94.26.14255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zhu H, Friedman MH. Relationship between the dynamic geometry and wall thickness of a human coronary artery. Arterioscler Thromb Vasc Biol. 2003;23:2260–2265. doi: 10.1161/01.ATV.0000095976.40874.E0. [DOI] [PubMed] [Google Scholar]