Testing limits to adaptation along altitudinal gradients in rainforest Drosophila

Abstract

Given that evolution can generate rapid and dramatic shifts in the ecological tolerance of a species, what prevents populations adapting to expand into new habitat at the edge of their distributions? Recent population genetic models have focused on the relative costs and benefits of migration between populations. On the one hand, migration may limit adaptive divergence by preventing local populations from matching their local selective optima. On the other hand, migration may also contribute to the genetic variance necessary to allow populations to track these changing optima. Empirical evidence for these contrasting effects of gene flow in natural situations are lacking, largely because it remains difficult to acquire. Here, we develop a way to explore theoretical models by estimating genetic divergence in traits that confer stress resistance along similar ecological gradients in rainforest Drosophila. This approach allows testing for the coupling of clinal divergence with local density, and the effects of genetic variance and the rate of change of the optimum on the response to selection. In support of a swamping effect of migration on phenotypic divergence, our data show no evidence for a cline in stress-related traits where the altitudinal gradient is steep, but significant clinal divergence where it is shallow. However, where clinal divergence is detected, sites showing trait means closer to the presumed local optimum have more genetic variation than sites with trait means distant from their local optimum. This pattern suggests that gene flow also aids a sustained response to selection.

1. Introduction

Geographic range limits are perplexing, because clines in fitness traits attest to the ability of species to diverge in ecological tolerances under some conditions (Endler 1977). What genetic and ecological factors prevent adaptive divergence (and therefore range expansion) at species or population margins? There are two contrasting explanations of why adaptation fails in nature. First, populations at species' edges may be unable to adapt to local conditions because they continually receive immigrants from nearby, well-adapted populations. Second, range margins may form where there is insufficient additive genetic variation for populations to track changing selective optima. This could be because populations at the edge of a range are isolated, or at low density, or because evolution in the direction required by selection is limited by condition dependence and correlations with other traits (Blows & Hoffmann 2005).

Several theoretical models have explored under what conditions organisms can adapt to an ecological optimum that varies linearly in space (an ecological gradient). These models couple population genetics with ecology, in that density increases as the trait mean approaches the value demanded by the local selective optimum (see Lenormand 2002; Bridle & Vines 2007).

Swamping effects of gene flow. Limits to adaptation along spatial ecological gradients occur because of two factors that reduce population mean fitness: standing load due to the genetic variance (V_G), and the strength of stabilizing selection (V_S: selection is stronger as this is reduced); and load due to gene flow along the gradient (σ, mean dispersal), which generates a mismatch between the trait mean and the optimum mean for that point on the ecological gradient.

As the gradient steepens above a critical value, $b_{\text{c}}\approx (2/\sigma )\sqrt{{\overline{r}}_{\text{max}}{V}_{\text{G}}}$, the population is typically unable to track the spatially changing optimum for a given value of r_max (the organism's growth rate at the optimum, for a logistic model), assuming that there is no environmental variance. This means that the gradient in trait mean is shallower than the fitness gradient (creating a load, which reduces local population density), and populations remain confined to a small part of the spatial gradient. Population densities within a limited range should therefore reflect the underlying selective gradient provided the population does not approach its carrying capacity, or it does not vary along the transect, as the difference between the trait mean slope (ΔZ) and the selective optimum increases as the ecological gradient (b) steepens. Such populations become extinct when $b>1/\sigma \left(V_{\text{G}}/\sqrt{V_{\text{S}}}+2{\overline{r}}_{\text{max}}\sqrt{V_{\text{S}}}\right)$ (Kirkpatrick & Barton 1997; Bridle et al. 2009; Polechová et al. Submitted).

Spreading effects of gene flow. When genetic variation in the trait is allowed to increase in the model due to gene flow along a gradient in trait mean, the increased response to selection means that the population can perfectly track the optimum for even very steep gradients (Barton 2001). The expected increase in additive genetic variance due to gene flow along a given trait gradient is $V_{\text{g}}=b\sigma \sqrt{V_{\text{S}}}$.

Barton's (2001) model predicts that local adaptation should continue without limit, until the demographic cost of this phenotypic variance equals the growth rate. This should occur when $b>2r_m\sqrt{V_{\text{S}}}/\sigma$.

These equations assume that (i) traits affecting fitness are controlled by biallelic loci, and (ii) all genetic variance is additive. However, nature departs from these assumptions. In particular, gene flow will increase non-additive variation (which can be substantial, owing to negative correlations between traits, and linkage disequilibria) as well as additive variation, so reducing mean fitness without increasing evolutionary potential. This means that the effects of gene flow on population mean fitness may actually be very large, for only a small increase in adaptive potential (Blows & Hoffmann 2005).

In reality, both these consequences of gene flow are likely to be important. Alternatively, range limits may result from successful adaptation to a spatially limited resource (Price & Kirkpatrick 2009). The challenge is to establish when and at what spatial scales these contrasting effects operate. There is therefore an urgent need for empirical data to test to what extent evolutionary models explain range limits in natural situations. Three issues, in particular, need to be addressed (Bridle & Vines 2007): (i) is adaptation to marginal habitat prevented by geographic regions where the selective optimum changes too quickly in space, (ii) do populations with trait means closer to the local optimum show higher densities than those far from the local optimum, and (iii) is adaptation to the local optimum limited by the amount of genetic variation in fitness available, or prevented by the continual introduction of unsuitable alleles from neighbouring, higher density, populations?

(a) Testing evolutionary models of marginal adaptation

Collecting empirical data to address these issues is difficult (Bridle et al. 2009) because it involves: defining the selective optimum, and measuring how quickly it changes in space; measuring the evolutionary response in traits allowing adaptation to this optimum; estimating gene flow; and quantifying additive genetic variation in those traits involved in this evolutionary response. Measuring these parameters is difficult enough in high-fitness populations where densities are likely to be high. It becomes even more difficult where populations fail to track local optima, as diminishing numbers of individuals survive to be collected and measured. Research should therefore focus on populations as they approach their margins, where they should show increasingly reduced fitness, rather than at the edge itself where too few individuals can be collected to estimate trait means and variances.

Variation in quantitative traits is dominated by gene flow along the ecological gradient, rather than by genetic drift and local population size (Bridle et al. in revision). Direct estimates of migration (e.g. based on mark–recapture analyses) are therefore more likely to be relevant to studies of evolutionary change at range margins than studies of neutral molecular markers. Given the high (and effectively equivalent) levels of gene flow assumed at the spatial scales considered in these models, studies of adaptation in a single species along similar ecological gradients provide an important opportunity to test causes of limits to adaptation at range margins. Altitudinal transects typically show predictable transitions in temperature and humidity, and in ecological communities. However, these repeated transitions occur at different spatial scales: along steep ecological gradients, the optimum changes rapidly, and a similar amount of gene flow should have a stronger swamping effect on local adaptation than along shallow gradients. A comparison of clinal divergence, local population density and variation in fitness and gene flow along ecological gradients of different steepness therefore allows an important test of the effect of gene flow on evolution at range margins.

In this paper, we present the results from using genetic divergence in stress-related traits along similar ecological gradients in the rainforest fruitfly Drosophila birchii (Dobzhansky & Mather; Drosophilidae). Unlike the highly cosmopolitan species Drosophila melanogaster, D. birchii is rarely collected outside of rainforest habitats in this part of Australia (Schiffer et al. 2006), suggesting the declines in density predicted by theoretical models, along spatial scales amenable to empirical study.

As with D. melanogaster, D. birchii shows latitudinal clines in several stress-related traits, including adult tolerance to desiccation, larval development time and (most strongly) adult resistance to starvation (Hoffmann et al. 2003a,b; Griffiths et al. 2005; van Heerwaarden et al. 2009). However, despite such latitudinal divergence, D. birchii retains a highly restricted latitudinal and habitat distribution. This may be because additive variation becomes limited in these traits (Hoffmann et al. 2003a; Kellerman et al. 2006), or because changes in selection become locally too steep to allow adaptation in the face of gene flow.

Populations of D. Birchii were studied along two similar altitudinal transects (1000–100 m altitude), one of which occurs over 10 km and the other over 4 km. Schiffer et al. (2007) showed virtually no evidence for isolation by distance in seven microsatellite loci between sites up to 1000 km apart, let alone between sites less than 10 km apart, suggesting that gene flow is very extensive in D. birchii. This pattern is also shown in other molecular markers such as mitochondrial DNA, as well as in other closely related Drosophila species (van Heerwaarden et al. 2009). Differences in clinal divergence along these gradients are therefore likely to reflect differences in gradient steepness per se, rather than any increased effect of isolation by distance along shallower gradients.

2. Material and methods

(a) Ecological analysis of altitudinal transitions

Collection of D. birchii isofemale lines and males was conducted along two altitudinal transects in northern Queensland during March and April 2004. One transect (Paluma) is 90 km south of the other (Kirrama). Dataloggers recorded temperature every 5 min at 18 sites along these transects for 5–28 days during the sampling period. Dataloggers at each transect's end were left in situ for a minimum of 18 days. The location, length and altitudinal and temperature/humidity range of these transects are given in table 1.

Table 1.

Environmental variation and D. birchii density along the two altitudinal transects studied. (Data are shown for altitude, mean temperature, mean daily minimum and maximum temperatures, and mean relative humidity at paired bottom and top sites, recorded over a three- to four-week period. Density is estimated as the average number of D. birchii males collected per site per day, averaged across the two highest or lowest sites. The overall change in these variables across each transect is given in italic. Steepness (S) is the change in altitude (L). All temperatures are in °C. Transect length is the shortest distance between the highest and the lowest sites. Steepness of transect is estimated as the change in altitude (m) per metre of distance from the highest to the lowest points.)

transect and position	altitudinal range (m)	mean temperature (°C)	mean minimum temperature (°C)	mean maximum temperature (°C)	mean relative humidity (%)	mean no. of D. birchii per site per day	transect length (km) [steepness]
Kirrama 18° 12′ 17″	83	24.6	21.6	29.3	88.6	4.08
	783	20.7	18.7	23.5	89.2	7.63	10.0
	+700	−3.9	−2.9	−5.8	+0.6	+3.55	[0.07]
Paluma 18° 59′ 0″	82	26.1	23.0	30.5	84.3	1.92
	953	20.1	18.3	22.0	99.1	7.29	3.7
	+871	−6.0	−4.7	−8.5	+14.8	+5.37	[0.24]

(b) Collection of Drosophila and estimation of population density

Ten sites were sampled at Kirrama, and eight at Paluma. At each site 5–10 buckets were placed 5 m apart and baited with mashed banana. Each of these buckets was swept every day for the next 4 days. Female Drosophila from the montium subgroup were isolated, and left to lay in 40 ml vials of Drosophila minimal media before being removed and stored in 100 per cent ethanol.

A total of 221 isofemale lines were established from these sites, of which 156 were identified as D. birchii (Schiffer & Mcevey 2006). Progeny numbers were increased to at least 400 individuals and maintained in five separate vials at 18°C under a 12 : 12 light cycle for 10–12 generations before trait measurement. There is no evidence for laboratory adaptation in similarly treated isofemale lines of D. birchii within six to eight generations, although some effects were identified after 20 generations (Griffiths et al. 2005). The number of lines per site varied from 1 to 16, with an average of 8.6.

Males from the montium subgroup of Drosophila (n=891) were collected from the field at the same time as the females, and stored in 100 per cent ethanol for identification using the microsatellite marker ‘Dbir7’, as described in Schiffer et al. (2007). Of these, 667 specimens (81%) were D. birchii, 141 (17%) were D. bunnanda and 17 (2%) were Drosophila serrata (the remaining 66 individuals failed to amplify reliably). Density estimates of D. birchii were calculated as the number of identified males collected, averaged across all traps within each site for each sampling day. A similar approach has been used by Kristensen et al. (2007). All statistical analyses were performed using available functions or custom scripts written in the R statistical language (www.R-project.org) unless otherwise specified.

(c) Screening of isofemale lines for stress-resistance traits

Each isofemale line was screened for adult chill coma tolerance (CCT: the time taken to stand up after chilling), heat resistance, and starvation and desiccation resistance. All of these traits show repeated latitudinal or altitudinal clines in Drosophila generally, and in D. birchii (Hoffmann et al. 2003b; Griffiths et al. 2005), and therefore they were chosen as candidate traits for a response to selection to altitudinal gradients, which (similar to latitudinal gradients) show deterministic changes in temperature and humidity. Candidate genes for these traits also show latitudinal clines in allele frequency in Drosophila (Hoffmann and Weeks 2007). These assays followed the procedures of Griffiths et al. (2005) for heat and cold tolerance, and Kennington et al. (2001) for starvation and desiccation resistance. CCT, heat tolerance and desiccation tolerance are all expected to decrease with altitude. Starvation tolerance should decrease with altitude, assuming food resources (rotting fruit) become more limiting at lower altitude.

Given the large number of isofemales lines screened per transect, the transects were screened separately to ensure that at least five flies were measured from each line for each trait in each screening batch. This is because our sole aim was to compare the organisms' response with the ecological gradient within transects at different localities. We therefore designed our screens to maximize the power to detect within-transect rather than between-transect divergence. Although assays within a screening run are highly repeatable (and internally controlled), trait values for distinct screening batches in Drosophila experiments cannot be compared owing to local effects during the screening, in particular differences in the food batch used for each screen.

All screens were conducted on females, controlled ± a maximum of 24 hours in age and reared at minimal density (to minimize larval competition) on a potato-based food media (Griffiths et al. 2005). All flies used for screening, and their parental generation, were reared at 21°C under a 12 L : 12 D  cycle on a single food batch to minimize the contribution of maternal effects to between-line variance. For each line, 30 mated females less than 10 days of age were allowed to lay for 72 hours on 50 ml of a food media in 500 ml bottles. Three to five bottles were set up per line.

Eclosing flies were collected over 4 days, 16–19 days after laying, and pooled across rearing bottles within lines. They were then aged in unyeasted vials, at densities of up to 100 flies per vial, for 4 days so that all females were mated. Females were then separated from males under CO₂ anaesthesia, and aged for a further 4–10 days (depending on the trait being screened) at a maximum of 50 females per vial, to reduce any adverse CO₂ effects.

(d) Chill coma tolerance

Between 5 and 52 fifteen-day-old adult females per line (total=4270; mean per line=19.3 flies) were screened in random order for cold tolerance. For each assay, a female was placed in an empty 40 ml glass vial, plugged with cotton wool. Vials were placed on ice in a 4°C constant temperature (CT) room. The temperature inside these vials was consistently 1°C. After 2 hours, the cotton wool was removed, the vials were taken off ice and placed upright in a 21° CT room. Recuperating flies were observed continuously for 2 hours, and the time taken for each one to stand up was recorded. If a fly had not stood up within 12 hours, it was scored as dead. If a fly stood up between 2 and 12 hours after chilling, its time to recovery was recorded as 2 hours.

(e) Heat tolerance

Flies were scored for the time taken to become incapacitated following exposure to a heat stress. Between 5 and 43 sixteen-day-old adult females (total=3960; mean individuals tested per line=17.6) from each isofemale line were tested in randomized batches of 12 individuals in twelve 40 ml vials immersed in a 39°C hot water bath, and monitored continuously until the female stopped moving any part of her body.

(f) Desiccation and starvation tolerance

Between 5 and 79 twelve-day-old females per line (total=15 413; mean=34.2 per line for each trait) were used to estimate starvation or desiccation tolerance for each line. Following Kennington et al. (2001), these were set up in random order, at 21°C under conditions of constant light. Between six and eight females were placed in five to ten 10×100 mm vials with (i) 7 ml of 1 per cent agar food, stuffed with cotton wool (for starvation tolerance) and (ii) 10×100 mm vials with a filter paper disc, covered in muslin (for desiccation resistance). This procedure imposes a lower level of desiccation stress on the flies over a longer period than that used by Hoffmann et al. (2003a) and Griffiths et al. (2005). Ambient humidity in the CT room varied between 50 and 55 per cent.

The number of flies remaining alive in each vial was recorded every hour for the desiccation resistance assay until all flies were dead. For starvation tolerance, observations began a maximum of 30 ours after a given vial were set up, and continued every 4–8 hours until all flies were dead. All desiccated flies were dead within 40 hours, and all starved flies were dead within 14 days.

3. Results

(a) Tests for clinal variation

The transects differ in the rate at which temperature and humidity change along their length (table 1). These differences at transect ends are comparable with those observed close to sea level across the entire species' range (Griffiths et al. 2005). A nested ANOVA of mean daily temperature also revealed that 72.2 per cent of the temperature variation was observed among sites within ecotones, compared with less than 0.1 per cent among transects. Variation in abiotic factors within transects is therefore greater than that observed between transects. Similar patterns were observed for minimum and maximum daily temperatures. Because the selective factors directly affecting fitness are unknown, the altitude of each site was used as an indicator of overall ecological difference along each transect. Altitude at each site was very highly correlated with mean temperature (r=−0.93, d.f.=29, p<0.001).

All data for each quantitative trait were logarithmically transformed to improve normality, and isofemale line means calculated. Tests for clinal divergence were conducted on site means for each trait using ANCOVA. The models contained transect (fixed effect), altitude (continuous variable) and their interaction as explanatory variables and were weighted by the number of lines sampled within each site. In these models, a significant transect-by-altitude interaction would indicate that relationships between trait means and altitude differed between transects, as would be expected if adaptation is affected by gradient steepness.

All traits differ significantly between transects, and these differences are in the direction predicted by selection, or by studies of latitudinal clines in these traits in D. birchii (Griffiths et al. 2005; table 2). However, we cannot exclude the possibility that these differences are due to differences in the food batch between screens. This does not apply to within-transect estimates of isofemale line mean, which were the focus of this study. No overall significant effects of altitude were observed for any trait, but a significant transect-by-altitude interaction was observed for CCT (F_1,14=7.37, p=0.017; table 2). Previous studies on D. birchii have used line means rather than site means of traits when testing for clinal variation (Hoffmann et al. 2003a; Griffiths et al. 2005). These studies argue that because each isofemale line was established from a different field female, line means represent independent points for a particular environment. If this approach is used, the transect-by-altitude interaction effect for CCT is also highly significant (F_1,148=10.26, p=0.002), and well below a Bonferroni-corrected significance level. No other significant transect-by-altitude interactions were observed using a line mean approach, but the effects of altitude were significant for CCT (F_1,148=6.63, p=0.011) and heat tolerance (F_1,146=3.99, p=0.048).

Table 2.

Analysis of covariance table for the effects of transect, altitude and their interaction on the site means for each of the quantitative traits measured.

source of variation	d.f.	MS	F	p-value
CCT
transect	1	0.201	69.29	<0.001
altitude	1	0.011	3.89	0.069
transect×altitude	1	0.021	7.37	0.017
residuals	14	0.003
heat tolerance
transect	1	0.259	67.35	<0.001
altitude	1	0.017	4.55	0.052
transect×altitude	1	0.001	0.00	0.999
residuals	14	0.004
desiccation tolerance
transect	1	0.103	10.14	0.007
altitude	1	0.001	0.05	0.825
transect×altitude	1	0.026	2.59	0.130
residuals	14	0.010
starvation tolerance
transect	1	0.102	18.30	<0.001
altitude	1	0.010	1.83	0.198
transect×altitude	1	0.010	1.77	0.205
residuals	14	0.006

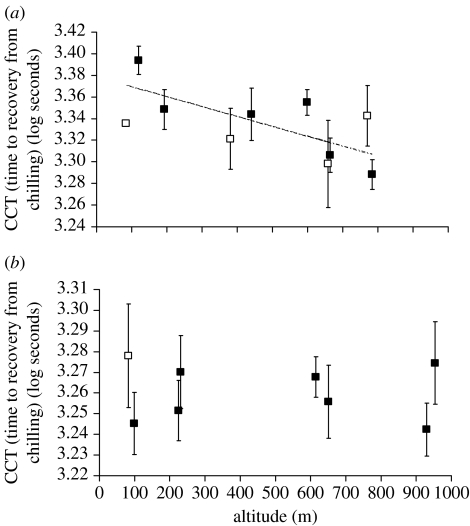
To examine the significant transect-by-altitude interaction for CCT, site means were regressed against altitude within each transect separately. If adaptation is influenced by the steepness of a gradient, we would expect clinal variation to be more evident in the shallow gradient at Kirrama. This analysis revealed a significant negative relationship with altitude at Kirrama (F_1,8=8.52, p=0.019; R²=0.52; figure 1), consistent with that expected by thermal selection, but not at Paluma (F_1,6=0.00, p=0.955; R²=0.00; figure 1). Confidence limits generated by resampling lines from within sites (n=1000) also revealed that the estimates of slope between Paluma and Kirrama significantly differ, with the best-fitted slope for Paluma being effectively zero (table 3). The power (1—type II error probability) to detect the maximum between-site variance in CCT found at Kirrama was 0.998 at Paluma. Our data therefore demonstrate significant clinal variation along the shallower transect (Kirrama), as well as being sufficiently powerful to detect an equivalent level of genetic divergence along the steeper transect (Paluma), had it been present.

Figure 1.

The relationship between altitude and the site mean of CCT for (a) the Kirrama (72 isofemale lines) and (b) Paluma transects (74 isofemale lines). Error bars represent standard errors. The linear regression at Kirrama is significant (F_1,8=8.52, p=0.019; R²=0.52). Sites represented by less than five lines are represented by open squares.

Table 3.

The bootstrapped 95% confidence intervals for the estimates of the best-fitted slope in a weighted linear regression between altitude and the site mean of CCT for each transect. CL, confidence limits.

transect	fitted slope	2.5% CL	97.5% CL
Kirrama (shallow)	−0.000092	−0.000143	−0.000041
Paluma (steep)	0.000001	−0.000034	0.000034

(b) Testing for coupling between population density and adaptation

Declines in population density at population margins should relate to how different in slope the trait mean is from the optimum. Provided population carrying capacity is never reached, or is constant within (but not necessarily between) transects different spatial patterns of density variation should be observed in these transects. Clinal divergence should be reflected by a shallower reduction in mean population fitness towards the low altitudinal margin at Kirrama (clinal divergence), but not at Paluma (no divergence).

We tested this prediction using ANCOVA, with the mean density of D. birchii as a response variable (logarithmically transformed) and transect, altitude and their interaction as explanatory variables. This transect-by-altitude interaction tests whether the relationship between density and altitude significantly differs between the different transects. Explanatory variables were added to the model sequentially starting with transect, followed by altitude, then the transect-by-altitude interaction. Mean density was weighted by the number of sampling days, so that sites for which densities were more accurately estimated had a higher leverage in the analysis.

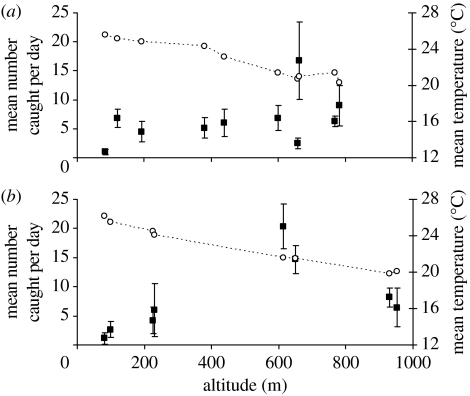
Altitude was significantly associated with the mean density of D. birchii males (table 4). In both transects, more flies were caught per day at cooler, high-altitude sites than in warmer, low-altitude sites (figure 2). However, although this decline in density towards lower altitudes appears more pronounced at Paluma than at Kirrama, there was no significant effect of transect or transect-by-altitude interaction on density. Linear fits of our density data therefore provide no evidence of a coupling between adaptation and density.

Table 4.

Analysis of covariance table for the effects of transect, altitude and their interaction on the mean number of D. birchii males caught per day.

source of variation	d.f.	MS	F	p-value
transect	1	0.047	0.11	0.107
altitude	1	3.754	8.67	0.011
transect×altitude	1	0.009	0.02	0.888
residuals	14	0.434

Figure 2.

The mean number of D. birchii males caught per day (filled squares) and the mean daily temperature (open circles) at each site of a given altitude along (a) the Kirrama and (b) Paluma transects. Error bars on density estimates represent the standard error.

The relationship between altitude and density may be nonlinear, because above a given altitude, all D. birchii populations may be at high fitness, even if clinal divergence has not occurred. We therefore compared the linear model with a model containing both a linear (altitude) and a quadratic term (altitude squared). The addition of a quadratic term to the ANCOVA improved the fit of the model significantly (F_14,13=6.34, p=0.026). However, there was no significant improvement of fit with the addition of a transect-by-altitude squared (F_13,12=1.39, p=0.261) or transect-by-altitude-by-altitude squared interaction term (F_13,11=0.38, p=0.693). Therefore, even when nonlinear relationships are explored, our data provide no clear evidence of a coupling between adaptation and density.

The power of these analyses to detect differences in the slope of density between transects was tested using the software package PS power and sample size calculations (v. 2.1.30, February 2003; Dupont & Plummer 1997), based on the sample sizes and standard deviations of the residuals. This analysis suggests that these data could have detected a significant difference in (logged) slopes of 0.0014. This is an order of magnitude greater that what the data suggest (figure 2), suggesting that more intensive estimates of density are necessary to provide a robust test for coupling based on this number of sampling days and sites.

(c) Effect of genetic variation on clinal divergence along the Kirrama transect

The swamping and spreading effects of gene flow along an ecological gradient make opposite predictions about why sites should fail to adapt to a local optimum. If swamping limits adaptation (Kirkpatrick & Barton 1997), sites with trait means distant from the optimum should have higher (or equal) levels of genetic variation compared with those close to the local optimum. By contrast, if gene flow aids adaptation by supplying new additive genetic variation (Barton 2001), such sites should show relatively lower levels of genetic variation. Similarly, if phenotypic distance from the local optimum is negatively correlated with density (coupling), then these sites should also show lower population densities.

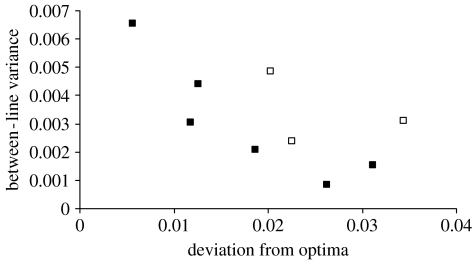
Without independent estimates of how isofemale line fitness varies at different altitudes, the clinal response of site mean to altitude along the Kirrama cline is our best estimate of the optimum for CCT. Deviations from this fitted linear regression for CCT and altitude at Kirrama were therefore correlated with between-line variance in CCT (figure 3) and with logged mean density of male D. birchii collected per day. This analysis of absolute residuals with density produced a marginally significant correlation in the expected (negative) direction (r=−0.463, d.f.=8, p=0.09). The analysis with between-line variance in CCT revealed a significant negative correlation between within-site, between-line variance and absolute residuals from the fitted line (r=−0.671, d.f.=7, p=0.048). The significance of this correlation increases (r=−0.765, p=0.016) if site values are weighted on the number of lines measured.

Figure 3.

Sites whose trait mean are different from the presumed optimum are associated with lower between-isofemale line variance compared with those close to the optimum along the Kirrama ecotone. Deviations from optima are the absolute distances between the site mean and the fitted line for the significant regression for CCT observed at Kirrama (figure 1). The correlation is significant (r=−0.67, p=0.048). Sites represented by less than five isofemale lines are represented by open squares.

To test the robustness of the correlation shown in figure 3, we repeated the analysis using 1000 random datasets. These data were generated by randomly selecting line means from the original data and recalculating site means and among-line variances for each site. Sample sizes and the altitudes for each site were kept the same as the original data. Analysis of these data revealed that there was a probability of 0.08 of a significant correlation between the regression residuals and the among-line variance. A similar probability (0.073) was obtained when the random data were generated by selecting values from a normal distribution. The relationship we observed above is unlikely to have arisen by chance or be a by-product.

Sites far from the fitted relationship between CCT and altitude therefore show lower levels of total genetic variation than those that lie close to the fitted line, suggesting that a lack of (suitable) genetic variation limits the ability of sites to track the local optimum. This effect is independent of any detectable effect of population density on genetic variance (r=−0.265, d.f.=7, p=0.490). Note also that this significant negative relationship is observed despite the underlying statistical bias towards a positive relationship between residuals from a regression on site means and within-site variance.

4. Discussion

Here, we develop the first tests of theoretical models of adaptation to marginal conditions, using natural populations of the fruitfly D. birchii distributed along two ecological gradients in northern Queensland. The key issues explored by these models are the effects of (i) the spatial scale at which selection changes on adaptive divergence, (ii) the fit to the local optimum on population density, and (iii) genetic variance on local adaptation. Our results suggest that: (i) clinal divergence in a stress-related trait is only observed where the selective optimum changes more slowly in space, (ii) this phenotypic divergence is not significantly correlated with local increases in population density, although the patterns are suggestive of this effect, and (iii) the fit of populations to their presumed local trait optimum along a cline is associated with increased, rather than reduced, levels of total genetic variation in that trait.

(a) Clinal divergence and ecotone steepness

Fine-scale clines in stress-resistant traits have been observed in Drosophila before, for example in alcohol tolerance, where differentiation was observed over 20–30 m (McKenzie & Parsons 1974; Gibson & Wilks 1988; Hoffmann & McKechnie 1991). Similar altitudinal clines in CCT have also been seen in Australian D. melanogaster (Collinge et al. 2006). However, this study is the first attempt to test how local adaptation depends on the rate of change in the selective optima in space. Both altitudinal gradients are characterized by similar changes in daily temperature and vegetation type (table 1; figure 2; Tracey 1982) but they vary in the steepness of these ecological gradients, from an average change of altitude of 0.07 m km⁻¹ (Kirrama) to 0.24 m km⁻¹ (Paluma) (table 1). Assuming that the amount of gene flow is extensive across both transects, as is suggested by neutral molecular markers (Schiffer et al. 2007), the observation of a cline in CCT at Kirrama but not at Paluma (figure 1) suggests that gene flow prevents adaptation because the swamping effect of gene flow is greater where the selective optimum changes rapidly in space compared with where it changes slowly.

(b) Coupling of population density with adaptive divergence

These data were also used to test for a relationship between clinal divergence and population density along these transects. This coupling of population genetics and ecology is central to many models of adaptation at the species' edge (Bridle & Vines 2007; Bridle et al. 2009), and predicts that density is inversely correlated with the distance of a given population's trait mean with the local optimum, provided population carrying capacity is equal along each transect (but not necessarily between them), or that food resources never become limiting within each transect. As adaptation occurs, this progressively reduces the steepness of the density gradient, and therefore the asymmetrical movement of individuals from the centre to the edge of the range. The positive feedback generated means that population margins should be characterized by sudden collapses as gene flow increases, or density is locally reduced.

Research into Drosophila population ecology (Atkinson 1985; Atkinson & Shorrocks 1984; Shorrocks et al. 1984) suggests that larval food (rotting fruit) rarely becomes limiting, meaning that competition is unlikely to be a strong limiting factor in natural populations, and that fly populations are more limited by abiotic stresses such as humidity and temperature. This is also supported by the lack of any cline in starvation resistance along these altitudinal gradients, although such clines are observed with latitude (Griffiths et al. 2005). Nevertheless, important species' interactions may differ along the transect (e.g. predation, parasitism), making it more difficult to detect the coupling predicted.

Collection of accurate density data is also difficult. Here, we have relied on the large number of traps used at each site, and the large number of revisits to each trap, to calculate an average number of D. birchii males collected per site per day. ANCOVA of these density estimates reveals a significant linear and nonlinear effect of altitude at both Kirrama and Paluma. Although the patterns observed (figure 2) are consistent with the expectations of theoretical models, the lack of a significant interaction term in this analysis indicates that the shape and slope of these fitted curves does not differ significantly between transects (table 4; figure 2). These data therefore do not provide evidence for a coupling between local adaptation and population density. However, a power analysis revealed that a much larger, more detailed study of density would be necessary to detect the suggested difference in density slope between the two transects.

As a more direct test of the effect of matching the local optimum on local density, absolute residuals from the CCT/altitude regression at Kirrama showed a marginally significant (p=0.09) correlation with population density in the predicted negative direction. Again, this pattern is consistent with the coupling predicted, but fails to provide substantial significant report.

(c) Effect of genetic variation on the match of trait mean to presumed optimum

A central issue in the population genetics of adaptation is the role of genetic variation. Both Kirkpatrick & Barton (1997) and Barton (2001) predict that the failure of populations to match their optimum is related to the amount of genetic variation available for the response to selection. However, the Kirkpatrick & Barton (1997) model assumes a fixed genetic variance, meaning that the ‘swamping’ effect of gene flow, in shifting trait means from their local optimum, is dominant. By contrast, Barton (2001) allowed genetic variation to be increased by gene flow, so increasing (‘spreading’) adaptive potential, and allowing adaptation to almost any ecological gradient. In natural situations, however, gene flow also increases non-additive variation, which does not contribute to increased adaptive potential, although it will still shift the trait mean from the local optimum.

In contrast to Hoffmann et al. (2003a) and Kellerman et al. (2006), who were able to partition additive and non-additive genetic variation, our estimates of genetic variation include such non-additive sources (e.g. epistasis, dominance). However, we assume that the total between-isofemale line variance is correlated with the levels of additive genetic variation. We used the fitted regression for CCT and altitude at Kirrama as our best estimate of the selective optima for that trait for a given altitude. Deviations from this fitted line were then used as estimates to the degree of mismatch at each site between the trait mean and the predicted optimum, and were correlated with total genetic variation in CCT at that site, based on within-site variance between isofemale line means. Although the fitted line for CCT and altitude is almost certainly shallower than the real change in selective optimum (because it measures the response to selection rather than selection itself), the negative correlation shown by our data suggests that the response to selection within the Kirrama transect is limited by the amount of genetic variation available. Gene flow along this transect (the main source of genetic variation at this spatial scale) is therefore likely to be aiding, rather than preventing, the match of the population's trait mean to the local trait optimum.

Taken together, these data suggest that gene flow can have contrasting effects at different spatial scales. At a large scale, that marginal adaptation is only possible below a critical rate of change of the optimum, indicating a swamping effect of gene flow. By contrast, once clinal divergence begins, sites with high levels of genetic variation more closely match the local optima than those with low levels of genetic variation. This observation supports the results from latitudinal clines in D. birchii, which showed that levels of additive variation in fitness-related traits (in this case, starvation and desiccation tolerance) are effectively zero at the range limits of these species, despite high levels of total variation (Hoffmann et al. 2003a; Kellerman et al. 2006).

Of the four quantitative traits known to affect fitness in D. birchii (starvation and desiccation tolerance, heat and CCT), our data reveal significant divergence only in CCT, which is either reduced at lower (hotter) altitudes or increased at higher altitudes. This implies that there must be a fitness cost to cold tolerance at low altitudes. This is supported by the observation that heat and cold tolerance are negatively correlated in other populations of Drosophila (Hoffmann et al. 2003b), and are negatively correlated between lines in our dataset (J. R. Bridle, S. Gavaz and W. J. Kennington, unpublished data, 2005–2006). It is surprising therefore that we also do not observe significant differentiation in heat tolerance. This may be because this trait is more difficult to measure reliably than CCT, as suggested by higher within-isofemale line variance in heat resistance than CCT.

Our data also show no divergence in desiccation and starvation tolerance, both of which show latitudinal clines throughout the range of D. birchii (Hoffmann et al. 2003a; Griffiths et al. 2005; van Heerwaarden et al. 2009). Similarly, no large-scale divergence in CCT is observed throughout the species' range (Griffiths et al. 2005). The response to selection therefore appears to vary at large and small spatial scales, and may differ depending on genetic architecture, as has been shown for development time and viability in D. birchii (Schiffer et al. 2006).

(d) Conclusions

This study highlights the potential for testing population genetic theory in natural populations, by comparing altitudinal transects of varying steepness, and also by the study of the mismatch between the trait mean and the local (presumed) optima within altitudinal transects, its effect on population density and its relationship with the amount of genetic variation available. Such an approach, focusing on evolutionary change towards (rather than at) population margins, where populations become increasingly unable to match the underlying spatial optimum, allows exploration of the critical parameters that limit evolutionary responses to ecological change. Although more data are needed to test the generality of our results, the current data are consistent with the predictions of theoretical models that: (i) clinal divergence is prevented above a critical rate of change of selective optimum and (ii) gene flow can improve the response to selection under some circumstances. The patterns shown with these data are also consistent with a third prediction that population density increases as a result of local adaptive divergence, and that the match of the trait mean to the local optimum is positively correlated with density.

Our research suggests that the population genetic factors explored by theoretical models do directly affect the distributional limits of populations in natural situations. They also show that empirical tests of maximum rates of evolutionary responses to ecological change are possible in the field, although obtaining sufficiently accurate estimates of key parameters is very data intensive. We hope that these data will encourage others to tackle this critical, but difficult, issue, allowing the predictions of theory to be applied to natural populations.