Fluctuating natural selection accounts for the evolution of diversification bet hedging

Abstract

Natural environments are characterized by unpredictability over all time scales. This stochasticity is expected on theoretical grounds to result in the evolution of ‘bet-hedging’ traits that maximize the long term, or geometric mean fitness even though such traits do not maximize fitness over shorter time scales. The geometric mean principle is thus central to our interpretation of optimality and adaptation; however, quantitative empirical support for bet hedging is lacking. Here, I report a quantitative test using the timing of seed germination—a model diversification bet-hedging trait—in Lobelia inflata under field conditions. In a phenotypic manipulation study, I find the magnitude of fluctuating selection acting on seed germination timing—across 70 intervals throughout five seasons—to be extreme: fitness functions for survival are complex and multimodal within seasons and significantly dissimilar among seasons. I confirm that the observed magnitude of fluctuating selection is sufficient to account for the degree of diversification behaviour characteristic of individuals of this species. The geometric mean principle has been known to economic theory for over two centuries; this study now provides a quantitative test of optimality of a bet-hedging trait in nature.

1. Introduction

Natural environments are stochastic (Halley 1996; Bell & Collins 2008). This unpredictable environmental change can lead directly to reduced survival, or to extinction of previously well-adapted organisms (Bell & Collins 2008). The likelihood of extinction under changing environments depends in part on evolutionary ‘tracking’ (Lynch & Lande 1993; Grant & Grant 2002; Bell & Collins 2008), which is limited jointly by the magnitude of environmental change and the extent of standing genetic and mutational variance (Burger & Lynch 1995; O'Hara 2005; Bell & Collins 2008).

However, a potentially major contributor to survival through unpredictable environmental change through time is often overlooked and alarmingly under-represented in the empirical literature: organisms may adapt to change itself through risk aversion or ‘bet hedging’ (Slatkin 1974; Seger & Brockmann 1987). Risk reduction is a well-established feature of human decision making. For example, the purchase of insurance is beneficial because—even though it carries the expectation of a net loss—it reduces the risk of financial disaster; the same argument holds for diversification of investment portfolios. Known to economics since 1738 (Stearns 2000), the idea of bet-hedging strategies has only relatively recently been incorporated into evolutionary theory. Bet-hedging traits are suboptimal under average conditions but reduce the variance in fitness (Gillespie 1974; Seger & Brockmann 1987), thus maximizing long run or geometric mean fitness across generations (Dempster 1955; Halley 1996; Simons 2002; Lee & Doughty 2003).

Assessments of bet hedging are rare, and quantitative tests of optimal bet hedging by individuals are completely lacking. Given that stochastic change is a fundamental quality of natural environments, an understanding of fluctuating selection (i.e. selection on a character that changes in magnitude or direction through time) and bet hedging seems central to appraisals not only of survival through rapid environmental change, but also to the concepts of fitness and optimality (Dempster 1955; Gillespie 1974). Furthermore, bet-hedging theory applies to evolutionary outcomes over any time scale (Simons 2002; Lee & Doughty 2003) and subsumes constant environments as a special case (Roff 1992).

Bet hedging may be accomplished either through the evolution of high phenotypic variance (diversification) or through the evolution of ‘safe’ (conservative) trait values (Seger & Brockmann 1987). Asynchrony in the timing of seed germination became the archetype diversification trait following publication of Cohen's (1966) classic model, but applies equally to a range of diversification traits including egg diapause and hatching asynchrony in animals. Phenotypic variance produced by individuals is well documented (Bull 1987; Simons & Johnston 2006) and is often cited as a bet-hedging strategy on the grounds that observed variance is higher than might be expected, and thus requires an explanation. However, an observation of unexplained high trait variance itself provides no evidence for diversification bet hedging: inferences of bet hedging, just like any adaptive explanation, must be based on quantitative tests of optimality.

A test of adaptation begins by establishing the optimal trait value (Orzack & Sober 1994). This is particularly onerous for a bet-hedging strategy because it requires assaying fluctuating selection acting on a trait across generations, and determining the extent of trait diversification that would maximize the long-term growth rate under the observed fluctuating selection. To test adaptation, this optimal diversification must then be compared quantitatively with diversification expressed at the individual level (Orzack & Sober 1994). A qualitative fit (diversification is both favoured by fluctuating selection, and it exists) offers some evidence for adaptation; a quantitative fit at the population level (fluctuating selection is sufficient to explain the quantity of diversification expressed by the population) offers more evidence; but, because adaptations are characters of individuals, a strong assessment of optimality must ask whether the degree of fluctuating selection is sufficient to account for the quantity of diversification expressed at the individual level (Orzack & Sober 1994). It is because of difficulties in characterizing the fitness effects of environmental variance over appropriate time scales that so little empirical work on bet hedging exists.

I am unaware of any studies that satisfy the requirements of a quantitative test of individual bet hedging, but a few particularly good qualitative or population-level tests stand out (Philippi 1993; Clauss & Venable 2000; Simons & Johnston 2003; Evans et al. 2007; Venable 2007; see §4). The focus of bet-hedging work has been on among-season germination delay in semelparous desert species because precipitation variance leads to ‘good’ and ‘bad’ years (Evans et al. 2007). The present study concerns a semelparous species, but of temperate regions in which complete reproductive failure is unlikely, and dormancy fractions are correspondingly low (Simons & Johnston 2006). If the germination timing that maximizes fitness were completely predictable at the time the germination ‘decision’ is made, then the evolution of germination synchrony or perfect adaptive plasticity would be expected. However, seedling mortality is high and variable within seasons, and if the germination timing that maximizes fitness is unpredictable at the time a germination decision is made, diversification within seasons is expected (Donohue et al. 2005b).

Lobelia inflata (L. Campanulaceae) is particularly well suited for a test of individual-level diversification for several reasons. Extensive and unexplained variance in timing of germination exists. Furthermore, seeds of L. inflata are known from previous studies to fulfil the basic requirements of bet-hedging traits (Simons & Johnston 2006): extensive phenotypic variation in germination timing—beyond variance generated by potentially adaptive phenotypic plasticity—exists among progeny within seed parents. Furthermore, L. inflata is obligately self-fertilizing, and variance expressed within naturally inbred lines cannot be explained by genetic variance. Also as predicted for a diversification trait, heritability in timing of germination is low, and this is attributable to a high environmental component of variance rather than to low additive genetic variance (Simons & Johnston 2006). Still, this unexplained germination variance at the individual level demonstrates only putative diversification. Required is a determination of whether diversification is favoured under natural environmental unpredictability, and whether this unpredictability is sufficient to explain the extent of diversification observed.

In a quantitative test of bet-hedging theory, I ask whether fluctuating natural selection on seedling survival throughout five growing seasons can account for the degree of diversification observed in the timing of seed germination within genotypes of L. inflata.

Optimal diversification bet hedging was obtained empirically by determining the fluctuating fitness functions for germination timing within each of five growing seasons. This assay of fluctuating selection was accomplished through phenotypic manipulation: seeds were germinated in the laboratory; newly germinated seedlings were translocated to the field at 71 regular intervals; and the fate of every seedling was followed. Phenotypic manipulation is not meant to mimic natural germination patterns; instead it allows the determination of the fitness surface over an extended range of phenotypes (Schmitt et al. 1999) without the confounding effects of traits not under study that typically plague correlational or observational studies. The continuous fitness functions assembled for each of the five study seasons were then used to calculate the diversification strategy that maximizes geometric mean fitness. Finally, this optimal diversification strategy was quantitatively compared with known germination variance expressed within genotypes of L. inflata.

2. Material and methods

(a) Sample collection and handling

Seeds of L. inflata (Campanulaceae) were collected from populations within a radius of 150 km of Ottawa, Ontario, the autumn prior to every study season. The 5-year fluctuating fitness functions were obtained by manipulating the timing of L. inflata seed germination in the laboratory and translocating newly germinated seedlings to the field at regular intervals. For each manipulated germination date within each season, seeds were germinated in Enconair SG-30 chambers (16 hours/8 hours, 24°C/18°C), and 100 seeds germinating during the peak (6–12 days) were used. Upon germination, seedlings were transferred singly into 8 cm fibre pots, placed briefly in a growth chamber to allow the radicle to re-establish, and transplanted (‘translocated’) to the field without being removed from the pot. The mean number of translocation dates was 14.2 (range: 12–19) per season for a total of 71 translocations. Seedlings were divided equally among four blocks and planted at randomly assigned positions within blocks.

(b) Computation of variable survival and fitness functions

Survival was scored throughout the growing season, extending into November or until snowfall precluded further observation. Care was taken to follow standardized procedures for each translocation batch. Because batches were transplanted to the field throughout the season, survival was observed over differing lengths of time. If survival probability changes with age, survival rate cannot be based simply on data extending to the end of the season. (Survival rate for seedlings in an early translocation, for example, would be based on more than three months, whereas that for a late batch would be based only on the first few weeks of life.) The observation window (t) common to all translocation batches was determined by the latest batch each year, and an observation period of t=23±4.4 (s.d.) days was used. Rate of survival (l_t) was measured as

$$l_t=1+\frac{\text{ln}(f_t)}{t},$$ (2.1)

where f_t is the survival fraction over the standard observation period (t).

Survival through this initial vulnerable period was strongly correlated with entire season survival (r=0.829; n=26; p<0.0001) for all batches of germinated seedlings transplanted through the end of July for all years, and is thus an appropriate proxy. This is because instantaneous mortality declined sharply with seedling age: over the entire study, 82 per cent of mortality over the more than 200-day observation period occurred by day 31.

High and variable seedling mortality means that fitness functions do not conform to a priori mathematical models. I thus used LOESS non-parametric smoothing (SAS 2003; Roff 2006) to estimate complex continuous fitness functions for survival (l_t) and 95 per cent CI for the 5 years of observation (SAS 2003). This procedure is similar to other smoothing techniques such as the cubic spline (Schluter 1988).

Rather than fitting data to an a priori model, LOESS asks what form best explains the data by fitting i least-squares regressions—within neighbourhoods centred on a predictor value x_i—using data weighted as a decreasing function of their distance from x_i. LOESS was performed in two stages. First, the smoothing parameter, which determines neighbourhood size, was obtained objectively based on the unbiased selection criterion AIC_C1 (SAS 2003)

$${\text{AIC}}_{\text{C}1}=n\text{log}({\hat{\sigma }}^2)+n\frac{{\delta }_1/{\delta }_2(n+{\nu }_1)}{{\delta }_1^2/{\delta }_2-2},$$

where n is the number of observations; σ² is the residual sum of squares; and δ₁, δ₂ and ν₁ are penalty functions. Second, the selected smoother was used to generate the fitness surface and 95 per cent confidence intervals (SAS 2003) for each year of study.

No evidence of temporal autocorrelation (AC) was found for survival within 2 of the 5 study years using a Durbin–Watson (DW) test for a first-order autoregression component (2002: AC=0.0005, DW=1.98, p=0.379; 2006: AC=−0.0488, DW=1.56, p=0.117), 2 years showed weak autocorrelation (2003: AC=0.111, DW=1.33, p=0.052; 2004: AC=0.344, DW=1.30, p=0.039), whereas 1 year showed stronger serial autocorrelation (2005: AC=0.597, DW=0.797, p=0.001).

Year-to-year fluctuation in overall seedling survival was also assessed. This estimate was based on instantaneous survival over the maximum calendar period common to all years of study in a random-effects ANOVA including a nested block effect. To avoid biased estimates of yearly survival caused by unequal sample size among batches within each year, the expected instantaneous survival, l_y, for each year was calculated for the mean survival fraction, $\overline{f}$, for the mean measurement period, $\overline{t}$, over all batches as

$$l_y=1+\frac{\text{ln}(\overline{f})}{\overline{t}}.$$

(c) Stochastic simulation

Analytical treatment of optimal diversification is precluded because observed fluctuating selection characterized by the 5-year fitness functions (above) cannot be meaningfully parametrized. Optimal diversification bet hedging under the observed environmental uncertainty was therefore analysed using stochastic simulation modelling in Mathematica (Wolfram Research 2003).

The geometric mean fitness associated with different diversification bet-hedging strategies was assessed in two main steps. First, I asked how parents would have fared in the field had they produced seeds characterized by a particular quantity of diversification, where fitness associated with each germination event is based on seedling success actually observed in the field. To do this, within-generation fitness associated with a range of diversification strategies was tested by generating germination distributions centred on the overall optimal date for germination and mapping these germination distributions onto the observed fitness functions. Germination events for 100 seeds produced by a parental genotype were randomly drawn from diversification strategies for mapping onto the fitness functions. A randomization approach is necessary because realized expression of diversification is dependent on seed number, which must be finite (Simons 2007). This procedure was repeated for 100 replicates for a range of germination distributions from s.d.=0 (synchronous germination) to s.d.=28d (high diversification). This entire procedure was then repeated for each empirical fitness function, thus obtaining replicate within-generation fitness estimates for each genotypic diversification strategy and for each observed fitness function.

In the final step, geometric mean fitness of each diversification strategy was calculated for 25 generations of fluctuating selection, where this sequence was a randomized draw from within-generation fitness distributions previously generated. To calculate confidence intervals for each diversification strategy, 100 independent estimates of geometric mean fitness were obtained. This simulation is a model in the sense that selection events observed in the field were randomized. Optimal diversification was obtained by solving for the diversification value at which fitness is maximized, i.e. where the first derivative of the geometric mean fitness function is zero. To obtain 95 per cent CI for the estimate of optimal diversification, the value for which the first derivative is zero was calculated for 100 replicate geometric mean fitness functions. These were generated by randomly sampling independent fitness values for each diversification strategy.

Finally, an F-test was used to compare this optimal bet-hedging diversification with observed germination variance expressed within genotypes. It is known from previous work (Simons & Johnston 2006) that extensive phenotypic variation in germination timing exists within individuals from naturally inbred lines. The low heritability of timing of germination was accounted for by a high environmental component of variance rather than by low additive genetic variance (Simons & Johnston 2006). By germinating seeds from the first two capsules for each genotype under constant conditions, potential confounding effects of adaptive phenotypic plasticity (environmental, within-maternal plant) were eliminated.

3. Results

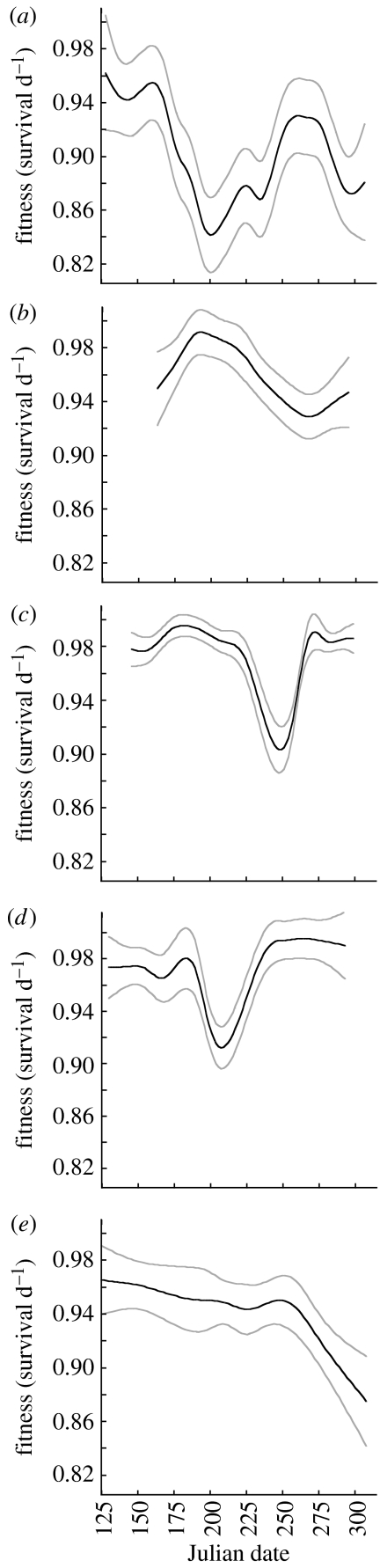
Natural selection on timing of germination, measured as instantaneous initial rate of survival, fluctuated widely within each of the five growing seasons; fitness functions were complex and, in some cases, multimodal (figure 1). Survival ranged from a high of 0.995 per day for a germination date of 3 July 2004 to a low of 0.845 per day for 15 July 2002. It should be noted that these values are expressed as daily rates; small differences in rates conceal their large multiplicative effect over time. These extreme survival rates, for example, translate to time to 50 per cent mortality of 139 and 6 days, respectively. LOESS analysis shows that the complex fitness functions differed significantly across the 5 years of study, with notable lack of coincidence in patterns of selection (figure 1). Optimal dates for germination fluctuated widely (see table 1 in the electronic supplementary material), and rate of seedling survival differed significantly (d.f.=19; F=6.55; p<0.0001) among growing seasons.

Figure 1.

Fluctuating selection acting on the timing of seed germination in L. inflata throughout five growing seasons ((a) 2002, (b) 2003, (c) 2004, (d) 2005 and (e) 2006). Seeds were manipulated to germinate at regular intervals throughout each season so that continuous fitness functions for seedling survival could be assembled. Fitness functions and their 95 per cent CI were evaluated using LOESS non-parametric smoothing and are based on instantaneous rates of seedling survival during the first few weeks of life (see §2). Note that because fitness is expressed as rate of seedling survival (per day), the y-axis corresponds to a wide range in survival over the season.

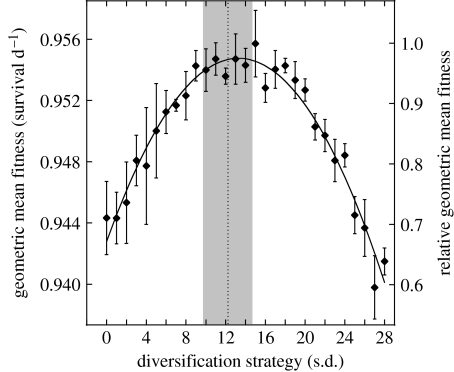
Under unpredictable selection characterized by the 5-year fitness functions, diversification at an intermediate level—and not synchronous germination on the expected optimal date—maximized geometric mean fitness (figure 2). The geometric mean fitness function over a range of diversification strategies was well described (r²=0.96) by a second-degree polynomial (figure 2). The optimal, or predicted, diversification strategy for the degree of fluctuating selection observed over 5 years in this study was thus given by the value at which the first derivative of the function is zero: the diversification strategy that maximized geometric mean fitness was s.d.=13.1 (95% CI: 12.64–13.50) (figure 2).

Figure 2.

Geometric mean fitness is maximized by an intermediate degree of diversification in seed germination timing. Geometric mean fitness is shown on the two y-axes: daily rate of seedling survival and geometric mean fitness relative to the fittest strategy over a 30-day period. Diversification strategies are reported as the standard deviation of the mean time to germination (days). Error bars indicate the standard error of geometric mean fitness estimates, and the solid line is the best-fit second-degree polynomial. The dotted line and grey area indicate observed germination variation (±s.d.) expressed within naturally inbred genotypes of L. inflata (Simons & Johnston 2006).

Observed germination variance expressed by individuals may be adaptive to the extent that it is explained by this predicted diversification. A previous study to partition variance in the timing of germination of seeds from 79 naturally inbred genotypes of L. inflata showed that 83.9 per cent occurs within genotypes (Simons & Johnston 2006). The within-genotype standard deviation was 12.28 days (s.d.=2.27; range=5.2–16.3; figure 2). Fluctuating selection resulting in predicted diversification (s.d.=13.1 days, above) was similar to and significantly greater than observed diversification (α=0.05; d.f.=1; F=10.72; p=0.0012; power=0.904).

4. Discussion

It is a truism to state that natural environments are variable, yet little empirical work has quantified the extent to which natural selection fluctuates, much less whether traits evolving under fluctuating selection fit theoretical bet-hedging predictions. Here, the magnitude of fluctuating selection across 71 periods within 5 years is found to be more than sufficient to explain within-season variance in the timing of seed germination in L. inflata, thus providing novel quantitative evidence for the adaptive significance of a bet-hedging trait. Although almost coincident, observed variance is significantly less than predicted diversification. This illustrates the difficulties inherent to quantitative tests of adaptation (Orzack & Sober 1994) in that the conventional roles of null and alternative hypotheses are reversed: a failure to reject the null hypothesis (of no difference between observed and expected) in a weak test would constitute a ‘positive’ result (optimality). Thus, a statistically powerful test might erroneously infer suboptimality even if the difference between observed and expected is biologically non-significant. Here, because the trait of interest that demands explanation—and thus the rationale for invoking bet hedging at all—is high germination variance, it is argued that the observation of environmental unpredictability that is more than sufficient to explain this observed germination variance must be interpreted as support for an adaptive explanation.

The close agreement, from a biological standpoint, of observed variance and predicted diversification in L. inflata suggests an adaptive, nearly optimal diversification strategy. However, as in any test of optimality, factors in addition to those under study may have contributed to the close match. Adaptive phenotypic plasticity may reduce selection for diversification (Donohue et al. 2005a), but only if environmental cues can be used to reliably predict the subsequent fitness effects of germination at the time this decision must be made; plasticity cannot replace diversification as a response to environments affecting post-germination fitness that is unpredictable. Furthermore, the fitness functions observed here suggest a strong unpredictable component (see §2). Although dormancy fractions are low in this species compared to in desert annuals, dormancy may reduce selection for diversification within seasons. No theoretical treatment of this relationship exists.

Tests of adaptation are impeded by constraints from which the present study is not immune. A good fit of observed-to-expected cannot be used in a deductive sense to infer optimality, because a suboptimal trait may fit well with an erroneous model. For example, the assumption that environmental variance observed during the study reflects that occurring during the evolution of the bet-hedging strategy is conservative because environmental variance is an ever-increasing function of time (Arino & Pimm 1995; Halley 1996; McKinney & Frederick 1999; Simons 2002; Bell & Collins 2008). It must be noted, however, that this assumption is no more onerous than assuming a single environment is representative in a test of optimality for non-bet-hedging characters.

Ideally, an ‘innate’ tendency for diversification in the field—without the effects of plasticity—would be compared with optimal germination diversification. In contrast to previous work, the estimate used here is not susceptible to effects of adaptive plasticity in the field because innate variance expression—that component expected to be an adaptation to unpredictable environmental variance—was assessed under a single environment (Simons & Johnston 2006). Whether this assessment reflects innate variance that would be expressed under a single, invariable environment in nature, however, cannot be determined, because such an invariable environment neither exists nor can be experimentally created.

Seed characters in the manipulation study may be influenced by environmental effects carried over from parents in the field. However, it is unlikely that parental effects generated differences in fitness functions among years. First, seeds were randomly sampled from many parental plants each year, which would contribute to within-year variance in fitness functions. Second, the use of seeds germinating only over a narrow time interval reduces the influence of maternal effects because of the negative relationship between seed size and time to germination (Simons & Johnston 2000).

Claims of bet hedging are typically based solely on the observation of trait variance. However, a few compelling qualitative, population-level tests using desert annuals have been performed. Philippi (1993), in a pioneering test, found that seeds not germinating during the first year germinate in subsequent years under the same conditions. Clauss & Venable (2000) showed that the rank order of dormancy fractions among populations closely matches the order predicted by differences in historical rainfall, but that adaptive plasticity was the primary influence on germination fraction. Evans and colleagues (2007) showed convincingly that fluctuating selection favours dormancy over non-dormancy under variably arid conditions. In a particularly strong interspecific test using long-term demographic data, Venable (2007) found a negative correlation between germination fraction and fitness variance. Conservative bet hedging has been implicated as a plausible explanation for apparently suboptimal timing of flowering in L. inflata (Simons & Johnston 2003) but, again, a quantitative fit of individual behaviour to an optimal strategy was not tested.

5. Conclusions

Because natural environments are variable over all time scales, knowledge of the evolutionary effects of environmental variance is fundamental to our understanding of adaptation (Grant & Grant 2002; Simons 2002; Lee & Doughty 2003). However, tests of bet hedging are rare. This study demonstrates that fluctuating natural selection in the field can explain observed diversification in a classic bet-hedging trait. This raises the general question of the extent to which evolutionary outcomes are shaped by environmental unpredictability. A mistaken interpretation of bet-hedging theory sees it as a special case; in reality, because natural selection is expected to maximize long-term growth rate, non-bet hedging is the special case—applicable to constant environments (Roff 1992). If unpredictability exerts a strong influence on trait evolution and results in traits that maximize the geometric mean fitness, our expectation to observe optimality under single environments or over short time scales will have to be re-evaluated. Furthermore, the present result suggests that bet-hedging expression must be considered in assessments of extinction vulnerability under rapid environmental change.

Supplementary Material

Table of seedling survival and optimal germination dates

Overall daily seedling survival rates and optimal dates for germination for the five years of study