Characteristics of air puffs produced in English “pa”: Experiments and simulations

Abstract

Three dimensional large eddy simulations, microphone “pop” measurements, and high-speed videos of the airflow and lip opening associated with the syllable “pa” are presented. In the simulations, the mouth is represented by a narrow static ellipse with a back pressure dropping to 1/10th of its initial value within 60 ms of the release. The simulations show a jet penetration rate that falls within range of the pressure front of microphone pop. The simulations and high-speed video experiments were within 20% agreement after 40 ms, with the video experiments showing a slower penetration rate than the simulations during the first 40 ms. Kinematic measurements indicate that rapid changes in lip geometry during the first 40 ms underlie this discrepancy. These findings will be useful for microphone manufacturers, sound engineers, and researchers in speech aerodynamics modeling and articulatory speech synthesis.

INTRODUCTION

The release burst and aspiration or “pop” associated with voiceless aspirated plosive consonants (e.g., ∕p^h∕, ∕t^h∕, and ∕k^h∕) in many languages is a potentially important cue in the perception of these sounds1 and a well-known challenge for audio engineers and microphone manufacturers.2, 3 Plosive release burst and aspiration contains both sound and what has been termed pseudo-sound.4, 5 While sound waves propagate through air at the speed of sound ($c=\sqrt{\gamma P∕\rho }$ for an ideal gas), pseudo-sounds are slower pressure fluctuations within the flow that are detectable by an ear or microphone. The present paper seeks to characterize the properties of flow (as opposed to sound) associated with English aspirated “p.”

While a good deal is known about the properties of air flow from an orifice in industrial applications, there exist a number of problems peculiar to modeling oral aspiration in speech that have not been previously addressed, including properties of the orifice, flow description, and simulation type.

Orifice

During the production of the labial plosive “p” release, the lips constitute a highly complex orifice, being elastic and continuously changing in geometry and rigidity. During English and Japanese bilabial stop releases, Westbury and Hashi6 used Westbury’s x-ray micro-beam data to demonstrate that the lips accelerate away from each other after the release, reaching a maximum velocity of about 200 mm∕s at 25 ms, and then decelerate until they reach an average opening of ∼20 mm after ∼200 ms. While this mouth opening time is quick, it is not negligible compared to the time scales under study. Pelorson et al.7 argued for the importance of modeling changes in the lip opening over time, but presumably did not simulate it due to computational complexity. The rate of lip opening is likely to have a large effect on initial flow rate as air flows faster through constrictions in a tube. However, disturbances due to interaction between the flow and lips are expected to have little effect on the general flow.8, 9

In an engineering setting there have been few studies of the effects of variable orifice geometry on the fluid mechanics. One such study, by Dabiri and Gharib,10 considered the starting jet formed by a circular orifice of time-varying diameter. They studied the effects of changing nozzle diameter on the flow and found that a temporally increasing nozzle diameter causes the leading vortex ring to have the strongest vorticity at a larger radius from the centerline than for a constant nozzle diameter, but they did not measure jet penetration distance, which is a primary quantity of interest here.

During the production of “pa’s,” lip aperture geometry is close to an ellipse,7 and so there is the need to consider whether modeling the general elliptical shape of the mouth opening is important in simulating airflow after a bilabial release. Noncircular jets have been previously studied as a means of providing passive flow control. Research results, both numerical and experimental, show significant differences between circular and elliptical jets;11, 12 thus simulating the general shape of the lip opening is likely to be important for accurate simulations.

Flow description

After a bilabial stop release into a vowel, the pressure in the mouth drops asymptotically to approximately 1/10th of its initial value in the first 60 ms of the flow (similar to Fig. 4).7, 13, 14 The pressure in the mouth is sufficiently great that the flow out of the mouth during an utterance such as “pa” is turbulent. In a turbulent flow a large range of scales is present, as opposed to the smaller range present in a smooth, laminar flow. One can confirm that a “pa” is turbulent by considering the Reynolds number, which is a dimensionless parameter important for characterizing flows:

$$\mathrm{Re}=\frac{\rho VD}{\mu }.$$

In this expression, ρ is the fluid density, V is the mean fluid velocity at the orifice, D is the orifice diameter, and μ is the dynamic viscosity. For a Reynolds number greater than 1000, round jets become turbulent a short distance from the nozzle.15D is approximated as 6.1 mm by finding the hydraulic diameter for the mouth (see Ref. 14 for similar hydraulic diameters), V=20 m∕s as a conservative estimate, and using typical values of air of ρ=1.2 kg∕m³ and μ=1.8×10⁻⁵ N s∕m², the Re is ∼8100, so this flow is turbulent.

Figure 4.

Transient boundary condition.

Turbulent starting jets (the initiation of a continuous flow from an orifice) and puffs (in which flow at the orifice is cut off soon after initiation) have been heavily studied for other applications such as fuel injection, and are typically studied with round nozzles. Sangras et al.9 (note correction16) provided a nice summary of starting jet and puff research. The leading edge of the burst follows the equation (dropping the virtual origin)

$$X=c{T}^n,$$

where X=x/D is the non-dimensional distance, c is an experimentally determined constant, T=tV/D is the non-dimensional time, and n=1/2 for starting jets and n=1/4 for puffs. Figure 1 shows the difference between a starting jet and a puff using the range of c reported in Ref. 9. The puff and starting jet penetration distances diverge significantly for T≳100. Using the characteristic diameter and velocity of a “pa” estimated above, puffs and jets would penetrate noticeably different distances after about 30 ms. Since there is a need to understand “pa” behavior to 100 ms or more, it is clearly necessary to model the actual transient pressure driving the flow.

Figure 1.

Starting puff and starting jet comparison.

Assuming the room temperature to be 22 °C and the air jet to be 37 °C (body temperature), then from the ideal gas law one finds the ratio ρ₀/ρ_jet=1.05. Diez et al.17 found the effects of buoyancy to be small for the temporal and spatial range considered in this study, and, while Diez et al. considered buoyant forces acting along the streamwise direction, in speech the buoyant force will be roughly perpendicular to the jet, presumably resulting in an even smaller effect on streamwise penetration. Temperature will also cause the jet viscosity to be ∼5% higher than the surrounding air, but this difference should also produce negligible effects on a flow at this Re.

Simulation type

One must consider whether the problem can be modeled in two dimensions, or if a more complex three dimensional (3D) model is required. If the domain is two dimensional (2D), then the mouth would have to be treated as a plane jet, as was done by Pelorson et al.7 Although turbulence is a 3D flow, it is possible to consider a 2D Reynolds-averaged Navier–Stokes (RANS) turbulence model. However, Reichert and Biringen18 and Stanley and Sarkan,19 among others, reported significant inaccuracies in 2D simulations of plane jets. Finally, RANS models average the flow, but the turbulent fluctuations themselves are of interest to us; therefore a more sophisticated technique such as large eddy simulation (LES) is needed. Thus, both the geometry and the flow compel us to model plosive aspiration in three dimensions using LES.

Hypotheses

Based on the above discussion, it is proposed that to adequately simulate air flow from the mouth after the release of a bilabial stop into a vowel, one needs to take into account the known decrease in air pressure following the release. It is also hypothesized that the mouth can be adequately modeled as a 2D narrow ellipse. Computational limitations require a static geometry. The validity of this assumption must be compared with lip aperture over time from a high-speed video experiment. Due to the fact that the airflow throughout most of the release is turbulent, it is necessary to resolve the turbulent properties, and because the lip aperture exists in 3D space, one needs a 3D LES to accurately model air flow after a bilabial release.

METHODS

These hypotheses were tested by comparing the results of two sets of experiments with simulations. The first experiment used a microphone located at varying distances from a participant repeating the syllable “pa” to record pressure fronts corresponding to microphone pops. The second experiment used high-speed video to record smoke particles. The microphone pops were compared to the simulation pressure front. The leading edge of the smoke particles recorded in the high-speed video was compared to the leading edge of the simulation particle front.

Microphone experiment

Data recording

For the microphone pop experiment, a single male participant was seated in a sound-proof room. Two microphones were placed in the room, one dummy microphone at 50 cm away from the mouth of the participant, and one SHURE SM58 set 5 cm away from the mouth of the participant. The cover of the microphone was removed to increase the effect of the pop on the recording, and the microphone was plugged into a Sound Devices USBPre microphone pre-amplifier plugged into a 1.42 Gbyte dual processor PowerMac G4 with 512 Mbytes of ram running Mac OSX 10.4.10 and recording with Audacity 3.3 at a sampling rate of 44 100 kHz. Both microphones were lined up and placed at exactly the mouth height of the participant.

The participant wore a set of direct sound extreme isolation headphones plugged into the USBPre and set to monitor microphone input in real-time. The self-monitoring allowed the participant to adjust his speaking angle to make sure that microphone pops were being picked up by the Shure SM58 microphone, a particularly difficult task at distances past 20 cm.

The participant was handed a thin rigid tube to place in the corner of his mouth. The tube was attached to a SCICON Macquirer 516 airflow meter set to record the mouth pressure of the participant during the experiment. The airflow meter was attached to the same powerMac and using MACQUIRER 8.9.5.

The participant was asked to say the word “pa” 15 times while focusing on the dummy microphone set 50 cm away. The experiment was repeated with the microphone moved back at 5 cm increments from 5 to 40 cm away from the participant.

Data analysis

For each token the maximum air pressure just prior to the release burst of “pa” was recorded along with the difference in time from the onset of the sound of each “pa” and the beginning of a microphone pop. Airflow perturbations, or microphone pops, affect microphone output through the production of a very low frequency wave caused by the airflow, and high frequency aperiodic sound. To measure how long the airflow took to reach the microphone, the time between the onset of the release burst and the onset of the first significant low frequency perturbation that looks and sounds like microphone pop was used, as illustrated in token 75 in Fig. 2a.

Figure 2.

Sound waves from a “pa” with microphone pop and “pa” without microphone pop (183 ms clip).

However, these perturbations are difficult to isolate, particularly from a sound signal for distances from 20 to 40 cm due to overlap with the high amplitude vocalic portion of the sound wave. Fortunately, microphone pops are also associated with turbulence at higher frequencies. The high frequency aperiodic sound is hard to isolate in the waveform, but easy to detect by listening to the sound. Therefore each token was also examined by listening for the onset of pops using a set of high-quality Sennheiser HD650 headphones and a Total Bithead pre-amplifier. This turbulent sound helped isolate the onset of the microphone pop. For cases where neither listening nor examining the original wave worked, the original sound file was low-pass filtered using a band pass elliptic filter set from 30 to 100 Hz in MATLAB with 30 Hz skirts. These frequencies are produced in the sounds of speech, but microphone pops produce these frequencies at higher amplitude making the leading edge of the microphone pop easier to detect.

The time between the onset of the original sound wave and the onset of the first visibly larger peak was selected, but only when there was an obvious increase in the amplitude of these low frequency waves clustered together. This filtering method can reduce the accuracy of measurements because it excludes relevant frequencies that cannot be used because they overlap the fundamental frequency and first harmonic. However, in some cases the method was very helpful, as in token 7 shown in Fig. 3 where it is hard to see the onset of the pop in the unfiltered waveform, but easy to see in the low-pass filtered waveform.

Figure 3.

Measurements from sound token 7, distance=40 cm, 437 ms clip.

If none of these three techniques produced a discernible result, the token was not used because the microphone did not record a loud enough pop to isolate.

The microphone pop timing corresponds to the leading pressure front recorded in the air puff simulation.

High-speed video experiments

Two sessions of high-speed video of the participant from the pop experiment saying the word “pa” while expelling white smoke were made. The smoke had a similar density as air, and was close to body temperature or approximately 37 °C at the time of expiration.

For the first round, digital videos of three productions of “pa” were captured using black foam board in the background and a standard tape measure pasted to the board for scale. The camera was placed approximately 460 cm away and focused on the tape measure such that the shot was 52.8 cm wide at the focal point. Bright sunlight was used to provide lighting. The participant then stood to the edge of the black bristol board such that their mouth opened just above the tape measure. The participant inhaled white smoke prior to the production of the “pa” so that the expelled air from the production of the “pa” would be visible during filming. Video was captured using a Bassler 504 kc high-speed color digital video camera with a Micro-Nikkor 70–180 mm telephoto zoom lens. The camera was plugged into an EPIX PIXCI CL3 SD frame grabber card with 1 Gbyte, of PC133 mHz memory in a P4 computer with 1 Gbyte of ram running Windows XP. Digital video was captured into the frame buffer using X-Cap Lite set to capture at 1024×768 resolution at 500 fps at maximum light gain and exported frame by frame into 1280×1024 32 bit tagged image file format (TIFF) files.

For the second round, digital video of 12 productions of “pa” was captured using black foam board background and meter sticks for scale. The camera was placed approximately 330 cm away and focused on the tape measure such that the shot was 53.0 cm wide at the focal point. A film light was placed facing the speaker to clearly illuminate the smoke particles. Video was captured using a Phantom v12 high-speed monochrome digital video camera with a Navitar 6.5× lens. Digital video was transferred from the camera’s built-in memory to 1280×800 resolution jpegs at 2000 fps.

Data analysis

For both rounds, the point of the opening of the mouth was captured using IMAGEJ’s point capture utility, and the leading edge of the white smoke was recorded frame by frame for the first 150 ms of recorded time. The points were converted to distance in centimeters and analyzed statistically.

For both rounds, exact measurements of initial mouth pressure could not be made because the air flow apparatus would have interfered with the visual recording of air puff travel. However, the pressure can be inferred from Kenneth Stevens data on initial intra-oral air pressure during the production of aspirated stops at normal volume and the previous recordings of louder “pa’s” during the microphone study which used the same subject (see Fig. 4 in Ref. 14).

For the second round, the rate of lip opening was also captured using IMAGEJ’s point capture utility. The position of the top of the mucous membrane of the upper lip and the crease that intersects the mental protuberance and the skin below the lower lip were recorded frame by frame for 40 ms for each of the 12 recordings. These points provided stable landmarks for measuring the rate of lip opening. The points were converted to distance in millimeters and analyzed statistically.

Numerical simulations

For the base numerical study, a domain of physical dimensions 350×100×100 mm³ which is meshed with 721 800, non-uniform, hexahedral control volumes was used. The mouth is shaped like a narrow ellipse in the x=0 plane, with r_y=2 mm and r_z=15 mm. A rough integration of upper and lower lip pellet velocities from the Westbury paper6 shows that the lips have a y radius of 2 mm ∼17 ms after they begin to separate.

Stevens14 showed the intra-oral pressure quickly dropping after the release burst for “pa;” thus the mouth was modeled as a transient pressure inlet which quickly drops to 1/10th of its initial value, as shown in Fig. 4. In the simulation, the mouth lies in a plane that is modeled as a wall, while the rest of the boundaries are pressure outlets set to atmospheric pressure. The air is incompressible and initially still. Nitrogen particles were injected and tracked as a dye, thus defining the leading edge of the jet. An implicit bounded central differencing spatial discretization and an implicit second-order time discretization with a LES to model this turbulent flow were used. LES resolves the large eddies within the flow, but eddies smaller than the mesh scale are approximated by a turbulence model (in this case dynamic Smagorinsky20). The model was performed over 4000 time steps of size Δt=0.025 ms (t_final=100 ms). Using FLUENT as the solver, and running on three parallel processors, this process took ∼6 days.

To explore the quality of the simulation methods and initial assumptions, numerous variations to this baseline simulation were run; Variation 1: A grid refinement study was performed with the standard hexahedral mesh using a simulation with a medium mesh of 88 380 control volumes and a course mesh of 11 925 control volumes; Variation 2: A similar simulation replacing the mouth-shaped and time-varying inlet with a circular and constant velocity inlet, thus modeling a starting jet from a circular nozzle, was run in order to validate the numerical methods. See Ref. 21 for general discussion of verification and validation; Variation 3: A simulation with the starting inlet pressure three times higher than normal (24 cm/H₂O) yet falling to the same final value (0.703 cm/H₂O) was run to simulate a loud utterance: Variation 4: A simulation with a constant pressure inlet of 7.03 cm/H₂O (690 Pa), which is the same initial pressure of the baseline simulation was also run to test the importance of the transient pressure inlet; Variation 5: A simulation where the initial pressure was raised by 1 Pa was run. This slight change has little effect on the physics, but it does cause the numerics to change slightly, thus providing a second realization of the turbulent flow; Variation 6: A simulation was run where the inlet pressure condition was unchanged, but the initial domain was perturbed with small velocities, thus providing realistic disturbances in the air which are greater than machine zero. Some preliminary simulations in two dimensions, using LES and RANS were also conducted, but these soon proved to be inadequate.

RESULTS

The results of the microphone and high-speed video experiments, along with the numerical simulations, are described below.

Microphone experiment

Of 120 tokens recorded, 90 had discernible pops according to the standards described in Sec. 2A. Individual measurements were highly variable, as seen in Fig. 5; the fit line is based on a loglinear quadratic fit with an assumed zero intercept. The fit line is highly significant, with an F(2,88)=4386, p<0.001 for each coefficient, and adjusted R²=98.9%. Linear, quadratic, cubic, and loglinear statistical models produced less significant results. As a result of trying to produce microphone pops in a microphone 50 cm away, the average intra-oral pressure was ∼25 cm of water, or three times higher than normal, with high variability. This variability is largely a question of repeatability. It is almost impossible for a person to produce a repeatable mouth shape, initial air pressure, rate of decrease in air pressure, rate and degree of mouth opening, and orientation of the mouth to the microphone.

Figure 5.

Experimental pressure fronts.

Many of these variables could not be measured and even initial mouth pressure could not be isolated from the other variables as no significant relationship was found between rate of air travel and intra-oral pressure prior to the release burst.

Nevertheless, the effect of many of these variables is known. Lower initial air pressure, faster rate of decrease in air pressure from the flow source, larger mouth opening, puff orientation away from the microphone, and perturbations in the air all decrease the rate of flow penetration. These effects combined can be quite significant.

High-speed video experiments

For the first round, three high-speed tokens were recorded, but only one was produced at a normal volume and voicing quality for an English “pa” syllable. This token was selected for comparison with the numerical simulations. For the second round of recordings, all 12 recordings were produced at a normal volume and voicing quality for an English “pa” syllable.

Results of measuring the leading edge of the smoke particles for each recording are shown in Fig. 6.

Figure 6.

Leading smoke particle trails for pilot and second-round high-speed video experiment.

Numerical simulations

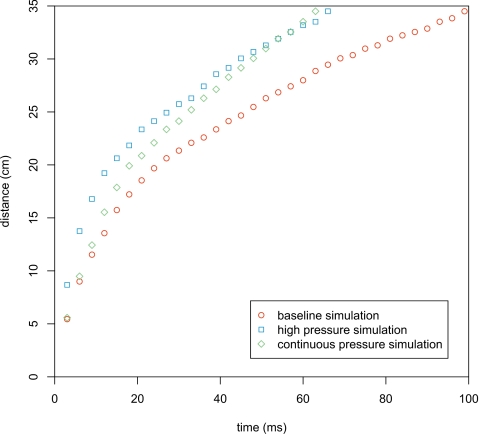
The validation study (variation 2) gives fine agreement with previous jet experiments described in the Introduction, as shown in Fig. 7. Figure 8 shows the grid refinement study (variation 1), along with the perturbed inlet simulation (variation 5) and the perturbed domain simulation (variation 6). The convergence is oscillatory, but outside of the asymptotic range. See Refs. 22, 23 for discussion of oscillatory convergence and complications of LES verification, respectively. A comparison of the baseline numerical simulation, the simulation of the loud utterance (variation 3), and the constant inlet pressure simulation (variation 4) is presented in Fig. 9. As suggested in the Introduction, 2D simulations did not yield realistic results; generally they resulted in a jet penetration rate that was too fast. The loss of the 3D geometry caused the flow to be that of a plane jet rather than a jet from a nozzle. The loss of the 3D flow means that turbulence could not be truly modeled by LES, and the time-averaging of the RANS simulations removed flow details that are of interest. Use of 2D simulations was quickly dropped; therefore these results are not presented in detail here.

Figure 7.

Numerical simulation validation: Starting jet range is defined by the constants reported in the summary of Sangras et al. (Ref. 9).

Figure 8.

Simulation verification: Range represents confidence interval.

Figure 9.

Comparison of leading particle front for baseline, high pressure onset, and continuous pressure simulation.

Comparison of simulation to microphone experiment

The simulation pressure front is defined as the distance at which the absolute value of the pressure reaches 1/10th of the maximum pressure for each time step. The simulation pressure front was compared to the results from the microphone experiment (Fig. 10). The green dots represent the mean measurements from the microphone experiment, the green line represents the loglinear quadratic fit, and the dashed green lines the 95% confidence interval. The simulation pressure front falls within the 95% confidence interval of the experiment.

Figure 10.

Average experimental and simulation pressure fronts.

Comparison of simulation to high-speed video experiment

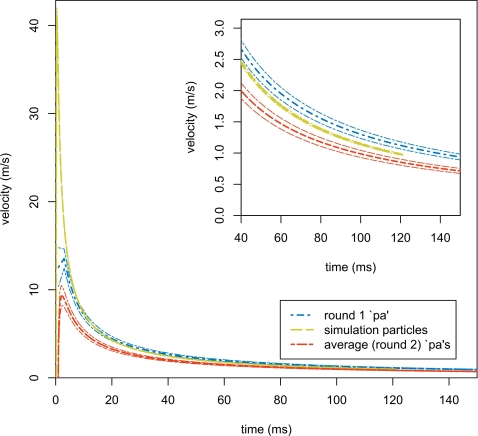
A comparison graph between distance over time of the particle front from the high-speed video recordings and the numerical simulation appears in Fig. 11. The graph shows the loglinear quadratic fit lines for the pilot puff [F(2,89)=1.125×10⁵, p<0.001, adjusted R²=99.9%], second-round puff average [F(3,3598)=7.479×10⁴, p<0.001, adjusted R²=97.7%], and numerical simulation [F(2,1208)=1.816×10⁶, p<0.001, adjusted R²=99.9%]. A comparison graph between the velocities over time of the particle front from the high-speed video recordings and the numerical simulation appears in Fig. 12. Note that the differences diminish dramatically after 40 ms, as shown in the inset within Fig. 12. There is a strong negative relationship between the rate of lip opening and leading particle edge distance traveled for the first 20 ms, diminishing after 30 ms and losing significance by 40 ms, as shown in Fig. 13. Both the significance and the t-value of the partial regression coefficient decrease over time as the leading edge of the puff moves away from the mouth opening. The results can be seen in Table 1.

Figure 11.

High-speed video particle front and simulation particle fronts (distance).

Figure 12.

High-speed video particle front and simulation particle fronts (velocity).

Figure 13.

Negative partial regression between the width of lip opening and leading edge distance.

Table 1.

Partial regressions of the interaction between the leading particle edge and lip opening averaged over 10, 20, 30, and 40 ms.

Coefficient	Time span (ms)	Estimate	Std. Err.	t	p
Puff travel	10	−1.69	0.34	−4.98	*<0.001
Distance	20	−0.81	0.18	−4.46	*<0.001
Lip opening	30	−0.36	0.11	−3.18	*=0.002
Width	40	−0.09	0.08	−1.03	0.304

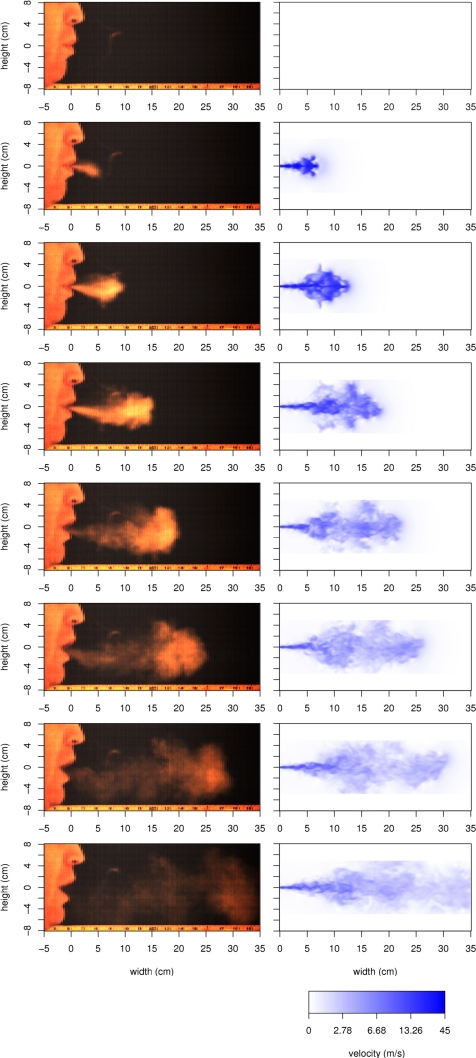
To illustrate the relationship between the smoke particle flow from high-speed film experiment and simulation results, a comparison of the video images from experiment round 1 and the baseline simulation is presented in Fig. 14. Round 1 video was selected to reduce the disparity between the images after time-alignment. Images were aligned such that the times at which the high-speed video’s particle flow penetrates 5, 10, 15, 20, 25, 30, and 35 cm are matched with the same times in the simulation. Because frames are spaced 2 ms apart, the first frame with visible particle flow is assumed to occur ∼1 ms after lip opening. This time-averaging, combined with the observation that the simulation flow rate matches closely, but not exactly with the high-speed video, creates distance alignment differences. As a result, the images do not align by particle front distance, and the differences can be seen in Table 2. The velocity field instead of the particle field is shown because FLUENT does not export the particle data in a usable format and because the particle field can be inferred from the velocity field. In the high-speed video, most of the smoke is expelled in the first 30 ms, so the air expelled after that time is not as visible in the video frames. A graph of the simulated airflow velocity as a function of time in which each curve shows the velocity at a particular distance from the front of the orifice is shown in Fig. 15. The data are spatially averaged over a 1 cm radius in the xz plane and 2.1 ms in time. These lines reveal velocity oscillations around 100 Hz that were not smoothed out by the averaging. The oscillations are caused by large eddies in the flow that are resolved by the LESs, but which would not have been resolved with a RANS simulation.

Figure 14.

“Pa” on high-speed video (left) compared with numerical simulation velocity field (right). From top to bottom, the times (in milliseconds) of the image are 0, 5, 11, 21, 35, 51, 75, and 121.

Table 2.

Time-alignment by distance for Fig. 14.

Time (ms)	Paticle distance (cm) by data source
	High-speed video	Simulation
5	5.3	8.1
11	9.7	12.8
21	15.2	18.5
35	20.1	22.3
51	25.1	26.3
75	30.0	31.0
121	35.0	>34.8

Figure 15.

Airflow velocity over time based on the distance from orifice aperture.

DISCUSSION

These results show some significant discrepancies between the microphone experiment, the high-speed video experiment, and the simulations, but upon examination, these errors make sense in light of the assumptions and experimental methods used.

The microphone experiments were expected to show faster penetration than normal because the average intra-oral pressure was three times higher than normal, which was needed to attain good recordings. This impact, however, was not expected to be too large because velocity scales with the square root of pressure, as derived from Bernoulli’s principle. Also, the air-pressure measurements showed that it quickly fell to the normal level predicted in Stevens’ book.14 Therefore, the effect of the intra-oral air pressure would be less than one might expect, and the differences would be most significant at distances closest to the mouth.

The microphone experiment had a high variance due in part to the difficulty in capturing the microphone pops, especially at increasing microphone distances. Because of this high variance, the simulations fell within the range of results from the microphone experiment.

The high-speed video experiments, on the other hand, were captured at pressures reasonable for speech and were deemed trustworthy.

The measurements taken from the high-speed video were much more accurate than those taken from the microphone pop experiment as there were no visual artifacts interfering with visibility of the leading edge of the smoke comparable to the interference of the acoustic waves on the capture of microphone pops. Most of the variability in recorded results was seen in the rate of particle penetration during the first 40 ms, and could be largely attributed to the rate of lip opening during the first 20 ms. The faster the lips opened, the slower the initial penetration. Very tiny differences were significant.

The measured strong negative relationship between the rate of lip opening and the “pa” leading edge velocity was unexpected. Boundary layer effects would tend to produce a positive relationship between lip opening and “pa” velocity, so the negative relationship implies a more complex phenomenon, perhaps related to the geometry of the mouth behind the lips.

As discussed in the Introduction, there were a number of simplifying assumptions made for the simulation, particularly concerning the mouth. Not including the lips in the model means that the boundary layer effects were not modeled; these effects slow the jet. Also, Pelorson et al.7 discussed the dominant role of viscous effects at the lips in the first milliseconds of a plosive, and Fujimura24 also emphasized the rapidity of the change in the first 10 ms. Figure 12 shows that most of the simulation error occurs in the first 10–20 ms of the burst where the simulation velocity is much higher than experiment, and the data in Fig. 13 and Table 1 confirm that the simulations suffer this error. This error largely accounts for the differences between the high-speed video experiment and the simulation.

Future work

The velocity data in this paper can be used to identify the maximum distance a perceiver can be positioned away from a speaker in order to detect puffs of air from labial plosives during their speech (though the minimum velocity at which skin receptors can detect air flow is as yet unknown), or as a basis for identifying the minimum distance a microphone needs to be from a speaker based on the microphone’s sensitivity to air-flow velocity.

While the simulations and the experiments match closely after 40 ms, the simulations predict faster airflow at the onset of the puff than that shown in the experiments. This difference was partially related to the fact that the mouth shape expands during the production of the “pa” syllable, but not in the simulation. Simulation of the change in oral aperture size would require changing the mesh throughout the simulation. This would be a challenging problem for further research. In addition, mesh and time step refinement may improve the quality of the simulations.

CONCLUSION

The results show that the hypotheses regarding the need for 3D LES with a mouth-shaped orifice and decreasing air pressure at the orifice are all reasonably valid for the accurate simulation of airflow after the release of an aspirated labial plosive. While the static elliptical orifice provided an adequate basis for simulation, the static and anatomically incorrect mouth shape contributed to the observed discrepancies in the results. Simulations involving a change in the orifice shape throughout the simulated time period, corresponding to known mouth shape changes in the production of labial plosives, may resolve this discrepancy.

By validating air-flow simulations to experimental data, it is possible to plot mean velocity in time as a function of downstream distance. This information can be used with experimental data to identify the distance away from the orifice or the time from the beginning of a speech release burst at which a person can perceive the airflow or a given microphone can pick up a pop.

These results provide the groundwork upon which future research in microphone manufacturing, sound engineering, speech perception research, and aerodynamic modeling of speech may be conducted.