Bone sonometry: Reducing phase aberration to improve estimates of broadband ultrasonic attenuation

Abstract

Previous studies suggest that phase cancellation at the receiving transducer can result in the overestimation of the frequency dependent ultrasonic attenuation of bone, a quantity that has been shown to correlate with bone mineral density and ultimately with osteoporotic fracture risk. Evidence supporting this interpretation is provided by phase insensitive processing of the data, which appear to reduce the apparent overestimates of attenuation. The present study was designed to clarify the components underlying phase aberration artifacts in such through-transmission measurements by conducting systematic studies of the simplest possible test objects capable of introducing phase aberration. Experimental results are presented for a Lexan phantom over the frequency range 300–700 kHz and a Plexiglas phantom over the 3–7 MHz range. Both phantoms were flat and parallel plates featuring a step discontinuity milled into one of their initially flat sides. The through-transmitted signals were received by a 0.6 mm diameter membrane hydrophone that was raster scanned over a grid coaxial with the transmitting transducer. Signals received by the pseudoarray were processed offline to emulate phase sensitive and phase insensitive receivers with different aperture diameters. The data processed phase sensitively were focused to demonstrate the results of planar, geometrical, and correlation-based aberration correction methods. Results are presented illustrating the relative roles of interference in the ultrasonic field and phase cancellation at the receiving transducer in producing phase aberration artifacts. It was found that artifacts due to phase cancellation or interference can only be minimized with phase insensitive summation techniques by choosing an appropriately large receiving aperture. Data also suggest the potentially confounding role of time-and frequency-domain artifacts on ultrasonic measurements and illustrate the advantages of two-dimensional receiving arrays in determining the slope of attenuation (nBUA) for the clinical assessment of osteoporosis.

INTRODUCTION

Phase cancellation at a phase-sensitive (piezoelectric) receiver has been known to result in artifacts in measurements of broadband ultrasonic attenuation (BUA) in a number of studies of cancellous bone.1, 2, 3, 4, 5, 6, 7 (Normalized broadband attenuation or nBUA is the slope of a line fit to the measured attenuation coefficient plotted as a function of frequency, a quantity sometimes referred to as the slope of attenuation.) Phase cancellation effects result in the overestimation of BUA, a quantity that has been shown to correlate with bone mineral density1, 8, 9, 10, 11, 12, 13, 14 and therefore osteoporotic fracture risk.15, 16, 17, 18, 19, 20, 21, 22

Measurements of bone are complicated by many factors associated with their inhomogeneous character and irregular shapes, making it difficult to sort out potential physical mechanisms underlying phase aberration artifacts. In vitro studies of calcaneus bone samples by Wear6 and Strelitizki et al.3 and studies in human subjects by Wear4 and Petley et al.2 appear to indicate that phase insensitive processing of array data yields improved estimates of the true ultrasonic attenuation. Studies by Langton et al.7, 23 and by Xia et al.5 suggest that phase aberration artifacts in cancellous BUA measurements are exacerbated by the surrounding cortical bone layer. Techniques by Ermert et al.,24 Defontaine et al.,25 and Eddin et al.26 incorporating the use of phased arrays, designed to adaptively correct for phase aberration in through-transmission and backscatter measurements of cancellous bone, support the hypothesis that phase aberration is a source of potential measurement artifacts.

The present study was carried out on simple phantoms whose intrinsic attenuation coefficients could be measured independently. This approach provides a starting point for differentiating between contributions to phase aberration artifacts from two sources, phase cancellation at the receiving transducer and interference effects in the ultrasonic field.

Interference in the ultrasonic field results from a spatial redistribution of energy without energy loss. That is, for any local reduction in the average amplitude of the pressure field (due to partial or total destructive interference) there will always be another region of higher-than-average amplitude of the pressure field. Energy is only ostensibly lost to interference; it may have simply been redistributed, potentially missing the receiving transducer.

In contrast, phase cancellation occurring at the surface of a phase sensitive receiver is an irreversible loss of energy, but is solely an instrumental effect. Local compressions and expansions produce surface charge distributions of opposite sign in the piezoelectric receiving transducer’s conductive plating.27 The associated currents in these electrodes result in an irrecoverable loss of energy as a result of current flow among locally produced positive and negative electrical signals.

The purpose of the present study is to illustrate how the size of the receiving aperture influences estimates of apparent attenuation as a result of diffraction and interference occurring in the field and phase cancellation occurring at the surface of a piezoelectric receiver. That is, artifacts due to phase cancellation or interference can only be minimized with phase insensitive summation techniques by appropriate choice of receiving aperture. In the present paper, through-transmission measurements of the apparent attenuation properties are conducted over two bandwidths, 300–700 kHz and 3–7 MHz, on the simplest possible test objects capable of introducing phase aberration. The two phantoms studied were flat and parallel Lexan and Plexiglas plates featuring a step discontinuity milled into one of their initially flat sides. Data were acquired over a two-dimensional receiving pseudoarray and processed phase sensitively and phase insensitively to emulate receiving apertures with different diameters. The phase sensitive data were further processed to represent a planar, spherical, and correlation-focused receiving phase sensitive transducer.

METHODS

Sample preparation

The two phase aberrating phantoms used in this investigation were constructed from single sheets of poly(methylmethacrylate) (Plexiglas) and polycarbonate resin thermoplastic (Lexan) initially machined into flat and parallel pieces. The piece used for the data collected over the bandwidth centered at 5 MHz was 50.8 mm (2 in.) long, 50.8 mm (2 in.) wide, and 12.7 mm (0.5 in.) thick. The piece used for data collected over a bandwidth centered at 500 kHz was 114.3 mm (4.5 in.) long, 114.3 mm (4.5 in.) wide, and 19.1 mm (0.625 in.) thick. Step discontinuities were then milled into the surfaces of both plates, resulting in each plate having two distinct thicknesses. For each plate the thinner of these two sides will be referred to as the thin side and the thicker of the two sides will be referred to as the thick side. The step milled into the Plexiglas sample for the 5 MHz data was approximately 0.32 mm (0.0125 in.) and the step milled into the Lexan sample for the 500 kHz data was approximately 4.6 mm (0.181 in.). These step sizes were chosen so that phase cancellation artifacts occurring at the surface of a phase sensitive receiver would arise at approximately the midbandwidth of each frequency range, 500 kHz and 5 MHz.28, 29

Experimental methods

Data centered about 500 kHz

Baseline attenuation measurements of Lexan over a bandwidth of 300–700 kHz were made using a matched pair of planar, 28.575 mm (1.125 in.) diam, single-element transducers nominally centered at 500 kHz (Panametrics v391, Waltham, MA). The two transducers were separated by 127 mm (5 in.), approximately twice the near field distance of either transducer. The transmitting transducer was excited by a single-cycle 500 kHz tone burst from a pulse∕function generator (HP 8116, Palo Alto, CA) passed through a 50 dB gain radio frequency (rf) amplifier (ENI 240L, Rochester, NY) and a Diplexer (Ritec, Warwick, RI). The received signal was sent to the 50 Ω input of an 8-bit digitizing oscilloscope (Techtronix 5052b, Beaverton, OR). The resulting time-domain signals were digitized at a rate of 125 MS∕s (800 ns∕pt) and temporally averaged 256 times.

The attenuation coefficient of the Lexan sample was measured at 25 individual sites over the flat and parallel Lexan plate (over a 5 by 5 site grid in the center of the sample) in through transmission mode to average over slight thickness variations occurring in the sample. These 25 measurements were then averaged to yield the true (unaberatted) attenuation coefficient over this bandwidth (300–700 kHz).

Apparent attenuation measurements of the stepped Lexan plate were performed using a through-transmission setup with the same 28.575 mm planar single-element transducer on transmit and a polyvinylidene fluoride (PVDF) membrane hydrophone (Sonic Industries, model 804, now Sonora Medical Systems, Longmont, CO) on receive. The stepped plastic plate was positioned so that the transmitted field was approximately “split in half” by the step, i.e., approximately 50% of the field insonified the thick part of the plate, and approximately 50% of the field insonified the thin part of the plate. This location has been found to maximize phase cancellation artifacts occurring at the surface of a phase sensitive receiver when transmitting through Plexiglas,29 the subject of the current investigation. The membrane hydrophone scanned the transverse receive plane in steps of 0.4 mm in a raster scan axially aligned with the transmitter from over a 57.6 by 57.6 mm area in the elevational and azimuthal directions. The transmitting transducer was excited by a single cycle 500 kHz tone burst from a pulse∕function generator (HP 8116, Palo Alto, CA) passed through a 50 dB gain rf amplifier (ENI 240L, Rochester, NY). The active element of the hydrophone was 0.6 mm in diameter. The transmitting transducer and the receiving membrane hydrophone were separated by 127 mm (5 in.), and the stepped plastic plate was placed approximately 64.5 mm (2.5 in.) away from the transmitter.

Data centered about 5 MHz

Baseline measurements of the attenuation coefficient of Plexiglas over a bandwidth of 3–7 MHz were carried out using the through transmission setup described in Baueret al.28 The attenuation coefficient was measured over 25 sites on the flat and parallel Plexiglas plate before it was milled using separate transmitting and receiving 6.35 mm (0.25 in.) diam, planar, immersion transducers nominally centered at 5 MHz. The transmitting transducer was excited by a pulser∕receiver (Panamtrics 5800 Waltham, MA) and the propagation path between the two transducers was approximately 76.2 mm (3 in.).

For the data collected over the stepped region of the plastic plate, the 6.35 mm (0.25 in.) transmitting transducer was excited by the Panametrics 5800 pulser∕receiver above, and similar to the Lexan sample above, the incident ultrasonic field was approximately split in half by the stepped plastic plate with approximately 50% of the field insonified the thick part of the plate, and approximately 50% of the field insonified the thin part of the plate to maximize phase cancellation artifacts. The PVDF membrane hydrophone described above was scanned over a 12.8 mm by 12.8 mm area in the transverse receive plane in steps of 0.1 mm across the through-transmitted field.

Data analysis

For both bandwidths investigated in this study, the amplitude attenuation coefficients of the flat and parallel and the stepped plastic plates were determined from a log-spectral subtraction technique

$$\alpha \left(\omega \right)=\frac{20\log \left(\mid {\tilde{U}}_w\left(\omega \right)\mid \right)-20\log \left(\mid {\tilde{U}}_s\left(\omega \right)\mid \right)+10\log \left(T_{\mathrm{ws}}^I{T}_{\mathrm{sw}}^I\right)}{d},$$ (1)

where $\mid {\tilde{U}}_w\left(\omega \right)\mid$ and $\mid {\tilde{U}}_s\left(\omega \right)\mid$ are the magnitudes of the measured response of the water (reference) and sample paths, and $T_{\mathrm{ws}}^I$ and $T_{\mathrm{sw}}^I$ are the intensity transmission coefficients of the water-sample and sample-water interfaces, respectively. The phase velocity and density were experimentally measured for the flat and parallel samples; these values were then used as the input to the formula [4Z₁Z₂∕(Z₁+Z₂)²] to specify the intensity transmission coefficient for all attenuation coefficient calculations. For the stepped plastic plates, the thickness d used in the calculation was the average thickness of the thin and thick sides of each plate. The responses were calculated offline by Fourier analysis of the processed digitized time-domain signals over the bandwidths investigated using the focusing and summation algorithms described below and in the Appendix.0

Summation of received signals

Phase sensitive analysis.

Phase sensitively summing the individual rf waveforms within the two-dimensional array emulates the response of a larger aperture piezoelectric receiver. The signals recorded at each array position are approximately what would be incident on a local region of this large diameter, single element piezoelectric transducer placed at a specific location in the field. For the phase sensitive analysis performed in this study, the rf signals recorded at each position in the array were focused one of three ways (planar, spherical, and correlation as described in the Appendix0), summed, and then normalized by the number of rf signals used for the sum. This procedure produces a single rf waveform for the whole array. This waveform, U_array(t_k), can be written as U_array(t_k)=(1∕N)∑_ijU_ij(t_k), where U_ij(t_k) is the focused (time-shifted) rf signal at the ijth position in the array and N is the number of positions in the array used in the sum. Dividing the sum by N normalizes all later analysis to the area one of the array elements. For the 500 kHz data, sampled rf signals within a radius of 28.575 mm (1.125 in.) from the center of the pseudoarray were used in all subsequent analyses in order to simulate a 57.15 mm (2.25 in.) diameter receiving transducer. For the 5 MHz data, rf signals within a radius of 6.35 mm (0.25 in.) from the center were used in all subsequent analyses in order to simulate a 12.7 mm (0.5 in.) diameter receiving transducer. Therefore, N=16 029 for the 500 kHz data and N=12 645 for the 5 MHz data. After the signals were focused and phase sensitively summed, a fast Fourier transformer (FFT) was performed on U_array(t_k) to obtain the squared magnitude of the frequency domain responses for the water and sample paths used in the amplitude attenuation coefficient calculation in Eq. 1.

Phase insensitive analysis.

Phase insensitive analysis was performed by calculating the squared magnitude of the frequency domain response obtained at each location in the two-dimensional pseudoarray and then summing these power spectra over the pseudoarray for the different aperture diameters described below. The power spectrum recorded at each array position is approximately what would be incident on a small, finite area of a larger power detector, or acoustoelectric receiver.27 The phase insensitive analysis performed in this study did not include any of the focusing techniques employed in the phase sensitive analysis because when a function is delayed (or advanced) by an amount Δt_ij, its Fourier transform is multiplied by a factor e^∓iωΔt_ij.30 Because the magnitude of the frequency domain response was calculated at each location before summation, and the temporal shifts were not of sufficient length to move the acquired temporally localized rf signals outside of the digitized record, the phase insensitive responses would not have been affected by temporal focusing.

The resultant phase insensitive frequency domain response of the array can then be written as

$${\mid {\tilde{U}}_{\text{array}}\left(\omega \right)\mid }^2=\frac{1}{N}\sum _{ij}{\left(\mid \mathit{FFT}\left[U_{ij}\left(t_k\right)\right]\mid \right)}^2.$$ (2)

For the 500 kHz data, masks of two different sizes were implemented in the phase insensitive data analysis to simulate two different diameter receiving apertures: 28.58 mm (1.125 in.) and 57.15 mm (2.25 in.). For the 5 MHz data, masks of two sizes were implemented in the phase insensitive data analysis to simulate two different diameter receiving apertures: 6.35 mm (0.25 in.), and 12.7 mm (0.5 in.).

Another method of phase insensitive summation of acquired rf data would be to sum and average the magnitudes of the rf signals at each array point and then square the average, essentially moving the left parenthesis in Eq. 2 to include the summation symbol; however, only the phase insensitive technique described above was performed for this study.

Nominally, phase insensitive analysis is not subject to artifacts due to phase cancellation at the surface of the receiver. The PVDF membrane hydrophone used is a phase sensitive receiver; however, the active element is only 0.6 mm in diameter. The wavelengths (in water) for the 300–700 kHz data are approximately 5–2 mm, respectively, and 0.5–0.2 mm for the 3–7 MHz data. Phase cancellation should be minimal across the active element of this receiver over both bandwidths studied.

Transverse plane analysis

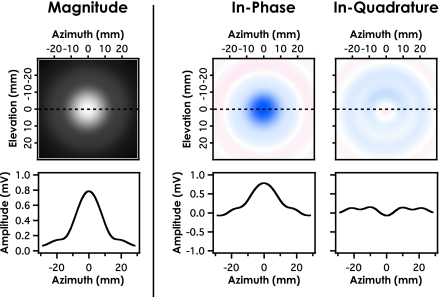
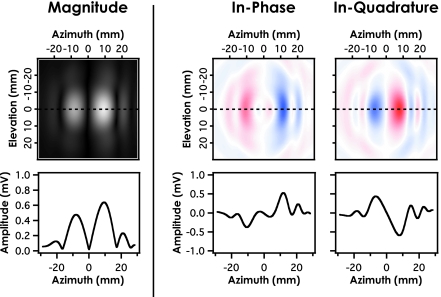
In order to illustrate the potential sources of apparent loss from both phase cancellation and interference for the stepped-Lexan phantom, for each position in the pseudoarray both the water-only reference path and the through sample path were processed to provide the magnitude, in-phase, and in-quadrature components for the 500 kHz component of the received signal. Resulting plots of the magnitude, in-phase, and in-quadrature components over the transverse cross section were analyzed by examining line profiles of each component for that frequency. For purposes of illustration, only the 500 kHz component is displayed in Figs. 45 because the size of the step discontinuity in the Lexan sample was specifically chosen to nominally cancel this particular frequency. The source of this apparent loss should therefore be made most clear at this frequency.

Figure 4.

Magnitude, in-phase, and in-quadrature components of the 500 kHz component of the water reference path. The three line profiles illustrate the symmetry in the pressure field as a function of aperture coordinate for an unaberated field.

Figure 5.

Magnitude, in-phase, and in-quadrature components of the 500 kHz component in the transverse plane as a result of insonifying a stepped (Lexan) plate. Interference artifacts result from local minima and maxima in the pressure field, while phase cancellation effects result from local positive and negative pressures simultaneously incident on the receiver.

RESULTS

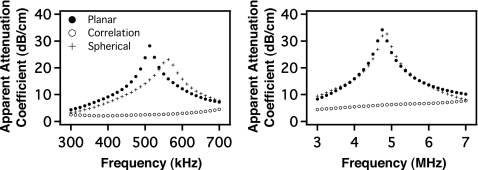
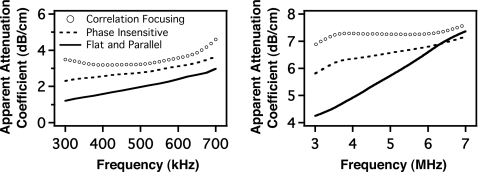
Figure 1 displays the apparent attenuation coefficient obtained with phase sensitive planar, spherical, and correlation focusing as a function of frequency for the data collected over the stepped region of each plate. The anticipated large phase cancellation artifact near band center observed with planar focusing is somewhat reduced by spherical focusing, and is significantly reduced with correlation focusing.

Figure 1.

Phase sensitively processed data collected over stepped plastic plates using three focusing algorithms: spherical, correlation, and planar. The pseudoarray scanned a diameter twice that of the transmitting transducer used for each bandwidth. The data centered at 500 kHz are from a Lexan sample, and the data centered at 5 MHz were collected from a Plexiglas sample.

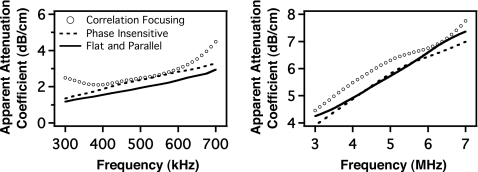
The results obtained with correlation focusing and those obtained with phase insensitive processing are compared with the results of measurements of the flat and parallel plate obtained prior to machining the step in Fig. 2. Error bars are too small to be seen and are not shown. For the relatively large aperture employed (twice the transmitting transducer’s aperture), both phase insensitive detection and correlation focusing with the maximum intensity through-sample signal yield values for the apparent attenuation coefficient that are quite comparable to the values obtained in a flat and parallel specimen free from the phase aberration-inducing artifact.

Figure 2.

Phase sensitively processed correlation data and phase insensitively processed planar data collected through the stepped region of each plate. The pseudo-array scanned a diameter twice that of the transmitting transducer used for each bandwidth. Data are plotted along with the results of insonifying a flat and parallel Lexan (500 kHz) and Plexiglas (5 MHz) sample.

Figure 3 displays data obtained by using a receiving aperture equal to that of the transmitting transducer (that is, one-half the diameter of that employed in Fig. 2). In contrast with the results shown in Fig. 2, neither phase insensitive processing nor correlation focusing is capable of producing results consistent with those obtained from the gold-standard flat and parallel sample. As discussed in Sec. 4, these overestimates of the attenuation coefficient presumably occur as a result of interference in the ultrasonic field that redistributes the energy in a fashion that cannot be overcome by phase insensitive or correlation processing.

Figure 3.

Phase sensitively processed correlation data and phase insensitively processed planar data collected through the stepped region of each plate for a pseudo-array scanning a diameter equal to that used on transmit for each bandwidth. Data are plotted along with the results of insonifying a flat and parallel Lexan (500 kHz) and Plexiglas (5 MHz) sample.

Figures 45 show the magnitude, in-phase, and in-quadrature components of the transverse, receive-plane signals detected by the entire 57.6 mm by 57.6 mm (2.25 in. by 2.25 in.) area hydrophone scan for both the water path signal and the through-sample path signal for the stepped Lexan phantom at 500 kHz. The range of the color map for each figure is different and scaled relative to the maximum amplitude of the magnitude profile at 0 mm elevation. The maximum red and blue value for each figure is the negative maximum amplitude and positive maximum amplitude value respectively. Line profiles taken across the receiver aperture are denoted by the dashed line at 0 mm elevation for all plots and shown below each magnitude, in-phase, and in-quadrature component.

Losses due to phase cancellation arise from the summation over the aperture of positive and negative values in either the in-phase or the in-quadrature components at a given frequency. For phase sensitive detection, the in-phase and in-quadrature components of the incident pressure field are summed separately across the surface, yielding the overall detected field. This instrumental effect is the source of phase cancellation occurring at the surface of a phase sensitive receiver.

Losses due to interference occurring in the ultrasonic field are attributed to local minima or maxima in the magnitude of the detect field. Regions of positive and negative pressures occurring in the field at a specific spatial location simultaneously will partially cancel, leaving a local pressure field of lower magnitude, while regions of same-signed pressures will additively contribute to the local magnitude of the pressure field. This interference that occurs in the field results in an overall redistribution of the total energy and not a loss in energy; any local region possessing a smaller than average pressure field will always be compensated by another region that contains a higher than average pressure field. This can be clearly seen in the magnitude panel of Fig. 5. Again, for purposes of illustration, only the 500 kHz signal is displayed to depict the effects of interference and phase cancellation occurring at the surface of the receiver.

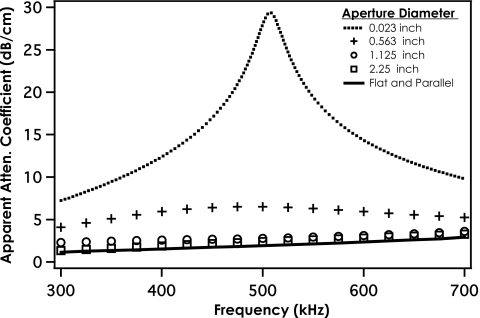
Figure 6 shows the relative impact of aperture size on phase insensitive measurements of the apparent attenuation of the stepped-Lexan phantom compared with the measurement of the true attenuation coefficient of flat-and-parallel Lexan. The four apertures investigated for this figure were 0.6 mm (point-like), 14.28 mm (0.5625 in.), 28.58 mm (1.125 in.), and 57.15 mm (2.25 in.) to simulate four different diameter receiving apertures. Although Figs. 16 are qualitatively similar, the source of apparent loss is quite different. Figure 1 displays the results of phase sensitively summing rf data over a 2.25-in. aperture, while Fig. 6 shows the results of phase insensitively summing rf signals over different aperture sizes.

Figure 6.

Phase insensitive measurements of the apparent attenuation coefficient of the stepped Lexan phantom vs frequency for different diameter apertures.

For the point-like aperture axially aligned with the transmitter in Fig. 6 apparent losses are largely due to interference effects because little phase cancellation can occur across the face of this 0.6 mm (0.023 in.) aperture. This can be seen by looking at the 0 mm elevational line profile of Fig. 5. The amplitude measured at this center location (0 mm azimuth) is very small. As the size of the aperture is increased, artifacts due to interference occurring in the field are reduced as the local minima in the pressure field are countered by local maxima in the pressure field. Therefore, artifacts due to phase cancellation become increasingly dominant for the larger aperture sizes, as more positive and negative (blue and red) pressures are incident over the aperture, as seen in Fig. 5. Measuring the true attenuation coefficient of the Lexan is only possible by scanning a sufficiently large cross-sectional area to recover all of the redistributed ultrasonic energy in conjunction with a phase insensitive detector to eliminate phase cancellation errors. This same behavior was seen in the 5 MHz data for Plexiglas and is not shown.

DISCUSSION

Studies of trabecular bone are complicated by the inhomogeneous structure and irregular shape. Differences in the speed of sound between the solid structure and the marrow (or water) result in significant aberration of the incident ultrasonic beam. Previous investigators have identified phase cancellation at the receiving transducer as a source of artifact in attenuation measurements such as BUA and have illustrated the use of phase insensitive and alternative forms of processing to reduce phase aberration effects.1, 2, 3, 4, 5, 6, 7, 23, 24, 25, 26, 27, 28, 29 In studies of very complicated structures represented by bone, it would be difficult to segregate effects arising from the irreversible loss of energy associated with phase cancellation at the receiving transducer from those arising from lossless redistribution of energy in the ultrasonic field. The present study was designed to permit the segregation of those effects and to illustrate the influence of the size of the receiving aperture on the interplay between these related but distinct phenomena.

Results presented in Figs. 12 establish that for these specimens phase insensitive detection and phase sensitive correlation processing are capable of minimizing artifacts arising from phase cancellation at the receiver, consistent with results previously reported in studies of bone.1, 2, 3, 4, 5, 6, 7 The data presented in Figs. 36, however, indicate that such processing is not sufficient to obtain the true attenuation coefficient if the receiver aperture is not of sufficient size. The presumption is that lossless redistribution arising from interference, and not phase cancellation at the receiver, is the source of the overestimation of the attenuation coefficient shown in Figs. 36. It is also interesting that for this smaller aperture size (Fig. 3), the slope of the measured apparent attenuation coefficient (nBUA) at 5 MHz appears to be underestimated, which counters the presumption that phase cancellation artifacts result in overestimations of nBUA, even though the attenuation coefficient at specific frequencies is still overestimated.

The phase insensitively processed data are in slightly better agreement with the flat and parallel data at 5 MHz than at 500 kHz. This might be due to the difference in the ratio of wavelength to aperture size at each center frequency. The wavelength (in water) to aperture ratio is larger at 5 MHz than at 500 kHz for the two largest apertures used in this experiment (12.7 and 57.15 mm). To compare properly the data at 5 MHz over the 12.7 mm aperture size, one would need a 127 mm (5 in.) diameter receiving aperture for the data centered at 500 kHz. It would be very difficult to employ this large aperture in a clinical setting. Therefore, for specific clinical or experimental investigations, a systematic study may be required to determine the appropriate dimensions for the receiving aperture.

SUMMARY

It has been shown that artifacts due to phase cancellation at the surface of a phase sensitive single element receiver can be minimized using pseudoarray data. The different focusing techniques used in this study reduce substantially the overestimation of the apparent attenuation of both Lexan and Plexiglas over two different bandwidths separated by a decade in frequency. A phase sensitive correlation technique yielded measurements comparable to those from a phase insensitive receiver thus avoiding artifacts arising from the processing of a multicomponent signal as if it were a single component signal. Results presented indicate that even phase insensitively processed data are subject to artifacts due to interference occurring in the field if an insufficiently large receiving aperture is chosen.

APPENDIX: FOCUSING ALGORITHMS

Stored ultrasonic waveforms acquired by the two-dimensional pseudoarray were processed using three focusing techniques: planar focusing, spherical focusing, and correlation focusing. Focusing of the array was achieved by applying the appropriate time shift to the individually acquired rf signals according to their position in the array and type of focusing employed. For the ijth position in the array, the acquired signal is represented by U_ij(t_k), where t_k is some timing marker of the captured rf waveform. Then the focused waveform,${\overline{U}}_{ij}\left(t_k\right)$, can be written ${\overline{U}}_{ij}\left(t_k\right)=U_{ij}(t_k+\Delta t_{ij})$, where Δt_ij is the focusing time shift applied to the array element.

1. Planar focusing.

For planar focusing of the two-dimensional receiver array, a time shift of zero was applied to each signal in the two-dimensional array, i.e., Δt_ij=0. The data approximately represent what a single-element, planar transducer would measure in the field in place of the membrane hydrophone.

2. Spherical focusing.

Spherical focusing was achieved by shifting the rf signals in the two-dimensional pseudoarray by the appropriate time delays according to their positions in the array and the desired focal distance. The time delays were determined by subtracting the time-of-flight of an ultrasonic wave in water from each element in the array to the focal point and the time-of-flight of an ultrasonic wave from the center of the array to the focal point. For the data centered about 500 kHz, the focal point was 63.4 mm (2.5 in.) from the center of the array, and for the data centered around 5 MHz, the focal distance was 38.1 mm (1.5 in.). These focal distances correspond to the distances from the sample to the center of the array in each experiment.

If the focal distance R represents the distance from the center of the array to a point along a line perpendicular to the plane of the array and r^′ is the distance between the center of the array and another point on the array, then the distance between any position in the array and the focal point is $r=\sqrt{r^{\prime 2}+R^2}$. The difference in distance between any array position and the focal point and the center array position and the focal point is then $\Delta r=r-R=\sqrt{r^{\prime 2}+R^2}-R$. Thus, the time shift Δt_ij required to focus any ultrasonic wave on the array to the specified focal point is then $\Delta t_{ij}=\Delta r∕c_w=(\sqrt{r^{\prime 2}+R^2}-R)∕c_w$, where c_w is the speed of sound in water.

3. Correlation focusing.

The correlation focusing method employed to focus the two-dimensional pseudoarray is based in part on techniques introduced previously by others.31, 32, 33 The correlation time shift applied to the rf waveform at each array position in the pseudoarray was chosen by maximizing the cross correlation between the waveform acquired at a given array position and the waveform at a reference position, that of the position of maximum intensity.

The cross-correlation function, C_ij(s) can be written as

$$C_{ij}\left(s\right)=\sum _{t_k=0}^{N-I}{U}^{\prime }\left(t_k\right)U_{ij}(t_k+s),$$

where U^′(t_k) is the time domain response at the reference position, U_ij(t_k) is the response at the ijth position in the array, t_k is a time index corresponding to the sampled points in the rf waveform, and s is the time shift of an integer number of sample points applied to the waveform. The correlation focusing time shift applied to the waveform recorded in each array position, Δt_ij, is then found by maximizing the correlation function, C_ij(s).