Abstract
The primary objective of this work was to develop and optimize the calibration techniques for ultrasonic hydrophone probes used in acoustic field measurements up to 100 MHz. A dependable, 100 MHz calibration method was necessary to examine the behavior of a sub-millimeter spatial resolution fiber optic (FO) sensor and assess the need for such a sensor as an alternative tool for high frequency characterization of ultrasound fields. Also, it was of interest to investigate the feasibility of using FO probes in high intensity fields such as those employed in HIFU (High Intensity Focused Ultrasound) applications. In addition to the development and validation of a novel, 100 MHz calibration technique the innovative elements of this research include implementation and testing of a prototype FO sensor with an active diameter of about 10 μm that exhibits uniform sensitivity over the considered frequency range and does not require any spatial averaging corrections up to about 75 MHz. The results of the calibration measurements are presented and it is shown that the optimized calibration technique allows the sensitivity of the hydrophone probes to be determined as a virtually continuous function of frequency and is also well suited to verify the uniformity of the FO sensor frequency response. As anticipated, the overall uncertainty of the calibration was dependent on frequency and determined to be about ±12% (±1 dB) up to 40 MHz, ±20% (±1.5 dB) from 40 to 60 MHz and ±25% (±2 dB) from 60 to 100 MHz. The outcome of this research indicates that once fully developed and calibrated, the combined acousto-optic system will constitute a universal reference tool in the wide, 100 MHz bandwidth.
Keywords: Nonlinear propagation, Spatial averaging, Piezoelectric polymer ultrasound hydrophone probes, Fiber optic hydrophone probe, Hydrophone calibration
1. Introduction
In the recent decade the importance of measurements in the frequency range above 20 MHz increased significantly. Modern ultrasound diagnostic systems routinely use harmonic imaging and operate at center frequencies close to 15 MHz. The existing AIUM/NEMA standards and FDA guidelines require the acoustic output characterization using hydrophone probes calibrated to eight times the center frequency of the imaging transducer [1-3]. Thus, the ultrasound field generated by imaging arrays in the 12-15 MHz range should be measured by a calibrated hydrophone probe having bandwidth on the order of 100 MHz [1-4]. Additional need for hydrophones calibrated and operating in 100 MHz bandwidth is due to growing interest in high frequency diagnostic applications. Specifically, catheter based systems often use frequencies beyond 20 MHz. Also, characterization of vasa vasorum and vulnerable plaque is being conducted using catheters operating in the frequency range of 20-60 MHz [5].
In addition to diagnostic applications, the characterization of High Intensity Focused Ultrasound (HIFU) fields is of interest. Detailed characterization of the HIFU produced fields is crucial for optimizing tissue ablation and minimizing collateral damage. The measurement of these fields is difficult as widely used piezoelectric hydrophone probes cannot withstand the temperatures and/or cavitation effects produced by HIFU or similar transducers in the focal region [6-8].
In this context, it is also important to point out the measurement challenges due to the finite aperture of existing hydrophone probes. A majority of the commercially available probes has a nominal active element diameter or aperture on the order of 500 μm. However, such aperture is too large for measurements in the fields beyond 3 MHz. This is because in order to eliminate the effects of spatial averaging, the hydrophones should be able to sample the field with at least half-wavelength resolution. At 100 MHz such resolution in water medium would require an active aperture on the order of 7 μm.
A design of the fiber optic hydrophone for application in the frequency range 1-50 MHz was recently reported [9], however, the frequency response presented was not uniform. The nonuniformity was most likely due to 10 microns thick polymer film sandwiched between two gold mirrors deposited on the tip of the sensor to improve its performance. As described in the following, to enhance the overall voltage sensitivity of the FO hydrophone the design described here uses 30 nanometers thick gold coating deposited on the tip.
In view of the above, it is clear that there is a well defined need for a novel, rugged hydrophone probe and associated measurement system that not only would be able to perform characterization of diagnostic ultrasound fields in the frequency range up to 100 MHz but also suitable to measure acoustic fields generated by HIFU transducers. Accordingly, the goal of this work was threefold; namely to develop and optimize the calibration technique for ultrasonic hydrophone probes up to 100 MHz, to use this technique to examine behavior of the sub-millimeter fiber optic (FO) sensor probe in this frequency bandwidth and to assess the need for such a sensor as an alternative tool for high frequency characterization of ultrasound fields. The implementation and verification of the novel calibration methods developed is described below along with the results of the preliminary testing. The discussion section summarizes the results obtained and examines the usefulness and applicability of the 100 MHz FO sensor.
2. Methods
In this section the acoustic measurements and acousto-optic instrumentation used to obtain the 100 MHz calibration data and to compare initially the performance of the spatial averaging-free FO sensor prototype with that of the finite aperture polymer hydrophones in time domain are described.
Acoustic measurements: piezoelectric hydrophones
Three unique acoustic methods (Time Delay Spectrometry (TDS) [10, 11], Time Gated Frequency Analysis (TGFA) [12] and semi-empirical nonlinear propagation model [13]) have been combined to determine the frequency dependent sensitivity of the finite aperture hydrophone probes and the frequency response of the 10 μm diameter FO prototype [14-16]. The application of TDS and TGFA equivalent technique in evaluation of the piezopolymer membrane hydrophone frequency response was independently reported in [17]. For the work described here, the TDS and TGFA were selected because they allow the hydrophone’s sensitivity to be determined as quasi-continuous function of frequency, which is of particular importance when the frequency response of needle-type hydrophones is needed. The results presented in the next section were obtained by employing TDS calibration from 1 to 40 MHz, TGFA method from 20-100 MHz and the nonlinear model [13] from 10-100 MHz. This overlapping of frequency ranges allowed verification of the developed calibration approach and minimized the overall uncertainty. To cover 100 MHz bandwidth with the swept frequency methods several acoustic sources were used. The sources employed up to 60 MHz have already been described in [11, 12]. Another customized wideband, focused acoustic source operating at the center frequency of 80 MHz was also used to obtain the frequency response up to 100 MHz. This source (having f-number 2) was designed by the NIH NCRR, The Resource Center for Medical Ultrasonic Transducer Technology, University of Southern California, Los Angeles, CA.
To ensure compliance with the traceability requirements [1-3] the validity of the calibration approach developed was independently confirmed by comparing the sensitivity of the hydrophones calibrated using the combined method described above with the calibration results received from a national laboratory (NPL, UK) up to 60 MHz. No independent verification was available beyond 60 MHz. Therefore, in the frequency range 60-100 MHz the absolute calibration data were obtained making use of the semi-empirical nonlinear model described in more detail in [12, 13]. This previously verified model [12, 13] was employed to predict the pressure-time (p-t) waveforms (and hence the absolute pressure amplitudes) generated by a circular, 10 MHz focused transducer [12]. Once the (point receiver) field prediction was obtained, the p-t waveforms were acquired experimentally at the focal plane of the 10 MHz source by recording the voltage at the hydrophone terminals. The voltage waveforms were corrected for spatial averaging caused by the hydrophone’s finite aperture. After applying FFT transform to the predicted and experimentally determined p-t waveforms, the hydrophone sensitivity in terms of V/Pa was calculated at each of the discrete (harmonic) frequencies generated by a 10 MHz source. The discrete calibration data were verified using the TDS and TGFA methods to yield virtually continuous sensitivity against frequency plot, as shown in Figs. 2 and 3 (Section III).
Figure 2.
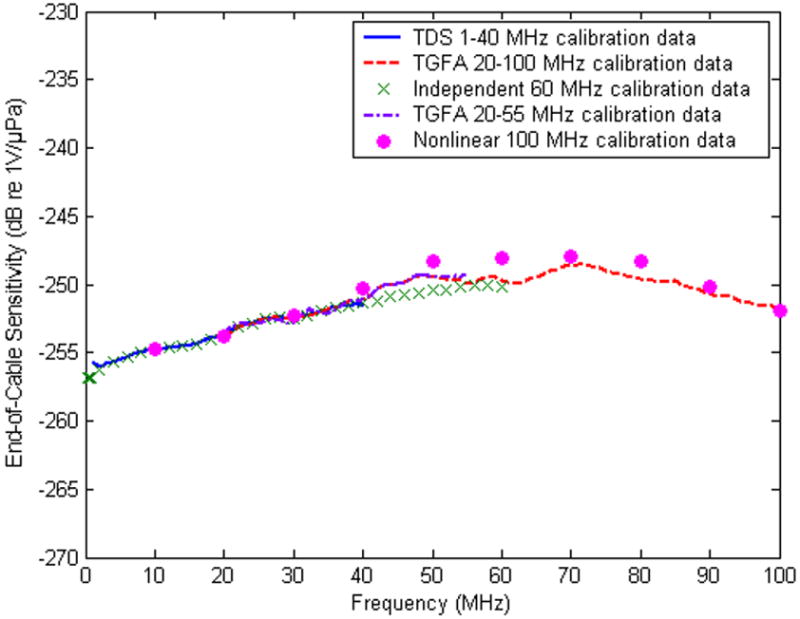
End-of-cable sensitivity (vertical units: dB re 1V/μPa) of a 400 μm diameter bilaminar membrane hydrophone calibrated up to 40 MHz using the TDS method and up to 100 MHz using both the TGFA and the nonlinear techniques in comparison with the independent calibration up to 60 MHz. Error bars were omitted for clarity; overall uncertainty: 1-40 MHz: ±1dB, 40-60 MHz: ±1.5dB, beyond 60MHz: ±2dB.
Figure 3.
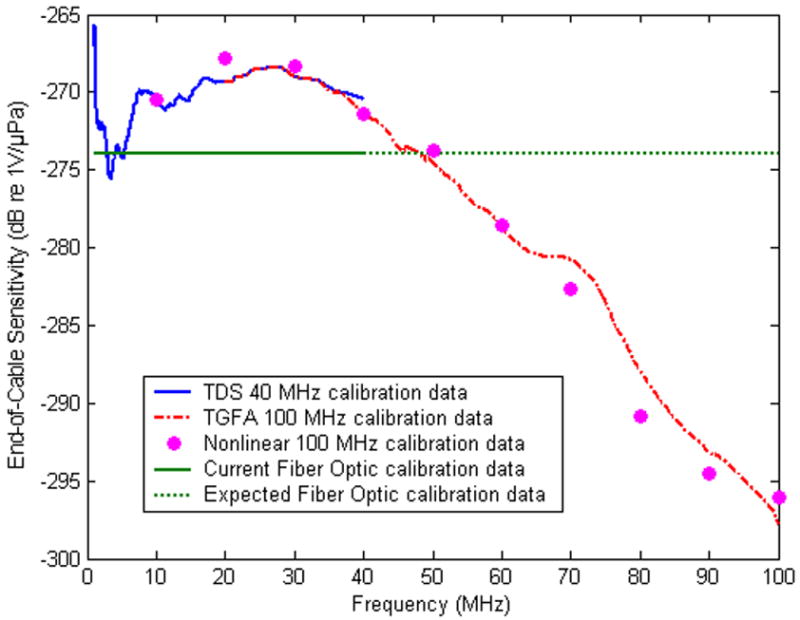
End-of-cable sensitivity (vertical units: dB re 1V/μPa) of a 150 μm diameter needle hydrophone calibrated up to 40 MHz using the TDS method and up to 100 MHz using both the TGFA and the nonlinear techniques. “Horizontal” line at the -274 dB re 1V/μPa level: preliminary data, up to 40 MHz for 10 micrometers diameter tip, early prototype, uncoated, fiber optic hydrophone (see text for details). Error bars were omitted for clarity; overall uncertainty: 1-40 MHz: ±1dB, 40-60 MHz: ±1.5dB, beyond 60MHz: ±2.5dB.
Acousto-optic measurements: fiber optic hydrophone probe
As mentioned earlier, the finite aperture of piezopolymer hydrophones introduces spatial averaging errors. To alleviate this problem, a fiber optic (FO) hydrophone probe was designed. The fiber optic hydrophone system was constructed using commercially available standard single mode, 10/125 μm fibers, which were FC/APC connectorized taking advantage of the higher return loss of the APC polish [16]. The sensitive tip of the FO prototype used here was about 10 μm in diameter, so effectively it could be treated as a point receiver up to about 75 MHz. The improved prototype being developed will extend the point receiver behavior up to 100 MHz by reducing the diameter to about 7 μm. An experimental set up of the acousto-optic measurement system is shown in Fig 1. The specific components of the set-up are briefly described below.
Figure 1.
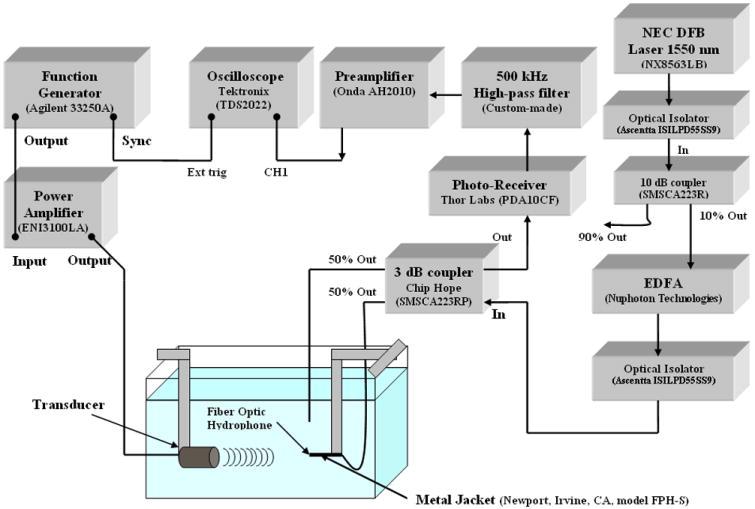
The experimental set up of the acousto-optic measurement system.
Optic source
As the optic source, the 1550 nm distributed feedback (DFB) Laser (NEC Electronics Inc., Japan) producing a minimum output power of 10 mW was used. The laser was “pigtailed” with a polarization maintaining fiber which ensured direct coupling of light and eliminated the need for collimation lenses and other optical instrumentation. The laser was connected to the optical isolator (Ascentta, Somerset, NJ, model ISILPD55SS9) and then coupled to a 10 dB optical coupler (Chip Hope Technology, Lemoyne, PA, model SMSCA223R). This configuration provided -12 dBm power at the input of the Erbium doped fiber amplifier, EDFA (Nuphoton Technologies, Inc., Murrieta, CA). The EDFA was a RS 232 controlled with an optical gain block of 40 dB capable of providing up to 30 dBm of optical output power.
Optic Receiver
The optic receiver used in the measurements was a wide band Indium Gallium Arsenide (InGaAs) detector (Thor Labs, Newton, NJ, model PDA10CF). It had a responsivity of 0.95 A/W at 1500 nm with a signal bandwidth of 150 MHz for a trans-impedance gain of 5 kΩ. The noise equivalent power was specified by the manufacturer as 1.2×10-11 W/(Hz)1/2.
Optic sensor
The EDFA output was connected to the optical isolator to ensure unilateral transmission of light. The signal was then divided equally using a 3 dB 2×2 coupler (Chip Hope Technology, Lemoyne, PA, model SMSCA223RP). One of the output leads was immersed in water whereas the other lead acted as the hydrophone probe and was controlled by a precision scanning system (Parker Hannifin Corporation, Compumotor Division, Rohnert Park, CA) that provided six-axis positioning. The precision of each axis was repeatable to within 0.1 μm. The fiber optic sensor was inserted through the barrel of a fiber optic metal jacket (Newport, Irvine, CA, model FPH-S) with approximately 1 mm of bare glass protruding beyond the metal jacket to minimize the ringing effect of the tip. Once the fiber had been inserted into the metal jacket, the jacket was mounted in the water tank and the FO hydrophone system was activated by turning on the laser source.
High pass filter, preamplifier and oscilloscope
As already noted, light launched into the first input lead from the laser diode module was passed through the optical isolator and then was attenuated by approximately 10 dB using a 10 dB optical coupler. The 10% power output of this coupler was fed to EDFA to boost the signal up to 30 dBm. The output from EDFA was connected to the optical isolator and then split equally using a 3 dB coupler. The output was then directed to both the test lead and the second output lead. The test lead was placed in the acoustic field, and its refractive index at the fiber end-face changed according to the pressure exerted by the acoustic source [18]. This caused the light signals to be directed back through the coupler (again being attenuated by about 3 dB) to each of the two input leads. The photo-receiver (Thor Labs, Newton, NJ, model PDA10CF) was used to convert the light signals to the electrical voltage. The voltage signals representing the acoustic pressure-time waveform were filtered by the custom-made 500 kHz high-pass filter, amplified using a 20 dB voltage preamplifier (Onda Corp., Sunnyvale, CA, model AH-2010) and displayed on an oscilloscope (Tektronix, model TDS 2022).
Acoustic source
In addition to above mentioned wideband acoustic sources that were employed to determine 100 MHz frequency response of the finite aperture piezoelectric hydrophones a high intensity focused (HIFU) transducer (Sonic Concepts, Woodenville, WA) was used to test the point receiver - FO sensor in time domain at the elevated pressure amplitude level. To maximize the longevity and stability of the HIFU source operation it was driven at about 100 Vpp and produced pressure amplitude of approximately 5 MPa. The source allowed operation at 2 center frequencies, 1.52 MHz and 5 MHz; the bandwidth of the fundamental and 3rd harmonic frequency ranged from 1.41-1.98 MHz and 5-5.7 MHz, respectively. The transducer had an active diameter of 20 mm and a focal length of 34 mm (focal number 1.9). It required an impedance matching network and was activated by an (50Ω) ENI power amplifier (ENI3100LA).
Voltage sensitivity of the fiber optic hydrophone probe
The sensitivity of the fiber optic hydrophone probe (S) was determined using substitution technique [14-15]. Briefly, a previously calibrated PVDF needle hydrophone probe (Force Institute, Copenhagen, Denmark) with the active diameter of 500 μm was used to acquire the pressure-time waveform and determine steady state peak-peak pressure amplitude (p). The needle hydrophone was then replaced by a fiber optic (FO) hydrophone probe and the voltage signal (Vo) produced by the fiber optic hydrophone probe was maximized and recorded. The fiber optic hydrophone’s sensitivity was calculated by dividing the voltage signal (Vo) measured by the fiber optic hydrophone probe by the acoustic pressure (p) measured by the needle hydrophone.
3. Results
All calibration measurements were performed at 22 deg C in deionized water and a tank having dimensions 1 m × 1 m × 60 cm. A 400 μm diameter bilaminar PVDF membrane hydrophone (Precision Acoustics, UK) calibrated by National Physical Laboratory (NPL), UK up to 60 MHz was used as a primary reference. Another, in-house calibrated 400 μm diameter bilaminar membrane hydrophone manufactured by Sonora Medical Systems, Inc (Longmont, CO, USA) was also used as an auxiliary reference. Representative calibration data for a membrane and needle type hydrophones are shown in Figs. 2 and 3.
The information on the hydrophones apertures and the overall uncertainty of the calibration is provided in respective captions. Agreement between the different calibration methods varied depending on frequency. Fig. 2 shows that in the frequency range up to 40 MHz this agreement is within ±0.5 dB or about ±5%. The discrepancy between TGFA and nonlinear calibration increases slightly beyond 40 MHz and exhibits a maximum of about 2.5 dB in the vicinity of 60 MHz. The reason for this discrepancy is currently being investigated. For the 150 μm needle hydrophone (Fig. 3) the agreement between the data obtained using the nonlinear method and the quasi-continuous one is less favorable with the discrepancies reaching 2 dB at 20 MHz, and 2.5 dB at 70 and almost 3 dB at 80 MHz. Again, the cause for these disagreements is being examined as there is no apparent reason for their existence.
Fig. 4 shows a comparison of the pressure-time waveforms measured by the FO hydrophone probe and a 500 μm diameter PVDF needle hydrophone probe under the same excitation conditions. To account for different voltage sensitivities of the probes the plot has been normalized. The acoustic source generating the tone burst waveforms was the 1.52 MHz HIFU transducer (focal number 1.9) transmitting a ten-cycle pulse at 5% duty cycle (pulse repetition period of 132 μs). The peak-to-peak pressure amplitude was determined to be approximately 5 MPa. The waveform received by the FO hydrophone probe was averaged using 128 point averaging prior to recording to improve the signal-to-noise ratio. In addition, before the waveform of the FO hydrophone probe was displayed on the oscilloscope (Tektronix TDS 2022), it was filtered by the custom-made 500 kHz high-pass filter and amplified by 20 dB voltage gain preamplifier (Onda Corp., Sunnyvale, CA, model AH-2010).
Figure 4.
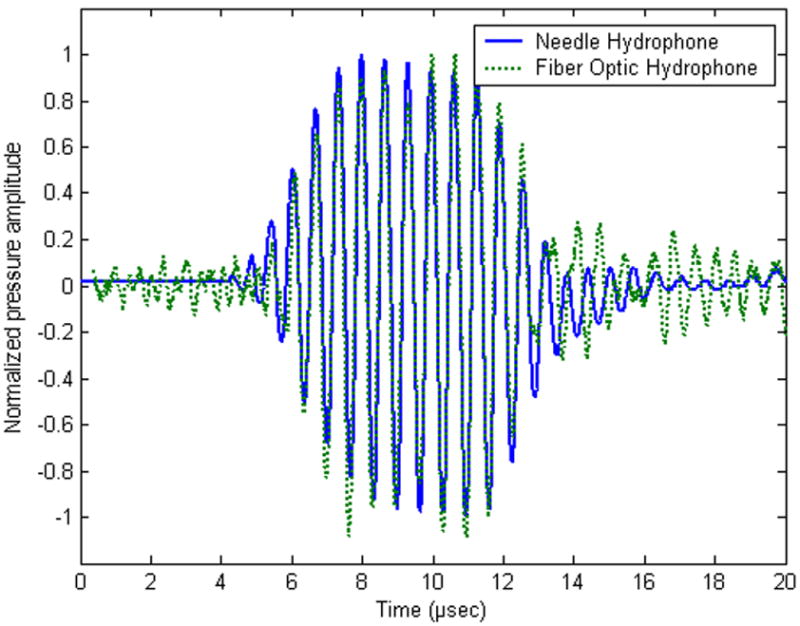
Normalized 5 MPa peak-to-peak pressure time waveforms obtained by a 500 μm diameter needle hydrophone probe and the fiber optic (FO) hydrophone probe using a 1.52 MHz HIFU acoustic source (focal number 1.9).
4. Discussion and conclusions
The results of Figs 2 and 3 confirm that quasi-continuous calibration of hydrophones in the frequency range up to 100 MHz is possible using a combination of TDS, TGFA and nonlinear methods. As anticipated, the frequency response of the membrane hydrophone shown in Fig. 2 does not exhibit any rapid variations in sensitivity as a function of frequency. These results are in agreement with those presented in [17] and [19].
The advantage of using quasi-continuous calibration methods such as TDS and TGFA is obvious from the analysis of the plot of 150 μm needle hydrophone shown in Fig. 3. The rapid variation in the sensitivity in the frequency range 1-10 MHz would not have been possible to detect in all details using a discrete frequency calibration approach.
For comparison, frequency response of the 10 μm diameter, uncoated, early prototype FO probe is also shown in Fig. 3. The FO probe sensitivity was obtained by the substitution technique using the 500 μm diameter PVDF needle hydrophone as a reference. Spatial averaging correction was applied to account for different active apertures of the probes [11]. The sensitivity shown in Fig. 3 was determined as 20 mV/MPa (or -274 dB re 1V/μPa). Although no calibration was performed beyond 40 MHz, the uniformity of the response indicates that similar response can be anticipated at the frequencies up to 100 MHz. Such uniform response would make the FO hydrophone useful in determining phase response of piezoelectric hydrophones. Although the phase can also be determined using the nonlinear propagation model [12, 13, 20] the phase measurement would be simplified by using a uniform response hydrophone [17, 19]. The sensitivity of the prototype design shown in Fig. 3 can be improved by almost an order of magnitude by employing a thin, tens of nanometers gold layer deposited at the tip of the fiber. Initial testing performed at 1.5 MHz using the HIFU transducer (see Fig.4) indicated that increasing the incident optic power to 1W (see Fig. 1) allowed 30 nm gold thickness layer design to reach the sensitivity level as high as -233 dB re 1V/μPa.
Although the data presented in Figs. 2 and 3 correspond to one membrane and one needle hydrophone, the technique developed was successfully employed to calibrate over 10 different hydrophone probes available and, as noted above, yielded results that were consistent with the independent laboratory (NPL) data up to 60 MHz. As pointed out earlier, in the frequency range between 60-100 MHz no independent confirmation of the absolute sensitivity data is available, but the consistency obtained up to 60 MHz with the NPL results and the agreement between the nonlinear discrete data and the virtually continuous TGFA ones indicate that the values of the sensitivity beyond 60 MHz as determined here are correct (to within the overall uncertainty given in Figs 2 and 3). Additional support for this notion comes from the theoretical modeling of the hydrophone responses using PiezoCAD (Sonic Concepts, Woodenville, WA).
In Fig. 4, the normalized pressure-time waveforms measured by the 500 μm diameter needle hydrophone and the fiber optic hydrophone probe using the 1.52 MHz HIFU acoustic source operating at 5 MPa peak-to-peak pressure amplitude are presented. Overall, the measurement results show very good agreement in terms of pulse repetition period, pulse duration and the number of pulse cycles. However, the noise level of the FO hydrophone probe was higher than that produced by the needle hydrophone. This was because the sensitivity of the FO probe was about 10 dB lower in comparison with that of the needle hydrophone and also the experimental set up of the FO probe was more susceptible to the extraneous noise than the measurement arrangement used to record the needle hydrophone signal. It is anticipated that the improvement in the signal-to-noise (S/N) ratio will be achieved by using a differential FO amplifier being currently tested [16].
The availability of a hydrophone probe that would perform as a point receiver in the frequency range considered (here, 100 MHz) and exhibit uniform frequency response is highly desirable. As noted earlier, such probe would be able to reproduce the pressure-time waveforms faithfully without the necessity of applying spatial averaging corrections and also be useful as a reference in determining phase characteristics of finite aperture and limited bandwidth hydrophone probes [17, 19]. In contrast to the optic measurement systems discussed in [19], which employ a fairly complex and expensive interferometric approach, the goal of this work was to examine a feasibility of using a less expensive option based on the designs described in [14, 15, 18]. Similar designs were proved to be useful in HIFU measurements [7, 8], however, the voltage sensitivity of the FO probes described in [7, 8] was inadequate for acoustic output measurements of diagnostic ultrasound imaging equipment. Also, the probes’ aperture was on the order of 100 μm, which would prevent point receiver behavior at frequencies beyond 7.5 MHz. The voltage sensitivity of the 10 μm diameter quasi-point receiver prototype tested here was determined to be about -274 dB re 1 V/μPa (see Fig. 3), however, as noted earlier, the gold coated design will provide voltage sensitivity close to 200 mV/MPa or -234 dB re 1V/μPa. The initial work on the sensitivity enhancement was reported in [15-16]; a more detailed description of the deposition procedure and testing of the gold plated FO hydrophones having different tip geometry (straight-cleaved and tapered) is being prepared for publication. It is anticipated that once fully developed the fiber optic (FO) measurement system described will constitute a universal, (i.e. applicable to both diagnostic and therapeutic ultrasound field measurements) reference tool that is spatial averaging free in the 100 MHz bandwidth.
From the results described in Section III, it can be inferred that both fiber optic and piezoelectric probes have their advantages and disadvantages depending upon the specific task. With the calibration approach presented, the PVDF probes in connection with an oscilloscope offer 100 MHz measurement assembly that is less complex and less expensive than the FO probe’s one. However, their finite aperture and limited bandwidth gradually introduce a phase shift that may have to be accounted for [17, 19, 20]. It was noted earlier that this phase shift could be determined using a nonlinear propagation theory, especially in case of membrane hydrophones [20], however, now and then it may be more convenient to use FO hydrophone probes because their sensitivity is frequency independent and they do not suffer from intrinsic mechanical resonances, so their phase shift will be zero in the whole frequency range considered. Although the FO probe described here was calibrated up to 40 MHz (Fig.3) its bandwidth should exceed readily 100 MHz as it is limited only by the associated electronics. Thus, although their measurement arrangement in more complex than that of the PVDF probes, once calibrated using e.g. the combined approach presented in this work, the FO probes could be conveniently used to determine phase characteristics of finite aperture piezoelectric polymer hydrophones. The only equipment that could limit the bandwidth of the acousto-optic probe assembly used here was the photo-receiver (Thor Labs, Newton, NJ, model PDA10CF) and preamplifier (Onda Corp., Sunnyvale, CA, model AH-2010). Both the photo-receiver and preamplifier exhibited the bandwidth of 150 MHz, which is well beyond 100 MHz considered here.
In conclusion, two swept frequency techniques together with a semi-empirical nonlinear propagation model were combined to form a consistent 100 MHz calibration tool. As the calibration techniques developed do not suffer from any fundamental limitations, they can be easily extended to frequencies beyond 100 MHz. Lower fundamental frequency sources (such as HIFU transducer described in Section 2) are planned to be used in the future to decrease the current 10 MHz frequency intervals used to obtain the discrete calibration data presented in Figs. 2 and 3. Up to 60 MHz, the calibration results were in agreement (see Fig. 2) with the ones obtained from a national laboratory (NPL, UK). As already noted, beyond 60 MHz no independent verification of the data was available but the consistency obtained up to 60 MHz with the NPL results and the agreement between the nonlinear discrete data and the virtually continuous TGFA ones indicate that the values of the sensitivity beyond 60 MHz are correct (to within the overall uncertainty less than ±2 dB). In addition, the results of the calibration of the FO probe indicate that its sensitivity should be uniform (to within the uncertainty of the measurements, ±1 dB). Current research efforts are focused on further improvement of the sensitivity of the FO hydrophone probe [15-16] by optimizing the thickness of the gold layer coating as discussed above and on verification of its uniform sensitivity response up to 100 MHz.
Acknowledgments
Mr. Jonathan Cannata of the NIH Center for Transducer Resources, USC, LA, CA, is thanked for his help with high frequency sources. This work was supported by the NIH grants 5 RO1 EB007117.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.AIUM, Laurel, MD. National Electrical Manufacturers Association (NEMA); Rosslyn, VA: 2004. Acoustic output measurement standard for diagnostic ultrasound equipment. [Google Scholar]
- 2.FDA. Revised FDA 510(k) Information for Manufacturers Seeking Marketing Clearance of Diagnostic Ultrasound Systems and Transducers. 1997 September 30; [Google Scholar]
- 3.American Institute of Ultrasound in Medicine (AIUM), Laurel, MD. National Electrical Manufacturers Association (NEMA); Rosslyn, VA: 2001. Standard for Real-Time Display of Thermal and Mechanical Acoustic Output Indices on Diagnostic Ultrasound Equipment, Rev. 1. [Google Scholar]
- 4.Bleeker HJ, Lewin PA. A novel method for determining calibration and behavior of PVDF ultrasonic hydrophone probes in the frequency range up to 100 MHz. Ultrasonics, Ferroelectrics and Frequency Control, IEEE Trans UFFC. 2000;47:1354–1362. doi: 10.1109/58.883524. [DOI] [PubMed] [Google Scholar]
- 5.Carlier S, Kakadiaris IA, Dib N, et al. Vasa vasorum imaging: a new window to the clinical detection of vulnerable atherosclerotic plaques. Curr Atheroscler Rep. 2005;7:164–169. doi: 10.1007/s11883-005-0040-2. [DOI] [PubMed] [Google Scholar]
- 6.Yang X, Roy RA, Holt RG. Bubble dynamics and size distributions during focused ultrasound insonation. J Acoust Soc Am. 2004;116:3423–3431. doi: 10.1121/1.1823251. [DOI] [PubMed] [Google Scholar]
- 7.Zhou Y, Zhai L, Simmons R, Zhong P. Measurement of high intensity focused ultrasound fields by a fiber optic probe hydrophone. J Acoust Soc Am. 2006;120:676–685. doi: 10.1121/1.2214131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Parsons JE, Cain CA, Fowlkes JB. Cost-effective assembly of a basic fiber-optic hydrophone for measurement of high-amplitude therapeutic ultrasound fields. J Acoust Soc Am. 2006;119:1432–1440. doi: 10.1121/1.2166708. [DOI] [PubMed] [Google Scholar]
- 9.Morris P, Hurrell A, Beard P. Development of a 50 MHz Fabry-Perot type Fibre-optic hydrophone for the characterisation of Medical Ultrasound Fields. Proc Institute of Acoustics. 2006;(Pt 1):717–725. [Google Scholar]
- 10.Radulescu EG, Lewin PA, Goldstein A, Nowicki A. Hydrophone spatial averaging corrections from 1 to 40 MHz. IEEE Trans UFFC. 2001;48:1575–1580. doi: 10.1109/58.971709. [DOI] [PubMed] [Google Scholar]
- 11.Radulescu EG, Lewin PA, Nowicki A. 1-60 MHz measurements in focused acoustic fields using spatial averaging corrections. Ultrasonics. 2002;40:497–501. doi: 10.1016/s0041-624x(02)00166-x. [DOI] [PubMed] [Google Scholar]
- 12.Radulescu EG, Lewin PA, Wojcik J, Nowicki A. Calibration of ultrasonic hydrophone probes up to 100 MHz using time gating frequency analysis and finite amplitude waves. Ultrasonics. 2003;41:247–254. doi: 10.1016/s0041-624x(03)00123-9. [DOI] [PubMed] [Google Scholar]
- 13.Radulescu EG, Lewin PA, Wojcik J, Nowicki A. Nonlinear propagation model for ultrasound hydrophones calibration in the frequency range up to 100 MHz. Ultrasonics. 2003;41:239–245. doi: 10.1016/s0041-624x(03)00124-0. [DOI] [PubMed] [Google Scholar]
- 14.Lewin PA, Mu C, Umchid S, Daryoush A, El-Sherif M. Acousto-optic, point receiver hydrophone probe for operation up to 100 MHz. Ultrasonics. 2005;43:815–821. doi: 10.1016/j.ultras.2005.05.003. [DOI] [PubMed] [Google Scholar]
- 15.Umchid S, Gopinath R, Srinivasan K, Bansal L, Lewin PA, Daryoush AS, El-Sherif M. IEEE International Ultrasonics Symposium. New York, NY, USA: 2007. 100 MHz sub-millimeter size fiber optic pressure sensors: luxury or necessity? pp. 2013–2016. [Google Scholar]
- 16.Gopinath R, Srinivasan K, Umchid S, Bansal L, Daryoush AS, Lewin PA, El-Sherif M. IEEE International Ultrasonics Symposium. New York, NY, USA: 2007. Improved fiber optic hydrophone Sensors; pp. 2319–2322. [Google Scholar]
- 17.Wilkens V, Moltenstruck W. Broadband PVDF Membrane hydrophone for comparisons of hydrophone calibration methods up to 140 MHz. IEEE Trans, UFFC. 2007;54:1784–1791. doi: 10.1109/tuffc.2007.462. [DOI] [PubMed] [Google Scholar]
- 18.Staudenraus J, Eisenmenger W. Fibre-optic probe hydrophone for ultrasonic and shock-wave measurements in water. Ultrasonics. 1993;31:267–273. [Google Scholar]
- 19.Koch C, Molkenstruck W. Primary calibration of hydrophones with extended frequency range 1 - 70 MHz using optical interferometry. IEEE Trans UFFC. 1999;46:1303–1314. doi: 10.1109/58.796135. [DOI] [PubMed] [Google Scholar]
- 20.Cooling MP, Humphrey VF. A Nonlinear Propagation Model-Based Phase calibration Technique for membrane Hydrophones. IEEE Trans UFFC. 2008;55(1):84–93. doi: 10.1109/TUFFC.2008.619. [DOI] [PubMed] [Google Scholar]


