Using blind source separation techniques to improve speech recognition in bilateral cochlear implant patients

Abstract

Bilateral cochlear implants seek to restore the advantages of binaural hearing by improving access to binaural cues. Bilateral implant users are currently fitted with two processors, one in each ear, operating independent of one another. In this work, a different approach to bilateral processing is explored based on blind source separation (BSS) by utilizing two implants driven by a single processor. Sentences corrupted by interfering speech or speech-shaped noise are presented to bilateral cochlear implant users at 0 dB signal-to-noise ratio in order to evaluate the performance of the proposed BSS method. Subjects are tested in both anechoic and reverberant settings, wherein the target and masker signals are spatially separated. Results indicate substantial improvements in performance in both anechoic and reverberant settings over the subjects’ daily strategies for both masker conditions and at various locations of the masker. It is speculated that such improvements are due to the fact that the proposed BSS algorithm capitalizes on the variations of interaural level differences and interaural time delays present in the mixtures of the signals received by the two microphones, and exploits that information to spatially separate the target from the masker signals.

INTRODUCTION

Much progress has been made over the last three decades in the development of new speech coding strategies for cochlear implants (CIs) (Loizou, 1998). Although CI recipients perform well in quiet listening conditions, several clinical studies have provided evidence that their ability to correctly identify speech degrades sharply in the presence of background noise and other interfering sounds, when compared against that of normal-hearing listeners (Qin and Oxenham, 2003; Stickney et al., 2004). Poor performance in noise can be generally attributed to the significantly reduced spectral resolution provided by current implant devices.

To improve speech intelligibility in noisy conditions, a number of single microphone noise reduction techniques have been proposed over the years (Hochberg et al., 1992; Weiss, 1993; Müller-Deile et al., 1995). Several pre-processing noise reduction strategies have been applied to cochlear implants, but most of these algorithms were implemented on first-generation cochlear implant processors, which were based on feature extraction strategies (e.g., see Loizou, 2006). A few pre-processing algorithms were also evaluated using the latest implant processors. Yang and Fu (2005) investigated the performance of a spectral-subtractive algorithm using subjects wearing the Nucleus22^®, Med−El^®, and Clarion^® devices. Significant benefits in sentence recognition were observed for all subjects with the spectral-subtractive algorithm, particularly for speech embedded in speech-shaped noise. Loizou et al. (2005) evaluated a subspace noise reduction algorithm that was based on the idea that the noisy speech vector can be projected onto “signal” and “noise” subspaces. Results indicated that the subspace algorithm produced significant improvements in sentence recognition scores compared to the subjects’ daily strategies, at least in continuous (stationary) noise.

In short, the previous pre-processing methods attempt to boost the overall speech quality and speech intelligibility by “denoising” the received signal before feeding it to CI listeners. Overall, tests with CI patients have demonstrated some relative improvement in speech recognition. To further improve on open-set speech recognition amidst noise, van Hoesel and Clark (1995) considered a two-microphone noise reduction technique, based on adaptive beamforming, by employing a generalized sidelobe canceller structure originally proposed by Griffiths and Jim (1982), in which a single directional microphone is mounted behind each implanted ear. Their results showed some improvement for all four CI patients tested, however, the effectiveness of the method is limited to only zero-to-moderate reverberation settings (e.g., see Greenberg and Zurek, 1992).

Hamacher et al. (1997) assessed the performance of two adaptive beamforming algorithms in different everyday-life noise conditions. The benefit of the two algorithms was evaluated in terms of the dB reduction in speech reception threshold. The mean benefit obtained using the beamforming algorithms for four CI users (wearing the Nucleus22^® device) varied between 6.1 dB for meeting-room conditions to 1.1 dB for cafeteria noise conditions. A number of studies focusing on speech perception in noise with bilateral cochlear implants, have indicated a substantial and consistent increase with regard to word recognition performance tasks with bilateral electric stimulation when compared to monaural listening conditions (e.g., see van Hoesel and Clark, 1997; Lawson et al., 1998; Müller et al., 2002; Tyler et al., 2002; van Hoesel and Tyler, 2003; Tyler et al., 2003). Positive findings, in terms of improvement on localization and speech reception, with bilaterally implanted adults and children, have been documented in both quiet and noisy settings. In the Tyler et al. (2002) study, a positive outcome was observed for eight out of ten subjects tested. Much of the benefit documented was due to the “head-shadow” effect (Shaw, 1974), which amounts to the advantage gained by placing a second ear with a better signal-to-noise ratio contralateral to the competing noise source. The true “binaural advantage” or “squelch” effect has been found to be considerably smaller (1–2 dB) than the head-shadow effect.

In this contribution, we aim to exploit the presence of two microphones using an adaptive multichannel processing technique other than beamforming. In the multisensor array configuration investigated in this work, speech is assumed to be collected simultaneously over several (two or more) spatially distributed sensors, possibly the microphones located in each of the two (one per ear) behind-the-ear (BTE) processors worn by the bilateral cochlear implant subjects. The main objective is to recover and perceptually enhance the waveform of the desired (target) source signal from a set of composite (or mixed) signals. This paper is organized as follows. The next section offers a general introduction to the topic of blind source separation (BSS) for linear convolutive speech mixtures and a mathematical description of the model and separation algorithm used throughout the paper. Section 3 investigates the performance of the BSS algorithm in anechoic settings (Experiment 1). Section 4 further evaluates the performance of the BSS algorithm in the challenging scenario of reverberant enclosures (Experiment 2).

BLIND SOURCE SEPARATION: BACKGROUND

BSS and independent component analysis (ICA), which is the most effective and most widely used technique to perform BSS (Comon, 1994), were first introduced in the early 1990s. Both methods quickly emerged as areas of intense research activity showing huge potential for numerous practical applications. By definition, BSS deals with the task of “blindly” recovering a set of unknown original signals, the so-called sources from their observed mixtures, based on little to no prior knowledge about the source characteristics or the mixing structure itself. The lack of any a priori knowledge regarding the origin of the linearly mixed observations can be compensated well by the statistically strong yet physically plausible1 assumption of statistical independence amongst all sources (Comon, 1994; Hyvärinen et al., 2001; Stone, 2004).

Proceeding blindly exhibits a number of advantages, with the most important one being that assumptions regarding the room configuration and the source-to-sensor geometry are relaxed (by being only implicitly used) in the separation process (Parra, 2000). The simplest approximation of this type of problem where the mixing coefficients are assumed to be just scaling factors (memoryless channel) has been extensively studied in the literature with the earliest of approaches tracing back to the pioneering work of Cardoso (1989); Jutten and Hérault (1991) and also Comon (1994). Still, this hypothesis of instantaneous (static) mixing is unrealistic for signal propagation inside a natural (or typical) acoustic environment. In reverberant enclosures, each microphone captures the weighted sum of multiple time-delayed versions of the sources instead, which in fact is the convolution of each signal with the acoustic transfer function of the room itself. Accordingly, the task of BSS then becomes equivalent to estimating the unknown room transfer functions (or their inverse) by relying only on combining information obtained from the observed convolutive mixtures captured in each input channel of the microphone array.

Over the years, a number of techniques have been developed to address the problem of separating convolutive mixtures (e.g., see Haykin, 2000; Hyvärinen et al., 2001). In time, the BSS framework has blossomed into a new discipline that has widely benefited the fields of signal processing and neural computation. Recently, some potential advantages stemming from the use of spatial separation schemes to improve speech intelligibility in hearing aid applications have been discussed by Zhao et al. (2002). The adaptive decorrelation filtering approach of Yen and Zhao (1999) was investigated in a “dinner-table” scenario, whereby the target speech is corrupted by a number of speech jammers, as well as noise. Experiments with eight normal-hearing and three hearing-impaired subjects produced an increase in speech reception, albeit the proposed method was somewhat limited to cases where the hearing and microphones were placed closer to the target sources than to the competing speakers.

Mathematical model

Focusing on the realistic dynamic scenario of signal propagation inside a typically reverberant acoustic environment, we are normally confronted with a set of m observed signals denoted here by vector x(t)=[x₁(t),…,x_m(t)^]T, which are considered to be convolutive mixtures of a set of n unknown, yet statistically independent (at each time instant) source signals s(t)=[s₁(t),…,s_n(t)^]T. In this paradigm, the transformation imposed on the sound sources can be essentially seen as being equivalent to linear convolution. As such, the proposed convolutive structure can take into account basic binaural cues used by the auditory system. In the model, these cues can be incorporated in the form of interaural time delays (ITDs) expressed as the delay or lag operator, and also interaural level differences (ILDs) modeled by the variation of the amplitude coefficients of the finite impulse response (FIR) filters.

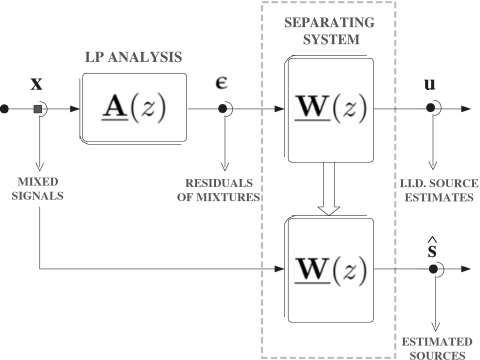
Consider the system shown in Fig. 1. In the context of convolutive BSS, the signal x_i(t) observed at the output of the ith sensor, after being transformed in the z-domain can be written as

$$X_i\left(z\right)=\sum _{j=1}^n{H}_{ij}\left(z\right)S_j\left(z\right),i=1,2,\dots ,m,$$ (1)

where in our case m=2 and n=2. Note also that here H_ij(z) represents the z-transform of the room transfer function or as otherwise referred to, the acoustic impulse response (AIR)2 observed between the jth sound source and the ith microphone (or sensor). The AIR is given by

$$H_{ij}\left(z\right)=\sum _{k=0}^{\ell -1}{h}_{ij}\left(k\right)z^{-k}$$ (2)

where k denotes the discrete-time index, z^−k is the time-shift (unit-delay) operator and finally ℓ defines the order of the FIR filters used to model the room acoustic (or channel transmission) effects. In the most general sense, the goal of BSS is to produce a set of n signals denoted by vector u(t)=[u₁(t),…,u_n(t)^]T, namely the source estimates, which when recovered would essentially correspond to the reconstructed waveforms of the original and otherwise unknown source signals, such that

$$U_j\left(z\right)=\sum _{i=1}^m{W}_{ji}\left(z\right)X_i\left(z\right),j=1,2,\dots ,n.$$ (3)

In practice, W_ji(z) defines the z-transform of the unmixing or separating transfer function between the ith sensor and the jth source estimate written as

$$W_{ji}\left(z\right)=\sum _{k=0}^{\ell -1}{w}_{ji}\left(k\right)z^{-k}.$$ (4)

The cascaded mixing and unmixing system in the case of a two-source two-sensor configuration is shown in Fig. 1. Normally, to use BSS one must presume that the number of microphones is greater than or equal to the number of observed signals, such that m⩾n. In addition, it is often assumed that the unknown mixing system of Eq. 1 can be modeled by using a matrix of FIR filter polynomials. In theory, AIR estimates need to be several thousands of coefficients long, especially when sampled at a sufficiently high sampling rate. However, considering relatively short reverberation times3 and assuming adequately long filters, virtually any source-to-sensor configuration can be adequately modeled by using an FIR filter.4 From a practical standpoint, such a task can be facilitated by resorting to the FIR matrix algebra proposed by Lambert (1996) and Lambert and Bell (1997). Based on this formalism, both mixing and unmixing systems may be ultimately expressed as FIR polynomial matrices, denoted here as $\underset{̱}{\mathbf{H}}(z{)}^{(i\times j\times k)}$ and $\underset{̱}{\mathbf{W}}(z{)}^{(j\times i\times k)}$ having complex-valued FIR polynomials as elements, which in turn are given by Eqs. 2, 4. Note also that in this case i=[1,2,…,m], j=[1,2,…,n], and k=[0,1,…,ℓ−1], are the indices corresponding to the observations, sources, and to each filter coefficient, respectively.

Figure 1.

Cascaded mixing and unmixing MBD system configuration in the two-source two-sensor convolutive mixing scenario.

Algorithm

Since its inception, the entropy maximization algorithm or INFOMAX (see Bell and Sejnowski, 1995) fairly quickly catalyzed a significant surge of interest in using information theory to perform ICA. The potential of entropy (or information) maximization in the framework of BSS for convolutive speech mixtures was explored shortly after by Lambert and Bell (1997) and also Lee et al. (1997). In short, it was shown that an efficient way of updating the separating FIR polynomial matrix $\underset{̱}{\mathbf{W}}$ with respect to its entropy gradient is to use the natural gradient algorithm (NGA) first devised by Amari et al. (1996). In this paper, we opt to use a more efficient implementation of the same algorithm. This employs a two-step optimization strategy. The first step is to use the NGA method to learn the unmixing filters shown in Eq. 4 with independently and identically distributed or temporally independent (white) observations of the sound sources written as

$${ϵ}_i\left(z\right)=\sum _{i=1}^m{A}_i\left(z\right)X_i\left(z\right),i=1,2,\dots ,m,$$ (5)

namely the outputs of the linear prediction (LP) analysis FIR polynomial matrix $\underset{̱}{\mathbf{A}}\left(z\right)$ such that:

$$\underset{̱}{\mathbf{A}}\left(z\right)=\mathrm{diag}[A_1\left(z\right),\dots ,A_m\left(z\right)]$$ (6)

with its elements subsequently given by

$$A_i\left(z\right)=1-\sum _{k=1}^p{\alpha }_i\left(k\right)z^{-k},$$ (7)

where each vector [α_i(k)] represents the LP coefficients and is defined for 1⩽k⩽p, as well as for every i=1,2,…,m. Following this, the second step is to apply the estimated unmixing filters to the initial streams of source observations in order to restore the signals back to their original form (e.g., see Kokkinakis and Nandi, 2004). This alternative “spatial-only” technique proposed for the separation of temporally correlated speech sources by modifying the popular NGA update rule is depicted in Fig. 2. By processing the observed mixtures in such manner, we avoid whitening5 the speech sources as we are successfully differentiating between the actual speech production system, namely the vocal tract and the influence of the acoustic path on the signals at hand. Ultimately, the filtering indeterminacies normally associated with existing BSS techniques are completely alleviated, and the source signals are recovered with their spectral information intact, by resorting to the following update rule (Kokkinakis and Nandi, 2004, 2006):

$${\underset{̱}{\mathbf{W}}}_{k+1}={\underset{̱}{\mathbf{W}}}_k+\lambda [\underset{̱}{\mathbf{I}}-\mathrm{FFT}\left(\phi \left(\mathbf{u}\right)\right){\mathbf{u}}^H]{\underset{̱}{\mathbf{W}}}_k$$ (8)

operating solely on the spatially and temporally independent outputs, written as

$$\mathbf{u}\left(z\right)=\underset{̱}{\mathbf{W}}\left(z\right)ϵ\left(z\right),$$ (9)

where (⋅)^H is the Hermitian operator, λ denotes the step-size (or learning rate), $\underset{̱}{\mathbf{I}}$ defines the FIR identity matrix, FFT[⋅] denotes the elementwise fast Fourier transform operation, and finally, vector φ(u)=[φ₁(u₁),…,φ_n(u_n)^]T represents the nonlinear monotonic activation (or score) functions. Note that here these functions operate solely in the time domain and can be further expressed as

$${\phi }_i\left(u_i\right)=-\frac{d}{d{u}_i}\log p_{u_i}\left(u_i\right)$$ (10)

with the term p_ui(u_i) denoting the (unknown) probability density function of each source estimate u_i. Optimal score activation functions used in the BSS update can be derived by resorting to a fixed family of densities or, alternatively, they can be learned adaptively (e.g., see Kokkinakis and Nandi, 2005).

Figure 2.

Schematic diagram of the alternative BSS system configuration, whereby the observations are first decorrelated through the LP analysis stage yielding a set of temporally independent signals, which are then used to adapt the spatial separation FIR filters.

Implementation

When using BSS, it is often necessary to employ many different FIR filters, and in realistic scenarios should contain thousands of filter coefficients. Conventional adaptive filtering techniques choose to operate solely in the time domain, in which case the filter updates are carried out on a sample-by-sample basis. In such cases, the complexity of the algorithm can become prohibitive. Instead, to reduce excessive computational requirements and potentially achieve considerable savings in complexity, we can make use of a frame-based—or as otherwise known block-based implementa-tion—by relying on the efficient use of the fast Fourier transform (FFT). Such efficient block-wise operations are based on the presumption that parameters remain invariant over a block of data, for example over a predetermined length of time. Block-based implementations demonstrate substantial savings, which in some cases have been reported to be up to 10× faster, when compared against conventional sample-by-sample iterative procedures (Shynk, 1992). In our implementation, all transforms have been assumed to be of length 2L, where L denotes the chosen block size. The overlap between successive frames (or blocks) of data has been set to 50% in all cases.

EXPERIMENT 1. SPEECH RECOGNITION BY BILATERAL COCHLEAR IMPLANT SUBJECTS IN ANECHOIC SETTINGS

Methods

Subjects

A total of five postlingually deafened adults were recruited for testing. The participants of the study, three females and two males, were all bilateral implant patients fitted with the Nucleus24^® multichannel implant device manufactured by Cochlear^®. Their ages ranged from 36 to 67 years old (M=61) and they were all native speakers of American English. Special provisions were made to acquire subjects having a minimum of at least 2 years of experience with their bilateral device. Biographical data for the subjects tested is given in Table 1.

Table 1.

Cochlear implant patient description and history.

	S1	S2	S3	S4	S5
Age	61	58	36	65	67
Gender	M	F	F	M	F
Etiology of impairment	Noise	Rubella	Unknown	Congenital	Hereditary
Years of implant experience (L∕R)	5∕5	4∕4	4∕3	3∕4	6∕6
Years of deafness	15	8	15	12	22

Stimuli

The speech stimuli used in this study, were sentences from the IEEE database IEEE (1969), which consists of a total of 72 phonetically balanced lists of 10 sentences each. Each sentence is composed of approximately 7 to 12 words, with 5 key words identified for the purposes of scoring. Every sentence in the IEEE speech corpus that was produced by a male talker was designated as the target speech. In order to simulate the speech interferer or competing voice in this experiment, a female talker uttering the sentence “Tea served from the brown jag is tasty” (also taken from the IEEE database) was chosen as the female masker (or non-target). Speech-shaped noise generated by approximating the average long term spectrum of the speech to that of an adult male taken from the IEEE corpus, was also selected to act as the second type of noise masker. This is an effective masker of speech. Twenty sentences (2 lists) were used for each condition. Different sets of sentences were used for each condition.

Signal processing

The test sentences were originally recorded with a sampling frequency of 25 kHz, but were later downsampled to 16 kHz to reduce overall computational time during the processing of the stimuli. In addition, each sentence was scaled to the same root-mean-square value, which corresponded to approximately 65 dB. The sound level of each masker was also adjusted relative to the fixed level of the target speech, yielding a target-to-masker ratio (TMR) equal to 0 dB. Both target and masker speech had the same onset, and, where deemed necessary, the masker signals were edited to have equal duration to the target speech tokens.

A set of free-field-to-eardrum (or anechoic) head-related transfer functions (HRTFs) measured in an acoustic manikin (Head Acoustics^®, HMS II.3) as described in the AUDIS catalog (see Blauert et al., 1998), were used to simulate different spatial locations of the speech target and the masker signals. HRTFs provide a measure of the acoustic transfer function between a point in space and the eardrum of the listener, and also include the high-frequency shadowing component due to the presence of the head and the torso. The length of the HRTFs was 256 sample points, amounting to a relatively short delay of 16 ms and no reverberation. To generate the multisensor composite (or mixed) signals observed at the pair of microphones, the target and masker stimuli for each position were convolved with the set of HRTFs for the left- and right-hand ear, respectively. For this experiment, the target speech source was assumed to be placed directly in front of the subject at 0° azimuth at the realistic conversational distance of 1 m. To generate stimuli in various spatial configurations, we set the azimuth angles of the masker positions to 0°, 30°, 45°, 60°, and 90°. In all cases, the vertical position of the sources was adjusted to 0° elevation.

The BSS algorithm, described in Sec. 2B, was implemented to run in an adaptive off-line mode with a multipass processing scheme. Thus, the estimation of the unmixing filters was performed iteratively over a block of data and the estimates obtained in the last iteration were then used to perform source separation for the same data block. By observing Eq. 8 we note that the separating system is characterized by the following two parameters: (1) The length of the separating filters composing the unmixing FIR polynomial matrix denoted by $\underset{̱}{\mathbf{W}}$ and (2) parameter λ that controls the adaptive step size (or learning rate). Theoretically, the BSS system can remove more interference with longer FIR filters, albeit at the cost of more computation and longer adaptation time. Here, in order to achieve the best separation quality possible, we chose the size of the unmixing filters to be twice the size of the HRTFs previously used to generate the target-masker signal mixtures. The BSS algorithm was run with 512 sample point adaptive FIR filters and a fixed large step size of λ=0.01 maximized up to the stability margin to ensure fast adaptation time and algorithm convergence. In addition, the algorithm was allowed to execute 20 passes through the data. This corresponds to a total of 60 s training time as the average sentence duration is 3 s. Each set of the mixtures was processed individually in order to extract the speech target estimates. Upon algorithm convergence, all the recovered (or enhanced) target speech segments were saved locally in the lab computer.

Procedure

All subjects were wearing the Cochlear Esprit^™ 3G BTE processor with two directional microphone elements (Knowles EL-7189). During their visit, however, all subjects were temporarily fitted with the new SPEAR3^® wearable research processor. SPEAR3^® has the ability to independently drive two implant devices and was developed by the Cooperative Research Center (CRC) for Cochlear Implant and Hearing Aid Innovation, Melbourne, Australia, in collaboration with HearWorks^®. Before the scheduled visit, we used the Seed−Speak^® GUI application to adjust the amplitudes for both threshold (T) and comfortable loudness levels (C) previously established for each electrode and subsequently program the processor separately for each patient. In addition, all participants used the device programmed with the advanced combination encoder (ACE) speech coding strategy (e.g., see Vandali et al., 2000) with the stimulation rates set to the values used in their daily processor. The volume of the speech processor (values between 0 and 9) was also adjusted to a comfortable loudness.

To evaluate recognition in anechoic conditions, the following conditions were used for each masker type and masker azimuth angle: (1) binaural unprocessed and presented bilaterally and (2) BSS-processed and presented diotically. Hence, in total there were 20 different conditions (2 maskers×5 angles×2 algorithms) using a total of 40 sentence lists. In the binaural unprocessed case, the two simulated sensor observations captured from one microphone were fed to one ear and similarly the composite signals observed in the other microphone, were presented to the other ear via the auxiliary input jack of the SPEAR3^® processor. In the processed case, the BSS-enhanced signal was presented diotically to the bilateral users via the auxiliary input jack of the SPEAR3^® processor. Prior to testing, all subjects were given a short practice session, in order to gain familiarity with the experiment. Separate practice sessions were used for single talker and noise maskers. No score was calculated for these practice sets. During the testing, the participants typed their response using the computer keyboard and were encouraged to guess if unsure. Feedback was provided during the practice session but not during the experimental sessions. The listeners participated in two separate experimental sessions with duration of 2–3 h each, that included several breaks. The list number presentation order was randomized across different participants, in order to counterbalance possible order effects in the test, such as learning or fatigue effects. After each test session was completed, the responses of each individual were collected, stored and scored off-line by the percentage of the keywords correctly identified.

Results and discussion

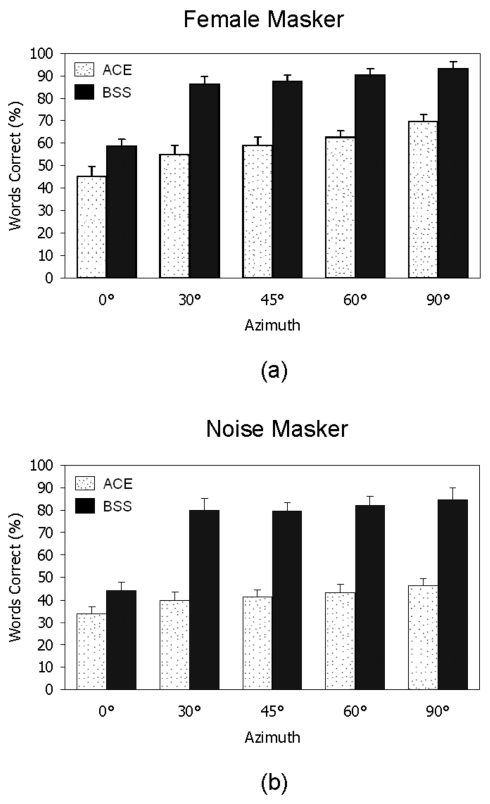
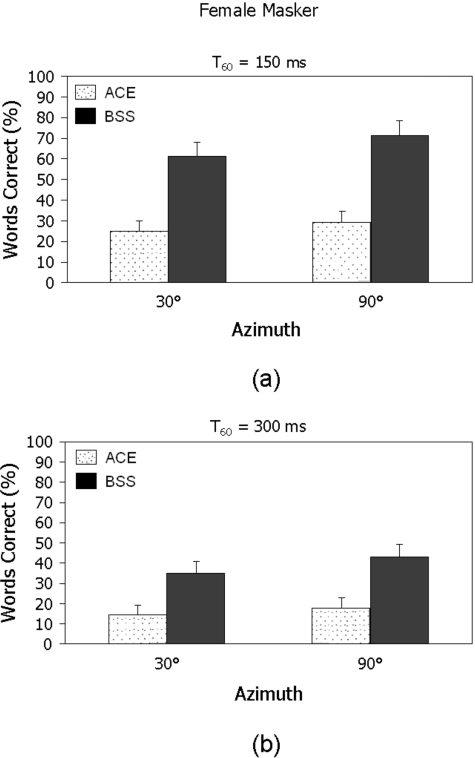
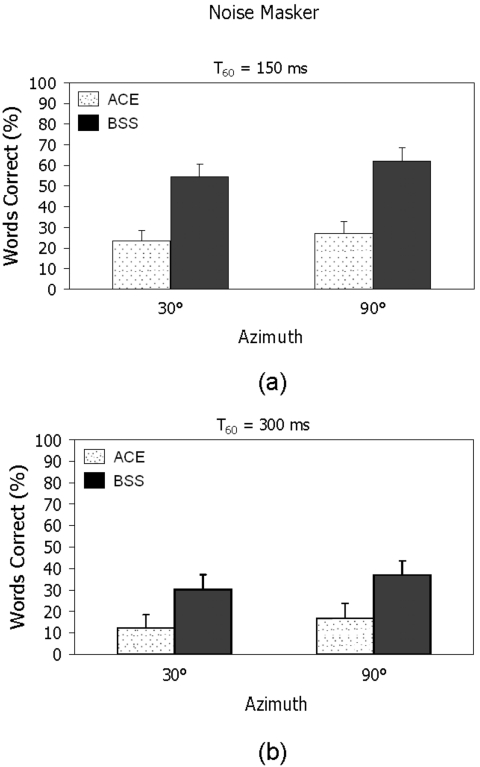
The mean scores on speech recognition obtained with and without BSS are shown in Fig. 3 for the female masker (top) and the noise masker (bottom).

Figure 3.

Mean percent word recognition scores for five Nucleus 24^® implant users on IEEE sentences embedded in female speech (top) and speech-shaped noise (bottom), both at TMR=0 dB. Scores for sentences processed only through the default processor ACE strategy are shown in white, and scores for sentences processed first through the BSS algorithm and then the ACE strategy are in black. Error bars indicate standard deviations.

Statistical analysis and comparisons

Two-way analysis of variance (ANOVA) (with repeated measures) was performed separately for each masker condition to assess significant effects of the processing algorithm and spatial configuration. ANOVA performed on the female masker data, indicated a significant effect [F(1,4)=1615.02,p<0.0005) of processing with the BSS algorithm, a significant effect [F(4,16)=419.2,p<0.0005] of the spatial configuration of the masker, and a significant interaction [F(4,16)=34.4,p<0.0005]. ANOVA performed on the noise masker data, also indicated a significant effect [F(1,4)=1311.5,p<0.0005] of processing with the BSS algorithm, a significant effect [F(4,16)=206.3,p<0.0005] of the spatial configuration of the masker, and a significant interaction [F(4,16)=127.7,p<0.0005]. Post-hoc comparisons using Fisher’s LSD between the scores obtained with the BSS algorithm and the subject’s daily processor indicated that the BSS algorithm yielded significantly (p<0.005) higher scores in all azimuth conditions and for both maskers. Interestingly, the BSS scores obtained at 0° azimuth were also significantly higher (p<0.005) than the scores obtained with the subject’s daily processor in both masker conditions. There is no theoretical explanation for this outcome, and hence we can make no claims that BSS is able to segregate co-located sources. This outcome may be instead attributed to small variations in intelligibility among individual IEEE sentence lists and the absence of counterbalancing on those sentence lists.6 These small variations in intelligibility might explain the differences in scores at 0° azimuth, but do not in general account for the comparatively larger differences in scores for other spatial configurations.

As shown in Figs. 3a, 3b, the scores obtained with the unprocessed sentences were higher in the 90° condition, where the masker and target signals were spatially separated, than in the 0° condition, in which case the masker and target signals originated from the same location. This suggests that the bilateral-implant subjects were able to benefit from spatial release of masking, an observation that is consistent with previous studies (e.g., van Hoesel and Tyler, 2003; Stickney et al., 2004; Tyler et al., 2002, 2003). That release, however, seemed to be largely dependent on the separation between the masker and target signals, as expected. According to Fig. 3, we can conclude that as long as the separation between the target and masker signals is at least 30° or more, the BSS algorithm can produce large improvements in intelligibility. In the noise masker condition for instance, word recognition scores improved from roughly 40% correct with unprocessed sentences to 80% correct with BSS-processed sentences. Large improvements in performance were obtained with the BSS algorithm for both maskers (female and noise). Spatially separating the target speech from its respective maskers by filtering the composite signals through a set of FIR unmixing filters results in a compelling release from masking. From a theoretical standpoint, the fact that BSS performs equally well in settings of both informational and energetic masking and for all configurations is to be anticipated, as the algorithm utilizes no prior knowledge with regard to the original signals or their underlying mixing structure.

Effect of different training strategies on speech recognition performance

Given that the BSS algorithm requires no previous information on the specifics of the acoustical setup, some amount of training is essential in order to achieve a considerable amount of masker suppression. In the present experiment, a total of 60 s was required to achieve the level of performance shown in Fig. 3. Logically, this raises the question of the amount of training required for the BSS algorithm to produce a reasonable separation performance and further to achieve similar word recognition scores as the ones previously obtained in Fig. 3. To thoroughly investigate the effect of training on speech recognition for bilateral users, the BSS algorithm was re-applied to enhance the male target embedded in female speech and speech-shaped noise, synthesized binaurally with HRTFs. The same subjects were used and an identical procedure to the one described in Sec. 3A was followed.

The main difference here is that training was not carried out individually for every single speech token as before. Instead, filters were adapted just for a randomly selected set of signals. The algorithm was executed with identical parameters as before. After convergence to a separating solution, the unmixing filters were saved, and then without any further modification used to enhance the remaining sentences. Note that in fact, we employed the same set of estimated filters to enhance signals embedded either in female speech or noise. The rationale behind this approach is that BSS should ideally remain truly “blind” to the original sources, and hence performance should not suffer. Based on this strategy, only a limited number of filters, namely one set for every spatial position of the maskers is required. This results in considerable savings in processing time. To further assess to what degree training affects separation quality the algorithm is allowed only 2, 3, and 5 passes (or iterations) through the data, which in effect correspond to 5, 10, and 15 s of total training time.

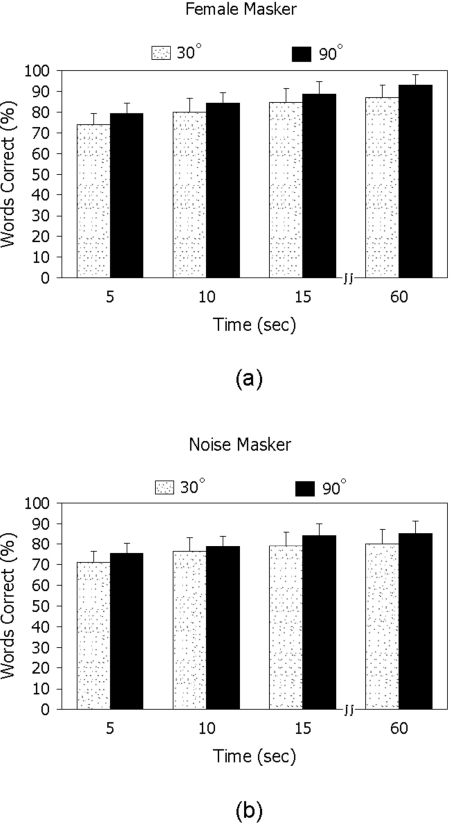
The results obtained for different training times are given in Fig. 4 for two spatial configurations (30° and 90°). The data obtained in Fig. 3 with 60 s of training are also included for comparative purposes. Nonlinear regression analysis was run to determine the minimum amount of training time required to achieve high levels of performance. Good fits, with correlation coefficients ranging from 0.67 to 0.77 (p<0.05), were determined with a log-shaped function in all conditions. The asymptote in performance was achieved with 15 s of training. Performance obtained with 15 s of training was not significantly (p=0.05) different to the performance obtained after a total of 60 s of training in all conditions. From Fig. 4 we can draw the following conclusions. First, as expected from theory, by increasing the adaptation time and hence the available signal length, the separation performance improves. This is reflected by the high recognition scores obtained when a total of 60 s (20 passes) of training is performed. Second, the BSS algorithm requires no more than a few seconds of data (5–10 s) in order to converge to a solution yielding an audibly distinguishable performance. Such observation can be confirmed by the plots in both Figs. 4a, 4b, showing relatively high word recognition scores for the 10 s case, for both types of maskers and for both the 30° and 90° azimuths.

Figure 4.

Mean percent word recognition scores plotted against training time for five Nucleus 24^® implant users on IEEE sentences embedded in female speech (top) and speech-shaped noise (bottom) at TMR=0 dB. Scores for sentences processed first through the BSS algorithm and then the default ACE strategy for a masker placed at 30° dB are in white. Scores for sentences processed first through the BSS algorithm and then the default ACE processor strategy for a masker placed at 90° dB are in black. Error bars indicate standard deviations.

EXPERIMENT 2. SPEECH RECOGNITION BY BILATERAL COCHLEAR IMPLANT SUBJECTS IN REVERBERANT ENVIRONMENTS

The previous experiment focused on assessing the performance of the BSS algorithm in anechoic environments. In the current experiment, we assess the performance of the BSS algorithm in more challenging (and more realistic) conditions, where reverberation is present.

Methods

Subjects

The same five postlingually deafened bilateral implantees tested in Experiment 1, were asked back to participate as subjects in this experiment.

Stimuli

The test material for the target and masker sentences was again selected from the IEEE corpus IEEE (1969) used in Experiment 1. None of the sentences previously used as the target speech (or masker) was reused in an effort to avoid potential learning effects.

Signal processing

To investigate the potential of BSS on speech intelligibility inside challenging reverberant environments, the target and masker stimulus for each position are convolved with a set of binaural room impulse responses (BRIRs) (Shinn-Cunningham et al., 2005). Before filtering the signals with the impulse responses, the level of each individual acoustic interference was adjusted relative to the fixed level of the target speech to reach a TMR=0 dB. The BRIRs were measured in a small rectangular classroom with dimensions 5×9×3.5 m and a total volume of V=157.5 m³ using the Knowles Electronic Manikin for Auditory Research (KEMAR), positioned at 1.5 m above the floor and at ear level as described in the study by Shinn-Cunningham et al. (2005). In contrast to the relatively smooth free-field anechoic HRTFs used in Experiment 1, these BRIRs exhibit rapid variations with frequency in both phase and magnitude and are in general, fairly difficult to invert even with FIR filters that employ a very large number of coefficients. Yet, only when resorting to such BRIRs we are capable of achieving a truly realistic binaural synthesis, and thus simulate a sound source at the desired location in space by filtering the audio stream with the left- and right-ear impulse responses corresponding to a specific sound location in the room. To reduce extraneous noise artifacts in their original measurements, Shinn-Cunningham et al. (2005) used Butterworth filters to bandpass filter the raw binaural responses in the 0.1–20 kHz range. These BRIRs were then multiplied by a 500 ms time window using a 50 ms cosine-squared fall time to produce the final BRIRs.

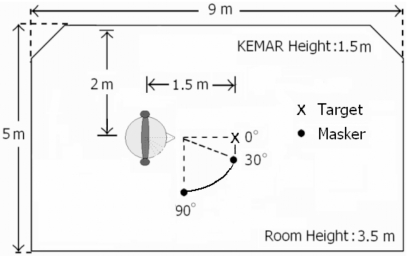
Before performing any filtering on the speech tokens, we downsampled the impulse responses to 16 kHz from their original 44.1 kHz recorded sampling rate. After convolving the signals with the pre-measured left- and right-ear responses obtained from the KEMAR, the target sound source was placed directly at the front of the listener in virtual space at 0° azimuth. Following the same procedure, the target speech was positioned at either a distance of 0.90 or 1.50 m away from the KEMAR dummy head. The female and noise maskers were placed at an angle of incidence of either 30° or 90°, and also at either a distance of 0.90 or 1.50 m away from the KEMAR. A total of 16 (2 distances×2 angles×2 maskers×2 algorithms) different conditions were considered in this experiment using a total of 320 sentences. Figure 5 provides a schematic representation of the aforementioned configurations, as well as the location of the KEMAR manikin inside the classroom where the actual measurements took place in the Shinn-Cunningham et al. (2005) experiment.

Figure 5.

Schematic diagram depicting the layout of the reverberant room and location of the KEMAR manikin where the BRIRs were measured.

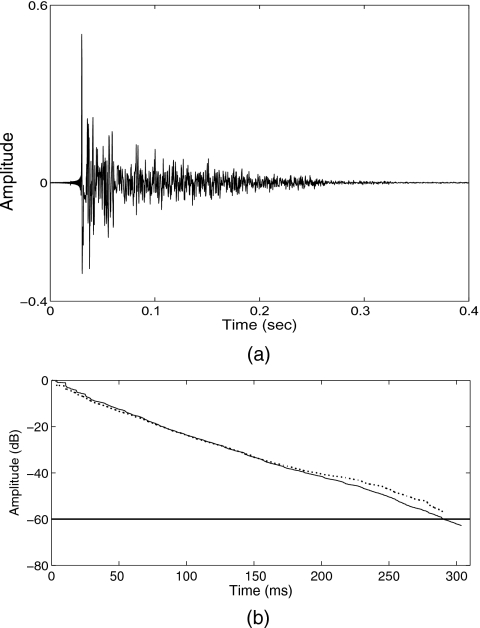
The broadband reverberation time of the room was calculated from the pre-measured impulse responses by resorting to the Schroeder integration procedure (Schroeder, 1965). This technique first estimates the energy decay curve and ultimately reveals the length of time required for the sound pressure to decrease by 60 dB. We choose, as an example, the topology where the source-to-sensor distance was equal to 1.50 m and the masker was placed at a 30° angle to the right of the target signal. As Fig. 6b reveals, for this particular enclosure, reverberation time is equal to around T₆₀=300 ms. In general, a rapidly decaying impulse response corresponds to a short reverberation time, whereas longer reverberation times are usually associated with impulse responses having much heavier tails. The first peak corresponds to the sound coming directly from the source, whereas the exponentially decaying tails, caused by successive absorption of sound energy by the walls, account for the later reflection paths in the enclosure. Figure 6a depicts one of the acoustic impulse responses used for the stimulus synthesis, measured inside the rectangular classroom when the KEMAR was placed 1.50 m away from the target speech (see Fig. 5).

Figure 6.

(Top) Center-target to left-ear impulse response recorded inside the classroom shown in Fig. 5. The reverberation time T₆₀ of this enclosure ranges from 150 to 300 ms depending on the source-to-sensor distance. (Bottom) Energy decay curves of the left-ear (solid line) and right-ear (dash line) impulse responses at 30°. The time taken for the amplitude to drop by 60 dB (thick line) below the original sound energy level is equal to 300 ms.

To generate a set of shorter (and less reverberant) binaural impulse responses, an exponential regression to the decay curve was calculated from the original 0.90 m impulse responses obtained in the Shinn-Cunningham et al. (2005) KEMAR experiment. These responses were then faded in a natural manner by applying an exponentially decaying time window that was flat for up to around 100 ms and had a cosine-squared fall time from 100 to 300 ms. This reshaping ensured that most reverberant energy was removed from the original set of the impulse responses, hence yielding a shorter reverberation time, which was adjusted to be approximately T₆₀=150 ms. Also computed were the averaged direct-to-reverberant ratios (DRRs) for the (0°,30°) and (0°,90°) configurations in both the 0.90 and 1.50 m settings. DRR is simply defined as the log energy ratio of the direct and reverberant portions of an impulse response and essentially measures how much of the energy arriving is due to the direct (source) sound and how much is due to late arriving echoes (e.g., see Zahorik, 2002). In general, the DRR will change depending on the source-to-listener distance. As perceived reverberation increases the DRR decreases, since the energy in the latter part of the impulse response will increase relative to that in the direct wave front. When the KEMAR is placed at 0.90 m away from the speech source, DRR₉₀=0.21 dB, whereas for the 1.50 m setting, the estimated DRR₁₅₀ is equal to −4.87 dB.

The main goal of the present experiment was not only to suppress the masker in order to allow the bilateral subject to better focus on the target speech, but also to remove the corrupting acoustic properties of the room and yield a nearly anechoic (or clean) target source. In this context, convolutive BSS is also usually referred to as multichannel blind deconvolution (MBD) (e.g., see Haykin, 2000; Haykin and Chen, 2005; Kokkinakis and Nandi, 2006; Lambert, 1996). Clearly, if a source is successfully canceled, the output is then statistically independent from the masker or interfering sound source. To do so and enhance the target speech, we applied the BSS algorithm to the binaural convolutive mixtures. The setting chosen for the unmixing filters was 4,096 sample points, which correspond to an overall delay of 256 ms at the sampling rate of 16 kHz. Such filter size should be adequate to invert the acoustic properties of the room in the moderately reverberant 0.90 m setting with DRR₉₀=0.21 dB and T₆₀=150 ms. However, note that the length of the impulse response in the 1.50 m distance condition with DRR₁₅₀=−4.87 dB and T₆₀=300 ms is somewhat longer than the length of the unmixing filters. Due to this, we anticipate that some degradation on the perceived speech due to reverberation will remain. As before, the BSS algorithm was executed in an adaptive off-line mode based on a multipass processing scheme with the learning rate equal to λ=0.001 to ensure prompt algorithm convergence. The training time in this case was set to approximately 30 s.

Procedure

The experimental procedure was identical to the one followed previously. The enhanced speech target signal processed by our BSS method, was presented identically to both implants (diotically), whereas the unprocessed speech signals were presented binaurally to the subjects. Overall, there were 16 different conditions that involved a total of 32 sentence lists (2 lists per condition). The invited subjects completed the data collection process over a period of 4–5 h with regular breaks provided as needed. Performance was scored separately for each subject as the percentage of words that were correctly identified in each condition.

Results

The mean subject scores obtained with the BSS method in reverberant conditions are shown in Figs. 78.

Figure 7.

Mean percent word recognition scores for five Nucleus 24^® implant users on IEEE sentences embedded in female speech at TMR=0 dB. Top graph corresponds to a source-to-sensor-distance of 0.90 m and T₆₀=150 ms, and bottom graph to 1.50 m and T₆₀=300 ms. Scores for sentences processed only through the default processor ACE strategy are shown in white, and scores for sentences processed first through the BSS algorithm and then the ACE strategy are in black. Error bars indicate standard deviations.

Figure 8.

Mean percent word recognition scores for five Nucleus 24^® implant users on IEEE sentences embedded in speech-shaped noise at TMR=0 dB. (Top) Corresponds to a source-to-sensor distance of 0.90 m and T₆₀=150 ms and (bottom) corresponds to 1.50 m and T₆₀=300 ms. Scores for sentences processed only through the default processor ACE strategy are shown in white, and scores for sentences processed first through the BSS algorithm and then the ACE strategy are in black. Error bars indicate standard deviations.

Speech recognition performance in 150 ms reverberation

Figures 7a, 8a show the mean word recognition score values for the female talker and noise maskers, respectively, in moderate reverberant conditions. The target speech was placed at 0° azimuth and the female and noise interferers were located at 30° and 90° both at a distance of 0.90 m away from the listener. For the female masker conditions, two-way ANOVA (with repeated measures) indicated a significant effect [F(1,4)=164.02,p<0.0005] of processing with the BSS algorithm, a significant effect [F(1,4)=106.3,p<0.0005] of the chosen spatial configuration for the maskers, and a significant interaction [F(1,4)=53.15,p=0.002]. Paired samples t-tests showed that the scores obtained with BSS were significantly (p<0.0005) higher than the scores obtained with the daily implant processor (unprocessed signals) in both the 30° and 90° masker positions. For the noise masker conditions, two-way ANOVA (with repeated measures) indicated a significant effect [F(1,4)=461.95,p<0.0005] of processing with the BSS algorithm, a significant effect [F(1,4)=111.455,p<0.0005] of the spatial configuration, and a nonsignificant interaction [F(1,4)=2.27,p=0.206]. Based on this analysis, we can reason that the scores obtained with BSS were substantially better than the scores obtained with the subjects’ daily processors alone for both masker configurations.

In the unprocessed conditions, both the single talker and noise maskers degraded speech intelligibility significantly. Compared to the anechoic condition, performance decreased in the female masker condition from nearly 60% correct as shown in Fig. 3, to nearly 30%. A similar degradation in performance was also observed in the noise masker conditions. The performance obtained at 90° was not significantly (p>0.05) better than the performance observed at 30° for either masker. This points to the conclusion that the performance of the BSS algorithm was not affected by the spatial configuration. Equally large improvements in intelligibility were noted in both angles and for both maskers. On average, the subjects’ scores were 2×better (and in some cases 3×better) when the mixtures were passed through the proposed BSS algorithm.

Speech recognition performance in 300 ms reverberation

Figures 7b, 8b show the mean word recognition scores for the female and noise maskers, respectively, in highly reverberant conditions. In this setup, the target speech was placed at 0° azimuth and the female talker and noise interferers were located at 30° and 90° both at a distance of 1.50 m away from the listener. The reverberation time as measured from the binaural impulse responses, was equal to around 300 ms [see Fig. 6b]. Two-way ANOVA (with repeated measures) in the female masker conditions, indicated a significant effect [F(1,4)=545.5,p<0.0005] of the BSS processing algorithm, a significant effect [F(1,4)=27.7,p=0.006] of the designated spatial configuration, and a nonsignificant interaction [F(1,4)=19.4,p=0.012]. Similar results were obtained for the noise masker. ANOVA showed a significant effect [F(1,4)=60.1,p=0.001] of processing with the BSS algorithm, a significant effect [F(1,4)=97.6,p=0.001] of the spatial configuration, and a non-significant interaction [F(1,4)=2.17,p=0.214]. Paired samples t-tests confirmed that the scores obtained after enhancing the target signals with BSS, were significantly (p<0.0005) higher than the scores obtained with the daily processor in both the 30° and 90°masker positions and for both maskers.

Speech intelligibility in the unprocessed conditions was reduced considerably as the reverberation time increased from 150 to 300 ms. Mean scores dropped to 17% correct in the female masker condition for 90° azimuth and to 15% correct in the noise masker condition (same angle). Equally low were the scores observed at the 30° configuration, where subjects scored 14% and 12% for speech signals embedded in speech-shaped noise. Performance improved significantly for the stimuli processed with the BSS algorithm in both masker conditions. Word recognition scores in the 90° position were found to be equal to 43% and 36% for the female and noise maskers, respectively. Equal improvements were noted in the 30° masker position. Overall, the above data demonstrate that the BSS method can yield substantial benefits in speech intelligibility even in reverberant listening conditions.

Discussion

Comparing the outcomes of Experiments 1 and 2, we observe that the bilateral cochlear-implant subjects’ abilities to communicate in reverberant conditions is severely compromised. This was found to be true in both the female masker [F(2,8)=344.1,p<0.005] and steady-noise masker [F(2,8)=78.4,p<0.005] conditions. As shown in Figs. 78, the subject’s ability to benefit from spatial release of masking is reduced substantially within reverberant settings. This is consistent with studies involving normal-hearing and hearing-impaired subjects (Culling et al., 2003; Nabelek et al., 1989; Nabelek and Picket, 1994; Freyman and Zurek, 2002; Shinn-Cunningham and Kopco, 2002). Culling et al. (2003) carried out experiments with normal-hearing subjects within a virtual room with controlled reverberation, and concluded that reverberation can abolish a listeners ability to exploit differences in spatial location, and hence to receive benefit from release of masking. Reverberation has been shown to blur temporal and spectral cues, to flatten formant transitions, reduce amplitude modulations associated with the fundamental frequency (F₀), and increase low-frequency energy which in turn results in greater masking of higher frequencies (e.g., see Bistafa and Bradley, 2000). In effect, reverberation can severely degrade consonant perception by smoothing out the envelope modulations that carry information about the abrupt onsets and offsets of consonants (Nabelek et al., 1989). In the context of cochlear implants, Poissant et al. (2006) were the first to demonstrate, using acoustic simulations, that the aforementioned temporal smearing effects can become even more detrimental when listening through only a limited number of spectral channels that are usually available to implant subjects.

Beamforming techniques are known to work well in anechoic settings, but their performance degrades in reverberant conditions (Hamacher et al., 1997; van Hoesel and Clark, 1995). In the study by van Hoesel and Clark (1995), beamforming attenuated (spatially separated) noise by 20 dB in anechoic settings, but only by 3 dB in highly reverberant settings. Additionally, beamformers are more prone to target signal cancellation, when longer adaptation filters are used (e.g., see Greenberg and Zurek, 1992). In contrast, the proposed BSS method seems to be robust in both anechoic and reverberant conditions. No comparisons were provided in the present study between the beamforming and BSS algorithms, as the main scope of this paper is to provide a proof of concept and establish the potential of BSS as an efficient pre-processing technique that can be used in bilateral cochlear implant devices. Nevertheless, further experiments are warranted comparing the performance of beamforming and BSS algorithms using the same filter parameters and data.

The proposed BSS method operates by gaining access to a single processor driving two implants. Such a processor, the SPEAR3^®, is currently made available from CRC for research purposes. As illustrated in Fig. 1, the signals acquired by the two microphones (placed in each of the two ears) are fed as input to the BSS algorithm running on a single processor. The main advantage in using this paradigm (single processor driving two implants) is that it provides access to intact binaural cues present in the incoming signals (left and right). As the BSS algorithm is formulated using a convolutive setup, we can take advantage of binaural cues, such as ITDs (expressed as filter delays) and ILDs (variations in the filters coefficients). Consequently, the ITD and ILD information is implicitly modeled and exploited by the BSS algorithm. It should be noted that the BSS technique described here, can also be easily applied to a unilateral implant configuration, as long as the speech processor is furnished with two microphones. An example of such speech processor is the Nucleus Freedom^™ implant system currently being marketed by Cochlear^®. The present study focused on the potential of BSS in providing benefits in intelligibility for bilateral implant subjects in anechoic and reverberant conditions. Further work will assess whether the BSS-processed signals (presented diotically) diminish the bilateral subject’s ability to localize sounds.

CONCLUSIONS

The present study assessed the performance of BSS, which has been largely unexplored in the context of bilateral cochlear implants. Evaluation of the proposed BSS algorithm with five bilateral cochlear implant users indicated significant benefits in intelligibility in both anechoic and reverberant conditions. The documented improvement in intelligibility was consistent for the two types of maskers tested and was quite substantial particularly in the 90° and 30° spatial configurations.

In our opinion, the established BSS framework is a crucial contribution to the future development of novel speech processing strategies for bilateral cochlear implants. Further work is needed to reduce the computational load involved with long adaptation filters, which can become increasingly heavy within reverberant conditions. One possibility, currently under investigation, is to apply the BSS algorithm to speech processed in subbands (e.g., see Kokkinakis and Loizou, 2007). This is similar to the subband processing schemes widely applied to several commercially available coding strategies to date.