Information transfer analysis: A first look at estimation bias

Abstract

Information transfer analysis [G. A. Miller and P. E. Nicely, J. Acoust. Soc. Am. 27, 338–352 (1955)] is a tool used to measure the extent to which speech features are transmitted to a listener, e.g., duration or formant frequencies for vowels; voicing, place and manner of articulation for consonants. An information transfer of 100% occurs when no confusions arise between phonemes belonging to different feature categories, e.g., between voiced and voiceless consonants. Conversely, an information transfer of 0% occurs when performance is purely random. As asserted by Miller and Nicely, the maximum-likelihood estimate for information transfer is biased to overestimate its true value when the number of stimulus presentations is small. This small-sample bias is examined here for three cases: a model of random performance with pseudorandom data, a data set drawn from Miller and Nicely, and reported data from three studies of speech perception by hearing impaired listeners. The amount of overestimation can be substantial, depending on the number of samples, the size of the confusion matrix analyzed, as well as the manner in which data are partitioned therein.

INTRODUCTION

Information transfer (IT) analysis, introduced by Miller and Nicely (1955), is an application of Shannon’s (1948) information measure to data obtained from a speech identification task. The data are typically categorized into distinctive features (e.g., voicing, nasality, affrication, manner and place of articulation, etc.) and then organized into a confusion matrix. An IT score is obtained from this matrix by calculating the number of bits received by the listener and dividing this result by the number of bits available in the stimuli. When the listener has received all the bits available in the stimuli, e.g., when no errors appear in the feature confusion matrix, an IT score of 100% is obtained. When the listener’s responses are independent of the stimuli, e.g., in a case of random guessing, the listener receives no bits of information producing an IT score of 0%. With IT analysis, one can construct a picture of how each speech feature contributes to the intelligibility of the phonemes as a whole. That is, when phonemes are viewed as a bundle of several distinctive features (Stevens, 2002), IT analysis tells us what fraction of the original information has been transmitted for each feature independently.

The IT metric is particularly advantageous over the percent correct score in cases where a listener’s responses are independent of the stimuli presented. For example, purely chance performance can yield different percent correct, depending on how speech stimuli are organized into features. If out of 16 consonants, say, 9 are voiced and 7 are voiceless, then purely chance performance produces an average percent correct score of 51%. If out of 16 consonants, say, 2 are nasal and 14 are non-nasal, then purely chance performance produces an average percent correct score of 78%. Even more anomalous is when a listener’s responses are biased even though the responses are independent of the stimuli presented. In the case of nasality, for example, if the listener always identified each consonant as non-nasal, the 2×2 matrix for this feature will yield a percent correct score of 87.5%. Conversely, if the listener always identified each consonant as nasal, the percent correct score in the 2×2 feature matrix for nasality becomes 12.5%. In all these cases, input and output are independent and the IT metric for these features yields a score of 0%, regardless of the type of feature or whether the listener’s responses are biased.

IT analysis is pertinent beyond the speech, language, and hearing sciences, having been applied to areas such as rehabilitation, acoustics, communication engineering, computer science, psychology, and neuroscience. The ISI Web of Science indicates more than 800 papers that have cited Miller and Nicely (1955). In IT analysis, the percent information transfer is obtained by applying a maximum-likelihood estimate (MLE) of the transmitted information to a confusion matrix. In a parenthetical note of their 1955 study, Miller and Nicely state, “like most maximum likelihood estimates, this estimate will be biased to overestimate [IT] for small samples.” They also state that in their study the bias can be safely ignored as each confusion matrix contained a total of 4000 entries, obtained by pooling data across subjects. Surprisingly few of the articles that cite Miller and Nicely (1955) mention this bias, or, to our knowledge, have provided a quantitative description of the overestimation, or a guideline as to the number of confusion matrix entries required to overcome the bias.

Previous efforts in other related fields have been made to describe the bias in information estimates (e.g., Miller, 1955; Rogers and Green, 1955; Carlton, 1969; Houtsma, 1983; Rabinowitz et al., 1987; Wong and Norwich, 1997; Sagi and Norwich, 2002). However, to provide an accurate bias correction for data sets with small numbers of samples, these methods require at least some model of how data will be distributed across confusion matrix elements. Such models are available for the more simple sensory stimuli such as pure tones varying in pitch or intensity. For speech stimuli, predicting how data will distribute across confusion matrix elements is a far more complicated affair.

The goal of this study is to examine the potential effect of the bias in information estimates on IT analysis, and to establish a rough guideline for avoiding this bias. First to be discussed is the case of IT overestimation bias that occurs in a situation of purely random performance, where IT should be 0%. Second, some data from Miller and Nicely (1955) will be used to demonstrate how the bias in IT estimates could arise in actual data obtained from a standard speech perception identification task. Finally, possible examples of overestimation bias in IT estimates reported in the literature shall be discussed.

METHODS

IT is defined as the ratio of transmitted information, I_t, to input entropy, H_x (Miller and Nicely, 1955), and is commonly expressed as a percent. The true probabilities that comprise the input entropy (denominator) are typically known a priori. Conversely, the probabilities that comprise the transmitted information (numerator) must be estimated from the contents of a confusion matrix. The MLE for the probability of a given event is obtained by dividing the number of times this event was observed by the number of times all events were observed. If N is the total number of observations of all events, n_x is the number of times input x was presented, n_y is the number of times output y was observed, and n_xy is the number of times x and y were observed together, then the MLE of the information transfer, $\mathrm{I}\widehat{\mathrm{T}}$ (the caret on top of $\mathrm{I}\widehat{\mathrm{T}}$ means “estimate”), is defined as

$$\mathrm{I}\widehat{\mathrm{T}}=\frac{{\widehat{I}}_t}{H_x}=\frac{-\sum _x\frac{n_x}{N}\log \frac{n_x}{N}-\sum _y\frac{n_y}{N}\log \frac{n_y}{N}+\sum _x\sum _y\frac{n_{xy}}{N}\log \frac{n_{xy}}{N}}{-\sum _x{p}_x\log p_x},$$ (1)

where p_x in the denominator is the true probability that the input x occurred. There are other ways to express the numerator in Eq. 1, but this form describes the MLE of the transmitted information as a summation of the input entropy plus the output entropy less the joint entropy. In a confusion matrix, N is equal to the total number of times all stimuli were presented, n_x is the sum of row x, n_y is the sum of column y, and n_xy is in the main body of the matrix at the intersection of row x and column y.

It is important to differentiate between information transfer as obtained from true probabilities and the estimation of information transfer from an experimental confusion matrix. The former will be depicted symbolically as IT, and the latter as $\mathrm{I}\widehat{\mathrm{T}}$. By definition, an estimator converges to its true value after a large enough number of samples. That is, $\mathrm{I}\widehat{\mathrm{T}}=\mathrm{IT}$ when N is large. However, to be considered an unbiased estimator, this result would have to be true on average for any value of N. That is, one calculates the estimate for a given number of samples N, repeats this process many times, and then computes the average of these estimates. If this average estimate equals IT for any value of N, then the estimator is considered unbiased. It will be shown that the average estimate of $\mathrm{I}\widehat{\mathrm{T}}$ is larger than IT when N is small, i.e. that $\mathrm{I}\widehat{\mathrm{T}}$ is a biased estimator, and that in some cases this bias can be large.

As a first step in demonstrating the bias in $\mathrm{I}\widehat{\mathrm{T}}$ we consider a situation where the true information transfer is equal to zero, i.e., IT=0%. This will occur whenever input and output are independent, for example when listeners guess their responses at random. Chance performance can be modeled by assuming that responses are drawn from a uniform distribution, i.e., when responses are equally likely given any stimulus. Three cases were considered. In the first case, the relationship between $\mathrm{I}\widehat{\mathrm{T}}$ and IT (i.e., the relationship between sample estimates and true values of IT) was examined as a function of two variables: the number of samples, N, and the size of the confusion matrix m (i.e., m rows and m columns). In the second case, the relationship between $\mathrm{I}\widehat{\mathrm{T}}$ and IT from the first case was reexamined as a function of the number of samples per matrix category, i.e., N∕m. In the third case the relationship between $\mathrm{I}\widehat{\mathrm{T}}$ and IT was examined as a function of N for matrices of equal size, but obtained using different partitions of a larger matrix.

For the first case, $\mathrm{I}\widehat{\mathrm{T}}$ was applied to nine confusion matrices ranging in size from 2×2 to 10×10 as each matrix was progressively filled with data. Data samples were obtained with a MATLAB subroutine instructed to generate two numbers for each sample, one “input” and one “output.” The input indicates the row and the output indicates the column of the confusion matrix to be updated by this sample. Both numbers are sampled pseudorandomly from a uniform distribution, but with one important difference. In many experiments, in addition to being presented in random order, stimuli are also presented the same number of times. This sampling constraint was employed strictly so that each input was repeated the same number of times every number of samples equal to the size of the confusion matrix. That is, for the 10×10 matrix, each input was represented exactly once every N=10 samples, whereas for the 5×5 matrix, each input was represented exactly once every N=5 samples, etc. In contrast to sampling of input, the uniform sampling of output was left otherwise unconstrained. $\mathrm{I}\widehat{\mathrm{T}}$ was calculated every cycle of samples for which all input were repeated until the number of samples reached closest to N=1000. This process was repeated 10 000 times so as to calculate the average $\mathrm{I}\widehat{\mathrm{T}}$ as a function of N. This average was then compared with the true value for IT, which is 0% for each confusion matrix in this case.

For the second case, the values of average $\mathrm{I}\widehat{\mathrm{T}}$ obtained in the first case were analyzed as a function of the number of samples per matrix category, from 1 to 100 samples per category. In the case of the 10×10 matrix, 100 samples per category are obtained after N=1000 samples. For the 2×2 matrix, 100 samples per category are obtained after N=200 samples, and so on.

For the third case, five 2×2 matrices were constructed from a 10×10 matrix as the latter matrix was filled with data using the strict sampling constraint described above. Each 2×2 matrix was constructed by using a different partition of the 10×10 matrix. For example, an equal partition of the 10×10 matrix would result in a 2×2 matrix with each category consisting of five categories from the original 10×10 matrix. Let us represent this partition as (5, 5). The other four 2×2 matrices were constructed using the following partitions: (4, 6), (3, 7), (2, 8), and (1, 9). $\mathrm{I}\widehat{\mathrm{T}}$ was calculated from each 2×2 matrix every N=10 samples until N=1000. This process was repeated 10 000 times to obtain an average $\mathrm{I}\widehat{\mathrm{T}}$ as a function of N.

The next example we used to demonstrate the overestimation bias employed data from Miller and Nicely (1955). Samples were drawn from the 16×16 consonant confusion matrix in Fig. 1 (Table II in Miller and Nicely, 1955). Normal hearing listeners were required to identify which of 16 consonants was heard in a stimulus that contained one of the consonants followed by the vowel ∕a∕. For this confusion matrix, stimuli were presented in the presence of background noise with a fairly low signal-to-noise ratio of −12 dB. From this matrix, one can produce 4000 input–output pairs. For example, consider the cell at the intersection of the first row and third column of the consonant confusion matrix. One observes that the number of times the consonant ∕p∕ was confused with consonant ∕k∕ is 65. Hence, there are 65 input–output pairs for the input ∕p∕ and the output ∕k∕. From the list of 4000 pairs, 1600 were selected at random and updated into a 16×16 consonant confusion matrix. The random selection of input–output pairs was constrained so that each input was represented exactly once every 16 samples. To achieve this, all responses to each input were randomly permuted, and then the first 100 responses for each input were entered into the matrix 16 at a time, once for each input. $\mathrm{I}\widehat{\mathrm{T}}$ was calculated from the matrix as each set of 16 samples were entered to obtain a measure of $\mathrm{I}\widehat{\mathrm{T}}$ as a function of N, for N=16,32,48,…,1600. This was repeated 10 000 times using a different random permutation of the original data to obtain a measure of the average $\mathrm{I}\widehat{\mathrm{T}}$ at each number of samples. The standard deviation about the mean was also calculated.

Figure 1.

16-consonant confusion matrix (top) from Miller and Nicely (1955) partitioned along gray lines into a 2×2 voicing feature matrix (bottom). In both matrices, correct responses are emphasized in bold.

This procedure for obtaining the curve of average $\mathrm{I}\widehat{\mathrm{T}}$ from the consonant confusion matrix in Fig. 1 was repeated for the following four features: voicing, nasality, affrication, and place of articulation. At the bottom of Fig. 1 is an illustration of how a 2×2 voicing matrix is constructed from the consonant matrix. The gray lines represent the partition of the consonant matrix into feature categories of voiced and voiceless consonants. The classification of consonants into feature categories for each of the four features is summarized in Table 1, taken from Miller and Nicely (1955). For a given input–output consonant pair sampled from Figure 1, Table 1 was used to reclassify the pair as an input and output for the appropriate feature confusion matrix. For example, the consonant pair ∕p∕ and ∕k∕ mentioned previously would yield a feature input–output pair of (0, 0) for voicing and (0, 2) for place. That is, both consonants are voiceless (i.e., 0), but ∕p∕ is produced with a constriction at the front of the oral cavity (i.e., 0) whereas ∕k∕ is produced with a constriction at the back of the oral cavity (i.e., 2). As with the 16×16 consonant matrix, the average $\mathrm{I}\widehat{\mathrm{T}}$ was calculated from each feature matrix at N=16,32,…,1600. For each feature, the a priori probabilities for the denominator of Eq. 1 were calculated from Table 1. For example, one can see from Table 1 that the a priori probabilities for nasal and non-nasal consonants are 2∕16 and 14∕16, respectively. To compare with the 16×16 consonant matrix, the standard deviation about the mean $\mathrm{I}\widehat{\mathrm{T}}$ was calculated for the voicing feature. For each of the above five cases, the consonant matrix in Fig. 1 as well as the four features in Table 1, the values of average $\mathrm{I}\widehat{\mathrm{T}}$ as a function of the number of samples N are compared with the true values for IT, approximated by the value of $\mathrm{I}\widehat{\mathrm{T}}$ at N=4000.

Table 1.

Miller and Nicely (1955) classification of feature categories for 16 consonants. Voicing: 0=voiceless and 1=voiced; nasality: 0=non-nasal and 1=nasal; affrication: 0=nonaffricate and 1=affricate; and place of articulation: 0=front, 1=middle, and 2=back.

Consonant	Features
	Voicing	Nasality	Affrication	Place
p	0	0	0	0
t	0	0	0	1
k	0	0	0	2
f	0	0	1	0
ϴ	0	0	1	1
s	0	0	1	1
ʃ	0	0	1	2
b	1	0	0	0
d	1	0	0	1
g	1	0	0	2
v	1	0	1	0
ð	1	0	1	1
z	1	0	1	1
ʒ	1	0	1	2
m	1	1	0	0
n	1	1	0	1

As an example of how bias in IT estimates appears in the IT literature, data sets from three studies with cochlear implant (CI) listeners are analyzed; Donaldson and Kreft (2006), van Wieringen and Wouters (1999), and Tye-Murray and Tyler (1989). In each case, the average $\mathrm{I}\widehat{\mathrm{T}}$ was reported for different speech features. In these investigations, the average was obtained by first calculating $\mathrm{I}\widehat{\mathrm{T}}$ from each listener’s confusion matrix, and then averaging across the group of listeners tested. Also reported in these studies was a confusion matrix containing data pooled from all listeners as well as a table depicting the classification of consonants into feature categories. We calculated $\mathrm{I}\widehat{\mathrm{T}}$ for each feature by applying their feature classification table to the pooled matrix, and compared the result with the average $\mathrm{I}\widehat{\mathrm{T}}$ reported in the respective papers. The difference between these two measures is that the former was calculated from a large number of samples, i.e., a confusion matrix with data pooled across listeners, whereas the latter consists of measurements obtained with far fewer samples, i.e., confusion matrices with data from individual listeners. If no small-sample bias existed in IT estimation, the two measures should be close. As IT estimates tend to overestimate the true value for smaller samples, we expect that the average $\mathrm{I}\widehat{\mathrm{T}}$ values reported would be larger than the $\mathrm{I}\widehat{\mathrm{T}}$ obtained from the pooled matrix.

In Donaldson and Kreft (2006), $\mathrm{I}\widehat{\mathrm{T}}$ averaged from 20 CI users was reported for the consonant features voicing, manner and place of articulation. Stimuli were 19 consonants in initial and medial position for three vowel contexts, produced by male and female talkers. Only the average $\mathrm{I}\widehat{\mathrm{T}}$ data reported for the initial consonants in three vowel contexts from female talkers was examined here. Each averaged estimate was obtained from matrices consisting of N=285 samples per listener. Also reported for each testing condition was a confusion matrix with data pooled across listeners. Each of these matrices contained N=5700 samples. We conducted IT analysis on the pooled matrices for the stimulus conditions examined here, for the features voicing, manner, and place of articulation using the feature table reported in Donaldson and Kreft (2006). The pooled $\mathrm{I}\widehat{\mathrm{T}}$ were compared with the reported averaged $\mathrm{I}\widehat{\mathrm{T}}$.

In van Wieringen and Wouters (1999), IT estimates were reported for vowel and consonant features for 24 CI users partitioned into three groups of better, intermediate, and poor performers with 8 listeners in each group. The vowel features analyzed were duration, first (F1) and second (F2) formant frequencies. The consonant features analyzed were voicing, burst, amplitude envelope, place, affrication, manner, and nasality. Two sets of IT estimates were reported for each group, an average score and a pooled score. The pooled confusion matrices for each group were also reported. We compiled three sets of IT estimates from the data of van Wieringen and Wouters (1999) for all speech features analyzed. The first set is the average of the 24 individual $\mathrm{I}\widehat{\mathrm{T}}$ values obtained by averaging the averaged estimates reported for the three performance groups. The matrices from which these estimates were obtained consist of N=120 samples per matrix for vowels and N=192 samples per matrix for consonants. The second set of estimates are the pooled $\mathrm{I}\widehat{\mathrm{T}}$ per group, averaged over the three performance groups. The matrices for these estimates contained N=960 samples per matrix for vowels and N=1536 samples per matrix for consonants. The second set of estimates is depicted as “Pool8” to indicate that each estimate represents the pooling of data from 8 listeners, pooled for each group, but averaged for the three groups. The third set of estimates is $\mathrm{I}\widehat{\mathrm{T}}$ obtained by pooling all data into one matrix of N=2880 for vowels and N=4608 for consonants. These estimates were obtained by combining the pooled matrices for the three performance groups into one matrix. The third estimate is depicted as “Pool24.” We compared the three sets of IT estimates, i.e., averaged, Pool8 and Pool24, to examine how much overestimation, if any, occurs as one moves from the Pool24 estimate to the averaged estimate.

In Tye-Murray and Tyler (1989) IT estimates were reported for users of several CI devices for the consonant features voicing, place, nasality, duration, frication and envelope. We examined their IT estimates reported for 7 Nucleus users and 10 Symbion users. The number of samples in the matrices from which IT estimates were obtained for each listener ranged from N=280 to N=630 samples per Nucleus user and N=280 to N=350 samples per Symbion user. We averaged the reported estimates for each feature across users for each device group. Also reported was the pooled confusion matrix for each device group, consisting of N=2940 samples for the Nucleus group and N=3430 samples for the Symbion group. We performed IT analysis on the pooled matrices to obtain $\mathrm{I}\widehat{\mathrm{T}}$ estimates for each feature and for each device group. The averaged and pooled $\mathrm{I}\widehat{\mathrm{T}}$ estimates obtained were compared to test for overestimation bias.

RESULTS

In a system where input and output are sampled independently from a uniform distribution, it is known from the outset that information transfer is zero, i.e., IT=0%. In Fig. 2 are values of the average estimate of information transfer as a function of the number of samples for confusion matrices ranging in size from 2×2 to 10×10 filled with uniformly distributed pseudorandom data. Two observations are worth noting. First, average $\mathrm{I}\widehat{\mathrm{T}}$ overestimates IT when the number of samples N is small, and approaches IT=0% as N becomes large. Hence, although $\mathrm{I}\widehat{\mathrm{T}}$ is an estimator for IT, it is a biased estimator. Second, the size of the overestimation depends on both the number of samples N and the size of the matrix. Larger matrices will tend to produce a larger overestimation and require more samples before $\mathrm{I}\widehat{\mathrm{T}}$ estimates will asymptote to their true value.

Figure 2.

Average information transfer estimate as a function of the number of samples for matrices filled with uniformly distributed pseudorandom data. Average was obtained from 10 000 iterations. Size of matrices ranges from 2×2 to 10×10. In each case, the true value for IT is 0%.

The sampling constraint we employed allowed us to examine the bias in another manner, as a function of the number of samples per matrix category. If an m×m matrix is filled with N samples so that each of the m possible inputs are presented the same number of times every cycle of m samples, then the number of samples per matrix category every m samples is N∕m. Could the overestimation bias be the same when examined on a per category basis, irrespective of matrix size? In Fig. 3, it is clear that this is not the case. For the same number of samples per matrix category, larger matrices will still tend to produce a larger overestimation. The data depicted in Fig. 3 are also summarized in Table 2, for matrix sizes ranging from 2×2 to 10×10 using up to 100 samples per matrix category. The overestimation in the 2×2 matrix is nearly negligible, less than 2%, after as few as 20 samples per category (N=40 samples). In contrast, the overestimation in the 10×10 matrix becomes less than 2% after as many as 100 samples per matrix category (N=1000 samples). Clearly, using too many feature categories relative to the number of samples collected could give rise to problematic estimates.

Figure 3.

Average information transfer estimate as a function of the number of samples per matrix category (N∕m) for m×m matrices of size m=2,…,10 filled with uniformly distributed pseudorandom data.

Table 2.

Average estimated information transfer as a function of samples per matrix category (N∕m) for m×m matrices of size m=2,…,10. Matrices filled with data sampled from a uniform distribution using the strict sampling constraint described in the text. The true value for information transfer should be 0%.

$I\widehat{T}$ (%)N∕m	Matrix size (m×m)
	2×2	3×3	4×4	5×5	6×6	7×7	8×8	9×9	10×10
10	4.0	7.0	9.6	11.9	14.1	15.9	17.7	19.3	20.8
20	1.9	3.2	4.4	5.5	6.5	7.5	8.4	9.4	10.2
30	1.2	2.1	2.8	3.5	4.2	4.8	5.4	6.0	6.5
40	0.9	1.6	2.1	2.6	3.1	3.5	3.9	4.4	4.8
50	0.7	1.2	1.6	2.0	2.4	2.8	3.1	3.4	3.7
100	0.4	0.6	0.8	1.0	1.2	1.3	1.5	1.7	1.8

One must keep in mind that the matrices in Table 2 were generated so that each category has the same number of samples per matrix category. Very often in IT analysis, feature matrices are produced by partitioning a larger matrix into feature categories where the numbers of samples per feature category are not equal. The effect of unequal samples per category on the overestimation bias is depicted in Fig. 4, where five 2×2 matrices were constructed using different partitions of a 10×10 matrix as the latter was filled with uniformly distributed data using the strict sampling constraint. For purposes of comparison, the bias due to a 3×3 matrix with a uniform partition is also plotted in Fig. 4 in gray (i.e., the same 3×3 data plotted in Fig. 2). The different 2×2 partitions are represented as (5, 5), (4, 6), (3, 7), (2, 8), and (1, 9), where (1, 9) means that the first category of the 10×10 matrix became the first category in the 2×2 matrix and the other 9 categories of the 10×10 matrix were combined to produce the second category in the 2×2 matrix. From Fig. 4, it is evident that a 2×2 matrix constructed from a less uniform partition of the 10×10 matrix tends to produce greater overestimation than a more uniform partition. That is, a less uniform partition will tend to require more samples than a more uniform partition before the bias becomes negligible. Indeed, after N=200 samples, the bias in the 2×2 matrix with the (1, 9) partition becomes very nearly equal to the bias in the 3×3 matrix with a uniform partition. Hence, a very extreme non-uniform partition in a smaller matrix can increase the bias, as if it came from a larger matrix size.

Figure 4.

Average information transfer as a function of the number of samples for five 2×2 matrices obtained from different partitions of a larger 10×10 matrix filled with pseudorandom data. For comparison, the bias due to a 3×3 matrix with a uniform partition filled with pseudorandom data is plotted in gray.

To understand the difference between the curves in Fig. 4, it is useful to refer to Table 2. For example, in Fig. 4, the average $\mathrm{I}\widehat{\mathrm{T}}$ for the (1, 9) 2×2 matrix at N=100 samples is 1.6%. In this matrix, the first input category consists of 10 samples whereas the second input category consists of 90 samples. In Table 2, 10 samples per category for a 2×2 matrix will result in an average $\mathrm{I}\widehat{\mathrm{T}}$ of 4% whereas 90 samples per category will result in an average $\mathrm{I}\widehat{\mathrm{T}}$ of 0.4%. The average $\mathrm{I}\widehat{\mathrm{T}}$ in the (1, 9) 2×2 matrix with 10 samples in one category and 90 samples in the other category falls in between these two extremes, and is largely determined by the input category with fewer samples per category.

Turning now to the data of Miller and Nicely (1955), the average $\mathrm{I}\widehat{\mathrm{T}}$ for the 16-consonant confusion matrix and 2×2 voicing matrix in Fig. 1 are plotted in Fig. 5 as a function of the number of samples (filled and empty circles respectively). When applying $\mathrm{I}\widehat{\mathrm{T}}$ to the 16×16 consonant matrix, each consonant is treated as a separate feature category. Although this is not the most common way of conducting IT analysis, it is presented here as a contrast to the 2×2 voicing matrix. Because each consonant stimulus was selected once every 16 samples, the average $\mathrm{I}\widehat{\mathrm{T}}$ are also plotted as a function of the number of stimulus repetitions (abscissa on top), i.e., the number of times all stimuli were repeated. Each value of average $\mathrm{I}\widehat{\mathrm{T}}$ includes an error bar (black for the 16-consonant matrix and gray for the voicing feature matrix) that represents ±2 standard deviations about the mean. The horizontal lines represent the value of $\mathrm{I}\widehat{\mathrm{T}}$ after 4000 samples in each case (24% for the 16-consonant matrix and 52% for the 2×2 voicing matrix). Although a small amount of bias may still exist after 4000 samples it is negligible at this point and the horizontal lines can be considered close enough to the actual asymptote, i.e., the true value of IT for each matrix. In both matrices, the average $\mathrm{I}\widehat{\mathrm{T}}$ is not equal to its true value for all numbers of samples (or stimulus repetitions) showing again that $\mathrm{I}\widehat{\mathrm{T}}$ is a biased estimator. Although in both matrices, the average $\mathrm{I}\widehat{\mathrm{T}}$ overestimates its true value for small numbers of samples, the bias is clearly different between the two cases. The average $\mathrm{I}\widehat{\mathrm{T}}$ for the voicing feature matrix approaches to within 1% of its true value after only 7 stimulus repetitions (112 samples), whereas even after 50 stimulus repetitions not only does the average $\mathrm{I}\widehat{\mathrm{T}}$ for the 16-consonant matrix overestimate its true value by 4%, but the true value remains lower than 2 standard deviations below the mean $\mathrm{I}\widehat{\mathrm{T}}$. Of course, the average $\mathrm{I}\widehat{\mathrm{T}}$ for the 16-consonant matrix will eventually approach the “true value” depicted in Fig. 5 as the latter was estimated from the same matrix filled with N=4000 samples.

Figure 5.

Average information transfer estimate as a function of the number of samples for the 16-consonant matrix (filled circles) and 2×2 voicing matrix (empty circles) depicted in Fig. 1. Averages were obtained from 10 000 iterations of randomly selecting samples from the consonant matrix using the strict sampling constraint. Black and gray error bars depict 2 standard deviations above and below the average for the 16-consonant and 2×2 matrices respectively. Horizontal lines depict approximate true value for IT.

Another difference in $\mathrm{I}\widehat{\mathrm{T}}$ values between the two matrices is that the 2×2 voicing feature matrix produces a larger standard deviation about the mean $\mathrm{I}\widehat{\mathrm{T}}$ than the 16-consonant matrix. Hence, for the voicing matrix, even though the average $\mathrm{I}\widehat{\mathrm{T}}$ reaches to within 1% of its true value after 7 stimulus repetitions, the amount of variability about this mean is ±9%. At the same number of stimulus repetitions the amount of variability about the mean $\mathrm{I}\widehat{\mathrm{T}}$ for the 16-consonant matrix is ±5%, though this mean overestimates the true value by 23%. The error bars for both matrices demonstrate that in addition to being a biased estimator $\mathrm{I}\widehat{\mathrm{T}}$ will also yield estimates that can vary considerably above and below the expected value, and that this variability will diminish as one uses a greater number of samples. This variability, due to the type of sampling error one encounters with any statistical estimator, is not explored further here.

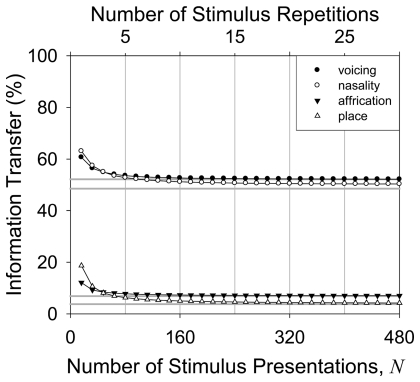
In Fig. 6 are plots of average $\mathrm{I}\widehat{\mathrm{T}}$ for the features voicing, nasality, affrication, and place using the data of Miller and Nicely (1955). The data are plotted both as a function of the number of samples N (abscissa on bottom) as well as the number of stimulus repetitions (abscissa on top), where each stimulus repetition occurs every 16 samples. The average $\mathrm{I}\widehat{\mathrm{T}}$ for the voicing feature is the same as in Fig. 5. The horizontal gray lines represent, approximately, the true value of IT for each feature. To reach within 1% of the true value, the average $\mathrm{I}\widehat{\mathrm{T}}$ required 7 stimulus repetitions (112 samples) for the voicing feature, 5 stimulus repetitions (80 samples) for the affrication feature, and 13 stimulus repetitions (208 samples) for the place feature. For nasality, even after 50 stimulus repetitions (800 samples) the average $\mathrm{I}\widehat{\mathrm{T}}$ failed to reach within 1% of its true value, though it did reach 3% of this value after 9 stimulus repetitions (144 samples).

Figure 6.

Average information transfer estimate as a function of the number of samples for the features voicing, nasality, affrication, and place of articulation. For each curve, average was obtained from 10 000 iterations of randomly selecting samples from the 16-consonant matrix depicted in Fig. 1 using the strict sampling constraint, and categorizing samples into features according to Table 1. For each feature, horizontal gray lines depict approximate true value for IT.

In Tables 3, 4, 5, 6 are examples of averaged and pooled IT estimates taken from three representative studies. The pooled estimate is obtained from one aggregate confusion matrix that includes the trial-by-trial data of all test subjects. Conversely, with the averaged estimate, each test subject’s confusion matrix is considered separately. As the number of samples in the aggregate matrix is much larger than the number of samples in each subject’s confusion matrix, we would expect that the pooled estimate would provide a less biased estimate of the true value for the average IT among all the subjects, whereas the averaged estimate of this true value would incur a larger overestimation. The number of samples per matrix for the pooled and averaged IT estimates and the number of feature categories per feature are specified in Tables 3, 4, 5, 6. In Table 3 are averaged and pooled IT estimates for three consonant features from the data of Donaldson and Kreft (2006). In each case the average $\mathrm{I}\widehat{\mathrm{T}}$ is larger than the pooled $\mathrm{I}\widehat{\mathrm{T}}$, but not by a large amount. The overestimation ranged from 2% to 6% with the largest overestimation coming from the manner feature with 4 categories. In Tables 4, 5 are averaged, Pool8 and Pool24 IT estimates from data reported in van Wieringen and Wouters (1999) for vowel (Table 4) and consonant (Table 5) features. In Tables 4, 5 there is a consistent drop in $\mathrm{I}\widehat{\mathrm{T}}$ between the average estimates and those pooled for 8 listeners, and between those pooled for 8 listeners and those pooled for 24 listeners. Overall, the average $\mathrm{I}\widehat{\mathrm{T}}$ overestimates the pooled $\mathrm{I}\widehat{\mathrm{T}}$ for 24 listeners by 9%–12% for the vowel features in Table 4, and by 6%–9% for the consonant features in Table 5. In Table 6 are averaged and pooled IT estimates from data reported in Tye-Murray and Tyler (1989) for six consonant features for users of the Nucleus and Symbion CI devices. The difference between the average and pooled estimates, i.e., average minus pooled, ranges between −2% and 9% with the largest overestimation occurring for the place and envelope features which comprise 4 feature categories; the other features consist of 2 feature categories. Differences in how phonemes were partitioned among the various features did not appear to play a large role in the amounts of bias reported in Tables 3, 4, 5, 6.

Table 3.

Information transfer estimates for consonant features in 20 cochlear implant users from Donaldson and Kreft (2006). Next to each feature in parentheses is the number of feature categories. Avg: average estimate per user, N=285 samples per matrix; Pool: estimate obtained from data pooled in one matrix with N=5700 samples; and diff=Avg-Pool. Without the small-sample bias, diff should be close to zero.

$I\widehat{T}$ (%)	∕Ca∕			∕Ci∕			∕Cu∕
	Avg	Pool	diff	Avg	Pool	diff	Avg	Pool	diff
Voicing (2)	59	56	3	63	60	3	67	65	2
Place (3)	35	33	2	23	21	2	27	25	2
Manner (4)	60	54	6	59	54	5	56	52	4

Table 4.

Information transfer estimates for vowel features in 24 cochlear implant users from van Wieringen and Wouters (1999). Next to each feature in parentheses is the number of feature categories. Avg: average estimate per user, N=120 samples per matrix; Pool8: estimate obtained by averaging the pooled estimate between better, intermediate, and poorer performers (8 listeners per group with N=960 samples per matrix); and Pool24: estimate obtained by pooling data from all 24 listeners into one matrix with N=2880 samples. Without the small-sample bias, numbers in a given row should be similar.

$I\widehat{T}$ (%)	Vowels
	Avg	Pool8	Pool24
Duration (2)	34	28	23
F1 (3)	28	24	19
F2 (3)	31	24	19

Table 5.

Information transfer estimates for consonant features in 24 cochlear implant users from van Wieringen and Wouters (1999). Next to each feature in parentheses is the number of feature categories. Avg: average estimate per user, N=192 samples per matrix; Pool8: estimate obtained by averaging the pooled estimate between better, intermediate, and poorer performers (8 listeners per group with N=1536 samples per matrix); and Pool24: estimate obtained by pooling data from all 24 listeners into one matrix with N=4608 samples. Without the small-sample bias, numbers in a given row should be similar.

$I\widehat{T}$(%)	Consonants
	Avg	Pool8	Pool24
Voicing (2)	41	35	33
Burst (2)	57	53	51
Amp Env (2)	63	59	56
Nasal (2)	43	41	37
Affrication (2)	52	46	43
Manner (3)	58	53	49
Place (4)	15	10	8

Table 6.

Information transfer estimates for consonant features in 7 Nucleus and 10 Symbion cochlear implant users from Tye-Murray and Tyler (1989). Next to each feature in parentheses is the number of feature categories. Avg: average estimate per user, about N=420 and N=343 samples per matrix for Nucleus and Symbion users, respectively; Pool: estimate obtained from pooled data in one matrix with N=2940 and N=3430 samples for Nucleus and Symbion users, respectively; and diff: Avg-Pool. Without the small-sample bias, diff should be close to zero.

$I\widehat{T}$ (%)	Nucleus			Symbion
	Avg	Pool	diff	Avg	Pool	diff
Voicing (2)	22	22	0	49	43	6
Nasality (2)	24	23	1	56	51	5
Frication (2)	17	19	−2	34	36	−2
Duration (2)	14	12	2	33	31	2
Place (4)	18	13	5	20	11	9
Envelope (4)	29	24	5	54	46	8

DISCUSSION

Miller and Nicely (1955) stated that the MLE for the information transfer will be biased to overestimate its true value for small samples. This study clarifies their assertion. Three approaches were followed to examine the small-sample bias in information transfer estimates. The first approach was to examine a case in which the bias is very clear and easy to interpret, where input and output are independent and drawn from a uniform distribution and the true value for the information transfer is 0%. The second approach was to reconstruct the bias in the original data set of Miller and Nicely (1955) by sampling data from one of the confusion matrices reported therein and calculating the amount of overestimation as a function of the number of samples for different speech features. Information transfer analysis was born out of this classic study and though the authors mentioned the small sample bias parenthetically, no indications or guidelines were presented about the magnitude of the bias or how to overcome it other than a statement to the effect that the bias is very small after a very large number of samples on the order of N=4000. Hence, the Miller and Nicely data set was included here to provide an explicit description of the bias referred to in their study. The third approach was to ascertain whether the problem of overestimation bias is relevant in a practical sense by examining the tendency of overestimation bias in information transfer estimates reported in three contemporary studies representative of how IT analysis is commonly used. Each of these approaches provides insight into the magnitude of the overestimation and a rough picture on the requirements to reasonably overcome this bias.

The case where input–output pairs are independent and drawn from a uniform distribution is a model of chance performance and demonstrates how the overestimation bias depends on the number of samples relative to the size of the confusion matrix, as well as how these samples are partitioned among the input categories of the matrix. In Fig. 2, the peak overestimation ranges from 50% to 76% depending on whether the confusion matrix was from 2×2 to 10×10. As for the number of samples before $\mathrm{I}\widehat{\mathrm{T}}$ drops below 2%, 40 samples were sufficient for the 2×2 case, whereas 1000 samples were required for the 10×10 case. Hence, larger matrices will tend to produce a larger overestimation and require more samples to reach the true information transfer. Figure 3 and Table 2 show how the effect of matrix size persists when the bias is examined as a function of the number of samples per matrix category. For example, at 10 samples per category, the bias ranges from 4% to 21% depending on whether the confusion matrix was 2×2 to 10×10. Figure 4 shows the effect on the bias when the number of samples per category is unequal among the matrix input categories. This occurs when a matrix is constructed from a non-uniform partition of a larger matrix. In such a case, the bias will be dominated by the input category with fewest samples and require more samples to be overcome relative to a matrix constructed from a uniform partition of a larger matrix. These model systems demonstrate how chance performance could yield a nonzero information transfer estimate depending on the number of samples, the size of the confusion matrix, and how samples are partitioned amongst the input categories of the matrix.

These three effects on the overestimation bias are also demonstrated in the curves of average $\mathrm{I}\widehat{\mathrm{T}}$ in Figs. 56, resampled from Miller and Nicely (1955). In Fig. 5, the bias in information transfer estimates for a 16-consonant matrix is contrasted with the bias when the consonants are partitioned into a 2×2 voicing matrix. Whereas the bias is fairly large for the 16×16 matrix and requires over 50 stimulus repetitions for the average information transfer to reach within 3% of its true value, the average bias in the 2×2 voicing matrix falls below 3% after just 3 stimulus repetitions, though considerable variability about the mean does exist (±15%). That is, although the average $\mathrm{I}\widehat{\mathrm{T}}$ in a small feature matrix can converge to its true value after relatively few stimulus repetitions, one should not expect the same from a single estimate of IT as considerable variability can remain even after a much larger number of stimulus repetitions. As depicted in Fig. 6, similar results for the average $\mathrm{I}\widehat{\mathrm{T}}$ were obtained for the other feature matrices. After a relatively small number of stimulus repetitions, the overestimation in the average information transfer became quite small. Even nasality, for which the bias persisted the most relative to the other features, reached within 3% of its true value using less than 10 stimulus repetitions (160 samples). This many stimulus repetitions is well within the number typically obtained in the speech and hearing fields and may be sufficient to overcome the bias when dealing with a small number of feature categories on the order of 2 or 3.

Some differences do exist amongst the curves of average $\mathrm{I}\widehat{\mathrm{T}}$ in Fig. 6. The order of features from least to greatest in terms of the number of stimulus repetitions required before the average $\mathrm{I}\widehat{\mathrm{T}}$ approached its true value was affrication, voicing, place, and then nasality. As one can observe in Table 1, the affrication and voicing features result in 2×2 matrices with partitions (8, 8) and (7, 9), respectively. The small matrix size accompanied by a fairly uniform partition of consonant stimuli results in a small bias that converges to its true value after relatively few stimulus repetitions. The place feature results in a relatively larger matrix (3×3) and hence requires more stimulus repetitions to converge to its true value. Finally, although the nasality feature results in a small matrix (2×2), its partition is highly skewed (14, 2) and so its bias is predominantly determined by the nasal category which accrues samples only twice every 16 samples. Hence, the effects of numbers of samples, matrix size, and how the samples are distributed among the feature categories combine to provide an account for the differences in small sample bias among the features in Fig. 6.

The three CI studies that were examined in this study, whose results are analyzed in Tables 3, 4, 5, 6, were chosen specifically because they published sufficient data to illustrate two different ways of calculating information transfer from a population of CI users. Each method can result in different amounts of overestimation bias. First, one can calculate the information transfer from each user’s confusion matrix and average the results. Second, one can pool data from all subjects into one aggregate confusion matrix and then calculate the information transfer. In general, the information transfer estimate obtained by averaging individual IT estimates from individual subject matrices will incur a larger overestimation than the information transfer estimate obtained from the pooled matrix. The averaging approach utilizes confusion matrices with a relatively smaller number of samples per matrix, whereas the pooled approach utilizes a confusion matrix with a relatively large number of samples. In addition to the number of samples, the amount of overestimation also depends on the size of the feature matrices analyzed.

In Table 3 and Table 6, one observes how the difference between averaged and pooled information transfer can be relatively small (3% or less) for feature matrices of 2×2 or 3×3 when the number of samples per matrix in the averaged estimate is larger than N=250. However, this difference becomes more substantial once the size of the feature matrix analyzed becomes 4×4. In Tables 4, 5, the individual matrices contained less than 200 samples resulting in a larger discrepancy between the averaged and pooled information transfer, even for features with 2 or 3 categories. For these matrices, an intermediate category between averaged and pooled results was included, showing a steady decrease in information transfer estimates between the averaged matrices and the pooled matrix, as the number of samples per matrix for each category was increased.

Some overestimation remained between features in the intermediate Pool8 category and features in the Pool24 category in Tables 4, 5, between 2% and 5%, even though the pooled matrices for the intermediate category consisted of about 1000 samples. Some overestimation also remained between the average and pooled estimates in Table 6 for the voicing and nasality features among Symbion patients, 5% and 6% respectively, even though the averaged estimates involved 2×2 feature matrices with more than 250 samples per matrix. These results may be attributed to the variability in information transfer estimates in addition to the bias, as depicted by the confidence intervals for the curves in Fig. 5. Indeed, the curves of Fig. 6 would suggest that the bias is nearly overcome after 200 samples for features with 2 or 3 categories. However, these curves were obtained from an average of 10 000 iterations. Hence, one should not presume that a number of samples on the order of N=250 will guarantee an information transfer estimate equal to its true value for small matrices since sometimes N=1000 might not be enough due to the randomness involved.

Both the averaged and pooled approaches to obtaining IT estimates have a disadvantage and an advantage. With the averaged approach, one is likely to obtain a result that overestimates the true value, whereas the pooled approach will likely yield an unbiased result. However, the averaged approach also yields confidence intervals with which one can conduct statistical analyses to test for differences between experimental groups. The pooled approach only yields one estimate for each condition, obviating any statistical comparisons between groups. So which approach should one follow?

If one is not interested in the absolute value of the information transfer for a given feature, but rather in relative differences between groups, then the averaged approach is a viable option and statistical differences thus obtained are valid. However, using a small number of samples per matrix will increase the inherent variability of IT estimates, in addition to inter-individual differences within the group, and thus make it more difficult to demonstrate significant differences between groups. Furthermore, if one decides to implement the averaged approach it is important to ensure that each confusion matrix, both between and within experimental groups, contains the same number of samples. Although the amount of bias in a group of IT estimates may differ within the group even when the number of samples obtained for each matrix within the group are the same, there is less chance of confounding the bias in the average IT for the group than if the number of samples per matrix is not fixed. Also, caution is required when comparing IT estimates between features with different numbers of feature categories or with very different partitions of the same phoneme matrix, because the bias becomes more prevalent as the number of feature categories increases and when the feature categories consist of very nonuniform partitions of phoneme stimuli.

If one is interested in the absolute value of the information transfer for the group, then one needs to ensure that the matrices to be analyzed have a sufficient number of samples. This can be achieved by pooling several matrices, or by ensuring that each individual matrix has an adequate number of samples. An example of when the absolute value of the information transfer is required is in sequential information transfer analysis (Wang and Bilger, 1973), where larger IT estimates determine the order for which features are sequentially partialed out of the confusion matrix. The effect of the small-sample bias on sequential IT analysis has not been explored here, and is yet to be determined.

CONCLUDING REMARKS

Until more sophisticated techniques are developed to correct for small-sample bias in IT estimates, it is important to keep the bias in mind when planning one’s experimental paradigm. For example, based on the results of this study, we would suggest obtaining at least 250 samples per subject when examining information transfer for features with 2 or 3 categories. For features with 4 or 5 categories, we would suggest obtaining at least 500 samples. This number of samples should yield an average IT estimate that is within 3% of its true value. However, this suggestion is more of a rough guideline than a hard rule, because the actual sample estimate may be higher or lower than the average. To assess the amount of overestimation bias, it may be useful to report the pooled IT estimate in addition to the average IT estimate for each group, and compare the two results.