Perception and cortical neural coding of harmonic fusion in ferrets

Abstract

This study examined the perception and cortical representation of harmonic complex tones, from the perspective of the spectral fusion evoked by such sounds. Experiment 1 tested whether ferrets spontaneously distinguish harmonic from inharmonic tones. In baseline sessions, ferrets detected a pure tone terminating a sequence of inharmonic tones. After they reached proficiency, a small fraction of the inharmonic tones were replaced with harmonic tones. Some of the animals confused the harmonic tones with the pure tones at twice the false-alarm rate. Experiment 2 sought correlates of harmonic fusion in single neurons of primary auditory cortex and anterior auditory field, by comparing responses to harmonic tones with those to inharmonic tones in the awake alert ferret. The effects of spectro-temporal filtering were accounted for by using the measured spectrotemporal receptive field to predict responses and by seeking correlates of fusion in the predictability of responses. Only 12% of units sampled distinguished harmonic tones from inharmonic tones, a small percentage that is consistent with the relatively weak ability of the ferrets to spontaneously discriminate harmonic tones from inharmonic tones in Experiment 1.

INTRODUCTION

Two fundamentally important auditory perceptual phenomena, spectral fusion and virtual pitch, are intimately associated with sounds having harmonic spectra. The importance of harmonic sounds in auditory perception is such that auditory theory for at least 150 years has been driven in part by a quest for understanding the mechanisms underlying pitch perception (von Helmholtz, 1954). Despite intense investigation, many aspects of pitch perception have resisted explanation. One such problem is identifying its cortical neural correlates. More generally, not just pitch but the cortical encoding of harmonic sounds is not well understood, and forms the topic of this paper.

Listeners typically hear a harmonic complex tone as a coherent unitary entity with a clear pitch; this perceptual fusion due to harmonicity is used by the brain to organize complex acoustic environments into separate auditory objects (Bregman, 1990). An example of this brain function is the improvement obtained in the ability to distinguish two talkers when a fundamental frequency difference is imposed (Brokx and Nooteboom, 1980). This study focuses on fusion of tone components due to harmonic relationships, seeking correlates of this fusion in single cortical neurons. The highly salient pitch evoked by spectrally resolved harmonic complex tones, known as virtual pitch (when there can be no actual energy at the frequency of the perceived pitch), makes this study relevant for understanding cortical neural coding of pitch. We distinguish this pitch due to spectrally resolved harmonics from that due to spectrally unresolved harmonics, and use the term residue pitch to refer to the latter in this paper. The pitch due to spectrally resolved harmonics is the most important of the many distinct percepts that come under the rubric of pitch, because it underlies speakers’ voices and speech prosody, as well as musical intervals and melody.

The percepts of virtual pitch and the spectral fusion of complex tones are closely related. There are a great many perceptual parallels, as in their similar insensitivity to the phases of low harmonics (Hartmann et al., 1993; Houtsma and Smurzynski, 1990; Moore and Glasberg, 1985). Moreover, models for virtual pitch apply well to harmonic spectral fusion as well (Duifhuis et al., 1982). For instance, in pattern recognition models, the pitch of a complex tone is equal to the fundamental frequency of the harmonic template that best fits the evoked neural activity arrayed along the tonotopic axis of the cochlea. In such models, template matching operates on the neural activity due to the resolved components of the complex tone (e.g., Goldstein, 1973; Srulovicz and Goldstein, 1983; Terhardt, 1974, 1979; Wightman, 1973). Such models predict well that the pitch of harmonic complex tones is not changed by the absence of the fundamental component: this is an important attribute for a model of pitch to possess (de Cheveigne, 2005). There is evidence that a template-matching operation also underlies the perceptual fusion of harmonically related components of a complex tone (Brunstrom and Roberts, 1998, 2000; Lin and Hartmann, 1998). However, the two processes are not entirely congruent, with virtual pitch depending on harmonic relations between components and perceptual fusion being due to spectral regularity (Roberts and Brunstrom, 1998, 2001, 2003). Nevertheless, the similarities of fusion and virtual pitch for harmonic stimuli suggest common mechanisms underlying the two and enable findings of one to be applied to the other. The study seeks to identify the neural basis for the special perceptual status of harmonicity; it approaches this issue from the perspective of the fusion or perceptual coherence of harmonic tones, and in the process it sheds light on the pitch evoked by such tones.

While spectral fusion and virtual pitch of complex tones are closely related, previous studies of the cortical coding of harmonic sounds have focused on the latter. One of the few studies that examined the role of human auditory cortex in harmonic fusion found support in measurements of event related potentials for the involvement of primary cortical areas (Dyson and Alain, 2004). Lesion studies show that the auditory cortex is needed for the perception of virtual pitch (Whitfield, 1980; Zatorre, 1988). Primary auditory cortex (AI) has failed, on the whole, to yield compelling correlates of virtual pitch. However, a study by Bendor and Wang (2005) in nonprimary auditory cortex of marmosets has yielded promising results that remain to be independently replicated and confirmed. See also further reservations discussed in McAlpine (2004).

In recordings from single neurons, Bendor and Wang (2005) found responses in rostral field tuned to the fundamental frequency of harmonic complex tones with and without the missing fundamental component. Such tuning to the fundamental frequency regardless of the physical presence of that component is suggestive of these neurons being tuned to pitch. Nevertheless, it is unclear if these neurons respond differently to harmonic tones than to inharmonic tones, as a pitch-selective or harmonicity-selective neuron might be expected to do.

Many studies of AI have examined pitch coding, and failed to yield harmonicity-selective neurons. Recordings from single units (Schwarz and Tomlinson, 1990) and multiple units (Fishman et al., 1998) of monkey AI in response to missing-fundamental harmonic complex tones failed to show any rate tuning to the fundamental frequency. Multi-unit activity and current-source-density patterns recorded in high-frequency areas of monkey AI directly encode the click rate of same- and alternating-polarity click trains in the temporal pattern of response (Steinschneider et al., 1998); this click rate corresponds to the weak residue pitch. Consistent with observations from single-unit recordings (Schwarz and Tomlinson, 1990), resolved harmonics were represented as local maxima of activity determined by the tonotopic organization of the recording sites. However, the virtual pitch that would be derived from these local maxima was not encoded directly, in that neither the temporal pattern of response nor spatial distribution of activity reflected the fundamental frequency. Finally, several studies have reported mapping of the envelope periodicity of amplitude-modulated tones on an axis orthogonal to the tonotopic axis in AI of Mongolian gerbils (Schulze et al., 2002; Schulze and Langner, 1997a, 1997b) and of humans (Langner et al., 1997). These findings may indicate the presence of a map of virtual pitch, but three aspects of the experiments make the assertion inconclusive. First, the neurons forming the map of envelope periodicity were primarily sensitive to high-frequency energy (>5 kHz), a frequency region that does not evoke virtual pitch in human and cats (Heffner and Whitfield, 1976). Second, an extensive body of psychoacoustical literature shows that envelope periodicity, in general, is not predictive of the virtual pitch evoked by a stimulus (e.g., de Boer, 1956, 1976; Flanagan and Gutman, 1960). Third, rather than reflecting the virtual pitch due to the spectrally resolved components of the stimulus, the findings could instead be a mapping of the fundamental frequency (or modulation frequency for an amplitude-modulated tone) reintroduced by nonlinear distortion in the cochlea (McAlpine, 2002, 2004).

The lattermost of these reservations is also applicable to observations in monkey AI of similar responses to a pure tone and a missing-fundamental harmonic complex of the same pitch (Riquimaroux, 1995; Riquimaroux and Kosaki, 1995). Sensitivity to harmonic combinations of resolved components that would show tuning to the fundamental frequency of complex tones has been found in marmoset AI (Kadia and Wang, 2003) (also in bats, Suga et al., 1983). Such neurons may underlie spectral fusion of harmonic complex tones. However, because these neurons preferred high frequencies and very high fundamental frequencies (typically greater than 4 kHz), the role of such neurons in the computation of virtual pitch and spectral fusion is unclear for sounds having predominantly low-frequency spectra such as speech, music, and many animal vocalizations.

In summary, previous studies of the cortical encoding of harmonic sounds have focused on correlates of virtual pitch. Several studies have yielded promising candidate neurons that encode pitch and may encode harmonic fusion, although these findings need to be further understood and replicated.

In this paper, we report experiments in domestic ferrets (Mustela putorius) aimed at understanding the cortical neural coding of harmonic sounds from the perspective of spectral fusion rather than virtual pitch. By comparing the neural representation of perceptually fused harmonic complex tones with that of perceptually unfused inharmonic complex tones in single AI and anterior auditory field (AAF) neurons, we expect to uncover neural computations specifically elicited by harmonic fusion in subcortical or primary cortical structures. The presence of such harmonicity-specific processing would have been missed by previous studies that employed harmonic sounds exclusively.

An assumption underlying the neurophysiology experiment is that ferrets automatically fuse components of harmonic complex tones, like humans do in typical listening conditions. Many animals can hear the pitch of the missing fundamental, including cats and monkeys (Heffner and Whitfield, 1976; Tomlinson and Schwartz, 1988), so it is not unreasonable to assume that ferrets might do the same. In order to hear the pitch of the missing fundamental, the feline and primate subjects must have been able to estimate the fundamental from the components that were actually present in the stimuli. However, the animals did not necessarily fuse these components into a unitary entity.1 The first experiment in this paper uses a conditioned avoidance behavioral-testing paradigm to study whether ferrets spontaneously fuse harmonic components of complex tones. Experiment 2 seeks neural correlates of harmonic fusion in ferret auditory cortex, specifically in areas AI and in AAF.

EXPERIMENT 1: PERCEPTION OF HARMONIC COMPLEX TONES

Rationale

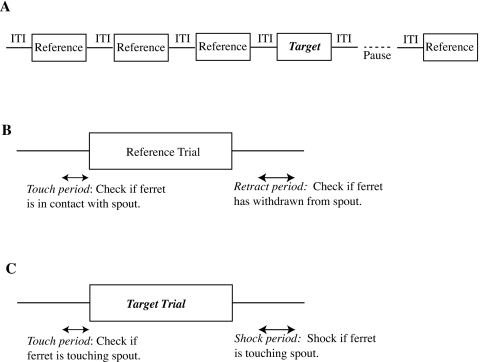
In order to address whether ferrets can automatically fuse components of a harmonic complex, we asked if they can distinguish inharmonic complex tones from harmonic complex tones without receiving training on the distinction between the two classes of sounds. The experiment was performed in two stages comprising baseline sessions and probe sessions (Fig. 1). In baseline sessions, the ferrets were trained to detect pure-tone targets in a sequence of inharmonic complex tone reference sounds. By eliminating or making unreliable the differences in frequency range, level, and roughness, we left two cues available for reliably distinguishing targets from references: (i) differences in the degree of perceptual fusion, and (ii) differences in timbre.

Figure 1.

Stimulus protocols for testing if ferrets automatically distinguish harmonic complex tones from inharmonic complex tones. (Top) In baseline sessions, ferrets were trained to detect pure-tone targets terminating a one-to-six-stimulus sequence of inharmonic complex tone reference sounds. Cues available for distinguishing the targets from the references were (i) differences in the quality of perceptual fusion and (ii) differences in timbre. (Bottom) In probe sessions conducted after ferrets attained proficiency in baseline sessions, a small fraction of the reference sounds were replaced by harmonic complex tone probe sounds. If harmonic complex tones were perceptually fused, then they might have been confused occasionally with the pure-tone targets, thereby indicating that ferrets can automatically distinguish harmonic tones from inharmonic tones.

When ferrets attained proficiency in these baseline sessions, probe sessions were conducted in which 10% of the reference sounds were replaced with harmonic complex tone probe sounds that were identical to the inharmonic complex tone references in every way except in the frequency relations between components. Because the timbre of the complex tones differs greatly from that of the pure tones, ferrets were expected, in most cases, to categorize the harmonic complex tones with the inharmonic complex tones based on similarity of timbre. This should be the case even if the ferrets heard the harmonic complex tones as fused. However, occasionally the putative fused nature of the harmonic complex tone might be confused with the unitary quality of the pure tone, prompting the ferret to respond to the harmonic probes as if it heard the pure-tone target. Therefore, detecting the probes at a rate greater than the false-alarm rate (i.e., the rate at which references were inadvertently detected as if they were targets) indicates that harmonic complex tones are heard differently than inharmonic complex tones. In contrast, failure to detect the probes in this experiment does not mean that the ferrets could not distinguish harmonic tones from inharmonic tones; they could simply have been using timbre exclusively to categorize the stimuli.

Methods

Behavioral testing

A conditioned-avoidance paradigm was used for testing how ferrets hear complex tones. The paradigm has been successfully used with many animals and it is described in detail by Heffner and Heffner (1995). We give a brief overview here.

A water-restricted ferret licked water from a continuously dripping spout while listening to reference sounds. At random intervals, an easily distinguishable target sound was presented followed by a light shock to the tongue delivered through the reward spout. Such pairings of stimulus and shock helped the ferret learn to break contact with the spout when it heard a target. The continuous water reward encouraged the ferret to maintain contact with the spout, providing a baseline behavior against which to measure responses. From the perspective of a ferret, the reference stimuli constituted safe trials because it could drink from the spout without getting shocked. On the other hand, target stimuli were warning trials, because they warned the ferret to break contact with the spout.

A computer registered successful withdrawal from the spout following a target as a hit and failure to withdraw as a miss. Because the animal occasionally withdrew in the absence of a target, a false-alarm rate was determined by registering how often it withdrew from the reward spout for reference trials. Both target and reference trials were ignored when the ferret did not contact the reward spout just before the trial; this was done in order to ensure that performance was evaluated only for trials on which the ferret attended to the stimuli. Figure 2 helps understand these measures by illustrating the presentation of trials and the timing of response intervals, while Table 1 shows which behaviors led to the different response categories.

Figure 2.

(A) Schematic representation of a trial sequence, where the target sound was presented on trial 4. The presentation of trials was paused after a target trial until the ferret returned to the spout. (B) Schematic representation of a reference trial shows two time intervals, one before the stimulus onset and the second after stimulus offset. During the second interval, the ferret’s contact with a reward spout determined the response class for the trial. If the ferret was not in contact with the spout during the first interval (the touch period), the response was classified as an “early” withdrawal and not counted toward overall performance on the experiment. If the ferret failed to contact the spout during the second interval (the retract period), the trial performance was scored as a “false alarm.” (C) Schematic representation of a target trial shows the same two intervals of time. The first interval played the same role as on a reference trial. The second interval (the shock period) was a period when contact with the spout elicited a shock, and the trial performance was scored as a “miss.” The touch period was 0.2 s while the retract and shock periods were 0.4 s in the experiment. The interval between the end of the stimulus and the start of the retract and shock periods was 0.2 s. Based on a figure from Heffner and Heffner (1995).

Table 1.

Relationship between stimulus timing, ferret response, and performance measures.

Trial type	Spout contact (touch period)	Spout contact (retract∕shock period)	Response class
Reference	Contact	No contact	Safe
Reference	Contact	Contact	False alarm
Reference	No contact	N∕A	Early
Target	Contact	No contact	Hit
Target	Contact	Contact	Miss
Target	No contact	N∕A	Early

During testing, two kinds of trial sequences were presented: (i) One to six reference trials followed by a target trial, and (ii) seven consecutive reference trials constituting a sham sequence. The number of reference trials in a given sequence was randomized such that the probability of the target sound occurring in trial position 2 through 7 was constant. This randomization was done so that the ferret could not preferentially respond on trials occurring at any given position. Sham sequences were interspersed between target sequences to discourage the ferrets from responding at regular intervals regardless of whether a target was presented. During probe sessions, probe trials were presented in exactly the same way as reference trials by replacing 10% of reference sounds by probe sounds; this percentage amounted, on average, to 40 probe sounds per session. Responses on the probe trials were scored in the same way as those on the reference trials. Probe hits and probe misses were equivalent to false alarms and safe responses respectively on reference trials.

Stimuli

For any given reference, target, or probe trial, stimuli were chosen randomly from a collection of inharmonic, pure-tone, and harmonic sounds that were synthesized and stored in memory just before placing a ferret in the testing cage. The stimuli were all 0.5 s long. Pure tones ranged in frequency from 150 to 4800 Hz. These frequencies were also the lower and upper bounds of the spectra of the complex tones, which had six components. To comply with these frequency limits, harmonic complex tones with components in random phase had fundamental frequencies between 150 and 800 Hz.

We constructed inharmonic complex tones by maintaining the same ratios or log spacings between consecutive components as in harmonic tones but reordering them to occur in different sequences than in harmonic tones. For example, a six-component harmonic tone had ratios between consecutive components of [2 3∕2 4∕3 5∕4 6∕5], and an exemplar inharmonic complex tone with lowest component at 200 Hz had components [200 267 320 480 960 1200] Hz corresponding to an ordering of the ratios of [4∕3 6∕5 3∕2 2 5∕4]. We constructed inharmonic complex tones in this manner so that these stimuli, if perceived as rough by ferrets, would have comparable roughness to the harmonic tones. The reasoning was that roughness is proportional to envelope fluctuations resulting from interactions between tone components within an auditory filter, and such interactions are comparable between harmonic complex tones and inharmonic complex tones constructed as above (Plomp and Levelt, 1965; Terhardt, 1974). The lowest component of the inharmonic complex tones was constrained between 150 and 800 Hz, so that any pitch cues from the edge of the spectrum were not reliably different from those generated by the spectral edge of the harmonic complex tones.

The levels of all stimuli were roved over a 6 dB range to prevent the use of intensity cues. Stimuli were played at a nominal level of 70 dB sound pressure level; this was the overall level of the complex tones, so individual components were lower in level. Levels were calibrated in an empty testing cage at the position occupied by the ferret’s head with a sound level meter (Bruel and Kjaer). All stimulus parameters were restricted to narrower ranges during training sessions to help the ferrets learn the task.

Experimental apparatus

Behavior of the ferrets was tested in a custom-designed cage mounted inside a Sonex-foam lined and single-walled soundproof booth (Industrial Acoustics, Inc.). Sound was delivered through a speaker (Manger) mounted in the front of the cage at approximately the same height above the testing cage as the metal spout that delivered the water reward.

The testing cage had a metal floor so that the ferret formed a low-resistance electrical pathway between the spout and the floor when licking. The lowered resistance between floor and spout was used by a custom “touch” circuit to register when the ferret contacted the spout. Electromechanical relays switched between the touch circuit and a fence charger in order to deliver shocks to the ferret’s tongue. All procedures for behavioral testing of ferrets were approved by the institutional animal care and use committee (IACUC) of the University of Maryland, College Park.

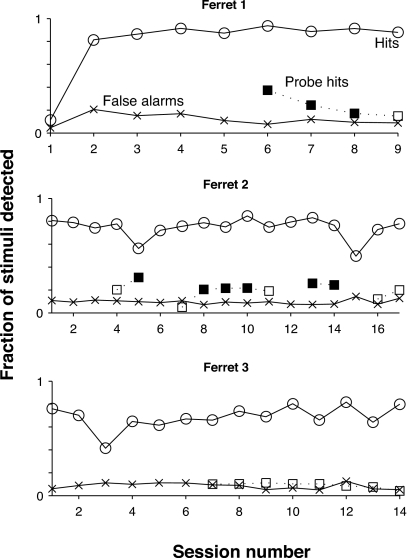
Results: Ferrets can weakly distinguish harmonic tones from inharmonic tones during spontaneous behavior

Results from testing three female ferrets, in Fig. 3, indicate that ferrets automatically distinguish harmonic complex tones from inharmonic complex tones on about 20% of trials. The figure shows performance on consecutive sessions after a training period lasting 15–75 sessions had been completed. Hit rates greater than 70% and false-alarm rates less than 20% show that all three ferrets attained proficiency at the baseline task of distinguishing pure-tone targets from inharmonic complex tone references. Two ferrets (top two panels) out of three also detected harmonic complex tone probes at a significantly higher rate than the false-alarm rate, especially in the earliest probe sessions. For the sessions indicated with filled symbols for the probe hit rate, the null hypothesis of no difference between the probe hit rate and the false-alarm rate was rejected (p<0.05) with a two-sided z test for independent proportions applied separately for each session and animal. The z test is a nonparametric test that is applicable when comparing two treatments (harmonic tones and inharmonic tones) and classifying measurements into two mutually exclusive types (hits and misses). Therefore, the ferrets, without receiving training on the distinction, occasionally heard harmonic complex tones to be different than inharmonic complex tones. Nevertheless, the considerable difference between the probe hit rate and the target hit rate indicates that harmonic tones were not treated equivalently to the pure tones.

Figure 3.

Performance of three ferrets on baseline and probe sessions of experiment. Several training sessions occurred prior to the first session indicated on the abscissa of the figure for each of the ferrets. All three ferrets attained proficiency at the baseline task of distinguishing pure-tone targets from inharmonic complex tone references, as indicated by the hit rate exceeding 70% and the false-alarm rate not exceeding 20%. Two ferrets (top two panels) had probe hit rates that were significantly greater than the false-alarm rate during probe sessions (statistically significantly greater probe hit rates are indicated with a filled symbol), indicating that they sometimes heard harmonic complex tones as being different from inharmonic complex tones.

Discussion

It is worth noting three points from the results. First, two ferrets heard harmonic complex tones to be different from inharmonic complex tones in about 15–20% of all trials. In these cases, they confused harmonic probes with pure-tone targets by responding to them as if they were pure tones, although the considerable difference between the hit rates for probes and targets suggests that these ferrets did not treat the two sound classes equivalently. A possible objection to the interpretation that probes and targets were confused, is that the ferrets simply heard the harmonic targets as a new kind of sound and responded (due to surprise) by withdrawing from the reward spout. This objection does not hold for two reasons. First, the parameters of the harmonic complex tones were matched in every way to those of the inharmonic complex tones. Thus, if harmonic probes were heard as a new category of sounds, it underscores the point that the ferrets could hear them to be different from inharmonic tones. Second, a novelty response should have declined rapidly as the ferret became accustomed to the harmonic probes. However, the elevated probe hit rate persisted for several sessions, especially in ferret 2.

Based on these results, we suggest that the ferrets sometimes distinguish harmonic tones from inharmonic tones on the basis of differences in perceived fusion. The results do not directly demonstrate that fusion was the relevant dimension for their judgments. However, we think it is a probable explanation because the harmonic and inharmonic complex tones were constructed to have no consistent differences in timbre or roughness. In analogy with human perception, we think perceptual fusion may be the logical dimension along which ferrets distinguish these two classes of sound. The results of the experiment also indicate that the ferrets occasionally distinguished harmonic tones from inharmonic tones automatically; it was automatic in the sense that they did not have to be taught the difference between these sound classes. In fact, the animals were not rewarded for making the distinction.

Second, the failure of ferret 3 to detect probes at a higher rate than the false-alarm rate does not necessarily indicate that it could not hear a difference between harmonic and inharmonic complex tones. Instead, the ferret may have learned to focus on the timbre cue in order to perform the baseline task. It may have continued to use the same cue during probe sessions and thus correctly categorized the harmonic probes to be similar to the inharmonic references along the perceptual dimension of timbre, while ignoring audible differences in fusion.

Finally, the probe hit rate for ferret 1 declined steadily after the first probe session. A probable reason is that the ferret, gradually learning that the harmonic probes were not associated with the shock, adjusted its judgments to use timbre exclusively rather than timbre in conjunction with fusion. Ferret 2, on the other hand, might not have adjusted its judgments simply because it more slowly learned that harmonic probes were not associated with the shock. Given more probe sessions, the ferret might have exhibited such a learning effect. Indeed, consistent with the notion that learning ability might underlie the difference between the declining probe hit rate for ferret 1 and the lack of such decline for ferret 2, the latter animal took almost five times more sessions than the former to attain proficiency at the baseline task.

In summary, two out of three ferrets discriminated harmonic tones from inharmonic tones. However, the low detection rate (15–20%) of harmonic tones was not comparable enough to that of pure tones to warrant a conclusion that these sound classes were perceptually equivalent to the animals.

EXPERIMENT 2: CORRELATES OF HARMONIC FUSION IN AUDITORY CORTICAL NEURONS

Rationale

To seek neural correlates of harmonic fusion, we recorded single-unit activity from primary auditory cortex (AI) and auditory anterior field (AAF) to a sequence of harmonic and inharmonic complex tones where all the sounds in the sequence shared a component at the best frequency (BF) of the unit under investigation (Fig. 4). The frequency of this shared component is known as the anchor frequency (AF) and the sequence is known as an anchored tone sequence in the rest of the paper. The anchor component was placed at the BF to ensure a robust response from the neuron for every complex tone. Any special cortical or upstream (subcortical) neural computation on harmonic sounds would be expected to result in a difference in the responses to the harmonic complex tones compared to those for inharmonic complex tones.

Figure 4.

Stimulus protocol for investigating cortical neural correlates of harmonicity in ferrets. Neural activity is recorded for a sequence of complex tones and a pure tone (anchored tone sequence), all of which share a component at the BF of the neuron under investigation. If cortical (or upstream) neurons treat harmonic sounds in a special manner, then the component at BF should elicit a qualitatively different response when presented in a harmonic context compared to an inharmonic context.

The effect of a harmonic context on the responses can be confused with the effects of spectro-temporal integration of stimulus spectrum by the spectro-temporal tuning of a cortical neuron (e.g., interaction of inhibitory sidebands with balance of spectrum above and below BF) (Depireux et al., 2001; Kowalski et al., 1996; Schreiner and Calhoun, 1994; Shamma et al., 1995). To account for spectrotemporal filtering, we measured a neuron’s spectro-temporal receptive field (STRF) and used it to predict the responses to the stimuli in the anchored tone sequences. An effect of harmonic context should then appear as a difference in the predictability of the responses to harmonic complex tones compared to those for inharmonic complex tones, because the predictions using the STRF account for the effect of the spectral context. The STRF is the best-fitting linear model for the transformation of the stimulus spectro-temporal envelope by a neuron. Because we measured STRFs using spectro-temporal envelopes imposed upon broadband noise (inharmonic) carriers, any effect of harmonic fusion is expected to manifest itself as a reduction in the predictability of responses to harmonic tones compared to that for inharmonic tones. A reduction is expected because the STRF, by definition, gives the best possible linear estimate of the response; any modification due to harmonicity must result in a degradation of this best estimate.

Methods

Experimental apparatus and methods

Experiments were performed at the University of Maryland, College Park and the University of Maryland, Baltimore. Animal preparation and neural-recording procedures were approved by the IACUCs of both institutions. Surgical procedures are described in detail in other publications (Dobbins et al., 2007; Fritz et al., 2003). We give a brief outline of the recording procedure here. During daily recording sessions lasting 3–6 h, ferrets were trained to lie motionless in a custom apparatus that restrained them. The auditory cortex was accessed through craniotomies of diameters in the range 0.5–6 mm. We took precautions to maintain sterility of the craniotomies at all times.

• In some experiments, the auditory cortex was accessed through a small hole of diameter less than 0.5 mm. Each hole was used for 5–7 days after which it was sealed with dental cement. The small size of the hole afforded stable recordings and lowered chances of infection. Closely spaced holes were made over auditory cortex, with particular focus on low-frequency areas for this study. Recordings were attributed to AI based on tonotopic organization and response properties (strong response to tones and relatively short response latency), but a few penetrations might have been from adjacent areas.

• In other experiments, we obtained recordings from both AAF and AI. In these experiments, the recordings were through relatively large craniotomies of diameter 5–6 mm. Larger craniotomies permitted us to identify recording locations as being from AI or AAF based on position relative to sulcal landmarks on the surface of the brain (Kowalski et al., 1995). Such attribution of location would not have been possible with microcraniotomies because sulcal landmarks are not readily visible.

A variety of different methods were used for the recordings. These methods are described below, but they are not distinguished in the reporting of results because they did not lead to noticeably different findings. Most of the recordings were with single parylene-coated tungsten microelectrodes having impedance ranging from 2 to 7 MΩ at 1 kHz. Electrode penetrations were perpendicular to the surface of the cortex. We used a hydraulic microdrive under visual guidance via an operating microscope to position the electrodes. A few recordings were made with NeuroNexus Technologies silicon-substrate linear electrode arrays (four arrays, with each array having four electrodes in a straight line) or silicon-substrate tetrode arrays (four tetrode arrays, with each array having four closely spaced electrodes in a diamond-shaped configuration). Recordings yielded spikes from 1–3 neurons on a single electrode that were sorted offline with a combination of automatic spike-sorting algorithms (Lewicki, 1994; MClust-3.3, A. D. Redish et al.; KlustaKwik, K. Harris) and manual techniques. A spike class was included as a single unit for further analysis if less than 5% of interspike intervals were smaller than 1 ms, the putative absolute refractory period, and the spike waveform had a bipolar shape.

In some experiments, sounds were delivered with an Etymotic ER-2 earphone inserted into the entrance of the ear canal on the contralateral side of the cortex being investigated. All stimuli were generated by computer and fed through equalizers to the earphone. An Etymotic ER-7C probe-tube microphone was used to calibrate the sound system in situ for every recording session. An automatic calibration procedure gave flat frequency responses below 20 000 Hz. In other experiments, sounds were delivered by a speaker (Manger) placed 1 m straight above the head of the ferret. Stimuli were generated by a computer and sound levels were calibrated at the position of the ferret’s head. Apart from a handful of cases, most of the recordings in these latter experiments were obtained without the sound system having been equalized to a flat frequency response, because the frequency response was flat even when not equalized.

Stimuli and analysis

a. Stimuli. After a cluster of single units was isolated using pure-tone and complex-tone search stimuli, its response area was measured with pure tones to get an estimate of the BF. The discharge rate was measured as a function of the level of pure tones at BF in order to estimate the threshold. Responses to a tone sequence anchored at the BF (as in Fig. 4) were measured at approximately 20 dB above BF-tone threshold. Finally, the neuron’s spectro-temporal filtering characteristics were estimated at the same level as the anchored-tone sequence by measuring the STRF with temporally orthogonal-ripple-combination (TORC) stimuli (Klein et al., 2000), which are described below.

b. Anchored tone sequences. Anchored-tone sequences consisted of six-component harmonic and inharmonic complex tones. Up to six different harmonic complex tones with components in random phase were part of the sequence, where each tone had a different component number at the anchor frequency. For most units, the first through sixth components were at the anchor frequency, but a few units had only the second through fifth or first through fifth components at the anchor frequency.

Inharmonic complex tones in the sequences were formed by reordering ratios between consecutive components of a harmonic complex tone, as in Experiment 1. The same sequences of ratios were used for almost all units.

In our later recording sessions, we imposed a slow sinusoidal amplitude modulation (4–20 Hz) with a modulation depth of 0.5 (peak to mean) upon the complex tones. All components were modulated coherently. We imposed this modulation to ensure that neurons responded vigorously throughout the complex tone, because cortical neurons are often unresponsive during the sustained portions of static stimuli (Clarey et al., 1992; Shamma et al., 1995) as was indeed the case for the majority of single units recorded during our early recording sessions. In contrast, most units responded vigorously to the amplitude-modulated complex tones. Sinusoidal amplitude modulation at slow rates may provide an additional grouping cue beyond that of harmonicity. However, this cue is in fact relatively weak compared to the unavoidable powerful (and quite similar) cue of the common rapid onset and offset of all (harmonic and inharmonic) tones. Since our goal is to compare the responses to the harmonic versus inharmonic complexes, then as they are treated the same, amplitude modulation should not confer any advantage to one complex over the other.

All components of the harmonic and inharmonic complex tones were presented at the same level.

c. Characterizing linear processing of spectro-temporal envelopes with STRFs. Underlying the measurement of a STRF is the observation (Kowalski et al., 1996; Schreiner and Calhoun, 1994; Shamma et al., 1995) that responses of many AI neurons have a large linear component with respect to the spectro-temporal envelope of sounds. The STRF (t,x), a two-dimensional function of time t and log frequency x=log(f∕f₀), describes the linear component of the transformation between the spectro-temporal envelope of an acoustic stimulus and the neural response. This response component is given by

$$r\left(t\right)=\int \int \mathrm{STRF}(\tau ,x)\cdot S(t-\tau ,x)d\tau dx,$$ (1)

where r(t) is the instantaneous discharge rate of the neuron and S(t,x) is the spectro-temporal envelope (or dynamic spectrum) of the stimulus; the equation describes a convolution in time and a correlation in log frequency. Intuitively, the neural response r at time t is the correlation of the STRF with the time-reversed dynamic spectrum of the stimulus S around that moment. This operation can be viewed as similar to a matched-filtering operation whereby the maximum response of the neuron occurs when the time-reversed dynamic spectrum most resembles the STRF.

The theory and practice of measuring STRFs with TORC stimuli are in Klein et al. (2000). A brief outline is given in the appendix. TORCs are composed of moving ripples (Depireux et al., 2001; Kowalski et al., 1996), which are broadband sounds having sinusoidal temporal and spectral envelopes. Moving ripples are basis functions of the spectro-temporal domain, in that arbitrary spectro-temporal envelopes can be most efficiently expressed as combinations of these stimuli. The accumulated phase-locked responses to individual moving ripples give a spectro-temporal modulation transfer function (parameterized by ripple periodicity and ripple spectral density) whose two-dimensional inverse Fourier transform is the STRF. TORCs are special superpositions of moving ripples such that two components having different ripple spectral densities do not share the same ripple periodicity. This special combination of moving ripples enables rapid measurement of the STRF. We used random-phase tones densely spaced on a log-frequency axis as carriers (100 tones∕octave, spanning 5–7 octaves) for the envelope of the TORC stimuli.

It is worth noting two properties of our STRF measurements.

• 1.Underlying our measurement of the STRF is an assumption that the neuronal system has reached a steady state (Schechter and Depireux, 2007). Consequently, the STRF quantifies changes of the discharge rate above and below a steady-state rate.
• 2.The mean of the STRFs is set to zero because the STRF is designed to predict response modulations, not the steady-state response. In order to predict the steady-state discharge rate, it is necessary to measure the terms of the STRF at a ripple periodicity of 0 Hz (i.e., static ripples). These responses cannot be measured by directly incorporating static ripples into TORC stimuli because responses to the static ripples are difficult to disambiguate from nonlinear responses to the moving ripples resulting from, for example, spiking rate saturation and positivity of spike rates. The 0 Hz ripple periodicity terms can be estimated separately using static ripples presented at a range of phases. We estimated such terms of the STRF for 13 units in some of the later recording sessions. However, because results from these units did not differ from other units, we do not distinguish them in the results.

d. Quantifying the effects of spectro-temporal filtering on responses to complex tones. In order to account for the effect of spectro-temporal filtering on responses of a unit to the anchored-tone sequence, we predicted the peri-stimulus time (PST) histogram of the response to each stimulus from the measured STRF. The lack of predictability of the PST histogram then served as a measure of the response to each stimulus that was not explainable by spectrotemporal filtering. Correlates of harmonic fusion were expected to show up as systematic differences in the predictabilities of the response for harmonic stimuli compared to those for inharmonic stimuli. In other words, the prediction of responses from the STRF accounts for the processing of slow spectrotemporal envelopes in the stimulus, a feature that has little to do with harmonic fusion and pitch. Any effects of harmonicity have to be in the remaining unpredicted portion of the response.

A discrete-time implementation of Eq. 1 was used to predict the response to each stimulus in the anchored tone sequence (visualized in Fig. 5). The predicted PST histogram (p[n]) for a stimulus was a function of the sum of two terms, one term due to spectrotemporal filtering (p_strf[n]) and a second term representing the steady-state discharge rate (p_ss). For a complex tone having L components, we used a two-step process to determine p_strf[n], which is simply the convolution of the stimulus spectrogram with the STRF.

• 1.
  Convolve stimulus envelope e[n] (flat in the early experiments that used unmodulated complex tones and sinusoidal in the later experiments that used modulated complex tones, both having 10 ms cosine-squared onset and offset ramps) with horizontal slices of the STRF at the frequencies xⁱ of the tone components, STRF [n,xⁱ], to get the contributions of individual components to the overall prediction.

  $$p_{\mathrm{strf}}^i\left[n\right]=\frac{1}{N}(\mathrm{STRF}[n,x^i]\ast e\left[n\right]),$$ (2)

  where N is the length of STRFⁱ[n] and  ^* indicates convolution in time.
• 2.
  Combine contributions of individual components to get the overall prediction from the STRF as the mean of the individual contributions.

  $$p_{\mathrm{strf}}\left[n\right]=\frac{1}{L}\sum _{i=1}^L{p}_{\mathrm{strf}}^i\left[n\right].$$ (3)

Finally, the predicted PST histogram was

$$p\left[n\right]=g(p_{\mathrm{strf}}\left[n\right]+p_{\mathrm{ss}}),$$ (4)

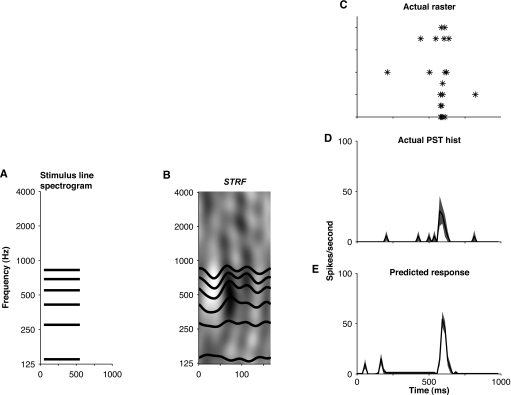
where g(⋅) indicates half-wave rectification representing the positivity of spike rates. Because the STRF does not predict the steady-state discharge rate (except in the handful of measurements where we measured responses to static ripples), we used the measured steady-state discharge rate r_ss instead of p_ss. In Fig. 5E, shading is used to indicate one standard deviation above and below the mean prediction,2 where the standard deviation is estimated by resampling the measured STRF using the bootstrap technique (Efron and Tibshirani, 1993; Klein et al., 2006). Figures 5C, 5D show raster and PST histograms of the actual response of the cell to the same stimulus, demonstrating the relatively high quality of the prediction in this case.

Figure 5.

Predicting responses to complex tones using STRFs. The predicted response (E) is the convolution of the spectrotemporal envelope of the stimulus (A, schematic spectrogram for complex tone having six components) with the STRF (B). More specifically, the operation can be seen as comprising two steps: (1) One-dimensional convolutions between the stimulus envelope (trapezoid-like with 10 ms cosine-squared onset and offset ramps) and horizontal slices of the STRF corresponding to the frequencies of each tone component; (2) Average of the results of the convolutions. These steps form part of an implementation of Eq. 4. Shown for comparison with the prediction are a raster plot (C) and a PST histogram (D) of the actual response of the neuron for ten stimulus presentations. Shading in D and E indicates one standard deviation above and below the mean prediction and the mean PST histogram, respectively, obtained with the bootstrap technique. The units of the STRF depicted in B are spikes∕s∕Pa. White pixels in the STRF indicate suppression, gray pixels indicate no change, and black pixels indicate elevation of discharge rate. Unit d‐46d, class 1.

We quantified the quality of the prediction with the cross-covariance between the response r[n] and the prediction p[n], defining it to be

$$\rho \left[m\right]=\frac{cov(r[n+m]\cdot p\left[n\right])}{{\sigma }_r\cdot {\sigma }_p}.$$ (5)

Because the covariance in the numerator is normalized by the standard deviations, ρ[m] is insensitive to the magnitudes of r[n] and p[n] but it captures the similarity of the waveform shapes. We used ρ=max(ρ[m]) to summarize the relationship of prediction and response independent of temporal misalignments between the waveforms; this quantity served as a measure of the neuron’s response after accounting for the effects of spectrotemporal filtering.

To quantify the extent to which a neuron distinguished a harmonic tone from each of the inharmonic stimuli, we used a measure analogous to the d-prime statistic from signal detection theory. We defined this measure to be the difference between the means of the distributions of ρ for each of the stimuli normalized by the geometric means of the standard deviations of the distributions, with the distributions having been generated by bootstrap replication.

$$d_{\rho }^{\prime }(Hx,\mathit{IH}x)=\frac{\overline{\rho \left(Hx\right)}-\overline{\rho \left(\mathit{IH}x\right)}}{\sqrt{{\sigma }_{\rho \left(Hx\right)}\cdot {\sigma }_{\rho \left(\mathit{IH}x\right)}}}.$$ (6)

We did not compute this quantity when either stimulus of a Hx, IHx pair (denoting harmonic and inharmonic tones, respectively) did not evoke a change in discharge rate or a change in phase-locked response by visual inspection because predictability of the temporal pattern of discharge of a no response is not meaningful. Figure 7B gives an example of distributions of ρ generated by bootstrap resampling for a harmonic tone and several inharmonic tones. We take d^′=1 as the threshold at which the two distributions are significantly different (equivalent to 76% correct identification in a two-alternative forced-choice discrimination task) to determine if a neuron reliably distinguished a harmonic tone from all of the inharmonic stimuli. We revisit this example in the Results section below.

Figure 7.

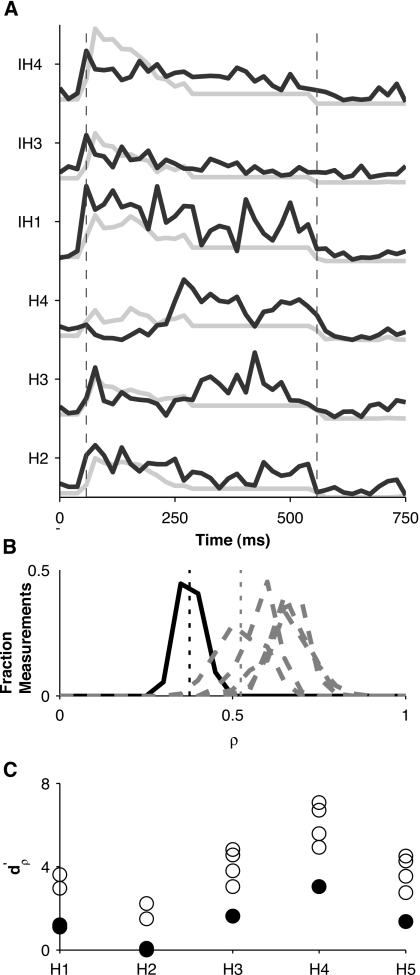
Predictability of temporal patterns of discharge for unit of Fig. 6. (A) Actual (solid) PST histograms overlayed on predicted (dotted) PST histograms for some select stimuli in the anchored-tone sequence. Dashed vertical gray lines indicate stimulus onset and offset. Predictions are normalized by the maximum across stimuli of all prediction waveforms and actual PST histograms are normalized by the maximum across stimuli of all actual responses, because the magnitudes of the predictions are consistently greater than the magnitudes of the PST histograms. (B) Histograms of the correlation coefficient (ρ) between predicted and actual PST histograms for harmonic stimulus H4 (solid) and histograms of ρ for each of the inharmonic stimuli (dashed), where histograms are obtained from 128 bootstrap replicates of predicted and actual responses. Dotted vertical lines indicate means of the distributions of ρ for stimulus H4 and for the inharmonic stimulus whose response predictability was closest to that of H4. $d_{\rho }^{\prime }$ is the difference between such means normalized by the geometric mean of their standard deviations. (C) $d_{\rho }^{\prime }$ for each of the harmonic tones relative to each of the inharmonic tones. The minimum $d_{\rho }^{\prime }$ for a given harmonic number (solid circles) is a measure of how discriminable that particular harmonic tone is from the most similar inharmonic tone in terms of the predictability of the temporal discharge pattern.

Results: A small fraction of cortical neurons distinguished harmonic complex tones from inharmonic complex tones

We selected data from 86 units in nine ferrets for this report, with many units rejected due to not having high enough signal-to-noise ratios. None of the nine ferrets were used in the behavioral study. The BFs of the units ranged from 210 to 13 600 Hz, with 11 having BF greater than 5000 Hz, 20 having BF greater than 3000 Hz, and 36 having BF greater than 1500 Hz. Of these units, 51 were from AI, 22 were from AAF, and 13 units were of uncertain location either in AI or AAF.

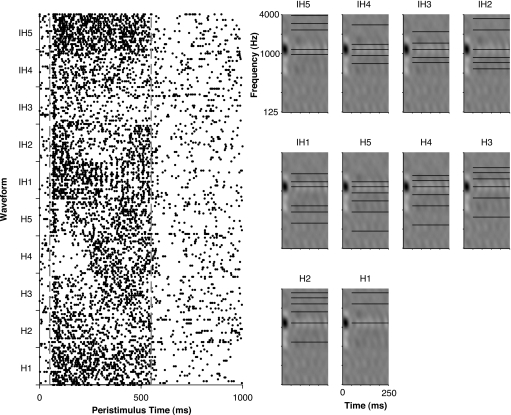
Figure 6 shows the responses of a single unit to unmodulated harmonic and inharmonic tones constituting the anchored tone sequences. Harmonic tones are labeled with the prefix “H” and the inharmonic tones are labeled with the prefix “IH;” the numerical suffix for the harmonic tones indicates the component at the AF (anchor frequency) while for inharmonic tones it is an arbitrary label not indicative of any status for the component at AF. The spectral context clearly influenced the responses of this unit to the different tones. For example, the harmonic tones labeled H3 and H4 (third and fourth components at the AF, respectively) were inhibited for the first half of stimulus presentation, while none of the other stimuli elicited such a response. Similarly, the unit responded far more weakly to the inharmonic tones labeled IH3 and IH4 than to any of the other stimuli.

Figure 6.

Response of a unit to an anchored-tone sequence. Dot rasters (left) and schematic spectrograms of each tone in the anchored tone sequence overlayed on the STRF of the unit (right). Stimuli labeled as Hx (where x indicates the component number at BF) are harmonic tones. Those labeled as IHx are inharmonic tones, but in contrast to that for the harmonic tones, the numerical suffix is an arbitrary label not indicative of any status for the component at anchor frequency. Unit d‐76b, class 1.

Interestingly for this unit, the response to stimulus IH1 shows temporal structure in the discharge pattern. This temporal structure reflects synchronization of discharges to envelope modulations resulting from interaction between tone components. Responses to all stimuli showed such synchronization to tone interactions up to 250 Hz. As a result of this 250 Hz upper limit, the temporal envelope for harmonic tones H1 through H4, where the fundamentals exceeded 250 Hz, was not reflected in the neural discharge patterns but the temporal envelope for H5 did produce synchronized discharges. The rate limit also makes such units unsuitable for encoding the virtual pitch of harmonic complex tones via synchronization to the envelope; instead, they are better suited for encoding residue pitch. A similar limit for synchronizing to the stimulus temporal envelope has been observed in previous studies of auditory cortex in awake animals (Bieser and Muller-Preuss, 1996; de Ribaupierre et al., 1972; Elhilali et al., 2004; Fishman et al., 2000; Liang et al., 2001; Steinschneider et al., 1998). No other unit in our population exhibited such discharge patterns.

In order to account for the effect of spectrotemporal filtering in this unit, we used the STRF to predict PST histograms for the complex tones. Figure 7A shows actual PST histograms overlayed on predictions for the unit of Fig. 6. The response was better predicted for the inharmonic stimuli than for stimuli H3 and H4 because the STRF was unable to predict the late response to these harmonic stimuli. We summarized the linear predictability of the response using the maximum cross-covariance ρ (see Methods), between the response PST histogram and the predicted wave-form. Figure 7B shows distributions of ρ for stimulus H4 and for all the inharmonic stimuli. We quantified the extent to which this neuron distinguished H4 from each of the inharmonic stimuli using $d_{\rho }^{\prime }$ (see Methods). If we take d^′=1 to be the threshold at which two distributions are significantly different, then this neuron reliably distinguished H4 from all of the inharmonic stimuli. Figure 7C summarizes $d_{\rho }^{\prime }$ for each of the harmonic stimuli compared to all of the inharmonic stimuli. The minimum $d_{\rho }^{\prime }$ for a given harmonic tone is a convenient measure of how well the neuron discriminated that harmonic tone from the inharmonic tone having the most similar response. This measure is greatest for H4 of all the harmonic tones, which means that this neuron was best at discriminating H4 from inharmonic tones.

Figure 8 shows an example of responses and predictions from a unit for amplitude-modulated complex-tone stimuli. Figure 8A shows period histograms of responses to a harmonic (H3) and an inharmonic tone3 along with a single period of predictions for the same stimuli. Both the magnitudes and phases of the responses are predicted well by the STRF of this neuron. Figure 8B shows histograms of bootstrap-replicate ρ for stimulus H3 and the inharmonic tone of panel A. The distributions of ρ for these stimuli overlap a great deal, suggesting that the predictability of temporal discharge pattern does not readily distinguish H3 from the inharmonic tone. Figure 8C summarizes $d_{\rho }^{\prime }$ for each of the harmonic tones compared to all of the inharmonic tones. The minimum $d_{\rho }^{\prime }$ for each harmonic tone is less than 1, confirming the observation for stimulus H3 that this neuron was not effective at discriminating any of the harmonic tones from inharmonic tones.

Figure 8.

Predictability of temporal patterns of discharge in a unit driven by amplitude-modulated complex tones. (A) A single period of predicted (dashed) and actual (solid) responses for harmonic tone H3 (thick gray) and an inharmonic tone (thin black). (B) Histograms of correlation coefficients between 128 bootstrap replicates of predicted and actual responses from panel (A). (C) $d_{\rho }^{\prime }$ for each of the harmonic tones relative to each of the inharmonic tones, with solid circles indicating the smallest $d_{\rho }^{\prime }$ for a given harmonic tone.

Neurons were no more effective at discriminating harmonic tones from inharmonic tones when the stimuli were unmodulated compared to when they were amplitude modulated. Distributions of $d_{\rho }^{\prime }$ for responses to unmodulated tones overlapped greatly with those for responses to modulated tones. A large-sample normal approximation of the Wald–Wolfowitz runs test, a nonparameteric test for determining whether two samples are identically distributed, yielded a test statistic z=1.42. At this value of the test statistic, the null hypothesis of $d_{\rho }^{\prime }$ for modulated stimuli and $d_{\rho }^{\prime }$ for unmodulated stimuli being identically distributed cannot be rejected (p>0.05).

Most units in the population were ineffective at discriminating the harmonic tones from the inharmonic tones; that is, they were mostly like the unit of Fig. 8 rather than the unit of Fig. 7. Figure 9 summarizes for our entire population of neurons how well the predictability of the temporal pattern of discharge discriminated the harmonic tones from the inharmonic tones. Histograms of minimum $d_{\rho }^{\prime }$ in Fig. 9A show that values exceeding 1 were infrequently observed, indicating that few neurons discriminated any of the harmonic tones from inharmonic tones. Figure 9B gives another view of the same information. The figure shows the minimum $d_{\rho }^{\prime }$ for each harmonic tone as a function of the BF of the unit, while identifying the harmonic tone by digits corresponding to the number of the anchor component. The 13 units that had a minimum $d_{\rho }^{\prime }$ greater than 1 had BFs between 500 and 10 000 Hz (all but one unit having BFs less than 4400 Hz). Location of the units (indicated by the font style of the symbol) that discriminated harmonic tones from inharmonic tones could be either AI or AAF. In summary, these few discriminative units were not likely to occur in a particular cortical location nor biased to a particular range of BFs within the 500–4400 Hz range.

Figure 9.

(Color online) Summary of how distinguishable harmonic tones are from inharmonic tones across all recordings. (A) Histograms of the minimum $d_{\rho }^{\prime }$ for each harmonic tone across all recordings. (B) Minimum $d_{\rho }^{\prime }$ for each harmonic tone as a function of the best frequency for the recording. The recording location is indicated by font style (bold: AI, italic: AAF, plain: undetermined) and the identity of the harmonic tone is indicated by the numeric symbol.

The maximum cross-covariance quantifies the similarity of the shapes of the predicted waveforms and the PST histograms. However, this measure fails to account for how the magnitude of the predicted waveform compares to the magnitude of the time-varying component of PST histograms, or any differences in latencies of the prediction and actual response. For modulated complex tones it fails to quantify synchronization of response to the amplitude modulation. Moreover, the steady-state discharge rate is not predicted by the STRF, but it must be affected by the interaction of the stimulus spectrum with the frequency tuning of the neuron. We accounted for these various other properties of response predictability in a manner similar to our examination of the maximum cross covariance (not shown). Our conclusions based on the maximum cross covariance were not significantly altered—between 10% and 15% of the units were capable of discriminating one of the harmonic tones from the inharmonic tones with these other measures.

Discussion

About 10%–15% of units in AI and AAF responded differently to harmonic tones than to inharmonic tones, so that they may be said to be sensitive to harmonicity. This relatively small fraction of harmonicity-encoding neurons may account for the weak ability of ferrets in Experiment 1 to discriminate harmonic tones from inharmonic tones.

The failure to find a robust neural discrimination of harmonic tones from inharmonic tones is consistent with the conclusion of previous studies that single AI neurons in naive animals for the most part are not concerned with the coding of harmonicity. On the other hand, the failure to find harmonicity coding in AAF neurons may be at odds with other studies. The correspondence of AAF in ferrets to cortical fields in other animals in uncertain (Bizley et al., 2005). If AAF corresponds to the rostral field in primates, then our failure to find a significant percentage of neurons to be selective for harmonicity may be surprising given the promising observations of neurons tuned to the fundamental frequency of harmonic tones in marmosets (Bendor and Wang, 2005).

There are several possible reasons for the lack of congruence between the marmoset data and the ferret data. One possible reason is that AAF in ferrets may not correspond to rostral field in marmosets or that the marmoset data were mostly at very low frequencies (<0.8 kHz), while our data are at higher frequencies [mostly between 1 and 5 kHz—see Fig. 9B]. Another reason might be that the marmoset neurons were not harmonicity selective but instead were selective to waveform modulation rate. Future ferret studies having more recordings from the low-frequency region of AAF may yield data that are in line with the marmoset data. Moreover, there are some caveats to our conclusion that there are few harmonicity-sensitive neurons in AI and AAF of ferrets. First, our recordings were from multiple cortical layers and we had relatively few recordings per cortex. These characteristics may lead to a false conclusion that single AI and AAF neurons do not encode harmonicity if a population of harmonicity-selective neurons is concentrated in a specific subfield and layer of auditory cortex that we failed to sample. Second, different animals were used for the physiology and the behavior and it is possible that the physiology animals were incapable of spontaneously distinguishing harmonic tones from inharmonic tones. Finally, it is of course conceivable that our criteria for identifying harmonicity-sensitive cells are simply inadequate. Other formulations in the future may prove successful, such as distributed coding requiring comparison of spike timing across nearby neurons.

On the whole, our failure to find a robust encoding of harmonicity is not inconsistent with most previous studies that have examined the encoding of harmonic sounds from the perspective of virtual pitch. Single-unit and multi-unit recordings have failed to reveal neurons selective to virtual pitch in AI (Fishman et al., 1998; Schwarz and Tomlinson, 1990). Recent neuromagnetic and functional magnetic resonance imaging studies also support the conclusion that virtual pitch is not extracted in AI. Instead, investigations with regular-interval noise and filtered harmonic complex tones suggest that pitch is extracted at the anterolateral border of AI in humans (Krumbholz et al., 2003; Patterson et al., 2003; Penagos et al., 2003; Warren et al., 2003). Nevertheless, this conclusion about the role of the anterolateral border of AI has also recently come under doubt (Hall and Plack, 2006, 2007).

Several studies have investigated neural coding of harmonic fusion by seeking correlates of the perceptual popout of a mistuned component from an otherwise harmonic complex tone. Sinex et al. (2002, 2005) found that single inferior colliculus neurons in chinchilla could distinguish harmonic tones from mistuned-component harmonic tones based on distinctive temporal patterns of discharge. These temporal discharge patterns were understood as arising from envelope modulations due to interaction between adjacent tone components. This finding of a neural correlate for harmonicity in inferior colliculus is not inconsistent with our failure to find a robust correlate in auditory cortex, because the majority of cortical neurons do not encode first-order envelopes (modulations due to tone-tone interactions) but instead encode slower second-order envelopes (modulation of the first-order envelope) (Elhilali et al., 2004).

The neural basis of the perceptual popout of a mistuned harmonic has also been investigated in human listeners with event-related brain potentials. These studies have found long latency (150–250 ms after stimulus onset) responses that are correlated with perceptual popout (Alain et al., 2002; Hiraumi et al., 2005; McDonald and Alain, 2005); such latencies imply an involvement of secondary auditory cortical areas. Involvement of primary auditory cortex is also suggested by small differences in middle latency responses between harmonic stimuli and mistuned-harmonic stimuli (Dyson and Alain, 2004). While these middle and long latency responses may reflect harmonicity processing, it is also possible that they indicate, more generally, the perception of concurrent auditory objects; this possibility may underlie our failure to find significant evidence for encoding of harmonicity.

In general, the present study differs in outlook from most previous single-unit and multi-unit neurophysiology studies of the cortical neural coding of harmonicity. Previous studies have sought correlates of harmonicity by focusing on two characteristics of the pitch percept: (1) virtual pitch is at the common fundamental of a sequence of harmonics, and (2) the pitch corresponds to that of a pure tone at the fundamental frequency. The former property is expected to endow the putative pitch neuron with inputs across a broad range of frequencies, while the latter property is expected to endow the neuron’s tuning to pure tones to be at low frequencies below 1100 Hz (the range of virtual pitch in humans). These studies may be seen as employing a pitch-equivalence method.

The present study, employing a fusion-based method, exploits the fact that the brain uses harmonicity as a cue for grouping spectral components of a sound. It assumes that the fusion of harmonic components leaves an imprint on the neural representation of the individual components themselves; i.e., the brain maintains a pitch- or harmonicity-tagged representation of sound that is a by-product of the harmonic fusion process. Neurons that have an imprint of this harmonicity tagging would span a broad frequency range of best tuning up to 5000 Hz, the existence region for virtual pitch (Ritsma, 1962). This frequency range is greater than the expected frequency range of tuning for neurons whose selectivity to fundamental frequency corresponds to the pure-tone best frequency. The larger candidate pool of neurons in the fusion-based method compared to the pitch-equivalence method can be seen as an advantage when seeking correlates of harmonicity processing. On the other hand, a desirable feature of the latter method is that it can better reveal the actual neurons that combine harmonic components across frequency. A further advantage of the fusion-based method over the pitch-equivalence method is the potential for distortion products and combination tones to complicate interpretation of data in the latter method (McAlpine, 2004). Distortion and combination tones can regenerate missing components of missing-fundamental harmonic tones used in pitch-equivalence experiments; such nonlinearities are not a problem for the fusion-based method because it does not use missing-fundamental stimuli.

GENERAL DISCUSSION

Our results show that ferrets can spontaneously distinguish harmonic tones from inharmonic tones, albeit weakly. We found relatively few neurons in AI and AAF that encoded harmonicity, which may explain the weak spontaneous behavior.

Perhaps one reason we did not find a large number of harmonicity-encoding neurons is that ferrets are not good at spontaneously distinguishing harmonic tones from inharmonic tones. Animals trained to discriminate harmonic tones from inharmonic tones may turn out to have significantly more harmonicity-encoding neurons. It is worth noting, however, that physiology studies that succeeded in finding candidate harmonicity-selective neurons were done on untrained animals (Bendor and Wang, 2005; Riquimaroux, 1995). Another possible explanation for finding few harmonicity-encoding neurons in AI and AAF is that such neurons exist aplenty, but elsewhere in the brain. If such is the case, then the relatively weak spontaneous behavior in Experiment 1 may be explainable if training is a necessary prerequisite for a strong behavioral response.

In conclusion, the neurons that confer a special perceptual status to harmonic sounds remain to be conclusively identified. Perhaps the puzzle of the cortical encoding of harmonicity will be unraveled by experiments having neural recordings coupled closely with functional brain imaging and behavioral measures in trained animals.

APPENDIX: MEASURING THE STRF OF A NEURON WITH TORC STIMULI

The TORC stimulus is a particular combination of broadband stimuli known as moving ripples, whose spectro-temporal envelope is given by

$$S(t,x)=a_0+a\cos [2\pi (\omega t+\Omega x)+\psi ].$$ (A1)

At each frequency location, the function describes a sinusoidal modulation of sound level at a rate of ω cycles∕s around a mean a₀ and amplitude a; the relative phases of these modulations at different log frequency, x=log(f∕f₀), produce a sinusoidal or rippled profile of density Ω cycles∕octave. The rippled profile drifts across the spectral axis in time, hence leading to the name of moving ripples for these stimuli. Analogous to sinusoids for one-dimensional signals, moving ripples are basis functions of the spectrotemporal domain in that any arbitrary spectrotemporal profile can be constructed from a combination of them. And analogous to estimating the impulse response of a one-dimensional system using reverse correlation with white noise stimuli that have equal representation of all sinusoidal frequencies within the system bandwidth (de Boer and de Jongh, 1978), it is possible to estimate the STRF by reverse correlation with spectrotemporal white noise (STWN), which is a stimulus that has an equal representation of all moving ripples within the spectrotemporal bandwidth of the system4 (Klein et al., 2000, 2006).

However, because the STRF (x,t) transforms a two-dimensional input to a one-dimensional output, moving-ripple components of STWN that are spectrally orthogonal (different ripple densities, Ω, but same ripple periodicities, ω) can evoke overlapping response components that cannot be disambiguated; reverse correlation with such stimuli can result in inaccurate and noisy estimates of the STRF. The TORC stimulus overcomes this problem by ensuring that each moving ripple in the stimulus has a different absolute ripple periodicity ∣ω∣, so that each linear response component is uncorrelated with every ripple component of the stimulus except for the one evoking it. Therefore, when using reverse correlation with a TORC stimulus, response components of a given ripple periodicity contribute only to a single [ω,Ω] component of the STRF.