Testing coherent reflection in chinchilla: Auditory-nerve responses predict stimulus-frequency emissions

Abstract

Coherent-reflection theory explains the generation of stimulus-frequency and transient-evoked otoacoustic emissions by showing how they emerge from the coherent “backscattering” of forward-traveling waves by mechanical irregularities in the cochlear partition. Recent published measurements of stimulus-frequency otoacoustic emissions (SFOAEs) and estimates of near-threshold basilar-membrane (BM) responses derived from Wiener-kernel analysis of auditory-nerve responses allow for comprehensive tests of the theory in chinchilla. Model predictions are based on (1) an approximate analytic expression for the SFOAE signal in terms of the BM traveling wave and its complex wave number, (2) an inversion procedure that derives the wave number from BM traveling waves, and (3) estimates of BM traveling waves obtained from the Wiener-kernel data and local scaling assumptions. At frequencies above 4 kHz, predicted median SFOAE phase-gradient delays and the general shapes of SFOAE magnitude-versus-frequency curves are in excellent agreement with the measurements. At frequencies below 4 kHz, both the magnitude and the phase of chinchilla SFOAEs show strong evidence of interference between short- and long-latency components. Approximate unmixing of these components, and association of the long-latency component with the predicted SFOAE, yields close agreement throughout the cochlea. Possible candidates for the short-latency SFOAE component, including wave-fixed distortion, are considered. Both empirical and predicted delay ratios (long-latency SFOAE delay∕BM delay) are significantly less than 2 but greater than 1. Although these delay ratios contradict models in which SFOAE generators couple primarily into cochlear compression waves, they are consistent with the notion that forward and reverse energy propagation in the cochlea occurs predominantly by means of traveling pressure-difference waves. The compelling overall agreement between measured and predicted delays suggests that the coherent-reflection model captures the dominant mechanisms responsible for the generation of reflection-source otoacoustic emissions.

INTRODUCTION

Most cochlear models represent the material properties of the cochlear partition by smooth and continuous functions of position. For example, to match trends in physiological data relating characteristic frequency to position, model parameters are varied so that the stiffness of the basilar membrane (BM) decreases exponentially from base to apex. But although continuity and smoothness can be realized in mathematics, the cochlea is a biological device assembled from discrete cellular components, each subject to developmental noise and other morphological aberrations (e.g., Finch and Kirkwood, 2000). Standard assumptions about smoothness certainly simplify the model equations, but real cochleae must be mechanically irregular.

How does mechanical irregularity affect cochlear model responses to sound? Simulations and analysis based on the application of Newton’s laws have answered this question in active cochlear models: The major functional consequence of modest mechanical irregularity in the organ of Corti is the production of long-latency evoked and spontaneous otoacoustic emissions (e.g., Zweig and Shera, 1995; Talmadge et al., 1998). When irregularities are introduced into the mechanics, model cochleae emit sound (or its computational equivalent); when irregularities are absent, the same models remain silent.

Biological cochleae are both intrinsically irregular (e.g., Engström et al., 1966; Bredberg, 1968; Wright, 1984; Lonsbury-Martin et al., 1988) and, as implied by the model analysis, also emit sound (e.g., Kemp, 1978). Buttressed by this empirical correlation, the theory of coherent-reflection filtering explains the generation of reflection-source otoacoustic emissions (OAEs) by analogy with the scattering processes that occur in cochlear models containing mechanical irregularity. In particular, the theory describes the coherent “backscattering” of cochlear traveling waves by mechanical irregularities distributed along the organ of Corti. When combined with a description of sound transmission and reflection by the middle ear, the theory provides a comprehensive account of spontaneous and reflection-source otoacoustic emissions as well as the microstructure of the hearing threshold (e.g., Shera and Zweig, 1993b; Zweig and Shera, 1995; Talmadge et al., 1998, 2000).

Standard cochlear-model assumptions

A number of important assumptions underlie the cochlear models in which the principles and predictions of coherent reflection have been most thoroughly elaborated. These model assumptions are not statements about the mechanisms of coherent reflection—coherent reflection is an emergent consequence of the physics, not a hypothetical process whose characteristics are chosen at the outset and then explicitly incorporated into the model definition. For example, the statement that “one of the fundamental premises of the [coherent-reflection theory is that]…SFOAEs originate at the sites where the BM traveling waves reach their peaks” (Siegel et al., 2005) puts the logical cart before the horse. Localization of the strongest scattering to the peak region of the traveling wave is not a built-in assumption of the model but a consequence of the physics; the statement is a conclusion, not a premise.

Rather than prescribing the details of stimulus re-emission, the model assumptions all involve basic statements about how the cochlea works. Although some model assumptions are almost entirely innocuous and merely simplify the analysis (e.g., the incompressibility of the cochlear fluids), other assumptions have important functional implications and ultimately help determine the characteristics of the emissions produced by the model. This latter group comprises the three principal assumptions or approximations common to most current models of cochlear mechanics (reviewed in de Boer, 1996):

• (1)The motion of the cochlear partition is driven primarily by forces that either originate locally or have been communicated from more distant locations through the scalae fluid pressure. In other words, the mechanics of the cochlear partition are well described by “point-admittance” functions that do not involve significant longitudinal coupling within the organ of Corti or tectorial membrane.
• (2)The forces produced by outer hair cells couple primarily into the slow-traveling transverse pressure-difference waves that drive the motion of the cochlear partition (e.g., Voss et al., 1996) rather than into longitudinal compression waves that travel at the speed of sound in a manner largely uninfluenced by mechanically tuned structures such as the organ of Corti (reviewed in Shera et al., 2007).
• (3)The hydrodynamics of cochlear fluid motion are well approximated by representing the tapered spiral geometry of the scalae using a rectangular box in which traveling waves transition from long-wave behavior in the tail region to short-wave behavior near the peak.

Although these standard assumptions have been employed in models that reproduce measurements of basilar-membrane motion, they—like the conventional assumption of smoothness—may not be entirely correct. Indeed, one of the three (2) has been questioned on the grounds that OAE phase gradients interpreted as roundtrip travel times appear too short to involve reverse propagation via slow pressure-difference waves (Ren, 2004; Ren et al., 2006; Ruggero, 2004; Siegel et al., 2005). Instead, OAE delays were taken to confirm the suggestion (Wilson, 1980) that the intracochlear forces giving rise to OAEs couple primarily if not exclusively into fast compression waves (for informal discussion, see Allen, 2003, 2006).

The studies contradicting assumption (2) base their conclusions on comparisons between otoacoustic phase gradients measured in the ear canal and mechanical delays measured on the BM or estimated from auditory-nerve responses. The specific hypotheses explored derive from conceptual models of OAE generation and∕or from approximate theoretical formulas (e.g., OAE delay≅2×BM delay) obtained using assumptions untested in the species employed. Although the results are suggestive, compelling tests of the assumptions and approximations underlying coherent reflection require more rigorous comparisons between model predictions and experiment. The fundamental character and near ubiquity of the assumptions under scrutiny would endow any definitive conclusions with broad significance, not only for interpreting otoacoustic emissions, where the issues appear especially salient, but also for understanding the most basic operation of the cochlea.

In this paper, we test coherent-reflection theory in chinchilla using the standard model assumptions enumerated above. In particular, we compare measured stimulus-frequency otoacoustic emissions (SFOAEs) (Siegel et al., 2005) with model predictions derived specifically for the chinchilla by analyzing measurements of auditory-nerve Wiener kernels (Recio-Spinoso et al., 2005; Temchin et al., 2005). Our strategy allows more rigorous and comprehensive tests of coherent-reflection theory than have previously been possible (e.g., Shera and Guinan, 2003; Cooper and Shera, 2004; Siegel et al., 2005).1

COHERENT REFLECTION IN STANDARD COCHLEAR MODELS

The theory of coherent-reflection filtering derives from an analysis of cochlear models based on Newton’s laws. For simplicity, we restrict attention to stimulus intensities in the near-threshold linear regime for which relative amplitudes of stimulus-frequency and transient-evoked OAEs are largest. In the standard cochlear model illustrated in . 1, the uncoiled cochlea appears as a rectangular box filled with incompressible, inviscid fluid and subdivided by a flexible membrane representing the cochlear partition. Linearized equations of fluid dynamics describe the motion of the fluid and its interaction with the membrane and the boundaries of the box, including the stapes and round window. We describe the mechanics of the partition by an equivalent point admittance that characterizes the transverse motion of the organ of Corti induced by a pressure difference across its surface. The admittance includes contributions from the active forces involved in cochlear amplification. Irregularities are represented as perturbations in the mechanics of the partition.

Figure 1.

Sagittal space-time slice through the symmetric two-dimensional box model of height H. The middle and external ears are represented by using balls and sticks. The cochlear partition is shown vibrating in response to a pure tone stimulus (P_stim) applied in the ear canal. Micromechanical irregularities (bottom panel) arising from the discrete cellular architecture of the organ of Corti appear superposed on the smooth secular variation of mechanical characteristics from base to apex. Analysis of the model equations shows that irregularities in any mechanical parameter (e.g., the effective damping) give rise to reverse-traveling waves that return to the ear canal as sound (P_SFOAE).

Predicting stimulus-frequency emissions

In previous papers, we solved cochlear model equations to determine the effects of mechanical irregularities on model responses (e.g., Zweig and Shera, 1995; Talmadge et al., 1998; Shera et al., 2005a). The solutions indicate that when stimuli are applied in the ear canal, model cochleae generate reverse-traveling waves that subsequently appear in the ear canal as sound (e.g., as SFOAEs when the stimuli are single tones). For example, . 2 shows the SFOAEs produced by a typical cochlear model supplemented with random mechanical irregularities. As the simulation demonstrates, the model reproduces the major qualitative features of measured SFOAEs: a rapidly rotating phase exhibiting occasional inflections and a slowly varying amplitude punctuated by sharp notches. By employing different spatial patterns of mechanical irregularities in the simulation, one can reproduce the intersubject variability seen in measured SFOAEs.

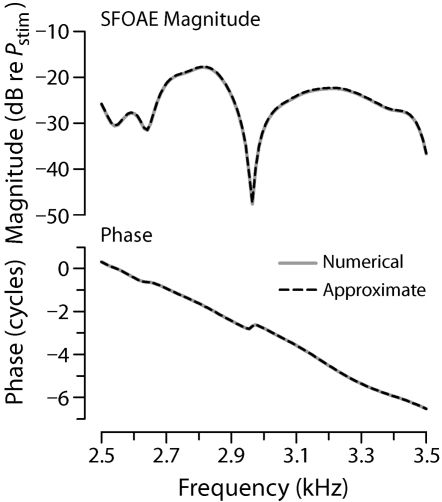
Figure 2.

Simulated SFOAEs. The figure shows the magnitude and phase of P_SFOAE(f) computed by using a two-dimensional model of cochlear mechanics supplemented with micromechanical irregularities (for details, see Shera et al., 2005a, Appendix D). Computations performed by using two different methods yield almost identical results. The solid gray line shows the SFOAEs computed by using numerical finite-difference algorithms; the dashed line uses the approximate perturbative expression given by Eq. 1. For simplicity, all calculations assume unity roundtrip middle-ear transmission gain and a stapes reflection coefficient of zero. [Adapted from Fig. 10 of Shera et al. (2005a).]

An approximate analytic formula

To facilitate comparisons between theory and experiment, we derived an approximate analytic expression for the SFOAE produced by the model (Shera et al., 2005a). By using perturbation theory to solve what amounts to a “scattering problem,” we found that the SFOAE pressure P_SFOAE(f) can be written in the form

$$P_{\mathrm{SFOAE}}\left(f\right)\sim P_{\mathrm{stim}}{G}_{\mathrm{ME}}\left(f\right){\int }_0^Lϵ(x,f){\mathcal{W}}^2(x,f)dx,$$ (1)

where the ∼ indicates approximate proportionality,2P_stim is the ear-canal stimulus pressure, G_ME(f) characterizes roundtrip middle-ear transmission,3 and the integral is proportional to the cochlear reflectance, which is defined as the ratio of the outgoing to the ingoing pressure wave at the stapes. The integral sums wavelets scattered by irregularities located throughout the cochlea. In the integrand, the dimensionless function ϵ(x,f) characterizes the mechanical perturbations. Contributions from different locations are weighted by the function W²(x,f), which describes both BM-fluid coupling and roundtrip wave propagation between the stapes and the site of scattering at cochlear position x. When written in a form convenient for future analysis, the weighting function is given by

$${\mathcal{W}}^2(x,f)=\alpha (x,f)V_{\mathrm{BM}}^2(x,f)∕k^2(x,f),$$ (2)

where V_BM(x,f) is the BM velocity normalized by the stapes velocity, k(x,f) is the complex wave number of the traveling wave, and α(x,f) is a dimensionless hydrodynamic factor whose value is well approximated by the expression

$$\alpha (x,f)\cong \frac{k(x,f)H}{\tanh \left[k(x,f)H\right]},$$ (3)

where H is the scala height (Duifhuis, 1988; Shera et al., 2005a). In terms of the wave number, the perturbations ϵ(x,f) are given by ϵ≡Δk²∕k², where the irregularities Δk² vanish in a hypothetical smooth cochlea. The mechanisms encapsulated in Eq. 1 for P_SFOAE(f) are those of wave scattering: Just as light scatters as it propagates through a medium of variable refractive index, so cochlear traveling waves partially reflect when they encounter irregularities in the partition mechanics.

Figure 2 establishes the validity of our semianalytic formula for P_SFOAE(f) [Eq. 1] by comparing it with the “exact” numerical result computed by solving Laplace’s equation using finite-difference algorithms (Shera et al., 2005a); the two solutions are indistinguishable on the scale of the figure. By providing knowledge of functional dependencies not available from numerical simulations, the semianalytic approximation proves crucial for subsequent comparisons between theory and experiment.

TAILORING PREDICTIONS TO CHINCHILLA

To compare model predictions with SFOAEs measured in chinchilla (e.g., Siegel et al., 2005), we need to evaluate Eq. 1 for P_SFOAE(f) using parameters appropriate to the species. The most important quantities to be determined are those defining the weighting function W²(x,f) given by Eq. 2. In particular, we need to know the BM velocity response V_BM(x,f) and the complex wave number k(x,f). The scalae height appearing in approximation 3 for α(x,f) can be obtained from anatomical measurements (Salt, 2001).

Estimating the traveling wave

By applying Wiener-kernel analysis to auditory-nerve fiber (ANF) responses to noise, Ruggero et al. were able to obtain estimates of BM mechanical transfer functions, both magnitude and phase, at characteristic frequencies (CFs) throughout the chinchilla cochlea (Recio-Spinoso et al., 2005; Temchin et al., 2005). As an example, the thin black line in Fig. 3A shows the function V_BM(x_o,f) obtained from a fiber innervating the base [CF(x_o)≅9 kHz]. The transfer function is plotted as a function of the “scaling variable,” ν(x,f), defined by (Shera, 2007)

$$\nu (x,f)\equiv \frac{f+{\mathrm{CF}}_1}{\mathrm{CF}\left(x\right)+{\mathrm{CF}}_1},$$ (4)

where the constant CF₁ represents the approximate characteristic frequency at which the cochlear map morphs from exponential to more linear behavior in the apex. In the chinchilla, CF₁≅140 Hz (Eldredge et al., 1981; Greenwood, 1990). At fixed position, the scaling variable ν(x,f) represents a modified normalized frequency that reduces to the conventional form f∕CF(x) at frequencies roughly two or more octaves above CF₁. At fixed frequency, equal intervals of ln ν represent constant distances along the BM.

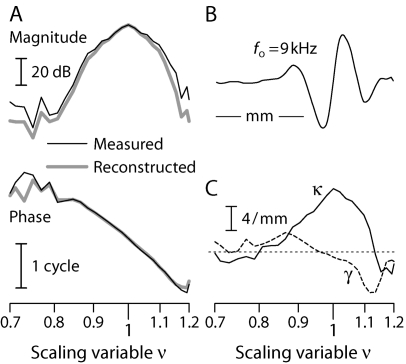
Figure 3.

Empirical estimation, inversion, and reconstruction of the BM velocity response in chinchilla. Panel (A): Thin black lines show the magnitude and phase of the ANF Wiener-kernel estimate of V_BM(x_o,f) at the cochlear location x_o tuned to approximately 9 kHz (Recio-Spinoso et al., 2005). The scaling variable ν(x,f) increases along the logarithmic abscissa. Thick gray lines show the function V_BM reconstructed from the derived wave number [see panel (C), with k=κ+iγ] using the WKB approximation (for details, see Shera, 2007). Panel (B): Snapshot of the 9 kHz wave whose envelope and phase are shown in panel (A). The traveling wave was obtained by reinterpreting the abscissa as a spatial axis at fixed frequency. The scale bar represents a distance of 1 mm (Eldredge et al., 1981; Greenwood, 1990). Panel (C): Solid and dashed lines show propagation and gain functions (κ and γ, respectively) obtained from V_BM in panel (A) using the wave number inversion formula [Eq. 5]. For reference, thin dashes mark the zero line. [Adapted from Figs. 2, 4, and 5 of Shera (2007).]

By regarding V_BM(x,f) primarily as a function of the single variable ν(x,f) rather than of the two variables x and f independently, we formalize the local scaling symmetry (Zweig, 1976) manifest by basilar-membrane transfer functions (Rhode, 1971; Gummer et al., 1987) and neural tuning curves (e.g., Kiang and Moxon, 1974; Liberman, 1978). As illustrated by the snapshot of the traveling wave shown in Fig. 3B, local scaling allows one to reinterpret the frequency response V_BM(x_o,f) measured at location x_o as an estimate of the spatial response (traveling wave) V_BM(x,f_o) at frequency f_o; both are given by the function V_BM(ν). The local scaling approximation is most accurate in the region about the peak of the response [i.e., for x near x_o and for f near CF(x_o)]. By converting transfer functions to traveling waves, local scaling permits computation of the spatial integral appearing in Eq. 1 for P_SFOAE(f).

Finding the complex wave number

We obtained the complex wave number of the traveling wave from the Wiener-kernel estimates of V_BM(x,f) by using the wave number inversion formula derived previously (Shera et al., 2005a; Shera, 2007),

$$k^2(x,f)=\raisebox{1ex}{$-V_{\mathrm{BM}}(x,f)$}\!\left/ \!\raisebox{-1ex}{${\int }_x^{L}d{x}^{\prime }{\int }_{x^{\prime }}^L{V}_{\mathrm{BM}}(x^{″},f)d{x}^{″}$}\right..$$ (5)

The real and imaginary parts of k, known as propagation and gain functions, are denoted as κ and γ, respectively. Figure 3C shows the values of κ(ν) and γ(ν) derived from the example Wiener-kernel estimate of V_BM(ν) shown in panel (A). The spatial integrals were performed by using local scaling.

The properties of the propagation and gain functions obtained from the chinchilla Wiener kernels are described and interpreted elsewhere (Shera, 2007). Here, we illustrate our procedure for validating the inversion procedure by using the derived wave number to reconstruct the BM velocity response. The thick gray line in Fig. 3A shows the function V_BM(ν) obtained from the wave number in panel (C) by using the Wentzel–Kramers–Brillouin (WKB) formula (Shera et al., 2005a).4 The agreement with the original measurements (thin black line) confirms that the propagation and gain functions obtained from Eq. 5 provide a valid representation of the complex wave number of the traveling wave.

As detailed elsewhere (Shera, 2007), we applied the inversion and reconstruction procedure outlined above to each of the 137 near-threshold Wiener-kernel BM click responses used to assemble the recently published map of near-CF BM group delays (see Fig. 13 of Temchin et al., 2005). Successful reconstructions were obtained for more than 60% of the responses, representing CFs throughout the cochlea.5 We restrict further attention to results derived by using these validated responses.

Modeling the perturbations

Evaluating the scattering integral in Eq. 1 for P_SFOAE(f) requires knowledge of the form and spatial distribution of any micromechanical irregularities. Although estimates of the weighting function W²(x,f) and wave number k(x,f) can be obtained for particular cochleae (e.g., by using the Wiener kernels), we have, as yet, no independent means of estimating the corresponding perturbations, ϵ(x,f)≡Δk²∕k²≅2Δk∕k. Although spatial irregularity presumably occurs in all mechanical parameters, it seems physiologically natural to associate the dominant contribution with irregularity in the active forces responsible for traveling-wave amplification. We therefore take Δk=r(x)γ(x,f), where the “roughness” r(x) characterizes the spatial pattern of irregularity and γ(x,f) is the traveling-wave gain function (Shera, 2007), whose value can be obtained from the wave number (γ≡Im k). In the short-wave region near the wave peak, irregularities in the gain function γ are equivalent to irregularities in the real part of the BM admittance.

Since the roughness r(x) remains unknown, we make no attempt to predict SFOAEs in individual ears. Instead, we compute their statistical behavior (in particular, the distribution of SFOAE phase-gradient delays6) across an ensemble of hypothetical ears, each having the same W² (i.e., the same BM velocity response and wave number) but different realizations of the roughness r(x). Lacking evidence for more ordered behavior, we also assume that r(x) varies randomly with position within an ear, displaying the same statistical features at all locations. The roughness used in the calculations therefore manifests no long-range correlations. Indeed, we assume that the gain function changes randomly and discontinuously from hair cell to hair cell. However, we obtain equivalent results with much smoother patterns so long as the roughness r(x) contains spatial frequencies within the passband of the “spatial-frequency filter” that arises through the dynamical action of the traveling wave (see Zweig and Shera, 1995, Figs. 6 and 10).

Accounting for middle-ear transmission

For our purposes here, the factor G_ME(f) describing middle-ear transmission can safely be ignored. Although the roundtrip pressure gain (∣G_ME∣) helps determine absolute emission levels, we cannot confidently predict SFOAE magnitudes for other reasons (e.g., we do not know the size of the irregularities, and the ANF Wiener kernels provide only a relative measure of tuning). Although the middle ear introduces a delay (characterized by the phase of G_ME), middle-ear delay appears negligible compared to cochlear delay in chinchilla (Ruggero et al., 1990; Songer and Rosowski, 2007) and, in any case, is already accounted for by the Wiener-kernel transfer functions,7 which were referenced to pressure at the eardrum (Recio-Spinoso et al., 2005).

COMPARING MEASURED AND PREDICTED SFOAEs

Qualitative comparison of SFOAE magnitude and phase

Figure 4 compares chinchilla SFOAE magnitude and phase (Siegel et al., 2005) with model predictions computed from Eq. 1 using the example Wiener-kernel estimate of V_BM(x,f) and derived wave number k(x,f) shown in Fig. 3. Both measured and computed SFOAEs span the frequency range of 8–10 kHz near the Wiener-kernel CF. The measured curves represent SFOAEs from 17 different chinchillas; the model curves show predictions for a single chinchilla (one Wiener kernel) using 17 different roughness functions r(x). Each of the 17 functions r(x) represents a different sample of Gaussian spatial noise (zero mean and constant variance) corresponding to rms fractional irregularities of 1%.

Figure 4.

Measured and simulated chinchilla SFOAEs. Panel (A) shows measured SFOAE magnitudes and phases from 17 chinchillas reported by Siegel et al. (2005). Stimulus probe levels were 30 dB SPL. Panel (B) shows simulated SFOAEs computed by using Eq. 1 for P_SFOAE(f) with parameters derived for the particular chinchilla whose ANF-derived BM velocity response and wave number are shown in Fig. 3. The model curves were computed by using irregularity functions consisting of 17 different samples of Gaussian spatial noise [rms value of r(x)=0.01]. Both measured and simulated SFOAEs are shown in a frequency range near the Wiener-kernel CF (≅9 kHz).

The simulated SFOAEs reproduce the major features of the measurements, including their noodling magnitudes and rapidly rotating phases. Although the measurements manifest a larger range of overall emission levels than the model, recall that all 17 simulations derive from the same Wiener-kernel transfer function; consequently, they do not include interanimal differences in mechanical gain that presumably contribute variability to the measured emissions. Furthermore, because the model roughness functions are all drawn from the same Gaussian distribution, their statistical features (e.g., rms value) are almost certainly more uniform than those of their biological counterparts. As for the phase, measured and predicted phase-gradient delays are similar; the mean delay obtained using the example Wiener kernel from Fig. 3 (1.4 ms) falls within the interquartile range of the 17 measurements. Undulations in emission magnitude (e.g., the occasional deep notches) correlate with wobbles in the phase, as expected from constraints imposed by causality (Sisto et al., 2007).

Because intra- and interanimal variations in middle-ear transmission and cochlear gain have considerable effects on OAE amplitude but are difficult to control for using these data, we focus our attention here on comparisons involving emission phase, specifically the SFOAE phase-gradient delay.

Preliminary comparison of delays throughout the cochlea

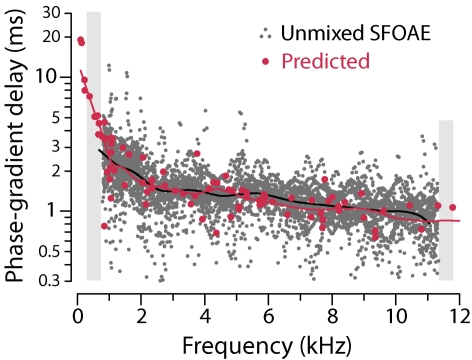
Figure 5 compares measured and predicted SFOAE delays at frequencies below 12 kHz, the upper limit for the SFOAE measurements. The gray dots form a scatterplot of the delays from all 17 chinchillas (Siegel et al., 2005). The red dots are median delays ${\widehat{\tau }}_{\mathrm{SFOAE}}$ computed using each of the 87 successfully reconstructed Wiener kernels; the error bars span the interquartile range, a robust measure of the spread. For each Wiener kernel, the predicted median SFOAE delay and spread are based on 300 simulations, each employing a different random roughness function and each performed by evaluating Eq. 1 at 21 frequencies straddling the CF. The corresponding phase-gradient delays were then computed by calculating the median slope of the unwrapped emission phase. Predicted mean, median, and modal delays were all essentially indistinguishable.

Figure 5.

(Color) Measured and predicted SFOAE phase-gradient delays. Gray dots show SFOAE delays vs frequency measured in 17 chinchillas at probe levels of 30 dB SPL (Siegel et al., 2005, Fig. 4). Red dots show predictions ${\widehat{\tau }}_{\mathrm{SFOAE}}$ obtained by using Eq. 1 for P_SFOAE(f) with parameters derived for chinchilla using each of the 87 successfully reconstructed Wiener kernels (Recio-Spinoso et al., 2005; Shera, 2007). Model values for each Wiener kernel represent the median near-CF phase gradient computed by using 300 different roughness functions (Gaussian spatial noise). Error bars show the interquartile ranges. Loess trend lines are shown in black and red.

The distributions of measured and predicted delays overlap in the base of the cochlea (f>4 kHz). At lower frequencies, however, the trend lines separate and SFOAE delays are substantially shorter than predicted by the model. At all frequencies, both measured and predicted delays manifest considerable scatter. The scatter in the predicted median delays arises from variations in mechanical tuning (e.g., bandwidths and delays), as captured by the ANF-derived Wiener kernels. Coherent-reflection theory predicts that on top of any scatter traceable to tuning, SFOAEs exhibit additional variability due to the micromechanical irregularity responsible for producing reverse-traveling waves. The error bars on the median model delays, which vary considerably from Wiener kernel to Wiener kernel, measure the variability originating in this way.

Complications from SFOAE source mixing

The mixed messages emerging from the comparisons in Fig. 5—compelling agreement in the base and clear disagreement in the apex—counsel taking a more careful look at the low-frequency behavior. Examination of the measured SFOAE magnitudes (Figs. 3 and 4 of Siegel et al., 2005) raises a potential complication: uncontrolled mixing of SFOAE components arising from different source mechanisms (e.g., Shera and Guinan, 1999; Talmadge et al., 2000; Schairer et al., 2003).

In the base of the chinchilla cochlea, the sharp notches characteristic of SFOAE magnitude spectra are typically spaced irregularly and appear separated by two to four or more cycles of phase variation. Human SFOAEs manifest a similar pattern (cf. Shera and Guinan, 1999, Fig. 9), at least above 1 kHz. According to coherent-reflection theory, widely and irregularly spaced spectral notches arise from chance spatial fluctuations in the perturbations that scatter the wave. At irregularly spaced frequencies, wavelets scattered from the many different perturbations within the scattering region happen to combine nearly out of phase with one another, causing near cancellation of the net reflected wave (see Fig. 2; see also Fig. 11 of Zweig and Shera, 1995). At frequencies below 4 kHz, however, the pattern of chinchilla SFOAE notches is rather different (see Fig. 6). Unlike the notches at higher frequencies, the notches below 4 kHz appear more evenly spaced, occurring at intervals corresponding to approximately one cycle of phase rotation.

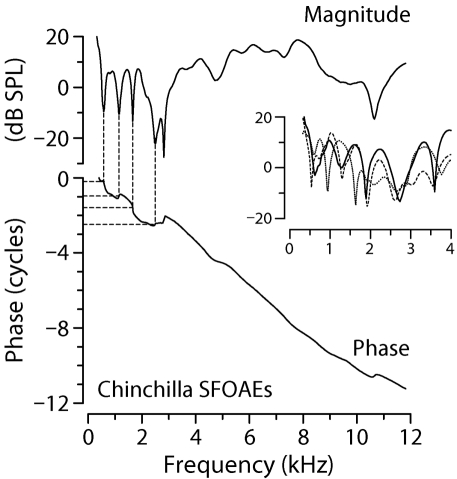
Figure 6.

SFOAE interference notches at low frequencies. Adapted from Fig. 3 of Siegel et al. (2005), the figure shows representative chinchilla SFOAEs (30 dB SPL probe). The solid lines in the main panel show SFOAE magnitude and phase vs frequency. The thin dashed lines connecting the top and bottom panels demonstrate that below 4 kHz, magnitude notches generally occur at intervals corresponding to about one cycle rotation of the phase. The inset shows three additional examples of magnitude notches, zooming in on the region below 4 kHz.

The more regular pattern of notches below 4 kHz provides strong evidence for interference between two SFOAE components with similar amplitudes but different phase-gradient delays. When the two emission components combine, they beat against each other as the stimulus frequency is varied, producing notches spaced at intervals of about one cycle of relative phase. Quasiperiodic interference notches of this sort are predicted by nonlinear models of SFOAE generation, where they result from near cancellation between reflection-source components with a steep phase slope and induced distortion components with a shallower slope (e.g., Talmadge et al., 2000). A similar interference between reflection- and distortion-source components generates distortion-product OAE microstructure (e.g., Kalluri and Shera, 2001).

SFOAE unmixing

We test for the existence of multiple SFOAE components by trying to separate them using signal-processing procedures previously applied to unmix distortion- and reflection-source components of DPOAEs (Kalluri and Shera, 2001; Knight and Kemp, 2001). Similar methods were previously applied to separate the stimulus from the emission during the measurement of SFOAEs (Shera and Zweig, 1993a; Kalluri and Shera, 2007a). The time-windowing method we employ derives from the correspondence between phase slope in the frequency domain and signal latency in the time domain (e.g., Papoulis, 1962). If the regular pattern of SFOAE notches occurs due to interference between two emission components with different phase slopes, then Fourier analysis should reveal two components with different latencies. Complete or partial separation of the two SFOAE components can then be achieved by using appropriate time windows.

To compensate for cochlear frequency dispersion, which smears out emission components in time, rendering them more difficult to separate by windowing, we perform the Fourier analysis with respect to a transformed frequency coordinate. The transformation we employ derives from the empirical place map of chinchilla near-CF BM group delays (τ_BMGD in the notation of Temchin et al. 2005), as estimated from the ANF Wiener kernels (Recio-Spinoso et al., 2005). Before computing the discrete Fourier transform, we interpolate the SFOAE measurements to frequencies spaced at intervals inversely proportional to τ_BMGD(f), where τ_BMGD(f)=a+b(f∕[kHz])^c with parameters {a,b,c}={0.496 ms,1.863 ms,−0.771} (Temchin et al., 2005; Siegel et al., 2005). By compensating for BM dispersion, the procedure yields sharper more well-defined peaks in the Fourier-conjugate “latency” domain. Previous studies used similar analysis procedures based on a log-frequency coordinate (Zweig and Shera, 1995; Knight and Kemp, 2000; Kalluri and Shera, 2001).

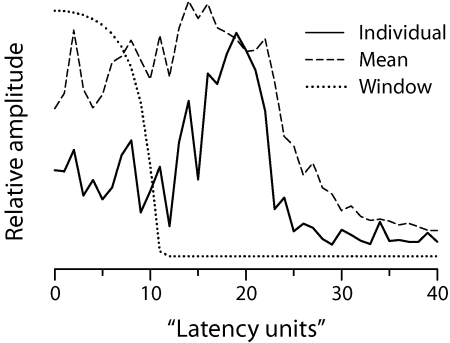
Figure 7 shows the latency-domain representation of the SFOAEs from an individual chinchilla, as well as the mean SFOAE latency function obtained by averaging the results computed from all 17 chinchillas reported by Siegel et al. (2005). Because of the quasi-power-law transformation applied before the Fourier analysis, the conjugate “latency units” (lu) along the abscissa have no simple physical interpretation.8 The peak centered near 18 lu represents the presumed long-latency component of the SFOAE; the short-latency component comprises all emission energy with latency below about 10 lu. We unmixed the SFOAE measurements for each chinchilla into components using the recursive exponential window (Shera and Zweig, 1993a; Kalluri and Shera, 2001) shown with the dotted line. Window durations in the range 10±3 lu yield quantitatively similar components.

Figure 7.

Chinchilla SFOAEs in the latency domain. The solid line shows the latency-domain representation of the SFOAEs for an individual chinchilla; the dashed line shows the mean of all 17 latency functions. Latency functions are the magnitudes of the discrete Fourier transforms of the SFOAE data obtained after compensating for BM dispersion by applying the quasi-power-law transformation described in the text. The conjugate Fourier variable, shown in latency units (lu) along the abscissa, has no simple physical interpretation. The dotted line shows the matched unmixing window (a 10th-order recursive exponential with a cutoff of 10 lu) used to separate putative short- and long-latency SFOAE components.

Figure 8 shows the results of unmixing the chinchilla SFOAEs into short- and long-latency components. Gray rectangles at the two extremes of the analyzed frequency range identify intervals where end effects associated with the windowing operation render the unmixed components unreliable (Kalluri and Shera, 2001). As expected, the two components have very different phase gradients. The short-latency component has a phase-gradient delay averaged across frequency of roughly 0.3 ms; the mean delay of the long-latency component is about four times longer. Since the two components have different phase gradients, their relative phase rotates with frequency. Summing the two components therefore produces alternating constructive and destructive interference.

Figure 8.

(Color) Unmixed short- and long-latency SFOAE components. Top and bottom sections show the magnitude and phase of the short-latency (blue) and long-latency (red) components unmixed from the total SFOAEs (black) by time windowing. The topmost panel shows magnitude results for the example highlighted in Fig. 6. Unmixing artifacts at the highest and lowest frequencies render the components unreliable in the intervals indicated by the tall gray rectangles. The total SFOAE data were measured by Siegel et al. (2005).

The interference pattern produced by the rotating phase depends on the component magnitudes. Figure 8 shows that the relative magnitude of the two components undergoes an abrupt transition near 4 kHz. At frequencies above 4 kHz, the long-latency component dominates the total emission, and the median level difference between the components exceeds 10 dB. Below 4 kHz, however, the median levels of the two components are nearly equal; on average, the short-latency component is about 1 dB larger than the long-latency component. In the low-frequency region, the similarity in component magnitudes, combined with the rotation of their relative phase, produces near cancellation at regular intervals. The two unmixed components therefore have properties consistent with the quasiperiodic interference notches observed below 4 kHz (and with their absence at higher frequencies). Although definitive conclusions require independent evidence for multiple SFOAE components, the unmixing analysis strongly suggests that chinchilla SFOAEs are indeed mixtures produced by multiple mechanisms, at least below 4 kHz.

Comparison of unmixed delays

When implemented in a linear cochlear model, the coherent-reflection mechanism generates only the long-latency reflection-source component of SFOAEs. Figure 9 compares model-predicted phase-gradient delays with those computed from the long-latency SFOAE components shown in Fig. 8. The unmixing procedure preserves the close agreement between theory and experiment in the base while substantially improving the agreement in the apex. Unfortunately, unmixing artifacts contaminate the empirical delays at the very lowest frequencies, where the discrepancy evident in Fig. 5 is largest. (Gray rectangles mask empirical delays subject to artifacts.) Nevertheless, wherever the comparison is meaningful, the agreement is striking. In particular, the model predictions capture both the magnitude and the frequency dependence of SFOAE delay.

Figure 9.

(Color) Unmixed and predicted SFOAE phase-gradient delays. Gray dots show delays computed from the long-latency SFOAE components shown in Fig. 8. Red dots show predicted delays reproduced from Fig. 5 (error bars have been omitted for clarity). Gray rectangles mask delay data contaminated by unmixing artifacts. Loess trend lines appear in black and red.

DISCUSSION

A wealth of newly published data in chinchilla (Recio-Spinoso et al., 2005; Temchin et al., 2005; Siegel et al., 2005) has enabled rigorous and comprehensive tests of the theory of coherent-reflection filtering. Although conceptually straightforward, the comparison between theory and experiment faced significant obstacles. On the theoretical side, meaningful quantitative comparisons with chinchilla SFOAEs require model predictions derived specifically for the species. By using inverse methods to derive parameters from data, we obtained model predictions that, within the framework of the assumptions, involve essentially no adjustable parameters. For this, three aspects of our approach proved critical: (1) The approximate analytic formula for P_SFOAE(f) [Eq. 1] revealed how SFOAEs depend on the BM traveling wave and its complex wave number; (2) The wave number inversion formula [Eq. 5] allowed estimation of k(x,f) from measurements of V_BM(x,f); and (3) The Wiener-kernel transfer functions provided indirect measurements of V_BM(x,f) at locations throughout the chinchilla cochlea and at intensities roughly comparable to those used to evoke the SFOAEs. Our strategy successfully reproduces the characteristic features of chinchilla SFOAEs, including their rapidly rotating phase and a slowly varying magnitude spectrum interrupted at irregular intervals by deep notches.

On the experimental side, the apparent mixing of SFOAE components produced by different mechanisms intervened to complicate more quantitative comparisons, especially in the apical half of the cochlea, where chinchilla SFOAEs show strong evidence for interference between two components with different phase-gradient delays. Since contamination by multiple OAE components confounds straightforward comparisons between theory and experiment, we used signal-processing techniques to “unmix” the measured SFOAEs. Although definitive characterization of SFOAE components requires independent corroboration, the unmixing analysis revealed emission components with the properties necessary to reproduce the interference pattern evident in the total SFOAE. As a result, we were able to compare model predictions with both the total SFOAEs and with their putative reflection-source components. Model comparisons with the total SFOAEs yield strong agreement in the base but substantial discrepancies below 4 kHz, where the relative magnitude of the short-latency component is greatest. Unmixing the SFOAEs preserves the model’s success in the base while significantly improving the agreement in the apex.

Relationship between SFOAE and BM delay

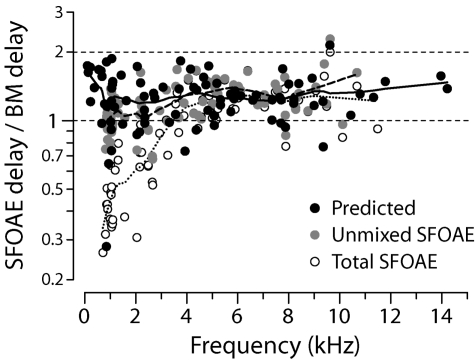
Our conclusions about the viability of the coherent-reflection model contrast with those of Siegel et al. (2005), who tested the relation ${\widehat{\tau }}_{\mathrm{SFOAE}}\cong 2\times \mathrm{BM}$ delay and found it wanting. Figure 10 demonstrates, however, that the tested relationship between SFOAE and BM delays provides only an approximate statement of the model predictions in chinchilla. The black dots show predicted delay ratios ${\widehat{\tau }}_{\mathrm{SFOAE}}∕{\widehat{\tau }}_{\mathrm{BM}}$ computed using the Wiener-kernel data. (The diacritical hat on the predicted τ_SFOAE denotes its median value; the hat on τ_BM indicates the Wiener-kernel delay near CF.9) The model generally predicts chinchilla delay ratios significantly less than 2 throughout the cochlea. Collapsing the predictions across frequency yields a mean delay ratio of 1.3±0.3 standard deviation. Although delay ratios appear to increase at both the highest and lowest frequencies, the data are too sparse to provide much confidence in the trend.

Figure 10.

Empirical and predicted delay ratios. Black dots give predicted delay ratios ${\widehat{\tau }}_{\mathrm{SFOAE}}∕{\widehat{\tau }}_{\mathrm{BM}}$ computed by using Eq. 1 tailored to chinchilla using the ANF Wiener kernels. Gray and white dots give empirical delay ratios computed using values of ${\widehat{\tau }}_{\mathrm{SFOAE}}$ obtained from the unmixed and total SFOAE measurements (Siegel et al., 2005), respectively. BM delays were estimated from the Wiener-kernel data (Recio-Spinoso et al., 2005; Temchin et al., 2005).

For comparison with the model predictions, Fig. 10 also shows empirical ratios estimated by combining the measured SFOAE and Wiener-kernel data. The empirical ratio ${\widehat{\tau }}_{\mathrm{SFOAE}}∕{\widehat{\tau }}_{\mathrm{BM}}$ was computed for each successfully reconstructed Wiener kernel by finding the median SFOAE phase-gradient delay (across all 17 chinchillas in the study of Siegel et al.) measured at frequencies within ±2% of the fiber’s CF. Gray dots show ratios computed using the unmixed long-latency component; open circles show the ratios computed using the total SFOAEs. Statistical tests corroborate conclusions evident from the trend lines (see also Figs. 59). At frequencies above 4 kHz, all three distributions (predicted, unmixed, and total) are statistically indistinguishable (Kolmogorov–Smirnov test), confirming the close agreement between the theoretical and empirical ratios in the base of the cochlea. Below 4 kHz, the ratios computed using the total SFOAEs stand out from the other two (Kolmogorov–Smirnov test, p<0.001), which are again statistically identical by the same test. Irrespective of its ultimate legitimacy, the unmixing procedure has at least substantially improved the agreement between theory and experiment in the apex.

The empirical delay ratios estimated from the chinchilla SFOAE and ANF data appear broadly consistent with, albeit somewhat smaller than, previous estimates obtained from the base of the cochlea in several species. In cat and guinea pig, Shera and Guinan (2003) report ratios of 1.7±0.2 and 1.6±0.3, respectively, values obtained by combining otoacoustic and mechanical data across studies. Direct mechanical and otoacoustic measurements in the same animals (ten guinea pigs and one chinchilla) gave a mean delay ratio of 1.8±0.2 (Cooper and Shera, 2004).

Interpretation in terms of traveling-wave delay

If coherent reflection involves roundtrip wave propagation, why are predicted delay ratios less than two? Why, in other words, is the intuitive formula SFOAE delay≅2×BM delay only approximate? To answer this question, we use the coherent-reflection model to derive a formula for ${\widehat{\tau }}_{\mathrm{SFOAE}}$ that reveals the origin of SFOAE delays in cochlear mechanics. To anticipate, we find that SFOAE delay corresponds to the roundtrip delay experienced by pressure-difference waves rather than BM traveling waves. These two waves, the transpartition pressure and the BM velocity, have different phase-gradient delays because they are related by a complex function of frequency, the BM admittance, whose phase varies appreciably near the wave peak.

Analysis of the integral in Eq. 1 for P_SFOAE(f) using the saddle-point approximation (e.g., Bender and Orszag, 1978) shows that its contribution to the emission phase-gradient delay is largely determined by the phase slope of the integrand (I) evaluated near its magnitude peak (Zweig and Shera, 1995, Appendix D; Shera et al., 2005). Since the integrand I≡ϵW², the median emission delay has the approximate value

$${\widehat{\tau }}_{\mathrm{SFOAE}}\cong {\widehat{\tau }}_{\mathcal{I}}={\widehat{\tau }}_{ϵ}+{\widehat{\tau }}_{{\mathcal{W}}^2},$$ (6)

where, for example,

$${\widehat{\tau }}_{{\mathcal{W}}^2}\equiv {\phantom{\mid }-{\partial }_{\omega }\arg {\mathcal{W}}^2\mid }_{\max \mid \mathcal{I}\mid },$$ (7)

and the notation ∂_ω is shorthand for ∂∕∂ω. The diacritical hat on τ_SFOAE denotes its median value and otherwise indicates evaluation at max ∣I∣. The delay τ_ϵ represents the phase-gradient delay associated with the smooth (nonstochastic) component of the perturbations. Equation 6 accurately predicts ${\widehat{\tau }}_{\mathrm{SFOAE}}$ in both one- and two-dimensional active cochlear models (cf. Fig. 12 of Shera et al., 2005a).

Approximation 6 for ${\widehat{\tau }}_{\mathrm{SFOAE}}$ can be expressed by using quantities determined by the Wiener-kernel measurements. We begin by examining the forms of ϵ and W² appearing in the integrand. Recall that we took ϵ(x,f)≅2Δk∕k with Δk=r(x)γ(x,f), where γ(x,f) is the gain function. Because Δk is real, it makes no contribution to the phase of ϵ. Hence, τ_ϵ≅−τ_k, where ${\widehat{\tau }}_k$ is the phase-gradient delay of the wave number (τ_k≡−∂_ω arg k); τ_k enters with a minus sign because k resides in the denominator (arg k⁻¹=−arg k). Equation 2 for W² simplifies in the short-wave regime near the wave peak. In the short-wave limit, α→kH so that ${\mathcal{W}}^2\equiv \alpha V_{\mathrm{BM}}^2∕k^2\cong H{V}_{\mathrm{BM}}^2∕k$. Hence ${\widehat{\tau }}_{{\mathcal{W}}^2}\cong 2{\widehat{\tau }}_{\mathrm{BM}}-{\widehat{\tau }}_k$, where the factor of 2 comes from the exponent on V_BM, and τ_k again enters with a minus sign.

Combining the expressions for ${\widehat{\tau }}_{ϵ}$ and ${\widehat{\tau }}_{{\mathcal{W}}^2}$ yields the approximation

$${\widehat{\tau }}_{\mathrm{SFOAE}}\cong 2({\widehat{\tau }}_{\mathrm{BM}}-{\widehat{\tau }}_k).$$ (8)

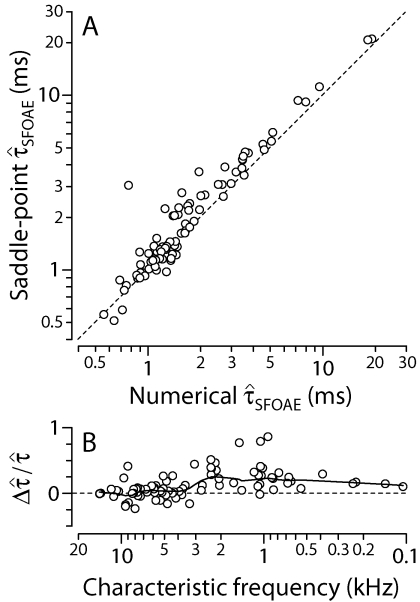
Estimates of ${\widehat{\tau }}_{\mathrm{BM}}$ and ${\widehat{\tau }}_k$ needed to evaluate Eq. 8 can be obtained by using the Wiener-kernel data. Figure 11 plots values of ${\widehat{\tau }}_{\mathrm{BM}}$ and ${\widehat{\tau }}_k$ calculated from the ANF data and the derived wave numbers.10 Figure 12 goes on to demonstrate that Eq. 8 for ${\widehat{\tau }}_{\mathrm{SFOAE}}$, based on the short-wave and saddle-point approximations, reproduces the model results shown in Figs. 59, which were obtained by evaluating Eq. 1 for P_SFOAE(f) numerically. Although the saddle-point formula slightly overestimates ${\widehat{\tau }}_{\mathrm{SFOAE}}$ at CFs below 4 kHz [Fig. 12B], the approximation appears quite respectable overall; it therefore provides a useful basis for interpreting the model predictions.

Figure 11.

BM and wave number delays. The black dots show values of the near-CF BM phase-gradient delay $\left({\widehat{\tau }}_{\mathrm{BM}}\right)$ computed from the Wiener-kernel estimates of V_BM(x,f). The gray triangles show corresponding values of ${\widehat{\tau }}_k$ computed from the same Wiener kernels. Loess trend lines are shown to guide the eyes.

Figure 12.

Numerical and approximate SFOAE delays. The scatterplot in panel (A) shows the correlation between median SFOAE phase-gradient delays computed by using the saddle-point approximation [Eq. 8] and values of ${\widehat{\tau }}_{\mathrm{SFOAE}}$ reproduced from Figs. 59 [obtained by using Eq. 1 for P_SFOAE(f)]. Each circle represents the results from an individual Wiener kernel. Short dashes show the line y=x. The scatterplot in panel (B) shows the fractional deviation $({\widehat{\tau }}_{\mathrm{approx}}-{\widehat{\tau }}_{\mathrm{numeric}})∕{\widehat{\tau }}_{\mathrm{numeric}}$ vs CF, which decreases along the abscissa. Short dashes mark the zero line and a loess trend guides the eyes. Generally quite accurate in the base of the cochlea, the saddle-point approximation overestimates the delay by roughly 10%–20% in the apex (CF<4 kHz). Overall, the approximation provides a useful framework for interpreting the model predictions.

The empirical values in Fig. 11 indicate that ${\widehat{\tau }}_k$ is positive$({\widehat{\tau }}_k>0)$. The sign of ${\widehat{\tau }}_k$, anticipated on theoretical grounds (Shera, 2001; Shera et al., 2005a), reflects the nature of cochlear amplification. In particular, the sign follows from the observation that near the peak of the traveling wave, the propagation function is positive (κ>0) and the gain function γ goes through a negative-going zero crossing (Shera, 2007).11 Because ${\widehat{\tau }}_k$ is positive, the predicted delay ratio is generally less than 2,

$${\widehat{\tau }}_{\mathrm{SFOAE}}∕{\widehat{\tau }}_{\mathrm{BM}}\cong 2(1-{\widehat{\tau }}_k∕{\widehat{\tau }}_{\mathrm{BM}})<2.$$ (9)

Since ${\widehat{\tau }}_k$ is perhaps 10%–20% of ${\widehat{\tau }}_{\mathrm{BM}}$, the approximation ${\widehat{\tau }}_{\mathrm{SFOAE}}\cong 2{\tau }_{\mathrm{BM}}$ is valid to within 2×(10–20)%. Since the ratio ${\widehat{\tau }}_k∕{\widehat{\tau }}_{\mathrm{BM}}$ decreases at lower frequencies, the model delay ratio increases slightly in the apex of the cochlea (see Fig. 10).

Approximation 8 can be interpreted physically by noting that V_BM is given by the product of the transpartition pressure P₀ and the BM admittance: V_BM=P₀Y_BM. In the short-wave regime near the peak, the relation Y_BM∼k²∕α (Shera et al., 2005a) becomes Y_BM∼k. Evaluating the delays gives ${\widehat{\tau }}_{\mathrm{BM}}\cong {\widehat{\tau }}_p+{\widehat{\tau }}_k$, where τ_p is the phase-gradient delay of the transpartition pressure. Thus, ${\widehat{\tau }}_p\cong {\widehat{\tau }}_{\mathrm{BM}}-{\widehat{\tau }}_k$; the pressure delay is just the difference between the curves in Fig. 11. Rewriting Eq. 8 in terms of ${\widehat{\tau }}_p$ gives

$${\widehat{\tau }}_{\mathrm{SFOAE}}\cong 2{\widehat{\tau }}_p.$$ (10)

In other words, the model predicts that SFOAE delay is approximately twice the pressure delay. Figure 13 illustrates this result with predictions obtained from individual Wiener kernels. Although the factor of 2 in Eq. 10 depends on the value of τ_ϵ (i.e., on the form of the irregularities that scatter the wave), it is consistent with the notion that energy propagation in the cochlea, both on the way in and on the way out, occurs not by means of waves on the BM but by means of traveling pressure-difference waves. Because the BM velocity and the transpartition pressure are related by a complex function of frequency—the BM admittance—the two kinds of waves have slightly different phase-gradient delays (with ${\widehat{\tau }}_p<{\widehat{\tau }}_{\mathrm{BM}}$ in an active cochlea).

Figure 13.

Predicted pressure delay ratios. The black dots and trend line give predicted delay ratios ${\widehat{\tau }}_{\mathrm{SFOAE}}∕{\widehat{\tau }}_p$ computed from Eq. (1) using parameters derived from the chinchilla ANF Wiener kernals. Transpartition pressures were estimated from the Wiener kernels using the formula P₀=V_BM∕Y_BM with Y_BM∼k²∕α (Shera, 2007).

Implications for compression-wave models

Although empirical delay ratios significantly greater than 1 but less than 2 agree with the predictions of the coherent-reflection model, they contradict suggestions that OAEs propagate back to the stapes primarily via fast compression (sound) waves (Ren, 2004; Ren et al., 2006; Ruggero, 2004; Siegel et al., 2005). Both heuristic models of fast-wave propagation (e.g., Ren, 2004) as well as more physically based models of fast-wave SFOAE generation (Shera et al., 2005b) predict unmixed delay ratios less than 1. Specifically, for the same types of irregularities employed here, they predict the value $1-{\widehat{\tau }}_k∕{\widehat{\tau }}_{\mathrm{BM}}<1$. This discrepancy between empirical delay ratios and fast-wave model predictions suggests that the forces involved in the production of long-latency OAEs couple primarily into transverse pressure-difference waves rather than into longitudinal compression waves. This conclusion is consistent with the results of “Allen–Fahey” and related experiments, which provide compelling independent evidence against the predominance of compression-wave OAEs in mammalian cochlear mechanics (Shera et al., 2007).

Prediction of a short-latency component

The mixing of emission components produced by different mechanisms can systematically distort measured phase-gradient delays (e.g., Talmadge et al., 2000). Depending on the relative amplitude of the components, the phase-gradient delay of the mixture falls somewhere between the delays of the components considered separately. Because the coherent-reflection model discussed here involves but a single mechanism—scattering from pre-existing perturbations—removing contributions from other mechanisms is logically necessary for any meaningful comparison between model predictions and experiment. By applying these ideas, we find that the discrepancy between measured and predicted delays apparent at low frequencies in Fig. 5 can be substantially reduced, perhaps even eliminated, by postulating the existence of and removing from the data a “contaminating” short-latency emission component presumed to arise by other means. [As discussed below, the coherent-reflection framework applied to a nonlinear cochlear model (Talmadge et al., 2000) yields a natural candidate for the short-latency component.]

Skeptics might object that unmixing renders the resulting agreement essentially vacuous—the procedure merely alters the data to match the theory. The criticism, however, is unwarranted for two reasons. First, nothing guarantees at the outset that simple unmixing will yield agreement between the measured and predicted delays at any frequency, let alone over the entire frequency range (e.g., that it will preserve the already outstanding agreement in the base), and yet it does so. Second, the procedure not only reconciles theory and experiment in the apex, it does so constructively by making what amounts to a testable prediction. In particular, our analysis implies that consistency between the model and the data at low frequencies requires the existence of a previously unrecognized short-latency SFOAE component whose relative amplitude is largest in the apical turns of the cochlea.

Prompted by these considerations, and encouraged by the model’s success in the base of the cochlea to take its predictions seriously throughout,12 we looked more closely at the low-frequency measurements. The examination corroborated predictions by revealing that at frequencies below 4 kHz, chinchilla SFOAEs show strong evidence for interference between two components with different phase-gradient delays (see Fig. 6). Thus, both the unmixing analysis and the measured fine-structure interference patterns strongly suggest that multiple emission mechanisms are at work in the apex. Our finding that the long-latency component matches the model predictions suggests that one of the mechanisms is linear coherent reflection. For the moment, the origin of the short-latency component remains unknown, and independent evidence of its existence is obviously needed. Verification of its existence and properties would provide powerful support for the overall modeling framework.

Candidates for the short-latency component

The short-latency SFOAE component could arise by one (or more) of many means. The component’s eponymous and shallow phase gradient immediately suggests an origin via induced (wave-fixed) sources, such as nonlinear distortion (e.g., Shera and Guinan, 1999). Indeed, wave-fixed sources provide a natural explanation for the paradox invoked by Siegel et al. (2005): That OAE phase-gradient delays can be substantially shorter than one-way stimulus propagation delays to the region of reverse-wave generation near the wave peak. If the cochlea were perfectly scaling symmetric, and middle-ear transmission instantaneous, wave-fixed sources would yield an emission with constant phase (i.e., zero phase-gradient delay). However, in the real ear, both violations of scaling, most salient in the apex (e.g., Kiang and Moxon, 1974; Liberman, 1978; Shera and Guinan, 2003; van der Heijden and Joris, 2006), and finite middle-ear delays (e.g., Dong and Olson, 2006) can produce small but nonzero phase-gradient delays at least qualitatively similar to those apparent in Fig. 9.

Helpfully, the coherent-reflection framework itself provides what may be the most natural candidate for the short-latency component: wave-fixed emissions that arise by scattering off wave-induced perturbations created by nonlinearities in the mechanics [i.e., the process dubbed “nonlinear reflection” (Talmadge et al., 2000)]. Although the present analysis employed linear cochlear models, the actual cochlea is nonlinear, even at the relatively low levels used for the SFOAE measurements. Adding both mechanical irregularity and nonlinearity to active models produces a mixture of wave- and place-fixed SFOAEs qualitatively similar to that seen here and in other studies (Talmadge et al., 2000; Goodman et al., 2003; Schairer et al., 2003). In addition, simple compression-wave models predict that OAEs generated by coupling into fast waves (e.g., via volume-velocity sources in the organ of Corti) are also essentially wave fixed (Shera et al., 2005b) and could, in principle, be contributing to the short-latency component.

The short-latency component could also comprise emission components that arise from the tail region of the cochlear traveling wave rather than the peak. Because the wavelength of the traveling wave is generally longer in the tail region, even place-fixed mechanisms acting in this region could produce emissions with relatively shallow phase gradients. Although their interpretation is not unequivocal (Shera et al., 2004), suppression experiments suggest that contributions from the tail of the traveling wave may, in fact, be significant in chinchilla (Siegel et al., 2003, 2004).

Alternatively, the appearance of a significant short-latency SFOAE component in the apex could simply be an artifact of the measurement method, which relies on nonlinear interactions between the probe and the suppressor to extract the emission. If the form and∕or frequency dependence of cochlear nonlinearities differ markedly between the base and the apex (e.g., Khanna and Hao, 1999; Cooper and Dong, 2003), then the suppression method may not always reliably extract the principal emission evoked by the probe (cf. Kalluri and Shera, 2007a). As an extreme example, suppose that the mechanics in the apex were completely linear and exhibited no two-tone suppression. Then, even if the apex were to generate strong reflection-source OAEs, suppression and other “nonlinear” methods would be unable to measure them. Hence, if low-frequency OAEs were actually recorded by using these methods, then the measured emissions could only have originated from more basal (nonlinear) regions of the cochlea (i.e., from regions corresponding to the tail of the traveling wave). As a result, the measured phase-gradient delays would be correspondingly reduced. In the actual ear, the suppression method may extract a mix of emissions from tip and tail regions of the traveling wave whose relative amplitudes vary with CF, depending on the form of cochlear mechanical nonlinearities.

Finally, and most speculatively, the short-latency component may arise through the involvement of nontraditional modes of energy propagation in the cochlea. If the relative magnitude of the short-latency component is any guide, these modes presumably play a more important role in the mechanics of the apex than in the base. Evidence for multiple modes of motion in this CF region can be found in ANF click responses (Lin and Guinan, 2004; Guinan et al., 2005) and in tuning curves, which have multilobed tips and group delays that change abruptly at the seams (e.g., Pfeiffer and Molnar, 1970; Kiang, 1984; van der Heijden and Joris, 2003).

An apical-basal transition

Independent of the status of the coherent-reflection model or of the existence or identity of any short-latency emission component, our analysis suggests that the chinchilla cochlea undergoes a transition between more “apical-like” and more “basal-like” behavior near the 4 kHz place. In Fig. 10, for example, empirical delay ratios ${\widehat{\tau }}_{\mathrm{SFOAE}}∕{\widehat{\tau }}_{\mathrm{BM}}$ computed from the total SFOAEs change slope rather abruptly near 4 kHz; they increase with frequency below 4 kHz but remain almost constant above. The appearance of this midfrequency transition is due almost entirely to a change in the frequency dependence of ${\widehat{\tau }}_{\mathrm{SFOAE}}$ rather than of ${\widehat{\tau }}_{\mathrm{BM}}$. Interestingly, a similar midfrequency bend in ${\widehat{\tau }}_{\mathrm{SFOAE}}$ occurs in other mammals, including cats, guinea pigs, and humans (Shera and Guinan, 2003). In chinchilla, the unmixing analysis suggests that the transition reflects a change in the composition of the total SFOAE: Whereas at frequencies above 4 kHz, chinchilla SFOAEs consist primarily of a single long-latency reflection-source component, at frequencies below 4 kHz, the emissions contain both short- and long-latency components in more equal proportions.

Interestingly, the 4 kHz location of the apical-basal transition in chinchilla SFOAEs corresponds closely with the CF region in which several properties of traveling-wave propagation and gain functions undergo quantitative changes (Shera, 2007). For example, the maximum value of the gain function γ(x,f) is generally smaller, and the spatial extent of the amplification region substantially larger, at CFs below 3–4 kHz than at CFs above (see Figs. 12–14 of Shera, 2007). In cat, the otoacoustic transition frequency corresponds approximately with the CF at which ANF tuning curves change from the classic tip∕tail form characteristic of high-CF fibers to the more complex multilobed shapes found in the apex (Liberman, 1978; Liberman and Kiang, 1978). Both the significance of these apical-basal transitions and the intriguing correlations between otoacoustic delays and cochlear physiology require further study.

Experimental and theoretical caveats

Notwithstanding the compelling agreement evident in Figs. 910, our comparison between theory and experiment requires important qualification. Necessary caveats generally fall into two partially overlapping and nonexclusive categories: limitations of the experimental data and uncertainties in the theoretical assumptions.

Wiggle room on the experimental side arises from:.

• (1)The different populations of chinchillas used for the ANF and SFOAE measurements. Comparisons done using data from the same individuals would control for possible systematic differences between the groups (e.g., the nature and extent of cochlear damage due to the surgical and measurement procedures). In addition, measurements on the same subjects would presumably reveal correlations between the otoacoustic and auditory-nerve data that now appear as random scatter, reducing the power of the comparison.
• (2)The different stimuli used for the otoacoustic and neural data (pure tones for the SFOAEs, wideband noise for the Wiener kernels). Due to suppression and other effects, systematic differences between responses to narrow- and wideband stimuli are expected in nonlinear systems. For example, although both data sets were measured at low intensities, the different stimulus bandwidths make it difficult if not impossible to match effective stimulus levels (cf. Kalluri and Shera, 2007b).
• (3)Possible systematic differences between ANF-derived and true BM mechanical transfer functions. Although Wiener-kernel responses corrected for synaptic and neural transmission delays resemble BM mechanical measurements made at corresponding locations and intensities (Temchin et al., 2005), the Wiener-kernel measurements characterize cochlear tuning as seen from the auditory nerve. They therefore presumably include contributions from internal motions of the organ of Corti or tectorial membrane visible to the inner hair cell but less prominent in the motion of the BM (e.g., Guinan et al., 2005; Nowotny and Gummer, 2006; Karavitaki and Mountain, 2007; Ghaffari et al., 2007). Whether (or how) these internal motions play a role in OAE generation remains unclear [cf. assumption (1) in Sec. 1A].
• (4)The uncertain legitimacy of the unmixing analysis. Although the evidence for a contaminating short-latency SFOAE component produced by other mechanisms seems compelling, corroborating data are needed to fully justify our procedures. The current analysis, although not entirely circular, appears at least disconcertingly spiral. If multiple SFOAE components do exist, perhaps they can be separated by using procedures that do not introduce unwanted artifacts at the edges; the unmixing artifact is especially unhelpful at the lowest frequencies, where discrepancies between theory and experiment appear largest. We note, however, that even if the unmixing analysis is entirely discarded, agreement between theory and experiment remains strong in the base (Fig. 5).
• (5)Possible biases introduced by the suppression method for measuring SFOAEs, as discussed in Sec. 5C.

On the theoretical side, the list of caveats includes:

• (1)Possible inaccuracy of the wave number inversion procedure. Although we limited our analysis to Wiener kernels and wave numbers validated by successful reconstruction, the inversion procedure is nevertheless approximate and depends on assumptions (e.g., local scaling) with the potential to produce systematic errors in the predicted SFOAEs. The local scaling approximation is also employed when evaluating Eq. 1 for P_SFOAE(f), where it serves to convert BM transfer functions into traveling waves. Any bias due to the local scaling approximation is expected to be largest in the apical half of the cochlea, where deviations from scaling are most pronounced.
• (2)Possible misrepresentation of the mechanical irregularities. Since the phase-gradient delay associated with the irregularities (τ_ϵ) contributes to ${\widehat{\tau }}_{\mathrm{SFOAE}}$ [Eq. 6], the form of the perturbations affects the predicted SFOAE delay. We took the dominant perturbations Δk to reside in the traveling-wave gain function, with the consequence that ${\widehat{\tau }}_{ϵ}\cong -{\widehat{\tau }}_k$. Although we regard these perturbations as physiologically natural—and other choices, such as placing the irregularities in the propagation function κ, produce identical results—the actual perturbations remain unknown and may even vary systematically along the cochlea. Currently, the strongest evidence supporting our approach may simply be the compelling overall agreement that results (i.e., it works). Because systematic discrepancies between measured and predicted phase-gradient delays can be introduced by appropriate adjustment of perturbation phases, the choice of perturbations is the closest thing to a free adjustable parameter in the model.
• (3)Deviations from one or more of the three principal assumptions about cochlear mechanics outlined in Sec. 1A. For example, conventional models assume that the mechanics of the partition are well described by point-admittance functions coupled together primarily by means of scalae fluid pressures. However, if spatial “feed-forward” or “feed-backward” forces play a significant role in cochlear amplification or if the normal operation of the cochlea involves additional modes of motion and∕or energy transport, then the analysis leading to Eq. 1 for P_SFOAE(f) becomes, at best, only approximate. In addition, the derivation assumes the simplified geometry of the two-dimensional box model. Therefore, even though our analysis encompasses both long- and short-wave behaviors, the predictions of Eq. 1 may deviate systematically from predictions that incorporate more realistic three-dimensional motions of both fluid and tissue.

Without minimizing the possible significance of these experimental and theoretical caveats, we note that the many ways that the model implemented here might seriously have failed—but evidently did not—strongly suggests that the coherent-reflection model captures at least the dominant mechanisms responsible for the generation of reflection-source otoacoustic emissions.