Estimation of the acoustic impedance of lung versus level of inflation for different species and ages of animals

Abstract

In a previous study, it was hypothesized that ultrasound-induced lung damage was related to the transfer of ultrasonic energy into the lungs (W. D. O’Brien et al. 2002, “Ultrasound-induced lung hemorrhage: Role of acoustic boundary conditions at the pleural surface,” J. Acoust. Soc. Am. 111, 1102–1109). From this study a technique was developed to: 1) estimate the impedance (Mrayl) of fresh, excised, ex vivo rat lung versus its level of inflation (cm H₂O) and 2) predict the fraction of ultrasonic energy transmitted into the lung (M. Oelze et al. 2003, “Impedance measurements of ex vivo rat lung at different volumes of inflation.” J. Acoust. Soc. Am. 114, 3384–3393). In the current study, the same technique was used to estimate the frequency-dependent impedance of lungs from rats, rabbits, and pigs of various ages. Impedance values were estimated from lungs under deflation (atmospheric pressure, 0 cm H₂O) and three volumes of inflation pressure [7 cm H₂O (5 cm H₂O for pigs), 10 cm H₂O, and 15 cm H₂O]. Lungs were scanned in a tank of degassed 37 °C water. The frequency-dependent acoustic pressure reflection coefficient was determined over a frequency range of 3.5–10 MHz. From the reflection coefficient, the frequency-dependent lung impedance was calculated with values ranging from an average of 1.4 Mrayl in deflated lungs (atmospheric pressure) to 0.1 Mrayl for fully inflated lungs (15 cm H₂O). Across all species, deflated lung (i.e., approximately 7% of the total lung capacity) had impedance values closer to tissue values, suggesting that more acoustic energy was transmitted into the lung under deflated conditions. Finally, the impedance values of deflated lungs from different species at different ages were compared with the thresholds for ultrasound-induced lung damage. The comparison revealed that increases in ultrasonic energy transmission corresponded to lower injury threshold values.

INTRODUCTION

Ultrasound-induced lung hemorrhage has been observed in animal experiments at exposure levels corresponding to those used for ultrasound examinations in humans (incidental exposure) (Child et al., 1990; Hartman et al., 1990; Penney et al., 1993; Raeman et al., 1993, 1996; Frizzell et al., 1994, 2003;Tarantal and Canfield, 1994; Zachary and O’Brien, 1995; Baggs et al., 1996; Holland et al., 1994; O’Brien and Zachary, 1997; Dalecki et al., 1997a, 1997b; AIUM, 2000; O’Brien et al., 2000, 2001a, 2001b, 2003a, 2003b, 2004, 2006; Zachary et al., 2001a, 2001b). Specifically, sharply defined thresholds on the order of 1 MPa were found with 10 μs length pulses and larger thresholds at 4 MHz than at 1 MHz (Child et al., 1990; Hartman et al., 1990). In addition, the lung damage was not found to be progressive, i.e., hemorrhage occurred only during exposure and did not continue after the termination of exposure (Penney et al., 1993). In further experiments, the threshold for lung damage was found to depend mainly on the pressure level and not on the exposure duration (Raeman et al., 1993, 1996). Similar results were obtained in larger animals, i.e., monkeys and swine (Tarantal and Canfield, 1994; Baggs et al., 1996). The dependence of ultrasound-induced lung damage was examined in terms of the age dependence of animals (Dalecki et al., 1997a, 1997b; O’Brien et al., 2003b). Although the thresholds for ultrasound-induced lung damage were similar for neonatal, juvenile, and adult mice, the sizes of the suprathreshold hemorrhages were significantly larger in adult mice than in neonatal or juvenile mice (Dalecki et al., 1997b). Furthermore, lung damage thresholds were examined across species with similar trends observed (O’Brien and Zachary, 1997). Ultrasound-induced lung damage was examined versus various ultrasound parameters including pulse duration (O’Brien et al., 2001a, 2003a), pulse repetition frequency (O’Brien et al., 2001a), beamwidth (O’Brien et al., 2001b), and use of contrast agents (O’Brien et al., 2004).

As a result of previous studies, several mechanisms for ultrasound-induced lung hemorrhage have been hypothesized including heating, inertial cavitation, and breaking of tissue layers from acoustic transfer of energy. In the case of tissue heating, several studies have indicated that heating cannot explain lung damage (Hartman et al., 1992; Zachary et al., 2006). The hypothesis that inertial cavitation was the mechanism underlying ultrasound-induced lung hemorrhage was also tested (Frizzell et al., 2003; O’Brien et al., 2000, 2004). These studies quantified lung damage thresholds when pulse polarity, energy, and overpressure values were varied. The studies suggested that inertial cavitation was not responsible for ultrasound-induced lung hemorrhage; however, the debate on the role of inertial cavitation in lung damage remains (Raeman et al., 1997; Carstensen et al., 2000; O’Brien et al., 2000; Frizzell et al., 2001a, 2001b, 2003; Apfel, 2001a, 2001b).

The third mechanism hypothesized to be responsible for ultrasound-induced lung damage is the breaking of tissue layers due to the transfer of acoustic energy. This could be due to a radiation-type force where tight junctions are transiently or permanently opened due to ultrasound exposure allowing hemorrhaging in the lung. In the case of a transiently opened junction, the hemorrhaging would stop after the exposure has terminated. This result would support early reports that ultrasound-induced lung damage was not progressive and did not continue after the termination of exposure (Penney et al., 1993). Later reports of superthreshold behavior in rats indicated that following exposure to pulsed ultrasound, lesions at zero days postexposure were characterized by areas of acute alveolar hemorrhage under the visceral pleural surface but without pleural or septal injury, resulting in no long-term residual effects on the lung (Zachary et al., 2001a). Superthreshold corresponds to pressure levels used in exposure above the threshold determined in previous studies to yield lung damage in rats (O’Brien et al., 2001a, 2001b).

In vivo experiments in rats demonstrated that deflated lung increased the occurrence and degree of hemorrhage when compared to a fully inflated lung (O’Brien et al., 2002). In the in vivo experiments, deflated lung corresponded to functional residual capacity or about 40% of total lung capacity (TLC). In this study, the respiratory systems of 12 rats were arrested (chemically inhibited and then ventilator used), and then the lungs at three volumes of inflation (inflated: approximately tidal volume; half-deflated: half-tidal volume; deflated: lung volume at functional residual capacity or about 40% of TLC) were exposed to two previously determined (from anesthetized breathing rats) superthreshold ultrasound conditions. Deflated lungs were more easily damaged than half-deflated lungs, and half-deflated lungs were more easily damaged than inflated lungs (inflated lungs had no lesions). The acoustic impedance difference between intercostal tissues and lungs was hypothesized to be much less for the deflated lung condition, suggesting that the extent of lung damage was related to the amount of ultrasonic energy that was propagated across the pleural surface boundary (tissue) into the lung (composed of tissue and fraction of air). These findings led to a better understanding of the ultrasonic properties of lungs as a function of inflation. As a result, it was suggested that ultrasound would be reflected from an inflated lung and less acoustic energy would be transferred into it.

The lung inflation studies led to the development of a model of the lung in terms of impedance (O’Brien et al., 2002). The lung was modeled as a two-component acoustic structure of air and bulk material. The impedance of the lung depended on the volume fraction of air in the lung. As the lung became more inflated, the lung impedance would approach that of air; however, as the lung became more deflated, the lung impedance would approach that of tissue. Based on estimates of the fraction of air and lung at the deflated and inflated cases in the in vivo experiments [volume fraction of air ∼0.76 for a deflated lung and ∼0.80 for an inflated lung (Gil et al., 1979)], the impedance estimated from the two-component model increases by 67% from an inflated to a deflated lung. Several other experiments have been conducted on ultrasound interaction with the lung that support the two-component bulk model of the lung (Dunn and Fry, 1961; Bauld and Schwan, 1974; Dunn, 1974, 1986; Pederson and Ozcan, 1986; Mikhak and Pederson, 2002). In these experiments, pressure reflection coefficients, attenuation values, and sound speed values were determined in lungs with varying levels of inflation. Table 1 summarizes the results of the lung reflection coefficient, attenuation, and sound speed values from these previous studies. The results indicate that the attenuation tends to be larger for higher air content in the lung. The sound speed tends to increase with decreasing air content while the density increases. The impedance tends to decrease with increasing air content, suggesting that more acoustic energy is transmitted into a lung with less air. Furthermore, the sound speed and attenuation both increase with increasing frequency at any one inflation level. In summary, the cumulative interpretation of results from these studies suggests that the amount of ultrasonic energy transmitting into and propagating within a deflated lung is much greater than in an inflated lung.

Table 1.

Summary of reflection coefficient, attenuation, and sound speed values for lung.

Air content (%)	Density (kg∕m3)	Sound speed (m∕s)	Attenuation coefficient(Np/cm)	Impedance(Mrayl)
100a				0.17a b, b
67c d, d	350–360c d, d	875.0,c 583.0d	8.83c	0.31,b c, c 0.21d
62.5b c, c	400c	918.7c	7.40c	0.37b c, c
60a d, d	430d	640.0d	7.40a b, b	0.28,d 0.80a b, b
57.7b c, c	450c	965.3c	6.83c	0.43b c, c
53b c, c	500c	1027c	5.83c	0.51b c, c
49d	540d	733.0d		0.40d
41.6a				0.92a b, b
40d	640d	842.0d		0.54d
34b c, c	700c	1202c	3.13c	0.84b c, c
32d	720d	948.0d		0.68d
16a			7.40a b, b	1.40a b, b

^aValues obtained from study by Bauld and Schwan (1974) using a frequency range of 2.4–7.4 MHz.

^bValues estimated from parameters given in the study.

^cValues obtained from study by Dunn (1986) using a frequency range of 1–5 MHz.

^dValues obtained from study by Pederson and Ozcan (1986) using a frequency range of 10–800 kHz.

In our previous study, a technique was introduced to measure directly the reflection coefficient from the lung surface incident from water and to calculate the impedance value of intact fresh lungs, ex vivo, from rats for different volumes of inflation (Oelze et al., 2003). In all of the previous studies on the acoustic properties of lungs, the reflection coefficient and impedance values were not estimated from intact fresh lungs. It was hypothesized that fresh lungs would have an impedance value dependent on the ultrasonic frequency and volume of inflation.

Measurements of the reflected ultrasound were made on seven rat lungs, ex vivo, under deflation (atmospheric pressure, 0 cm H₂O) and three volumes of inflation pressure (7, 10, and 15 cm H₂O) (Oelze et al., 2003). From the measurements, the frequency-dependent pressure reflection coefficient for the lung was estimated, and the frequency-dependent impedance of the lung was then estimated from the pressure reflection coefficient. The estimates indicated that the greater the volume of the inflation, the larger the magnitude of the reflection coefficient and, correspondingly, the smaller the impedance value of the lung. Estimates also indicated that the impedance value of the lung was always less than the characteristic impedance of water at 37 °C (pressure release surfaces relative to water). The frequency-dependent lung impedance ranged from an average of 1 Mrayl in deflated lungs to 0.2 Mrayl for fully inflated lungs; deflated lungs had an impedance closer to water (1.52 Mrayl) than inflated lungs. Using the two-component model of the lung, as the level of inflation increases more air fills the lung, and the impedance value of the lung approaches that of air (O’Brien et al., 2002). As a result of the increased impedance mismatch between the inflated lung (which approaches that for air) and the surrounding fluid or tissue, more ultrasonic energy is reflected from the lung surface and less is transmitted. Therefore, more ultrasonic energy was transferred into the deflated lungs than into the inflated lungs.

In the case of an incidental clinical exposure of the lungs by ultrasound through intervening tissues, the degree of lung inflation will determine the amount of ultrasonic energy transferred into the lungs. Most of the sound will be reflected from the lung surface with just a little inflation. With the deflated lung, the pressure reflection coefficient is small (∼0.25 for the rat lungs), the impedance is closely matched to the surrounding tissue, and more acoustic energy is transmitted into the lung. Because the deflated lung was less dense than water, the pressure transmission coefficient was ∼0.75. If increased ultrasonic energy transmitted into the lung causes an increase in the incidence of lung damage, then the increased ultrasonic energy transmitted into the deflated lung due to more closely matched impedance supports earlier observations of higher probability of lung lesions in rats with deflated lungs.

In the present study, the reflection coefficient and impedance of intact fresh lungs, ex vivo, were estimated at four different levels of inflation from three species of animals, i.e., rats, rabbits, and pigs, in populations with varying ages. Using the same experimental techniques and statistical approach to examine the threshold for ultrasound-induced lung damage across species, the thresholds for ultrasound-induced lung damage were found to be consistent across species (O’Brien et al., 2006). Furthermore, the morphology of ultrasound-induced lesions was similar in all species and age groups studied. In studies of the age-dependent effect of ultrasound-induced lung damage, threshold values were found to have a dependence on age in pigs (O’Brien et al., 2003b). If the mechanism of ultrasound-induced lung damage results from the fraction of ultrasonic energy transmitted into the lung, then the impedance values of the lung should also correlate to species and age-dependent threshold values.

The study was conducted to further elaborate the dependence of ultrasonic energy transfer into the lungs and the effects of different species and age on the transfer of ultrasonic energy into the lung. Corresponding lung damage thresholds for different species of animals at different ages were then correlated to their respective lung impedance values under deflated conditions. Section 2 briefly discusses the theory and methodology used to estimate the reflection coefficient and the corresponding impedance value of the lung at different levels of inflation. Section 3 presents the results of the experiments. Section 4 discusses the results of the experiments, and the final section ends with some concluding remarks.

METHODOLOGY

Measurements

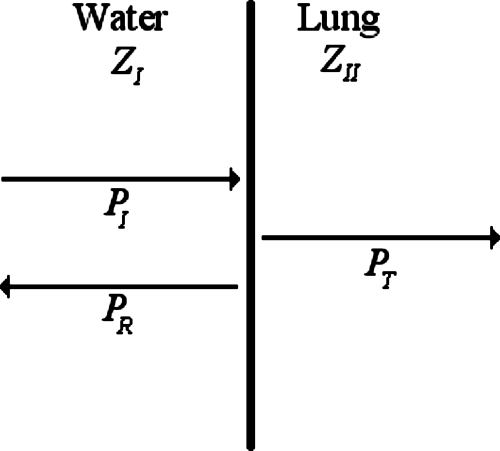
Estimates of the impedance of the ex vivo lung were obtained by measuring the pressure reflected from the lung surface. The reflected ultrasound would come from the interface between the lung surface and the surrounding water. Figure 1 shows a diagram of the interface between the lung and water. The acoustic pressure reflection coefficient (for plane waves) of sound reflecting at normal incidence from a planar boundary of two different media (media I and II) with a frequency, f, is defined as (Kinsler et al., 2000)

$$R\left(f\right)=\frac{P_R\left(f\right)}{P_{\mathrm{I}}\left(f\right)},$$ (1)

where P_R(f) is the pressure amplitude of the reflected sound and P_I(f) is the amplitude of the incident pressure wave. The sign of the reflection coefficient is positive if the impedance of medium I is smaller than the impedance of medium II and is negative if the impedance of medium I is greater than that of medium II. Actual estimates of the pressure reflection coefficient were obtained through a planar reference technique outlined in a previous study (Oelze et al., 2003).

Figure 1.

Diagram representing the interface between water with impedance Z_I and the lung with impedance Z_II and corresponding incident (P_I), reflected (P_R), and transmitted (P_T) pressure waves.

The pressure reflection coefficient is related to the impedance of the two media by (Kinsler et al., 2000),

$$R\left(f\right)=\frac{Z_{\mathrm{II}}\left(f\right)-Z_{\mathrm{I}}\left(f\right)}{Z_{\mathrm{II}}\left(f\right)+Z_{\mathrm{I}}\left(f\right)},$$ (2)

where Z_I(f) and Z_II(f) represent the frequency-dependent impedance of media I and II, respectively. Solving Eq. 2 for the impedance of medium II yields

$$Z_{\mathrm{II}}\left(f\right)=Z_{\mathrm{I}}\left(f\right)\frac{1+R\left(f\right)}{1-R\left(f\right)}.$$ (3)

If the impedance of medium I is known (i.e., water) and the pressure reflection coefficient at the boundary of media I and II is determined, then the impedance of medium II can be estimated by Eq. 3.

A single-element weakly focused ultrasonic transducer (GE Panametrics Inc., Waltham, MA) was used to make measurements of the pressure reflection coefficient from the planar reference material (a smooth Plexiglas™ plate) and the lung tissues. The transducer had an aperture diameter of 19 mm and a focal length of 51 mm measured from the planar reference material. The center frequency of the transducer was 7.1 MHz with a −6 dB pulse-echo frequency bandwidth of 5.5 MHz and a −6 dB pulse-echo beamwidth of ∼550 μm. The analysis bandwidth ranged from 3.5 to 10 MHz (−9 dB pulse-echo bandwidth).

The transducer was operated in a pulse-echo mode by using a Panametrics 5800 pulser∕receiver (GE Panametrics, Inc., Waltham, MA). The incident amplitude of the pulse used for the reflection coefficient study was determined to be 1.4 MPa at the focus of the transducer with a calibrated Polyvinylidene Fluoride (PVDF) membrane hydrophone (Marconi Model Y-34-6543, Chelmsford, UK). Measurements were digitized on an oscilloscope (LeCroy 9354TM, Chestnut Ridge, NY) that had a dynamic range of 48 dB and downloaded to a PC for postprocessing. The sampling rate was 50 MHz. Reflection measurements from both the planar reference and the lung surface were taken near the focus of the transducer where the wave fronts could be approximated as a plane wave within the narrow beamwidth (Lizzi et al., 1983).

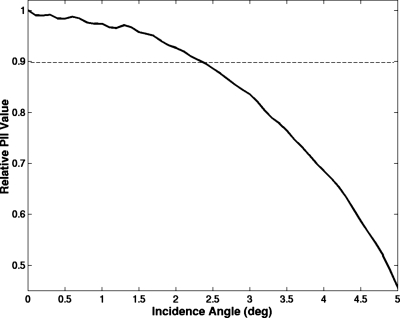
While the planar reflector is a flat surface, the lung is not a flat surface. One of the difficulties in the experimental setup was in aligning the lung with the transducer so that the sound reflected from the lung was at normal incidence. Failure to align the lung properly or a local curvature of the lung surface would lead to a reduced reflected signal relative to sound reflected at normal incidence. To quantify the possible alignment error, the plastic plate was used to record the relative reflected signal at several angles of incidence. A smooth plastic plate was placed normally incident to the transducer at the focus and rotated axially by several degrees. The plastic plate was rotated about the z-axis, and the magnitude of the signal decrease was then recorded. Figure 2 shows the relative pulse intensity integral (PII) of the reflected signal as the angle of incidence changes from normal. The angle of incidence could be off normal by 2.5° and still have a PII value within 10% error of true normal.

Figure 2.

Relative loss in magnitude of the PII value of the reflected signal as the angle of incidence moves away from normal.

The lung surface was measured similarly to the reflection from the plastic plate. In order to obtain a smooth flat surface on the lung that would be near-normal incidence, the lung was gently pressed up against a plastic holder that was aligned perpendicular to the beam axis. The holder had a small circle cut out in the middle with a diameter of 18 mm that allowed for a scanning window onto the lung surface; the lung surface was in direct contact with the water. The large size of the scanning window (18 mm) compared to the beamwidth (∼550 μm) ensured negligible diffraction effects. The lung was setup so that its surface would be near the focus of the transducer. A 5×5 mm² square perpendicular to the beam axis of the transducer (y-z plane) was scanned on the surface of the lung. RF data waveforms were acquired at intervals of 100 μm in the y and z directions.

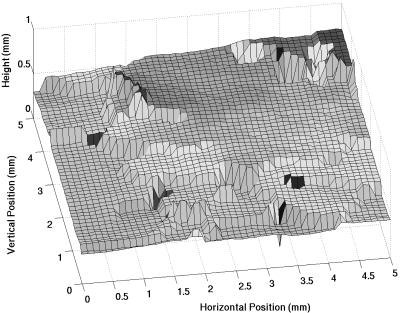
In order to reduce the measurement error of reflections from off-normal incidence, waveform sections were used in the calculations that coincided with flat areas at near-normal incidence on the lung surface. A surface plot of the lung over the 5×5 mm² scanned area was constructed from waveforms measured off the lung surface. The surface plot was constructed by finding the distance from the source to the peak with a maximum magnitude in each reflected waveform. Figure 3 shows a graph of a surface plot from one of the lungs. The flat regions shown by the surface plots were used to determine smooth regions at near-normal incidence from which the reflection coefficient calculations were made. The angle of incidence at a particular point in the scan region was calculated from the average of the arctangents of the slopes between the particular scan point and four immediately surrounding scan points. Only reflected pulses from scan points that showed angles of incidence less than 0.5° from normal were used. This procedure does not account for surface roughness smaller than a beamwidth, which could result in a frequency-dependent loss of some reflected signal relative to the reference signal. However, because the size of the roughness would be small compared to the beamwidth (and wavelength), the contribution from the roughness was assumed to be negligible compared to the direct reflection from the lung surface.

Figure 3.

Surface plot of a deflated rabbit lung recorded from the maximum peak magnitude of waveforms scanned over a 5×5 mm² window.

Reference pulses were measured from a smooth plastic plate of known reflectivity. The transducer was aligned perpendicular to the reflecting surface. The same equipment and settings were used for the pulse∕echo measurement of the reference pulse as used for the lung reflection measurements. Reflection measurements from the planar surfaces were made at different depths relative to the transducer by scanning axially along the transducer beam. The scan measured reflected values over an axial length of 1 cm centered about the focus with a step size of 100 μm (approximately half the wavelength).

Animal procedures

The experimental protocol was approved by the Institutional Animal Care and Use Committee at the University of Illinois at Urbana-Champaign and satisfied all campus and National Institutes of Health (NIH) rules for the humane use of laboratory animals. Animals were housed in an Association for Assessment and Accreditation of Laboratory Animal Care, Rockville, MD (AAALAC)-approved animal facility. Water was provided ad libitum for all species. Rabbits and pigs were fed a measured amount, and rats were provided food ad libitum.

Age-dependent lung impedances (reflection coefficients) were determined in four 2-week-old, four 3-week-old, four 7-week-old, seven 17-week-old, and five 52-week-old Sprague Dawley rats (Harlan, Indianapolis, IN); seven 12-week-old, three 3-yr-old, and three 5-yr-old New Zealand White rabbits (Myrtle’s Rabbitry, Thompson Station, TN); and seven 1-week-old, seven 4- to 5-week-old, and seven 7–8-week-old crossbred pigs (University of Illinois Veterinary Research Farm, Urbana, IL). Animals were weighed and anesthetized. Rats and rabbits were anesthetized with ketamine hydrochloride (87.0 mg∕kg, rats; 50.0 mg∕kg, rabbits) and xylazine (13 mg∕kg, rats; 10 mg∕kg, rabbits) administered intraperitoneally in rats and subcutaneously in rabbits. Pigs were anesthetized with ketamine hydrochloride (2.2 mg∕kg), xylazine (2.2 mg∕kg), and Telazol (4.4 mg∕kg) administered intramuscularly. The animals were immediately euthanized by cervical dislocation (rats) or carbon dioxide (rabbits and pigs) while under anesthesia. The lungs (with heart attached) and trachea (cut transversely at the thoracic inlet) were removed by opening the thorax with a midline incision extending from the thoracic inlet to the caudal most aspect of the sternum. Following the removal, the lungs were rinsed with a 0.9% (isotonic) saline solution. Saline was not allowed to enter the trachea. All lungs were used immediately after harvest.

A 20-gauge needle (2- and 3-week-old rats), a 16-gauge needle (7-week, 17-week, and 52-week-old rats), a 0.25-in. diameter stainless steel tube (1-week-old pigs and rabbits), and a 0.50-in.-diameter stainless steel tube (4–5- and 7–8-week-old pigs), with the tips blunted, were inserted into the open end of the trachea and sealed airtight. Plastic hosing was then used to attach the needle to the lung inflation apparatus. The lung inflation apparatus consisted of a plastic tube connected to two pressure regulators, a tank of compressed air, and a ruler to determine the pressure level (for a diagram of the apparatus, see Fig. 4). Pressure in the ex vivo lungs was measured in terms of centimeters of H₂O (1 cm H₂O=98 Pa). When a pressure level of 30 cm H₂O in an ex vivo lung was reached, the lung was considered fully inflated or inflated to TLC (Bachofen et al., 1982). In terms of common lung parameters (i.e., the TLC), 15-, 10-, 7-, 5-, and 0 cm H₂O were estimated to correspond to 90%, 82%, 70%, 61%, and 7% TLCs, respectively (Gil et al., 1979).

Figure 4.

Photograph of the inflation apparatus including a compressed air tank, pressure gauge regulators, and a water barometer.

All measurements were made in degassed water at 37±0.5 °C. Water temperature was controlled by a proportional temperature controller (Yellow Springs Instrument Co., Inc., Yellow Springs, OH). A digital thermometer (Control Company, Friendswood, TX), with an accuracy of 0.2 °C, in the water tank served as the temperature standard.

Measurements for the pressure reflection coefficient were taken at four different volumes of inflation for each lung. The waveforms reflected from the lung surface were normal to the axis of the transducer. The first measurements were taken on the deflated lungs (0 cm H₂O). After the deflated measurement was taken, the lung was slowly inflated at a rate of 1 cm H₂O∕min, to 20 cm H₂O. The lung was held at that pressure for a minimum of 5 min to allow the pressure and air inside the lung to equilibrate. The pressure was then reduced to 15 cm H₂O at 2 cm H₂O∕min and held for 15 min to ensure pressure equilibrium. Measurements were then taken from the inflated lung at 15 cm H₂O. For a normal animal, 15–20 cm H₂O pressure is required for adequate but not full inflation (Hayatdavoudi et al., 1980). The next two pressure volumes (7 and 10 cm H₂O) were used to observe lung impedance at intermediate levels of inflation. The pressure was reduced to 10 cm H₂O and 7 cm H₂O (5 cm H₂O for the pigs) at 2 cm H₂O∕min, and held for 15 min at each pressure level to ensure pressure equilibrium. Measurements were then taken from the inflated lung at 10 and 7 cm H₂O (5 cm H₂O for the pigs). 7 cm H₂O (5 cm H₂O for the pigs) was the lowest pressure that could be maintained without the lung visibly deflating during the measurement procedure.

Data analysis

The acquired echo waveforms were downloaded to a computer for postprocessing. MATLAB^® (The Mathworks Inc., Natick, MA) was used to perform the waveform analysis. The frequency spectrum of each waveform reflected from the lung was calculated by taking its Fourier transform. Each reflection waveform was made up of 2000 points. A Hanning window was constructed based on the width of the pulse reflected from the reference surface. The Hanning window was applied to each pulse reflected from the lung by centering the window at the point in the waveform where the peak had its maximum magnitude. To account for the spectral influence of the Hanning window, the reference pulse was also multiplied by the same Hanning window. A 5×5 mm² section from each lung was scanned at a 100 μm step size, yielding many waveforms per lung examined. The absolute values of the Fourier transforms from the waveforms were taken, and all the Fourier spectra were averaged for each lung to obtain an overall representation of the pressure reflection coefficient from the lung. The exact number of waveforms acquired per inflation level depended on the amount of surface area of the lung that was flat and perpendicular to the transducer axis. Therefore, while the minimum number of waveforms from each animal was greater than 10, the number of waveforms acquired for each animal was different. The impedance was then calculated over a frequency range of 3.5–10 MHz according to Eq. 3, where Z_I(f) represented the acoustic impedance of water at 37 °C [Z_I(f) is the product of the density of water, 998 kg m⁻³, and the speed of sound in water at 37 °C, 1525 m s⁻¹].

RESULTS

Estimates of the pressure reflection coefficient from ex vivo lungs of different species of animals at various ages for four levels of inflation were acquired with the ultrasonic system. The impedance values of the lung for the four levels of inflation were calculated from the pressure reflection coefficients. Because the TLC and functional residual capacity of the lung scale approximately linearly with animal weight across species (Stahl, 1967), estimates of the fraction of air in the lung from previous studies of rabbit lung in terms of TLC versus pressure (cm H₂O) were used to predict the impedance at each pressure level (Gil et al., 1979). Based on the study by Gil et al. (1979), the fraction of air corresponding to 0, 5, 7, 10, and 15 cm H₂O in the lung is 0.39, 0.84, 0.85, 0.86, and 0.89, respectively. Using the two-component model of the lung, this leads to predictions of 0.26, 0.013, 0.011, 0.099, and 0.0062 Mrayl for the acoustic impedance of the lung at the different inflation levels, respectively (O’Brien et al., 2002).

Rats

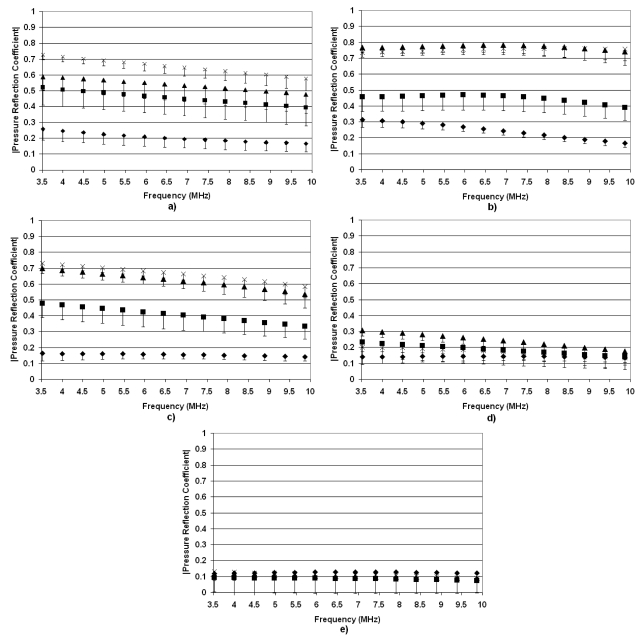
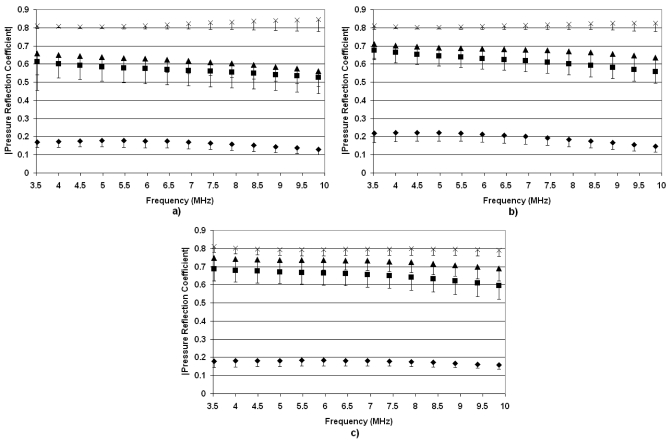
Figure 5 shows the absolute value of pressure reflection coefficients, ∣R(f)∣, from rat lungs at the four levels of inflation as a function of frequency. For the deflated lungs for all ages of rats, ∣R(f)∣ ranged between 0.1 and 0.3 across all frequencies examined, indicating that a large percent of the ultrasonic energy was transmitted into the lung. ∣R(f)∣ at higher levels of inflation suggests an age-dependent effect. ∣R(f)∣ in the inflated lung is greater in the older rats. In the case of the 2-week-old rats, no differences are observed between ∣R(f)∣ at deflation and various levels of inflation. Furthermore, minimal changes in ∣R(f)∣ versus inflation level are observed for the 3-week-old rats. Based on our hypothesis, this suggests that the young rats would have a lower threshold for ultrasound-induced lung damage because no matter the inflation level, a larger percentage of ultrasonic energy would be transmitted into the lung.

Figure 5.

Pressure reflection coefficients vs frequency for deflated rat lungs (◆) and inflated lungs at 7 cm H₂O (◼), 10 cm H₂O (▲), and 15 cm H₂O (×). The measurements were taken from (a) 52-week-old rats, (b) 17-week-old rats, (c) 7-week-old rats, (d) 3-week-old rats, and (e) 2-week-old rats. The error bars represent one standard error.

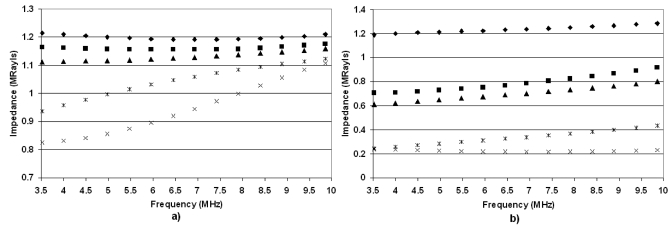
The impedance values for the deflated and fully inflated (15 cm H₂O) rat lungs reveal similar trends (Fig. 6). The impedance values for the deflated lungs range between 0.8 and 1.25 Mrayl across all age ranges. However, in the case of the inflated lungs, the 2- and 3-week-old rats have impedance values larger than 0.7. Note also that the 2-week-old rats have essentially the same impedance values for both inflation levels. The 17- and 52-week-old rats have the lowest impedance values for the deflated and inflated cases. Based on the hypothesis that lung damage is caused by the transfer of ultrasonic energy into the lung, this would suggest that the threshold for lung damage would be lower for less developed (younger) rats. Finally, the predicted impedance values based on extrapolating measurements and estimates from Gil et al. (1979) were consistently smaller than estimates of impedance derived from reflection coefficient measurements from ex vivo lungs at all levels of inflation.

Figure 6.

Estimates of the rat lung impedance vs frequency for (a) deflated lungs and (b) fully inflated lungs from 52-week-old rats (×), 17-week-old rats (*)s, 7-week-old rats (▲), 3-week-old rats (◼), and 2-week-old rats (◆).

Rabbits

Figure 7 shows ∣R(f)∣ versus ultrasonic frequency for the rabbit lungs at different stages of development. Across all ages of rabbits, ∣R(f)∣ is consistent with the level of inflation and ∣R(f)∣ increases with increasing level of inflation. This would suggest that an age-dependent threshold is not observed for the rabbits (at least spanning the ages explored in these experiments). The only biological differences observed between the rabbits and rats were the smaller thickness of the pleural surface for the rats. Therefore, we hypothesize that the thickness of the pleural membrane, which will increase with increasing maturity of the animal, might be responsible for the differences observed between the rats and rabbits. However, at this time the hypothesis has not been tested.

Figure 7.

Pressure reflection coefficients vs frequency for deflated rabbit lungs (◆) and inflated lungs at 7 cm H₂O (◼), 10 cm H₂O (▲), and 15 cm H₂O (×). The measurements were taken from (a) 5-yr-old rabbits, (b) 3-yr-old rabbits, and (c) 12-week-old rabbits. The error bars represent one standard error.

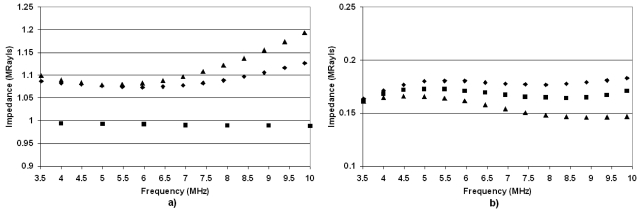
The impedance values (Fig. 8) reveal that for all ages of rabbits, the deflated lungs have impedances typically greater than 1.0 Mrayl and close to that of tissue or water (1.4–1.6 Mrayl). The close impedance match between the deflated lung and tissue suggests that a large percentage of incident ultrasonic energy would be transferred into the lung. The impedance values for the deflated lungs also increase with frequency by as much as 15% from 3.5 to 10 MHz. The impedance values for the fully inflated (15 cm H₂O) lungs range from 0.15 to 0.18 Mrayl, or almost an order of magnitude smaller than the impedance of tissue. The frequency dependence of the inflated rabbit lungs does not reveal a significant increase in impedance values with higher ultrasonic frequency. The large impedance mismatches between the inflated lungs and tissue would suggest little transfer of ultrasonic energy into the lungs. Furthermore, as in the case of the rats, the predicted impedance values based on extrapolating measurements and estimates from Gil et al. (1979) were consistently smaller than estimates of impedance derived from reflection coefficient measurements from ex vivo lungs at all levels of inflation.

Figure 8.

Estimates of the rabbit lung impedance vs frequency for (a) deflated lungs and (b) fully inflated lungs from 5-yr-old rabbits (▲), 3-yr-old rabbits (◼), and 12-week-old rabbits (◆).

Pigs

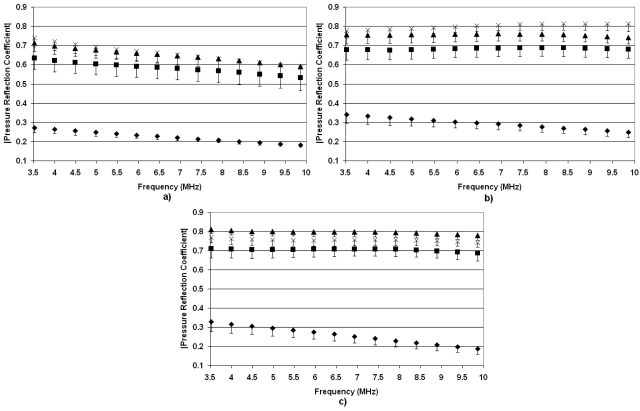
The ∣R(f)∣ versus ultrasonic frequency for the pigs is shown in Fig. 9. Results for the pigs are similar to those of the rabbit in that ∣R(f)∣ is observed to increase with increasing inflation, and similar trends were observed for each age group of pigs examined. Like the rabbits, the largest increase in the pigs ∣R(f)∣ is observed from deflated to just partially inflated (5 cm H₂O) lungs. Similar to the rabbits, the thickness of the pleura for the pigs will be larger than for the rats and may explain the differences observed between the lungs of the rats and the lungs of the pigs and rabbits.

Figure 9.

Pressure reflection coefficients vs frequency for deflated pig lungs (◆) and inflated lungs at 5 cm H₂O (◼), 10 cm H₂O (▲), and 15 cm H₂O (×). The measurements were taken from (a) 7–8-week-old pigs, (b) 4–5-week-old pigs, and (c) 1-week-old pigs. The error bars represent one standard error.

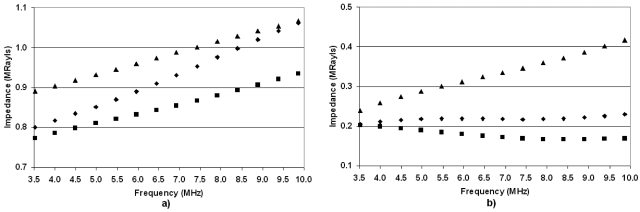
The impedance values for the pig lungs are shown in Fig. 10. Again, the impedance values for all ages in the deflated case are always within 20% of each other. However, compared with the rabbit lung, deflated pig lungs exhibit greater frequency dependence. The impedance values increase by more than 20% from 3.5 to 10 MHz with the pigs, whereas with the rabbits, the increase in impedance values over the same range is at most 15%. The rat impedance values reveal similar trends of increasing impedance with frequency in the deflated lungs for the older rat populations. In the case of the fully inflated (15 cm H₂O) lungs, the impedance values for the pigs have very small slopes except for the oldest pigs, where the impedance value increases by almost 77% from 3.5 to 10 MHz. In terms of lung impedance and age, the impedance is greatest for the oldest pigs, least for the 4–5-week-old pigs, and in between for the youngest pigs. Furthermore, as in the case of the rats and rabbits, the predicted impedance values based on extrapolating measurements and estimates from Gil et al. (1979) were consistently smaller than estimates of impedance derived from reflection coefficient measurements from ex vivo lungs at all levels of inflation.

Figure 10.

Estimates of the pig lung impedance vs frequency for (a) deflated lungs and (b) fully inflated lungs from 7–8-week-old pigs (▲), 4–5-week-old pigs (◼), and 1-week-old pigs (▲).

DISCUSSION

In most cases examined, ∣R(f)∣ increased with increasing level of inflation. The increase in ∣R(f)∣ corresponded to a decrease in the impedance of the lung with increasing inflation level. These results corroborate earlier results from a study on rat lungs alone (Oelze et al., 2003). The results further support the acoustic model of the lung as a two-component structure whose impedance is determined by a combination of the bulk properties of air and tissue (O’Brien et al., 2002). The higher the level of inflation of the lung, the more the lung impedance approaches that of air and subsequently the smaller the fraction of ultrasonic energy transmitted into the lung.

However, while the two-component model of the lung predicted an increase in the acoustic impedance with decreasing inflation levels, the actual predicted values of acoustic impedance were much smaller than impedance values estimated from the reflection coefficient measurements. The largest impedance value predicted by the two-component model when the fraction of air is zero is 0.77 Mrayl. Compared to the acoustic impedance values estimated for the deflated lungs, whose fraction of air is estimated to be approximately 0.39, all estimates were above 0.77 Mrayl (with the exception of the 4–5-week old pigs), while the predicted value from the model was 0.26 Mrayl. This discrepancy between predicted acoustic impedance values and acoustic impedance values estimated for the deflated and inflated lungs suggests that the two-component model of the lung, while conceptually sound, needs improvement to better predict the acoustic impedance versus the level of lung inflation.

The only exceptions to the observations that the acoustic impedance values decreased with increasing level of inflation were found in the measurements from the 2- and 3-week-old rats. The impedance values did not appear to decrease as much with increasing level of inflation, suggesting that with 2- and 3-week-old rats the threshold of lung damage could be less than for 7-, 17-, and 52-week-old rats. The thickness of the pleura was smallest for the youngest rats, which has been hypothesized to play a role in the threshold value for lung damage. Therefore, the difference in the pleural thickness with the age of rats may play a role in the age dependence observed in the rats.

One way to test this hypothesis is to examine the frequency-dependent impedance from the lung surface. The frequency dependence of the impedance may yield some clues to the underlying mechanism of the age-dependent effect. In the case of the deflated lungs, the impedance values were typically observed to increase with increasing frequency, the exception being the youngest rats. One hypothesis explaining this effect is the presence of the pleural surface surrounding the freshly excised lungs, a mechanism similar to that used to explain the frequency dependence of ultrasonic thresholds in a mammalian brain (Johnston and Dunn, 1976). In rats and rabbits, the thickness of the pleura is 8–25 μm, and for pigs and humans this thickness is 100–150 μm (AIUM, 2000; Tyler and Julian, 1992). The thickness of the pleura will increase with age from young to adult animals. Mice, rats, rabbits, cats, dogs, and monkeys, which are members of the thin group, have scant but varying quantities of collagen fibers within the pleura. Sheep, pigs, humans, cattle, horses, and other large animals, which are members of the thick group, have abundant but varying quantities of collagen fibers within the pleura (AIUM, 2000; Tyler and Julian, 1992). A thin layer surrounding the lung will act as a filter for ultrasonic energy, allowing ultrasound at certain frequencies to pass through more efficiently than other frequencies. A simple equation for the pressure reflection coefficient of ultrasound through a thin layer is given by (Kinsler et al., 2000)

$$R\left(f\right)=\frac{(1-Z_1∕Z_3)\cos k_{2}L+j(Z_2∕Z_3-Z_1∕Z_2)\sin k_{2}L}{(1+Z_1∕Z_3)\cos k_{2}L+j(Z_2∕Z_3+Z_1∕Z_2)\sin k_{2}L},$$ (4)

where k₂ refers to the acoustic wave number in the layer, L is the layer thickness, and the subscripts 1, 2, and 3 refer to the front medium, layer, and back medium, respectively. From Eq. 4, the frequency-dependent impedance can be calculated from Eq. 3.

Another hypothesis that might explain these differences is roughness of the pleural surface. Roughness will cause some of the ultrasonic energy incident on the surface to scatter in many directions. Therefore, the backscattered energy will be less if the surface was smooth (Sagar et al., 1978). In addition, the backscatter from a rough surface will be frequency dependent (Oelze et al., 2001). Future studies will be required to thoroughly test both hypotheses.

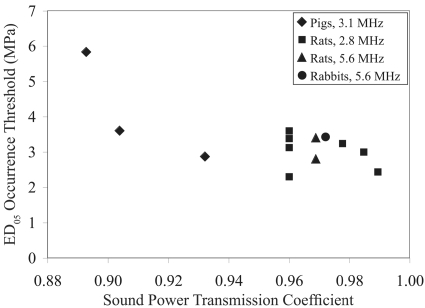
Finally, literature-based thresholds of ultrasound-induced lung damage were related to the impedance values determined herein from the different species of animals examined (Table 2). Assuming that the surrounding material (water or tissue) had an impedance of 1.5 Mrayl, the normal-incidence sound power transmission coefficient (SPTC) was calculated (Kinsler et al., 2000) for each lung (using the mean lung impedance values). Furthermore, the SPTC was calculated for each of the animals for which ED₀₅ occurrence thresholds were assessed. Figure 11 shows the ED₀₅ occurrence threshold versus SPTC. For the deflated lung, there is a general trend whereby as the SPTC increases, the ED₀₅ threshold decreases. For the fully inflated (plot not shown), no clear trend was observed. These observations support the view that the ultrasonic energy transmitted into the lung (deflated lung received the most ultrasound energy) determines the lung hemorrhage threshold.

Table 2.

Comparison between the sound power transmission coefficient (SPTC) calculated from the deflated (0 cm H₂O) lung impedance values (Z_def) determined herein at the indicated frequency f using an incident (water) impedance value of 1.5 Mrayl and the comparable literature-based ultrasound-induced lung damage ED₀₅ occurrence threshold (ED_{05 occ}). Selected rat Z_def values were interpolated (Int) because the literature-based rat ages were slightly different from those evaluated herein. Also, the Z_def values at frequencies less than 3.5 MHz were extrapolated to either 2.8 or 3.1 MHz.

From impedance study			From threshold studies
	Zdef (Mrayl)	SPTC	⟨age⟩	ED05occ(MPa)	f(MHz)	Reference
1 week pigs	0.79	0.904	5 d	3.60	3.1	O’Brien et al., 2003b
4–5 week pigs	0.76	0.893	39 d	5.83	3.1	O’Brien et al., 2003b
7–8 week Pigs	0.88	0.932	58 d	2.87	3.1	O’Brien et al., 2003b
2 week rats	1.22	0.989	12–14 d	2.44	2.8	O’Brien et al., 2008
2 week rats	1.20				5.6
3 week rats	1.17	0.985	22–24 d	3.00	2.8	O’Brien et al., 2008
3 week rats	1.16				5.6
7 week rats	1.11	0.978	53–62 d	3.24	2.8	O’Brien et al., 2008
7 week rats	1.12				5.6
Int (rats)	1.00	0.960	72 d	3.38	2.8	O’Brien et al., 2008
Int (rats)	1.00	0.960	10–11 week	2.30	2.8	Zachary et al., 2001a, 2001b
Int (rats)	1.05	0.969	10–11 week	2.80	5.6	Zachary et al., 2001a, 2001b
Int (rats)	1.00	0.960	10–11 week	3.60	2.8	O’Brien et al., 2001a, 2001b
Int (rats)	1.05	0.969	10–11 week	3.40	5.6	O’Brien et al., 2001a, 2001b
Int (rats)	1.00	0.960	10–11 week	3.13	2.8	O’Brien et al., 2003a
17 week rats	0.81				2.8
17 week Rats	0.88				5.6
52 week rats	0.91				2.8
52 week rats	1.02				5.6
12 week rabbits	1.07	0.972	76 d	3.43	5.6	O’Brien et al., 2006
3 year rabbits	1.00				5.6
5 year rabbits	1.08				5.6

Figure 11.

ED₀₅ occurrence threshold vs SPTC under deflated lung conditions.

Furthermore, as noted earlier, for the pigs the impedance was greatest for the oldest pigs, least for the 4–5-week-old pigs, and in between for the youngest (neonate) pigs. This suggests that the oldest pigs would have the lowest threshold for lung damage (i.e., lung damage occurs at lower pressure values), and the 4–5-week-old pigs would have the highest threshold for lung damage. A comparison of these impedance values with ultrasound-induced lung damage thresholds in pigs reveals the same trend (O’Brien et al., 2003b). The oldest pigs had the lowest threshold for damage (2.87±0.29 MPa), followed by the neonate pigs (3.60±0.44 MPa), followed lastly by the 4–5-week old pigs (5.83±0.52 MPa).

CONCLUSION

The pressure reflection coefficient was determined, and the impedance values versus frequency were estimated from freshly excised lungs at different levels of inflation from rats, rabbits, and pigs of various ages. The data revealed consistent trends whereby lungs that were deflated had smaller pressure reflection coefficient values than inflated lungs. The only exceptions were with the rats, where rats younger than 3 weeks old were observed to have minimal increases in pressure reflection coefficients versus level of inflation. These observed trends corresponded to earlier experiments that revealed that ultrasound-induced lung damage was related to the level of inflation; i.e., deflated lungs were more likely to have damage from ultrasound. The impedance values of deflated lungs across all species and ages were found to be much closer to tissue impedance values than inflated lungs. This supported the hypothesis that ultrasound-induced lung damage was related to the transfer of ultrasonic energy into the lung.

A few mechanisms were proposed to explain the frequency dependence of the pressure reflection coefficients and the impedance values. These mechanisms were the modeling of the lung with a thin layer, i.e., the visceral pleura, the roughness of the lung surface, and a combination of both. Future studies will be required to determine the extent to which the proposed mechanisms contribute to the frequency dependence of the estimated pressure reflection coefficients and impedance values.