Acoustic characterization of high intensity focused ultrasound fields: A combined measurement and modeling approach

Abstract

Acoustic characterization of high intensity focused ultrasound (HIFU) fields is important both for the accurate prediction of ultrasound induced bioeffects in tissues and for the development of regulatory standards for clinical HIFU devices. In this paper, a method to determine HIFU field parameters at and around the focus is proposed. Nonlinear pressure waveforms were measured and modeled in water and in a tissue-mimicking gel phantom for a 2 MHz transducer with an aperture and focal length of 4.4 cm. Measurements were performed with a fiber optic probe hydrophone at intensity levels up to 24 000 W∕cm². The inputs to a Khokhlov–Zabolotskaya–Kuznetsov-type numerical model were determined based on experimental low amplitude beam plots. Strongly asymmetric waveforms with peak positive pressures up to 80 MPa and peak negative pressures up to 15 MPa were obtained both numerically and experimentally. Numerical simulations and experimental measurements agreed well; however, when steep shocks were present in the waveform at focal intensity levels higher than 6000 W∕cm², lower values of the peak positive pressure were observed in the measured waveforms. This underrepresentation was attributed mainly to the limited hydrophone bandwidth of 100 MHz. It is shown that a combination of measurements and modeling is necessary to enable accurate characterization of HIFU fields.

INTRODUCTION

High intensity focused ultrasound (HIFU) is an evolving medical technology for noninvasive surgery and cancer therapy. HIFU devices are currently under investigation for use as surgical tools, for example, to thermally ablate solid tumors of the prostate,1 liver,2 breast,3 kidney,4 and brain,5 as well as for cauterizing internal bleeding.6

In HIFU medical treatments, ultrasound (US) energy is focused into a small volume to heat and destroy the targeted tissue while ideally not damaging tissue outside the focal region. The acoustic characterization of HIFU fields is important both for the accurate prediction of US induced bioeffects in tissues and for the development of standards to ensure the safety and efficacy of treatments. Modern HIFU devices operate at very high focal intensity levels from 1000 W∕cm² to greater than 25 000 W∕cm²in situ and are highly focused to a millimeter or even a submillimeter sized focal spot.2, 7 The high pressures and tight focusing of HIFU devices make accurate acoustic field measurements challenging.

For medical work, the characterization of acoustic output is often performed in two parts. First, measurements are performed in water. Next, a method is used to relate the measurements in water to what is expected in tissue. Although this approach is widely used in medical US, the challenge of directly measuring and modeling HIFU fields is worth revisiting since experimental tools and numerical models may improve over time, and no standard method, such as that for diagnostic US,8 has yet been agreed upon for HIFU devices.9

The most common parameter to characterize the acoustic output of a HIFU device is the spatially averaged intensity (I_SAL).10 The calculation of I_SAL for a given source is achieved through measurement of the acoustic power output of the device and the focal cross-sectional area of the HIFU beam. The acoustic power output is measured using a radiation force balance. The focal cross-sectional area is determined by scanning a hydrophone across the focal plane of the source. The spatially averaged intensity is then calculated by dividing the acoustic power that passes within the −6 dB pressure contour11 by the area of the contour. Acoustic propagation is assumed to be linear in that the frequency content of the pressure waveform and the corresponding beam width are assumed to be independent of the source power. The peak positive and peak negative pressures for sinusoidal waveforms are therefore equal and only one needs to be measured. The low-power measurements of I_SAL are then linearly extrapolated to higher output levels of the HIFU device. That is, the focal pressure amplitude is assumed to scale linearly with applied source voltage so that the focal intensity (I_SAL) increases as a square of the voltage.

Once the output intensity is determined in water, it can be used to estimate the focal intensity in tissue. This step is achieved by multiplying by a compensation factor depending only on the propagation path and linear attenuation coefficient of tissue at the operating frequency of the source. This approach is useful for comparing exposures at relatively low intensities as it provides an estimate of the in situ focal intensity. Tissue heating, the common bioeffect of interest, can also be estimated from the product of the tissue absorption coefficient and I_SAL. However, the acoustic fields of most HIFU clinical devices are nonlinear; therefore, errors are introduced at every characterization step where linear acoustic propagation is assumed.12, 13

At currently reported HIFU intensity levels, the combined effects of nonlinear propagation and diffraction in water or in tissue lead to generation of higher harmonics, narrowing of harmonic beam widths, asymmetric distortion of pressure waveforms, and formation of steep shock fronts.14, 15 Nonlinear broadening of the spectrum to higher frequencies and the formation of shocks can significantly increase the amount of energy converted to heat, as absorption in tissue increases with frequency.16, 17 Since nonlinear effects accumulate with propagation distance and depend on the initial pressure amplitude, waveforms have different shape and spectral content at different locations of a HIFU beam and at different source power levels. Acoustic characterization of a nonlinear HIFU field thus requires measurements not only of the pressure amplitude or intensity but of the entire acoustic waveform at each source power and location. At a minimum, the focal waveform, which contains the broadest spectral content, is necessary to obtain the spatial peak heating rate under nonlinear propagation conditions. Because nonlinear effects accumulate differently in water and in tissue, the focal waveform measured in water cannot necessarily be directly translated to tissue.

The characterization of medical acoustic devices that operate at high output levels has been a research topic and an issue of practical concern for several decades.18 The importance of nonlinear effects has been considered and addressed even at diagnostic levels of US.13, 19 In lithotripsy and HIFU, these effects are critical as acoustic pressures of up to 100 MPa or higher can be reached; such pressures are two or even three orders higher in magnitude than diagnostic US. Direct measurements of pressure waveforms in HIFU or lithotripsy fields require a hydrophone that is robust to mechanical damage from cavitation and that has a large bandwidth to capture sharp shock fronts than can develop at the focus. Waveform measurements in HIFU are even more difficult than in lithotripsy because of the explicit need to accurately measure peak amplitudes of shock waves within a relatively small focal region. Accurate measurement of peak pressures is especially relevant in HIFU because the prediction of heating rates is sensitive to shock amplitudes. When shocks are present, the amount of heat deposition is determined by the cube of the shock amplitude.17 This imposes additional requirements on hydrophone bandwidth. In addition, focal beam dimensions of clinical HIFU devices are usually much smaller than in lithotripsy. The typical size of the HIFU focal zone is about an order of magnitude smaller in both the transverse and axial directions. As such, a hydrophone with a very small active diameter is required to accurately measure HIFU fields.

As mentioned, direct measurements of high amplitude fields can be performed in water. Methods have been described to measure nonlinear fields of diagnostic US transducers13, 19 and lithotripters.18 Recently, shocked waveforms from a HIFU source were measured using a fiber optic probe hydrophone (FOPH).20 Such hydrophones claim advantages of self-calibration, small size, and broad bandwidth relative to polyvinylidene fluoride (PVDF) hydrophones.20, 21

Alternatively, numerical modeling has been used to predict high amplitude acoustic fields from medical devices. One advantage of modeling is that it can be used to determine the acoustic field in both water and tissue. Numerical algorithms, most commonly based on the nonlinear parabolic Khokhlov–Zabolotskaya–Kuznetsov (KZK) equation, have been developed and applied to the nonlinear fields of lithotripters,22 unfocused ultrasonic piston sources,23, 24 diagnostic US transducers operating in tissue harmonic imaging mode,25, 26 focused US sources,27 and HIFU sources.17, 28, 29 For highly focused sources, the Rayleigh integral can be used to capture diffraction effects more accurately in the model.30, 31 More comprehensive models based on full-wave nonlinear equations have also been developed, but they are much more computationally intensive.32

In this study, a new method to characterize HIFU field parameters at and around the focus is proposed and examined in water and in a tissue-mimicking gel phantom. First, at low source excitation, the pressure amplitude along and across the HIFU axis beyond the −6 dB points is measured using a hydrophone with a spot size smaller than the HIFU wavelength. Second, the voltage amplitude applied to the source and focal pressure is measured. Third, the source is modeled as a curved uniform piston using nominal measures of curvature and aperture and the axial and transverse pressure plots are calculated in the linear regime and compared with the measurements. The exact source geometry to be used in the model is determined by adjusting the curvature and aperture to best fit the dimensions of the measured focal region. Fourth, the source pressure amplitude, p₀, is determined by matching the measured and calculated focal pressures. In this last step, the source voltage measured at any excitation can be converted to a source pressure, p₀, used as an input to the model. With these steps completed, the model can then be used to calculate the nonlinear fields in water or in tissue. Here, the simulations are validated against experimental measurements in water and in a tissue-mimicking phantom. Methods for further refining the techniques and for broadening them to other source geometries are also discussed.

The clinically relevant goal of this work is to demonstrate methods for accurately determining HIFU pressure waveforms. This paper is timely as new clinical devices enter the market and many of them operate at amplitudes much higher than used in previous research. The problems of measuring and modeling nonlinear shocked HIFU waveforms as well as potential reasons for discrepancies observed between measured and modeled results are examined and discussed. While direct low amplitude measurements of a HIFU field in water are necessary to characterize the spatial pattern of the field and to establish precise boundary conditions for the model, simulations provide more accurate results than measurements at high source amplitude levels.

MATERIALS AND METHODS

A 2 MHz single element HIFU transducer with a diameter and focal length of 44 mm was used in measurements and calculations and is representative of many HIFU sources. Intensity levels in situ reached 24 000 W∕cm², a level used by some clinical devices.7 Calibration measurements and modeling were performed in water and in a transparent tissue-mimicking gel phantom. The gel phantom consisted of polyacrylamide and a 7% concentration of bovine serum albumen (BSA) and has been used in several studies as a test phantom for HIFU dosimetry studies.28, 33, 34, 35 While the acoustic properties of the phantom material such as sound speed and density are similar to tissue, the absorption coefficient is about three times lower than in tissue. The lower absorption leads to more pronounced nonlinear effects than might be observed in tissue at similar source power levels.

Numerical model

Numerical modeling of experimental conditions was performed using a KZK-type nonlinear parabolic equation, generalized for the frequency-dependent absorption properties of the propagation medium:

$$\frac{\partial }{\partial \tau }[\frac{\partial p}{\partial z}-\frac{\beta }{{\rho }_0{c}_0^3}p\frac{\partial p}{\partial \tau }-L_{\mathrm{abs}}\left(p\right)]=\frac{c_0}{2}{\Delta }_{\perp }p,$$ (1)

where p is the acoustic pressure, z is the propagation coordinate along the axis of the beam, τ=t−z∕c₀ is the retarded time, c₀ is the ambient sound speed, ρ₀ is the ambient density of the medium, β is the coefficient of nonlinearity, Δ_⊥ is the Laplacian with respect to the transverse coordinate r, and L_abs is the linear operator that accounts for the absorption and dispersion of the medium.17, 28

For simulations in water, thermoviscous absorption was included as

$$L_{\mathrm{abs}}=\frac{b}{2{\rho }_0{c}_0^3}\frac{{\partial }^{2}p}{\partial {\tau }^2},$$ (2)

where b is the dissipative parameter of water. For simulations in gel, the propagation path for US comprised a two-layer medium consisting of water followed by tissue-mimicking gel phantom. The frequency-dependent absorption of US in the gel was included in the model according to a nearly linear power law combined with a weak thermoviscous absorption, as in water:

$$\alpha \left(f\right)=2{\pi }^2{f}^{2}b∕{\rho }_0{c}_0^3+{\alpha }_0{(f∕f_0)}^{\eta }.$$ (3)

Here α₀ is the absorption parameter of the gel at the fundamental frequency, f₀, and variation of the sound speed with frequency was calculated for the power law term (η) in Eq. 3 using the local dispersion relations.36, 37

The boundary condition for Eq. 1 was set by translating the pressure amplitude, p₀, uniformly distributed over the curved surface of the source to the plane z=0. The translation of the amplitude was performed using a geometrical acoustics approximation following the spherical convergence of the field. The focusing phase shift along the radial coordinate was introduced in the parabolic approximation as

$$p(z=0,r,\tau )=\frac{p_0}{\sqrt{1+r_0^2∕F^2}}\sin \left(2\pi f_0(\tau +r^2∕2c_{0}F)\right),$$ (4)

if $r<r_0∕\sqrt{(1-r_0^2∕F^2)}$ and p(z=0,r,τ)=0 elsewhere. Here, 2r₀ is the aperture of the source and F is its radius of curvature. To account for nonuniform vibration of the surface of the transducer,38 additional simulations were performed with more accurate boundary conditions that were reconstructed using an experimental acoustic holography method.39

Equation 1 was solved numerically in the frequency domain using a previously developed finite difference algorithm.17, 24 The acoustic pressure waveform was represented as a Fourier series expansion as

$$p(z,r,\tau )=\sum _{n=1}^{\infty }{c}_n(z,r)e^{-in2\pi f_0\tau },$$ (5)

where c_n is the complex amplitude of the n th harmonic. A set of nonlinear coupled differential equations for the amplitudes of the harmonics was derived and integrated numerically using the method of fractional steps and an operator-splitting procedure. The simulations were performed assuming radial symmetry of the HIFU source.

To characterize the HIFU output level in the focal zone in water or in gel, two values of the spatial peak intensity were introduced. These values will be referred to in the paper as focal intensities. The first value, I_N, was calculated from the numerically modeled nonlinear waveform as a combination of the focal intensities of all harmonic components:

$$I_N=f_0{\int }_0^{1∕f_0}\frac{p^2}{{\rho }_0{c}_0}d\tau =\frac{2}{{\rho }_0{c}_0}\sum _{n=1}^{\infty }{\mid c_n\mid }^2.$$ (6)

The second value, I_L, was calculated based on the results of the linear acoustic propagation modeling as

$$I_L=p_F^2∕2{\rho }_0{c}_0,$$ (7)

where p_F is the focal (i.e., spatial peak) pressure amplitude in situ. The linear focusing gain of the source was defined as a ratio of the focal and source pressure amplitude obtained from linear modeling in water:

$$G=p_F∕p_0.$$ (8)

The values of the physical constants used for the modeling in water were ρ₀=1000 kg∕m³, c₀=1486 m∕s, β=3.5, and b=4.33×10⁻³ kg s⁻¹ m⁻¹. In the gel phantom, the constants were ρ₀=1044 kg∕m³, c₀=1544 m∕s, β=4, α₀=1.6 m⁻¹ at 1 MHz, η=1, and L=0.033 mm.33

The simulations were performed for the following parameters of the numerical scheme: Δz∕z=2.5×10⁻⁵ and Δr∕r₀=0.5×10⁻³ were the steps in the axial and transverse directions, respectively, z_max=2F and r_max=1.25r₀ were the spatial windows, and N_max=1000 was the maximum number of harmonics retained in the code. To suppress reflections from the radial boundary of the grid, an artificial absorption was introduced for the last 100 radial grid points. Within this layer, the absorption coefficient increased quadratically with the radial coordinate from zero to 100 Np∕cm and was equal for all harmonics included in calculations.

Experimental arrangement

A diagram of the experimental arrangement used to perform the high-power measurements is shown in Fig. 1. The US source was a single element spherically focused piezoceramic crystal (PZ 26, Ferroperm Piezoceramics, Denmark) with a resonant frequency of 2.158 MHZ that was air backed and mounted in a custom-designed brass housing. The transducer was driven by a function generator (Agilent 33250A, Agilent, Palo Alto, CA) and a linear rf amplifier (ENI A-300, ENI, Rochester, NY). A high-voltage probe was attached in parallel with the transducer for monitoring the driving voltage amplitude to the source. The transducer was operated in a pulse mode with a 30-cycle sine-wave burst. Waveforms from the hydrophones and the driving voltage were recorded using a digital oscilloscope (500 megasamples∕s, model LT344, Lecroy, Chestnut Ridge, NY). Waveform averaging was performed of multiple tone bursts to increase the signal-to-noise ratio. The US source was attached to a three-axis computer-controlled positioning system (Velmex Inc., Bloomfield, NY) for alignment with the hydrophone. A custom LABVIEW (National Instruments, Austin, TX) computer program was used to control the function generator, oscilloscope, and the positioning system during measurements. All of the experiments were performed in a large water tank at room temperature (20 °C). The water was purified using a reverse osmosis system and was degassed prior to measurements using a pinhole degassing system to limit cavitation.40 The dissolved oxygen content of the water was measured using an oxygen meter (WTW Oxi 330i, Weilheim, Germany) and was less than 25% of saturation during all experiments.

Figure 1.

A diagram of the experimental arrangement used for measurements of pressure waveforms.

Calibration measurements in water

Experiments performed to establish the boundary conditions for the numerical model involved measurements in water with two different hydrophones. First, a SEA needle hydrophone [uncalibrated, model GL-150-1A with 150 μm active diameter, Specialty Engineering Associates (SEA), Soquel, CA] was used for measuring axial and transverse profiles of the source under linear propagation conditions. Next, a calibrated NTR PVDF membrane hydrophone (0.168 V∕MPa sensitivity, model MHA-200 with 200 μm active diameter, NTR Systems, Seattle, WA) was used as a reference hydrophone to measure focal waveforms to establish the source pressure amplitude, p₀, for a given source driving voltage. The FOPHs were not used for these measurements because their sensitivity is too low. Focal waveforms were then measured at moderate source powers using both the NTR and the FOPH to ensure agreement between the calibrated hydrophones. Two FOPHs (FOPH 500 and FOPH 2000 with 100 μm active diameters, RP Acoustics, Germany) were used for pressure measurements at the higher levels of operation of the HIFU source. The FOPH 500 and 2000 are similar in design but differ in the stated bandwidth of the photodiode in each unit—30 MHz for the FOPH 500 and 100 MHz for the FOPH 2000. Pressure waveforms were measured with the fiber parallel to and the sensitive cleaved face of the fiber perpendicular to the HIFU axis. Measured waveforms were deconvolved using the impulse responses of the hydrophones provided by the manufacturers. Calibration of FOPH signals from voltage to acoustic pressure in water was performed using the manufacturer’s calibration equations and protocols.41

Waveform measurements in gel phantom

Although fiber optic hydrophones have been employed in various calibration measurements of high-power lithotripsy and HIFU fields in water,20, 41 no results have been reported on the application of such techniques to measurements in tissues or phantoms. In this study, the FOPH was used to measure pressure waveforms at the focus of the HIFU source in a transparent tissue-mimicking gel phantom. To perform measurements in the phantom, the fiber tip was cast in a large rectangular mold that was designed for HIFU dosimetry experiments with tissue phantoms. The mold’s dimensions were 6 cm in the axial direction, 5 cm in the transverse direction, and 13 cm in the other transverse direction. Preparation of the gel phantom comprised three steps: degassing of the unpolymerized liquid mixture, positioning of the FOPH tip in the liquid, and lastly addition of a polymerization agent. For these experiments, the propagation path from the transducer to the focus included water, then 33 mm of the phantom.

The FOPH signal measured in the gel phantom was converted from voltage to acoustic pressure based on the method described by the manufacturer for measurements in water. However, the method could not be directly applied to measurements in gel. Therefore, we discuss here the main equations and explain how they can be modified for using the FOPH in gel phantom.

The output of the FOPH photodiode is a voltage that is proportional to the reflection coefficient of laser intensity, R, at the FOPH tip. If the tip is embedded in some medium, the calibration of the measured signal is performed based on three equations.41 The first equation is the relation between the reflection coefficient, R, and the optical refractive index of the medium:

$$R={(n-n_g)}^2∕{(n+n_g)}^2.$$ (9)

Here n_g is the refractive index of the glass fiber and n is the refractive index of the surrounding medium. The acoustic measurements rely on the fact that n is a function of the medium density, ρ, which changes with acoustic pressure: ρ=ρ(p).

The second equation is the relation for refractive index as a function of density, which can be obtained based on the Gladstone–Dale model:

$$\frac{n\left(\rho \right)-1}{\rho }=\mathrm{const}=\frac{n_0-1}{{\rho }_0}.$$ (10)

The static refractive index n₀=n(ρ₀) of the gel phantom in Eq. 10 was calculated from Eq. 9 by comparing dc voltage output levels of the photodiode with the FOPH tip embedded in the gel phantom or placed in water, which has a known refractive index of n₀=1.329 at 20 °C. Using this method, the refractive index of the gel was measured as n₀=1.357.

The third equation used for calibration of the hydrophone is the relation between the change of the density and acoustic pressure ρ=ρ(p). It can be used in the form of the Tait equation (P+Q)∕ρ^γ=const, where P is the sum of the acoustic and ambient pressure and Q and γ are constants. The manufacturer used the Tait equation for water measurements with parameters Q=295.5 MPa and γ=7.44.41 However, the values of Q and γ are not available for the gel. Moreover, the Tait parameters (Q,γ) for water were originally obtained by fitting experimental data for which pressure varied isothermally up to 600 MPa using pressure steps of 50 MPa.42, 43 For the pressure range less than 100 MPa that typifies HIFU and lithotripsy, the inaccuracy of this approach is obvious from the fact that the Tait equation gives the wrong value of the nonlinear parameter of water β=(γ+1)∕2≈4.2 at 20 °C whereas acoustic measurements give β≈3.5.14

The relation ρ=ρ(p) in the gel was obtained from the expansion used in nonlinear acoustics to second order:14

$$\rho ={\rho }_0+\left(\frac{1}{c_0^2}\right)p-\left(\frac{\beta -1}{{\rho }_0{c}_0^4}\right)p^2+\cdots .$$ (11)

The neglected terms in Eq. 11 depend on the acoustic pressure to a power greater than 2 and on entropy changes, which are insignificant for pressure changes of less than 100 MPa, as considered in this paper. The necessary parameters of the medium (ρ₀,c₀,β) in Eq. 11 are known for both water and gel.14, 33

The combination of Eqs. 9, 10, 11 is used here to determine the change of the refractive index with the acoustic pressure in the gel phantom. For measurements in water, calibrations using both the Tait equation and Eq. 11 were compared. At the highest output level (p₀=0.57 MPa), peak pressures of 61.8 and 60.4 MPa were obtained with the Tait equation and Eq. 11, respectively. The small discrepancy of about 2% validates the calibration approach for the gel phantom using Eq. 11. For measurements in water, calibrations were performed with the Tait equation.

The calibration described above is applicable only to low frequency measurements when the fiber diameter is much smaller than the acoustic wavelength. At higher frequencies, the signal is distorted because of diffraction of the acoustic wave at the fiber tip.44 Additional damping of high frequencies is introduced by the FOPH electronics. To compensate for these effects, a deconvolution procedure must be applied using the frequency response of the hydrophone. For measurements in water, this response was provided by the manufacturer. For measurements in gel, the response was assumed to be the same because the acoustic properties of the gel and water (provided in Sec. 2) are very close and therefore diffraction effects at the fiber tip should be similar.

RESULTS

Low amplitude calibration of the HIFU source in water

The radius of curvature and diameter of the transducer were nominally stated by the manufacturer as 44.5 mm and 44.45 mm, respectively. However, both the transducer housing and surface waves might limit and distort the vibration of the source. Therefore, to model the source as a uniform piston, it was necessary to obtain the effective operational aperture and radius of curvature of the source. These parameters were determined by measuring pressure distributions along the axis of the HIFU beam and transverse to the axis in the focal plane. Measurements were acquired with the SEA hydrophone under low amplitude linear propagation conditions. The acoustic axis of the transducer relative to the mechanical axis of the positioning system was determined using methods described by Cathignol et al.45 to ensure that the axial scan corresponded to the true axial field distribution. Measured distributions were compared to results of simulations based on a linearization of Eq. 1. Simulations were performed for various values of the source aperture and radius of curvature to obtain the “best fit” with hydrophone measurements in the focal zone. The effective aperture of the transducer, 2r₀, and radius of curvature, F, were found to be 40.0 mm and 44.4 mm, respectively. A comparison of measurements and simulation results for the one dimensional axial and transverse focal field is shown in Fig. 2. In addition, pressure distributions calculated using analytic O’Neil solutions for the linear focused field11 (with 2r₀=42 mm and F=44.4 mm) are also shown in Fig. 2. The results of both models, calculated with the best fit aperture and radius of curvature, are in good agreement with the experimental data within the focal region of the pressure field of the HIFU transducer. These plots demonstrate that simplified models of uniformly vibrating focused transducers can be applied to model the focal zone of a single element HIFU source. However, discrepancies between simulations and measurements in the axial prefocal distributions were observed; therefore, more precise boundary conditions should be employed in the modeling to capture the nearfield of a real transducer with better accuracy. The location of the spatial pressure peak pressures determined by both modeling and measurements essentially coincided with the geometric focus of the transducer. Consequently, further measurements and calculations of the focal waveforms were performed at the distance z=F from the source.

Figure 2.

Comparison of axial and focal scans of the low amplitude (“linear”) pressure field measured in water by the SEA hydrophone and calculated with the linearized KZK equation, along with the O’Neil analytic solution (Ref. 11). The beam plots were used to determine the radius of curvature and aperture of the source input to the KZK model.

After establishing the effective radius of curvature and aperture of the source, the relationship between the voltage applied to the source and the source pressure amplitude was determined. First, a focal maximum pressure (spatial peak) of 0.47 MPa was measured using the NTR hydrophone at a low driving voltage for linear propagation conditions. The hydrophone was positioned at the geometric focus of the source (44.4 mm) using time-of-flight measurements. The linear focusing gain of the source as defined by Eq. 8 was determined from the linear modeling results and was found to be G=48. Hence, the source pressure amplitude in the model that corresponds to a focal peak pressure of 0.47 MPa can be calculated as p₀=p_F∕G=0.0097 MPa. As calculated from Eqs. 6, 7, a peak focal pressure of 0.47 MPa corresponds to focal intensities of I_L=I_N=7 W∕cm². For other output levels, the source pressure amplitude, p₀, was assumed to be linearly proportional to the driving voltage to the source.23

To compare calibration of the NTR and FOPH 2000 hydrophones, further measurements of focal waveforms were performed with both hydrophones at a higher source level, p₀=0.1 MPa (I_L=700 W∕cm², I_N=720 W∕cm²). Figure 3 shows the focal waveforms obtained with the NTR and FOPH 2000 hydrophones as well as with the KZK nonlinear model. At this output level, the waveforms are slightly distorted due to nonlinear propagation. All three waveforms show very good agreement with a peak positive pressure of 6 MPa and a peak negative pressure of −4 MPa. This comparison demonstrates that under conditions of nonlinear propagation, the numerical modeling agrees with experimental measurements, while the FOPH calibration is accurate in comparison with a reference hydrophone.

Figure 3.

Comparison of focal waveforms simulated with the KZK model and measured with the FOPH 2000 and NTR hydrophones in water for a source pressure amplitude of p₀=0.1 MPa (I_L=700 W∕cm², I_N=720 W∕cm²). Under slightly nonlinear propagation conditions, the focal pressure level was sufficiently high to be measured with two calibrated hydrophones.

High amplitude calibration of the HIFU source in water and gel phantom

At pressures above those described above, waveforms were measured with the FOPH 2000 and modeled in both water and the gel phantom. Measurements and simulations included source pressure levels up to p₀=0.57 MPa.

Water measurements and modeling

Figure 4 shows the focal waveforms and corresponding envelopes of the spectra measured and modeled for p₀=0.29 MPa (I_L=6500 W∕cm², I_N=8200 W∕cm²), p₀=0.39 MPa (I_L=11 000 W∕cm², I_N=16 000 W∕cm²), and p₀=0.57 MPa (I_L=24 000 W∕cm², I_N=29 000 W∕cm²). At an initial pressure amplitude of p₀=0.29 MPa, the experimental and simulated waveforms are noticeably distorted with a measured peak positive pressure of 35 MPa and a peak negative pressure of −10 MPa and show excellent agreement. At higher-power levels, the waveforms also agree well, particularly in the smooth rarefaction part of the waveform and corresponding peak negative pressure values. However, some discrepancy between the measurement and modeling is observed within the sharp positive part of the waveform. The peak positive pressure obtained with modeling is consistently higher than in the measured waveform. For p₀=0.39 MPa, the peak positive pressure modeled is 63 MPa, which is 10 MPa or 19% higher than the measured pressure of 53 MPa. The peak negative pressure for both waveforms is −11 MPa. For p₀=0.57 MPa, the peak negative pressure is −14.5 MPa, but the peak positive pressure is 25% higher in the model (81 MPa versus 65 MPa from the measurement). The discrepancy between measurements and modeling is also apparent in the frequency domain, wherein measurements consistently exhibit less energy content at high frequencies.

Figure 4.

Comparison of focal waveforms and corresponding spectra simulated with the KZK model and measured with the FOPH 2000 in water for p₀=0.29 MPa (I_L=6500 W∕cm², I_N=8200 W∕cm²), p₀=0.39 MPa (I_L=11 000 W∕cm², I_N=16 000 W∕cm²), and p₀=0.57 MPa (I_L=24 000 W∕cm², I_N=29 000 W∕cm²). The horizontal arrows in the waveform plots depict the peak positive pressure measured and modeled. At these output levels, the waveforms are strongly distorted, contain shocks, and the harmonic content of the waveforms extends beyond 100 MHz. The agreement between modeling and measurement results is good, although, when sharp shocks are present (p₀=0.39 and 0.57 MPa), the measurements show lower peak positive pressures and lower values of harmonic amplitudes at high frequencies.

Distributions of the peak positive (p+) and peak negative (p−) pressures were also measured and modeled along the acoustic axis and in the transverse focal plane. In Fig. 5, axial and transverse peak pressure distributions are shown along with distributions of the first four harmonics for p₀=0.39 MPa. As indicated by Fig. 4 for the same drive level, asymmetric shocks develop in the focal region and the measured peak positive pressure is slightly lower in value than the modeled one. Both experiment and simulation show that the peak positive pressure has a dramatic increase in gain from the linear value of G=48 to G_p+=130 in measurements and G_p+=160 in modeling. The −6 dB spatial distribution of the peak positive pressure becomes less than half the width in the transverse direction (0.4 mm in modeling versus 1 mm in the linear case) and shorter in the axial direction (35 mm in modeling versus 70 mm in the linear case) compared to linear propagation conditions, which are shown in Fig. 2.

Figure 5.

Comparison of measured and modeled pressures axially and in the focal plane in water for p₀=0.39 MPa (I_L=11 000 W∕cm², I_N=16 000 W∕cm²). Shown on the left are the transverse distributions for the peak positive, p₊, and peak negative, p₋, pressures as well as for the first four harmonics. The axial data are shown on the right. The combination of nonlinear propagation and diffraction results in narrowing of the harmonic beamwidths and asymmetry of the waveform at the focus, which was captured by both measurement and modeling.

The measured and modeled distributions of the first four harmonics from Fig. 5 show good agreement and demonstrate that higher frequencies are increasingly localized. Only four harmonics are shown in Fig. 5, but as seen in Fig. 4, the focal waveform has a frequency content beyond 100 MHz. Stronger focusing of higher harmonics will result in enhanced localized heating of the propagation medium because the absorption coefficient grows with frequency, as described by Eqs. 2, 3. This effect will significantly increase if shock fronts develop. Figure 4 shows qualitatively that the shock amplitude is nearly equal to the value of the peak positive pressure. Because heat deposition at a shock front is proportional to the cube of its amplitude,14 the spatial distribution of heating in the presence of shocks will be even sharper than the highly localized distribution of peak positive pressure. Moreover, an underrepresentation of the peak positive pressure and thus of the shock amplitude in measurements can have a large impact on predictions of heat deposition rates.

The agreement in the distribution of peak negative pressure is excellent between measurements and simulations. In contrast with the impact of nonlinear propagation on peak positive pressures, the focusing gain for the peak negative pressures is reduced to G_p−=30 and the −6 dB size of the focal zone (1.25 mm in the transverse direction and 80 mm in the axial direction) is larger than in the linear case. Because peak negative pressure in the acoustic waveform is primarily responsible for cavitation effects, the volume of cavitation in nonlinear focused fields is much less localized than that of absorptive heating. To characterize the acoustic field with regard to possible cavitation effects, direct measurements or nonlinear modeling of focal waveforms is necessary to avoid overestimation of peak negative pressures.

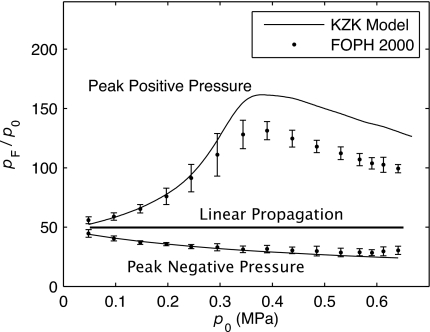
A summary of the measured and modeled spatial peak pressures over the range of power levels used in experiments and modeling is shown in Fig. 6. Peak positive and negative pressure values are normalized by the source pressure amplitude and therefore represent the focusing gain of the transducer. The focusing gains for p+ and p− are plotted versus the source pressure amplitude. The error bars show the standard deviations of three separate measurements. At low source pressure, the linear focusing gain of the transducer is 48 for both peak positive and peak negative pressures. Under nonlinear conditions, the peak positive pressure focusing gain grows higher (a maximum of 160 is obtained in modeling) and then decreases as shocks form proximal to the focus and result in higher prefocal losses. Meanwhile, the gain for peak negative pressures monotonically decreases with increasing source pressure amplitude. Figure 6 again illustrates that the measured and modeled peak negative pressures show an excellent agreement over the range of input source amplitudes, while the peak positive pressures are lower in the measurement than in the modeling.

Figure 6.

Summary of focal pressures measured and modeled with increase in the source operation level. The pressures are normalized by the source pressure amplitude, p₀, illustrating the change in the focusing gain due to combined nonlinear and diffraction effects. The error bars indicate the standard deviation of three different measurements. Nonlinear propagation effects, which are stronger at higher p₀, lead first to a higher gain in peak positive pressure. However, the gain falls off as shocks form prefocally, leading to increased attenuation before reaching the focus. The focusing gain for the peak negative pressure monotonically decreased as the source pressure amplitude increased.

Gel measurements and modeling

Before waveform measurements were made in the gel phantom, an experiment was performed to test the calibration method that is described in Sec. 2. In this experiment, the focal waveform was measured with the FOPH tip in both water and gel phantom and then the calibrated waveforms were compared. First, the FOPH tip was cast in a 7% BSA-acrylamide gel phantom. The gel phantom was cast in the mold described in Sec. 2, but was only 1 cm thick in the axial direction. The FOPH tip was cast so that it was embedded less than 1 mm into the gel phantom. The HIFU transducer was aligned so that the FOPH tip was positioned at the spatial maximum of the peak positive pressure and waveform measurements were recorded up to a source level of p₀=0.39 MPa. Next, measurement of the focal waveform was taken with the FOPH tip positioned in water, less than 1 mm behind the 10 mm thick slab of gel phantom. The voltage signals measured in water and in gel were calibrated following the method of Sec. 2 and compared for the same source pressure levels. Note that the difference in absorption between the two cases is negligible, but the pressure slightly changes in transmission from gel to water. The corresponding transmission coefficient is T=2Z_water∕(Z_water+Z_gel)=0.96, where Z=ρc denotes the acoustic impedance of the water or gel. The relevant material parameters used to calculate Z are provided in Sec. 2. When waveforms were compared over a range of source levels, they showed very good agreement (within 5%), thus validating the proposed calibration approach for using the FOPH to measure pressure waveforms in the gel phantom.

The method of testing the theoretical gel calibration described above can also be viewed as a “substitution” calibration of the FOPH in the new medium (gel phantom). The calibration equations of the FOPH and the results of waveform measurements “in” and “out” of the gel phantom lead to the result that after the waveforms are deconvolved with the impulse response of the hydrophone, the transfer function from voltage to pressure is nearly linear. If the calibration for water was used for measurements in gel, then pressure waveforms in gel were linearly shifted to a value 20% higher. The “linear” sensitivity of the FOPH thus was found to be 20% higher in gel than in water. Accordingly, the FOPH calibration for water can be corrected for measurements in gel without requiring the explicit calibration technique described in Sec. 2D.

The measurements and modeling in the gel phantom with the FOPH 2000 show very good agreement. At low drive levels, the agreement was excellent. However, at higher-power levels when shocks were present, there was again a discrepancy between the measured and modeled peak positive pressures in the waveforms. Figure 7 depicts one such comparison of a focal waveform in the gel phantom at p₀=0.1 MPa (I_L=I_N=560 W∕cm²in situ) and p₀=0.39 MPa (I_L=9100 W∕cm², I_N=12 000 W∕cm²in situ). The peak positive pressure in the shocked waveform is 46 MPa by measurement and 56 MPa (i.e., 22% higher) by modeling; the peak negative pressure for both waveforms is −11 MPa. The peak pressures in gel are lower than in water for the same values of p₀ because of the higher attenuation in gel (see Figs. 34). These results demonstrate that measurements can be made in a tissue-mimicking phantom and that the FOPH can be calibrated in media other than water using the proposed method based on medium properties (β,n₀).

Figure 7.

Comparison of focal waveforms measured and modeled in a 7% BSA-acrylamide tissue-mimicking gel phantom for p₀=0.1 MPa (I_L=I_N=560 W∕cm²) and p₀=0.39 MPa (I_L=9100 W∕cm², I_N=12 000 W∕cm²). The arrows in the p₀=0.39 MPa plot indicate the peak pressures measured and modeled. The agreement is good, but the peak positive pressure is lower for the measured waveform when the shock is present. The waveforms were able to be measured in the phantom, and although of lower amplitude because of increased attenuation, they are of identical shape to comparable amplitude waves measured in water.

Reasons for discrepancy in measured and modeled peak positive pressure

The results summarized in Fig. 6 for measurements in water indicate that at lower drive levels (p₀<0.25 MPa) there is very good agreement between the simulated and measured focal waveforms. At higher drive levels, the values of the peak positive pressure and thus the shock amplitude are lower in the experiment than in the modeling. Accurate measurement of the peak positive pressure is important for predicting thermal effects during HIFU treatments. For example, a 25% difference in measured and modeled values of p₊ in Fig. 4 results in a twofold difference in the heat deposition rate at the focus, as calculated using weak shock theory.17 Several hypotheses for the discrepancy in focal waveforms between measurement and modeling were tested and are discussed below.

Spatial averaging

One of the factors that can affect acoustic measurements is the finite size of the receiver used to measure pressure waveforms.9 If the acoustic field at the point of measurement does not have a uniform planar pressure distribution over the active area of the receiver, then the true acoustic pressure at the focus can be underestimated. This effect is referred to as spatial averaging.46, 47, 48

Although the 100 μm diameter FOPH hydrophone used in this study is much smaller than the transverse dimensions of the acoustic field under linear acoustic propagation conditions (1 mm at −6 dB level), it may not be sufficiently small in the nonlinear field. For example, the field distribution for the peak positive pressure becomes narrower with increasing source pressure amplitude. Thus, the measurement would become increasingly sensitive to spatial averaging at higher output levels. This hypothesis is consistent with the increasing discrepancy in measured and modeled focal values of peak positive pressure for higher values of the source pressure amplitude. The results of modeling show that the narrowest distribution of the peak positive pressure occurs at p₀=0.39 MPa, in which case the shock fronts form very close to the focus. This output level corresponds to the maximum focusing gain of p₊ (shown in Fig. 6). For higher source pressures, shocks form prefocally and the beam width at the focus widens.15

To determine whether spatial averaging had an effect on the measurement of focal waveforms, the KZK model was used to predict the waveform that would be measured by a hydrophone of finite diameter. Waveforms were simulated in the focal plane around the focus and then were averaged over a circular area corresponding to virtual hydrophones of a range of diameters. The results of these simulations are shown in Fig. 8. The predicted waveforms that would be measured by 100 (FOPH diameter), 300, and 500 μm (commonly used in lithotripsy49) diameter hydrophones are shown. The predicted focal waveform for a 100 μm diameter hydrophone was only 2% lower in peak positive pressure than the waveform predicted for an ideal “point” receiver at p₀=0.39 MPa, the drive level at which the −6 dB positive pressure region was the smallest. However, when a 500 μm diameter hydrophone was simulated, there was a significant distortion of the measured waveform. Spatial averaging results mainly in a decrease in the measured value of the peak positive pressure and a widening of the shock front. Nevertheless, for the conditions of this study, it was determined that spatial averaging was not a significant source of error in the measured waveforms.

Figure 8.

The waveforms for p₀=0.39 MPa calculated using the KZK model at focus and averaged over 100, 300, and 500 μm diameter circular cross sections, representing increasing hydrophone sizes. Spatial averaging over the finite hydrophone size caused less than <2% reduction in peak amplitude at the narrowest beamwidth for the 100 μm diameter FOPH hydrophone but would cause a significant reduction with larger hydrophones.

Nonuniform vibration of the HIFU source

In the modeling described in Sec. 2, it was assumed that the vibration pattern of the transducer surface was uniform. However, few real transducers operate as perfect uniformly vibrating pistons. The piezoceramic transducer used in this study, like others, had a nonuniform vibration pattern due to the excitation of surface waves.38, 45 Nonuniform vibration can influence the acoustic field generated by the device and lead to prefocal differences between the actual acoustic field and the calculated field assuming uniform vibration. The effect of nonuniform vibration can be observed in the axial pressure distributions shown in Fig. 2, in which the measured axial scan has two prefocal peaks that are different than those obtained using the O’Neil formula. Since nonlinear effects accumulate as the acoustic wave propagates to the focus, the discrepancy observed in modeling the transducer nearfield may affect the focal waveform.

To determine whether nonuniform source vibration had an effect on modeled waveforms, the transducer vibration pattern was measured using acoustic holography39 and included in the numerical model. The holographic technique was implemented by measuring the amplitude and phase of a small amplitude signal in a plane located at a distance of 30 mm in front of the transducer perpendicular to its acoustic axis. The measurements were performed in water using the SEA hydrophone. A square grid, 60 mm in width, was raster scanned with a step size of 0.3 mm. The Rayleigh integral was then used to reconstruct the velocity distribution at the plane z=0 (where the boundary conditions to the KZK model are specified) by backpropagating the measurements obtained at z=30 mm. Figure 9 depicts the normal velocity distribution in the plane z=0 after the reconstruction. The annular pattern shown in Fig. 9 demonstrates that the transducer did not operate with a uniform velocity distribution.

Figure 9.

The reconstructed velocity distribution across the transducer surface from low amplitude measurements using acoustic holography (top left). The surface is seen to have very periodic radial surface waves where black color corresponds to higher and white to lower values of velocity. A cross section of the radially averaged source velocity that was used as the boundary condition in the numerical model assuming uniform (dashed) and nonuniform (solid) vibrations (top right). Comparison of low amplitude axial pressures measured and modeled with uniform and nonuniform boundary conditions (bottom).

The reconstructed nonuniform velocity distribution was incorporated into simulations by altering the boundary conditions of the KZK model. First, the two dimensional velocity distribution was transformed to an axisymmetric form by radially averaging over 300 equally spaced rings. The number of rings used in the model was chosen to be similar to the step size of the grid used for holographic reconstruction. Next, the source pressure amplitude in the numerical model was adjusted so that the focal pressure predicted by linear modeling matched experimental measurements. Figure 9 shows the uniform and nonuniform boundary conditions used in the model as well as the axial pressure distribution of the transducer. For the axial distribution, the experimentally measured result is shown as well as the results of linear modeling using both uniform and nonuniform boundary conditions. The agreement between both uniform and nonuniform models with measurements is excellent in the focal region, although prefocally, the uniform and nonuniform models yield different pressure patterns. The results of the nonuniform model in the nearfield are closer to measurements, but a discrepancy is still observed. Imperfect agreement in the nearfield is caused by the parabolic approximation used to govern diffraction effects in the KZK equation.

Nevertheless, further simulations performed up to the highest source pressure level considered in this work indicate that nonuniform boundary conditions did not have a significant effect on calculated focal waveforms. The excellent agreement is illustrated by Fig. 10, which shows the axial distributions for the peak positive (the curves above the “zero” axis) and peak negative pressures (the curves below the zero axis) as well as focal waveforms modeled assuming either uniform (p₀=0.39 MPa) or nonuniform boundary conditions. Although there is disagreement between the results of the two models prefocally, the pressures within the focal region agree very well. Most nonlinear effects occur within the high amplitude focal region; therefore, differences that occur prefocally do not contribute significantly to nonlinear distortion of the pressure field at the focus. The calculated focal waveforms, shown in Fig. 10, are almost identical. The difference in peak positive pressure values of the waveforms is less than 5%. Thus, nonuniform source vibration was not a significant source of error in this study.

Figure 10.

Axial distributions of the peak positive and negative pressures calculated for p₀=0.39 MPa with uniform and nonuniform boundary conditions. The vertical line in the picture indicates the location of the focus, where pressure waveforms are calculated under the same conditions and shown on the top right. The nonuniform boundary condition is more accurate in modeling nearfield pressure patterns and may be useful for predicting side effects such as skin burns. However, the focal waveforms are almost indistinguishable when calculated with both uniform and nonuniform boundary conditions.

Frequency response of the FOPH

In the experiments performed in this paper, the FOPH fiber was oriented parallel to the HIFU acoustic axis. In this orientation, as compared to the case when the FOPH tip is at an angle with respect to the acoustic axis, the effect of averaging of the received signal along the FOPH face is minimized. However, besides spatial averaging, diffraction effects at the hydrophone tip also alter the measured waveform. An effective doubling of the measured pressure occurs at frequencies above 10 MHz, resulting in a nonuniform frequency response of the hydrophone.44 To determine the actual acoustic pressure waveform, the measured signal must be deconvolved with the impulse response of the hydrophone. For the fiber optic hydrophones used in this study, the impulse responses provided by the manufacturer were used to deconvolve the measured signal. Typical shocked waveforms obtained with the FOPH 2000 system are shown in Fig. 11. The figure depicts a waveform that is calibrated to acoustic pressure with and without deconvolution with the FOPH impulse response. If deconvolution is not performed, the measured peak positive pressure is overpredicted and the waveform shape is distorted. Thus, deconvolution is necessary to obtain accurate pressure waveforms when using the FOPH.

Figure 11.

A typical focal waveform measured using the FOPH hydrophone at p₀=0.39 MPa calibrated with and without deconvolution with the manufacturer’s impulse response. At low values of p₀, where the wave is sinusoidal, the need for deconvolution is not obvious and a linear calibration from volts to pressure can be used. However, at higher p₀, the directly measured waveform significantly overpredicts the peak positive pressure and distorts the waveform shape; therefore deconvolution is necessary.

Thus far, only measurements with the FOPH 2000 have been presented. To examine the effect of different bandwidth hydrophones on pressure measurements, the focal waveforms were recorded using two models of fiber optic hydrophones. At low-power levels, where the focal waveforms were nearly sinusoidal, the agreement between the two hydrophones was excellent. As the power increased and shocks developed at the focus, the FOPH 500 measured shocks with longer rise times and smaller values of peak positive pressure than those obtained with the FOPH 2000. The bandwidth difference between the two hydrophones is illustrated in Fig. 12, which is composed of three subfigures—the step response, the transfer function, and a waveform comparison. The step response of the FOPH 500 and FOPH 2000 hydrophones is shown, as calculated by integrating the impulse response provided by the manufacturer. The transfer function of the FOPH hydrophone is shown and is composed of five plots. The first plot, labeled (1), is the published result that accounts for diffraction at a 100 μm diameter hydrophone oriented perpendicular to the propagation direction.44 The next two plots depict the transfer function of the FOPH 2000. The first one (2a) was calculated by taking the discrete Fourier transform of the manufacturer’s provided impulse response. The second (2b) was calculated by dividing the spectra of the measured peak focal waveforms without deconvolution by the modeled peak focal waveforms when shocks formed. The curve (2b) is an average of five different measurement and model comparisons (using waveforms from p₀=0.39 MPa to p₀=0.57 MPa) and the error bar at 40 MHz depicts the standard deviation. Lastly, the FOPH 500 transfer function calculated using the impulse response (3a) and the measured and modeled results (3b) are shown in the same way as for the FOPH 2000. Comparison of the focal pressure waveforms measured with the FOPH 2000 and FOPH 500 hydrophones and deconvolved by the respective impulse responses provided by the manufacturer at p₀=0.39 MPa is shown at the bottom of Fig. 12. The peak positive pressure measured with the FOPH 2000 is more than 10 MPa higher than that obtained with the FOPH 500 and thus closer to the value obtained in modeling (Fig. 4). As this result demonstrates, the bandwidth of the receiver is important for capturing the shock fronts and the peak positive pressure. Our conclusion is that despite the increased bandwidth of the FOPH 2000, the shock front at the focus of the HIFU source was still not resolved with sufficient accuracy.

Figure 12.

The step response of the FOPH 500 and FOPH 2000 hydrophones calculated by integrating the manufacturer’s provided impulse response (top). A comparison of the transfer function of the FOPH hydrophone (middle). The figure is composed of five different curves. Labeled (1) is the theoretical transfer function resulting from diffraction at a 100 μm tip (Ref. 44). The frequency transfer functions for the FOPH 2000 (2) and FOPH 500 (3) calculated from the step response (a) and obtained by comparison with the model predictions (b). Comparison of focal waveform measured with the FOPH 2000 and FOPH 500 hydrophones for p₀=0.39 MPa (bottom). The smaller bandwidth of the FOPH 500 hydrophone results in a diminished peak positive pressure and shock amplitude as compared to the FOPH 2000.

DISCUSSION

The Food and Drug Administration in the U.S. and other regulatory agencies have required waveform measurements in water as part of the approval process for US medical devices. Specific protocols have been described for diagnostic US (Ref. 8) and shock wave lithotripsy (SWL),50 but not yet for HIFU. The US and SWL protocols alone are insufficient for HIFU because HIFU operates with higher amplitudes and is more focused than US. Moreover, even the US and SWL regulatory protocols are still debated despite the fact that such devices are in widespread clinical use.

The specific challenges of designing protocols for US device approval depend on what part of the waveform is critical to measure for determining bioeffects. The combined amplitude and duration of the negative pressure phase is responsible for cavitation, which contributes to bioeffects such as tissue injury in US and stone comminution in SWL. The spatially averaged intensity, I_SAL, has been used in HIFU as a metric for reporting exposure levels. In the linear case, the product of twice the pressure attenuation coefficient and the intensity describes the heating rate, and heating is the primary mechanism responsible for inducing bioeffects in HIFU treatments. However, at intensities typically used in HIFU (order of 1000 W∕cm²) and certainly at higher intensities used in newer HIFU devices (order of 10 000 W∕cm²), the heating depends on the frequencies generated due to nonlinear acoustic propagation. At these intensity levels, nonlinear effects lead to shock formation where energy loss at the shock is the dominant heating mechanism.17 The energy loss at the shock is proportional to the shock amplitude cubed,14 as opposed to the square of the pressure amplitude in linear acoustics. Hence, the heating rate becomes more sensitive to accurate measurement of shocks when they are present. Therefore, the peak positive pressure, which determines the peak of the shock, is perhaps the most critical feature in the HIFU waveform.

Comparison of the measured waveforms using two models of fiber optic hydrophones demonstrated that waveforms acquired with the wider bandwidth hydrophone resulted in better agreement between measurements and simulations. Even though agreement was significantly better, it was nevertheless concluded that modeling provided better accuracy in predicting shock waveforms than measurements. Additional evidence for trusting that the calculated peak pressures were more accurate than the bandwidth limited measurements has been demonstrated by comparing time to boiling in a gel phantom due to shock wave heating.51 Initiation of boiling in milliseconds was detected using high speed video imaging and calculated using weak shock theory from the measured and modeled focal waveforms. The measured time to observe boiling agreed better with calculated time to achieve 100 °C when modeled, not measured waveforms were used.

However, it remains possible to improve the measurements made with the FOPH. In this work, each measured FOPH signal was deconvolved with a hydrophone impulse response provided by the manufacturer. It was concluded that the limited bandwidth of the hydrophones caused a reduction in the peak positive pressure. If the hydrophones were completely insensitive above a critical frequency, this would be the major measurement limitation. However, it is more likely that the hydrophone is simply less sensitive at high frequencies than was indicated by the impulse response. Figure 12 indicates that this is more likely the case, at least for the FOPH 2000. Therefore, the impulse response of the hydrophone can be refined to improve the accuracy of the measurements. Refined impulse responses can be determined directly from curves (2b) or (3b) in Fig. 12 or can be obtained from a recent publication that reports newly measured impulse response curves for fiber optic hydrophones.52

This paper underscores the importance of very broad bandwidth (and accurate correction for variable sensitivity in that bandwidth) and of small active spot size hydrophones when measuring HIFU waveforms at clinical excitation levels. Nonlinear acoustic propagation causes spectral broadening of the wave as well as narrowing of the transverse distribution of the peak positive pressure. The −6 dB peak positive pressure beam width was as small as 300 μm for the high gain 2 MHz source used in this study. For this case, the 100 μm active diameter of the FOPH was sufficient but HIFU devices that have higher gains or that operate at higher fundamental frequencies may require an even smaller hydrophone.

The position of the hydrophone for all of the focal waveform measurements presented in this paper was at the geometric focus of the source and was not adjusted to compensate for possible small changes in the axial focal position of the spatial maximum that can occur with changes in source power. For a source with a high gain and small amplitude (linear) propagation, the geometric focus nearly corresponds to the location of the spatial pressure maximum on the acoustic axis. However, the location of the maximum can shift in the axial direction with an increase in the source amplitude. Moreover, the axial shift is different for the peak positive and peak negative pressures. From the modeling results, the accuracy of measurements performed in the geometric focus can be assessed by determining how much the pressure maxima shift axially over the range of source power levels used. Here, the maximum shift was less than 300 μm in either direction from the geometric focus. Furthermore, the difference in peak pressure values at the position of the true maximum, as compared to the geometric focus, was less than <2% for the peak positive pressure and negligible for the peak negative pressure.

In light of these measurement challenges, modeling provided a potentially more accurate determination of the pressure field in water at high amplitudes as well as the ability to readily determine the acoustic field in either absorptive phantoms or tissue. However, low amplitude measurements were necessary for obtaining the boundary conditions for the model. The source curvature and aperture were determined by matching the dimensions of the modeled and measured focal regions. Next, the source pressure amplitude was determined by matching the modeled and measured focal pressure; i.e., the source pressure p₀ was the measured focal pressure p_F divided by the linear gain G. Alternatively, the source pressure amplitude could be calculated using acoustic radiation force balance (ARFB) measurements by dividing the acoustic power of the device by the transducer area and then using the plane-wave relation between intensity and pressure.53 The effect of focusing could be included in the force balance calculation using Beissner’s correction factor.54 However, when this calibration method was applied, the focal pressures predicted by the model were 22% higher than the measured pressures. This discrepancy occurs because part of the source power goes to sidelobes radiated by the nonuniform velocity distribution. These sidelobes are directed away from the focus and thus do not contribute to the focal pressure.45 The ARFB method therefore does not provide an accurate calibration of the uniform piston model for simulating nonuniformly vibrating transducers. On the contrary, the method proposed in Sec. 2 is not influenced by the source nonuniformity.

A uniform piston model was used to simulate the focal field of a single element transducer. It was shown that even though the transducer vibrated nonuniformly, the simplified piston model provided a good agreement for pressure waveforms within the focal lobe both in water and in gel up to 24 000 W∕cm²in situ. A holographic method was reported to refine the boundary conditions used in calculations by measuring and modeling the nonuniform vibration of the source as caused in this study by surface waves or as might be caused by individual array elements in a more complex source. The majority of clinical devices are much more complex and can involve hundreds to thousands of individual elements to allow for electronic steering of the transducer focus. The method of matching measured and modeled focal beamwidths and the techniques to model a nonlinear source described here provide a framework applicable to characterizing focal fields of these more complex sources.

A further development of the proposed method of HIFU characterization would be to better govern the nearfield of the HIFU source in modeling. The modifications would include a more accurate diffraction approach based on using the Rayleigh integral, extension of the code to nonaxisymmetric sources, and the use of acoustic holography to obtain appropriate boundary conditions for the model. For the single element transducer considered in this paper, we have shown that the holographic technique and incorporation of nonuniform boundary conditions in the numerical model did not have a significant effect on focal pressure values. However, for more complicated sources, the holographic method may be more significant for correctly determining focal pressures. Nonuniform source vibration or complicated array designs can also lead to larger pressures in the nearfield than expected with the uniform piston model. These nearfield peaks are important during HIFU surgery because they can contribute to skin burns or other unintentional tissue damage.7

CONCLUSIONS

Acoustic characterization of HIFU fields is difficult and a standard method has not yet been established. The root of the difficulty is nonlinear acoustic propagation effects, especially since the clinical trend has been toward increasing pressure amplitudes in HIFU.

In this paper, a new characterization method based on measurement and modeling was proposed and validated at clinical output intensities in water and in a tissue-mimicking phantom. In summary, the focal pressure and beam dimensions are first measured with a hydrophone at low output levels where acoustic propagation is linear. Using these measurements, the boundary conditions to the model can be defined. The model then can be used to determine pressure waveforms in and around the focus at higher source operation levels. With the described technique, the source can be modeled as a uniformly vibrating focused piston. It was further demonstrated that acoustic holography can be used to improve the boundary conditions to the model or to model more complex source geometries.

Simulations and measurements were compared in water and in tissue phantom at high source pressure levels and agreed well. To obtain these results, the FOPH, was extended to in situ pressure measurements in a material other than water. Strongly asymmetric waveforms with a peak positive pressure of up to 80 MPa and a peak negative pressure of up to 15 MPa were obtained both numerically and experimentally found in very good agreement. However, when steep shocks were present in the waveform at focal intensity levels higher than 6000 W∕cm², lower values of the peak positive pressure were observed in the measured waveforms. The lower measured values were attributed to the broad, but still limited, hydrophone bandwidth. It was therefore concluded that both measurement and modeling were needed. Low amplitude calibration measurements in water were necessary to establish boundary conditions for modeling, but at higher amplitudes, simulations of shocked waveforms were more accurate than measurements. In addition, once validated, the model can be used without further modification to translate the pressures determined in water to in situ pressures in tissue.