Auditory brainstem responses to a chirp stimulus designed from derived-band latencies in normal-hearing subjects

Abstract

In an attempt to compensate for the temporal dispersion in the human cochlea, a chirp has previously been designed from estimates of the cochlear delay based on derived-band auditory brain-stem response (ABR) latencies [Elberling et al. (2007). “Auditory steady-state responses to chirp stimuli based on cochlear traveling wave delay,” J. Acoust. Soc. Am. 122, 2772–2785]. To evaluate intersubject variability and level effects of such delay estimates, a large dataset is analyzed from 81 normal-hearing adults (fixed click level) and from a subset thereof (different click levels). At a fixed click level, the latency difference between 5700 and 710 Hz ranges from about 2.0 to 5.0 ms, but over a range of 60 dB, the mean relative delay is almost constant. Modeling experiments demonstrate that the derived-band latencies depend on the cochlear filter buildup time and on the unit response waveform. Because these quantities are partly unknown, the relationship between the derived-band latencies and the basilar membrane group delay cannot be specified. A chirp based on the above delay estimates is used to record ABRs in ten normal-hearing adults (20 ears). For levels below 60 dB nHL, the gain in amplitude of chirp-ABRs to click-ABRs approaches 2, and the effectiveness of chirp-ABRs compares favorably to Stacked-ABRs obtained under similar conditions.

INTRODUCTION

The chirp stimulus

The concept of the chirp was first applied to auditory electrophysiology by Shore and Nutall (1985), and has since been studied intensively for its use within the auditory field; for a recent review see, e.g., Elberling et al. (2007). A chirp stimulus—or more specifically an upward chirp—is designed to compensate for the temporal dispersion in the cochlea related to the traveling wave delay, e.g., Shore and Nutall (1985), Lütkenhöner et al. (1990), and Dau et al. (2000). In response to a brief stimulus, as, for example, a click, the cochlear traveling wave takes some time to reach from the base of the cochlea to its apical end. Therefore, the different neural units along the cochlear partition will not be stimulated at the same time and the neural activity across all nerve fibers will be smeared. This lack of temporal synchrony can be partly neutralized by an upward chirp stimulus, in which higher frequency components are delayed relative to lower frequency components. The design of such a chirp must be based on a model of the cochlear delay as it is reflected in the broadband click response—being either the auditory compound action potential (ACAP) or the auditory brain-stem response (ABR). It has been shown repeatedly that a chirp is more efficient than a corresponding click both in the recording of the ACAP, the ABR, and of the auditory steady-state response (ASSR)—see, e.g., Elberling et al. (2007).

Latency-frequency functions obtained from derived-band ABRs

One of the chirps used in the ASSR-study by Elberling et al. (2007) was based on latencies from derived-band ABRs originally obtained from a group of normal-hearing subjects by Don et al. (2005). The mean latencies were fitted to a power-function model, which described the average latency-frequency function or the cochlear delay in normal-hearing adults. More specifically, the latency model was used to represent the group delay of a linear cochlear two-port system that modifies the phase of the applied stimulus—e.g., a click. Subsequently, the inverse group delay was used to design a chirp that theoretically should be able to compensate for the delay introduced by the cochlea.

The individual derived-band ABR latencies—described above—showed a relatively large variation across the group of normal-hearing individuals, and further it was unknown whether the power-function model (originally described by Anderson et al., 1971) was adequate in describing the individual latency-frequency relationship.

This raises therefore the following questions:

• (1)What is the interindividual variation of the derived-band ABR latencies in a large group of normal-hearing adults?
• (2)What are the implications of this variance?
• (3)Is the power-function model a relevant descriptor of the latency-frequency function based on individual derived-band latencies?

Chirps based on derived-band ABR latencies at different stimulus levels

Fobel and Dau (2004) described an interesting effect of stimulus level in an ABR study on normal-hearing subjects using three different chirp stimuli. The results implied that two of the chirps designed using different values of the cochlear delay would be optimal at different ranges of stimulus levels. One of the chirps, the M-chirp, was based on cochlear delay values from a model of the mechanical characteristics of the cochlea (de Boer, 1980). Another chirp, the A-chirp, was based on cochlear delay values derived from the latencies of frequency-specific tone-burst ABRs in normal-hearing subjects (Neely et al., 1988), which resulted in cochlear delays that changed significantly with stimulus level.

In the study by Elberling et al. (2007) a set of three chirps was used to record the ASSR at 50 and 30 dB nHL in 49 normal-hearing adults. The three chirps were as follows: (1) the chirp based on cochlear delay values in accordance with the above mentioned power-function model fitted to the mean derived-band ABR latencies obtained by Don et al. (2005). (2) The chirp based on the above mentioned tone-burst ABR latencies described by Neely et al. (1988), but only using the values for the cochlear delay that was described for one specific stimulus level. This level was approximately 65 dB nHL and the chirp based on Neely et al. (1988) turned out to correspond to the A-chirp at 50 dB SL used by Fobel and Dau (2004) (for further details see the discussion in Elberling et al., 2007 p. 2781). (3) The chirp based on de Boer (1980) similar to the M-chirp used by Fobel and Dau (2004). In this study (Elberling et al., 2007), it was found that the ASSRs in response to the chirp based on Don et al. (2005) were larger than the ASSRs to any of the other two chirps; however, this finding was only statistical significant at 50 dB nHL.

These results lead to the following question: What is the effect of stimulus level on the latency-frequency function described by the derived-band ABRs?

Derived-band ABR latencies and the traveling wave delay

In several publications about chirp stimuli, the latency-frequency functions that are used to design the chirps are thought to represent the cochlear traveling wave delay in normal-hearing adults (e.g., Dau et al., 2000, Fobel and Dau, 2004, Stürzebecher et al., 2006, Elberling et al., 2007). Recently, however, Ruggero and Temchin (2007) analyzed the different latency-frequency functions obtained from electrophysiological recordings in humans—specifically tone-burst ABRs and derived-band ABRs—and questioned whether or not these functions were in accordance with their own estimate of the group delay of the basilar membrane (BM) traveling wave. For the derived-band responses, Ruggero and Temchin (2007) concluded that the precise relationship between BM delays and derived-band estimates cannot be specified at present with any certainty. With updated information about the latency-frequency function obtained from derived-band ABR-latencies in a large group of normal-hearing adults, the question should be revisited: How does such an average latency-frequency function relate to an estimate of the group delay of the BM traveling wave in humans?

The efficiency of a chirp based on derived-band ABR latencies

In the study by Elberling et al. (2007) the efficiency of a chirp based on derived-band ABR-latencies [chirp based on Don et al. (2005)] was evaluated by recording the ASSR (stimulus rate 90∕s) from 49 normal-hearing adults. The chirp ASSRs were compared with the corresponding click ASSRs at two stimulus levels, viz 50 and 30 dB nHL. From the grand average ASSR waveforms obtained from the different recording conditions (see Elberling et al., 2007, Fig. 6) the average gain (ratio) in peak-peak response amplitude between the chirp and the click can be evaluated: at 50 dB nHL the ratio was 820∕340∼2.4, and at 30 dB nHL the ratio was 560∕280∼2.0. These gain values are of the same order of magnitude as those found for the ABR by Fobel and Dau (2004, Fig. 4) using chirps designed in a different way.

In the paper by Elberling et al. (2007), the terms input compensation and output compensation were introduced. By input compensation, the temporal dispersion in the cochlea is compensated for by using a chirp stimulus, whereas by output compensation the cochlear delay is compensated for by means of the Stacked ABR technique. This latter technique is based on the derived-band method (Teas et al., 1962) using the same underlying concept as the chirp, namely, to increase the temporal synchronization of activity across the different neural elements in the cochlea (for further description of the Stacked ABR technique see, e.g., Don et al., 1994, 2009).

In the paper by Don et al. (2009), ABR recordings obtained previously from a group of normal-hearing subjects (Don et al., 2005) were evaluated. Both click ABRs and derived-band ABRs were obtained at 60 dB nHL and three different Stacked ABRs were constructed from the individual recordings and compared to the corresponding click ABR. The different Stacked ABRs were formed by aligning the derived-band ABRs according to (1) the individual’s peak latencies (named standard Stacked ABR), (2) the group mean latencies (named mean Stacked ABR), and (3) the modeled latencies in accordance with a power-function model fitted to the group mean latencies (named modeled Stacked ABR). This latter power-function model corresponds to the model used by Elberling et al. (2007) to design the chirp based on Don et al. (2005). The average gain (ratio) in peak-peak response amplitude between each of the three Stacked ABRs and the click was evaluated as follows: (1) for the standard Stacked ABR, the ratio was ∼2.59; (2) for the mean stacked ABR, the ratio was ∼2.36; and (3) for the model Stacked ABR, the ratio was ∼2.27.

This leads to the following questions:

• (1)What is the gain in peak-peak amplitude of the chirp ABR over the click ABR in normal-hearing adults?
• (2)How do these gain values compare to those obtained by the Stacked ABR?
• (3)What are the differences between the waveforms of the click ABR, the chirp ABR, and the Stacked ABR obtained under comparable recording conditions in normal-hearing adults?

The aims of the present study

In order to address the questions raised above, there are four specific aims of the present study.

First, to create a combined dataset with derived-band ABR latencies obtained from a total of 81 normal-hearing subjects. All data are retrieved from previous experiments (Don et al., 1998, 2005). This combined dataset will be used to describe the interindividual variations and to evaluate the effectiveness of using a power-function model to describe the latency-frequency relationship in the individual. Subsequently, the dataset will be used to design a chirp stimulus.

Second, to describe how the latency-frequency relationship varies with stimulus level over a range of 60 dB. The data underlying this analysis also originate from a previous experiment (Don et al., 1998).

Third, to analyze the differences between the latencies of the derived-band responses and the estimated delays of the BM traveling wave. This analysis will include a modeling of the derived-band responses.

Fourth, to evaluate the efficiency of chirp ABRs (input compensation) with Stacked ABRs (output compensation). This will be achieved by evaluating the amplitude ratios between chirp and click ABRs recorded in normal-hearing subjects. The distributions of these ratios will be compared with similar distributions between Stacked and click ABRs that recently have been described by Don et al. (2009). Finally, the waveform morphology of click ABRs, chirp ABRs, and Stacked ABRs will be compared.

COMBINED DERIVED-BAND ABR LATENCY DATA

Two different datasets

Two datasets of derived-band ABR latencies are combined for the present evaluation. Dataset I consists of derived-band latencies recorded by Don et al. (1998) and dataset II consists of corresponding data subsequently recorded in the same laboratory at House Ear Institute by Don et al. (2005). Dataset II was used previously for the design of a chirp stimulus as reported by Elberling et al. (2007). Details about the recording procedures, etc., can be found in the original publications but will be briefly summarized in the following.

Subjects

Both investigations (Don et al., 1998, 2005) received approval from the Institute Review Board (IRB). Prior to testing, the purpose and procedure of the study were orally presented to each test subject by the experimenter. The experimenter then answered any questions the subject had regarding his∕her participation. Finally, each subject read and signed an IRB approved informed consent form.

The test group for dataset I (Don et al., 1998) consisted of 42 normal-hearing subjects1 (23 females and 19 males) with ages 18–38 years. The test group for dataset II (Don et al., 2005) consisted of 39 normal-hearing subjects (20 females and 19 males) with ages 18–39 years. Normal hearing was defined as pure-tone thresholds of 10 dB HL or better for frequencies between 500 and 4000 Hz and 15 dB HL or better for 6000 and 8000 Hz.

Stimuli

The stimuli were rarefaction clicks produced by applying 100 μs electric pulses to the earphones. For the recording of dataset I, a TDH 50P earphone was used, whereas dataset II was obtained using an ER-2 insert earphone. The clicks were presented at a rate of about 45∕s (interstimulus interval=22 ms) and at a level of approximately 60 dB nHL.2

Ipsilateral pink-noise masking was used to obtain the derived-band ABRs by means of the high-pass masking technique. The noise was presented at a level which was sufficient to mask the ABR to the clicks. There were six stimulus conditions: clicks presented alone (unmasked condition), and clicks presented with ipsilateral pink noise high-pass filtered at 8000, 4000, 2000, 1000, and 500 Hz. The slope of the high-pass filtered masking noise was 96 dB∕octave.

ABR recordings

The subjects were placed in a reclining chair in a double-walled sound-treated room (IAC). ABRs were recorded differentially between electrodes applied to the vertex (C_z) and the ipsilateral mastoid (M₁ or M₂); the electrode at the contralateral mastoid was used as ground. The EEG was bandpass filtered from 100 to 3000 Hz using filter slopes of 12 dB∕octave. ABRs were obtained using noise estimation techniques (Elberling and Don, 1984) and weighted averaging techniques (Elberling and Wahlgreen, 1985; Don and Elberling, 1994). These techniques reduce the destructive effects of episodic physiological background noise variation on the ABR average by weighting the average toward those blocks of sweeps with low estimated background noise. Data collection for a run was terminated when the estimated residual background noise in the average reached 20 nV (rms) or less. Thus, all recordings had approximately the same low residual background noise levels.

The derived-band responses were subsequently produced from ABR recordings first to a broadband click presented alone and then to a series of simultaneous ipsilateral presentations of the click and high-pass noise with varying cutoff frequencies as described above. By subtracting the response for one run from the previous, a derived-band response is formed. This method for generating a series of five derived-band ABRs has been presented before in a number of studies (Don and Eggermont, 1978; Parker and Thornton, 1978; Don et al., 1997; 2005) and is based on the high-pass masking technique (Teas et al., 1962). Each derived-band response represents octave-wide activity with a theoretical center frequency equal to the geometrical mean of the high-pass cutoff frequencies of the two maskers used to form the derived-band ABR.

Derived-band latencies

For both datasets, the wave V latencies of the unmasked click ABR and of the five derived-band responses were collected. In order to relate this activity to the level of the cochlea—e.g., the traveling wave and the action potentials in the peripheral part of the auditory nerve—the wave I-V latency difference of 4.1 ms (Elberling and Parbo, 1987) was subtracted from all observed latency values. Additionally, 0.86 ms was subtracted from the values in dataset II in order to compensate for the acoustical delay in the long tube of the ER-2 earphone (i.e., 292 mm). After these corrections were made, the Kolmogorov–Smirnov test of normality (Siegel, 1956) was performed on the values from each dataset and each condition. The results indicated that none of the data distributions deviates significantly from a Gaussian distribution described by the observed mean and standard deviation. Thus, it was assumed that all the data reported here are normally distributed, justifying the use of normal parametric statistics in the analyses. Mean and standard deviation for both studies are calculated and shown in Table 1.

Table 1.

Observed derived-band latencies (mean and standard deviation) from dataset I and II, as well as the calculated values for the combined dataset (N=81 Ss). The observed latencies are corrected for the wave I-V delay (4.10 ms) and the values in dataset II also for the acoustical delay (0.86 ms), in the ER-2 earphone. The column to the right shows the mean latencies of the combined dataset subtracted a value of 1.0 ms (for explanation see text).

Band center frequency (Hz)	1998 (N=42) latency (ms)		2005 (N=39) latency (ms)		Combined (N=81) latency (ms)		Corrected (N=81) latency (ms)
	Mean	SD	Mean	SD	Mean	SD	Mean-1.0 ms
Unmasked	2.13	0.27	2.15	0.27	2.14	0.27
11300	2.09	0.36	2.10	0.27	2.09	0.32
5700	2.14	0.29	2.19	0.35	2.17	0.32	1.17
2800	2.89	0.42	2.82	0.39	2.86	0.40	1.86
1400	4.07	0.58	3.79	0.54	3.93	0.56	2.93
710	5.66	0.73	5.48	0.85	5.57	0.79	4.57

The two datasets produce mean latencies that differ very little from each other except for the 1400 Hz band, where the derived-band latency difference is 0.28 ms (4.07–3.79 ms) longer for dataset I; this difference is significant (p<0.05; t-test). Analysis of the frequency characteristics of the two earphones (amplitude and phase) reveals no obvious differences between their group delays in the 1000–2000 Hz frequency range, which could explain a latency difference of the observed magnitude (see Sec. 4A and endnote 3).3 In the four derived bands: 5700, 2800, 1400, and 710 Hz, the variances (standard deviations) of the two datasets have the same order of magnitude and do not differ significantly from each other (NS, F-test). Since the observed difference for the 1400 Hz band is small (<0.30 ms), the two datasets can meaningfully be combined by calculating the weighted means and standard deviations of the two sets of latencies. These combined values are shown in Table 1.

Describing the combined dataset

In the further analysis of the combined data, the values corresponding to the highest band center frequency, i.e., 11 300 Hz, are excluded; the values for this derived band are regarded to be uncertain because the level of activation is much lower in this frequency region given the ear’s sensitivity curve and the falling spectrum of the click above 8000–9000 Hz (Don et al., 1979; Elberling et al., 2007). The remaining four data points represent an observed latency-frequency function.

Such latency functions of electrophysiological data can be described by a power function as suggested by Anderson et al. (1971):

$$\tau =k\cdot f^{-d},$$ (1)

where τ is the latency in seconds, f is the frequency in Hertz, and k and d are constants. This formula was also used by Eggermont (1979) to describe derived-band ACAP latencies and was used recently by Elberling et al. (2007) to describe the latency-frequency functions of different sets of compound latency data.

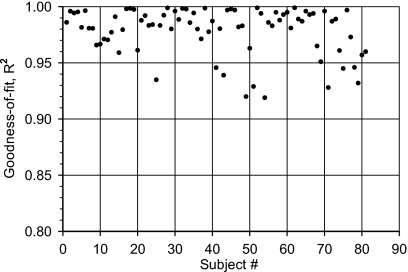
The latency-frequency data for each individual test subject (N=81) as well as the mean values (Table 1) were submitted to a curve fitting using the above power function [Eq. 1]. Each fitting was characterized by its Goodness-of-fit (R²) and the two constants (k and d). The distribution of the goodness-of-fit values across subjects is plotted in Fig. 1. Most values (N=71) are greater than 0.95 and no values smaller than 0.91. This indicates that the observed derived-band latencies as a function of frequency are described reasonably well by the proposed power function [Eq. 1].

Figure 1.

Distribution across subjects of the goodness of fit (R²) obtained by fitting the corrected derived-band latencies from each individual to a power-function model (N=81 Ss).

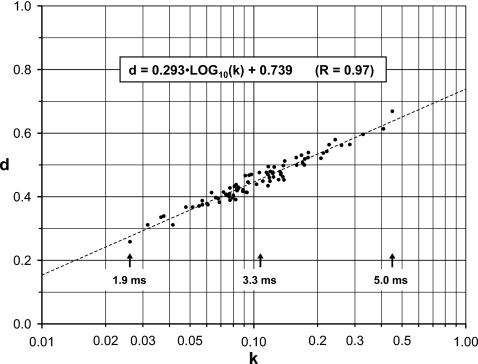
The paired values of k and d are shown in Fig. 2, with k plotted on a logarithmic axis. The two fitting constants appear to have a logarithmic relationship as indicated by the regression line and the corresponding formula. Figure 2 demonstrates a significant interindividual spread in the latency-frequency functions. For each fitted power function, the latency delay between any two frequencies can be found from Eq. 1 by using the corresponding values of the two fitting constants k and d. Whereas the power function fitted to the mean values (Table 1) has a latency delay of 3.3 ms between 5700 and 710 Hz, the individual power functions exhibit latency delays ranging from 1.9 to 5.0 ms.

Figure 2.

Paired values of the two parameters, k and d, which define the power-function model [Eq. 1] fitted to the corrected derived-band latencies from each individual (N=81 Ss). With k plotted on a logarithmic axis, there appears to be a linear relationship between d and k (indicated by the formula and the corresponding plotted broken line; R=0.97). The locations of the mean and the two end points of the distribution (k,d) are shown by the arrows together with the corresponding latency differences between the 5700 and 710 Hz derived bands.

Discussion

The combined dataset is based on data from both genders in a reasonably balanced way (43 females and 38 males). By analyzing the data from the females and males separately, the average derived-band latencies across the four frequency bands are 0.48 ms longer for the males than for the females. Further, the fitted power functions result in a latency delay between 5700 and 710 Hz which is 0.26 ms longer for the males than for the females. These gender differences have been examined more closely in the original publications by Don et al. (1993, 1998, 2005) and will not be discussed further.

The differences between the average values in datasets I and II are very small. This is quite surprising since the recordings for the two datasets are obtained seven years apart, with different groups of normal-hearing test subjects, with different earphones and by different examiners. However, the basic recording principles are identical. When the two sets of mean values are fitted to a power function which describes the latency-frequency relationships, the maximum difference between the two datasets appears at 710 Hz and is only 0.32 ms (within the frequency range 710–5700 Hz). At this frequency, the two fitted power functions deviate symmetrically (±0.16 ms) around the corresponding power function fitted to the mean values of the combined dataset. For all practical purposes, this means that there is only a marginal difference between using dataset I, dataset II, or the combined dataset.

Analysis of the derived-band latencies from all 81 normal-hearing test subjects reveals that the power-function model is able to describe each individual set of recorded latencies fairly accurately (goodness of fit, R²>0.91). This indicates that the determined fitting constants (k and d) may be regarded as relevant descriptors of the fitted data. The paired k and d values are plotted in Fig. 2, which displays the interindividual variance of the latency-frequency information obtained from the derived-band ABRs.

In order to compensate for the cochlear traveling wave delay, chirp stimuli have previously been designed based on data representing the average cochlear delay in normal-hearing adults (e.g., Elberling et al., 2007). The variance described above corresponds to a substantial variation (1.9–5.0 ms) in the latency delay between 5700 and 710 Hz across the group of 81 normal-hearing individuals. Even between the adjacent bands of 5700 and 2800 Hz, large differences in latency were reported earlier by Don et al. (1994). This implies that a chirp using a latency-frequency model based on the mean values of the combined dataset will not be optimal for all normal-hearing individuals. In an attempt to investigate this further, Don et al. (2009) formed three different Stacked ABRs from the derived-band responses underlying dataset II (N=39) and evaluated the amplitudes of the resulting waveforms. The different Stacked ABRs were formed by aligning the derived-band ABRs according to (1) the individual’s peak latencies (standard procedure for the Stacked ABR), (2) the group mean latencies, and (3) the modeled latencies in accordance with a power-function model fitted to the average values of dataset II. The average peak-peak amplitudes for the three different Stacked ABRs were found to be 1014, 929, and 888 nV. This demonstrates that on the average the amplitude drops to about 0.88 (888∕1014) or by 12% when modeled latencies are used instead of individual latencies. However, across the normal-hearing group in dataset II, the corresponding drop in amplitude ranges from −7% to 34%. Therefore, in normal-hearing subjects, we may expect response amplitudes up to about 35% lower than would have been produced by an individualized compensation of the cochlear delay.

DERIVED-BAND LATENCIES AT DIFFERENT STIMULUS LEVELS

Additional level information

In the study by Don et al. (1998), derived-band ABRs were obtained from normal-hearing subjects at a click level of 93 dB p.-p.e. SPL. The latencies from these recordings formed dataset I described above in Sec. 2. In the same study, derived-band recordings were also obtained at other click levels and the results were reported from N=43 normal-hearing subjects at levels in 10 dB steps in the range from 93 to 53 dB p.-p.e. SPL (Don et al., 1998). The wave V latency in all four derived bands could not be measured at all click levels and in all subjects and therefore the latency delays (differences) between the derived bands at 5700 and 1400 Hz were the only ones that could be thoroughly analyzed. The results were described as follows: …“These data suggest that the delay between these two bands is, for most part, not dependent on stimulus level” (Don et al., 1998).

The reported data, however, represented only a subset of the derived-band responses recorded from a total of N=55 normal-hearing subjects and for click levels all the way down to 43 dB p.-p.e. SPL. In the present study, we therefore reanalyze the obtained recordings in order to look more closely at the effect of level changes on the derived-band latencies. From the complete data pool, derived-band latencies were extracted from those normal-hearing subjects (N=35) from which the wave V in both the 5700 and the 1400 Hz band could be identified at all the levels 93, 83, 73, 63, and 53 dB p.-p.e. SPL. At the lowest level, i.e., 43 dB p.-p.e. SPL, wave V in both bands could only be identified in the recordings from N=14 subjects (a subgroup of the larger group of N=35 subjects). The Kolmogorov–Smirnov test of normality (Siegel, 1956) was performed on each dataset and indicated that none of the distributions deviates significantly from a Gaussian distribution described by the observed mean and standard deviations. The mean and standard deviations of the extracted latencies corrected for the wave I-V delay (4.1 ms) are shown in Table 2 and plotted in Fig. 3. The mean and standard deviations of the corresponding latency delays (differences) between the two bands are also shown in Table 2.

Table 2.

Observed latencies (mean and standard deviation) for the 5700 and 1400 Hz derived-bands for different click levels. The observed latencies are corrected for the wave I-V delay (4.10 ms). The column to the right shows the calculated latency differences (delays) between the two derived bands

	Click level (dB p-p.e. SPL)	5700 Hz band latency (ms)		1400 Hz band latency (ms)		5700–1400 Hz difference (ms)
		Mean	SD	Mean	SD	Mean	SD
	93	2.16	0.29	4.10	0.56	1.94	0.42
	83	2.43	0.29	4.32	0.62	1.89	0.48
N=35	73	2.75	0.34	4.75	0.75	2.00	0.55
	63	3.18	0.35	5.20	0.86	2.03	0.67
	53	3.68	0.54	6.06	0.93	2.38	0.73
N=14	43	4.25	0.58	6.56	1.18	2.31	0.91

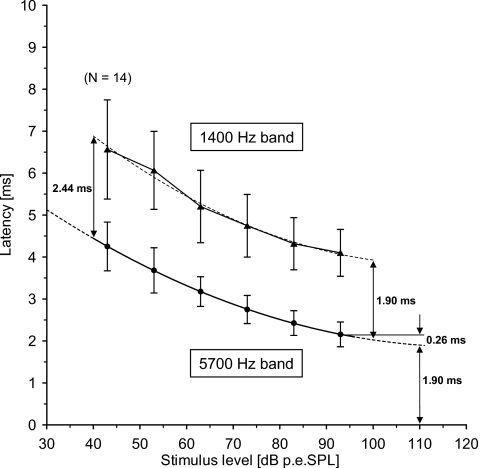
Figure 3.

Latencies (mean and ± one standard deviation) for the 5700 and 1400 Hz derived bands plotted as a function of click level (Table 2). The mean values for the 5700 and the 1400 Hz derived bands are each fitted to a second-order polynomial, shown by the broken lines. The polynomial for the 5700 Hz band indicates that the latency in this band flattens off at about 110 dB p.-p.e.SPL with a value of 1.90 ms; this latency is 0.26 ms shorter than the observed mean value at 93 dB p.-p.e.SPL. The latency delay between the two bands estimated from the two fitted polynomials is 1.90 ms at 100 dB p.-p.e.SPL, and 2.44 ms at 40 dB p.-p.e.SPL.

Because the different datasets do not have the same variance (standard deviation, see Table 2), comparison across stimulus level is done by means of nonparametric testing. By using Wilcoxon matched-pair signed-rank test (Siegel, 1956) on successive level pairs (including Bonferroni’s correction for repeated testing—Hochberg and Tamhane, 1987) no difference was found in the latency delays between the two bands (5700 and 1400 Hz) at 93 versus 83 dB p.-p.e. SPL; 83 versus 73 dB p.-p.e.-SPL; and 73 versus 63 dB p.-p.e.SPL. Contrary to this, a significant difference (p<0.01) was found between the latency delays at 63 versus 53 dB p.-p.e. SPL. However, the mean difference between the delays at 63 and 53 dB p.-p.e. SPL is only 0.35 ms. Finally, no significant difference could be found in the latency delays at 53 versus 43 dB p.-p.e. SPL (N=14).

In Fig. 3, a curve (second-order polynomial) is fitted through the mean 5700 Hz derived-band latencies obtained in 10 dB steps within the range 43–93 dB p.-p.e. SPL. By extrapolation, it is estimated that this derived-band latency flattens off at about 110 dB p.-p.e. SPL with a value of 1.90 ms (see Fig. 3). This value is about 0.26 ms shorter than the corresponding value at 93 dB p.-p.e. SPL (2.16 ms).

Discussion

With the paired analysis, we cannot demonstrate statistically any change in the latency delay between the 5700 and 1400 Hz derived bands over the 30 dB range from 63 to 93 dB p.-p.e. SPL. This is in agreement with the general description originally made by Don et al. (1998). However, at 53 dB p.-p.e. SPL, the latency delay increases significantly, which indicates that the derived-band responses from the two bands do not produce latency functions with a constant latency delay. It is conceivable that the latency function of the 1400 Hz band is more steeply sloping than that of the 5700 Hz band. A second-order polynomial is therefore also fitted to the mean latencies for the 1400 Hz band and compared to the fitted curve for the 5700 Hz band data, as shown in Fig. 3. The difference between the two fitted curves is 1.90 ms at 100 dB p.-p.e. SPL and 2.44 ms at 40 dB p.-p.e. SPL. If the two fitted curves represent the true underlying latency structure, the delay between the two bands only changes about 0.55 ms over a 60 dB range. Consequently, for all practical purposes, the two latency functions may be described as having a constant latency delay.

Derived band ABR’s cannot readily be recorded at very high stimulus levels—mainly because these levels are perceived uncomfortably loud by the test subjects and because of risks of permanent damage from the high noise exposures. Derived band data are therefore not available for click levels higher than about 60 dB nHL (about 90–95 dB p.-p.e. SPL). From the latency data for the 5700 Hz band reported herein, we have therefore attempted to estimate the corresponding response latency at higher click levels. As shown in Fig. 3, the fitted curve indicates that the latency function flattens off at about 110 dB p.-p.e. SPL. The latency at this level could therefore be used as a reference in the comparison of derived-band and BM latency data observed at high stimulus levels (see Sec. 4).

DERIVED-BAND LATENCIES AND THE TRAVELING WAVE

Observed derived-band latencies and the cochlear traveling wave delay

In order to compare the mean observed derived-band latencies from normal-hearing subjects [i.e., the combined dataset (N=81) in Table 1], with the traveling wave delay, the recorded latencies have to be adjusted appropriately. All latencies in Table 1 include a subtracted value of 4.1 ms, corresponding to the average latency difference between ABR wave V and wave I (or ACAP wave N₁) found in a previous study (Elberling and Parbo, 1987).

No acoustical corrections were needed for the latencies in dataset I (Don et al., 1998) in Table 1. However, the latencies in dataset II (Don et al., 2005) were corrected for the delay introduced by the tubing of the ER-2 earphone. Acoustical control measurements3 demonstrated that the two earphones used in the two studies produce reasonably flat group delays across the frequency range 500–8000 Hz with average group delays of approximately 0.2 ms (after correcting the ER-2 for the sound tube delay). If correction is made for this average group delay the latency reference (0 ms) will approximate the time of arrival of the click at the tympanic membrane and the latencies would then represent traveling delays between the ear drum and the spiral ganglion cells in the cochlea—the site where the ACAP is generated (see, e.g., the Discussion in Kiang et al., 1976).

The observed derived-band latencies (Table 1) are not corrected for temporal delays caused by the synaptic gap. For this delay, we have chosen the value of 0.8 ms, which is similar to the value used by Eggermont (1979) and by Ruggero and Temchin (2007, p. 158).

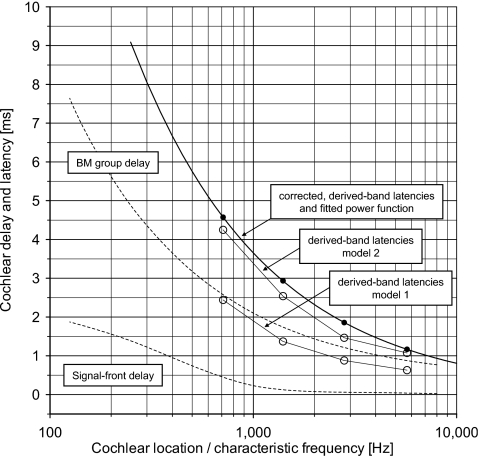
Therefore, from the combined latency values in Table 1, a value of 1.0 ms (=0.2+0.8) is finally subtracted. The corrected latencies are shown in Table 1 (last column—Corrected mean) and plotted in Fig. 7 together with a power function fitted to the four corrected data points.

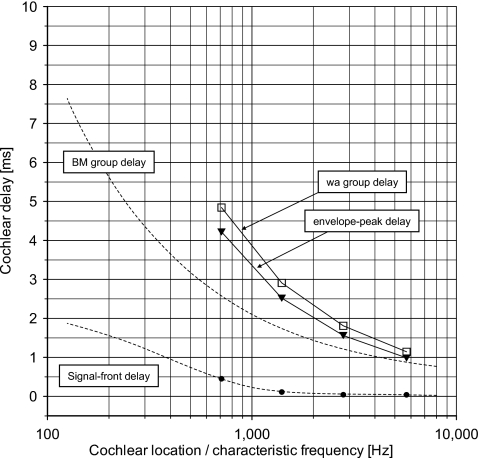
Figure 7.

Cochlear delay and latency vs cochlear location indicated by characteristic frequency. The broken lines show the signal front delay and the group delay of the BM estimated to be valid for humans at intense levels of stimulation by Ruggero and Temchin (2007, Fig. 7). The figure shows the corrected derived-band latencies (●) (Table 1, last column) and the corresponding fitted power-function model (full line). The peak latencies (○) of the two sets of modeled derived-band responses (models 1 and 2; Fig. 5, right) are also included.

How latencies of derived-band responses relate to delays of the cochlear traveling wave in humans—or the BM traveling wave—has recently been discussed by Ruggero and Temchin (2007). In that paper, the authors presented estimates of the signal-front delay and the weighted-average group delay of the BM as a function of location (characteristic frequency) in the cochlea of humans as well as of other species (see, e.g., Fig. 7 in Ruggero and Temchin, 2007). The estimates of the signal-front delay and the group delay suggested to be valid for humans at intense levels of stimulation are plotted in Figs. 67. From Fig. 7, it is quite clear that the corrected derived-band latencies deviate significantly from the suggested BM group delay.

Figure 6.

Cochlear delay vs. cochlear location indicated by characteristic frequency. The broken lines show the signal front delay and the group delay of the BM estimated to be valid for humans at intense levels of stimulation by Ruggero and Temchin (2007, Fig. 7). The following delay values of the standard functions in Fig. 5 are shown: the signal front delay (●), the envelope-peak delay (▾), and the calculated weighted-average group delay (◻).

Modeling derived-band responses

In order to look closer on this difference, a mathematical modeling of the derived-band responses is carried out by using a band-limited version of the formula originally proposed by Goldstein and Kiang (1958) to describe the formation of the ACAP N₁:

$${\mathrm{ACAP}}_{ab}\left(t\right)=\sum _{n=a}^b{\int }_{-\infty }^t{p}_n\left(\tau \right)\cdot u_n(t-\tau )\cdot d\tau ,$$ (2)

where ACAP_ab(t) is the derived-band ACAP from the frequency band between frequencies a and b; p_n(t) is the firing probability of the nth nerve fiber represented by its poststimulus-time histogram, PST_n(t), and u_n(t) is the unit response describing the contribution from the nth nerve fiber discharge to the activity at the remote recording electrode. In the original version of the formula, Goldstein and Kiang (1958) presumed the unit response to be the same for all nerve fibers. More recently, however, it has been suggested (e.g., Chertoff, 2004) that the shape of the unit response changes with the characteristic frequency of the nerve fibers. In this version of the formula, we only include contributions from nerve fibers within the frequency band in question. The right-hand side of the formula expresses the sum over the frequency band of the convolution of the firing probability function of each nerve fiber and the unit response. If the shape of the unit response can be regarded as being constant across the frequency band, the formula can be written as follows:

$${\mathrm{ACAP}}_{ab}\left(t\right)=\sum _{n=a}^b{\mathrm{PST}}_n\left(t\right)\ast u_n\left(t\right),$$ (3)

where ${\sum }_{n=a}^b{\mathrm{PST}}_n\left(t\right)$ is the sum of the PST histograms over the frequency band and ∗ is the convolution operator. The formula expresses that the derived-band response equals the sum of the PST histograms (in the following abbreviated ∑PST) filtered by the spectral characteristics of the unit response.

Modeling the ∑PST

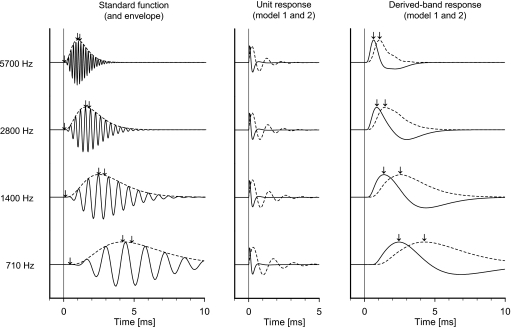
To represent the ∑PST, we use a model of the auditory nerve fibers’ temporal activity in response to click stimulation. Under the assumption of linearity, the revcor function is an approximation to the impulse response of the filtering process in each neural unit, e.g., Evans (1977) and de Boer and de Jongh (1978). Therefore, in a model of the ACAP in the cat, de Boer (1975) used a revcor template to model a standard function, for each fiber’s impulse response (see Appendix A). A set of standard functions is shown in Fig. 5 (left).

Figure 5.

(Left) Standard functions and envelopes (de Boer, 1975) corresponding to the center frequency of each of the four derived bands. The arrows indicate (left to right) the signal front delay, the envelope-peak delay, and the weighted-average group delay (see Appendix A); these latencies are plotted in Fig. 6. (Middle) Unit responses in accordance with models 1 (—) and 2 (- - -) (see Appendix B). (Right) Modeled derived-band responses obtained by convolution of the standard function envelopes (left) with each of the two unit responses (middle). The arrows indicate the peak latencies of the modeled derived-band responses; these latencies are plotted in Fig. 7.

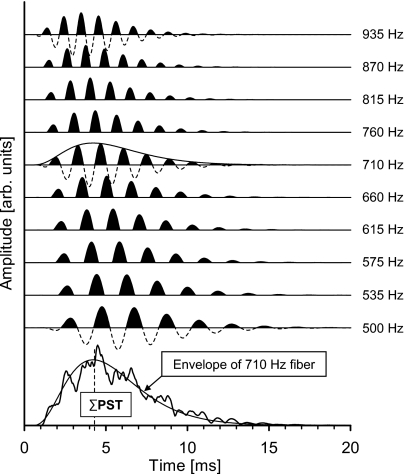
If the click stimulus can be regarded as an approximation to a unit-impulse function within the frequency range from approximately 200 to 10 000 Hz, the standard function is the impulse response of the linear filter associated with a single nerve fiber. With this assumption, we have first attempted to model the derived-band activity from the low-frequency octave band (500–1000 Hz). Figure 4 (top) shows the simulated activity from ten single fibers uniformly distributed on a logarithmic frequency scale within the band. The neural activity—or simulated PST-histograms—is indicated by the black areas of the positive parts of the standard functions representing the activity of each nerve fiber. The standard functions are given signal-front delays (t_front=α_f; see Appendix A) in accordance with the values estimated by Ruggero and Temchin (2007), and plotted in Figs. 6 and 7. The sum of the PST histograms (∑PST) across the octave band is shown in Fig. 4 (irregular curve, bottom). For comparison, the temporal envelope of the standard function for the nerve fiber with a characteristic frequency of 710 Hz, which corresponds to the geometrical center frequency of the band, is shown. This latter envelope is scaled in a way that enables visual comparison with the ∑PST curve. The broken vertical line indicates the peak latency of the 710 Hz response envelope (=4.3 ms). Thus the temporal waveform of the 710 Hz response envelope, including its peak latency, approximates the temporal waveform of the total firing probability of the group of single nerve fibers within the derived band. This corresponds to the suggestion by de Boer (1975, p. 1034) to replace the neural activity with its envelope when modeling the ACAP.

Figure 4.

(Top) Simulated activity from ten single nerve fibers, i.e., standard functions (de Boer, 1975) uniformly distributed on a logarithmic frequency scale of the low-frequency octave band. The neural activity or simulated PST histograms is indicated by the black areas. Each standard function is given a signal-front delay corresponding to the values estimated by Ruggero and Temchin (2007) and plotted in Figs. 67. (Bottom) The sum of the PST histograms (ΣPST) across the octave band (irregular curve). A scaled version of the temporal envelope of the standard function for the 710 Hz nerve fiber (the geometrical center frequency of the band) is plotted for comparison. The broken vertical line corresponds to the peak latency (4.3 ms) of the 710 Hz envelope.

The envelope of the standard functions corresponding to the geometrical center frequencies of the four octave bands are subsequently used in Eq. 3 to represent the temporal activity to click stimulation—or the ∑PST—in each band. For the frequencies 710, 1400, 2800, and 5700 Hz, the four standard functions (and their envelopes) are shown in Fig. 5 (left). On each curve, the signal-front delay, the envelope-peak delay, and the weighted-average group delay are successively indicated and the values plotted in Fig. 6.

Modeling the unit response, u_n(t)

Different unit responses are reported in the literature—either derived theoretically, from masking experiments or from triggered averaging procedures in experimental animals as reviewed by Chertoff (2004). Since the reported unit responses deviate significantly from each other, we have used two models which are markedly different: the unit response originally proposed by de Boer (1975) (model 1) and the unit response proposed by Chertoff (2004) (model 2) (see, Appendix B). de Boer’s unit response is the same for all nerve fibers, whereas Chertoff’s unit response changes with characteristic frequency of the nerve fiber. The two unit responses are shown in Fig. 5 (middle) and are used for the convolution in Eq. 3.

Modeling of the derived-band ACAP

By convolving the envelope of the standard functions with the unit response (models 1 and 2), the modeled derived-band response waveforms are computed [Eq. 3] and shown in Fig. 5 (right) with indication of the peak response latencies. It is apparent that the modeled derived-band response waveforms and their latencies depend significantly on the characteristics of the unit response. The resulting modeled latencies are plotted in Fig. 7. As can be seen, the corrected observed derived-band latencies deviate significantly from the latencies of the modeled derived-band ACAPs using model 1, whereas they are more in agreement with those obtained using model 2.

Discussion

The high-pass masking paradigm, which has been used to record the derived-band ABR, presumes linearity (additivity of the high-pass masked responses as well as the corresponding derived-band responses). For the interpretation of the derived-band responses, it is also assumed that the fibers with characteristic frequencies inside the derived band respond fully and the fibers with characteristic frequencies outside the derived band do not respond at all. Prijs and Eggermont (1981) analyzed derived-band ACAPs from guinea pigs and concluded that the derived-band responses reflect the average behavior of activity from single fibers with characteristic frequencies corresponding to the center of the derived bands. In a high-pass masking experiment (Evans and Elberling, 1982), the activity in single auditory nerve fibers in the cat was studied. Apart from “remote masking” or lateral “two-tone” suppression between the click and the high-pass noise maskers which seemed to operate for low-frequency fibers, a general confirmation of the high-pass masking technique and therefore of the derived-band concept for the ACAP was supported. Therefore, we assume that the activity in each derived band reflects synchronized firing from nerve fibers with characteristic frequencies within the range between the two cutoff frequencies of the corresponding high-pass maskers.

The derived-band ABRs which produce datasets I and II (in Sect. 2) were recorded at a moderate stimulus level i.e., 93 dB p.-p.e.SPL (∼60 dB nHL). The observed latencies are therefore longer than would have been found at very intense click levels. However, we could attempt to calibrate the observed latencies for this level effect by subtracting 0.26 ms (Fig. 3) from the observed corrected latency values. However, this calibration would not bring the derived band latencies in line with the suggested BM group delay.

The data plotted in Fig. 3 indicate that the latency delay between the 5700 and 1400 Hz derived bands appears to be constant in the range between 93 and 63 dB p.-p.e.SPL (∼60–30 dB nHL). For lower levels, i.e., 53 and 43 dB p.-p.e.SPL (∼20 and 10 dB nHL), the latency delay becomes larger. For levels decreasing from 93 to 63 dB p.-p.e.SPL (from ∼60 to 30 dB nHL), the derived-band latency-frequency curve in Fig. 7 would be shifted toward longer latencies. However, at 53 and 43 dB p.-p.e.SPL, the resulting latency-frequency curves would be shifted toward even longer latencies but more for the lower than for the higher bands, and the latency-frequency curves would therefore exhibit slightly more curvature than the 93 dB p.-p.e.SPL (∼60 dB nHL) curve shown in Fig. 7.

In order to use the ABR wave V latency as a descriptor of the ACAP N₁ latency (ABR wave I), the same amount has been subtracted from the observed wave V latencies in all four derived bands (=4.1 ms). If the wave I-V difference in the low-frequency band were larger than in the high frequency band, a systematic error would be made. Such an error could then explain part of the observed differences between the experimental data and the modeled data and the suggested BM group delay. However, in a maturation study by Ponton et al. (1992), derived-band ABRs were recorded from newborns, infants, children, and adults in response to clicks presented at 91 dB p.-p.e.SPL (approximately 60 dB nHL). From the derived-band responses from the adults (N=18) the wave I-V delay was found to be constant across the derived bands (see Ponton et al., 1992, Table 1).

What is of more concern in the present context is the difference between the observed and the modeled derived-band latencies. It appears that this difference depends not only on the cochlear filter buildup time but also on the characteristics of the unit response used to model the derived-band response.

The revcor model is derived from the application of the reverse correlation method to the recordings from single auditory nerve fibers in the cat by, e.g., de Boer (1967), Evans (1977), and de Boer and de Jongh (1978). For low to moderate levels of the applied noise stimuli (up to 70 dB SPL per one-third octave) the revcor-functions are almost invariant (de Boer and de Jongh, 1978, p. 119) and are able to describe the filtering properties of the nerve fibers even at stimulus levels well above fiber saturation (Evans, 1977, p. 191). The click level used to record the derived-band ABRs in the present study is not excessive (93 dB p.-p.e. SPL ∼60 dB nHL) and corresponds to a long-term level of about 67 dB SPL.4 The click level complies therefore with the limitations given by de Boer and de Jongh (1978) and Evans (1977). However, regardless of the validity of this argument, we do not know with any certainty if the revcor function is an adequate first-order descriptor of the filtering process in the auditory nerve fibers for the data reported herein.

At very high click levels, we would expect the revcor functions to have significantly shorter rise times corresponding to the broader tuning of the neural units. The ∑PST curves in each octave band would then display earlier peak latencies than the ∑PSTs we have used for our modeling. These shorter latencies would be more in line with the BM group delay proposed by Ruggero and Temchin (2007).

The two unit responses used in the modeling represent different bandpass filters. The unit response proposed by de Boer (1975) corresponds to a filter with a slope of about 6 dB∕octave in the frequency range of interest (below 700–900 Hz) and therefore acts almost as a differentiator. Consequently, the peak latencies of the modeled ACAPs (model 1) coincide with the maximum slope of the envelope of the standard functions (see Fig. 5). Contrary to this, the family of unit responses proposed by Chertoff (2004) corresponds to filters with a relatively flat response in the frequency range of interest. Consequently, the peak latencies of the modeled ACAPs (model 2) approach the actual peak latencies of the envelope of the standard functions (see Fig. 5).

Since neither the precise filtering process corresponding to the level of the click used to obtain the derived-band ABR nor the precise waveform of the unit responses of the involved nerve fibers are known, we are not able to provide a detailed explanation of the difference between the observed derived-band latencies and the suggested BM group delay. We therefore must agree with Ruggero and Temchin (2007, p. 158) that at present we have insufficient information to specify the relationship between the BM delays and derived-band latencies.

DESIGNING A CHIRP AND TESTING ITS EFFICIENCY

Designing a chirp

Individual nerve fiber responses or derived-band responses are obtained by measuring the activity from one individual nerve fiber or one group of nerve fibers at the time and thus regarding the cochlea as a tapped delay line. Contrary to this, broadband ACAPs or ABRs are formed by the activity from the whole auditory nerve thus regarding the cochlea as a two-port system. For the design of chirp stimuli response latencies from specific locations along the BM obtained either from mechanical observations (von Bèkèsy, 1960; Ruggero and Temchin, 2007) or from responses from individual nerve fibers or group of nerve fibers have been used to characterize this two-port system (Fobel and Dau, 2004). In this way, estimates of the traveling wave delay have been used to characterize the group delay of the (linear) cochlear two-port system (e.g., Dau et al., 2000; Wegner and Dau, 2002, and Elberling et al., 2007). However, it is assumed that each derived band represents a neural activity pattern that arises from stimulation with frequency components within the frequency range of the derived band; this regardless of which location in the cochlea that actually generates the corresponding neural activity. Therefore, the derived-band latencies can be used to specify the group delay of a cochlear two-port system where the term frequency does not relate to position along the cochlear partition but to the input stimulus. This group delay then specifies how different groups of frequency components, for instance, a broadband click, and their resulting neural responses are delayed from the input to the output of the cochlear two-port system. The inverse group delay can subsequently be used to construct a chirp that attempts to compensate for the observed derived-band delay.

This approach has also been applied here. From the power function fitted to the mean latencies of the combined dataset (Table 1, but offset to have zero delay at 10 000 Hz), a chirp was generated using the frequency-domain method described in detail by Elberling et al. (2007). Similarly, a standard 100 μs click was also generated by using a constant zero group delay.

The chirp used by Elberling et al. (2007) was generated from the mean latencies in dataset II. Since the differences are very small between dataset II and the combined dataset (Table 1), the present chirp deviates only marginally from the one used previously (Elberling et al., 2007)

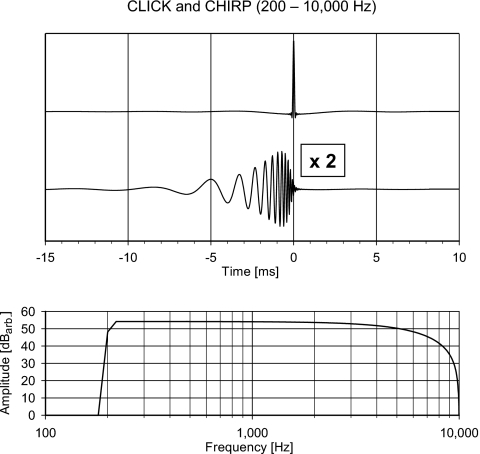
The chirp and the click have different temporal characteristics. Therefore, if the efficiencies of the two stimuli are to be compared, it should be assured that they have identical amplitude spectra5 and thus differ only in their phase spectra. The waveforms and amplitude spectra of the click and the chirp are shown in Fig. 8.

Figure 8.

(Top) The temporal waveform of the click and the chirp. The stimuli are band limited to the frequency range from 200 to 10 000 Hz. The amplitude of the chirp has been multiplied by 2. The two stimuli are temporally aligned so the phase delay at 10 000 Hz of both stimuli corresponds to 0 ms. (Bottom) The (identical) amplitude spectra of the two stimuli. The lower cutoff corresponds to −6 dB at 200 Hz and the higher cutoff corresponds to the falling spectrum of a 100 μs click, having its first null at 10 000 Hz (see endnote 5).

Testing the chirp against the click

Subjects

The clinical testing is part of a quality control procedure with CE-marked6 equipment (used as intended), which complies with the general rules of the Central Ethical Committee and Danish Medicines Agency in Denmark. No written approvals are therefore needed. However, the following procedure was applied: Prior to testing, the purpose and procedure of the study were orally presented to each test subject by the experimenter. The experimenter then answered any questions the subject had regarding his∕her participation. Finally, each subject read and signed an informed consent form.

The test group consisted of ten normal-hearing subjects (five females and five males) with ages 24–42 years. Normal hearing was defined as pure-tone thresholds of 10 dB HL or better for frequencies between 500 to 4000 Hz and 15 dB HL or better for 6000 and 8000 Hz. Both ears were tested sequentially on all test subjects.

Stimuli

The two test stimuli a 100 μs rarefaction click and the corresponding chirp (200–10 000 Hz) were applied to a set of ER-2 insert earphones. The stimuli were presented at a rate of 27∕s (interstimulus interval=37 ms) at the levels 60 and 50 dB nHL.

ABR recordings

The present recordings were made with an Interacoustics Eclipse EP25 ABR-system®. The subjects were placed on a couch in an electrically shielded booth. ABRs were recorded differentially between electrodes applied high on the midfrontal area (F_z) and the ipsilateral mastoid (M₁ or M₂); an electrode on the lower midfrontal area (F_pz) was used as ground. The EEG was bandpass filtered from 100 to 3000 Hz using filter slopes of 12 dB∕octave. ABRs were obtained using noise estimation techniques (Elberling and Don, 1984) and weighted averaging techniques (Elberling and Wahlgreen, 1985; Don and Elberling, 1994). These techniques reduce the destructive effects of episodic physiological background noise variation on the ABR average by weighting the average toward those blocks of sweeps with low estimated background noise. For the purpose of collecting the data presented here, averaging was continued in each run until the estimated residual background noise level was 40 nV (rms) or lower. For all test subjects and all recordings, an average residual background noise level of 34.6 nV was obtained after 3150 sweeps.

Wave V parameters

The Wave V peak-to-trough amplitude and peak latency were identified and measured automatically from the recordings. To compensate for the acoustical delay in the sound tubing of the ER-2 earphones, 0.86 ms was subtracted from all measured latency values. In six of the recordings from one subject, significant postauricular muscle (PAM) response precluded the automatic amplitude measurements because the trough following the wave V was obscured by the PAM activity. In these cases, the location of the trough was found by judgments made by two independent observers. The Kolmogorov–Smirnov test of normality (Siegel, 1956) was performed on the values from the data from each condition. The results indicated that none of the data distributions deviates significantly from a Gaussian distribution described by the observed mean and standard deviations. Thus, it was assumed that all the data reported here are approximately normally distributed, justifying the use of a normal parametric description of the data. However, because the samples from the different conditions do not have the same variance, we have applied nonparametric testing for the statistical analyses: The Wilcoxon matched-pair signed-rank test for analysis of paired data and the Mann–Whitney U test for the analysis of unpaired data (Siegel, 1956).

Results

The mean and standard deviations of peak-peak amplitude and peak latency for all four sets of recordings (from both ears in ten subjects) are shown in Table 3. At both 60 and 50 dB nHL, there are marked differences between the click and chirp data: the chirp amplitudes are significantly larger than the corresponding click amplitudes (p<0.001, Wilcoxon) and the chirp latencies significantly shorter than the click latencies (p<0.001, Wilcoxon). Whereas the relative standard deviations for the chirp amplitudes are about the same as those for the corresponding click amplitudes, the standard deviations for the chirp latencies are significantly larger than those for the corresponding click latencies [p<0.001 (60 dB) and p<0.05 (50 dB), F-test].

Table 3.

Observed wave-V peak-peak amplitudes and peak latencies (mean and standard deviation) of the recorded click and chirp ABRs at the stimulus levels 60 and 50 dB nHL (N=20 ears). The column to the right shows the calcualted ratios between the chirp and the click ABR-amplitudes.

Stimulus level (dB nHL)	Click				Chirp				Amp. ratio
	Amp. p-p (nV)		Latency (ms)		Amp. p-p (nV)		Latency (ms)
	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
60	331	69	6.12	0.22	501	104	4.62	0.66	1.54	0.32
50	305	58	6.55	0.41	531	132	5.43	0.66	1.78	0.47

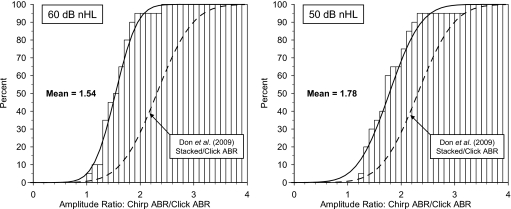
At both 60 and 50 dB nHL, the ratio between the chirp amplitudes and the click amplitudes are calculated and the mean and standard deviations shown in Table 3. At 60 dB nHL, the mean ratio is 1.54 and at 50 dB nHL it is 1.78. The two observed cumulative distributions of the amplitude ratios are plotted together with their estimated Gaussian distributions in Fig. 9.

Figure 9.

Cumulative distribution of the ratios between the chirp and the click ABR amplitudes (N=20 ears) obtained at 60 dB nHL (left, mean value=1.54) and at 50 dB nHL (right, mean value=1.78). Both the observed distribution of the individual amplitude ratios and the corresponding continuous Gaussian distribution using the observed mean and standard deviation (Table 3) are shown. The continuous Gaussian distribution of the ratios between the modeled Stacked and the click ABR amplitudes obtained at 60 dB nHL by Don et al. 2009 [Fig. 1(c)] are shown for comparison (broken line).

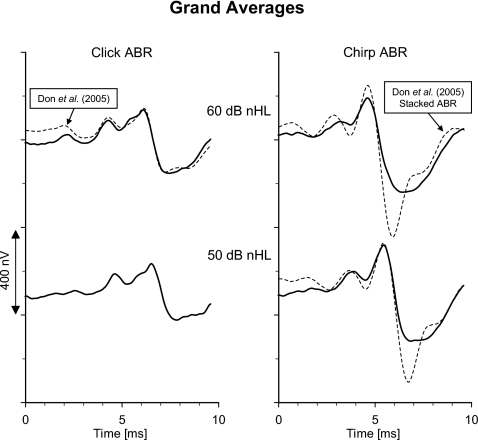
In order to study the ABR waveform morphology, grand averages are constructed as follows: First, each recording is time shifted so the latency of wave V coincides with the mean latency for the actual recording condition (mean latencies for each stimulus type and level, Table 3). Next, the average across each set of 20 time-adjusted recordings is calculated. The four grand average waveforms are shown in Fig. 10. For comparison, the grand averages of the click ABR and Stacked ABR7 obtained at 60 dB nHL by Don et al. (2005) [dataset II (N=39), Sec. 2] are constructed in a similar way, as described above. In Fig. 10, these latter grand averages are plotted so their peak latencies coincide with those from the present study. Further, the two grand averages (click and Stacked ABR, Don et al., 2005) are multiplied by a scaling factor=0.88 which enables the grand average click ABR to be presented with the same peak-peak amplitude as the grand average click ABR from the present study.8 Since the waveform of the time and amplitude-adjusted grand average click ABR (Don et al., 2005) resembles that from the present study (R²=0.90), the click ABRs at 60 dB nHL serve as a common reference and the chirp ABR can then meaningfully be compared with the Stacked ABR. At 60 dB nHL the waveform of the Stacked ABR is slightly different from the chirp ABR (R²=0.80) and also significantly larger, but at 50 dB nHL the two waveforms become more similar (R²=0.85).

Figure 10.

Grand average waveforms of click ABR (left) and chirp ABR (right) obtained at 60 and 50 dB nHL (N=20 ears). The corresponding grand averages of the click ABR and the modeled Stacked ABR obtained from the original recordings at 60 dB nHL by Don et al. (2005) are shown for comparison (broken lines): left, click ABR; right, modeled Stacked ABR. These latter waveforms are scaled and time shifted as described in detail in the text.

Discussion

As found in other studies (e.g., Dau et al., 2000, Fobel and Dau, 2004, and Elberling et al., 2007), we find the chirp ABR amplitude to be larger than the corresponding click ABR amplitude. The chirp∕click amplitude ratio is significantly lower at 60 than at 50 dB nHL (1.54 versus 1.78, p<0.01, Wilcoxon), because when the level of stimulation drops from 60 to 50 dB nHL the click ABR amplitude decreases whereas the chirp ABR increases. This finding is in agreement with the findings by Fobel and Dau (2004, Fig. 4), and from their results the amplitude ratios 1.42 (60 dB SL) and 2.059 (50 dB SL) can be estimated (for their M-chirp).

It should be noted that the observed (shorter) latencies of the chirp ABRs have significantly larger standard deviations than the corresponding latencies of the click ABRs. However, the analysis of the chirp data demonstrates a very high correlation between the latencies at 60 and 50 dB nHL (R=0.95), whereas for the click the corresponding correlation is much lower (R=0.80). The higher the correlation, the more the observed variance is due to individual differences than due to random fluctuations. The result therefore seems to indicate that the chirp ABR systematically emphasizes individual characteristics—at least for the two stimulus levels used herein.

In the study by Elberling et al. (2007), the terms “input compensation” and “output compensation” were introduced: Input compensation refers to the use of a chirp stimulus which attempts to compensate for the traveling wave delay at the input to the cochlea and output compensation refers to the application of the Stacked ABR which attempts to compensate for the traveling wave delay at the output from the cochlea. In the study by Don et al. (2009), the click ABR at 60 dB nHL and the corresponding Stacked ABR were evaluated in the recordings from 39 normal-hearing subjects and three different Stacked ABRs were formed (also described above in Sec. 2C). One of these—called the modeled Stacked ABR—was made in an attempt to simulate the effect of using a chirp stimulus which in principle would compensate for the traveling wave delay similar to the Stacked ABR when based on the same average latency-frequency model. The mean ratio of the modeled Stacked ABR amplitudes to the corresponding click ABR amplitudes across the group of 39 normal-hearing subjects was found to be 2.27 [sd=0.50 (Don et al., 2009, Fig. 1c)]. For comparison with the present findings, the corresponding Gaussian cumulative distribution is shown in the two graphs in Fig. 9.

At 60 dB nHL, the chirp∕click amplitude ratio is significantly lower than the corresponding modeled stacked∕click amplitude ratio (p<0.001, Mann–Whitney). This means that the gain in amplitude relative to the click ABR is higher for the modeled Stacked ABR than for the chirp ABR. For both compensation methods, it can be observed that no recordings produce a ratio <1.0. However, the distribution of the chirp∕click ratio is much steeper than the modeled stacked∕click ratio, corresponding to a significantly lower observed standard deviation (Table 3) of 0.32 versus 0.50 (p<0.02, F-test), but the relative standard deviations are about the same (0.21 versus 0.22).

At 50 dB nHL, the modeled stacked∕click amplitude ratio (obtained at 60 dB nHL) is also higher than the corresponding chirp∕click amplitude ratio. However, here the two distributions appear almost equally steep corresponding to an observed standard deviation (Table 3) of 0.47 versus 0.50 (NS, F-test), and the relative standard deviations are only slightly different (0.26 versus 0.22).

In Fig. 10, the corresponding waveforms are evaluated by means of the time-adjusted grand averages. All the recordings by Don et al. (2005) are scaled down with the purpose of presenting the two grand average click ABRs at 60 dB nHL with the same peak-peak amplitude. By using the click ABR as an anchor point or common reference for the two sets of recordings, the waveforms of the modeled Stacked ABR and the chirp ABRs can be compared. The differences in the amplitude ratios as found above repeat itself in the waveforms. At 60 dB nHL, the waveform of the chirp ABR has some similarities with the modeled Stacked ABR but is much smaller. However, at 50 dB nHL, the two waveforms become more similar and more equal in magnitude.

Therefore, at 50 dB nHL, the efficiency of input compensation (chirp ABR) and of output compensation (the estimated modeled Stacked ABR) in generating larger ABRs appear to be comparable when obtained using similar recording conditions.

That the chirp is more efficient at 50 dB nHL than at 60 dB nHL could be related to the spread of excitation by the individual frequency components of the chirp. At lower levels of stimulation, each frequency component excites only a restricted area of the cochlea, but at higher levels the excitation spreads—especially toward the base of the cochlea (upward spread of excitation). Each frequency component of the chirp arrives at the cochlea with one specific delay, which is designed to compensate for the cochlear delay at the location with a characteristic frequency corresponding to the frequency component in question. If each frequency component at higher levels excites a broader area of the cochlea, the effect will be a desynchronization, because each location will now be excited by a broader range of frequency components each arriving at a different point in time. If this explanation is correct, there might be an upper level of stimulation beyond which the chirp no longer will be more effective than the click—at least not in normal-hearing individuals.

SUMMARY AND CONCLUSION

There are only small differences between the two datasets (I and II) that are used to create the combined dataset describing the latency-frequency relationship of derived-band ABRs obtained at 60 dB nHL in normal-hearing individuals.

The proposed power-function model is an adequate descriptor of the combined dataset as well as the latency-frequency relationship in the individual.

There is a large interindividual variance in the delay between the derived-band ABRs across normal-hearing individuals, corresponding to a range from 1.9 to 5.0 ms between the 5700 and 710 Hz bands.

The observed variance indicates that a chirp constructed from the mean values in the combined dataset may cause reductions of up to 35% in response amplitude relative to an individualized compensation of the cochlear delay in normal-hearing subjects.

Inferred from derived-band ABRs obtained at different click levels there seems to be no major effect on the relative cochlear delay (<0.55 ms—between 5700 and 1400 Hz) over a 60 dB range of stimulation (∼10–70 dB nHL).

Extrapolation of the average latency values obtained for click levels from 10 to 60 dB nHL indicates that the 5700 Hz derived-band latency function flattens off at ∼80 dB nHL (110 dB p.-p.e.SPL).

The observed latency of derived-band ABRs depends not only on the cochlear filter buildup time but also on the waveform (or frequency spectrum) of the unit response, which characterizes the contribution to the activity at the remote recording electrode of the discharge in single nerve fibers.

In humans neither the shape of the cochlear filter response nor the waveforms of the unit responses are known in detail. Therefore, the relationship between the derived-band latencies and the suggested group delay of the BM cannot be specified.

Chirp ABRs generate higher response amplitudes than the corresponding click ABRs. However, the gain in amplitude is lower at 60 dB nHL than at 50 dB nHL where it approaches a factor of 2.

The drop in response amplitude of the chirp ABR over the click ABR for higher levels of stimulation in normal-hearing individuals implies that there might be an upper level of stimulation beyond which the chirp is no longer more effective than the click.

From the latency behavior of the chirp ABR, it is suggested that the chirp emphasizes individual characteristics more than the corresponding click.

Chirp ABRs are lower in magnitude than Stacked ABRs at 60 dB nHL. However, at 50 dB nHL, the magnitude of chirp ABRs seems to approach that of modeled Stacked ABRs, and the two methods of compensation appear therefore to be equally efficient.

APPENDIX A: REVCOR FUNCTIONS

In a model of the ACAP in the cat, de Boer (1975) used a revcor template to model a standard function, h(t), for each fiber’s impulse response:

$$h\left(t\right)=\mathrm{env}\left(t\right)\cdot \cos (2\pi \cdot f_C\cdot t+{\phi }_{f_C}),$$ (A1)

where t is the time in seconds, f_c is the fiber’s characteristic frequency in Hertz, and env(t) is the temporal envelope of h(t) defined as follows:

$$\mathrm{env}\left(t\right)=0\text{for}t<{\alpha }_{f_C},$$ (A2)

$$\mathrm{env}\left(t\right)={[(t-{\alpha }_{f_C})∕{\beta }_{f_C}]}^{(\gamma -1)}\cdot e^{-[(t-{\alpha }_{f_C})∕{\beta }_{f_C}]}\text{for}t⩾{\alpha }_{f_C},$$

where α_fC is a delay time dependent on f_c, β_fC is a decay $\text{constant}=0.0975f_C^{-0.663}$, γ is a degree of complexity of the associated filter (chosen by de Boer to be=4.0), and φ_fC is the phase of the “carrier” or characteristic frequency (chosen by de Boer (1975) to be be=−α_fC⋅2π⋅f_C).

Several different delays are associated with this standard function: the signal-front delayt_front (=α_f), the envelope-peak delay t_peak, and the weighted-average group delayt_group, (see Goldstein et al., 1971, Ruggero 1980, 1994). In a linear system, the weighted-average group delay corresponds to the center of gravity of the impulse response energy (see, e.g., Goldstein et al., 1971). A corresponding numerical calculation demonstrates that for a signal-front delay=0, de Boer’s standard function, Eq. A1, gives a weighted-average group delay which is approximately 17% longer than the envelope-peak delay, i.e., t_group=1.17t_peak(α_f=0).

APPENDIX B: UNIT RESPONSES

Model 1: Unit response proposed by de Boer

This unit response is constant across nerve fibers and is defined in the s-domain through its Laplace transform:

$$U_n\left(s\right)=\frac{s^2}{(1+s)\cdot (1+\xi \cdot s+s^2)},$$ (B1)

where the constant ξ=1.2 and s=1 corresponds to a frequency of 1000 Hz. The corresponding time function is rather complex and does not have a zero-mean value. Therefore, we have used the following mathematical approximation:

$$u_n\left(t\right)=e^{-at}\sin (2\pi \cdot (b\cdot e^{-ct})\cdot t),$$ (B2)

where the constants are given the values (in s⁻¹): a=2900, b=3600, and c=1250, which ensures the unit response a zero-mean value.

Model 2. Unit response proposed by Chertoff

This unit response changes with the characteristic frequency of the nerve fiber, and consists of a damped sinusoidal function given as follows:

$$u_n\left(t\right)=e^{-kt}\sin (2\pi f\cdot t),$$ (B3)

where the damping factor k is in s⁻¹ and the oscillation frequency f in Herz. From the information provided by Chertoff (2004, Figs. 4 and 5), we have approximated the two constants with the following values as a function of the characteristic frequency: (characteristic frequency,f,k)⇒(710,700,750), (1400, 850, 900), (2800, 900, 1050), and (5700, 950, 1250).