Abstract
A survey of papers using auditory evoked potentials (AEPs) published over the last 10 years (Table I) demonstrates that most AEP studies in animals have used subjective methods for auditory threshold determination. Subjective methods greatly reduce the value of statistical hypothesis testing and jeopardize tests of hypothetical experimental group differences in hearing sensitivity. Correspondingly, many attempts have been made to develop objective threshold determination methods, but these have not been used widely. Further, they seldom include an appreciation of the effects of residual noise in the AEP. In this study, AEPs evoked by tonal and noise stimuli in goldfish (Carassius auratus) were recorded and the residual background noise was measured and analyzed in detail. High variability was found in residual noise, but can be effectively controlled with a simple modification of averaging routines. Considerable interobserver disagreements were found using subjective threshold estimation. An objective method of threshold determination was developed based on comparison between AEP amplitude and controlled residual noise, using a signal detection theory approach to set specific threshold criteria. The usefulness of AEP in hypothesis testing for auditory function requires more control over residual background noise amplitudes and the use of objective threshold determination techniques.
INTRODUCTION
The surface recording of auditory evoked potentials (AEPs) utilizes synchronous averaging of far-field neuronal potentials evoked by repetitive presentations of auditory stimuli. The technique remains popular for many reasons, but especially because it is a noninvasive and time-efficient means of measuring auditory system function. It has now become widely used in clinical and basic hearing research in both human and diverse vertebrate animal models [mammals (e.g., Boettcher, 2002), birds (e.g., Brittan-Powell et al., 2002), reptiles (e.g., Higgs et al., 2002), amphibians (e.g., Katbamna et al., 2006), and fishes (e.g., Kenyon et al., 1998)].
Most recently, AEP audiometry has been used to statistically test a wide variety of hypotheses on the function, development, and evolution of audition. Examples include the effect of chemical and noise exposure on auditory sensitivity (e.g., Lu and Tomchik, 2002; Le Prell et al., 2004; Popper et al., 2005; Porter et al., 2006; Cordova and Braun, 2007), ontogenetic changes in hearing abilities (e.g., Boettcher, 2002; Higgs et al., 2003; Song et al., 2006), or comparative studies of closely related species (e.g., Ramcharitar and Popper, 2004; Ramcharitar et al., 2006). The vast majority of publications reporting AEP threshold estimates (in animals) in this and three other prominent journals over the last 10 years used subjective response determinations to estimate thresholds (Table 1). In some publications, no mention of threshold determination technique at all was given. Typically, subjective response determination relies on visual inspection of the repeatability of replicate AEP averages using a subjective yes∕no decision, occasionally based on expected minimal response amplitudes (e.g., Boettcher, 2002) and∕or within a particular latency window (e.g., Ramcharitar and Popper, 2004). The heavy reliance on visual inspection techniques in the animal AEP literature is especially unfortunate because unsatisfactory interobserver agreements of visual inspection have been shown in several independent studies of experienced observers or clinicians (Arnold, 1985; Gans et al., 1992; Vidler and Parker, 2004; Lv et al., 2007). Unfortunately, the use of such unreliable subjective threshold determination techniques raises the possibility that hypothesis testing could be compromised by confirmation bias, particularly in the absence of double-blind protocols (Nickerson, 1998).
Table 1.
Summary of literature review. The table gives the number of studies using AEP for animal hearing threshold determination with different methods, including subjective methods of visual inspection and objective methods based on the measure of the response amplitude or correlation analysis. Some publications did not describe threshold determination techniques at all (not given). The nonexhaustive survey covered four journals for the years 1997–2006. HR: Hearing Research; JASA: The Journal of the Acoustical Society of America; JEB: The Journal of Experimental Biology; JCPA: Journal of Comparative Physiology A: (Neuroethology) Sensory, Neural, and Behavioral Physiology.
| HR | JASA | JCPA | JEB | |
|---|---|---|---|---|
| Visual inspection | 178 | 20 | 8 | 7 |
| Response level | 12 | 11 | 2 | 1 |
| Correlation | 1a | 5a | ||
| Not given | 29 | |||
| Total | 220 | 31 | 15 | 8 |
One paper in each category used both correlation analysis and visual inspection; they are both counted only in the correlation category.
Because of the obvious shortcomings of the subjective threshold determination methods, attempts to objectively determine AEP threshold have been made repeatedly, especially in clinical research (see Hyde et al., 1998, for a review). Two general approaches to objective AEP threshold determination have been proposed: (1) Response repeatability measurement, i.e., a graphical correspondence should exist in responses evoked by repeat stimulus presentations, which can be measured with mathematical algorithms rather than judged by subjective visual inspection. The implementation of this method has been generally based on correlation analysis, either between AEP replicates evoked by the identical stimuli at the same level, or between recorded AEP and a predetermined response template (e.g., Elberling, 1979; Ozdamar et al., 1994; Yan, 1998; Lu and Tomchik, 2002). (2) AEP amplitude analysis, wherein the amplitude (from either time or frequency domain) of the AEP is used to determine if a stimulus-evoked response is present. Studies employing response-amplitude-based threshold estimations mainly involve a combination of three steps: (i) Measurement of the response amplitude, usually in terms of peak-to-peak (e.g., May et al., 2002) or root mean square (rms) (e.g., Elberling and Don, 1984) voltage in the time domain or power in the frequency domain (e.g., Supin et al., 2001; Popper et al., 2005); (ii) Estimation of the background noise remaining in the average (see below); and (iii) Definition of a criterion minimum AEP amplitude for an evoked response, such as 3 dB above the background noise (Popper et al., 2005), two standard deviations (SDs) above the average background amplitude (May et al., 2002), or simply using an arbitrary value with no stated relation to the background noise (e.g., 0.1–0.2 μV in Mitchell et al., 1996). A simpler AEP amplitude threshold determination approach uses the relationship between response amplitude and stimulus level to determine which stimulus levels are linearly related to AEP amplitude, regardless of background noise amplitudes. The threshold level can then be defined as the zero-crossing value or inflection point, below which the response amplitude does not change monotonically with the stimulus level (e.g., Supin et al., 2001; Brittan-Powell et al., 2002).
AEP amplitude analysis, while providing much needed objectivity, cannot be simply applied if the experimental conditions change. The amplitude of any AEP average is a reflection of both the response and the residual background noise in an average (RBN); the latter reflects multiple sources, including other neural activity, muscular contractions, and ambient electrical pollution. When the stimulus level is just above threshold levels, the AEP amplitude is expected to be just greater than the RBN amplitude, thus when the background noise amplitude varies greatly, either spontaneously or as a result of experimental condition [such as with or without administration of neuromuscular blocker (Kenyon et al., 1998)], the estimate of threshold based on response amplitude will be contaminated by variability in noise amplitude, accordingly. Thus, AEP amplitudes cannot be directly compared without concurrent measures of RBN amplitude. Any estimates of response strength will be contaminated unless RBN amplitude differences are also considered.
Residual noise amplitudes in an AEP average roughly reflect the number of signal sweeps composing the average AEP, with a theoretical relationship of BN∕√N, where BN is the instantaneous background noise amplitude and N is the number of sweeps (Wong and Bickford, 1980). This relationship holds only if the background noise is stationary, so collecting a fixed number of sweeps [e.g., 500 sweeps by Katbamna et al. (2006), 1000 sweeps by Brittan-Powell et al. (2002), and 2000 sweeps by Kenyon et al. (1998)] does not ensure that RBN will be the same in each average. The instantaneous noise amplitude may vary across trials depending on the status of the test subject and the experimental setup. More damagingly, episodic noise from different sources can change the noise amplitude during averaging, weakening the relationship between sweep number and RBN amplitude. Therefore, objective response-amplitude threshold determination techniques should be combined with the control of RBN amplitude, especially in studies using statistical hypothesis testing. Bayesian averaging techniques may also be used to differentially weight individual sweeps (or blocks of sweeps) in an average (Eberling and Wahlgreen, 1985).
The RBN amplitude can be measured in many ways. Some authors have proposed to directly measure the amplitude (e.g., rms amplitude) of averages composed of an equal number of no-stimulus sweeps (e.g., Mann et al., 2001) or of averages within separate prestimulus or postresponse windows of the stimulus sweep (e.g., May et al., 2002). This approach may be a good approximation of the RBN amplitude presented in AEP averages containing responses, however, it does require additional data collection, and it may also be inaccurate if ongoing noise amplitude changes greatly during the course of data collection.
To circumvent these complications, other authors have proposed methods of directly estimating the RBN amplitude in AEP averages that also contain a response. Elberling and Don (1984) recorded the instantaneous voltage of a single time-point from each sweep composing the AEP average. If the noise is random and normally distributed, the standard deviation of these instantaneous voltages should be equal to the rms amplitude of the RBN embedded in the AEP average, after being corrected by the total number of sweeps. The ratio of the variance of the AEP to the single-point variance can be used as an F statistic, which allows for the estimation of thresholds within specific confidence windows using approximated degrees of freedom (Elberling and Don, 1984). In their subsequent studies, Don and Elberling and colleagues showed that this method is also an effective means of estimating noise amplitudes in human audiometric data and can be used to determine how many sweeps should be included in an average (Don et al., 1984; Don and Elberling, 1994; 1996). In the present report, the estimated RBN amplitude using this method will be presented as the RBNSP.
Signal averaging in AEP measurements is based on the assumptions that the neural potential evoked by the repetitive stimulus is identical in each sweep, and the averaging process only reduces the amplitude of noise, i.e., potentials that do not have a fixed time relationship with the stimulus presentation. Based on this idea, an alternate method of RBN amplitude estimation was proposed by Wong and Bickford (1980), following Schimmel (1967). The RBN in an average AEP was estimated from the plus-minus (±) average, the average of all sweeps following a polarity-reversal of one half of the recorded sweeps. This ± average represents the same sweeps composing the AEP average, except that all time-locked features have been effectively removed by the polarity reversal of half of the sweeps. The rms of this ± average is an indirect estimate of the RBN amplitude in the AEP average (assessed from the same sweeps) and is termed as the RBN± hereafter.
The present report describes the measurement of RBN in goldfish AEP averages, and provides the range and variability of RBN amplitudes in multiple replicates of AEP tests. We also report on the interobserver consistency of threshold determination using visual inspection. Subsequently, we present an evaluation of RBNSP and RBN± and conclude that RBN± is an effective and simple means of noise estimation. Finally, we describe an objective method of threshold determination based on comparing the AEP amplitude and RBNSP with fixed RBN amplitudes. We also show how the principles of signal detection theory can be used to estimate the equivalent hit and false alarm rates of specific AEP threshold criteria.
GENERAL METHODS
Goldfish (Carassius auratus, comet variety) [N=21; standard length: 10±0.8 (SD) cm; body mass: 39±11.4 g] were obtained from a commercial distributor, maintained in filtered aquaria under 12L:12D light cycle and fed commercial food. The protocol of animal use in the study was approved by the Institutional Animal Care and Use Committee of Hunter College, CUNY.
Each animal was lightly anesthetized in 100 mg L−1 MS222 (3-aminobenzoic acid ethyl ester, Sigma) before an intramuscular injection with Flaxedil (gallamine triethiodide, Sigma; 5 μg g−1 body weight). The animal was then held in a sling constructed of a foam-lined aluminum strip strung from the sides of the tank [6 mm acrylic: 45×40×15 (depth) cm]. The tank contained 10 cm deep water and the animal was suspended with the top of skull above the water surface (no more than 2 mm). The exposed part was covered with a small piece of tissue paper to retain moisture. The animal was respirated by a gravity-fed water circulation system through a tube inserted in the mouth. To reduce the disturbance from environmental vibration and noise, the tank rested on a vibration-isolation table (Nano-K™, Minus K Technology, Inc., Inglewood, CA) within a 1.2×1.2×2 m single wall sound-attenuating booth (Controlled Acoustical Environments, Industrial Acoustics Company, Inc., New York, NY).
All stimuli presentation, data acquisition, and data management were operated via a TDT System 3 system (Tucker-Davis Technologies, Inc., Gainesville, FL; sampling frequency=24.4 kHz) controlled by customized routines in MATLAB® 7 and TDT RPvdsEx© 5.4.
Two stimulus types were presented to evoke the AEPs: 1000 Hz tone pips of 9 ms duration, with 2 ms linear rise∕fall ramps, and band-limited (600–1400 Hz) white noise bursts of 7 ms duration with 0.01 ms linear ramps. These were presented with an interstimulus interval of 33.17 ms. The stimuli were generated by a TDT RP2.1 processor. Analog outputs were attenuated (TDT PA5), amplified (Crown D-75A), and broadcasted from a JBL Control® 29AV Speaker (frequency response: 45 Hz–18 kHz±3 dB), suspended ∼60 cm above the water surface. To monitor the stimulus level, a B&K 8103 hydrophone was placed underwater adjacent to the fish. The hydrophone signal was fed through a B&K Nexus conditioning amplifier (with a 30–10 000 Hz band-pass filter) and digitized by the TDT RP2.1 processor. Estimation of tone pip level was based on averaged hydrophone signals, expressed as the largest rms value obtained over any 1-ms window (one stimulus cycle) during the burst [following Burkard (1984)]. To estimate noise-burst levels, ∼2% of the individual stimulus sweeps were evenly sampled. The rms amplitude of each sweep was estimated over a 7-ms window, starting at stimulus onset. The stimulus level was calculated as the mean rms of all the samples and was expressed in dB re 1 μPa.
The AEPs were measured with a pair of silver-wire electrodes. The active electrode was positioned on the midline of the skull above the medulla region, and the reference one between the nostrils. The tank water near the fish was grounded to the ground of the headstage (TDT RA4LI). Electrical activity was amplified (TDT RA4PA preamplifier), then band-pass filtered (30–3000 Hz) and digitized with a TDT RA16 processor. Sweeps with peak-to-peak amplitude higher than 15 μV were rejected by an artifact rejection circuit. The average AEP responses were recorded over an 800-point (i.e., 32.8 ms long) window, beginning with stimulus onset.
EXPERIMENT 1: THRESHOLD ESTIMATION WITH UNCONTROLLED VARIATION IN RBN AMPLITUDE
Introduction
Repeated AEP tests were carried out to examine the variation in RBN amplitudes and the interobserver reliability of visual inspection for hearing threshold estimation.
Methods
Sixteen animals were tested with tone (N=10) and∕or noise (N=15) bursts in this experiment. Stimulus level was decreased initially with steps of 10 dB (starting at 120–130 dB re 1 μPa) and then by 5 dB near threshold, until several steps below a provisionally estimated threshold. At each level, the stimuli were presented in four blocks of 500 sweeps, with alternating stimulus polarity by block (starting phases of 0° and 180°), forming a total of 2000 sweeps. These blocks were used to create two subaverages of 1000 sweeps each composed of an equal mix of both stimulus polarities. We defined threshold as the lowest stimulus level that evokes a response with all higher stimulus levels also evoking responses. The presence or absence of a response was judged by both visual inspection and by comparison of AEP and RBN amplitudes.
Visual inspection
Visual inspection of two replicate 1000 sweep subaverages for each single trial was performed by three experienced observers independently. The waveforms of the two subaverages were graphically overlapped and visually examined for their repeatability by each observer. The recorded signal was determined to contain a response when the two traces were judged to be repeatable.
Measurement of AEP and RBN amplitudes
The AEP rms amplitude was calculated over the first 16.4 ms (400 samples) rather than the whole sampling window (800 samples) from the average AEP of all 2000 sweeps. We adopted a shorter window because the duration of the response decreases as the stimulus level declines. Close to threshold, the response itself may only last a few milliseconds, so longer windows will underestimate the amplitude of near threshold AEP. We chose a 16.4-ms window as a compromise between accurate RBN± measurements (see below) and sensitive AEP amplitude measures. Noise amplitudes in the AEP were estimated as RBNSP and RBN±. To calculate RBNSP, the instantaneous voltage at one fixed time-point (sample number 144, ∼6 ms) was recorded in every sweep. The amplitude of the RBN presented in the average AEP was estimated as RBNSP=SDSP∕√N, where SDSP is the standard deviation of the instantaneous voltages and N is the total number of sweeps in the average (Elberling and Don, 1984). For tests with tonal stimuli (where stimulus polarity was alternated to reduce stimulus artifacts), the variances in instantaneous voltages were calculated individually from the sweeps of each stimulus polarity and averaged before calculating the overall SDSP. To calculate RBN±, we used the two 1000 sweep subaverages for each trial as described for visual inspection, each representing both stimulus polarities. One subaverage was subsequently reversed (multiplied by −1) before averaging with the other subaverage to generate the ± average. The RBN± was calculated as the rms of this ± average based upon all 2000 sweeps (Wong and Bickford, 1980). The AEP amplitude was then compared with the RBN amplitude estimate to determine the threshold (see below).
Results
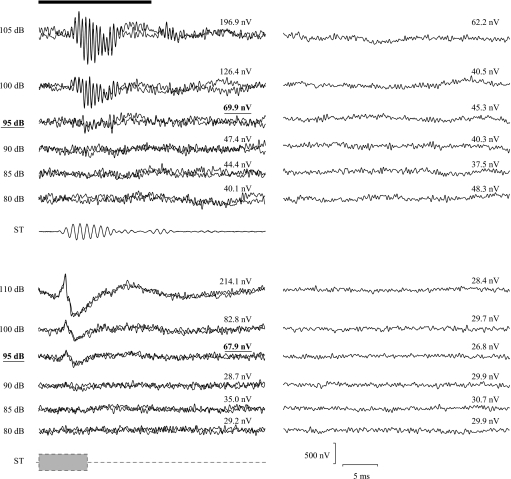
Figure 1 shows pairs of representative mean AEP waveforms (each from 1000 sweeps) and the corresponding ± average noise waveforms (and the rms amplitude of each). Characteristic features can be seen from the AEP waveforms, such as declining amplitude, increasing latency and decreasing response duration with decreasing stimulus level, as have been observed before in this (Cordova and Braun, 2007) and other laboratories (e.g., Kenyon et al., 1998; Lu and Tomchik, 2002).
Figure 1.
Representative waveforms of average AEPs (two replicate averages of 1000 sweeps each are superimposed) evoked by tonal pips (top) and noise bursts (bottom). Corresponding ± average waveforms are plotted beside the average AEPs. Amplitude (rms) amplitudes of the average of all 2000 sweeps and of the ± average are given on the top of corresponding traces. Values on the left side of AEP traces are the sound pressure level of the evoking stimuli (re 1 μPa) and the threshold values are in bold font. A sample waveform of the tonal stimulus is given below the AEP waveforms. The schematic envelope of noise burst is also given as a rectangular shape. The time-window used to measure AEP amplitude is indicated as a heavy black bar at the top of the figure.
Interobserver reliability of visual inspection
Each observer judged 25 detection thresholds using visual inspection of pairs of 1000 sweep averages at each stimulus level. The interobserver disagreement was profound. Cohen’s Kappa values, which measure interobserver reliability (Cohen, 1960), were 0.76, 0.80, and 0.87 for the three pairs of observers. Complete agreement (all three observers in agreement) only occurred 16% of the time, and the three observers made entirely different decisions for 20% of the judgments. The average maximum difference between any two observers was 8±6.1 dB for all the tests, and the average difference between all three observers was 6±4.0 dB. Across all the tests, 28% of the mean differences between all three observers were at least two stimulus level-steps (⩾10 dB), and only 52% of the average differences were within one level-step (5 dB).
When the observers made different judgments, the median judgment was reported as threshold for that stimulus level in that subject. Across animals, the mean detection threshold was 91±3.2 dB re 1 μPa (N=10) for tonal stimuli and 92±4.1 dB re 1 μPa (N=15) for noise stimuli.
Noise estimation accuracy
Since one of the basic assumptions behind the use of RBNSP is that noise is normally distributed, we examined the distribution of instantaneous voltages to assess the validity of this assumption. In our recordings, instantaneous voltages frequently deviated from a normal distribution (judged by Kolmogorov–Smirnov tests). The single-point recordings in 221 of 1028 (21.5%) 500-value blocks were not drawn from normal distributions. The non-normal percentages were 21.7% and 21.4% for responses evoked by tonal and noise stimuli, respectively. Examining the dataset by individual subject, the portion of data that appears to contain non-normal noise varied from 9.6% to 50.0%, with a mean of 22.6%±13.18%. Further examination of the distribution of the single-point recordings showed that most of the non-normal 500-value blocks were not significantly skewed (84.6%) but were kurtotic. Of those blocks with significant kurtoses beyond a 95% confidence interval, the vast majority were leptokurtic (97.9%), rather than platykurtic (2.1%).
To further evaluate the accuracy of both noise estimates, we compared them to the rms amplitude of the AEP evoked by the stimuli at the lowest level presented in each series for all animals (at least 10 dB below threshold, mean difference from threshold was ∼15 dB for tonal stimuli and ∼28 dB for noise bursts). At these stimulus levels, the AEP may be expected to contain only noise, and the rms of the average should be equal to the true RBN amplitude using the same sweeps. Therefore, we compared these no-response AEP rms values with the corresponding estimates obtained with both single-point and ± average methods. Since the evoked activity measured from the subject was filtered between 30 and 3000 Hz, but a 16.4-ms analysis window limits the noise to a bandwidth above 61 Hz (1∕.0164), we recalculated the no-response AEP rms with the full 800-point window when comparing the AEP rms and the RBNSP. Results of the comparisons showed no significant difference between the AEP rms and the RBN± (Wilcoxon matched-pairs signed-ranks test: P=0.9158, N=25). However, the RBNSP estimates were significantly higher than the no-response AEP rms (P<0.0001, N=25). Similar results were found for both stimulus types: comparing RBN± and no-response AEP rms, P=0.2324 for tonal stimuli (N=10) and 0.3028 for noise bursts (N=15); using RBNSP estimates, P=0.0195 (tone, N=10) and 0.0001 (noise, N=15). Based on these results, further analysis was based on RBN± rather than RBNSP
Background noise variation
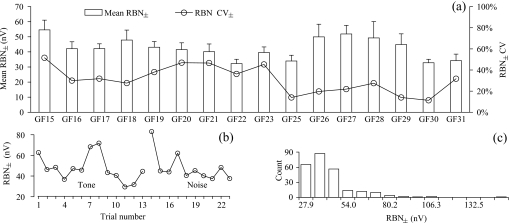
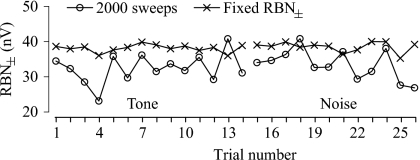
Across the 16 individual animals tested, the mean RBN± rms ranged between 32.2 and 54.6 nV after averaging 2000 sweeps. The overall average was 42.5±6.96 nV rms (N=16), with a CV (coefficient of variation) of 16.4%. Obvious fluctuation in RBN amplitudes was observed both within individual test series and among series collected on different days (Fig. 2). The CV of RBN for each individual test day varied from 11.3% to 51.6% around a mean of 30.9±12.65% (N=16).
Figure 2.
Variation of RBN amplitude in experiment 1, illustrated with (a) interindividual variation of the mean RBN± (with error in SD) and CV of the RBN± after 2000 sweeps, (b) within-individual variation of RBN± obtained in consecutive trials from one representative animal, and (c) the frequency distribution of all RBN± levels in 2000 sweep averages collected from all 16 animals.
Quantitative threshold estimation
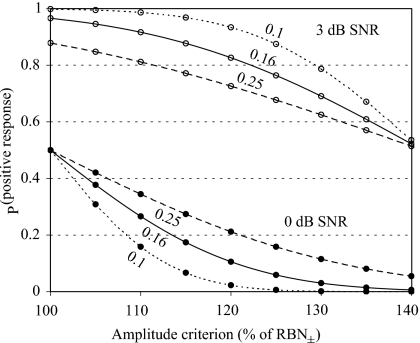
The direct measure of RBN amplitude from AEPs recorded at very low stimulus levels (no response) was further used to estimate the error in RBN± measures. We calculated the mean ratio of the no-response AEP to RBN± amplitudes and its variance. If RBN± was identical to the true noise amplitude (as estimated by the no response condition), this ratio should equal one and its deviation from that value represents the degree of error in the RBN± estimate. In our data, this noise estimate error ratio (NER) did not significantly deviate from a normal distribution (Kolmogorov–Smirnov tests, P=0.1855, N=16). The distribution of NER (mean=1.0 and SD=0.16) can be used to estimate the distribution of AEP amplitudes at specific signal-to-noise ratios (SNRs). For example, with a 3 dB SNR in the AEP, 82.7% of average AEP amplitudes would be expected to be at least 20% larger than the corresponding RBN. Conversely, when there is no response present (AEP amplitude is equal to RBN on average: 0 dB SNR), only 10.6% of the individual AEP averages will be at least 20% greater than their corresponding RBN estimates. Thus, using a criterion of 120% of RBN± to define a threshold response, we correctly categorize over 80% of responses positively when the SNR in the AEP is at least 3 dB, with a false positive rate of approximately 10%.
Greater or lesser stringency may be achieved by using higher or lower criteria, respectively. Differences in NER SD between datasets will result in altered hit and false alarm rates, but a SD as high as 0.25 (while mean NER=1.0) still provides high detectability of 3 dB AEP signals (Fig. 3). Similarly, changes in the mean NER can also affect the hit and false alarm rates slightly, by increasing both rates with increasing mean NER and vice versa (figure not shown). However, dividing the present dataset into two subgroups of eight animals resulted in similar NER estimates (1.0±0.15 and 1.0±0.22), and other samples from unpublished datasets and from the same subjects (not shown) also produced very similar values (also see Sec. 4C).
Figure 3.
Probabilities of positive judgments (false alarms at 0 dB SNR, filled circles, and hits at 3 dB SNR, open circles) as functions of varying amplitude criteria (percentage of the corresponding RBN level estimate). Curves are based on the NERs obtained from experiment 1, expressed as the ratio of no-response AEP amplitude to corresponding RBN± with an average of 1.0±0.16. Predictive curves (dotted lines) are also given for datasets with the same average NERs but different SDs (values beside the curves).
Using 20% above the corresponding RBN± as the criterion to define a minimum response amplitude, the mean detection threshold is 89±4.6 dB re 1 μPa (N=10) for 1000 Hz tonal burst and 92±5.3 dB re 1 μPa (N=15) for noise burst.
EXPERIMENT 2. THRESHOLD ESTIMATION USING STANDARDIZED AND CONTROLLED RBN AMPLITUDES
Introduction
Because intra- and interindividual RBN variation can be quite large, we adopted an averaging technique advocated by Don and Elberling (1996), wherein stimulus presentations were stopped after RBN amplitudes decreased below a fixed criterion, rather than after collecting a fixed number of sweeps. Given the results of experiment 1, we used the RBN± rms estimate and collected as many sweeps as needed to produce AEP averages with less than 30 nV RBN± rms. We then compared threshold estimates in individual animals at varying target RBN amplitudes.
Methods
Five animals were tested with both tone pips and noise bursts, as in experiment 1. The stimulus level was decreased in steps of 2.5 dB near threshold level, until several (3–5) steps below a provisionally estimated threshold. Unlike the test in experiment 1, each trial in experiment 2 was composed of flexible number of 200 sweep blocks, each containing four subblocks of 50 sweeps, with alternating stimulus polarity by subblock (100 sweeps per stimulus polarity in each block). The cumulative RBN amplitude after each additional block (200 sweeps) was monitored by calculating the RBN± of all accumulated sweeps after each block. At each stimulus level, data collection continued until the cumulative RBN± decreased below 30 nV rms (if this was reached with fewer than 2000 sweeps, additional sweeps were collected to allow for comparisons with 2000 sweep averages). In order to test the effects different RBN amplitudes might have on the threshold estimates, we extracted subaverages with RBN± amplitudes of 50, 40, and 30 nV rms from each trial. We also used the first 2000 sweeps (unfixed RBN±) of this sample in our comparisons. Following the results in experiment 1, the minimal AEP amplitude containing an evoked response was defined as 120% of the corresponding RBN±.
Results
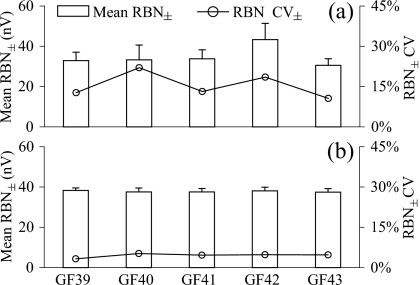
The mean RBN± after the first 2000 sweeps (34.8±4.94 nV rms, N=5) was slightly lower than that observed in experiment 1 [Fig. 4a]. In four of five animals, target noise amplitudes of 40 nV rms (the average amplitude in experiment 1) were obtained in fewer than 2000 sweeps (mean sweep number=1633±501; N=5).
Figure 4.
Interindividual variation of RBN± obtained in experiment 2 after (a) 2000 sweeps and (b) collecting enough sweeps lowering the RBN± below the fixed target RBN amplitude (40 nV rms). Error bars are SDs.
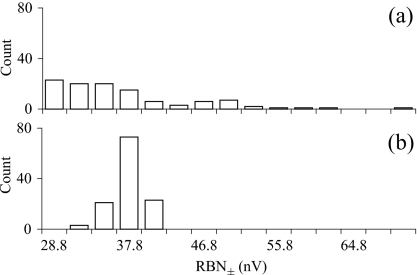
As shown in Figs. 4a, 56a, the noise amplitude varied considerably within and between individuals when using a fixed number (2000) of sweeps, as observed in experiment 1. The CV of mean RBN± across all individuals after 2000 sweeps in experiment 2 was 14.2%. Within individuals (or per experimental day) noise variability was similar, ranging from 10.6% to 22.0% (mean within-individual CV=15.4%±4.71; N=5). As expected, however, the cumulative background noise amplitudes were less variable when averaging was stopped at a target RBN amplitude [Figs. 4b, 56b], even though the decision to stop averaging is made rather coarsely, based on the cumulative noise amplitudes after each 200 sweep block. Using a target amplitude of 40 nV rms as an example, the RBN± showed a much narrower distribution compared to 2000 sweep averages (CV across individuals=1.0%). Variability within a subject was also greatly reduced, with a mean CV of 4.5%±0.74 (N=5).
Figure 5.
Within individual fluctuation of RBN± obtained in consecutive trials from one representative animal in experiment 2 after (a) 2000 sweeps and (b) collecting enough sweeps to lower the RBN± below the fixed target RBN amplitude (40 nV rms).
Figure 6.
Frequency distribution of RBN± obtained from all five animals used in experiment 2 after (a) 2000 sweeps and (b) collecting enough sweeps to reach the criterion RBN± amplitude (40 nV rms).
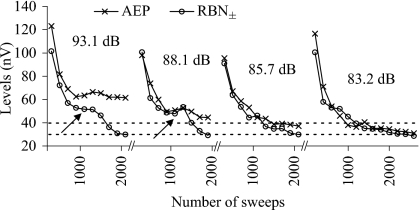
Figure 7 shows a detailed view of the effects of sweep number on RBN amplitudes. With increasing number of sweeps, the cumulative noise amplitude generally decreases monotonically as a power function of the number of sweeps. The AEP amplitude also declines initially as well, although it appears to asymptote or decreases its rate of attenuation after some minimum number of sweeps, if a response is contained in the average. If a criterion of the absolute amplitude of the AEP average or one relative to the RBN amplitude is used to judge the presence of an evoked response, it is clear that stopping averages at different RBN amplitudes could produce different threshold estimates. For instance, the AEP amplitude evoked by a 85.7 dB re 1 μPa tone was not 20% larger than the RBN if averaging was stopped at a target RBN amplitude of 40 nV rms, but if enough sweeps were collected to reduce the RBN± to less than 30 nV rms, then this stimulus did evoke a response 20% above RBN (Fig. 7). It is also important to note, as did Don and Elberling (1994), that the noise declines only as an approximate function of sweep number. Episodic noise sources, such as muscular contraction or external pollution can cause substantial deviations from the expected attenuation of RBN as a function of 1∕√N (Fig. 7, arrows).
Figure 7.
Cumulative AEP and RBN± amplitudes of one representative animal in experiment 2 as functions of number of sweeps collected at several different stimulus levels (values given above the plots; re 1 μPa). Horizontal dashed line indicates two potential target RBN levels, the cumulative RBN± lower than which the collecting and averaging more sweeps can be stopped. Threshold was determined to be 88.1 dB for 40 nV rms target RBN and 85.7 dB for 30 nV rms. Arrows indicate where the cumulative RBN amplitude did not decrease at the theoretical rate of 1∕√N (number of collected sweeps).
The mean NER obtained from this dataset at a target RBN amplitude of 40 nV rms was 1.0±0.18 (the NERs were computed using AEPs evoked by stimulus levels at least 5 dB lower than the estimated threshold, on average 14.0±6.79 dB below threshold). Since it was very similar to what we found and used to determine the response criterion in experiment 1, the same response criterion, 120% of the corresponding RBN±, was used to estimate the threshold in this experiment.
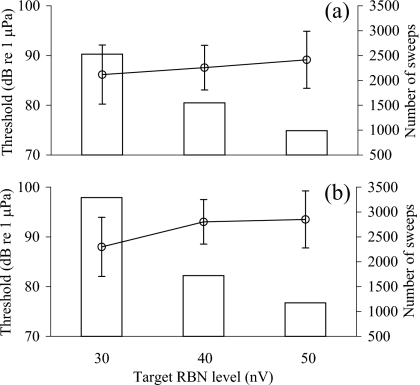
Figure 8 shows mean detection thresholds (±SD) estimated with this method at three target RBN amplitudes. Over a range between 50 nV rms and 30 nV rms, the estimated threshold decreased by 3 dB for tonal pips (from 89±5.7 dB re 1 μPa to 86±5.9 dB re 1 μPa) and 6 dB for noise bursts (from 94±7.0 dB re 1 μPa to 88±7.1 dB re 1 μPa), respectively. Repeated measures analysis of variance found significant differences among the thresholds for tonal pips (P=0.0049; P=0.1723 for noise bursts). However, significant differences in threshold were only found between those with target RBN amplitudes of 30 nV rms and higher amplitudes for tonal stimuli (30 nV rms versus 40 nV rms: P>0.05; 30 nV rms vesus 50 nV rms: P>0.01; post hoc multiple Tukey comparison), and to decrease the RBN± from 40 nV rms to 30 nV rms, an average of 77% more sweeps (mean sweep number for 30 nV rms=2894±1025 sweeps; N=5) were required. Nonetheless, it is clear that RBN amplitude has an impact on estimated threshold and should be reported with AEP results.
Figure 8.
The mean threshold estimates (±SD) for (a) tonal and (b) noise stimuli based on average AEPs with fixed target RBN amplitudes of 30, 40, and 50 nV rms. Histograms show the mean number of sweeps required to reach the target RBN levels.
DISCUSSION
As a method of threshold estimation, visual inspection has the clear advantage of being immediate and easy to implement. It is potentially effective, given the great human capability for visual pattern recognition and the general robustness of AEP average waveform shape. Multiple trained observers are not highly consistent, however. Both the present study and studies of trained audiologists (Arnold, 1985; Gans et al., 1992; Vidler and Parker, 2004; Lv et al., 2007) have reported poor agreement between observers in judging AEP threshold. In the present study, we reported that disagreement between all three observers was found for 20% of all threshold judgments, which is higher than what Lv et al. (2007) reported for three experienced audiologists (one out of twelve judgments in their Fig. 4). Cohen’s Kappa values, which measure observer agreements, were very similar in Arnold (1985), Lv et al. (2007), and the present study and were all below 0.9, a standard minimum criterion for independent observer reliability. This lack of reliability makes visual inspection particularly unsuited for hypothesis testing using AEP unless double-blind data collection and examination is carried out, which is generally not practical. Moreover, the need to have the AEP examined by multiple experienced observers, which might be necessary for reducing the subjective bias, is not always satisfied in AEP studies on animals. Nor is there a clear method for resolving observer discrepancies, other than averaging. Given these reasons, an objective method of threshold determination is highly desirable.
The determination of detection threshold depends on the quality of recorded average responses, and is therefore very likely affected by changes in background noise amplitude. Methods that depend on response repeatability (e.g., visual inspection or correlation analysis) can be affected by the distorting effects of noise in near threshold AEP waveforms (Elberling and Don, 1984). Methods that depend on response amplitude (e.g., Supin et al., 2001) must also consider noise amplitude because the AEP amplitude reflects the sum of the RBN and the evoked potential together, rather than the size of the evoked response alone. Moreover, even methods based on the relationship between AEP and RBN amplitude, like the one proposed herein, may still differ in sensitivity if different target RBN amplitudes are sought (or if RBN is not controlled). For example, we found a significant effect of reducing RBN amplitudes on threshold estimation when using tonal stimuli (Fig. 8). In our samples, and in similar reports in the literature (Elberling and Don, 1984), RBN amplitude can vary greatly after equal numbers of sweeps, and it is also possible that experimental treatments (such as drug-effects) could alter background physiological noise amplitudes. Standardized noise amplitudes would therefore minimize one confounding source of variability in AEP studies and should be used in all studies, regardless of threshold estimation technique. We therefore suggest that the presence of a response should be judged in relation to background noise amplitude, and that in hypothesis testing all comparisons should be made at equal or similar RBN amplitudes.
One advantage of the present method over subjective methods is that it allows for estimation of the accuracy of the technique based on the particular combinations of empirical noise reliability estimates and amplitude criteria (e.g., Fig. 3), as do other objective methods (Elberling and Don, 1987). Elberling and Don (1984) have advocated a parametric statistical approach using the F-distribution to compare the ratio (FSP) of EP variance (the square of AEP rms) to noise variance (the square of RBNSP). After estimating the degrees of freedom in an AEP average, the FSP can be compared to standard critical values of the F-distribution. The variance in single point amplitudes is a robust estimate of RBN variance and is thought to have degrees of freedom equal to the number of samples (i.e., sweeps). The AEP rms, however, is a different kind of time average whose degrees of freedom are not equal to the number of sweeps, but rather are limited by the frequency content present in the averaged time-window. Elberling and Don (1984) have provided estimated degrees of freedom for AEPs that range from 8 to 22. Unfortunately, much of our single-point values were not normally distributed and our attempts to fit an F-distribution to no-signal AEP ratios were not effective for estimating the degrees of freedom of our AEP rms. Instead we used an estimate of noise reliability that was amenable to a detection theory analysis rather than analysis by F-distribution critical values. Although the RBN± has lower degrees of freedom than RBNSP, it is equal in degree of freedom to the AEP rms estimate.
Error rates (misses and false alarms) can be predicted using our measure of noise estimate reliability (Fig. 3). Different values used as a minimum response amplitude (120% in present study) would result in different error rates (for both false alarms at 0 dB SNR and misses at higher SNRs) if the reliability of the noise estimate is unchanged, as shown in Fig. 3. Further, if the reliability of the RBN estimate differs, error rates will also change for any specific criterion value. Nevertheless, as long as the NER is empirically measured and a minimum response criterion is chosen, hit and false alarm rates for any specific SNR of AEP averages can be easily predicted. Moreover, our approach could also be used to estimate the expected detectability [in standard signal detection measures such as d′ (Green and Swets, 1988)] of a given SNR or the lowest SNR that would result in a specific d′ value. For instance, if NER=1.0±0.16 and a criterion of 120% of RBN± is used to judge the presence of a response, d′ values greater than 1 are expected to occur whenever the AEP SNR is greater than 1.24 dB.
The choices of target RBN amplitudes and the criteria depend on the experimental preparation and the amount of environmental noise present in the laboratory, both of which will influence the time required (number of sweeps) to reach the target noise amplitudes. Although a lower target RBN amplitude might provide a more sensitive threshold estimate (Figs. 78), the number of sweeps required will also increase and may prolong data collection beyond practical limits (Fig. 8). Therefore, the choice of the target RBN amplitude can only be made by a tradeoff between the desired quality of the AEP, i.e., the RBN amplitude, and the affordable time expense.
The choice of noise measurement may also affect the sensitivity of the threshold estimation (e.g., Cebulla et al. 2000; Stürzebecher et al., 2001). In the present study, measures of RBNSP were not always normally distributed, which did not match the assumptions required to use this measure in the statistical fashion proposed by Elberling and Don (1984). It is difficult to explain the difference in our data from those presented by Elberling and Don (1984). One potential explanation may be that the noise distribution was skewed by episodic noise from either the subject (e.g., muscle activity) or nearby electronics. However, we did not find obvious correlation between the non-normal blocks and the RBN amplitude or the number of sweeps rejected within the collection of the data, and few of the non-normal single-point blocks were significantly skewed. In any case, we found that RBN± was statistically indistinguishable from no-response AEP amplitudes while RBNSP was significantly higher than direct measures of RBN amplitude in no-response averages. Other studies (in humans) have not reported such difficulties, and some have indicated that RBNSP may be a more sensitive measure than RBN± (Don et al., 1984; Stürzebecher et al. 2001).
We also prefer the RBN± because it can be easily measured by most commercial software packages with few modifications; the procedure with a controlled RBN amplitude can be simply implemented by postprocessing of blocks of small numbers of sweeps and manually deciding to continue or stop collecting sweeps. It can be performed either with or without a true on-line analysis or the storage of single sweeps. In any case, the procedures advocated above, including controlling RBN and using an AEP:RBN ratio to determine threshold, may be applied using any potential method of noise amplitude estimation, including FSP. Further, we advocate an internal measure of RBN reliability that can be used in a signal detection analysis. Specific hit and false alarm rates can be achieved by adjusting the exact AEP:RBN ratio criterion based on each noise estimate, much like defining α in an F-ratio with a given degree of freedom (as with FSP: Elberling and Don, 1987).
The threshold values reported herein are higher than most behavioral thresholds (see Fay, 1988 for review; but also see Wolski et al., 2003 for a discussion of differences between behavioral and AEP thresholds in the same subjects) and some AEP thresholds (e.g., Kenyon et al., 1998, 65 dB re 1 μPa), but are similar to those published by Lu and Tomchick (2002, ∼80 dB re 1 μPa) and are consistent across multiple groups of subjects in this laboratory (e.g., Cordova and Braun, 2007, 83 dB re 1 μPa). Similar large differences between laboratories have been greatly discussed (Popper et al., 1973; Hawkins, 1981; Fay, 1988), and may reflect large differences in the acoustics of underwater sound propagation in different tanks (Parvulescu, 1967; Akamatsu et al., 2002). Stimuli with wavelengths larger than the arena (the wavelength of 1000 Hz underwater is 1.5 m) result in hydrodynamic fields with great (and unpredictable) inhomogeneities in the particle velocities in the sound field. The size, shape, and material properties of the arena greatly influence the pressure-to-velocity ratio for any given sound source, thus the position of the fish and speaker will change the true stimulus to the subject. A threshold measured only in pressure will not guarantee equivalent stimuli across different positions within the arena. Laboratories also differ in the method of holding the subject, which could easily affect the response of displacement sensitive otolithic organs. These factors greatly complicate the comparison of threshold values across laboratories, and future studies should examine the role of tank acoustics and AEP methodologies for measuring fish auditory thresholds.
It is less appreciated, however, that objective measures of AEP threshold are even more important for comparisons of hearing function within the same laboratory. Subjective threshold determination techniques are not consistent across observers, which raises the potential for subjective bias. Since physiological experiments are generally not conducted in a double-blind fashion, some objective thresholding technique is essential for statistical hypothesis testing. We suggest that controlled and clearly reported RBN amplitudes will effectively eliminate potential bias and intralaboratory variability in AEP audiometry.
SUMMARY AND CONCLUSIONS
In this report, we evaluated the interobserver reliability of subjective response determination in goldfish AEP audiometry using tone and noise stimuli. We found, as has been reported in several similar studies of clinical audiologists, that visual inspection and subjective evaluation is only modestly reliable at best. Among the three experienced observers in this study, complete and partial agreement on threshold level was found in 80% of their judgments. One potential explanation for this disagreement is that low signal-to-noise ratios in near-threshold AEPs make these judgments difficult. This phenomenon raises the added problem that if noise amplitudes vary, either between animals or experimental treatment groups, the difficulty, and hence, the reliability of subjective threshold determination techniques will differ between groups. This represents a serious pitfall for the use of AEPs in testing hypotheses about auditory function, for example after sonic or toxic insult. To develop a more objective response determination technique and measure the potential for noise variability, we evaluated two measures of residual noise in AEP averages. We found that while both measures provided relatively similar estimates of noise amplitude, RBNSP did not meet the normality assumption required for its use (Elberling and Don, 1984) in our data. Noise estimates as RBN± were indistinguishable from direct measurements of AEP physiological noise from no-response AEP recordings and has the added advantage of being easy to calculate with nearly any commercial evoked-potential software package. We further described the statistical structure of the ratio between RBN± and direct measures of AEP noise to estimate the reliability of our noise estimate, and to estimate the hit and false alarm rates of objective criteria for specific minimal response AEP SNRs. We conclude that objective measures of threshold determination with RBN amplitude control are relatively simple to apply and should be used in hypothesis testing using AEP audiometry. At a minimum, future AEP studies should include the verification of equal noise amplitudes in experimental treatment groups.
ACKNOWLEDGMENTS
The authors thank Dr. Manuel Don for his encouragement and advice during the development of this technique. Micah Cordova acted as our third subjective observer and they thank him for his contribution. Financial support for this research was provided by NIH awards 1 S06 GM60654 and 1 R03 MH067808 to C.B.B. The National Center for Research Resources of the NIH supports research infrastructure at Hunter College through the Research Centers in Minority Institutions (RCMI) award RR-03037.
References
- Akamatsu, T., Okumura, T., Novarini, N., and Yan, H. Y. (2002). “Empirical refinements applicable to the recording of fish sounds in small tanks,” J. Acoust. Soc. Am. 10.1121/1.1515799 112, 3073–3082. [DOI] [PubMed] [Google Scholar]
- Arnold, S. A. (1985). “Objective versus visual detection of the auditory brain stem response,” Ear Hear. 6, 144–150. [DOI] [PubMed] [Google Scholar]
- Boettcher, F. A. (2002). “Susceptibility to acoustic trauma in young and aged gerbils,” J. Acoust. Soc. Am. 10.1121/1.1513364 112, 2948–2955. [DOI] [PubMed] [Google Scholar]
- Brittan-Powell, E. F., Dooling, R. J., and Gleich, O. (2002). “Auditory brainstem responses in adult budgerigars (Melopsittacus undulatus),” J. Acoust. Soc. Am. 10.1121/1.1494807 112, 999–1008. [DOI] [PubMed] [Google Scholar]
- Burkard, R. (1984). “Sound pressure level measurement and spectral analysis of brief acoustic transients,” Electroencephalogr. Clin. Neurophysiol. 57, 83–91. [DOI] [PubMed] [Google Scholar]
- Cebulla, M., Stürzebecher, E., and Wernecke, K.-D. (2000). “Objective detection of auditory brainstem potentials.” Scand. Audiol. 29, 44–51. [DOI] [PubMed] [Google Scholar]
- Cohen, J. (1960). “A coefficient of agreement for nominal scales,” Educ. Psychol. Meas. 10.1177/001316446002000104 20, 37–46. [DOI] [Google Scholar]
- Cordova, M. S., and Braun, C. B. (2007). “The use of anesthesia during evoked potential audiometry in goldfish (Carassius auratus),” Brain Res. 1153, 78–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Don, M., and Elberling, C. (1994). “Evaluating residual background noise in human auditory brain-stem responses,” J. Acoust. Soc. Am. 10.1121/1.411281 96, 2746–2757. [DOI] [PubMed] [Google Scholar]
- Don, M., and Elberling, C. (1996). “Use of quantitative measures of auditory brain-stem response peak amplitude and residual background noise in the decision to stop averaging,” J. Acoust. Soc. Am. 10.1121/1.414560 99, 491–499. [DOI] [PubMed] [Google Scholar]
- Don, M., Elberling, C., and Waring, M. (1984). “Objective detection of averaged auditory brainstem responses,” Scand. Audiol. 13, 219–228. [DOI] [PubMed] [Google Scholar]
- Elberling, C. (1979). “Auditory electrophysiology. The use of templates and cross correlation functions in the analysis of brain stem potentials,” Scand. Audiol. 8, 187–190. [DOI] [PubMed] [Google Scholar]
- Elberling, C., and Don, M. (1984). “Quality estimation of averaged auditory brainstem responses,” Scand. Audiol. 13, 187–197. [DOI] [PubMed] [Google Scholar]
- Elberling, C., and Don, M. (1987). “Threshold characteristics of the human auditory brain stem response,” J. Acoust. Soc. Am. 10.1121/1.395019 81, 115–121. [DOI] [PubMed] [Google Scholar]
- Elberling, C., and Wahlgreen, O. (1985). “Estimation of auditory brainstem response, ABR, by means of Bayseian inference,” Scand. Audiol. 14, 89–96. [DOI] [PubMed] [Google Scholar]
- Fay, R. R. (1988). Hearing in Vertebrates: A Psychophysics Databook (Hill-Fay Associates, Winnetka: ). [Google Scholar]
- Gans, D., Del Zotto, D., and Gans, K. D. (1992). “Bias in scoring auditory brainstem responses,” Br. J. Audiol. 26, 363–368. [DOI] [PubMed] [Google Scholar]
- Green, D. M., and Swets, J. A. (1988). Signal Detection Theory and Psychophysics (Peninsula, Los Altos: ). [Google Scholar]
- Hawkins, A. D. (1981). “The hearing abilities of fish,” in Hearing and Sound Communication in Fishes, edited by Tavolga W. N., Popper A. N., and Fay R. R. (Springer, New York: ), pp. 109–133. [Google Scholar]
- Higgs, D. M., Brittan-Powell, E. F., Soares, D., Souza, M. J., Carr, C. E., Dooling, R. J., and Popper, A. N. (2002). “Amphibious auditory responses of the American alligator (Alligator mississipiensis),” J. Comp. Physiol., A 10.1007/S00359-002-0296-8 188, 217–223. [DOI] [PubMed] [Google Scholar]
- Higgs, D. M., Rollo, A. K., Souza, M. J., and Popper, A. N. (2003). “Development of form and function in peripheral auditory structures of the zebrafish (Danio rerio),” J. Acoust. Soc. Am. 10.1121/1.1536185 113, 1145–1154. [DOI] [PubMed] [Google Scholar]
- Hyde, M., Sininger, Y. S., and Don, M. (1998). “Objective detection and analysis of auditory brainstem response: an historical perspective,” Semin. Hear. 19, 97–113. [Google Scholar]
- Katbamna, B., Brown, J. A., Collard, M., and Ide, C. F. (2006). “Auditory brainstem responses to airborne sounds in the aquatic frog Xenopus laevis: Correlation with middle ear characteristics,” J. Comp. Physiol., A 192, 381–387. [DOI] [PubMed] [Google Scholar]
- Kenyon, T. N., Ladich, F., and Yan, H. Y. (1998). “A comparative study of hearing ability in fishes: the auditory brainstem response approach,” J. Comp. Physiol., A 10.1007/s003590050181 182, 307–318. [DOI] [PubMed] [Google Scholar]
- Le Prell, C. G., Yagi, M., Kawamoto, K., Beyer, L. A., Atkin, G., Raphael, Y., Dolan, D. F., Bledsoe, S. C. J., and Moody, D. B. (2004). “Chronic excitotoxicity in the guinea pig cochlea induces temporary functional deficits without disrupting otoacoustic emissions,” J. Acoust. Soc. Am. 10.1121/1.1772395 116, 1044–1056. [DOI] [PubMed] [Google Scholar]
- Lu, Z., and Tomchik, S. M. (2002). “Effects of a red-tide toxin on fish hearing,” J. Comp. Physiol., A 188, 807–813. [DOI] [PubMed] [Google Scholar]
- Lv, J., Simpson, D. M., and Bell, S. L. (2007). “Objective detection of evoked potentials using a bootstrap technique,” Med. Eng. Phys. 29, 191–198. [DOI] [PubMed] [Google Scholar]
- Mann, D. A., Higgs, D. M., Tavolga, W. N., Souza, M. J., and Popper, A. N. (2001). “Ultrasound detection by clupeiform fishes,” J. Acoust. Soc. Am. 10.1121/1.1368406 109, 3048–3054. [DOI] [PubMed] [Google Scholar]
- May, B. J., Prosen, C. A., Weiss, D., and Vetter, D. (2002). “Behavioral investigation of some possible effects of the central olivocochlear pathways in transgenic mice,” Hear. Res. 171, 142–157. [DOI] [PubMed] [Google Scholar]
- Mitchell, C., Kempton, J. B., Creedon, T., and Trune, D. (1996). “Rapid acquisition of auditory brainstem responses with multiple frequency and intensity tone-bursts.,” Hear. Res. 10.1016/S0378-5955(96)00081-0 99, 38–46. [DOI] [PubMed] [Google Scholar]
- Nickerson, R. S. (1998). “Confirmation bias: A ubiquitous phenomenon in many guises,” Rev. Gen. Psychol. 2, 175–220. [Google Scholar]
- Ozdamar, O., Delgado, R. E., Eilers, R. E., and Urbano, R. C. (1994). “Automated electrophysiologic hearing testing using a threshold-seeking algorithm,” J. Am. Acad. Audiol 5, 77–88. [PubMed] [Google Scholar]
- Parvulescu, A. (1967). “The acoustics of small tanks,” in Marine Bio-Acoustics, edited by Tavolga W. N. (Pergamon, Oxford: ), pp. 7–13. [Google Scholar]
- Popper, A. N., Chan, A. T. H., and Clarke, N. L. (1973). “An evaluation of methods for behavioral investigations of teleost audition,” Behav. Res. Methods Instrum. 5, 470–472. [Google Scholar]
- Popper, A. N., Smith, M. E., Cott, P. A., Hanna, B. W., MacGillivray, A. O., Austin, M. E., and Mann, D. A. (2005). “Effects of exposure to seismic airgun use on hearing of three fish species,” J. Acoust. Soc. Am. 10.1121/1.1904386 117, 3958–3971. [DOI] [PubMed] [Google Scholar]
- Porter, C. A., Martin, G. K., Stagner, B. B., and Lonsbury-Martin, B. L. (2006). “Distortion-product otoacoustic emission suppression growth in normal and noise-exposed rabbits,” J. Acoust. Soc. Am. 10.1121/1.2211407 120, 884–900. [DOI] [PubMed] [Google Scholar]
- Ramcharitar, J., and Popper, A. N. (2004). “Masked auditory thresholds in sciaenid fishes: A comparative study,” J. Acoust. Soc. Am. 10.1121/1.1771614 116, 1687–1691. [DOI] [PubMed] [Google Scholar]
- Ramcharitar, J. U., Higgs, D. M., and Popper, A. N. (2006). “Audition in sciaenid fishes with different swim bladder-inner ear configurations,” J. Acoust. Soc. Am. 10.1121/1.2139068 119, 439–443. [DOI] [PubMed] [Google Scholar]
- Schimmel, H. (1967). “The (±) reference: accuracy of estimated mean components in average response studies,” Science 157, 92–94. [DOI] [PubMed] [Google Scholar]
- Song, L., McGee, J., and Walsh, E. J. (2006). “Frequency- and level-dependent changes in auditory brainstem responses (ABRs) in developing mice,” J. Acoust. Soc. Am. 10.1121/1.2180533 119, 2242–2257. [DOI] [PubMed] [Google Scholar]
- Stürzebecher, E., Cebulla, M., and Wernecke, K.-D., (2001). “Objective detection of transiently evoked otoacoustic emissions,” Scand. Audiol. 29, 78–88. [DOI] [PubMed] [Google Scholar]
- Supin, A. Y., Popov, V. V., and Mass, A. M. (2001). The Sensory Physiology of Aquatic Mammals (Kluwer, New York: ). [Google Scholar]
- Vidler, M., and Parker, D. (2004). “Auditory brainstem response threshold estimation: Subjective threshold estimation by experienced clinicians in a computer simulation of the clinical test,” Int. J. Audiol. 43, 417–429. [DOI] [PubMed] [Google Scholar]
- Wolski, L. F., Anderson, R. C., Bowles, A. E., and Yochem, P. K. (2003). “Measuring hearing in the harbor seal (Phoca vitulina): Comparison of behavioral and auditory brainstem response techniques.,” J. Acoust. Soc. Am. 10.1121/1.1527961 113, 629–637. [DOI] [PubMed] [Google Scholar]
- Wong, P. K. H., and Bickford, R. G. (1980). “Brain stem auditory evoked potentials: The use of noise estimate,” Electroencephalogr. Clin. Neurophysiol. 50, 25–34. [DOI] [PubMed] [Google Scholar]
- Yan, H. Y. (1998). “Auditory role of the suprabranchial chamber in gourami fish,” J. Comp. Physiol., A 10.1007/s003590050259 183, 325–333. [DOI] [PubMed] [Google Scholar]