Analytical time-domain Green’s functions for power-law media

Abstract

Frequency-dependent loss and dispersion are typically modeled with a power-law attenuation coefficient, where the power-law exponent ranges from 0 to 2. To facilitate analytical solution, a fractional partial differential equation is derived that exactly describes power-law attenuation and the Szabo wave equation [“Time domain wave-equations for lossy media obeying a frequency power-law,” J. Acoust. Soc. Am. 96, 491–500 (1994)] is an approximation to this equation. This paper derives analytical time-domain Green’s functions in power-law media for exponents in this range. To construct solutions, stable law probability distributions are utilized. For exponents equal to 0, 1∕3, 1∕2, 2∕3, 3∕2, and 2, the Green’s function is expressed in terms of Dirac delta, exponential, Airy, hypergeometric, and Gaussian functions. For exponents strictly less than 1, the Green’s functions are expressed as Fox functions and are causal. For exponents greater than or equal than 1, the Green’s functions are expressed as Fox and Wright functions and are noncausal. However, numerical computations demonstrate that for observation points only one wavelength from the radiating source, the Green’s function is effectively causal for power-law exponents greater than or equal to 1. The analytical time-domain Green’s function is numerically verified against the material impulse response function, and the results demonstrate excellent agreement.

INTRODUCTION

The attenuation coefficient for biological tissue may be approximated by a power law1 over a wide range of frequencies. Measured attenuation coefficients of soft tissue typically have linear or greater than linear dependence on frequency. For example, breast fat has a power-law exponent of y=1.5, while breast tissue ranges1 from y=1 to y=1.5. This nonquadratic frequency-dependent loss conflicts with the classical thermoviscous attenuation and, by the Kramers–Kronig relations, predicts a frequency-dependent phase speed or dispersion. Mathematically, the power-law frequency dependence of the attenuation coefficient cannot be modeled with standard dissipative partial differential equations with integer-order derivatives such as the Stokes wave equation2 or the telegrapher’s equation.3 However, fractional partial differential equations (FPDEs) sucessfully capture this power-law frequency dependence.

Power-law attenuation has been incorporated in the time-domain via FPDEs, which add loss to the wave equation with a time-fractional derivative4, 5, 6, 7 or a space-fractional derivative.8, 9 Unlike loss models that utilize integer-order derivatives,10, 11 these FPDEs support power-law attenuation coefficients for a range of noninteger exponents y. The Szabo wave equation is one such FPDE that interpolates between the telegrapher’s equation (y=0) and the Blackstock equation (y=2), allowing a large range of lossy behavior to be encapsulated in an expression with two loss parameters: an attenuation coefficient and a power-law exponent.4 Frequency-domain formulations, based on the Kramer–Kronig relations12, 13, 14 between attenuation and dispersion, have also been proposed for linear frequency dependence15 and power-law dependence.16, 17, 18

The bulk of the above work is numerical, which motivates additional analytical modeling of the combined effects of power-law loss and diffraction with Green’s functions in the time-domain. Unfortunately, few closed-form solutions that describe the effects of dispersion in the time domain have been reported. To date, approximate closed-form Green’s function solutions have only been provided for the special cases of y=0 (frequency-independent media) and y=2 (viscous media). In order to construct Green’s functions for general power-law exponents y, stable law probability distributions, which have previously been used to study fractional diffusion, are required. These stable distributions facilitate analytical descriptions of power-law attenuation directly in the time domain.

The purpose of this paper is to derive analytical time-domain three dimensional (3D) Green’s functions for power-law media for 0<y<2 in terms of stable probability densities. These Green’s functions are exact solutions for power-law media and approximate Green’s functions to the Szabo wave equation. In Sec. 2, the Szabo wave equation and the power-law wave equation corresponding to these solutions are formulated as FPDEs. 3D Green’s functions are then calculated in Sec. 3, allowing solutions to be obtained for fractional power-law media in terms of the Fox H-function19 and the Wright function.20 These functions have previously been used in the study of fractional diffusion,21 fractional relaxation,22 and fractional advection dispersion.9 In the special cases of y=0, 1∕3, 1∕2, 2∕3, 3∕2, and 2, Green’s function is expressed in terms of standard functions (Dirac delta, exponential, Airy, hypergeometric, and Gaussian functions). In the remaining cases, asymptotic expressions are provided. Numerical results and discussions of these results are provided in Secs. 4, 5, respectively, followed by the conclusion in Sec. 6 and the Appendix.

FPDE FORMULATIONS OF THE SZABO AND POWER-LAW WAVE EQUATIONS

Szabo wave equation

The Szabo wave equation4 approximates power-law media with an attenuation coefficient given by

$$\alpha \left(\omega \right)={\alpha }_0{\mid \omega \mid }^y.$$ (1)

The Szabo wave equation was originally derived as an integro-differential equation for fractional power-law media. Subsequently, Ref. 23 expressed the Szabo wave equation in terms of fractional derivatives, thereby allowing the machinery of fractional calculus to be utilized. For y≠1, the Szabo wave equation is written as

$${\nabla }^{2}p-\frac{1}{c_0^2}\frac{{\partial }^{2}p}{\partial t^2}-\frac{2{\alpha }_0}{c_0\cos (\pi y∕2)}\frac{{\partial }^{y+1}p}{\partial t^{y+1}}=0,$$ (2)

where the third term accounts for dispersive loss. In the special cases of y=0 and y=2, the fractional derivative term reduces to first and third temporal derivatives, respectively. For fractional y, the third term is defined by the Riemann–Liouville fractional derivative defined in Appendix A.

For fractional y, Eq. 2 is a FPDE that approximates lossy dispersive media satisfying a power-law. As discussed in Ref. 4, Eq. 2 is valid for α₀⪡1 in the (a) high-frequency limit for y<1 and (b) low-frequency limit for y>1. As shown below, a more general model for power-law media is obtained by including a higher-order temporal derivative. As in the case of the Stokes wave equation, the particle velocity and velocity potential also satisfy Eq. 2. From the definition of the fractional derivative given in Appendix A, Eq. 2 is also recognized as a singular integro-differential equation, where the fractional derivative term depends on the past history of the pressure p(r,t).

Frequency-independent (y=0) and viscous (y=2) media

In the special cases of frequency-independent media (y=0) and viscous media (y=2), the Szabo wave equation reduces to well-known integer-order PDEs which are solved via standard methods. The y=0 case corresponds to the telegrapher’s equation

$${\nabla }^{2}p-\frac{1}{c_{\infty }^2}\frac{{\partial }^{2}p}{\partial t^2}-\frac{2{\alpha }_0}{c_{\infty }}\frac{\partial p}{\partial t}=0,$$ (3)

which models one-dimensional (1D) damped string motion and electromagnetic wave propagation in conductive media. The reference frequency c_∞ is the phase speed in the limit of infinitely high frequency, and α₀ is the attenuation coefficient for ω=1. The 3D Green’s function for Eq. 3 consists of two terms: an exponential attenuated spherical wave, which is localized at time R∕c_∞, and a wake involving a modified Bessel function, which extends for infinite time. If α₀ is small, the modified Bessel function term is of order ${\alpha }_0^2$, yielding the high-frequency approximation3

$$g(R,t)\approx u\left(t\right)e^{-{\alpha }_{0}R}\frac{\delta (t-R∕c_{\infty })}{4\pi R}$$ (4)

where u(t) is the Heaviside step function. Equation 4 is an attenuated spherical wave, which is localized in time and hence is nondispersive.

In the viscous case (y=2), the Szabo equation reduces to the Blackstock equation

$${\nabla }^{2}p-\frac{1}{c_z^2}\frac{{\partial }^{2}p}{\partial t^2}+\frac{2{\alpha }_0}{c_z}\frac{{\partial }^{3}p}{\partial t^3}=0,$$ (5)

which models acoustic wave propagation in viscous media24 under a plane wave approximation for small α₀ and for small frequencies. The reference frequency c_z is the phase speed in the limit of zero frequency. Since the spatial bandwidth of a wavefield is large near the source, Eq. 5 fails to capture the high-frequency content in the extreme near field of a radiator.2, 24 The 3D Green’s function of Eq. 5 is calculated via standard Fourier transform techniques, yielding

$$g(R,t)\approx \frac{1}{4\pi R}\sqrt{\frac{1}{4\pi R{\alpha }_0}}\exp (-\frac{{(t-R∕c_z)}^2}{4R{\alpha }_0}),$$ (6)

which is an approximate solution to Eq. 5. Similar to the asymptotic solution to the Stokes wave equation,25 Eq. 6 predicts Gaussian spreading of a spherical wave as the field radiates away from the source. However, Eq. 6 is noncausal, which means that Eq. 6 specifies nonzero field values for t<0. However, for α₀ small and R sufficiently large, Eq. 6 and the causal Green’s function for the Stokes wave equation [see Eq. (3) in Ref. 26] are virtually indistinguishable, which is demonstrated numerically in Ref. 2 for the 1D case.

By utilizing the loss operator defined in Eq. A2, the Szabo wave equation interpolates between the telegrapher’s equation and the Blackstock equation. The telegrapher’s equation is causal and hyperbolic, whereas the Blackstock equation is noncausal and parabolic. Mathematically, Eq. 2 is a second-order hyperbolic equation for y<1. For y>1, however, Eq. 2 becomes an order y+1 parabolic equation where high-frequency components propagate with infinite velocity. As y→1⁻ in Eq. 2, c_∞→∞, and as y→1⁺ in Eq. 2, c_z→∞, which agrees with the transition between hyperbolic and parabolic behaviors at y=1. Thus, the Szabo wave equation interpolates between the two different behaviors as the power-law exponent y varies from 0 to 2.

Power-law wave equation

As discussed in Ref. 4, Eq. 2 is an approximate model for wave propagation in a power-law medium for small values of α₀. To facilitate the analytical solution of wave propagation in power-law media, a FPDE that exactly describes power-law attenuation for arbitrary α₀ is derived, and the Szabo wave equation is an approximation to this FPDE. This exact FPDE is then solved for a point source in space time, thereby yielding desired Green’s function solution. Since both temporal and spatial Fourier transforms are utilized extensively throughout the derivation, the Fourier transform given by Eq. 3 in Ref. 4 is utilized throughout this paper. In order to derive the analytical time-domain Green’s function solution, a power-law dispersion relationship relating wavenumber k and angular frequency ω is required. This dispersion relationship should yield (1) a power-law attenuation coefficient and (2) a frequency-dependent phase speed. The power-law dispersion relationship that satisfies these requirements is

$$k=\frac{\omega }{c_0}-\frac{{\alpha }_0{(-i)}^{y+1}{\omega }^y}{\cos (\pi y∕2)},$$ (7)

for ω⩾0 and k(−ω)=k^*(ω) to ensure real solutions. The imaginary part of Eq. 7 yields the power-law attenuation coefficient given by Eq. 1. The real part produces

$$\frac{1}{c\left(\omega \right)}=\frac{\mathrm{Re}k\left(\omega \right)}{\omega }=\frac{1}{c_0}+{\alpha }_0\tan \left(\frac{\pi y}{2}\right){\mid \omega \mid }^{y-1}.$$ (8)

Letting c₁ denote the phase speed at ω₀=1 yields the expression

$$\frac{1}{c\left(\omega \right)}=\frac{1}{c_1}++{\alpha }_0\tan \left(\frac{\pi y}{2}\right)({\mid \omega \mid }^{y-1}-1),$$ (9)

which is valid for all y≠1. Equation 9 corresponds to the phase velocities computed via the Kramers–Kronig relations14, 27 and the time-causal theory.13 In addition, Eq. 8 is in close agreement with the experimental dispersion data presented in Refs. 12, 13, 14, 17. Thus, Eq. 2 supports the power-law attenuation and dispersion that is predicted by the Kramers–Kronig relationships and supported by experimental measurements.

In order to invert the wavenumber-frequency relationship into space time, the fourfold Fourier transform $\widehat{P}(\mathbf{k},\omega )$ of the time-domain pressure p(r,t) is multiplied by the dispersion relationship. Squaring both sides of Eq. 7 and multiplying by $\widehat{P}(\mathbf{k},\omega )$ yield

$$[-k^2+\frac{{\omega }^2}{c_0^2}-\frac{2{\alpha }_0}{c_0\cos (\pi y∕2)}{(-i\omega )}^{y+1}-\frac{{\alpha }_0^2}{{\cos }^2(\pi y∕2)}{(-i\omega )}^{2y}]\widehat{P}(\mathbf{k},\omega )=0.$$ (10)

Performing an inverse spatial Fourier transform produces the power-law Helmholtz equation

$${\nabla }^2\widehat{p}+[\frac{{\omega }^2}{c_0^2}-\frac{2{\alpha }_0}{c_0\cos (\pi y∕2)}{(-i\omega )}^{y+1}-\frac{{\alpha }_0^2}{{\cos }^2(\pi y∕2)}{(-i\omega )}^{2y}]\widehat{p}=0.$$ (11)

Finally, performing an inverse temporal Fourier transform using Eq. A3 yields the power-law FPDE

$${\nabla }^{2}p-\frac{1}{c_0^2}\frac{{\partial }^{2}p}{\partial t^2}-\frac{2{\alpha }_0}{c_0\cos (\pi y∕2)}\frac{{\partial }^{y+1}p}{\partial t^{y+1}}-\frac{{\alpha }_0^2}{{\cos }^2(\pi y∕2)}\frac{{\partial }^{2y}p}{\partial t^{2y}}=0,$$ (12)

which satisfies the dispersion relationship, Eq. 7, exactly. For small α₀, the fourth term in Eq. 12 is negligible, thus yielding the Szabo wave equation given by Eq. 2.

3D GREEN’S FUNCTION

Time-domain 3D Green’s functions for power-law media are derived in this section. These Green’s functions are exact solutions to the power-law wave equation in Eq. 12 and approximate solutions to the Szabo wave equation in Eq. 2. Applying a point source at time t=0 to Eq. 12 and considering Green’s function g(R,t) yield

$${\nabla }^{2}g-\frac{1}{c_0^2}\frac{{\partial }^{2}g}{\partial t^2}-\frac{2{\alpha }_0}{c_0\cos (\pi y∕2)}\frac{{\partial }^{y+1}g}{\partial t^{y+1}}-\frac{{\alpha }_0^2}{{\cos }^2(\pi y∕2)}\frac{{\partial }^{2y}g}{\partial t^{2y}}=-\delta \left(\mathbf{R}\right)\delta \left(t\right),$$ (13)

where R is the relative displacement between the source and the observer and R=∣R∣. Applying a temporal Fourier transform to Eq. 13 yields

$${\nabla }^2\widehat{g}+k^2\left(\omega \right)\widehat{g}=-\delta \left(\mathbf{R}\right),$$ (14)

where k(ω) is given by Eq. 7. The well-known Green’s function for Eq. 14 is given by

$$\widehat{g}(R,\omega )=\frac{e^{ik\left(\omega \right)R}}{4\pi R}.$$ (15)

Inserting Eq. 7 into Eq. 15 and grouping terms yield

$$\widehat{g}(R,\omega )=\left[\frac{\exp (i\omega R∕c_0)}{4\pi R}\right]\left[\exp (-{\alpha }_{0}R({\mid \omega \mid }^y-i\tan (\pi y∕2)\omega {\mid \omega \mid }^{y-1}))\right],$$ (16)

where the first factor solves the lossless Helmholtz equation. The time-domain Green’s function for y≠1 is recovered by applying an inverse Fourier transform and the convolution theorem, yielding

$$g(R,t)={\mathcal{F}}^{-1}\left[\widehat{g}(R,\omega )\right]=\left[\frac{\delta (t-R∕c_0)}{4\pi R}\right]{\mathcal{F}}^{-1}\left[\exp (-{\alpha }_{0}R({\mid \omega \mid }^y-i\tan (\pi y∕2)\omega {\mid \omega \mid }^{y-1}))\right],$$ (17)

which is expressed as a temporal convolution

$$g(R,t)=g_D(R,t)\ast g_L(R,t).$$ (18)

Within the framework of linear time-invariant filters, Eq. 18 combines the effects of dispersive loss and diffraction as a cascade of two system functions. The first factor in Eq. 18 is the Green’s function for the lossless wave equation given by

$$g_D(R,t)=\frac{\delta (t-R∕c_0)}{4\pi R},$$ (19)

which is responsible for the effect of propagation and diffraction. The second term is a loss function defined via

$$g_L(R,t)={\mathcal{F}}^{-1}\left[\exp (-{\alpha }_{0}R({\mid \omega \mid }^y-i\tan (\pi y∕2)\omega {\mid \omega \mid }^{y-1}))\right].$$ (20)

Interestingly, the inverse Fourier transform defined by Eq. 20 may be calculated in closed form using the machinery of stable distributions.28 The expression within the square brackets in Eq. 20 is identified as the characteristic function of a stable distribution with index y, center 0, skewness 1, and scale (Rα₀)^1∕y. The inverse transform given by Eq. 20 is then expressed concisely as

$$g_L(R,t)=\frac{1}{{\left({\alpha }_{0}R\right)}^{1∕y}}{\tilde{f}}_y\left(\frac{t}{{\left({\alpha }_{0}R\right)}^{1∕y}}\right),$$ (21)

where the function ${\tilde{f}}_y\left(t\right)$, which is independent of R and α₀, is the maximally skewed stable distribution of index y with scale 1. This family of functions has been studied extensively.29, 30, 31 Software is available for the computation of stable probability density functions (PDFs) and cumulative distribution functions32 based on formulas developed in Ref. 33. In the following analysis, an alternate parametrization f_y(t) is defined via

$$f_y\left(t\right)={\mid \sec (\pi y∕2)\mid }^{1∕y}{\tilde{f}}_y\left({\mid \sec (\pi y∕2)\mid }^{1∕y}t\right),$$ (22)

in order to utilize existing expressions for the stable density f_y(t). In the case of both sublinear power-law media (y<1) and superlinear power-law media (y>1), f_y(t) possesses the following analytical properties: (1) f_y(t)⩾0 for all t, (2) f_y(t) is infinitely continuously differentiable (or smooth), (3) f_y(t) is unimodal, and (4) ${\int }_{-\infty }^{\infty }{f}_y\left(t\right)dt=1$. Although these properties are common to all maximally skewed stable distributions, the behavior of f_y(t) differs for y<1 and y>1. Properties of these functions are studied in the following two subsections for sublinear (y<1) and superlinear (y>1) power-law media. The special case of y=1 is discussed in Sec. III D.

Equation 18 is approximate Green’s function, valid for small α₀, for the Szabo wave equation given by Eq. 2. However, Eq. 18 is an exact solution to the power-law FPDE given by Eq. 12 for linear homogeneous media since the imaginary part of Eq. 7 exactly describes the power-law behavior that the Szabo wave equation approximates. Thus, analytical Green’s function given by Eq. 18 is not restricted to small α₀ and large R.

Sublinear power-law media (0<y<1)

For the general case of 0<y<1, f_y(t) was first considered in Ref. 34 and later in Ref. 35 as an inverse Laplace transform. Rewriting Eq. 22 as a inverse Laplace transform yields

$$f_y\left(t\right)={\mathcal{L}}^{-1}\left\{e^{-s^y}\right\}=\frac{1}{2\pi i}{\int }_L{e}^{-s^y}{e}^{\mathrm{st}}ds,$$ (23)

where L is a contour in the left half plane. The notation is Eq. 23 was previously utilized in Ref. 36. The following analytic properties of f_y(t) for 0<y<1 are known:29, 30 (1) f_y(t) has support on [0,∞) and (2) as t→∞, f_y(t)∼t^−y−1. The inverse Laplace transform defined by Eq. 23 is expressed in terms of the Fox H-function19 using formulas presented in Ref. 22. The Fox H-function, which is defined in terms of a contour integral by Eq. B1, generalizes many of the special functions, such as Bessel, hypergeometric, and Mittag-Leffler.20 Using Eq. (62) in Ref. 22, the fractional exponential possesses the representation

$$\exp (-s^y)=\frac{1}{y}{H}_{0,1}^{1,0}(s\mid \begin{array}{c}(1,1)\\ (0,1∕y)\end{array}),\phantom{\mid }$$ (24)

and the inverse Laplace transform is then calculated using Eq. (30) in Ref. 22, yielding

$$f_y\left(t\right)=\frac{1}{yt}{H}_{1,1}^{1,0}(\frac{1}{t}\mid \begin{array}{c}(0,1)\\ (0,1∕y)\end{array}).\phantom{\mid }$$ (25)

For y=0, 1∕3, 1∕2, and 2∕3, Eq. 25 possesses the following exact representations:

$$f_0\left(t\right)=\delta \left(t\right),$$ (26a)

$$f_{1∕3}\left(t\right)=\frac{u\left(t\right)}{{\left(3t^4\right)}^{1∕3}}\mathrm{Ai}\left[\frac{1}{{\left(3t\right)}^{1∕3}}\right],$$ (26b)

$$f_{1∕2}\left(t\right)=u\left(t\right)\frac{1}{2\sqrt{\pi }{t}^{3∕2}}\exp (-\frac{1}{4t}),$$ (26c)

$$f_{2∕3}\left(t\right)=u\left(t\right)\frac{2}{3\sqrt{\pi }{t}^2}\exp (-\frac{4}{27t^2}){}_{2}F_0(\frac{1}{6},-\frac{1}{6};;-\frac{27t^2}{4}),$$ (26d)

where Ai(z) is the Airy function and ₂F₀(a,b;;z) is the confluent hypergeometric function of the second kind.

For the general case, an asymptotic expression, valid for t⪡1, is derived using the asymptotic form19 of $H_{1,1}^{1,0}\left(z\right)$. Alternatively, the inverse Laplace transform may be approximated via the method of steepest descents,36 yielding

$$f_y\left(t\right)\approx u\left(t\right)\frac{A}{t^{\nu }}\exp (-\frac{B}{t^{\mu }}).$$ (27)

The coefficients A, B, ν, and λ depend only on y and are given by

$$A=\frac{y^{1∕(2-2y)}}{\sqrt{2\pi (1-y)}},$$ (28a)

$$B=y^{1∕(1-y)}\frac{1-y}{y},$$ (28b)

$$\nu =\frac{2-y}{2-2y},$$ (28c)

$$\mu =\frac{y}{1-y}.$$ (28d)

Equations 18, 27, 28a, 28b, 28c, 28d provide a closed-form asymptotic approximation to the time-domain 3D Green’s function for sublinear power-law media (y<1). These equations exactly satisfy Eq. 26c at all times t for y=1∕2 and are valid for y≠1∕2 when t⪡1. For y≈1∕2, Eq. 27 also provides an excellent approximation37 for all values of t. For t>0, f_y is infinitely continuously differentiable (or smooth); moreover, $f_y^{\left(n\right)}\left(t\right)=0$ as t→0⁺ for all n⩾0, implying strong causality.2, 36 However, for y≠1∕2 and t⪢1, the asymptotic solution given by Eq. 27 decays exponentially for large times, while f_y(t) decays algebraically. Therefore, for large t, the first term in the asymptotic series for Eq. 25 is utilized, yielding29

$${\tilde{f}}_y\left(t\right)\approx \frac{\sin (\pi y∕2)\Gamma (y+1)}{\pi t^{y+1}},$$ (29)

which indicates a slowly decaying tail.

To show the behavior of f_y(t) for 0<y<1, the PDFs for the sublinear attenuation cases y=1∕3, 1∕2, 2∕3, and 9∕10 are displayed in Fig. 1. Since the ordinate f_y(t) is a PDF, the abscissa t is unitless. The expressions given by Eqs. 26a, 26b, 26c, 26d are evaluated for y=1∕3, 1∕2, and 2∕3, while the STABLE toolbox is utilized for y=9∕10. In all of these cases, f_y(t) is identically zero for t<0 and smooth. As y increases from 1∕3 to 9∕10, the main plume spreads out, while the asymptotic decay accelerates from t^−4∕3 to t^−19∕10 due to the behavior predicted by Eq. 29.

Figure 1.

Plots of maximally skewed stable PDFs f_y(t) for four sublinear attenuation cases: y=1∕3, 1∕2, 2∕3, and 9∕10. Equations 26a, 26b, 26c, 26d are evaluated for y=1∕3, 1∕2, and 2∕3, while the y=9∕10 case is evaluated with the STABLE toolbox (Ref. 32).

As y→0, f_y(t)→δ(t), while as y→1⁻, f_y(t)→δ(t−1). Thus, there is a delay incorporated into the stable distribution which accounts for the slower phase velocity in a dispersive medium. This delay is apparent in the asymptotic representation given by Eq. 27. For very small t, the argument of the exponent in Eq. 27 is very large, causing f_y(t) to approach zero. The delay t_d of f_y(t) can be approximated by setting the exponential argument of Eq. 27 equal to unity, yielding t_d≈B^1∕μ. Letting y vary from zero to 1, t_d is also seen to increase smoothly from zero to one.

Superlinear power-law media (1<y⩽2)

In superlinear power-law media, the qualitative behavior of the loss function g_L(R,t) differs from that observed in sublinear power-law media. The maximally skewed stable distributions possess the additional analytical properties for 1<y⩽2: (1) f_y(t) has support on (−∞,∞), (2) as t→∞, f_y(t)∼t^−y−1 for y<2, and (3) as t→−∞, f_y(t) decays with exponential order. For y>1, f_y(t) is nonzero for all times t. Since the 3D Green’s function is simply a delayed and scaled version of f_y(t), the power-law Green’s function g(R,t) is nonzero for all t and is therefore noncausal for superlinear power-law media for all values of y such that 1<y⩽2. Since f_y(t) decays with exponential order as t→−∞, the solution is very small. This property, which was discussed by Szabo4 for the quadratic case (y=2), where f_y(t) is Gaussian, is also true for all 1<y⩽2 according to the stable law properties listed above.

The stable distribution f_y(t) is evaluated in terms of the Fox H-function [see Eq. (2.13) in Ref. 38] via

$$f_y\left(t\right)=\frac{1}{y}{H}_{1,1}^{1,0}(-t\mid \begin{array}{c}(1-1∕y,1∕y)\\ (0,1)\end{array}\phantom{\mid }),$$ (30)

where 1<y⩽2. Equation 30 may be simplified in terms of the Wright function ϕ(a,b;z), yielding

$$f_y\left(t\right)=\frac{1}{y}\varphi (-\frac{1}{y},1-\frac{1}{y};t),$$ (31)

which is a known solution of the time-fractional diffusion problem.39 For the special cases of y=3∕2 and y=2, Eq. 31 is expressed in terms of the confluent hypergeometric function of the second kind and a Gaussian, respectively:

$$f_{3∕2}\left(t\right)=\{\begin{array}{ll}\frac{3}{4\sqrt{\pi }{t}^{5∕2}}{}_{2}F_0(\frac{7}{6},\frac{5}{6};;-\frac{27}{4t^3})& \text{if}t>0\\ -\frac{2\exp (4t^3∕27)}{3\sqrt{\pi t}}{}_{2}F_0(\frac{1}{6},-\frac{1}{6};;\frac{27}{4t^3})& \text{if}t<0\end{array}\phantom{\}}$$ (32a)

$$f_2\left(t\right)=\frac{\exp (-t^2∕4)}{\sqrt{4\pi }}.$$ (32b)

Note that the y=2 case in Eq. 32b yields Eq. 6, which approximately solves the Blackstock equation24 in Eq. 5.

Unlike the solution described earlier for sublinear power-law attenuation (y<1), f_y(t) is nonzero for all t. Therefore, three separate cases are considered: early time (t⪡R∕c₀), late time (t⪢R∕c₀), and times near the wavefront. To obtain an early-time estimate, Eq. 30 is expanded in a Taylor series.38 If t⪡R∕c₀, then t_r→∞, allowing an asymptotic representation of Eq. 30 to be utilized:38

$$f_y\left(t\right)\approx A{\mid t\mid }^{\nu }\exp (-B{\mid t\mid }^{\mu })$$ (33)

where

$$A=\frac{y^{-1∕(2y-2)}}{\sqrt{2\pi (y-1)}},$$ (34a)

$$B=y^{-y∕(y-1)}(y-1),$$ (34b)

$$\nu =\frac{2-y}{2y-2},$$ (34c)

$$\mu =\frac{y}{y-1}.$$ (34d)

For y=2, Eq. 33 reduces to f₂(t) for all t, yielding the noncausal Blackstock solution. Equation 33 has the form of a “stretched exponential,” which is a characteristic of anomalous diffusion.40 In other words, the early-time response of superlinear power-law media is characterized by fractional diffusive behavior. For large t, the asymptotic formula given by Eq. 29 is utilized.

Since Eq. 33 is nonzero for all t, power-law Green’s functions are noncausal for 1<y⩽2. However, the rapid exponential decay for t⪡R∕c₀ makes the solution very small for large negative times (t⪡−1). Thus, the noncausal nature of Green’s function for 1<y⩽2 is not evident in numerical evaluations for small α₀. From a physical perspective, the phase velocity becomes unbounded as frequency increases, implying that high-frequency components propagate infinitely fast. However, as noted in Ref. 2 for the special case of y=2, these high-frequency components experience high absorption and attenuate over a short distance, implying Green’s function g(R,t)⪡1 for t⪡R∕c₀.

To show the behavior of f_y(t) for 1<y⩽2, the stable PDFs for the superlinear power-law attenuation cases y=11∕10, 3∕2, 19∕10, and 2 are displayed in Fig. 2. The expressions given in Eqs. 32a, 32b are evaluated for y=3∕2 and 2, while the STABLE toolbox32 is utilized for y=11∕10 and 19∕10. In all cases, f_y(t) is nonzero for all t and smooth. For y=11∕10, f_y(t) is skewed to the right and decays very rapidly for t<−1. As y increases from 11∕10 to 2, the PDF becomes increasingly symmetric, eventually converging to a Gaussian. Although y=11∕10, 3∕2, and 19∕10 decay like t^−y−1, y=2 decays much more rapidly.

Figure 2.

Plots of maximally skewed stable PDFs f_y(t) for four superlinear attenuation cases: y=11∕10, 3∕2, 19∕10, and 2. Equations 32a, 32b are evaluated for y=3∕2 and 2, while the y=11∕10 and 19∕10 cases are evaluated with the STABLE toolbox (Ref. 32).

Linear power-law media (y=1)

The FPDE formulations of both the Szabo wave equation, given by Eq. 2, and the power-law wave equation, given by Eq. 12, break down as y→1 since cos(πy∕2)→0 in the denominator. To circumvent this problem, the frequency-domain solution at a reference frequency ω₀=1 is considered. The phase velocity is computed by taking the limit of Eq. 9 as y→1. Without loss of generality, let y approach one from the right. Defining y=1+ϵ and letting ϵ→0, then

$$\frac{1}{c\left(\omega \right)}=\frac{1}{c_1}+{\alpha }_0\tan (\pi (1+ϵ)∕2)({\mid \omega \mid }^{ϵ}-1)=\frac{1}{c_1}-{\alpha }_0\frac{{\mid \omega \mid }^{ϵ}-1}{\tan (\pi ϵ∕2)}\to \frac{1}{c_1}+\frac{2{\alpha }_0}{\pi ϵ}({\mid \omega \mid }^{ϵ}-1),$$ (35)

where the limit tan z→z is used in the last line. To finish the computation, the following limit is invoked:41

$$\frac{w^{\gamma }-1}{\gamma }\to \ln \left(w\right),$$ (36)

yielding

$$\frac{1}{c\left(\omega \right)}=\frac{1}{c_1}-\frac{2{\alpha }_0}{\pi }\ln \mid \omega \mid .$$ (37)

Equation 37 is identical to the Hilbert dispersive model derived in Ref. 15 and the Kramers–Kronig relation given by Eq. (13) in Ref. 14. Combining Eqs. 1, 37 yields a dispersion relationship between the wavenumber k (spatial frequency) and the temporal frequency ω:

$$k\left(\omega \right)=i{\alpha }_0\mid \omega \mid +\frac{\omega }{c_1}-\frac{2}{\pi }{\alpha }_0\omega \ln \mid \omega \mid .$$ (38)

The 3D time-domain Green’s function is computed by inserting Eq. 38 into the frequency-domain Green’s function given by Eq. 15 and assigning the delay term ω∕c₁ to ${\widehat{g}}_D(R,\omega )$. Inverse Fourier transforming this product of diffraction and loss factors yields Eq. 18 with a loss function

$$g_L(R,t)={\mathcal{F}}^{-1}\left\{\exp [-{\alpha }_{0}R\mid \omega \mid (1+\frac{2i\mathrm{sgn}\left(\omega \right)\ln \mid \omega \mid }{\pi })]\right\},$$ (39)

where the signum function sgn(ω) is introduced to enforce conjugate symmetry. Equation 39 is recognized as a stable distribution with index 1, center 0, skewness 1, and scale α₀R using the parametrization in Ref. 28. Thus, the inverse Fourier transform is expressed as

$$g_L(R,t)=\frac{1}{{\alpha }_{0}R}{\tilde{f}}_1\left(\frac{t}{{\alpha }_{0}R}\right),$$ (40)

where ${\tilde{f}}_1\left(t\right)$ is the inverse Fourier transform of Eq. 39 with α₀R=1. Carrying out the transform by integrating over the negative and positive frequencies and expressing the cosine in terms of complex exponentials yield

$${\tilde{f}}_1\left(t\right)=\frac{1}{\pi }{\int }_0^{\infty }\exp (-\omega )\cos [\omega t+\frac{2}{\pi }\omega \ln \omega ]d\omega .$$ (41)

Although ${\tilde{f}}_1\left(t\right)$ cannot be expressed in terms of the Fox or Wright functions, this expression is computable using the STABLE toolbox.32 Moreover, ${\tilde{f}}_1\left(t\right)$ has the same analytical properties as the superlinear power-law solutions shown earlier, including smoothness and exponential decay as t→−∞. Since f_y(t) is nonzero for all t, the power-law Green’s function is noncausal for y=1. For t⪢1, the asymptotic behavior of ${\tilde{f}}_1\left(t\right)$ is given by Eq. 29, which estimates the tail of the Green’s function.

NUMERICAL RESULTS

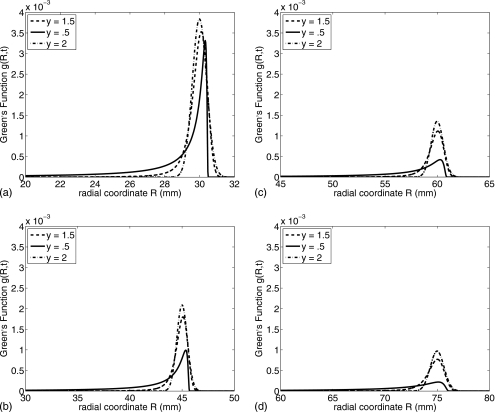
To numerically verify the analytical results presented above, the analytical Green’s function was compared to the material impulse response function (MIRF) approach developed in Ref. 16. In Fig. 3a, the 3D Green’s function is computed in a power-law medium with parameters y=1.5, c₀=0.15 cm∕μs, and α₀=0.1151 Np∕MHz^1.5∕cm using the analytical formula in Eq. 18. In Fig. 3b, the inverse Fourier transform defined by Eq. 20 was calculated numerically via an inverse fast Fourier transform (FFT). The two panels demonstrate excellent agreement. For power-law exponents y=1∕3, 1∕2, 2∕3, 3∕2, and 2, the function f_y(t) is represented in terms of the Airy, hypergeometric, exponential, and Gaussian functions. Equations 26a, 26b, 32a, 32b are evaluated numerically using the GNU Scientific Library.42 For other values of y, the function f_y(t) is represented as a maximally skewed stable distribution computed using the software package STABLE,32 which is a general-purpose software for analyzing stable distributions. The results of STABLE have been independently verified using codes developed by Robinson43 and a combination of asymptotic expressions, power series, and inverse power series. All demonstrate excellent numerical agreement. Transient fields are then evaluated using FFT-based convolutions.

Figure 3.

Comparison of 3D Green’s functions using (a) the MIRF approach and (b) the analytical Green’s function approach given by Eq. 18. Green’s functions are displayed at three different depths with y=1.5, c₀=0.15 cm∕μs, and α₀=0.1151 Np∕MHz^1.5∕cm.

Figure 4 shows the 3D power-law Green’s function for y=1∕2, 3∕2, and 2 for α₀=0.05 mm⁻¹ MHz^−y. The Green’s functions are shown as functions of the radial coordinate R for times t=20, 30, 40, and 50 μs in order to emphasize the spatial distribution of acoustic energy in power-law media. The qualitative properties of sublinear power-law media (y=0.5), superlinear power-law media (y=1.5), and viscous media (y=2) are displayed in these plots. In these figures, the impulsive excitation has been stretched and smoothed by the filtering effect of the medium. The Green’s function for sublinear power-law media (y=0.5) has a sharp wavefront at R=c₀t, where the field is identically zero to the right of this wavefront. Neither the superlinear power-law attenuation Green’s function nor the viscous Green’s function has this sharp wavefront. In the y=1.5 case, most of the energy is located in the slowly decaying tail of the Green’s function, whereas in the viscous case (y=2), energy is symmetrically distributed about the location R=c₀t.

Figure 4.

Snapshots of the 3D power-law Green’s function for y=0.5, 1.5, and 2.0 for α₀=0.05 mm⁻¹ MHz^−y. Snapshots of the Green’s function are shown for t=20, 30, 40, and 50 μs.

As time evolves in Figure 4, the peak amplitudes of all three of the Green’s functions decrease, thus accounting for the transfer of acoustic energy into random thermal energy within the intervening medium. In the y=0.5 and y=1.5 cases, the duration of the Green’s function increases, which is a consequence of the heavy tail behavior predicted by the asymptotic expression in Eq. 29. In the viscous case (y=2), spreading of the main plume occurs, although the Green’s function is more localized relative to the fractional cases due to the rapid decay of the Green’s function for large times. The absence of a slowly decaying tail is a consequence of the minimal dispersion associated with viscous and thermo-viscous loss.

To explore the effect of frequency-dependent attenuation on broadband pulse propagation, the velocity potential due to a point source at the origin was computed by convolving Eq. 18 with the pulse44, 45

$$v\left(t\right)=A_0{t}^3\exp (-\beta t)\sin \left(2\pi f_{0}t\right)\mathrm{rect}\left(\frac{t}{W}\right).$$ (42)

The following simulations utilize the center frequency f₀=2.5 MHz, pulse length W=1.2 μs, damping factor β=9.3750 μs⁻¹, and a normalization factor of A₀=616.3 mm∕μs. Two examples of velocity potential calculations are shown in two power-law media using parameters from Ref. 1: (1) a fat-like medium with y=1.5, c₀=1.432 mm∕μs, and α₀=0.086 Np∕MHz^1.5∕cm and (2) a liver-like medium with y=1.139, c₀=1.569 mm∕μs, and α₀=0.0459 Np∕MHz^1.139∕cm.

Figure 5 displays the velocity potential as a function of time t at radial distances 10, 25, 50, and 100 mm to show the effect of dispersion on the pulse shape. As R increases in Fig. 5, several qualitative features become evident. First, the pulse experiences rapid attenuation due to the combined effects of loss and spherical spreading. Second, the pulse changes shape due to the more rapid attenuation of the high-frequency components. In other words, the spectrum of the pulse experiences a frequency downshift. There are significant differences between the fat-like medium and the liver-like medium. The fat-like medium is more dissipative; therefore, greater attenuation and greater frequency downshifts are observed for large depths (R=100 mm). Although the liver-like medium is increasingly attenuated as the propagation distance increases, there is little change in the pulse shape. The pulse distortion in the fat-like medium indicates that the effects of dispersion become significant for large depths, which is consistent with the conclusion reached in Ref. 27.

Figure 5.

Velocity potential produced by a point source excited by a broadband pulse defined by Eq. 42 in two power-law media: (1) a fat-like medium with y=1.5, c₀=1.432 mm∕μs, and α₀=0.086 Np∕MHz^1.5∕cm and (2) a liver-like medium with y=1.139, c₀=1.569 mm∕μs, and α₀=0.0459 Np∕MHz^1.139∕cm. The velocity potential is displayed at radial distances 10, 25, 50, and 100 mm.

DISCUSSION

Causality and the superlinear attenuation paradox

In Ref. 4, the “quadratic loss paradox” associated with the 1D solution of the Blackstock equation given by Eq. 5 is presented. In the discussion of Sec. VII of Ref. 4, Szabo notes that the 1D solution is noncausal yet provides an excellent approximation to the thermoviscous wave equation for small values of ϵ=α₀c₀∣ω∣^y−1, where ω is the upper frequency limit. Szabo’s analysis is applied to three dimensions for superlinear power-law media (y>1).

By letting $\widehat{R}=R∕\lambda$, where λ is the wavelength associated with ω, the ratio of Green’s function at time t=0 to the peak value is given by

$$\eta =\frac{f_y(-R∕c_0∕{\left({\alpha }_{0}R\right)}^{1∕y})}{\max f_y\left(z\right)}=\frac{f_y(-{\widehat{R}}^{1-1∕y}\chi )}{\max f_y\left(z\right)}$$ (43)

where $\chi ={\mid \sec (\pi y∕2)\mid }^{1∕y}∕\left(c_0{\alpha }_0^{1∕y}\right)$. Letting the normalized distance $\widehat{R}=1$ in Eq. 43 yields the upper limit 20 log₁₀ η<−136 dB for 1<y⩽2. However, values of η are typically much smaller than this upper limit. For instance, for y=1.5, 20 log₁₀ η<−360 dB. Similar computations for other y⩾1 demonstrate that for observation points only one wavelength from the radiating source, Eq. 18 is effectively causal for all 0<y⩽2.

Physical interpretation and application to ultrasonic imaging

Unlike the Green’s function for lossless media, the Green’s function for power-law media is not localized in space. Rather, the energy radiated by a point source is smeared out over a wide volume. For viscous media (y=2), the Green’s function, given by a shifted and scaled Gaussian, decays rapidly for observation points distant from c₀R. For y<2, however, the Green’s function decays as an inverse power of distance for observation points between the origin and R. This slow decay is interpreted as the gradual relaxation of the medium after the initial wavefront has passed. As time evolves from t=20 μs to t=50 μs in Fig. 4, the tail of the Green’s function increases in both amplitude and duration, indicating that acoustic energy is being transferred from an organized spherical wavefront to a slowly decaying wake. Since this slow decay is not evident in the viscous case (y=2), a mechanism other than viscous dissipation (such as scattering by subwavelength structures) may be responsible for the observed wake.

Understanding the effect of attenuation on ultrasonic fields is important in B-mode image synthesis46 and full-wave simulations in heterogeneous media.47 Although the predicted change in phase velocity in most biological tissue is small,12 the effects of dispersion accumulate with propagation distance and may alter pulse shape over acoustically large distances.27 For instance, the change in phase velocity in the fat-like medium over the bandwidth of the pulse is less than 3 m∕s, yet the incident pulse undergoes a significant frequency downshift at a depth of R=100 mm.

The 3D power-law Green’s functions derived in Sec. 3 facilitate the study of 3D sound beams in dispersive power-law media. In particular, the impulse response produced by baffled circular and rectangular pistons may be constructed by integrating power-law Green’s function over the radiating aperture. Specifically, the methodology developed in Ref. 26 for circular apertures in viscous media and Ref. 48 for rectangular apertures in viscous media may be extended to power-law dispersive media by utilizing the analytical Green’s functions derived above. Since the power-law Green’s function is efficiently evaluated using the STABLE toolbox,32 the analytical expressions presented here may be used to either validate fields generated by dispersive full-wave linear solvers7 or construct efficient single-scattering codes based on the Born approximation. Therefore, the analytical tools developed in this paper may further the understanding of the influence of dispersive loss on ultrasonic scattering and image formation.

Figure 5 provides an example of one such evaluation. For large depths (R=50 mm and R=100 mm), the distortion of the pulse is clearly evident in the fat-like medium but much less apparent in the liver-like medium. In fat, attenuation increases with frequency at a greater rate (y=1.5) than in liver (y=1.139), yielding a larger frequency downshift. Since attenuation and dispersion increase with frequency, increasing the center frequency f₀ of the pulse will increase both the absolute magnitude of frequency downshift and time delay, thereby degrading the ultrasound image in a diagnostic application. To address this problem, the analytical Green’s functions presented in this paper may be used to select and evaluate pulse sequences for different imaging applications.

Comparison to frequency-domain models

To further validate the power-law Green’s function, the Green’s function for linear with frequency attenuation (y=1) was compared to the dispersive tissue model presented in Ref. 15, which incorporates a logarithmic frequency-dependent phase delay that is equivalent to Eq. 37. Since Ref. 15 utilizes a 1D model, the 1∕(4πR) factor in the power-law Green’s function was omitted from this evaluation. The impulse response associated with the dispersive tissue model shown in Fig. 2 of Ref. 15 was then reproduced by evaluating Eq. 40 using the STABLE toolbox at times t retarded by a bulk delay given by τ_b=1∕c₁=6.67 μs∕cm. The minimum phase τ_m presented in Ref. 15 is not required in the evaluation since this additional delay is incorporated into the stable density ${\tilde{f}}_1\left(t\right)$.

The analytical time-domain Green’s functions presented in this paper may serve as references for calculations in a dispersive tissue model. These analytical models may prove advantageous relative to the frequency-domain models proposed in Refs. 15, 16, 27, which require the evaluation of numerical inverse Fourier transforms. To expedite these inverse transforms, FFTs are utilized, which require (1) uniform discretization in time and (2) adequate sampling of $\widehat{g}(R,\omega )$ in the temporal frequency domain. In contrast, the time-domain power-law Green’s functions presented above are not limited by these two requirements. These Green’s functions may be evaluated on a nonuniform grid of time samples without sacrificing efficiency. For example, these power-law Green’s functions may be used to validate finite difference time domain codes which use nonuniform time stepping. In addition, the error tolerance associated with evaluating f_y(t) via the STABLE toolbox is user specified,32 thus making these analytical Green functions an ideal reference for MIRF and dispersive tissue model calculations.

Alternate fractional models

FPDEs have previously been utilized in hydrogeology to model advection due to microheterogeneity.9, 49 These FPDE models utilize a 1D advection-dispersion equation to capture the dispersion in heterogeneous aquifers. Like the solutions to the power-law wave equation, the solutions to the advection-dispersion equation are translated and scaled stable distributions, thus suggesting a connection between the hydrogeologic and ultrasonic models. Also, sound speed heterogeneity has been proposed as a mechanism for attenuation in marine sediments.50 Since one possible mechanism for ultrasonic absorption is Class 0 scattering due to microheterogeneity,51 the power-law wave equation may approximate scattering due to heterogeneity at the macromolecular level. The explicit connection between macromolecular scattering and power-law attenuation requires advanced mathematical tools such as homogenization theory and∕or subordinated random processes.30

Alternate FPDE models for power-law attenuation have been reported, including models by Chen-Holm8 and Wismer.7 The Chen-Holm model utilizes a space-fractional derivative of order y, while the Wismer model utilizes a fractional time derivative of order y−1. Both the Chen-Holm and the Wismer models support power-law attenuation with exponent y in the zero-frequency limit, which is desirable for biomedical applications. Analysis of these models using the mathematical tools developed in this paper is an intended topic of future research.

CONCLUSION

3D Green’s functions in power-law media have been analytically computed in the time domain using the tools of fractional calculus. This paper shows that Green’s functions for a medium with an attenuation coefficient given by Eq. 1 are maximally skewed stable distributions, shifted by a delay R∕c₀, scaled by (α₀R)^1∕y, and multiplied by a spherical diffraction factor of 1∕(4πR). Mathematically, power law Green’s functions are represented by a transient spherical wave, which embodies the diffractive process, convolved with a loss function g_L(R,t), which embodies both the attenuation and dispersion of the medium. Physically, therefore, the solutions to the power-law wave equation are represented as the linear coupling of diffraction and dispersive loss. The time-domain power-law Green’s functions presented here are exact solutions to the power-law wave equation in Eq. 12 and approximate solutions to the Szabo wave equation given by Eq. 2.

By solving for the time-domain power-law Green’s function with the machinery of stable distributions, efficient numerical evaluation is available via the STABLE toolbox.32 For all y<1, these Green’s functions are expressed in terms of Fox H-functions, while for y>1, the Green’s function is expressed in terms of the H function and Wright functions. For y=0, 1∕3, 1∕2, 2∕3, 3∕2, and 2, the Green’s function solutions are expressed in terms of widely known special functions. The analytical Green’s function was numerically verified against the MIRF result16 and Hilbert dispersive model,15 and example fields were computed. The results show that power-law Green’s function is causal for y<1 and noncausal for 1⩽y⩽2. Despite being noncausal for 1⩽y⩽2, power-law Green’s function provides an excellent causal approximation even for observation points very close to the radiating source. For 0<y<2, the Green’s function decays as t^−y+1, leaving a slowly decaying wake behind the primary wavefront. The Green’s functions reported in this paper may be used to construct solutions to diffraction and scattering problems in power-law media.

APPENDIX A: RIEMANN–LIOUVILLE FRACTIONAL DERIVATIVES

The Riemann–Liouville fractional derivative is formally defined via a hypersingular integral52

$$\frac{d^{y}f}{d{t}^y}=\frac{1}{\Gamma (-y)}{\int }_{-\infty }^t\frac{f\left(t^{\prime }\right)}{{(t-t^{\prime })}^{1+y}}d{t}^{\prime }.$$ (A1)

The nonintegrable singularity is removed from Eq. A1 by recognizing a differentiation operator, yielding

$$\frac{d^{y+1}g}{d{t}^{y+1}}\equiv \{\begin{array}{ll}\frac{1}{\Gamma (1-y)}\frac{d^2}{d{t}^2}{\int }_0^t\frac{g\left(t^{\prime }\right)}{{(t-t^{\prime })}^y}d{t}^{\prime }& \text{if}0<y<1\\ \frac{1}{\Gamma (2-y)}\frac{d^3}{d{t}^3}{\int }_{-\infty }^t\frac{g\left(t^{\prime }\right)}{{(t-t^{\prime })}^{y-1}}d{t}^{\prime }& \text{if}1<y<2.\end{array}\phantom{\}}$$ (A2)

In the literature, the 0<y<1 case is known as the Riemann–Liouville form, whereas the 1<y<2 case is the Liouville form. The following Fourier transform relationship for fractional derivatives is essential:52

$$\mathcal{F}\left(\frac{d^{y}g}{d{t}^y}\right)={(-i\omega )}^y\widehat{g}.$$ (A3)

In the 0<y<1 case, Eq. A3 assumes g(t) vanishes for t<0.

APPENDIX B: THE FOX-H FUNCTION

The Fox H-function20, 52 is defined via a complex contour integral

$$H_{p,q}^{m,n}\left(z\mid \begin{array}{c}(a_p,A_p)\\ (b_q,B_q)\end{array}\phantom{\mid }\right)\equiv \frac{1}{2\pi i}{\int }_L\chi \left(s\right)z^{s}ds,$$ (B1)

where (a_p,A_p)=(a₁,A₁),(a₂,A₂),…,(a_p,A_p), (b_q,B_q)=(b₁,B₁),(b₂,B₂),…,(b_q,B_q), and the integral density χ(s) is defined as

$$\chi \left(s\right)=\frac{{\prod }_{j=1}^m\Gamma (b_j-B_{j}s){\prod }_{j=1}^n\Gamma (1-a_j+A_{j}s)}{{\prod }_{j=m+1}^q\Gamma (1-b_j+B_{j}s){\prod }_{j=n+1}^p\Gamma (a_j-A_{j}s)}.$$ (B2)

Since the Gamma function is singular when the argument is a negative integer, Eq. B2 contains an infinite number of poles in general. Therefore, the contour L is chosen to separate the poles of Eq. B2. Note that Eq. B1 is the inverse Mellin transform of Eq. B2. The Fox H-function, which generalizes most of the special functions of mathematical physics, is discussed in great detail in Refs. 19, 22.

APPENDIX C: THE WRIGHT FUNCTION

The Wright function ϕ(α,β;z) is defined by an infinite series [see Eq. (1.11.1) in Ref. 52]:

$$\varphi (\alpha ,\beta ;z)\equiv \sum _{k=0}^{\infty }\frac{1}{\Gamma (\alpha k+\beta )}\frac{z^k}{k\text{!}}.$$ (C1)

The Wright function and the more general H-function are related [see Eq. (6.2.66) in Ref. 52] via

$$H_{1,1}^{1,0}\left(z\mid \begin{array}{c}(b,\alpha )\\ (0,1)\end{array}\phantom{\mid }\right)=\varphi (-\alpha ,b;-z).$$ (C2)

Equation C2 is computed by evaluating the contour integral definition of the H-function, which possesses an infinite number of poles, with Cauchy’s residue theorem. The resulting infinite series is identified as Eq. C1.