WITHIN-SESSION TRANSITIONS IN CHOICE: A STRUCTURAL AND QUANTITATIVE ANALYSIS

Abstract

The present study used within-session transitions between two concurrent schedules to evaluate choice in transition. Eight female Long-Evans rats were trained to respond under concurrent schedules of reinforcement during experimental sessions that lasted 22 hr. The generalized matching equation was used to model steady-state behavior at the end of each session, while transitional behavior that emerged following the change in reinforcement schedules was modeled using a logistic equation. The generalized matching and logistic equations were appropriate models for behavior generated during single-session transitions. A local analysis of behavior on the two response alternatives during acquisition was used to determine the source of preference as revealed in response ratios. The number of “low-response” visits, those containing three to five responses, remained stable. Preference ratios largely reflected a sharp increase in the number of visits with long response bouts on the rich alternative and a decrease in the number of such visits to the leaner alternative.

While considerable work has been dedicated to modeling steady-state behavior, relatively little attention has been paid to modeling behavior in transition. Transitional behavior occurs during the shift from one steady state to another (Johnston & Pennypacker, 1993; Sidman, 1960), is characterized by significant changes in the behavior ratio, B₁/B₂, and is usually observed following a change in reinforcement contingencies (Newland & Reile, 1999). Mazur and colleagues (Bailey & Mazur, 1990; Mazur, 1992, 1997; Mazur & Ratti, 1991) and Davison and Baum (Davison & Baum, 2000) have conducted some of the most recent work on transitional behavior by describing the behavior that emerges following a change from one concurrent schedule to another. Using random ratios of reinforcement, Bailey and Mazur and Mazur and Ratti employed hyperbolic equations to model transitional behavior in pigeons, and demonstrated that the rate of acquisition of choice was a function of the magnitude of the reinforcement ratio on two response keys rather than the absolute difference between the two reinforcement probabilities. Specifically, they showed that it was the magnitude of the reinforcement ratio, and not the difference between the two ratios, that was important. More recently, Davison and Baum and colleagues have evaluated the acquisition of choice when reinforcer ratios changed rapidly throughout one experimental session. This research showed that preference for a rich alternative developed quickly, and while slope estimates fell short of those calculated from multisession experiments, they reached 59% to 72% of asymptotic slope values after only 10 to 12 reinforcers had been delivered.

Another approach to modeling transitional behavior within a single session was proposed by Newland, Yezhou, Lögdberg, and Berlin (1994) in a study of how developmental exposure to environmental contaminants disrupts choice. Their approach was modified and further described by Newland and Reile (1999) and Newland, Reile, and Langston (2004). Here, a logistic function is used to model transitional behavior, and takes the form

1

where B₁/B₂ is the ratio of responses on alternative 1 to alternative 2, X is the number of reinforcers that have been delivered. The free parameters are X_half, the number of reinforcers that have been delivered when the transition is half-way complete; k, the slope of the S-shaped portion of the function; and Y_m, the magnitude of the transition (i.e., difference between the asymptotic and baseline response ratios; see Figure 1).

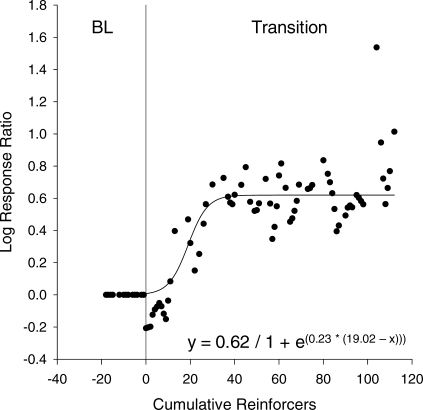
Fig 1.

Representative 32:1 transition (from subject 102). Log response ratio is plotted as a function of cumulative reinforcers earned. Data points are LOWESS smoothed values and the function was fitted by Equation 2. The vertical line indicates the beginning of the transition (x  =  0). Negative values of x are reinforcers delivered prior to the transition. This transition had a magnitude of 0.62, the half-maximal reinforcers value was 19.02, and the slope at the inflection point was 0.23. The last term indicates that the middle 1/e (∼1/2.7) of the transition was 1/0.23 or 4.3 reinforcers in length. BL  =  baseline.

Newland et al. (2004) applied Equation 1 to concurrent schedule behavior derived from a new experimental procedure in which a transition between two reinforcement ratios occurs in a single session. At the beginning of each session, behavior was reinforced under a concurrent variable interval-variable interval (conc VI VI) schedule in which the reinforcer ratio was 1:1 (baseline). Thirty min into the session, the reinforcer ratio changed such that one alternative became rich (i.e., delivered reinforcers at a higher rate than the other alternative), while the overall rate of reinforcement was the same as during the baseline period. This transition period lasted an additional 2 hr. Log response ratios were plotted as a function of cumulative reinforcers earned on a visit-by-visit basis, where one visit consisted of a bout of responding on one lever followed by a bout of responding on the other lever. Data were smoothed using a 9-point locally weighted scatterplot smoothing (LOWESS) algorithm (see Method section for further discussion of the LOWESS algorithm; see also Cleveland, 1979, for an in-depth description of the procedure), and Equation 1 was fitted to the smoothed data. In addition to transition analyses, response ratios during the last 30 min of each session were plotted as a function of scheduled reinforcer ratio and the generalized matching equation (Baum, 1974) was fitted to the data, allowing for the analysis of steady-state behavior. This equation takes the form

2

Here, B₁/B₂ is the ratio of responses on alternative 1 to alternative 2, R₁/R₂ is the ratio of reinforcers obtained (or, sometimes, scheduled) on alternative 1 to alternative 2, log c is the y-intercept, and a is the slope of the linear function. Log c is a measure of response bias, or a preference for responding on one alternative that is independent of the reinforcer ratio. The slope parameter, a, is a measure of behavioral sensitivity to changes in the reinforcer ratio.

While changes in response ratios did not reach the magnitude observed when behavior is given many weeks to stabilize (Baum, 1979) , Newland et al. reported that slope estimates approximated those obtained when behavior is allowed to stabilize over the course of several days.

The present study was designed to examine the structure of choice in transition. We focused on the role of reinforcer ratio by charting choice from a 30-min baseline, in which the reinforcer ratio from the two alternatives was 1:1, to a period during which the ratio either remained the same or abruptly changed to 4:1, 8:1, 16:1, or 32:1. We also examined how the number of responses per visit shifted in response to these changes in contingencies. Specifically, we examined whether preference for the richer alternative is due to a wholesale shift in the number of responses on that alternative (i.e., a change in both the mean and mode of the distribution of visit lengths), an increase in the number of visits with long response bouts (e.g., a change in the right tail of the distribution but with little variation in the mode), or some combination of the two. Finally, we evaluated the degree to which Equations 1 and 2 are able to describe terminal and transitional behavior, respectively, when transitions occur in a single session.

METHOD

Subjects

Subjects were 8 female Long-Evans rats obtained from Harlan Laboratories that ranged from 160-180 days in age at the beginning of the experiment. They were housed in an AAALAC accredited facility (the Biological Research Facility) at Auburn University on a 12h-12h dark/light cycle (lights on at 0600h). Rats were housed in pairs in single Plexiglas cages measuring 42 × 21.5 × 20.5 cm, and containing a clear plastic divider designed to divide the cage in half diagonally. Rats were fed ad libitum for several weeks to determine asymptotic body weights. Once weights stabilized, food restriction was initiated to reduce and maintain each rat at 230-240 gm (approximately 85-90% of their ad libitum weights).

Apparatus

Experiments were conducted in eight operant chambers purchased from Med Associates and housed in sound-attenuating cabinets. Each chamber contained two levers on the front panel and one on the back. The levers on the front panel were retractable and were calibrated to 0.20 N. The rear lever was not retractable, and while responses to it were recorded, there were no programmed consequences for these responses. One light emitting diode (LED) was located above each front lever and a 20 mg sucrose pellet dispenser was located equidistantly between the two levers. A 2.8-W house light was located near the ceiling of the chamber on the front panel and was aligned with the center of the pellet dispenser.

Experimental events were programmed and controlled by a computer using MED-PC IV software (Med Associates) with 0.01-s resolution. This computer was located in a room adjacent to that which housed the operant chambers.

Procedure

Once body weights stabilized, rats were trained to lever press for 20-mg sucrose pellets in an overnight session using an autoshaping procedure similar to that used by Paletz, Day, Craig-Schmidt, & Newland (2007). Training on the initial lever was considered complete following 90 independent responses (i.e., responses made after autoshaping trials ended). Responding on the adjacent lever was trained in a similar fashion the following evening.

Concurrent schedule training commenced after all subjects successfully completed autoshaping on both levers. At the beginning of each session, the house light and LEDs above each lever were illuminated and remained on throughout the session. Initially, responding was reinforced on an independently programmed conc VI 60-s VI 60-s schedule for the duration of a 120-min session. This yielded an average overall scheduled reinforcement rate of two pellets per min. Once stability criteria were met (the proportion of responses occurring on the left lever was between 0.4 and 0.6 for the last three consecutive sessions with no systematic changes in overall response rate), single session transitions began. The overall average scheduled reinforcement rate was held constant at two per min throughout each session. For most sessions, the scheduled reinforcement ratio changed from 1:1 (baseline portion) to one in which either the left or right alternative became rich (transition portion) 30 min into the session. For other sessions, no transition occurred. Each subject was exposed to the following transition magnitudes: 32∶1, 1∶32, 16∶1, 1∶16, 8∶1, 1∶8, 4∶1, 1∶4, and 1∶1 (no transition). Each subject experienced all transitions twice except for the 4:1 and 1:4 transitions (4:1 and 1:4 transitions only occurred once per rat). A 10-s timeout immediately preceded the change in reinforcement ratio. The time out was unsignaled, and responding during this period had no programmed consequences. The timeout was included because this condition served as a control for additional experimental manipulations that will be described in another paper.

Reinforcers were scheduled on a conc VI 60-s VI 60-s schedule of reinforcement during the first 30 min of the session, and on a conc random interval t₁ random interval t₂ (conc RI t₁ RI t₂) for the remainder of the session. To construct the intervals for the first 30 min of the session, a sequence of interreinforcer intervals (IRIs) for the left and right alternatives was generated in advance of the session. This was done by determining when a reinforcer would occur by selecting a random number between 0 and 1 with equal probability (seeded differently on different applications) and multiplying that number by a constant to generate the targeted reinforcement rate. For the first 10 min of the baseline period, that reinforcer was assigned to the left side with probability 0.5. For the period from 20 min to 30 min of baseline, a reinforcer was assigned to the left alternative with probability of 0.5 but with the constraint that neither alternative would provide less than 40% or more than 60% of the reinforcers. New IRIs were calculated frequently to avoid repeated scheduling of the same reinforcer sequence. Specifically, 30 such sequences were generated to create a new one for each day of the month.

Transition sessions occurred on Tuesdays and Fridays, and sessions in which the reinforcement ratio remained 1:1 for the duration of the 120-min session were conducted on Mondays, Wednesdays, and Thursdays. Transition magnitudes were presented in the order listed above, and the order was the same for all subjects. Given the presence of intervening days in which the reinforcement ratio remained 1:1 throughout the session, it is unlikely that order effects would be observed. A changeover delay (COD) of 2 s was employed throughout each condition. That is, when a subject switched from responding on one lever to responding on the other, no reinforcers were delivered for responses that occurred during the first 2 s of the visit on the new lever.

Data Analysis

Response and changeover (CO) rates

Response and CO rates were analyzed separately for each transition magnitude. Baseline, transition, and terminal response rates were calculated independently for the first 30, middle 60, and last 30 min of each session, respectively. Baseline, transition, and terminal response and CO rates were then averaged individually for each animal at each transition magnitude regardless of whether the left or right lever became the rich alternative. This was also done for transition and terminal response and CO rates for 16∶1, 8∶1, and 4∶1 transitions. Repeated measures analyses of variance (RMANOVA) with two within-subjects variables (magnitude and session segment) were used to evaluate differences in response and CO rates.

Steady state

To evaluate steady state behavior that emerges at the end of the transition period, response ratios (Y_m) from the last 30 min of each session were plotted as a function of scheduled and obtained reinforcement ratios using least-squares linear regression. Matching functions for each subject were constructed by fitting Equation 1 to these data.

Transitions

Log response ratio was plotted as a function of cumulative reinforcers on a visit-by-visit basis, where each visit consisted of one bout of responding on the right lever and one bout of responding on the left lever. To calculate the magnitude of the transition as compared with that day's baseline, and in order to fit a logistic equation with only three free parameters, data were normalized by calculating the median log response ratio during the baseline portion of the session and subtracting this from each data point during the transition. This yields a function with a lower asymptote of 0 and an upper asymptote that reflects the difference between terminal response ratios and the median baseline response ratio. This difference is the magnitude of the transition (Y_m). A 9-point LOWESS smoothing algorithm was applied to normalized data collected during the transition and terminal segments of the session (i.e., the last 90 min of the session). This algorithm weights points close to the targeted point (point 5) heavily and progressively less for more distal points, out to points 1 and 9. It removes visit-by-visit noise while retaining sensitivity to fluctuations in choice. Equation 2 was then fitted to the smoothed data, yielding three parameters per subject per transition: k, X_half, and Y_m. Data were combined within each reinforcement magnitude (i.e., 4∶1, 8∶1, 16∶1, and 32∶1) by taking the median parameter estimates of the left (e.g., 32∶1) and right (e.g., 1∶32) transitions for each subject. These values were then averaged across animals, yielding mean k, mean X_half, and mean Y_m values for each transition magnitude. RMANOVAs with transition magnitude as a within-subjects factor were performed to test for magnitude effects on transition parameters. Because slope parameters were nonnormally distributed, k values were log-transformed prior to conducting statistical analyses.

Transition sessions were excluded from all statistical analyses if they met both of the following criteria: (1) Y_m estimates exceeded the transition magnitude observed at the end of the session and (2) X_half estimates exceeded the total number of reinforcers delivered during the session. Also, slope estimates greater than 1 were set equal to 1. The number of sessions included for each transition magnitude and reasons for exclusion are presented in Table 1. Exclusion criteria are discussed in further detail in the Discussion section.

Table 1.

Number of Sessions Included in Statistical Analyses.

	Transition Magnitude
	4∶1	8∶1	16∶1	32∶1
Number of sessions included	14	30	31	22
Excluded for Ym and Xhalf criteria	0	1	1	6
Excluded for other reasons1	2	1	0	4

¹Other reasons include a failure of the statistical algorithm to converge on parameter estimates or due to missing sessions.

For comparison, transitions were also fit to LOWESS data using the hyperbolic equation

3

where p is the upper asymptote and c is the number of reiniforcers delivered when the transition is half-way complete. These parameters correspond to Y_m and X_half, respectively.

Histograms

To examine how changes in preference over the course of a transition are influenced by response bouts on the rich and lean levers, histograms were constructed for response bout length on each lever during the baseline, transition, and last 30 min of each session. This was done for each transition magnitude. Normal, Weibull, and log-normal functions were fitted to these histograms to determine which type of distribution best described the data. Only log-normal functions adequately modeled the data. Therefore, they are the only ones presented here.

For all statistical analyses, a Type I error rate of 0.05 was used, and all degrees of freedom for within-subjects tests were adjusted using the Huynh-Feldt correction.

RESULTS

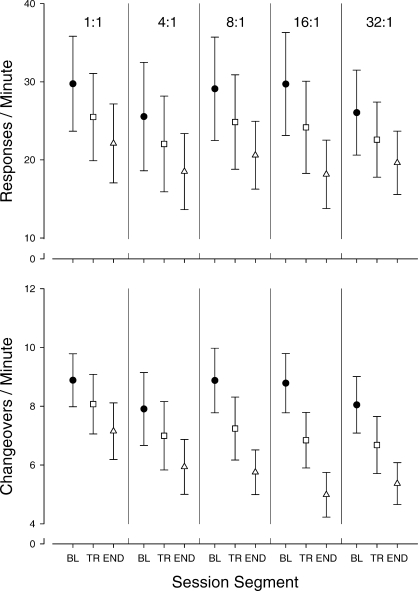
Figure 2 shows response (top panel) and CO (bottom panel) rates as a function of transition magnitude and session segment. An RMANOVA with two within-subjects factors (magnitude × session segment) showed a significant effect of session segment on response rate, F (2, 14)  =  17.674, p  =  0.003, ε  =  0.56, but no effect of reinforcer ratio and no interaction. Response rates decreased through the course of the session independently of the magnitude of the reinforcer ratio (Figure 2, top) For CO rates, there were significant main effects of segment, F (2,14)  =  35.617, p < .001, ε  =  0.78, and magnitude, F (4,28)  =  3.702, p  =  0.015, ε  =  1.0, and a significant interaction between the two, F (8,56)  =  4.583, p < 0.001, ε  =  0.98. CO rates decreased across the session at all transition magnitudes, and this effect became more pronounced as the transition magnitude increased (Figure 2, bottom).

Fig 2.

Response and changeover rates as a function of session segment and transition magnitude. Error bars are ± 1 standard error of the mean (SEM). BL  =  baseline, TR  =  transition, END  =  last 30 min of session.

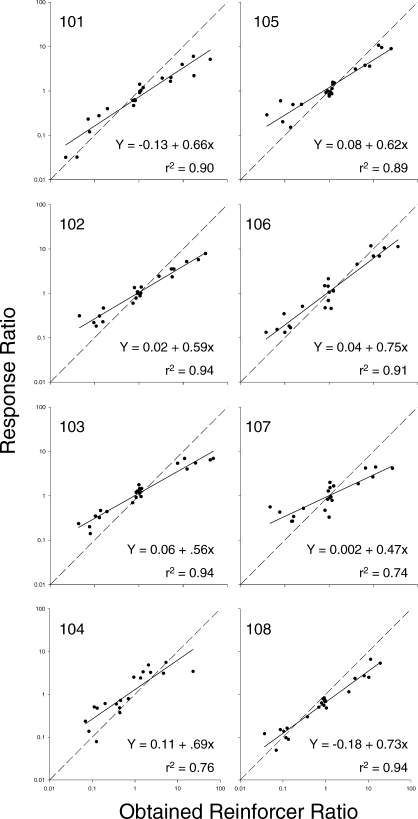
Matching functions (Equation 1) were estimated using response and reinforcer ratios from the last 30 min of each session. Parameter estimates from matching functions fitted using both scheduled and obtained reinforcer ratios are provided in Table 2. Slope values ranged from 0.41 to 0.71 and from 0.46 to 0.75 for functions fitted with scheduled and obtained reinforcers, respectively. Both independent variables accounted for a substantial amount of variance in response ratios. Scheduled reinforcer ratios accounted for an average of 81% of the variance in response ratios (range: 42 to 94%), while obtained reinforcer ratios accounted for an average of 88% of the variance (range: 74 to 94%). Figure 3 shows matching functions generated with obtained reinforcer ratios for individual subjects.

Table 2.

Parameter Estimates for Matching Functions.

Rat	Slope		Intercept (log c)		r2
	SCH1	OBT2	SCH	OBT	SCH	OBT
101	0.60	0.66	-0.18	-0.13	0.76	0.90
102	0.53	0.59	0.001	0.02	0.93	0.94
103	0.55	0.56	0.08	0.06	0.94	0.94
104	0.45	0.69	0.01	0.11	0.42	0.76
105	0.57	0.62	0.09	0.08	0.86	0.89
106	0.71	0.75	0.07	0.04	0.90	0.91
107	0.42	0.47	0.01	0.002	0.75	0.74
108	0.64	0.73	-0.23	-0.18	0.90	0.94
Ave.	0.56	0.63	0.083	0.083	0.81	0.88

¹Functions calculated with scheduled (SCH) reinforcer ratios.

²Functions calculated with obtained (OBT) reinforcer ratios.

³Averages calculated with absolute value of the intercept.

Fig 3.

Matching functions for individual animals. Matching equations and variance accounted for are provided in the lower right hand corner of each figure. Dashed diagonal line represents strict matching (i.e., B₁/B₂  =  R₁/R₂).

Appendix A provides parameters estimated for each transition using both the logistic and hyperbolic models. These data, along with visual examination of the fits, suggest that the logistic model was better suited for describing the data described here. While r² and SER values are similar for the two models, closer examination of Appendix A reveals that a greater number of transitions would have to be eliminated from analyses when fitted with the hyperbolic as compared to the logistic model due to over-estimation of Y_m and/or X_half. Therefore, the remainder of the paper focuses on data generated by Equation 1.

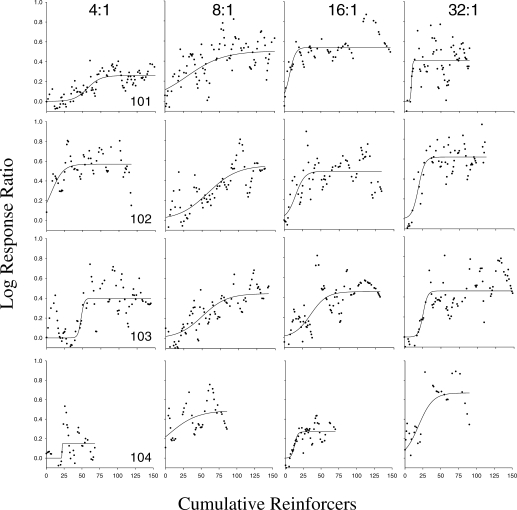
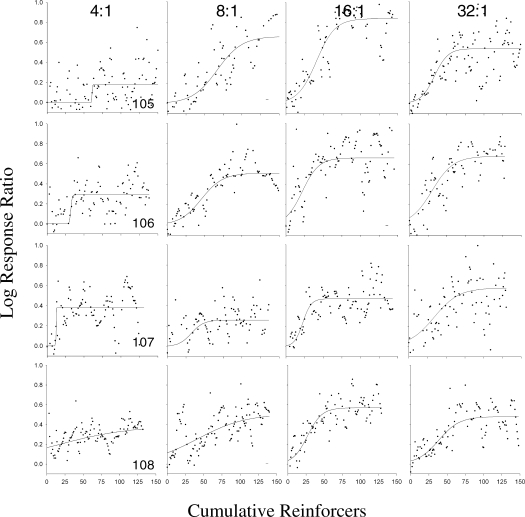
Figures 4 and 5 provide exemplar transitions for each animal at each of the transition magnitudes. Data points are those calculated by the 9-point LOWESS smoothing algorithm, and axes have been adjusted to promote across-subject comparisons.

Fig 4.

Sample transitions for 4 animals at 4:1, 8:1, 16:1, and 32:1 magnitudes, reading from the left to the right columns. Each row represents a different subject. Data points are those calculated by the 9-point LOWESS smoothing algorithm. The curves are the best-fitting functions generated with the logistic equation.

Fig 5.

Sample transitions for the other 4 animals at 4:1, 8:1, 16:1, and 32:1 magnitudes, reading from the left to the right columns. Each row represents a different subject. Data points are those calculated by the 9-point LOWESS smoothing algorithm. The curves are the best-fitting functions generated with the logistic equation.

Summary transition parameters are plotted as a function of transition magnitude in Figure 6. Only two 4:1 sessions were conducted, the data from these sessions were highly variable, and combined parameter estimates were strongly influenced by extreme values (because the median was always equal to the mean). Therefore, data from 4:1 transitions were excluded from all statistical analyses and figures. RMANOVAs for 8:1, 16:1, and 32:1 transitions showed no significant effects of magnitude on X_half, slope, or Y_m (ps  =  0.08, 0.48, and 0.15, respectively) .

Fig 6.

Average X_half, slope, and Y_m as a function of transition magnitude. Closed symbols represent group means, and error bars are ± 1 SEM. Open symbols are parameters from individual matching functions. *Data from the 4:1 transitions are not included in statistical analyses.

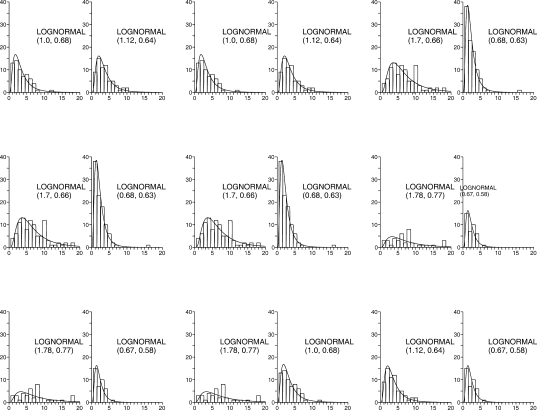
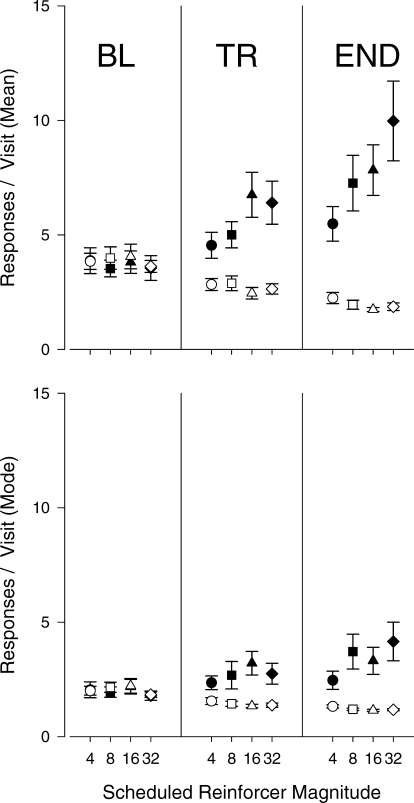
Figure 7 consists of six histograms showing the distribution of response bout lengths for a single representative subject during a 1:4, 1:16, and 1:32 transition. Panels on the left show data from the lean lever, while panels on the right show data from the rich lever. The top, middle, and bottom panels show bout length distributions from baseline, transition, and last 30 min of the session, respectively. Histograms were constructed using a bin width of one response. The geometric mean and standard deviation from the log-normal distribution are shown in parentheses in each panel. Summary data averaged across all subjects are shown in Figure 8. These values were derived from the parameters describing the log-normal distribution. RMANOVAs for arithmetic mean bout length on the rich lever (top panel, closed symbols) showed a significant interaction between magnitude and session segment, F (6, 42)  =  8.336, p  =  0.001, ε  =  0.63, and significant main effects for magnitude, F (3, 21)  =  8.063, p  =  0.006, ε  =  0.61, and segment, F (2, 14)  =  25.955, p  =  0.001, ε  =  0.57. RMANOVAs for arithmetic mean bout length on the lean lever (top panel, open symbols) showed a significant main effect of session segment, F (2, 14)  =  37.386, p < 0.001, ε  =  0.71. These results demonstrate that average bout lengths on the rich lever increased across the session, and that the magnitude of this increase depended on the magnitude of the transition. Specifically, as the transition magnitude increased, so did the change in average bout length. For the lean lever, average bout lengths decreased across a session, but were not affected by transition magnitude. RMANOVAs for modal bout lengths indicated a significant magnitude × segment interaction on the rich lever, F (6, 42)  =  4.028, p  =  0.005, ε  =  0.87, and significant main effects of session segment on both the rich, F (2, 14)  =  14.815, p  =  0.003, ε  =  0.60, and lean levers, F (2, 14)  =  23.310, p  =  0.001, ε  =  0.62. The pattern of changes in modal bout lengths is similar to that observed among mean bout lengths. However there was a much greater increase in mean than modal bout lengths on the rich lever, and the influence of reinforcer ratio was greater for means than for modes.

Fig 7.

Frequency distributions of responses per visit for a single subject (Rat 105) during three different transitions. The magnitude of the transition is shown above each pair of columns. The left and right columns show frequency distributions for responses on the lean and rich alternatives, respectively. The top row shows histograms from the first 30 min of a session during which the programmed ratio of reinforcers for each alternative was 1∶1. The second row shows frequency distributions during the transition period (30 – 90 min.), at which point the programmed ratios changed from 1∶1 to 1∶4, 1∶16, or 1∶32. The bottom panel shows data from the last 30 min of a session. The geometric mean and standard deviation for each distribution are given in parentheses. Distributions exclude responses that occurred during the changeover delays.

Fig 8.

Average and modal response rate as a function of transition magnitude and session segment. Means and modes are presented in the top and bottom panels, respectively. Error bars are ± 1 SEM. Closed symbols  =  rich lever, open symbols  =  lean lever, BL  =  baseline, TR  =  transition, END  =  last 30 minutes of session.

DISCUSSION

Single-session transitions were used to study the choice in transition for rats responding under concurrent schedules of reinforcement. The generalized matching relation (Equation 2) was used to model behavior from the last 30 min of each session, by which time behavior ratios were changing only very slowly even though they had likely not reached their ultimate steady-state value. By examining choice on a visit-by-visit basis, we were able to model the acquisition of choice with good resolution. It was evident that an acquisition phase could be described by a brief period of near stasis, or very slow change, followed by a rapid transition, and finally, an approach to an asymptote. A logistic function (Equation 1) was employed to model behavior during the transition phase because it provided the S-shape required for modeling this biphasic transition.

Overall Measures of Behavior

In the present study, response rates and CO rates were used to compare overall responding under concurrent schedules of reinforcement as a function of session segment and reinforcer ratio. A key element of these experiments was that the overall rate of reinforcement was held constant across all reinforcer ratios. Accordingly, overall response rates were relatively consistent across all reinforcer ratios employed.

Both response rates and CO rates decreased within sessions. A decline in response rates over the course of a session has been noted previously (McSweeney & Murphy, 2000), and may reflect habituation. Of particular importance is that they remained sufficiently high that choice could be modeled using data from the last 30 min of each session. Statistical analyses showed that the decline in CO rate interacted with the size of the reinforcer ratio. This may be a joint function of habituation (as with response rate) and of the well-known inverse relationship between changeover rate and reinforcer ratio (Baum, 1974; Myerson & Hale, 1988; Stubbs & Pliskoff, 1969).

Terminal Behavior

The generalized matching equation was well-suited for describing terminal behavior ratios that emerged at the end of single-session transitions. Equation 1 accounted for a large proportion of the variance in response ratios when obtained reinforcement ratios were used as the independent variable. Bias, as indicated by Equation 1, was generally low and unsystematic. Slope values, said to reflect sensitivity to reinforcement or the difference in the reinforcement rates between the two alternatives (Baum, 1974; Davison & McCarthy, 1988; Davison & Nevin, 1999), were generally lower than those reported in multisession studies. In the single session transitions described here, slope values averaged 0.63 as compared with averages of approximately 0.88 for rats in multisession transitions (Baum, 1979). Nonetheless, it is noteworthy that this level of sensitivity emerges over the course of a 2-hr session. In fact, Davison and Baum (2000) have shown that average slope estimates reach values between 0.52 and 0.63 within 10 reinforcers following a condition change. Taken together, these data suggest that initial preference for a newly rich lever is acquired rapidly, but that a slower rise to asymptotic ratios emerges after extended exposure.

For purposes of comparison, two matching functions were fitted for each subject: one using obtained reinforcer ratios as the independent variable and one using scheduled reinforcer ratios. In most cases, slope and r² values were only slightly lower for scheduled than for obtained reinforcer ratios. With one notable exception (subject 104), scheduled reinforcer ratios accounted for between 75% and 94% of the variance in response ratios, indicating that fits constructed with obtained ratios described the data only slightly better than those obtained with scheduled ratios. This is not surprising considering that scheduled and obtained ratios are discrete and continuous variables, respectively.

Whereas obtained reinforcer ratios have traditionally been used in concurrent schedule research, scheduled ratios are helpful in assessing the effects of other variables on matching, such as impairments due to neurotoxicant exposure, or when an extreme bias exists. In such cases, obtained and scheduled reinforcement ratios may produce different matching functions, and therefore may provide different information about choice. For example, in utero exposure to lead or methylmercury produced matching functions that revealed a strong bias and diminished sensitivity to reinforcer ratios when scheduled reinforcers were used as an independent variable. This was interpreted as a deficiency in how the structure of behavior reflected the structure of reinforcement contingencies (Newland et al., 1994). The discrepancy occurred because monkeys exposed to high levels of lead or methylmercury sometimes perseverated on an initially rich lever that became lean after a transition was imposed (see also Paletz et al., 2007; Reed, Paletz, & Newland, 2006). Obtained reinforcer ratios are a joint function of the scheduled ratios and of behavior, and work well when there is adequate responding on both alternatives. The use of scheduled ratios allows for the assessment of changes in behavior as a sole function of changes in the environmental contingencies, and this approach can be important when describing impaired performance.

Choice in Transition

The distributions of the number of responses during a visit across key segments of the transition (Figure 7) suggest that the transition from indifference to preference for the richer alternative can be characterized as a sharp change in number of long-response visits on the two alternatives. There was dramatic increase in the number of visits with very long response runs on the richer alternative, as indicated by the long right tail of the distribution, and a concomitant reduction in such visits on the leaner alternative. The number of low-response visits (the left tail) changed less dramatically, if at all. This increased skewness in the distribution appeared in the group means as a growing difference between the mean and the mode of the distributions as the session progressed and as the reinforcer ratios became more extreme. Thus, choice was driven not by a wholesale shift in the distribution of responses per visit, but rather by the emergence of visits that consisted of long response bouts on the rich lever.

In the present study, single-session transitions provided a way to describe transitional behavior mathematically within an individual session using parameters that reflect actual physical properties of that behavior (Newland & Reile, 1999). While there is some degree of variation both between and within subjects and between and within transition magnitudes as evidenced in Figures 4 and 5, some general conclusions can be drawn. First, 4:1 transitions appear to have the steepest slopes in the S-shaped portion of the functions. This suspicion is further supported by the summary measures presented in Figure 6 (recall that 4:1 transitions were not included in statistical tests; see Method section for rationale). This is interesting because it suggests that transitions to the lowest magnitude proceeded most quickly, which contradicts the idea that transitions should proceed more rapidly as the discrepancy between reinforcement rates on alternatives increases (Davison & Nevin, 1999). Several factors make us reticent to draw this conclusion, however. First, the slope parameter of the logistic equation is the most volatile and sensitive to small changes in the dependent variable (see below). Second, the other measure of transition rate, X_half, is more stable and does not seem to confirm that 4:1 transitions proceed any more quickly than the others. Also, there is no evidence of such an inverse relationship when considering the full range of transition magnitudes. The absence of a relationship between rate of behavior change and the magnitude of the reinforcer ratio in the present study is consistent with previous research (Mazur, 1992), but conflicts with other reports (Bailey & Mazur, 1990; Mazur & Ratti, 1991).

One variable that has been shown to affect the rate of behavioral adjustment to changes in concurrent schedules is the overall rate of reinforcement (Alsop & Elliffe, 1988; Davison & Baum, 2000; Elliffe & Alsop, 1996). In our study, this variable remained constant throughout all conditions. This may account for why we failed to observe changes in the rate parameters, k and X_half. Replicating the current study and incorporating multiple overall rates of reinforcement would help determine whether the parameters generated by the Equation 1 are sensitive to such manipulations.

While the absence of magnitude effects on rate was not completely unexpected, what was somewhat surprising was the lack of magnitude effects on Y_m. Previous research (Mazur, 1992) suggests that asymptotic response ratios vary as a function of reinforcement ratio magnitude. One important difference between Mazur's study and the data presented here is that Mazur allowed behavior to stabilize for four sessions following a transition. Mathematical models were then applied to data collected over the course of all of these sessions. Here, a transition occurred and was modeled within each session. Given that the overall reinforcement rate was held constant at two per min, and that each transition lasted 90 min, the maximum number of reinforcers a subject could earn during a transition was 180 (most animals earned well below 180 pellets per transition). Given the parameters of the current study, it is possible that this was not enough reinforcers to allow for the development of significant magnitude-related differences in the terminal response ratio.

The Logistic Equation for Modeling Acquisition of Choice

Equation 1, a form of the logistic equation, was selected largely for empirical reasons. First, it provides the appropriate shape with which to describe transitions, and it produces parameters that are easily interpretable in terms of behavior. That is, Y_m, X_half, and k reflect the terminal behavior ratio, the number of reinforcers required for the transition to reach half of the maximum response ratio, and the rate of behavior change, rather than functioning as hypothetical constructs. By using these terms, it is possible to describe concretely the course of a transition and make meaningful comparisons between conditions.

Second, the logistic model provided a good fit for the transitional behavior that occurred over the course of a single session. This equation was superior to concave functions such as hyperbolic or exponential functions, but was indistinguishable from other S-shaped functions, such as Gompertz equations (Newland & Reile, 1999). It might be noted that both the logistic and Gompertz arise in models of population dynamics, selectionistic models that might be adapted to describe choice (Edelstein-Keshet, 1988).

While Equation 2 modeled behavior in transition well, there remain a few issues that require further investigation. Most of these issues involve cases in which estimated parameters either did not describe the data well or could not be interpreted meaningfully. In some cases, the slope parameter was estimated to be greater than 1. In a literal sense, this means that a transition has occurred within one reinforcer, or in practice, during the course of one visit. For example, a slope value of 38 is literally interpreted as follows: during the transition, the delivery of each additional reinforcer yields an increase of 38 in the log response ratio. Alternatively, it can be shown algebraically that 1/k  =  the number of reinforcers that span the middle third of the transition. Therefore, a slope of 38 means that 1/38 reinforcers were required to span 1/3 of the transition. From a practical standpoint, this is indistinguishable from saying that the transition occurred within a single visit, and as such, is no different from a situation in which k  =  1. Further, the error in the estimate of slopes of this magnitude was generally very large, which led to a lack of confidence that this number was different from 1. Because we cannot resolve more finely than a single visit, the error bars showed that such slopes are indistinguishable from 1, and because the extreme slope values caused estimate averages to be unstable, all slope values greater than 1 were set equal to 1 in the present study. This happened rarely, and was carried out for three 8:1, three 16:1, and two 32:1 transitions.

A more difficult situation arose when behavior ratios were still increasing at the end of a session and failed to reach an estimable asymptote. This was usually manifested as extremely high Y_m values and X_half estimates that exceeded the range of the data obtained, and confidence intervals that overlapped with zero. Typically, these involved cases in which there was no discernable transition or, for some reason, transitions that proceeded very slowly. Unfortunately, there is no simple or logical remedy for this issue. In this study, transitions that produced (a) magnitude estimates that were never achieved, and (b) X_half estimates that exceeded the total number of reinforcers delivered, were eliminated from analyses. This occurred for relatively few transitions, but appeared to happen most frequently in the 32:1 condition. It is possible that larger reinforcer ratios produce poorer fits because response ratios did not have time to completely stabilize over the course of 2 hr.

An assumption embedded in the use of the logistic model might be noted here. This equation is symmetric about the half-max value, yielding a function that is symmetric about the inflection point. That is, the rising portion to the left of the inflection point is a mirror image of the asymptotic portion to the right of that value. The Gompertz model does not make this assumption of symmetry but, instead, produces a rapidly rising portion followed by a slower asymptote to the right of the inflection point. Conceptually, this has some appeal, but was not used here for two main reasons. In comparisons using variance accounted for and standard error of regressions as markers of the quality of the fit, the Gompertz model was indistinguishable from the logistic model (Newland & Reile, 1999). Moreover, the Gompertz model is more complex and the parameters are somewhat more difficult to interpret. However, future investigations might focus on the issue of symmetry and functional forms of the Gompertz that yield interpretable parameters.

Single Session Transitions Enable the Study of Pharmacological or Neural Determinants of Choice

The ability to study the acquisition of choice in a single session is a methodological advance over approaches that require several days to weeks, and could facilitate the study of other factors that may influence choice and its acquisition. For example, despite a huge literature on behavioral determinants of choice and the growing importance of choice in the neuroscience of the cerebral cortex and basal ganglia (e.g., Schultz, Tremblay & Hollerman, 2000; Tremblay & Schultz, 1999), very little drug research has been conducted on potential neural or pharmacological influences on the acquisition of choice. This is likely due to the time-intensive nature of the traditional procedure. If we conservatively estimate that it takes 2 weeks for behavior to stabilize under each of five reinforcer ratios, it would take 10 weeks to construct a full matching function. To determine a dose-effect curve using five conditions (control, saline, and three drug doses), it would take a minimum of 60 weeks to collect the necessary data. This is nearly half of a rat's life span and introduces age as a confounding factor. Using a single-session paradigm, dose-effect curves can be evaluated over the period of a few months.

In the present study, we have built upon previous work (Newland et al., 1994; Newland et al., 2004) and demonstrated the utility of single-session transitions in assessing both transitional and steady-state behavior generated under concurrent schedules of reinforcement. This procedure provides a method for collecting data on choice and its acquisition in relatively short periods of time, and the logistic equation used to model the transition provides idemnotic parameters (Johnston & Pennypacker, 1993) that can be used to chart the course of acquisition and to make meaningful comparisons across a variety of experimental conditions. In addition, we have presented a method for describing changes in response distributions throughout the course of a transition. The use of distribution analyses suggests that changes in behavior ratios result from an increase in the number of long response bouts on the rich lever, and a corresponding decrease in such bouts on the lean lever. We hope that future research will incorporate similar assessments to further elucidate the nature of the shift in behavior that occurs during the transition from one concurrent schedule to another.

Appendix A.

Transition parameters generated with both the logistic and hyperbolic functions.

Condition	Rat	Ymax		Xhalf		r2		SER1
		L	H	L	H	L	H	L	H
L4_1	101	0.32	0.35	7.69	10.52	0.82	0.83	0.13	0.13
	102	0.17	0.18	2.27	2.76	0.6	0.57	0.14	0.14
	103	23.642	4091.62	372.282	12868002	0.64	0.6	0.17	0.18
	104	0.15	0.272	22.03	71.352	0.36	0.18	0.17	0.19
	105	0.18	184892	60.93	114460002	0.34	0.34	0.18	0.18
	106	0.29	0.442	32.14	45.4	0.7	0.67	0.16	0.17
	107	0.38	0.44	11.98	9.54	0.77	0.73	0.2	0.21
	108	0.39	0.38	14.98	14.02	0.91	0.91	0.09	0.09
L8_1	101	0.652	0.912	65.72	104.52	0.87	0.85	0.13	0.13
	102	0.74	1.292	27.48	64.262	0.93	0.91	0.11	0.12
	103	0.79	293762	74.76	55726002	0.82	0.81	0.14	0.14
	104	0.2	0.25	3.97	5.77	0.5	0.49	0.19	0.19
	105	1.462	4.752	114.37	626.752	0.89	0.89	0.17	0.17
	106	0.74	2.792	49.45	322.232	0.83	0.82	0.21	0.21
	108	0.41	0.49	9.45	11.21	0.88	0.88	0.14	0.13
L8_2	101	0.17	0.17	3.62	0.04	0.61	0.61	0.13	0.13
	102	0.79	0.56	42.13	7.4	0.87	0.86	0.18	0.19
	103	0.45	3.642	50.5	787.952	0.82	0.82	0.13	0.13
	104	0.49	0.48	4.53	4.56	0.89	0.88	0.15	0.15
	105	0.56	1.682	53.51	250.932	0.81	0.82	0.17	0.17
	106	1.142	2.172	78.21	207.022	0.86	0.86	0.2	0.2
	107	0.58	0.912	42.09	79.26	0.79	0.79	0.21	0.2
	108	0.51	0.61	41.27	42.19	0.84	0.85	0.15	0.15
L16_1	101	1.22	5.552	87.17	741.632	0.86	0.86	0.15	0.15

	102	38.082	425752	161.542	42819002	0.91	0.89	0.11	0.12
	103	0.53	0.6	7.56	7	0.89	0.87	0.17	0.19
	104	0.35	0.5	11.74	20.21	0.85	0.83	0.14	0.14
	105	0.84	1.33	40.8	71.86	0.92	0.9	0.19	0.21
	106	0.66	0.84	21.81	25.36	0.9	0.9	0.19	0.19
	107	0.47	0.67	22.52	37.19	0.88	0.88	0.15	0.15
	108	0.57	0.9	26.96	49.79	0.93	0.93	0.13	0.13
L16_2	101	0.19	0.18	10.21	0.88	0.48	0.47	0.18	0.19
	102	0.48	0.51	8.34	5.13	0.88	0.88	0.17	0.16
	103	0.45	0.54	18.02	19.07	0.91	0.9	0.12	0.13
	104	0.72	0.73	3.84	0.69	0.97	0.96	0.12	0.14
	105	0.53	0.57	15.64	9.94	0.89	0.87	0.17	0.18
	106	1	1.19	17.38	16.62	0.96	0.93	0.19	0.24

	107	0.58	0.85	49.8	76.5	0.76	0.77	0.2	0.2
	108	0.46	0.57	21.11	22.27	0.85	0.84	0.16	0.16
L32_1	101	0.62	0.89	27.37	44.19	0.95	0.95	0.1	0.11
	102	0.46	0.65	9.5	17.61	0.89	0.85	0.15	0.17
	103	0.58	1	19.76	47.51	0.92	0.93	0.14	0.13
	105	0.83	1.25	39.61	69.44	0.93	0.93	0.16	0.16
	106	0.68	1.08	30.21	57.81	0.93	0.93	0.15	0.14
	107	1.092	1.72	136.882	340.012	0.82	0.81	0.14	0.14
L32_2	101	0.41	0.51	9.8	12.52	0.86	0.83	0.16	0.17
	102	0.62	0.94	19.02	35.96	0.91	0.9	0.17	0.18
	103	0.46	1.01	25.53	100.74	0.88	0.88	0.15	0.15
	104	0.69	1.152	21.03	42.59	0.88	0.9	0.15	0.13
	105	4.722	4.012	300.622	715.882	0.93	0.92	0.13	0.13
	106	10.622	7.152	316.582	787.552	0.89	0.89	0.24	0.24
	107	0.952	25.192	118.52	6103.82	0.77	0.77	0.2	0.2
	108	0.67	1.792	47.83	197.912	0.93	0.93	0.12	0.11

Condition	Rat	Ymax		Xhalf		r2		SER1
		L	H	L	H	L	H	L	H
R4_1	101	0.26	421.42	56.18	1938102	0.85	0.8	0.08	0.09
	102	0.57	0.6	6.64	4.5	0.93	0.92	0.16	0.16
	103	0.4	1.642	47.75	359.5	0.81	0.69	0.15	0.19
	105	0.49	1.03	70.12	209.392	0.78	0.78	0.15	0.15
	106	0.28	0.642	40.11	132.9	0.75	0.73	0.14	0.15
	107	0.35	1.082	55.74	278.242	0.62	0.63	0.19	0.18
R8_1	101	0.5	0.61	30.53	35.14	0.87	0.87	0.14	0.14
	102	0.55	2.392	58.18	425.32	0.86	0.85	0.14	0.15
	103	0.35	2.152	60.79	648.762	0.73	0.71	0.14	0.14
	104	171.382	633582	189.212	65974002	0.81	0.72	0.17	0.2
	105	0.49	102082	81.27	32896002	0.7	0.69	0.18	0.18
	106	0.78	1.28	44.16	86.27	0.88	0.89	0.21	0.21
	107	0.26	0.52	32.07	90.02	0.62	0.61	0.17	0.17
	108	0.51	0.54	20.97	16.47	0.91	0.91	0.12	0.13
R8_2	101	0.49	0.56	2	4.14	0.83	0.84	0.21	0.21
	102	1.432	1.272	116.23	94.74	0.91	0.9	0.16	0.17
	103	0.65	1.192	35.24	84.95	0.82	0.81	0.25	0.25
	104	0.49	0.5	1.06	0.9	0.95	0.94	0.11	0.12
	105	0.66	619452	66.86	122830002	0.79	0.78	0.18	0.18
	106	0.51	0.83	45.6	86.3	0.9	0.87	0.12	0.14
	107	0.61	1.382	62.11	201.752	0.87	0.88	0.13	0.13
	108	0.882	1.22	78.51	121.44	0.93	0.91	0.12	0.13
R16_1	101	0.54	0.62	7.21	7.34	0.96	0.97	0.11	0.1
	102	0.64	0.8	23.78	25.11	0.96	0.96	0.11	0.11
	103	0.46	0.952	35.85	101.26	0.84	0.84	0.15	0.15
	104	0.27	0.48	12.68	32.1	0.89	0.87	0.08	0.09
	105	0.25	0.26	8.79	3.44	0.65	0.63	0.18	0.18
	106	0.6	0.73	25.92	22.28	0.84	0.78	0.22	0.26
	107	0.4	0.54	17.33	25.07	0.84	0.84	0.15	0.15
	108	0.41	0.43	9.05	4.03	0.88	0.88	0.14	0.14
R16_2	101	0.75	6.912	44.67	828.332	0.95	0.9	0.1	0.15
	102	0.48	0.55	15.35	12.13	0.89	0.89	0.15	0.16
	103	0.6	0.81	30.13	40.36	0.88	0.88	0.18	0.18
	104	0.36	0.36	2.07	0.84	0.6	0.59	0.3	0.29
	105	0.93	7.722	71.78	1109.52	0.89	0.89	0.18	0.18
	106	0.66	1.17	40.12	91	0.84	0.84	0.21	0.21
	107	0.57	0.69	25.55	31.23	0.87	0.86	0.18	0.18
	108	0.7	0.95	29.59	42.77	0.94	0.96	0.13	0.11
R32_1	101	0.5	1.052	50.23	133.892	0.91	0.86	0.11	0.14
	102	1.262	1.082	132.072	119.24	0.88	0.87	0.14	0.15
	103	0.73	1.432	43.7	119.67	0.95	0.94	0.12	0.12
	105	1.872	1.732	154.122	180.852	0.88	0.87	0.17	0.18
	106	1.632	300752	108.47	41090002	0.94	0.92	0.15	0.17
	108	0.48	0.75	38.15	68.21	0.89	0.88	0.13	0.14
R32_2	101	4.62	188732	220.432	29213002	0.85	0.83	0.18	0.19
	102	0.58	0.67	10.73	10.91	0.94	0.94	0.13	0.13
	103	0.63	2.62	55.27	379.472	0.81	0.79	0.19	0.2
	104	0.67	0.89	19.15	25.85	0.91	0.89	0.16	0.18
	105	0.54	0.94	33.53	73.57	0.85	0.85	0.18	0.19
	106	0.76	1.12	35.04	55	0.92	0.92	0.17	0.17
	107	0.58	0.81	33.64	46.2	0.82	0.81	0.21	0.21
	108	0.57	0.8	36.38	49	0.91	0.9	0.14	0.14

¹Standard error of regression.

²Over-estimate of parameter warranting removal of transition from analysis.