Skip to main content
PMC home page
UKPMC Funders Author Manuscripts logoLink to UKPMC Funders Author Manuscripts
. Author manuscript; available in PMC: 2009 May 6.
Published in final edited form as: Nature. 2003 Oct 23;425(6960):828–832. doi: 10.1038/nature02058

Independent rate and temporal coding in hippocampal pyramidal cells

John Huxter 1,*, Neil Burgess 1,2, John O’Keefe 1,2
PMCID: PMC2677642  EMSID: UKMS4620  PMID: 14574410

Abstract

Hippocampal pyramidal cells use temporal 1 as well as rate coding 2 to signal spatial aspects of the animal’s environment or behaviour. The temporal code takes the form of a phase relationship to the concurrent cycle of the hippocampal EEG theta rhythm (Figure 1​; 1). These two codes could each represent a different variable 3,4. However, this requires that rate and phase can vary independently, in contrast to recent suggestions 5,6 that they are tightly coupled: both reflecting the amplitude of the cell’s input. Here we show that the time of firing and firing rate are dissociable and can represent two independent variables, viz, the animal’s location within the place field and its speed of movement through the field, respectively. Independent encoding of location together with actions and stimuli occurring there may help to explain the dual roles of the hippocampus in spatial and episodic memory 7 8 or a more general role in relational/declarative memory9,10.

A cell must fire to manifest either a temporal or rate code. Place cells are hippocampal pyramidal cells that increase their firing rate in a particular portion of the environment 2,11 (the ‘place field’, see Fig1b). As such, they provide a coarse rate code for the animal’s location within which a temporal code provides additional information1,12,13. In addition we propose that the rate of firing within the field can vary to encode for other information without disrupting this temporal code.

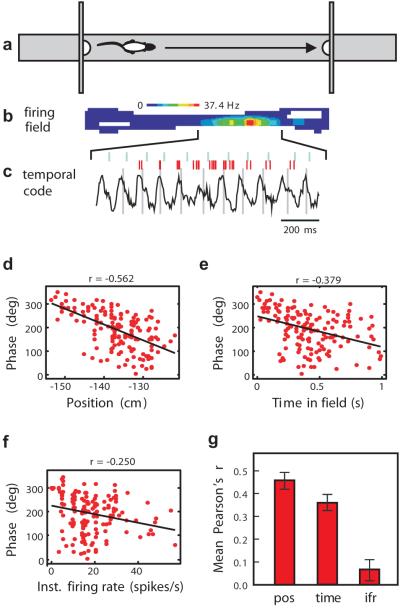
Figure 1.

Figure 1

Open in a new tab

(a) Behavioural task: rat shuttles back and forth along linear track between food rewards contained in cups attached to moveable walls. (b) False-colour firing field of a place cell created from multiple runs in the eastward direction. (c) EEG theta rhythm and place cell firing (in red) for the same cell on a single eastward run. Ticks above the spikes indicate + to − zero crossings (0°/360° phase) for each theta wave, lines through theta waves indicate 270°. Bursts of spikes occur at higher than theta frequency causing each successive burst to move to an earlier phase of the theta cycle, despite initially rising, then falling firing rate. Theta cycle phase of spikes from multiple runs is plotted against position (d), time (e) and instantaneous firing rate (f) in the place field. g) Phase (adjusted for circularity, see Methods) is better correlated with location than with time or firing rate across the population of cells. Here and in subsequent figures, vertical bars represent +/− s.e.m.

We recorded the firing of place cells and the EEG from the hippocampi of rats as they ran back and forth on a linear track for food reward at each end (see Figure 1a and Methods). During this behaviour, the EEG shows the prominent theta oscillation and each place cell fires in a specific region of the track (Figure 1b). The cell’s bursting rate through the field (Figure 1c) is slightly higher than the concurrent EEG theta frequency so that the average phase of firing moves earlier on each theta wave as the animal progresses through the field (Figure 1d). The phase of firing correlates with spatial variables such as the animal’s position on the track or within the field (Fig. 1d), and also with non-spatial variables such as the time since entry into the field (Fig. 1e) or instantaneous firing rate (Figure 1f), but in general the correlation with position is stronger than with either (Figure 1g; see also 1,5,6,12). Some process must align the phase of each spike relative to the concurrent theta wave so that the phase codes for location despite the different speeds of each run through the field.

Must the phase and rate codes always co-vary with each other or is it possible for them to dissociate? Harris et al 5 reported an overall relationship between phase and rate in spikes recorded on a linear track, and our data show a similar relationship (Figures 1g​, S1a,b). However, it is much weaker than the relationship between phase and position (Figure 1d, phase correlates better with position than rate in 66/77 cells p=5.3 × 10-11), and may result directly from the relationship both phase and rate hold with position (Figure S1c). Mehta and colleagues 6 reported that, over the first few runs of a session, the firing fields become more negatively skewed versus position and the phase precession strengthened – suggesting that both rate and phase reflect the net input to the cell and that this input becomes ramp-shaped: increasing with distance through the field. Our fields show a continuous range of negative, zero, and positive skew, however there was no correlation between skew and the rate or amount of phase precession (Figure S2). Thus a causal relationship between negative field skew and phase precession is unlikely, despite both effects strengthening over the first few runs of a session.

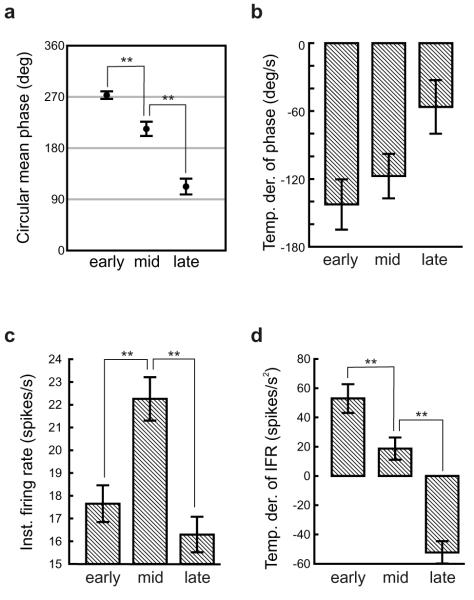
To see whether phase and rate dissociate within a place field, each field was divided into three equal segments: the beginning, middle, and end. The mean instantaneous firing rate (IFR) and mean firing phase per theta cycle, and their respective temporal derivatives (TDIFR & TDPhase) for runs through each segment of the field were averaged across the population, see Figure 2. The mean phase per cycle continues to precess throughout the entire run, despite the firing rate rising in the early part of the field and then falling, and despite the increasing variance of firing phase through the field 6,14. TDIFR is positive in the early part of the field and negative in the late part, while TDPhase is negative throughout, demonstrating that phase precession occurs during both accelerating and decelerating spike trains, and that the firing rate rises and falls within each run. Thus, again, a causal relationship between phase precession and increasing rate is unlikely, consistent with the much lower correlation of phase with firing rate than with position (Figure 1).

Figure 2.

Figure 2

Open in a new tab

Phase precession is independent of instantaneous firing rate. (a) Phase depends on location, being highest in the early third of each field, lower in the middle third, and lowest in the late third. (b) Temporal derivative of phase is negative in each portion of the field (68/76 fields in the early portion, p< 1 × 10-12; 57/76 in the middle, p<1 × 10-5; 46/76 late, p< 0.05, binomial test). (c) Instantaneous firing rate starts low, increases in the middle third and then decreases in the late part of the field. (d) Temporal derivative of instantaneous firing starts high, falls towards zero in the middle third, and then goes negative in the last third. Here and in subsequent figures, * denotes p < 0.05 & ** denotes p < 0.01.

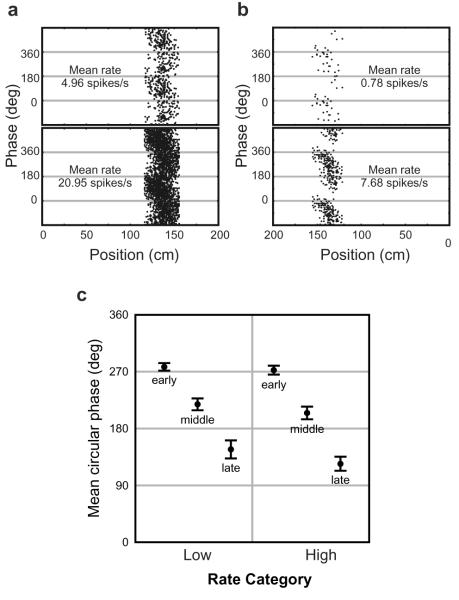
To see whether rate and phase dissociate on a run-by-run basis, the runs with the highest and lowest firing rates for each cell were identified so that the phase precession in both data sets could be compared. Across the population, we found no difference in mean phase precession between the high and low firing rate runs. Figure 3 shows that phase precession takes place equally on trials with low as well as high firing rates, and even under conditions of very low firing rates with 2 or fewer spikes per run (Figure 3b). Thus the dissociation of firing rate and firing phase is not due to effects specific to the second part of the field such as habituation, spike frequency accommodation, or to high and low rate runs being combined in the overall mean rate. In addition, the above data rule out any necessary coupling between phase precession and the TDIFR cf. ​5.

Figure 3.

Figure 3

Open in a new tab

Phase is correlated with track location on low as well as high firing rate runs. (a) A single cell for which average firing rate on high rate runs (below) is four times that on lower rate ones (above) with no discernible effect on the phase precession. (b) The same analysis for the cell shown in Figure 1. Phase precession can occur despite very low firing rates. Above: 35 spikes from 66 low-rate runs, mean spikes/run .53, SEM 0.09, range 0-2 (0 spikes on 41 runs, 1 on 15, and 2 on 10); Below: 194 spikes from 36 high-rate runs mean spikes/run 5.40, SEM 0.53, range 2-14. (c) Population data (n=34): phase precesses across early, middle and late parts of the field on both high and low rate runs.

If the phase and firing rate can be independent, what variables does each encode? Previous work has suggested that the firing rate of place cells correlates with running speed through the field 15-18. We confirm that relationship for the present data set (Figure 4), where place fields reconstructed from faster runs were associated with higher firing rates (30 of 34 fields, t1,33 = −5.88, p < 0.001, Figure 4a ). In contrast the temporal code did not vary between fast and slow runs, as measured by mean rate of phase precession in space (t1,33 = 0.301, p = 0.77, Figure 4b); total extent of phase precession (t1,33 = −4.32, p = 0.67, Figure 4c); phase at firing onset (F1,32 = 0.066, p = 0.799) or offset (F1,32 = 1.281, p = 0.266, data not shown). The correlation between mean firing rate per run and running speed on individual runs, averaged across the population, is 0.223 (Figure 4d) - higher than the correlation between speed and any other variable we have measured.

Figure 4.

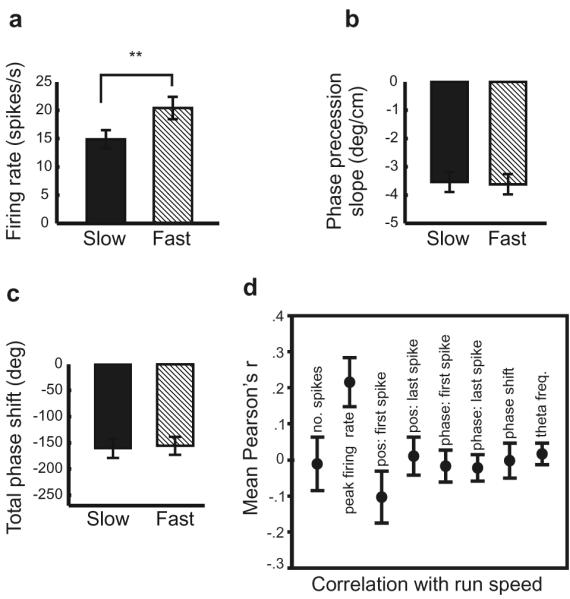
Figure 4

Open in a new tab

Firing rates differ on fast and slow runs through the field. (a) Significant difference in average peak firing rates but no difference in (b) rate of phase precession, (c) total phase shift. (d) Firing rate is the only variable measured that consistently correlates with running speed (1.5 metre track, mean r= 0.223, 23/29 fields with significant positive correlations p< 0.05)

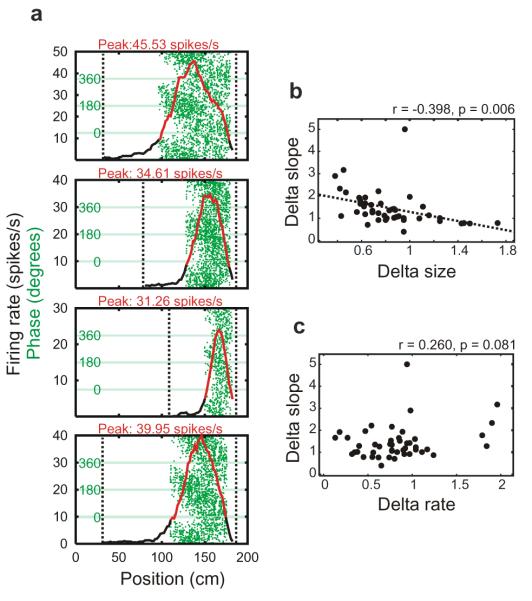
To identify the spatial correlate of firing phase more precisely, we varied the length of the track from 1.5 metres to 1.0 or 0.75 metres by moving the walls closer together. The rats ran slower on the shortened tracks (F1,29 = 12.536, p = 0.001), the fields were smaller (F1.29 = 16.834. p < 0.001) and firing rates were reduced (F1,29 = 11.068, p = 0.002) (Figure 5a). When the fields shrank, there was a strong correlation between the shortening of a field and the increase in the rate of change of phase in space (Fig. 5b). By contrast, the change in the rate of phase precession was not correlated with changes in its firing rate (Figure 5c). We tentatively conclude that the phase is coding for the proportion of the field traversed, which is also consistent with the finding that blocking LTP produces shorter fields on average (by preventing their asymmetric expansion 19) but does not reduce the amount of phase precession 18. The correlation between running speed and firing rate per run observed on the full length track was also found on the shortened track (mean r= 0.18), showing the robustness of this effect within different environmental configurations.

Figure 5.

Figure 5

Open in a new tab

Phase Precession on the shortened tracks. Single cell: (a) phase angle vs position (green) gets steeper as the field size shrinks and the firing rate (spikes dividing by dwell time, in red) drops due to shortening of the track. Bottom panel shows the second baseline trial on full-length track carried out after short track trials. Population: slope of phase precession (i.e. rate of change in space) increases with shorter track length (b) in the absence of systematic changes in other correlations such as firing rate (c), ‘Delta’ values refer to the change from the preceding baseline trial to the trial on the shortened track, see Methods.

What mechanisms might underlie phase coding of location independent of rate? One model1,20 views CA3 place cell firing as an interference pattern between an inhibitory theta input and an intrinsically oscillatory membrane potential, see e.g.21, whose frequency increases above theta frequency as the input to the cell increases, see e.g. 22. Under this model modulation of the amplitudes of the response, possibly by input from the dentate gyrus (DG), need not affect its phase, while the rate of precession naturally adjusts to cover the extent of the field. If the frequency of the variable oscillator reflects distance from landmarks as measured by external and internal signals including motor efference, this model could also account for the phase precession observed in running wheels as well as linear tracks 5. Alternative possibilities include phase of firing reflecting the directions of the stimuli defining the place field3,23, or early- field firing being driven by input from other place cells while late-field firing is driven by sensory input 19,24-26. In this latter model, delays in synaptic transmission mean that early-field firing occurs later in a theta cycle than that driven by sensory input (note however that the drive from other place cells should not depend on LTP18).

The present experiments show that, on linear tracks, the phase of firing relative to the hippocampal EEG theta wave and the instantaneous firing rate code for two independent aspects of the animal’s spatial behaviour: proportion of distance through the place field and in-field velocity. However the correlation of rate with velocity varies between cells and is low overall, suggesting that it might also code for other variables. Previous experiments 2,16,27,28 suggest that firing rate in the place field is influenced by such variables as direction of turning along the rat’s trajectory and the presence (or absence) of particular objects, or of smells or sounds associated with reinforcers. Thus we propose that the strong spatial relation with phase leaves modulation of the firing rate free to represent additional information regarding the behaviours performed and the salient objects or features encountered in specific places. This dual code may provide the neural basis for the involvement of the hippocampus in both spatial and more general episodic/declarative memory 7-10 by simultaneously encoding and binding together the location of the event and its behavioural and sensory content. Theta EEG activity has also been demonstrated in many different neocortical regions in human patients 29 suggesting that the ability to code for more than one variable by using rate and temporal codes may be a general property of cortical pyramidal cells.

Methods

Nine male Lister Hooded rats were implanted with pairs of movable tetrodes in the dorsal hippocampus1,30 and placed on a food deprivation schedule (initially 90% of body weight with a gain of 5 gms/week). After one week of post-operative recovery, they were trained to shuttle between the ends of a linear track for food reward (track dimensions: 150×10cm, bounded by 25cm side walls and 61cm end walls that could be moved to shorten the length of the track). Above the walls, the rats could see the experimental room. A recording session consisted of a series of 8-minute trials, the first always a set of runs on the full-length track followed by a series of trials including trials on shortened tracks, interspersed with baseline full-length track trials. Further series were then run in which the size of the end walls was modified or the belt which comprised the floor of the track was moved. Only the results from the first series are reported here.

An overhead camera tracked an array of infrared LED’s fixed to the rat’s head (sampled at 50 Hz with a theoretical resolution of 3mm). Simultaneously, EEG field potentials (sampled at 250Hz, band-pass filtered at 0.34-125Hz) and extracellular action potentials (spikes, sampled at 48kHz, band-pass filtered at 500-6700Hz) were recorded from the pyramidal cell layer. Half-sinusoids in the theta frequency range (6-16Hz) were aligned to negative-going deflections in the EEG and the goodness-of-fit used to detect the presence of theta. The firing phase (0-359°) of a spike reflects its temporal distance between successive zero crossings during theta. Where absolute phase values from different fields are combined, each field is first adjusted by a constant so that least frequent phase corresponds to 0°/360°.

Place Field Definition

For a given cell, firing rates were calculated in 2cm bins along the length of the track (i.e. the ratio of the total number of spikes to occupancy duration in each bin) and then boxcar averaged using the five bins centred on it. Place fields were defined as the bin with the highest firing rate and all contiguous bins in which the firing rate exceeded 20% of this peak rate.

General Data Analysis

Only well-isolated units with good spatial selectivity and a peak firing rate of > 1 Hz were analysed, yielding 73 cells with 94 place fields: 75 from CA1, 19 from CA3, the dentate gyrus or hilar region. All further analyses concerned data from runs through the place field in its preferred firing direction at above 10cm/s. Positions are plotted such that the ordinate increases for runs from East to West and decreases for runs from West to East. The initial trial on the full-length track from each place field was used to compare field characteristics like peak firing rate, field skew, and rate of phase precession versus position. Correlations and regression on phase data were adjusted to take account of its circular nature, minimising the squared angular distance from the line (not more than 180°) rather than the absolute distance, see also 1. Correlations were done on the 77 fields contributing at least 100 spikes to the initial full-length trial.

Instantaneous firing rate (IFR) was calculated as the number of spikes in a time window up to one theta cycle on either side of the reference spike, divided by the size of the window (after 5). The temporal derivative of the IFR (TDIFR) is the difference between the IFR for any two consecutive spikes, divided by the time interval between them. Only IFRs based on time windows greater than 100 ms were included. Mean phase per cycle is the circular mean phase of spikes within a theta cycle, and the temporal derivative of this (TDphase) is the circular difference between the mean phase in successive theta cycles divided by the duration of the first cycle.

For analyses comparing fast vs. slow runs and high-rate vs. low-rate runs, separate fields were constructed from subsets of runs (combining multiple baseline trials with r > 0.9 field correlations). ‘Slow runs’ comprised the bottom quartile of runs ordered by the speed of the run through the firing field (i.e. the length of the path through the field divided by its duration), ‘fast runs’ comprised the top quartile. Four fields for which this produced fewer than 200 spikes in each subset were simply split at the 50th percentile. Runs ordered by firing rate were divided into ‘high’ and ‘low’ rate runs at the 50th percentile. In both cases, only fields for which there were at least 100 runs through the composite field were included (n=34).

Shortened Runway

Field characteristics on two shortened runway trials (created by moving one of the end walls 50 or 75 cm towards the middle of the track) were compared with the two flanking baseline trials and analysed using a repeated measures ANOVA. The wall which was moved and the amount by which it was moved varied pseudo-randomly across trials. Changes in firing rate, running speed, and field size were measured as the ratio of the score on each manipulation trial compared to the preceding baseline. Changes in the rate of precession were measured as the difference between scores on manipulation trials and the preceding baseline and were only performed on trials with 100 or more spikes.

Supplementary Material

SIcaptions
SIfigures

Acknowledgements

We thank Colin Lever, Francesca Cacucci, Tom Wills, John Ryan, Dave Edwards and Tom Hartley for technical assistance. This work was supported by the MRC and the Wellcome Trust. JH was a Rothermere Fellow.

Footnotes

Supplementary Information accompanies the paper on Nature’s website (http://www.nature.com).

Competing interests statement The authors declare that they have no competing financial interests.

References

  • 1.O’Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 1993;3:317–330. doi: 10.1002/hipo.450030307. [DOI] [PubMed] [Google Scholar]
  • 2.O’Keefe J. Place units in the hippocampus of the freely moving rat. Exp. Neurol. 1976;51:78–109. doi: 10.1016/0014-4886(76)90055-8. [DOI] [PubMed] [Google Scholar]
  • 3.O’Keefe J. In: Brain and Space. Paillard J, editor. Oxford University Press; Oxford, UK: 1991. pp. 273–295. [Google Scholar]
  • 4.Buzsaki G. Theta oscillations in the hippocampus. Neuron. 2002;33:325–340. doi: 10.1016/s0896-6273(02)00586-x. [DOI] [PubMed] [Google Scholar]
  • 5.Harris KD, et al. Spike train dynamics predicts theta-related phase precession in hippocampal pyramidal cells. Nature. 2002;417:738–741. doi: 10.1038/nature00808. [DOI] [PubMed] [Google Scholar]
  • 6.Mehta MR, Lee AK, Wilson MA. Role of experience and oscillations in transforming a rate code into a temporal code. Nature. 2002;417:741–746. doi: 10.1038/nature00807. [DOI] [PubMed] [Google Scholar]
  • 7.O’Keefe J, Nadel L. The hippocampus as a cognitive map. Oxford University Press; Oxford, UK: 1978. ( www.cognitivemap.net) [Google Scholar]
  • 8.Burgess N, Maguire EA, O’Keefe J. The human hippocampus and spatial and episodic memory. Neuron. 2002;35:625–641. doi: 10.1016/s0896-6273(02)00830-9. [DOI] [PubMed] [Google Scholar]
  • 9.Squire LR. Memory and the hippocampus: a synthesis from findings with rats, monkeys, and humans. Psychol. Rev. 1992;99:195–231. doi: 10.1037/0033-295x.99.2.195. [DOI] [PubMed] [Google Scholar]
  • 10.Eichenbaum H, Cohen N. From conditioning to conscious recollection. Oxford University Press; Oxford, UK: 2001. [Google Scholar]
  • 11.Muller R. A quarter of a century of place cells. Neuron. 1996;17:813–822. doi: 10.1016/s0896-6273(00)80214-7. [DOI] [PubMed] [Google Scholar]
  • 12.Skaggs WE, McNaughton BL, Wilson MA, Barnes CA. Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus. 1996;6:149–172. doi: 10.1002/(SICI)1098-1063(1996)6:2<149::AID-HIPO6>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
  • 13.Jensen O, Lisman JE. Position reconstruction from an ensemble of hippocampal place cells: contribution of theta phase coding. J. Neurophysiol. 2000;83:2602–2609. doi: 10.1152/jn.2000.83.5.2602. [DOI] [PubMed] [Google Scholar]
  • 14.Yamaguchi Y, Aota Y, McNaughton BL, Lipa P. Bimodality of theta phase precession in hippocampal place cells in freely running rats. J. Neurophysiol. 2002;87:2629–2642. doi: 10.1152/jn.2002.87.6.2629. [DOI] [PubMed] [Google Scholar]
  • 15.McNaughton BL, Barnes CA, O’Keefe J. The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely-moving rats. Exp. Brain Res. 1983;52:41–49. doi: 10.1007/BF00237147. [DOI] [PubMed] [Google Scholar]
  • 16.Wiener SI, Paul CA, Eichenbaum H. Spatial and behavioral correlates of hippocampal neuronal activity. J. Neurosci. 1989;9:2737–2763. doi: 10.1523/JNEUROSCI.09-08-02737.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Hirase H, Czurko HH, Csicsvari J, Buzsaki G. Firing rate and theta-phase coding by hippocampal pyramidal neurons during ’space clamping’. Eur. J. Neurosci. 1999;11:4373–4380. doi: 10.1046/j.1460-9568.1999.00853.x. [DOI] [PubMed] [Google Scholar]
  • 18.Ekstrom AD, Meltzer J, McNaughton BL, Barnes CA. NMDA receptor antagonism blocks experience-dependent expansion of hippocampal “place fields”. Neuron. 2001;31:631–638. doi: 10.1016/s0896-6273(01)00401-9. [DOI] [PubMed] [Google Scholar]
  • 19.Mehta MR, Barnes CA, McNaughton BL. Experience-dependent, asymmetric expansion of hippocampal place fields. Proc. Natl. Acad. Sci.USA. 1997;94:8918–8921. doi: 10.1073/pnas.94.16.8918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Lengyel M, Szatmary Z, Erdi P. Dynamically detuned oscillators account for the coupled rate and temporal code of place cell firing. Hippocampus. 2003;13:700–714. doi: 10.1002/hipo.10116. [DOI] [PubMed] [Google Scholar]
  • 21.Pike FG, et al. Distinct frequency preferences of different types of rat hippocampal neurones in response to oscillatory input currents. J. Physiol. 2000;529:205–213. doi: 10.1111/j.1469-7793.2000.00205.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Kamondi A, Acsady L, Wang XJ, Buzsaki G. Theta oscillations in somata and dendrites of hippocampal pyramidal cells in vivo: activity-dependent phase-precession of action potentials. Hippocampus. 1998;8:244–261. doi: 10.1002/(SICI)1098-1063(1998)8:3<244::AID-HIPO7>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
  • 23.Burgess N, Recce M, O’Keefe J. A model of hippocampal function. Neural Networks. 1994;7:1065–1081. [Google Scholar]
  • 24.Tsodyks MV, Skaggs WE, Sejnowski TJ, McNaughton BL. Population dynamics and theta rhythm phase precession of hippocampal place cell firing: a spiking neuron model. Hippocampus. 1996;6:271–280. doi: 10.1002/(SICI)1098-1063(1996)6:3<271::AID-HIPO5>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
  • 25.Jensen O, Lisman JE. Hippocampal CA3 region predicts memory sequences: accounting for the phase precession of place cells. Learn. Mem. 1996;3:279–287. doi: 10.1101/lm.3.2-3.279. [DOI] [PubMed] [Google Scholar]
  • 26.Wallenstein GV, Hasselmo ME. GABAergic modulation of hippocampal population activity: sequence learning, place field development, and the phase precession effect. J. Neurophysiol. 1997;78:393–408. doi: 10.1152/jn.1997.78.1.393. [DOI] [PubMed] [Google Scholar]
  • 27.Wood ER, Dudchenko PA, Eichenbaum H. The global record of memory in hippocampal neuronal activity. Nature. 1999;397:613–616. doi: 10.1038/17605. [DOI] [PubMed] [Google Scholar]
  • 28.Moita MA, Rosis S, Zhou Y, LeDoux JE, Blair HT. Hippocampal place cells acquire location-specific responses to the conditioned stimulus during auditory fear conditioning. Neuron. 2003;37:485–497. doi: 10.1016/s0896-6273(03)00033-3. [DOI] [PubMed] [Google Scholar]
  • 29.Kahana MJ, Sekuler R, Caplan JB, Kirschen M, Madsen JR. Human theta oscillations exhibit task dependence during virtual maze navigation. Nature. 1999;399:781–784. doi: 10.1038/21645. [DOI] [PubMed] [Google Scholar]
  • 30.O’Keefe J, Burgess N. Geometric determinants of the place fields of hippocampal neurons. Nature. 1996;381:425–428. doi: 10.1038/381425a0. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SIcaptions
NIHMS4620-supplement-SIcaptions.doc (23KB, doc)
SIfigures
NIHMS4620-supplement-SIfigures.pdf (1.8MB, pdf)

RESOURCES