Abstract
An optimization approach for diffusion tensor imaging (DTI) technique is proposed, aiming to improve the estimates of tensors, fractional anisotropy (FA), and fiber directions. With the simulated annealing algorithm, the proposed approach simultaneously optimizes imaging parameters (gradient duration/separation, read-out time, and TE), b-values, and diffusion gradient directions either with or without incorporating prior knowledge of tensor fields. In addition, the method through which tensors are estimated, least squares in our study, was also considered in the optimization procedures. Monte-Carlo simulations were performed for three different scenarios of prior fiber distributions including fibers orientated in 1 (CONE1) and 3 (CONE3) cone areas (50 tensors orderly oriented within a diverging angle of 20° in each cone) and a uniform fiber distribution (UNIF). In addition, three imaging acquisition schemes together with different signal-to-noise ratios were tested, including M/N=1/6, 2/12, and 5/30 for each prior fiber distribution where M and N were the number of b=0 and b>0 images, respectively. Our results show that the optimal b-value ranges between 0.7 and 1.0 × 109 s/m2 for UNIF. However, the optimal b-value ranges become both higher and wider for CONE1 and CONE3 than that of UNIF. In addition, the biases and standard deviations (SD) of tensors, and SD of FA are substantially reduced and the accuracy of fiber directional estimates is improved using the proposed approach particularly in CONE1 when compared with the conventional approaches. Together, the proposed unified optimization approach may offer a direct and simultaneous means to optimize DTI experiments.
INTRODUCTION
Diffusion tensor imaging (DTI) has become an invaluable non-invasive imaging tool to provide insights into the microstructural integrity of white matter. While its clinical utility has largely been demonstrated, DTI demands a much higher signal-to-noise ratio (SNR) than that of conventional MR imaging sequences in order to provide accurate and quantitative diffusion measures. Therefore, extensive effort has been devoted to optimizing DTI (Basser and Pierpaoli, 1996), in an attempt to improve the accuracy and precision of tensor estimation. These optimizations include the choices of imaging parameters (Alexander and Barker, 2005; Andreisek et al., 2008; Armitage and Bastin, 2001; Brihuega-Moreno et al., 2003; Hasan, 2007; Jones et al., 1999; Kingsley and Monahan, 2004; Lee et al., 2006; Naganawa et al., 2004; Xing et al., 1997), the approaches through which tensors are estimated (Basser et al., 1994; Salvador et al., 2005; Stieltjes et al., 2003), and the design of diffusion gradient directions (Hasan et al., 2001; Papadakis et al., 1999; Skare et al., 2000). While intriguing results have been reported, demonstrating the improved tensor estimations using these optimization approaches, all of the existing approaches thus far have separately optimized different aspects of DTI such as imaging parameters or gradient directions alone. Given the fact that all aspects of a DTI experiment, including image acquisition as well as methods for tensor calculations will affect the accuracy of tensor estimates, it is thus highly desirable to having a unified approach where the essential aspects of DTI are optimized simultaneously. In addition, one of the main assumptions of the existing optimization procedures is that all tensors are uniformly distributed in a sphere. While this assumption is valid for most of the applications, in some cases, i.e. in the pediatric brain, only the major white matter fibers are well mylinated, leading to a non-uniform distribution of these major fibers (Fig. 1). As a result, a uniformly distributed diffusion gradient scheme may no longer be the most efficient scheme to provide accurate measures of tensors. Recently, Peng and Arfanakis (Peng and Arfanakis, 2007) proposed an approach where the prior directional information of selected fiber tracts was incorporated in the design of the diffusion gradient orientations. A significant reduction of the standard deviation of FA was obtained with their approach, underscoring the importance of considering the prior information. Nonetheless, similar to other existing DTI optimization approaches, only the design of the gradient directions was considered.
Fig. 1.
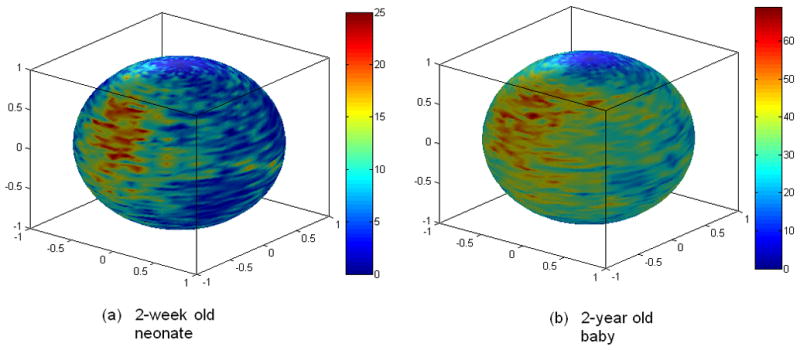
Examples of fiber distribution patterns in a neonate (a) and a 2-year old baby (b) are shown. Fiber orientations are obtained using voxels with a FA larger than 0.3 in the 2-week old neonate and 0.4 in the 2-year old baby based on a 6 direction DTI experiment and visualized on a sphere representing the 3D directions. Color codes represent number of fibers in a specific orientation block (4° span in azimuth angle and 2° span in elevation angle).
In this paper, we propose a unified optimization approach that simultaneously optimizes most of the essential imaging parameters, including gradient separation/duration, TE, read-out time, and b-values, and gradient orientations either with or without considering the prior information of fiber distributions. In addition, the means through which tensors are calculated is also considered in the optimization procedures. Monte-Carlo simulations were performed to evaluate the performance of the proposed method. Simulation results demonstrate that our approach provides similar results to that reported in the literature when fibers are uniformly distributed while outperforming the existing methods when fibers are not uniformly distributed.
METHOD
In this section, the formulation of the optimization criteria, the optimization procedures, and the information on simulation/evaluation parameters are provided.
Design criteria
Assuming the SNR is moderately high, a Gaussian distribution instead of the Rican distribution (Rice, 1944) can be employed to model MR signal. With a pulsed gradient spin echo experiment, the MR signal with the diffusion tensor and weighting matrix can be written as:
| (1) |
where S is the measured signal, S0 is the expected baseline signal intensity, r is the unit vector representing one gradient direction, and b is the scalar value of gradient weighting strength. Moreover, η represents Gaussian noise with a zero mean and a variance of and D0 represents (Andreisek et al., 2008) the true tensor. Taking the logarithm of both sides of Eq. (1) leads to . Subsequently, taking Taylor expansion of the last term and neglecting the higher order terms, we can obtain:
| (2) |
where and 〈S〉 = S0 exp(−brTD0r).
Thus, ln(S) is approximately normally distributed with a mean of ln(S0) − brT D0r and variance for moderate to large 〈S〉/ση (Anderson, 2001; Zhu, 2007). Eq. (2) can be rewritten using a matrix formulation as:
| (3) |
where Y⃗ = [log(S̃1), log(S̃2),....log(S̃n)]T represents the measured signal intensities, n is the total number of acquisitions at each voxel and β⃗ = [log(S0), (D0)11, (D0)12, (D0)13, (D0)22, (D0)23, (D0)33]T. In addition, the i-th row of the design matrix X⃗ has the form of . The unbiased least squares (LS) estimator of β⃗ is β̃LS = (XTX)−1 XTY⃗, and its corresponding covariance matrix is
| (4) |
where Σε is the covariance matrix of ε. Assuming the signal intensities are independent,
| (5) |
By defining and θ = [(D0)11, (D0)12, (D0)13, (D0)22, (D0)23, (D0)33], Eq. (5) can be written as
| (6) |
The trace of ΣβLS was then used as the cost function for the following optimization procedures. The main justification for the use of Eq. (12) as the cost function for subsequent optimization is due to the fact that the main goal of our study is to improve the accuracy and precision of tensor estimates which can be characterized by the bias and covariance of the estimated DT. Therefore, it is common in the field of experimental design to choose the covariance matrix of the estimated DT when the bias of the estimated DT is small (Atkinson, 1992; Federov, 1972). It should be noted that the same procedures can be used to derive criteria for weighted least squares estimation (Basser et al., 1994; Zhu, 2007) as outlined in Appendix B.
Incorporating imaging parameters
In the previous section, we derived the design criteria for tensor estimation. In this section, procedures on how imaging parameters can be integrated into Eq. (6) will be outlined. A sequence structure (Fig. 2) similar to that illustrated in Alexander and Barker (Alexander and Barker, 2005) was employed in our study, although slight modifications were made to accommodate our optimization process. The durations of the 90° and 180° pulses were P90 and P180, respectively, δ was the diffusion gradient duration, Δ was the time interval between diffusion gradients, and R and RH were the readout time before and after the echo, respectively. Assuming a fixed image resolution, RH would be fixed and independent of other parameters. Four time intervals, τ1, τ2, τ3, and τ4 were included. The durations of these four time intervals along with P90 and P180 were considered fixed based on the hardware constraints and were independent of other imaging parameters.
Fig. 2.
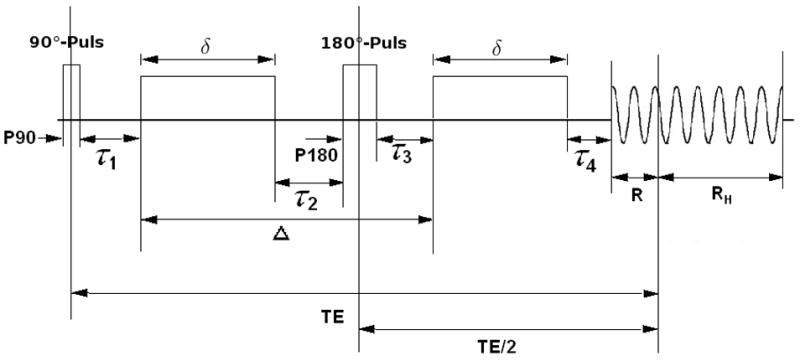
The pulsed-gradient spin-echo (PGSE) sequence diagram is shown.
The echo time TE was then defined as
| (7) |
and the applied b-value was given by
| (8) |
where γ is the gyro-magnetic ratio, g is the gradient strength, is the “effective” diffusion time under the assumption of rectangular gradient pulses and the Gaussian density function of particle displacements (Callaghan, 1991) (Stejskal and Tanner, 1965). We assume that the expected baseline intensity S0 is given by
| (9) |
and
| (10) |
where P0 depends on the intrinsic signal of the tissue (spin density). If we further assume that the underlying noise is constant, then the SNR can be incorporated into S0 as follows:
| (11) |
Substituting Eq. (11) in Eq. (6) yields
| (12) |
Notice the gradient directions are represented in the X and Z matrices. This formulation incorporates most of the important imaging parameters together with the LS approach for tensor estimation and diffusion gradient directions. The trace of ΣβLS was then used as the cost function for the following optimization procedures. The use of Eq. (12) as the cost function for subsequent optimization is justified due the fact that the main goal of our study is to improve the accuracy and precision of tensor estimates which can be characterized by the bias and covariance of the estimated DT. Therefore, it is common in the field of experimental design to choose the covariance matrix of the estimated DT as the cost function when the bias of the estimated DT is small (Atkinson, 1992; Federov, 1972). Nevertheless, although the trace of the covariance matrix is used in our approach, other measures such as the determinant or smallest eigenvalue are also eligible for this purpose.
Optimization
The incorporation of fiber orientations into the optimization processes for DTI imaging parameters, gradient directions, and LS tensor estimation is one of the main motives of the present study. Once the values of Δ and R are chosen, the values of δ, TE and b-values can be calculated according to P90, P180, RH, τ1, τ2, τ3, and τ4. By further choosing the gradient direction vectors and incorporating the tensor field information, the covariance matrices represented by Eq. (12) can be fully determined, allowing the minimization of the cost function – the trace of covariance matrix.
A simulated annealing algorithm (Kirkpatrick et al., 1983) was used to minimize the cost function. The optimization procedures are described below.
Setting values of P90, P180, RH, τ1, τ2, τ3, and τ4 according to the hardware limitations (P90=0.005s; P180=0.004s; τ1, τ2, τ3, and τ4 =0; Gradient Strength: 40 mT/m; readout time after echo=0.0338s according to our 3.0-T MR imaging unit (Allegra; Siemens Medical Systems, Erlangen, Germany)). T2 was set to be 0.08s.
Initializing values of Δ, R and gradient direction vectors which were represented by N×3 (N: number of gradient directions) matrix and were independently simulated from the standard Gaussian distribution.
Calculating the values of δ, TE and b-value, respectively.
Calculating the covariate matrix as in Eq. (12) for each prior DT and then summing the trace of matrices for all DTs in the corresponding tensor field as the cost function values.
Updating values of Δ, R and gradient direction vectors according to the random-walk Metropolis algorithm.
Repeating the steps c)–e) until the stopping criteria were met.
After optimization, the values of Δ, R, δ, TE, b-value and gradient direction vectors that provided the minimal cost function values (minimum×(1+5%)) were defined as the optimal values. Detailed descriptions of the simulated annealing algorithm are given in Appendix A.
Simulation
In this section, parameters for Monte Carlo simulation and how simulated DW images were obtained are provided.
Prior-Knowledge of fiber directions
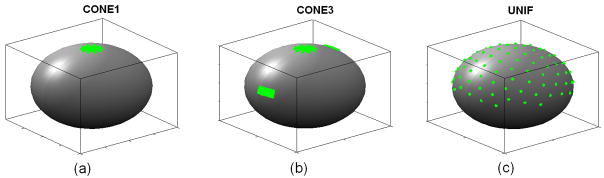
Three different fiber distributions as represented by the corresponding tensor fields were simulated as prior information: I) CONE1 – fibers orientated in 1 cone area (50 tensors orderly oriented within a diverging angle of 20°); II) CONE3 – fibers orientated in 3 well separated cone-like areas (50 tensors in each cone and the diverging angle for each cone was 20°); and III) UNIF – uniformly distributed fibers (100 tensors with random orientations) (Fig. 3). In each of the tensor fields, a “rice-shaped” diffusion tensor D diag = (λ1, λ2, λ2) with λ1 = 1.7 × 10−9m2s−1 and λ2 = λ2 = 0.2 × 10−9 m2 s−1 was selected and different fiber orientations were generated using a rotation around the z axis D = RT (α, φ)diag(λ1, λ2, λ2)R(α, φ), where R(α, φ) represents the rotation matrix defined by azimuth angle α and elevation angle φ.
Fig. 3.
Simulations of three different fiber distributions, including (a) a single fiber cone area with 50 fibers, (b) three fiber cone areas with 50 fibers in each cone and (c) the uniform fiber case with 100 randomly distributed fiber orientations.
Three different imaging acquisition schemes were tested, including DIFF6 – M=1/N=6; DIFF12 – M=2/N=12, and DIFF30 – M=5/N=30 for each prior tensor field where M and N are the numbers of b=0 and diffusion weighted images (b>0), respectively.
Reconstruction
The expected baseline signal intensity S0 was computed from Eq. (11) assuming a constant spin density P0. The “ideal” DW signals were then calculated 〈S〉 = S0 exp(−brT D0r) from for each of the corresponding prior tensor fields. Constant complex noise with independent real and imaginary parts, each with a normal distribution (μ/σ =0/2) was added to S0 and 〈S〉 separately and the magnitude was then calculated to obtain the synthetic measurement for the baseline image intensity and diffusion weighted image intensity, respectively. By assuming a constant noise level, four different P0 levels [250, 450, 600, 800] were tested to simulate different SNRs. Finally, DTs were reconstructed using LS estimation. This process was repeated 100 times for each experimental setting.
Performance indices
To assess the performance of the proposed optimization procedures, the bias (B(D)) and the standard deviations (σ(D)) of the tensor elements, the standard deviation of reconstructed FA (σ (FA)) and Mean Angular Difference (MAD) (Landman et al., 2007) of the reconstructed principle eigenvectors were employed. Detailed information on these four parameters is provided below.
B(D): In each experimental setting, the square error of each DT element was calculated by subtracting the estimated values from the true tensor elements. The square errors of the six independent elements were then added together and averaged over all trials and all experimental settings to obtain a scalar value at each SNR and b-value to assess the accuracy of tensor estimation.
σ(D): Standard deviations of the six independent elements across 100 trials were summed together and averaged over all experimental settings to assess the precision of tensor estimation.
σ(FA): Standard deviations of FA values across 100 trials were averaged over all experimental settings to assess the precision of FA estimation.
MAD: The MAD was calculated using the following formula (Landman et al., 2007) for each experimental setting: where N=100 for 100 trials, PEVi is the reconstructed principle eigenvector of each experimental setting and PEVtr is the “true” principle eigenvector.
Evaluation of optimal imaging parameters and gradient directions
For each optimization set, an optimal b-value range was obtained as outlined in the optimization section together with the corresponding Δ, R, δ and TE values. To validate this optimal b-value range, a series of 11 different b-values (Appendix A) together with the corresponding Δ, R, δ, TE and gradient directions were tested through the reconstruction process to produce performance indices at each specific b-value, which provided the comparison across different b-values and hence the validation of the proposed optimal ranges.
In order to determine the performance of the optimal gradient directions in the presence of prior knowledge of the tenor fields, a direct comparison was made between the optimized diffusion gradient directions obtained using the proposed approach and the conventional gradient scheme based on the minimal energy method as proposed by Jones et al (Jones et al., 1999). For each comparison, the prior tensor field was considered as the “true tensor field.” To ensure a fair compassion between the proposed and the conventional scheme, all imaging parameters including b-value were kept identical. The four performance indices as outlined above were employed to compare the two optimization approaches of diffusion gradient directions. In addition, an improvement ratio (performance of the proposed optimization scheme/performance of the conventional scheme) was also calculated.
In order to further assess the directional sensitivity of the proposed gradient scheme, another synthetic tensor field which consisted of 10000 uniformly distributed “test samples” on the sphere was also simulated. The proposed optimization and conventional schemes were used to perform reconstruction at a specific b-value based on this “true” tensor field so that their directional performance can be compared.
RESULTS
Optimal Δ, R, TE, and b-value
Fig. 4 shows the optimal b-value ranges for all combinations of tensor fields and gradient directions. In the UNIF case, the optimal b-value ranges between 0.7 × 109 s/m2 and 1.0 × 109 s/m2 independent of the number of diffusion gradient directions, consistent with that reported by Alexander and Barker (Alexander and Barker, 2005) for one fiber case. In contrast, the optimal ranges become both wider and higher for CONE3 and CONE1.
Fig. 4.
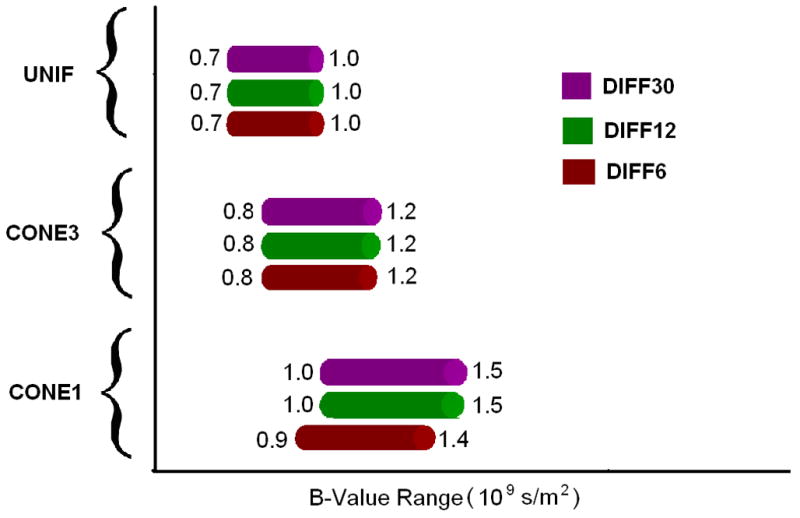
Optimal b-value ranges defined by the proposed scheme. CONE1: one cone area; CONE3: three cone areas; and UNIF: uniform fiber case. DIFF6: M/N=1/6, DIFF12: M/N=2/12, DIFF30: M/N=5/30.
Table 1 lists the optimal values of Δ, R, and TE (rounded to ms) at the optimal b-value (rounded at 0.1 × 109 s/m2) which corresponds to the lowest cost function value (the center of the optimal range) of all three prior fiber distributions. It is evident that the optimal parameters are rather stable for each prior tensor distribution independent of the M/N. In order to better compare our approach and that reported by Alexander and Barker (Alexander and Barker, 2005), the optimal values calculated based on their approach are listed in parentheses at the same b-values for comparison. It is immediately apparent that the optimal Δ, R, and TE are consistent between both approaches.
Table 1.
Optimal values of Δ, R, TE at the optimal b-value corresponding to the minimal cost function values (the center of the optimal range) of all three prior fiber distributions
| CONE1 | CONE3 | UNIF | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DIFF6 | DIFF12 | DIFF30 | DIFF6 | DIFF12 | DIFF30 | DIFF6 | DIFF12 | DIFF30 | |
| B(109s/m2) | 1.1 | 1.2 | 1.2 | 1.0 | 1.0 | 1.0 | 0.8 | 0.8 | 0.8 |
| TE (ms) | 51 (51) | 52 (53) | 52 (53) | 50 (50) | 50 (50) | 50 (50) | 46 (46) | 46 (46) | 46 (46) |
| Δ (ms) | 27 (28) | 28 (28) | 28 (28) | 27 (27) | 27 (27) | 27 (27) | 25 (25) | 25 (25) | 25 (25) |
| R (ms) | <0.01 (0.4) | 0.01 (1.2) | <0.01 (1.2) | 0.1 (1.1) | <0.01 (1.1) | <0.01 (1.1) | <0.01 (0.2) | <0.01 (0.2) | 0.01 (0.2) |
The four performance indices with DIFF6 and CONE1 for different SNR are shown in Fig. 5. The two dotted lines indicate the ranges of the optimal b-values as shown in Fig. 4. With the exception of s(FA), the optimal b-value ranges coincide with the “valley” of the B(D), σ(D) and MAD curves, demonstrating the effectiveness of the proposed optimization approach which yields reduced biases and SD of tensors and improved accuracy of the estimates of tensor directions. However, the optimal b-value range for FA appears slightly higher than that obtained using the proposed optimization approach. This finding is reasonable since our optimization criteria are based on the variance properties of the six independent tensor elements rather than FA, and a more specific criterion may be needed if one is particularly interested in FA estimation. Similar findings were also reported by Alexander and Barker (Alexander and Barker, 2005) where they showed that the optimal b-value for FA estimation is higher than that for fiber orientation estimation.
Fig. 5.
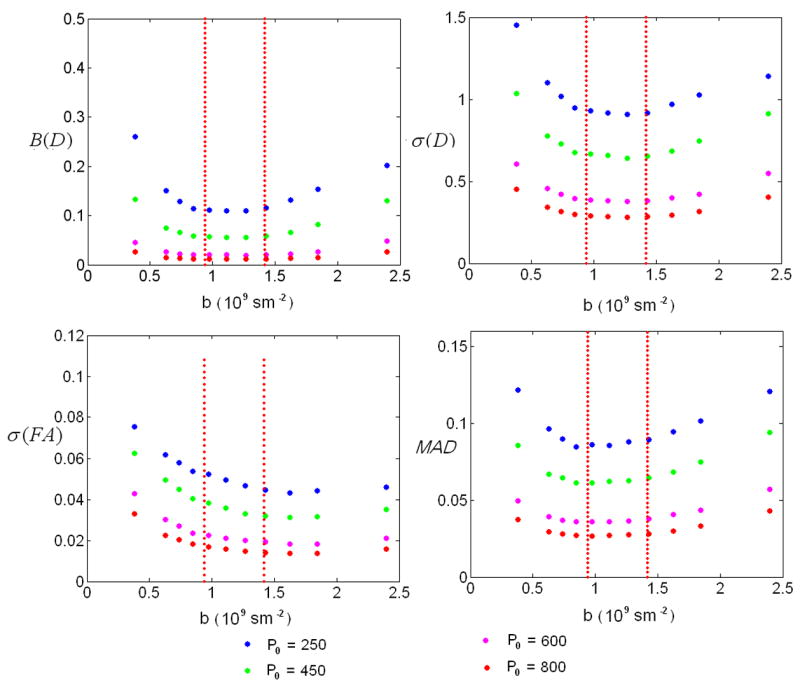
Results of the four performance indices: Bias of D-B(D), standard deviation of D-σ(D), standard deviation of FA-σ(FA) and mean angular difference-MAD for DIFF6 and CONE1. X-axis represents b-value in109s/m2, y-axis represents the corresponding performance indices values. Red lines indicate the optimal b-value ranges defined by the proposed optimization scheme.
Optimal diffusion gradient directions
Fig. 6 demonstrates the diffusion gradient directions using the conventional and the proposed optimization schemes, respectively. As expected, the conventional scheme results in a highly uniform coverage of the entire sphere (Fig. 6a). However, the gradient scheme using the proposed method shows a very different pattern especially in CONE1 (Fig. 6b) and CONE3 (Fig. 6c), respectively. In CONE1, the optimized gradient directions exhibit an orderly pattern around the direction of the prior tensor field (red points). Similarly, although the gradient directions spread out, they maintain an orderly pattern around the three tensor fields (red points) in CONE3. Finally, the optimized diffusion gradient directions for UNIF (Fig. 6d) using our approach resemble that obtained using the conventional scheme (Fig. 6a); the gradient directions are uniformly distributed across the sphere.
Fig. 6.

Diffusion gradient orientations are shown for the conventional scheme (a) and the proposed optimization scheme in CONE1 (b), CONE3 (c) and UNIF (d), respectively. Red points represent the center directions of the predefined fiber distributions (CONE1 and CONE2). Green points are the orientations of the diffusion gradients. In each panel, the diffusion gradient directions are plotted on a spherical coordinate with azimuth angle θ (X-axis) ranging from −π to π and elevation angle ϕ(Y-axis) from 0 to π/2.
Comparison of Optimal and Conventional Gradient direction schemes
The improvement ratios (proposed/conventional schemes) for all four performance indices in CONE1 (Fig. 7a), CONE3 (Fig. 7b) and UNIF (Fig. 7c) conditions with P0=450 (which corresponds to a SNR~30 in our simulation) are shown. The proposed optimization scheme substantially reduces the bias (B(D)) and standard deviation (s(D)) of the tensors by ~40% – 60% and ~20–30%, respectively within the optimal b-value range (red lines) for CON1 (Fig. 7a). It appears that these improvements are independent of the number of diffusion gradients. In contrast, although the proposed scheme remains superior to that of conventional approach, the extent to which σ(FA) and MAD are improved depends on the number of diffusion gradients. Specifically, the largest improvement is observed with DIFF6 (~50%), followed by DIFF12 and DIFF30 for σ(FA) at a b-value of 1.2×109s/m2. For MAD, a comparable performance is observed between the optimized and the conventional schemes with DIFF6 while a 30% improvement is observed for DIFF12 and DIFF30, suggesting that it is imperative to employ more than 6 diffusion gradient directions in order to obtain an accurate estimate of tensor directions. Comparing to CONE1, the degree of improvements for CONE3 is reduced for both B(D) and σ(D) (Fig. 7b). In addition, the improvement is minimal for σ(FA) and MAD (within 5%). Finally, the performance is comparable for all four measures between the proposed and conventional schemes in UNIF condition (Fig. 7c). The improvement ratios of other P0 levels show a similar improvement pattern and the results are summarized in Table 2.
Fig. 7.
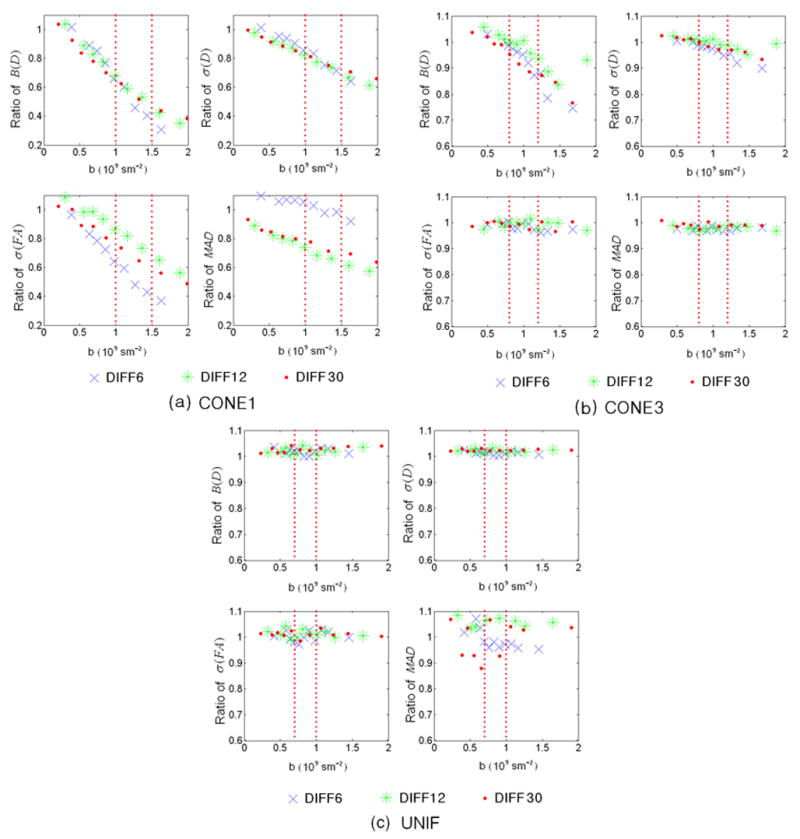
Improvement ratios of the four performance indices are shown for CONE1 (a), CONE3, and UNIF (c), respectively, where P0=450. X-axis represents b-value in 109s/m2 and Y-axis represents the performance indices values. Dashed red lines indicate the rages of optimal b-value using the proposed optimization approach. Blue crosses, green asterisks, and red filled circles represent DIFF6, DIFF12, and DIFF30, respectively.
Table 2.
Improvement ratios at four different P0 levels for the four performance indices of CONE1
| b(10 9s/m2) | B(D) | σ (D) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| P0=250 | P0=450 | P0=600 | P0=800 | P0=250 | P0=450 | P0=600 | P0=800 | ||
| DIFF6 | 0.4 | 1.07 | 1.02 | 1.04 | 1.03 | 1.03 | 1.01 | 1.01 | 1.01 |
| 0.6 | 0.91 | 0.89 | 0.92 | 0.90 | 0.96 | 0.95 | 0.97 | 0.96 | |
| 0.7 | 0.83 | 0.85 | 0.83 | 0.85 | 0.93 | 0.94 | 0.92 | 0.94 | |
| 0.9 | 0.77 | 0.77 | 0.75 | 0.74 | 0.91 | 0.91 | 0.90 | 0.89 | |
| 1.0 | 0.61 | 0.66 | 0.65 | 0.65 | 0.84 | 0.86 | 0.85 | 0.85 | |
| 1.1 | 0.54 | 0.60 | 0.57 | 0.59 | 0.80 | 0.83 | 0.82 | 0.82 | |
| 1.3 | 0.49 | 0.46 | 0.46 | 0.49 | 0.77 | 0.75 | 0.75 | 0.77 | |
| 1.4 | 0.48 | 0.40 | 0.37 | 0.37 | 0.76 | 0.71 | 0.69 | 0.69 | |
| 1.6 | 0.53 | 0.30 | 0.27 | 0.30 | 0.81 | 0.64 | 0.61 | 0.64 | |
| 1.8 | 0.56 | 0.35 | 0.25 | 0.21 | 0.90 | 0.69 | 0.58 | 0.55 | |
| 2.4 | 0.41 | 0.36 | 0.30 | 0.24 | 1.00 | 0.89 | 0.75 | 0.62 | |
| σ(FA) | MAD | ||||||||
| 0.4 | 0.99 | 0.97 | 0.94 | 0.92 | 1.11 | 1.10 | 1.09 | 1.09 | |
| 0.6 | 0.89 | 0.83 | 0.85 | 0.81 | 1.07 | 1.06 | 1.09 | 1.09 | |
| 0.7 | 0.84 | 0.78 | 0.77 | 0.77 | 1.07 | 1.07 | 1.09 | 1.11 | |
| 0.9 | 0.78 | 0.73 | 0.72 | 0.71 | 1.05 | 1.07 | 1.09 | 1.09 | |
| 1.0 | 0.70 | 0.64 | 0.63 | 0.62 | 1.04 | 1.05 | 1.08 | 1.06 | |
| 1.1 | 0.63 | 0.59 | 0.57 | 0.56 | 1.02 | 1.03 | 1.06 | 1.04 | |
| 1.3 | 0.57 | 0.48 | 0.49 | 0.48 | 0.97 | 0.98 | 1.03 | 1.04 | |
| 1.4 | 0.52 | 0.43 | 0.39 | 0.39 | 0.94 | 0.98 | 1.00 | 1.00 | |
| 1.6 | 0.49 | 0.37 | 0.34 | 0.35 | 0.89 | 0.92 | 0.95 | 0.95 | |
| 1.8 | 0.47 | 0.34 | 0.30 | 0.27 | 0.78 | 0.86 | 0.89 | 0.87 | |
| 2.4 | 0.44 | 0.33 | 0.28 | 0.24 | 0.56 | 0.63 | 0.72 | 0.77 | |
| DIFF12 | B(D) | σ(D) | |||||||
| 0.3 | 1.01 | 1.04 | 1.04 | 1.01 | 0.97 | 0.98 | 0.98 | 0.97 | |
| 0.6 | 0.88 | 0.89 | 0.92 | 0.90 | 0.92 | 0.92 | 0.93 | 0.92 | |
| 0.7 | 0.82 | 0.83 | 0.84 | 0.85 | 0.89 | 0.89 | 0.90 | 0.91 | |
| 0.8 | 0.77 | 0.78 | 0.76 | 0.79 | 0.87 | 0.87 | 0.86 | 0.88 | |
| 1.0 | 0.68 | 0.68 | 0.70 | 0.69 | 0.83 | 0.82 | 0.83 | 0.83 | |
| 1.2 | 0.59 | 0.59 | 0.62 | 0.61 | 0.78 | 0.78 | 0.79 | 0.79 | |
| 1.4 | 0.49 | 0.53 | 0.53 | 0.53 | 0.72 | 0.74 | 0.74 | 0.74 | |
| 1.6 | 0.43 | 0.42 | 0.44 | 0.45 | 0.67 | 0.67 | 0.68 | 0.69 | |
| 1.9 | 0.43 | 0.35 | 0.36 | 0.36 | 0.68 | 0.61 | 0.62 | 0.63 | |
| 2.2 | 0.49 | 0.34 | 0.28 | 0.28 | 0.75 | 0.61 | 0.55 | 0.55 | |
| 3.0 | 0.38 | 0.36 | 0.25 | 0.19 | 0.94 | 0.79 | 0.55 | 0.46 | |
| σ(FA) | MAD | ||||||||
| 0.3 | 1.10 | 1.08 | 1.07 | 1.03 | 0.88 | 0.89 | 0.90 | 0.87 | |
| 0.6 | 1.01 | 0.99 | 1.00 | 1.01 | 0.83 | 0.82 | 0.83 | 0.82 | |
| 0.7 | 0.98 | 0.99 | 0.98 | 1.01 | 0.81 | 0.80 | 0.81 | 0.80 | |
| 0.8 | 0.94 | 0.94 | 0.92 | 0.93 | 0.78 | 0.78 | 0.78 | 0.78 | |
| 1.0 | 0.88 | 0.86 | 0.90 | 0.87 | 0.75 | 0.74 | 0.74 | 0.73 | |
| 1.2 | 0.85 | 0.82 | 0.82 | 0.80 | 0.71 | 0.68 | 0.70 | 0.70 | |
| 1.4 | 0.77 | 0.73 | 0.75 | 0.75 | 0.67 | 0.66 | 0.66 | 0.65 | |
| 1.6 | 0.69 | 0.65 | 0.67 | 0.68 | 0.62 | 0.61 | 0.61 | 0.62 | |
| 1.9 | 0.62 | 0.56 | 0.56 | 0.56 | 0.61 | 0.58 | 0.56 | 0.57 | |
| 2.2 | 0.56 | 0.52 | 0.47 | 0.46 | 0.64 | 0.55 | 0.51 | 0.51 | |
| 3.0 | 0.49 | 0.45 | 0.38 | 0.33 | 0.66 | 0.61 | 0.48 | 0.43 | |
| DIFF30 | B(D) | σ(D) | |||||||
| 0.2 | 1.04 | 1.04 | 1.03 | 1.04 | 0.99 | 0.99 | 0.99 | 0.99 | |
| 0.4 | 0.91 | 0.92 | 0.91 | 0.90 | 0.94 | 0.95 | 0.95 | 0.94 | |
| 0.5 | 0.84 | 0.83 | 0.86 | 0.87 | 0.92 | 0.91 | 0.92 | 0.93 | |
| 0.7 | 0.76 | 0.78 | 0.80 | 0.80 | 0.88 | 0.88 | 0.90 | 0.90 | |
| 0.9 | 0.69 | 0.70 | 0.70 | 0.71 | 0.84 | 0.85 | 0.85 | 0.85 | |
| 1.1 | 0.60 | 0.62 | 0.62 | 0.62 | 0.80 | 0.81 | 0.81 | 0.81 | |
| 1.3 | 0.53 | 0.52 | 0.54 | 0.54 | 0.76 | 0.75 | 0.76 | 0.77 | |
| 1.6 | 0.48 | 0.44 | 0.44 | 0.44 | 0.72 | 0.70 | 0.70 | 0.70 | |
| 2.0 | 0.47 | 0.38 | 0.35 | 0.35 | 0.74 | 0.66 | 0.64 | 0.64 | |
| 2.4 | 0.44 | 0.38 | 0.30 | 0.27 | 0.81 | 0.68 | 0.59 | 0.58 | |
| 3.5 | 0.21 | 0.24 | 0.23 | 0.21 | 0.95 | 0.85 | 0.63 | 0.54 | |
| σ(FA) | MAD | ||||||||
| 0.2 | 1.04 | 1.02 | 1.01 | 1.02 | 0.91 | 0.93 | 0.92 | 0.89 | |
| 0.4 | 0.96 | 1.00 | 0.94 | 0.96 | 0.88 | 0.86 | 0.89 | 0.87 | |
| 0.5 | 0.92 | 0.89 | 0.94 | 0.92 | 0.85 | 0.85 | 0.86 | 0.85 | |
| 0.7 | 0.88 | 0.88 | 0.90 | 0.88 | 0.81 | 0.81 | 0.84 | 0.84 | |
| 0.9 | 0.81 | 0.80 | 0.81 | 0.82 | 0.79 | 0.80 | 0.79 | 0.79 | |
| 1.1 | 0.70 | 0.73 | 0.73 | 0.73 | 0.77 | 0.77 | 0.77 | 0.76 | |
| 1.3 | 0.65 | 0.65 | 0.65 | 0.66 | 0.73 | 0.71 | 0.73 | 0.72 | |
| 1.6 | 0.59 | 0.56 | 0.55 | 0.54 | 0.68 | 0.69 | 0.68 | 0.68 | |
| 2.0 | 0.56 | 0.49 | 0.46 | 0.45 | 0.66 | 0.63 | 0.64 | 0.63 | |
| 2.4 | 0.54 | 0.46 | 0.38 | 0.37 | 0.68 | 0.62 | 0.59 | 0.58 | |
| 3.5 | 0.48 | 0.45 | 0.35 | 0.29 | 0.67 | 0.65 | 0.54 | 0.50 | |
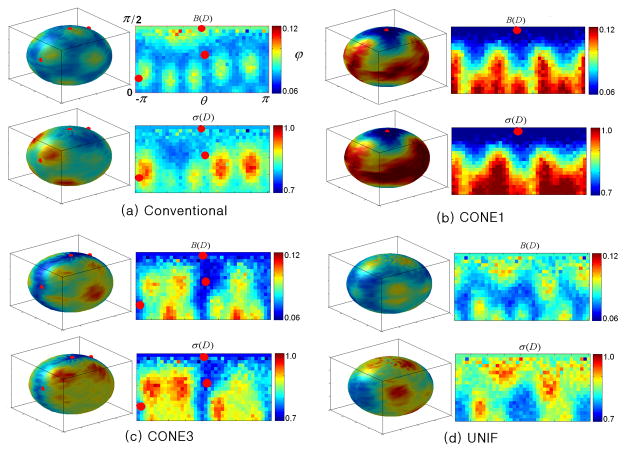
The comparison of directional sensitivity between all three different fiber distributions is shown in Fig. 8 for DIFF6. As expected, the directional dependence of both bias and precision of tensors are apparent for all schemes. A decreased bias as well as standard deviation of the tensors are observed using the proposed scheme for both CONE1 (Fig. 8b) and CONE3 (Fig. 8c), suggesting that the optimized diffusion gradient scheme offers a better estimate of the tensors around the fiber distributions. Nevertheless, it is not surprising that both the bias and standard deviations of the tensors are increased away from the cones. Finally, Fig. 8d exhibits no obvious improvements between the proposed and the conventional scheme since both schemes are optimized for a uniform fiber distribution. Similar patterns were observed for both DIFF12 and DIFF30.
Fig. 8.
Comparison of the directional sensitivity of different schemes (M/N=1/6, b-value=1*109 s/m2, P0=450) are shown for conventional scheme (a) and the proposed optimization approach for CONE1 (b), CONE3 (c), and UNIF (d), respectively. In each panel, the first row shows the spatial distribution of B(D) and the second row is σ(D). Red points represent the center of the prior fiber distribution (CONE1 or CONE3). In each panel, the performance values are plotted on a spherical coordinate with azimuth angle θ (X-axis) ranging from −π to π and elevation angle ϕ(Y-axis) from 0 to π/2.
DISCUSSION
Most of the existing optimization methods for DTI have separately considered different aspects of a DTI experiment, including either sequence parameters such as gradient duration/separation, read-out time, TE, and b-values (Alexander and Barker, 2005; Armitage and Bastin, 2001; Brihuega-Moreno et al., 2003; Jones et al., 1999; Kingsley and Monahan, 2004; Xing et al., 1997), diffusion gradient orientations (Hasan et al., 2001; Papadakis et al., 1999; Peng and Arfanakis, 2007; Skare et al., 2000), or the postprocessing schemes for tensor estimations (Basser et al., 1994; Pajevic and Basser, 2003; Salvador et al., 2005). While these approaches have yielded improvements on the parameters that were targeted to be optimized, they are prone, potentially, to be trapped in local minima when the cross-talk effects are difficult to be dealt with. Therefore, an approach capable of simultaneously optimizing most of the essential aspects of a DTI experiment is highly desirable. In this study, we proposed a unified optimization approach for DTI to simultaneously consider imaging parameters, fiber distributions and methods through which tensors are calculated. To the best of our knowledge, this is the first reported approach that offers the ability to simultaneously consider most of the important aspects of DTI experiments in the optimization processes. Specifically, with the simulated annealing algorithm (Appendix A), the proposed approach simultaneously optimizes different parameters in image acquisition (gradient duration/separation, readout time, TE, and b-values), tensor estimation, and diffusion gradient directions by considering the prior knowledge of tensor fields while minimizing the cross-talk between all parameters so as to enhance the probability of finding the global minimum. Our results show that compared with the conventional scheme (Jones et al., 1999), the proposed optimization approach substantially reduces the biases and standard deviations of tensor estimations as well as the standard deviations of FA and MAD when a nonuniform fiber distribution prior is assumed, particularly in the CONE1 condition. In addition, our results also demonstrate that a higher and wider range of b-values can be employed without compromising the accuracy and precision of tensor estimates when the information of fiber distribution is considered in the design of diffusion gradient orientations. Finally, an extension of our approach is provided in Appendix B where the weighted least squares approach is employed for tensor estimates, demonstrating the flexibility of the proposed approach in adapting different post-processing schemes for tensor estimation.
Optimal b values
With the assumption that fibers are uniformly distributed, Alexander and Barker (Alexander and Barker, 2005) evaluated a series of different b-values in an attempt to identify the optimal b-value ranges for tensor estimation. They found that b-values ranging between 0.7 and 1.0 × 109s/m2 were optimal for fiber direction estimates in one-fiber case, consistent with the optimal range of b-values obtained using our approach in the UNIF experimental setting (Fig. 4). However, the optimal ranges of b-values change when the prior information of non-uniform fiber distributions was incorporated in the design of the diffusion gradients. Specifically, the optimal ranges of b-values become higher and wider for both CONE3 ([0.8, 1.2] × 109s/m2) and CONE1 ([0.9, 1.5] × 109s/m2). These findings suggest that by incorporating the prior information of tensor fields for optimizing the diffusion gradient directions, a higher and wider range of b-values can be used without compromising accuracy and precision, potentially facilitating diffusion spectrum imaging (Wedeen et al., 2008) where high b-values are needed.
Optimal gradient directions
It is evident that the optimized gradient schemes using the proposed approach for nonuniform fiber distributions (CONE1 and CONE3) (Fig. 6) exhibit a very different pattern when compared with that of using the conventional approach (Fig. 6) (Jones et al., 1999). With our approach, the optimized diffusion gradient directions appear to be more symmetrically distributed around the direction of the fibers (Figs. 6b and 6c). This pattern is particularly apparent in CONE1 (Fig. 6b) where the diffusion gradients (green points) tend to align themselves in two lines covering evenly in the elevation dimension while spanning throughout the whole range of the azimuth dimension. With these optimized gradient direction arrangements, the accuracy (B(D)) and precision (σ(D)) of tensor estimates together with the estimated FAs (σ(FA)) and fiber orientations (MAD) are substantially improved when compared to that obtained using the conventional approach where a uniformly distributed tensor field was assumed (Fig. 7). Nevertheless, the improvement ratios decrease as the number of cones increases (Figs. 7a vs. 7b). This finding is not surprising since as the number of cones increased, it would eventually approach a uniform distribution and the advantages of incorporating prior information would be diminished (Fig. 7c).
It is worth pointing out that some of the optimized diffusion gradient directions using our approach appear to be very close to each other, particularly for DIFF30 (Fig. 6) in both CONE1 and CONE3. Although it is plausible that the imperfection of the proposed optimization approach leads to the observed pattern of the diffusion gradient orientations, the most likely explanation may be the utilization of the LS approach for tensor estimation in our study. The LS approach does not account for the noise variance and assumes equal variance. We have also performed the same optimization processes with the exception that WLS was employed for tensor estimates (Appendix B). The results demonstrate that the previously observed clustered pattern using the LS approach no longer existed (result not shown), supporting the notation that the assumption of equal variance for LS accounts for the clustered diffusion gradient directions.
Comparisons with an optimization approach incorporating prior information
Peng and Arfanakis (Peng and Arfanakis, 2007) have recently proposed an approach to optimize diffusion gradient directions by taking into account the prior information of the fiber orientations. However, unlike our proposed approach considering most of the essential aspects of a DTI experiment, only the σ(FA) was employed as the criterion for optimization in their approach. Specifically, they considered fibers oriented within a 30° cone along the z-axis, which is similar to the CONE1 condition in our studies, allowing a direct comparison between our and Peng and Arfanakis’ approaches. Fig. 9 shows the improvement ratios of the four performance indices for Peng and Arfanakis’ approach over the conventional scheme (Fig. 9a) and our over Peng and Arfanakis’ schemes (Fig. 9b), respectively. Since their approach specifically optimized FA measurements, it is not surprising that σ(FA) is less than 1 with the exception of the lowest b-values evaluated when compared with those obtained using the conventional approach. In contrast, a much poorer performance for MAD is observed using Peng and Arfanakis’ approach than that of using the conventional scheme. The performance for both B(D) and σ(D) is largely dependent on the b-values; Peng and Arfanakis’ approach outperforms the conventional approach for b ~> 1.2 × 109s/m2 or otherwise is worse than the conventional approach. Comparing the improvement ratios between our and Peng and Arfanakis’ approaches (Fig. 9b), it is evident that with the exception of σ(FA) where a comparable performance is observed, our approach outperforms that proposed by Peng and Arfanakis for the remaining three performance indices, underscoring the importance of optimizing the essential aspects of DTI experiments simultaneously and demonstrating the effectiveness of our approach.
Fig. 9.
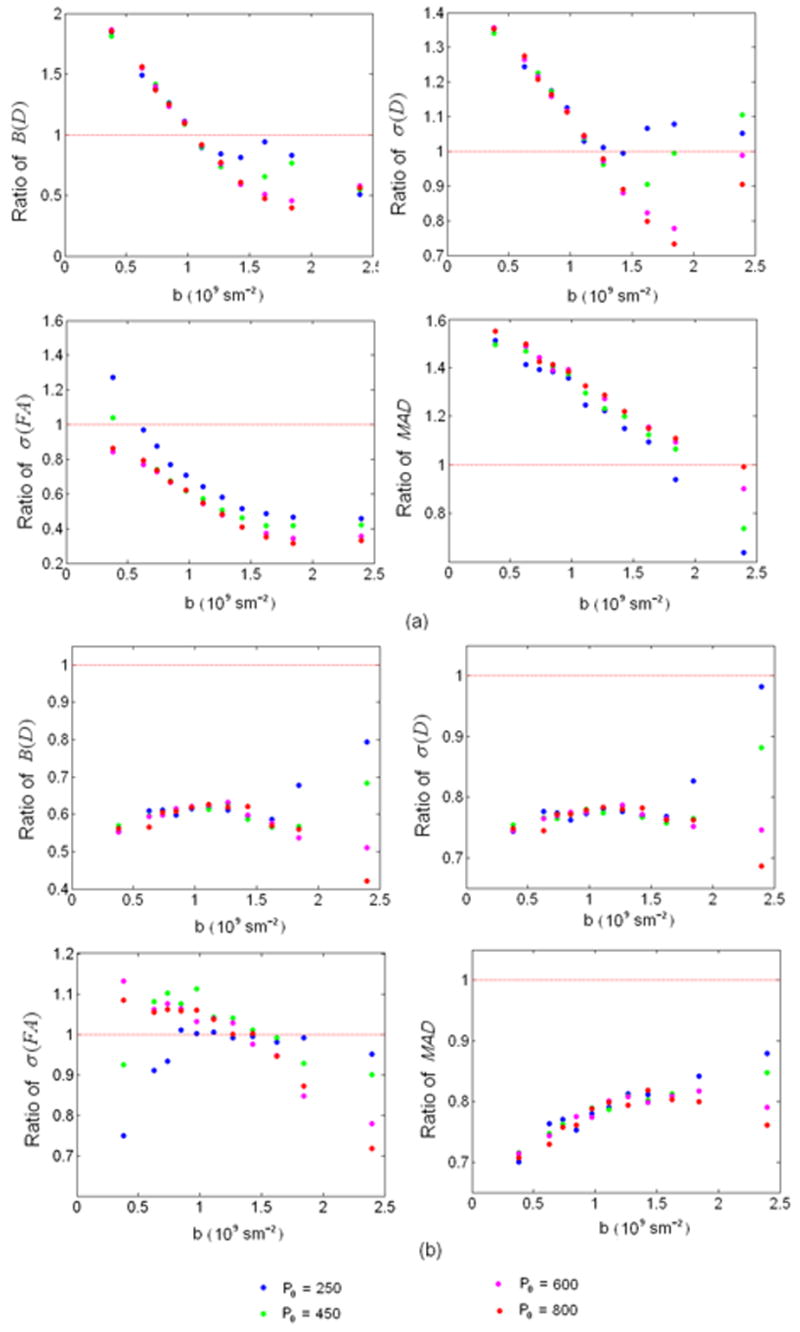
Ratios of the four performance indices between Peng and Arfanakis’ over the conventional approaches (a) and the proposed over Peng and Arfanakis’ approaches are shown, respectively, where results using M/N=1/6 and CONE1 are shown. X-axis represents b-value in 109s/m2 and Y-axis represents the ratios of performance index values.
One of the major findings of our study is that the prior tensor information can be employed for optimizing gradient orientations so as to improve the accuracy of tensor estimates. While the directional distribution of white matter is most likely to be uniformly distributed throughout the entire sphere in adults, the directional distribution in very young pediatric subjects may have preferential directions and is non-uniform (Fig. 1). Under this condition, the prior tenor information should be considered in optimizing diffusion gradient directions. This can potentially be accomplished by building a fiber distribution atlas for each age group and from which the proposed optimization approach can be applied to form an optimal set of imaging parameters for each age group. By the same token, in the case when a specific white matter tract is of interest, our optimization approach can again be applied to improve the accuracy of the DT estimates of the specific fiber tracts.
Another advantage of our approach is the flexibility of incorporating different DT postprocessing approaches into the optimization framework. This flexibility is important considering different estimation methods may become necessary in different conditions. For example, in the case of a low SNR ratio, the Gaussian assumption of MR signal will no longer hold. The expectation of such a “log Rician” distribution could deviate from the real signal intensity, which may lead to systematic biases using the least squares estimates (Salvador et al. 2005). In this case, either weighted least squares (WLS) estimation (Basser et al., 1994, Zhu et al., 2007) or maximum likelihood estimation of the Rician distribution (Goodlett et al., 2007, Andersson, 2008) can be applied to minimize or correct for this bias. As demonstrated in Appendix B, the proposed optimization framework can be easily adapted to the WLS approach by modifying the covariance matrix of the estimated DT, demonstrating the potential wide applicability of the proposed approaches.
Finally, while the proposed approach enables simultaneously optimization of a variety of imaging and DTI parameters, including gradient duration/separation, read-out time, TE, b-value and diffusion gradient directions, these parameters do not include all aspects of a DTI experiment. Both theoretic analysis and experimental tests have been performed to study the effects of the number of diffusion-encoding gradient directions (Papadakis et al., 2000) (Jones, 2004) (Landman et al., 2007) (Ni et al., 2006), the ratio of M (b=0 images) and N (diffusion weighted images) (Hasan, 2007) and the size/shape of imaging voxels (Oouchi et al., 2007). Although it is feasible to potentially incorporate these additional parameters into a more generalized optimization framework, further studies will be needed and are beyond the scope of this paper.
Acknowledgments
This work was supported by National Institutes of Health grants R01NS055754 (Lin), and 1-UL1-RR025747-01, SES-0643663 and BCS-0826844 (Zhu)
APPENDIX A
The simulated annealing (SA) method is suitable for optimization problems of large scales, especially when the desired global minimum is hidden among many local extremes. The specific elements of the SA algorithm are listed below:
a) Generator of random changes
Δ and R
Δ and R were taken as the square of two numbers A and B setting to random walk to avoid negative b-values at each step. Random numbers choosing from a standard Gaussian distribution scaled by 10−3 were added to every A and B, respectively, at each step.
Gradient directions
All 3D vectors of the diffusion gradient directions were first transferred to a spherical coordinate so that each diffusion gradient direction corresponds to two elements: azimuth angle theta and elevation angle phy. At each step, a random number choosing from a scaled standard Gaussian distribution was independently added to each of these two angles of every diffusion gradient direction. For better performance against local minima, the scale factor S (the magnitude of each random number) depended on the current temperature T, i.e., if T>=1000, S=0.001*T and if T<1000, S=0.001. After random walk of each step, these directional vectors in the spherical coordinate were transferred back to the Cartesian coordinate for cost function evaluation.
b) The acceptance-rejection algorithm
The Metropolis-Hastings algorithm (Hastings, 1970; Metropolis, 1953) was applied for decision making on acceptance or rejection. Specifically, the system altered its configuration from energy E1 to E2 according to the probability p = exp(− (E2 − E1)/T). If E2 < E1, then the system always accepted E2, otherwise the system accepted E2 with a probability p < 1. The probability p = exp(− (E2 − E1)/T) became smaller as T increased.
c) Cost function
The cost functions were the sum of the trace of every covariance matrix resulted from ach known θ, .
d) Default settings
Initial Δ and R: 0.01 ms
Initial gradient directions: 3D vectors with random entries choosing from a standard Gaussian distribution but normalized to be unit vectors;
Initial temperature: 2000 Kelvin;
Stop temperature: 10−18 Kelvin;
Stop energy (value of cost function): infinitely small;
Cooling schedule: 0.98*T (current temperature);
Maximum number of consecutive rejections: 1000;
Maximum number of tries within one temperature: 1000;
Prior information θ was derived from the predefined tensor field;
e) Recording of parameters and cost function values
A term referred to as “E_best” was used to track the most minimal cost function value. After each run, the cost function value was compared to the current E_best and if this value was less than the current E_best, this value was recorded together with the random-walk parameters that result in this value. However, we only kept the latest 10000 sets of values and defined the optimal ranges of each parameter based on this set. After optimization, a series of 11 different b-values corresponding to the 1st, 1000th, till 10000th at a 1000 interval of the recorded 10000 b-values (sorted) were chosen to evenly cover the whole sampled b-value range and used for optimal b-value range testing.
APPENDIX B
Although we only presented results with the LS estimation method, our optimization scheme can be applied with different estimation methods if proper design criteria can be established accordingly. In this section, the derivation of the design criteria for WLS estimation is provided.
The WLS estimator of β⃗ is and its covariance matrix is given by
| (B1) |
Again by defining
and θ = [(D0)11, (D0)12, (D0)13, (D0)22, (D0)23, (D0)33], Eq. (B1) can be written as
| (B2) |
The incorporation of other imaging parameters follows the same deduction as that for LS estimation as described in the Method section, which resulted in the following expression:
| (B3) |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alexander DC, Barker GJ. Optimal imaging parameters for fiber-orientation estimation in diffusion MRI. Neuroimage. 2005;27:357–367. doi: 10.1016/j.neuroimage.2005.04.008. [DOI] [PubMed] [Google Scholar]
- Anderson AW. Theoretical analysis of the effects of noise on diffusion tensor imaging. Magn Reson Med. 2001;46:1174–1188. doi: 10.1002/mrm.1315. [DOI] [PubMed] [Google Scholar]
- Andersson JL. Maximum a posteriori estimation of diffusion tensor parameters using a Rician noise model: why, how and but. Neuroimage. 2008;42:1340–1356. doi: 10.1016/j.neuroimage.2008.05.053. [DOI] [PubMed] [Google Scholar]
- Andreisek G, White LM, Kassner A, Tomlinson G, Sussman MS. Diffusion tensor imaging and fiber tractography of the median nerve at 1.5T: optimization of b value. Skeletal Radiol. 2008 doi: 10.1007/s00256-008-0577-6. [DOI] [PubMed] [Google Scholar]
- Armitage PA, Bastin ME. Utilizing the diffusion-to-noise ratio to optimize magnetic resonance diffusion tensor acquisition strategies for improving measurements of diffusion anisotropy. Magn Reson Med. 2001;45:1056–1065. doi: 10.1002/mrm.1140. [DOI] [PubMed] [Google Scholar]
- Atkinson AC, Doney AN. Optimum Experimental Designs. Oxford University Press; Oxford, U K.: 1992. [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B. 1994;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B. 1996;111:209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- Brihuega-Moreno O, Heese FP, Hall LD. Optimization of diffusion measurements using Cramer-Rao lower bound theory and its application to articular cartilage. Magn Reson Med. 2003;50:1069–1076. doi: 10.1002/mrm.10628. [DOI] [PubMed] [Google Scholar]
- Callaghan PT. Principles of Magnetic Resonance Microscopy. Oxford Science Publications; Oxford, UK: 1991. [Google Scholar]
- Federov VV. Theory of Optimal Experiments. Academic Press; New York: 1972. [Google Scholar]
- Goodlett C, Fletcher PT, Lin W, Gerig G. Quantification of measurement error in DTI: theoretical predictions and validation. Med Image Comput Comput Assist Interv Int Conf Med Image Comput Comput Assist Interv. 2007;10:10–17. doi: 10.1007/978-3-540-75757-3_2. [DOI] [PubMed] [Google Scholar]
- Hasan KM. A framework for quality control and parameter optimization in diffusion tensor imaging: theoretical analysis and validation. Magn Reson Imaging. 2007;25:1196–1202. doi: 10.1016/j.mri.2007.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasan KM, Parker DL, Alexander AL. Comparison of gradient encoding schemes for diffusion-tensor MRI. J Magn Reson Imaging. 2001;13:769–780. doi: 10.1002/jmri.1107. [DOI] [PubMed] [Google Scholar]
- Hastings WK. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometika. 1970;57:97–109. [Google Scholar]
- Jones DK. The effect of gradient sampling schemes on measures derived from diffusion tensor MRI: a Monte Carlo study. Magn Reson Med. 2004;51:807–815. doi: 10.1002/mrm.20033. [DOI] [PubMed] [Google Scholar]
- Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42:515–525. [PubMed] [Google Scholar]
- Kingsley PB, Monahan WG. Selection of the optimum b factor for diffusion-weighted magnetic resonance imaging assessment of ischemic stroke. Magn Reson Med. 2004;51:996–1001. doi: 10.1002/mrm.20059. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick S, Gelatt CD, Jr, Vecchi MP. Optimization by Simulated Annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Landman BA, Farrell JA, Jones CK, Smith SA, Prince JL, Mori S. Effects of diffusion weighting schemes on the reproducibility of DTI-derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5T. Neuroimage. 2007;36:1123–1138. doi: 10.1016/j.neuroimage.2007.02.056. [DOI] [PubMed] [Google Scholar]
- Lee JW, Kim JH, Kang HS, Lee JS, Choi JY, Yeom JS, Kim HJ, Chung HW. Optimization of acquisition parameters of diffusion-tensor magnetic resonance imaging in the spinal cord. Invest Radiol. 2006;41:553–559. doi: 10.1097/01.rli.0000221325.03899.48. [DOI] [PubMed] [Google Scholar]
- Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equations of State Calculations by Fast Computing Machines. Jorirrlol of Cherniciil Physics. 1953;21:1087–1081. 1092. [Google Scholar]
- Naganawa S, Koshikawa T, Kawai H, Fukatsu H, Ishigaki T, Maruyama K, Takizawa O. Optimization of diffusion-tensor MR imaging data acquisition parameters for brain fiber tracking using parallel imaging at 3 T. Eur Radiol. 2004;14:234–238. doi: 10.1007/s00330-003-2163-6. [DOI] [PubMed] [Google Scholar]
- Ni H, Kavcic V, Zhu T, Ekholm S, Zhong J. Effects of number of diffusion gradient directions on derived diffusion tensor imaging indices in human brain. AJNR Am J Neuroradiol. 2006;27:1776–1781. [PMC free article] [PubMed] [Google Scholar]
- Oouchi H, Yamada K, Sakai K, Kizu O, Kubota T, Ito H, Nishimura T. Diffusion anisotropy measurement of brain white matter is affected by voxel size: underestimation occurs in areas with crossing fibers. AJNR Am J Neuroradiol. 2007;28:1102–1106. doi: 10.3174/ajnr.A0488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pajevic S, Basser PJ. Parametric and non-parametric statistical analysis of DT-MRI data. J Magn Reson. 2003;161:1–14. doi: 10.1016/s1090-7807(02)00178-7. [DOI] [PubMed] [Google Scholar]
- Papadakis NG, Murrills CD, Hall LD, Huang CL, Adrian Carpenter T. Minimal gradient encoding for robust estimation of diffusion anisotropy. Magn Reson Imaging. 2000;18:671–679. doi: 10.1016/s0730-725x(00)00151-x. [DOI] [PubMed] [Google Scholar]
- Papadakis NG, Xing D, Huang CL, Hall LD, Carpenter TA. A comparative study of acquisition schemes for diffusion tensor imaging using MRI. J Magn Reson. 1999;137:67–82. doi: 10.1006/jmre.1998.1673. [DOI] [PubMed] [Google Scholar]
- Peng H, Arfanakis K. Diffusion tensor encoding schemes optimized for white matter fibers with selected orientations. Magn Reson Imaging. 2007;25:147–153. doi: 10.1016/j.mri.2006.10.013. [DOI] [PubMed] [Google Scholar]
- Rice SO. Mathematical analysis of random noise. Bell Syst Technol J. 1944;23:282–332. [Google Scholar]
- Salvador R, Pena A, Menon DK, Carpenter TA, Pickard JD, Bullmore ET. Formal characterization and extension of the linearized diffusion tensor model. Hum Brain Mapp. 2005;24:144–155. doi: 10.1002/hbm.20076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skare S, Hedehus M, Moseley ME, Li TQ. Condition number as a measure of noise performance of diffusion tensor data acquisition schemes with MRI. J Magn Reson. 2000;147:340–352. doi: 10.1006/jmre.2000.2209. [DOI] [PubMed] [Google Scholar]
- Stieltjes B, Schluter M, Hahn HK, Wilhelm T, Essig M. [Diffusion tensor imaging. Theory, sequence optimization and application in Alzheimer’s disease] Radiologe. 2003;43:562–565. doi: 10.1007/s00117-003-0930-7. [DOI] [PubMed] [Google Scholar]
- Wedeen VJ, Wang RP, Schmahmann JD, Benner T, Tseng WY, Dai G, Pandya DN, Hagmann P, D’Arceuil H, de Crespigny AJ. Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers. Neuroimage. 2008;41:1267–1277. doi: 10.1016/j.neuroimage.2008.03.036. [DOI] [PubMed] [Google Scholar]
- Xing D, Papadakis NG, Huang CL, Lee VM, Carpenter TA, Hall LD. Optimised diffusion-weighting for measurement of apparent diffusion coefficient (ADC) in human brain. Magn Reson Imaging. 1997;15:771–784. doi: 10.1016/s0730-725x(97)00037-4. [DOI] [PubMed] [Google Scholar]
- Zhu HT, Zhang HP, Ibrahim JG, Peterson BS. Statistical analysis of diffusion tensors in diffusion-weighted magnetic resonance imaging data. Journal of the American Statistical Association. 2007;102:1085–1102. [Google Scholar]