The boundary vector cell model of place cell firing and spatial memory

Abstract

We review evidence for the boundary vector cell model of the environmental determinants of the firing of hippocampal place cells. Preliminary experimental results are presented concerning the effects of addition or removal of environmental boundaries on place cell firing and evidence that boundary vector cells may exist in the subiculum. We review and update computational simulations predicting the location of human search within a virtual environment of variable geometry, assuming that boundary vector cells provide one of the input representations of location used in mammalian spatial memory. Finally, we extend the model to include experience-dependent modification of connection strengths through a BCM-like learning rule, and compare the effects to experimental data on the firing of place cells under geometrical manipulations to their environment. The relationship between neurophysiological results in rats and spatial behaviour in humans is discussed.

Introduction

The hippocampus has become the most studied neuronal system in the mammalian brain. Its popularity derives from several sources, including the discovery of place cells/^1,2/ and long-term synaptic potentiation/³/ in the hippocampus, its suggestive and well-described architecture/⁴/, and the association of hippocampal damage with amnesia/⁵/ and navigational impairments/⁶/. In this paper we focus on the role of the mammalian hippocampus in the representation of, and memory for, location within large-scale environments. More specifically, we focus on the place cells, each of which fires whenever the animal enters a specific region of its environment (the corresponding ‘place field’). These data, relating to the neural representation of location, tie in with the observation of deficits in finding unmarked goal locations following hippocampal lesions/⁷/ suggesting the place cell representation is directly involved in spatial memory; an idea first put forward by O'Keefe and Nadel, who suggested that the hippocampus acts as a cognitive map /⁸/. To understand the role of the hippocampus in spatial memory, it is important to find out how it controls behaviour in spatial memory tasks. To address these issues, we have developed a simple computational model of why place cells fire where they do, and how that information might guide behaviour: the Boundary Vector Cell (BVC) model/^{9,10,11,12,13,14,15}/.

The BVC model posits the existence of ‘boundary vector cells’ to explain the effects of geometrical manipulations of an environment on the firing of place cells. The model is also able to make explicit, testable predictions of firing patterns for specific cells in a novel environment/¹²/. In the main section of the paper, we describe preliminary experimental evidence for this model concerning the effect on place cell firing of adding barriers to an environment, or removing barriers from it. We next consider how the BVCs might support memory for spatial locations, and provide new simulations of the predicted search of human subjects when remembering a location in a virtual reality environment subject to geometric manipulations/¹⁵/. We then describe novel evidence that BVCs may exist in the hippocampal formation. Finally we introduce an extension to the model, which by incorporating the BCM learning rule/¹⁶/, is able to begin to capture some of the experience-dependent changes observed in the place cell representation. First, however, we provide a brief overview of the relevant neurophysiological data, and describe the existing BVC model.

Place cells, head direction cells, and their inputs

Place cells, hippocampal pyramidal cells that exhibit spatially localised activity, were first identified by O'Keefe and Dostrovsky/¹/. Since the initial discovery, cells with spatially modulated firing have been found in almost all areas of the hippocampus and in some surrounding areas (entorhinal cortex/¹⁷/, subiculum/¹⁸/). Although early work was conducted on rats, similar cells have been subsequently been found in other species of rodent/²⁰/, monkeys/^21,22,23,24/ and more recently humans/²⁵/.

The striking quality of place cells is that they seem to provide a precise representation of an animal's position in its environment. The background firing rate of place cells is very low. When an animal enters the receptive field (place field) of a cell its firing rate rapidly increases, typically to a maximum between 5hz and 15hz (for example see figure 1A). In open field environments firing seems to be independent of the animal's orientation: in essence, firing is best correlated with the position of an animal's head/²⁶/, and can be used to infer it/²⁷/. Interestingly, the complementary representation, of orientation independent of location, is found in the ‘head-direction’ cells of the lateral mammillary bodies, anterior thalamus and presubiculum/^28,29,30/. These cells fire whenever the animal's head is pointing in a given direction, independent of the animal's location within an environment/^28,31/.

Figure 1.

Effect of barrier insertion on real and simulated place fields. A. Place fields of 4 place cells (i-iv) in three successive trials in a 65cm square walled environment. First column: 10 minute first trial. Second column: first 10 minutes of 40 minute second trial, after the insertion of a 40cm barrier. Third column: final 10 minute trial, barrier removed. Three outcomes inserting a barrier are illustrated: (i) inhibition of firing; (ii-iii) doubling of field with duplicate on either side of the barrier (the most common outcome); (iv) firing unaffected by the barrier (less common). B. Three simulated place fields from the Boundary Vector Cell (BVC) model in 65cm square environments with and without the 40cm barrier. Similar outcomes to experimental fields i-iii are illustrated: inhibition of firing (i); doubling of existing field in presence of barrier (ii, the most common outcome); double place field induced by presence of the barrier (iii). Here and below, plots shows firing rate as a function of the rat's location while it explores for randomly scattered food. These are calculated as the number of spikes divided by the animal's dwell time in each bin of a 64×64 spatial grid, and smoothed with a 5×5 kernel. Peak rate (Hz) is indicated by the value above the plot and corresponds to the area shaded black. Each gradation represents 20% of the peak.

Place fields seem to be randomly distributed across an environment, with perhaps a tendency to be smaller and more numerous near to the environmental boundaries/³²/. Place cell firing can be detected within the first few minutes of an animal's entrance into a novel environment/²⁷/. Although initially quite noisy, the cellular representation of the environment rapidly becomes stable. Indeed, in invariant conditions place fields are extremely stable, in some cases persisting for months/³³/. During a single exposure to an environment a place cell will continue to fire each time an animal moves through its field; although it does so with curiously high variability/³⁴/. Removal from an environment and then replacement does not affect stability either.

So what causes place cells to fire where they do? Early studies showed that place fields are not defined by a single modality of sensory information, but will make use of whichever are available, including visual, tactile and auditory inputs/³⁵/. The representation of a given environment is robust to the removal of subsets of cues/^36,37/. The absence of spatial cues from one modality tends to be compensated for by cues from other modalities/³⁸/, for example congenitally blind rats exhibit normal place fields/³⁹/. In addition, in the temporary absence of other cues, path integration (dead reckoning) which provides a method for animals to navigate/⁴⁰/, can also support a place cell representation/^2,41,42/, although the path integration process rapidly succumbs to cumulative error in the absence of sensory information/⁴²/. In terms of the hierarchy of influence of these various inputs, it seems that, when present, stable visual cues at or beyond the edge of the reachable environment exert a powerful control over the orientation of the place cell/^36,43/ and head-direction cell/²⁹/ representations. Muller and Kubie/⁴⁴/ recorded place cells from rats foraging in a cylindrical environment polarised by a single cue card. They showed that rotation of the cue, without the animal's knowledge, caused a complementary rotation in the entire place cell ensemble. Hence a 90° clockwise rotation resulted in a similar rotation of the place fields (although note that removal of the cue did not result in loss of place firing: the ensemble rotated by an arbitrary amount but remained intact). In the absence of reliable and stable/⁴³/ visual cues, similar effects can be produced by rotation of a sloped environment/⁴⁵/, and even of the rat itself/⁴³/. If rats are systematically disoriented between trials, the orientations of the place and head-direction representations can be made to rotate – failing to maintain a stable correspondence to the external world. Interestingly, in this situation, both representations rotate in synchrony with each other/⁴⁶/.

The above results pertained to cues that orient place cells in a rotationally symmetrical environment of constant dimensions. Changes to the shape or topography of an environment have been also been used to investigate the nature of the inputs driving place cell activity. Comparing recordings from the same cells made in rectangular environments of varying shape and size, O'Keefe and Burgess/¹⁰/ noted that the location of peak firing typically maintained a constant position to the nearest walls. In addition to this, several fields were stretched along the axes of the environment, with some becoming bimodal in the larger environments. More recently, similar parametric responses to geometric changes to an environment have been seen across a variety of different shaped environments/⁴⁷/. O'Keefe and Burgess/¹⁰/, see also /⁹/, proposed that place cells received inputs that are tuned to respond to the presence of a barrier at a given distance along a given allocentric direction, with sharper tuning at shorter distances. Related, but more localised, effects have also been observed by Muller/⁴⁴/; he showed that bisecting a place field with a barrier would often cause the cell to stop firing, while those with more distant fields remained unchanged. Our own data (reviewed below) confirm Muller's early result and also demonstrate that the addition of a barrier can promote the addition, deletion or duplication of place fields adjacent to the barrier (figure 1A). In short, it seems that impediments to movement, be they the walls of the environment, a free standing barrier or even a sheer drop at the edge of a platform, play a key role in defining place cell firing. In contrast to the influence of extended barriers, Cressant et al./⁴⁸/, showed that isolated objects within the environment failed to affect place cell firing, unless moved to the edge of the environment, where they acted as orientation cues, or put in line to form an extended barrier.

In this paper, we concentrate on experimental manipulations that have parametric effects on cell firing, for their explanatory value. However, a topic of increasing interest concerns the large, non-parametric, effects on place cell firing caused by sufficiently large perturbation of the animal's surroundings - which can cause some or even all of the cells in a representation to change their behaviour (remapping/⁴⁹/). The change exhibited by one cell need not share a trivial relationship with its neighbours in the brain or with cells that have neighbouring fields. Sufficient changes to the geometry/⁵⁰/ and colour/⁴⁹/, odour/⁵¹/ of an animal's environment, or to its behaviour/⁵²/, have all been shown to promote remapping. However, the experimental variables controlling the occurrence or extent of remapping have yet to be fully understood/⁵³/. By first attempting to understand the parametric effects on place cell firing of experimental manipulations we hope to create a model that also serves as a framework within which to understand remapping.

The Boundary Vector Cell model

Many previous models have considered place cell firing as a feed-forward transformation of environmental inputs, most notably /^54,55/, see /^56,57/ for reviews. These have assumed that place cell firing depends on various functions of the relative location of the rat from point-like landmark-locations. The boundary vector cell (BVC) model describes place cell firing as a continuous function of the relative location of the barriers in and around the animal's environment. Place cell activity is driven by feed-forward connections from putative BVC inputs whose firing is determined by the presence of extended barriers (e.g. walls, large objects, an impassable drop). More specifically, each BVC fires optimally when a barrier is encountered at a defined distance and allocentric direction from the rat (figure 2A), i.e. each BVC has a Gaussian tuned response to the presence of a barrier, peaked at a preferred distance and direction. The firing of BVC i (tuned to preferred distance d_i and angle φ_i) to a boundary at distance r and direction θ, subtending an angle δθ at the rat, is given by:

$$\delta f_i=g_i(r,\theta )\delta \theta ,$$ (1)

where:

$$g_i(r,\theta )\propto \frac{\exp [-{(r-d_i)}^2∕2{\sigma }_{\mathit{rad}}^2\left(d_i\right)]}{\sqrt{2\pi {\sigma }_{\mathit{rad}}^2\left(d_i\right)}}\times \frac{\exp [-{(\theta -{\varphi }_i)}^2∕2{\sigma }_{\mathit{ang}}^2]}{\sqrt{2\pi {\sigma }_{\mathit{ang}}^2}},$$ (2)

the angular width σ_ang is constant, but radial tuning width increases linearly with the preferred tuning distance: σ_rad(d_i)= d_i + c. For each location x in the environment, the contribution of all boundaries to the firing of BVC i is determined by integrating equation 1 over θ. The firing of place cell j at that location F_j(x) is then proportional to the thresholded linear sum of the N BVCs that happen to be connected to it:

$$F_j\left(\underset{‒}{x}\right)=A\Theta \left(\underset{i=1,N}{\Sigma }{f}_i\left(\underset{‒}{x}\right)-T\right),$$ (3)

where the threshold T and coefficient A are constants, and Θ is the Heaviside function (i.e. Θ(x)=x if x>0; Θ(x)=0 otherwise). Firing does not depend upon the rat's heading and the direction tuning of all BVCs is determined relative to the same allocentric reference frame (assumed to be provided by the head-direction system). For example, a place cell that received input from BVCs tuned to respond to nearby barriers to the North and to the East would fire when the ‘rat’ was in the Northeast corner of its environment. More generally, the sharper tuning of BVCs with short preferred directions implies that boundaries near to the location of peak firing will tend to have more influence than boundaries further away.

Figure 2.

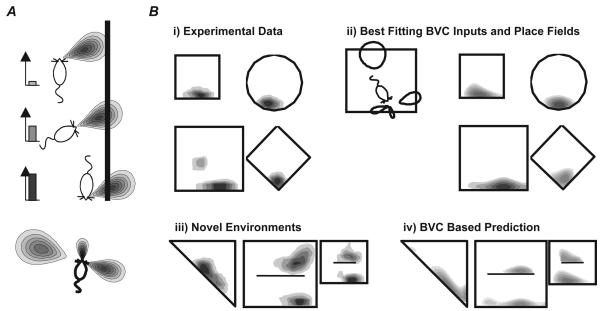
The Boundary Vector Cell (BVC) Model. A. A BVC responds to the presence of a boundary at a preferred distance and (allocentric) direction. Its firing rate (bar charts on left) decreases as a boundary's distances and direction differs from the preferred values. The tuning to distance is shaper for shorter distances (bottom). B. i) Place fields from the same place cell recorded in different shaped environments. ii) Simulation of the place cell's firing in the 4 shapes using 4 BVC inputs (BVCs shown on the left). iv) Predicted firing of modelled place cell in 3 new shapes. iii) Observed firing of actual place cell in 3 new shapes. (Adapted from (/¹²/ and /⁹⁵/)

Simulated firing produced by the BVC model has similar properties to that obtained experimentally. In response to topographic changes of the environment simulated cells responded like those observed by O'Keefe and Burgess/¹⁰/. The majority of cells maintain their position relative to nearby walls, while some stretch and become bimodal and a smaller number turn on or off, in the appropriate proportions. It also explains consistencies across more radical changes in shape/^12,50/. Furthermore, by determining the subset of BVCs which best fit a set of firing data from a given cell, it is possible to predict how that cell will respond to a novel change in the environment (figure 2B). The likely BVC nature of the input to places is also beginning to be recognised in other modelling studies /^58,59/.

The above discussion implies that the BVC model accounts satisfactorily for shifts in firing as result of topographical changes to an animal's environment. It is also able to describe coherent field rotation, as the preferred allocentric tuning of BVCs are determined relative to the same reference frame. One recent experiment looked at the effect on place fields of manipulating two cue-cards (one black and one white) mounted on the wall of a grey cylindrical environment/⁶⁰/. Either card alone would control the orientation of the place cell representation, however, when both cards were rotated inconsistently (together or apart) a rather complex pattern of movement was observed in the place fields. The BVC model can account for these data/¹⁴/, given the added assumption that BVCs can also become specific to barrier colour, and that the cue-cards have differential local effects on the head-direction system (each one preferentially affecting the overall sense of head direction when the rat is nearby, or preferentially affecting those directions closest to its bearing from the rat), see also /⁵⁹/ for a similar approach.

Effects of inserting or removing barriers on place fields

Inserting barriers

The clearest novel prediction of the BVC model was the formation of double fields in response to the addition of an extended barrier into the environment. For instance, a BVC which fires strongly when the rat is a short distance South of the northern boundary of the environment will also fire strongly when it is a short distance South of a newly-inserted East-West barrier. This implies that some of the place fields near to the North wall of the environment would be predicted to develop a second field in a similar location relative to the barrier: which fields do this depends on the distribution of other BVCs connected to the place cell. Another prediction is that place fields will tend to have fields oriented parallel to the walls of the environment. For instance in circular environments, the model predicts that most fields close to the walls are crescent shaped. In rectangular model environments, asymmetric fields should generally be extended parallel to one of the axes, and fields with a clear diagonal orientation are rare.

Experimental data from several sources concord with these predictions. In terms of field shape, cells recorded in circular environments tend to have crescent fields/³⁴/ and elongation of a rectangular environment produces elongated fields that run parallel to the direction of stretch/¹⁰/. Several experimenters have produced field doubling. Skaggs et al./⁶¹/ recorded from two visually identical environments connected via a corridor. They observed a large number of cells with similar fields in both environments. Similarly, Lever et al./⁴⁷/ have observed field doubling in response to barrier insertion. More recently we recorded 10 cells in square box before and after the addition of a north-south barrier (figure 1A). Three cells exhibited duplicate fields as predicted (e.g. figure 1A ii-iii) and a further 3 cells either turned on or moved to have fields adjacent to one side of the barrier. Two cells were unaffected (e.g. figure 1A iv), 1 turned off (e.g. figure 1A i) and the final cell moved away from the barrier. During these recordings the barrier used was made from the same black foam board as the environment walls. On the last day of recording however, we substituted a white barrier. Fields were unaffected by this change, responding to the presence of a barrier regardless of its colour or other associated local cues. It is hard to explain these observations without invoking geometry sensitive inputs which mean that (at least on initial exposure) place cells act as if barrier and boundary are equivalent.

In the BVC model, the addition of a new barrier in the middle of an environment typically has two effects: it can provide additional loci at which short-range BVCs will fire, which can produce field doubling as described above; but it can also shift the firing of longer-range BVCs by occluding the environmental perimeter in the direction to which the BVC is tuned. This shifting may disrupt formerly convergent BVC inputs to a place cell so that they no longer coincide, and no longer exceed the place cell's firing threshold. This cessation of firing for barriers and fields near the centre of an environment, was seen by Muller/⁴⁴/. More generally, while the net input to each place cell will tend to have two spatially distinct peaks, one on each side of the barrier, this input will not necessarily exceed the firing threshold on both sides. However, the model does predict a fair proportion of cells in which firing fields are unambiguously doubled on initial exposure to an environment containing a barrier.

Removing barriers

The BVC model suggests that environmental boundaries are the crucial ingredient determining the location of place cell firing. More specifically, the overall amount of BVC firing at a given location will depend on the angle subtended at that location by extended boundaries (i.e. the angle over which equation 1 can be integrated), and the proximity of these boundaries (reflecting the increased density and sharpness of tuning of BVCs). A completely enclosed environment will provide complete BVC input, while a single extended boundary provides at most 180° when the animal is right next to it.

In this section we address the question: to what extent are extended boundaries required for the generation of normal place fields? Two obvious problems impede our pursuit of this question. First, nearly all models excepting only those wholly based on path integration/⁴⁰/ would predict absent or unstable place fields in a totally denuded environment. However, there are alternative sources of spatial information that should allow a rat to self-localise. For example, environments containing a point-like landmark and a directional cue theoretically provide enough information to uniquely localise any point in two-dimensional space (although it should be noted that remembering a goal location relative to this type of configuration of cues does not appear to depend on the hippocampus/⁶²/). Second, there are practical difficulties associated with removing environmental boundaries: they are often required for mundane reasons such as preventing the subject escaping, holding up the roof etc.

Although recording place cells in a wide open space is obviously impractical, we attempted to simulate such a space. Rats were allowed to forage on the floor of a large room in almost complete darkness (a weak patch of illumination high up on the walls provided the sole orientation cue), so that they could not in general see the walls and were therefore deprived of visual information about their location. The walls and floor of the room were covered with, respectively, black drapes and black wipeable and moveable polypropylene tiles. Tiles were wiped with alcohol, rearranged and rotated pseudo-randomly between trials to prevent olfactory and other local cues gaining control of place fields. The rats were prevented from escaping, or from using touch to determine the location of the walls, by means of a computer tracking a head-mounted LED and generating a burst of white noise whenever the animals strayed too far from the centre of the room. A circular threshold centred on the room defined the point at which the sounds barrier was activated and deactivated. The radius of this threshold was varied dynamically between 720mm and 1180mm to prevent it from serving as a spatially constant reference point. This auditory discouragement procedure kept the rats confined to the centre of the room, and enabled us to from record place cells in open environments, see below.

Recordings were made from 2 adult male Lister Hooded rats prepared using a standard procedure/⁶³/ as they foraged for rice thrown directly onto the floor. Four clear Perspex sheets (60cm × 55cm) provided the walls of the rats' local environment. Plastic tubes, cut to accommodate the Perspex, were used at the corners of the environments to support the walls. The walls were initially arranged to form a closed square with 60cm sides. A single wall and redundant pillars were removed in successive trials. Adjacent walls were removed one at a time in a pseudo-random order until just a single pillar was left. The animals did not receive a training period; recordings were made from first exposure to the experimental room. At the start of each recording session the rat was brought into the main recording room in an opaque covered transport box, and the lights were turned off. The rat was confined inside the transport box whenever the lights were on (e.g. while stimulus changes were made). The lights were turned off again before the rat was placed in the local environment (aligned with and next to the North wall, facing East). Trials in the closed square lasted 5 minutes, while trials in which the rat could explore the room lasted 15 minutes. Between trials, rats were held in the opaque box placed onto the floor of the recording room. The location of each trial within the room was varied between 9 positions arranged in a 3 by 3 grid, with adjacent positions 30cm apart.

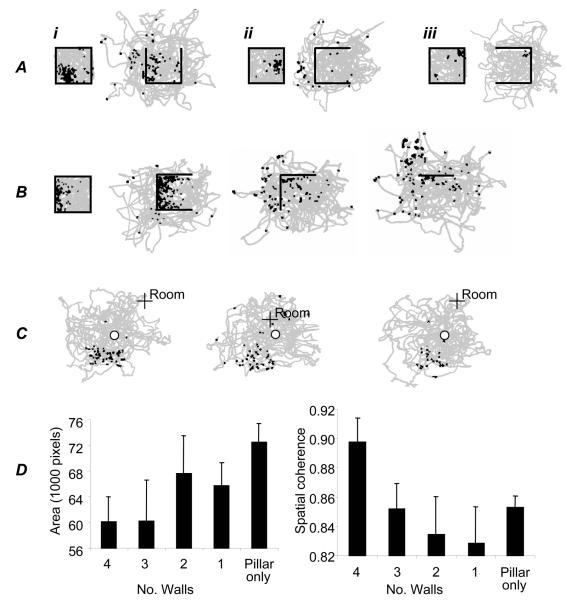
The deconstruction of the four-walled enclosure produced a marked change in the firing pattern of most observed cells. Twenty five place cells were recorded from the two rats. Eight cells ceased firing completely after the first wall removal. Figures 3 Ai,iii and B show examples of cells that retain aspects of their spatial firing after removal of the first wall. Seventeen cells showed activity in the closed environment plus at least one of the others, and seven of these had activity in all five kinds of environment (four-walled, three-walled, two-walled, one-walled and single-pillared). The most common response to wall removal was a dramatic breakdown of the place fields, especially for fields close to the removed wall (see e.g. figure 3Aii) rather than for fields more distant from the removed wall (e.g. figure 3 Ai,iii and B). Occasionally, an existing field would disappear but a new field would appear, or a field would appear where a cell had previously been silent. Overall, the change in the boundedness and reachable extent of the environment had a profound impact on the hippocampal place representation. Fields became less coherent and more diffuse as the number of walls decrease (figure 3D). An example of this effect for a single cell is shown in figure 3B.

Figure 3.

Effect of wall removal on place cell firing. A. Effect of removing one wall. Three place cells are shown (i-iii). Plots show the locations at which spikes were fired (black squares) and the path of the rat (grey). Walls are shown as black lines. B. Effect of successive removal of walls on the firing of one place cell. Removal of the first wall produced limited change in the place field – three surrounding walls were sufficient to support spatial firing. Removal of the second wall, however, caused a profound break down in spatial firing. C. A rare place cell (one of two) with a coherent field in the pillar-only condition (after removal of all 4 walls). The location of the pillar is shown by ‘o’, a fixed point within the room is shown by ‘+ Room’. D. Effect of successive wall removal on 17 place fields: they increase in area (left: Kilo-pixels above half of the peak firing rate, entire camera view is 262Kpix) and decrease in spatial coherence (right, see /²⁶/, note that evenly scattered low firing produces high coherence).

Stable spatially localised firing was observed in the single pillar condition in only two cells. These fields followed the pillar, on trials in which it occupied different room-locations, rather than remaining fixed with respect to uncontrolled room cues or the noise boundary. One of these fields was located at a distance from the pillar (figure 3C). In general however, fields in the single-pillar condition tended to be unstable.

In summary, the behaviour of place fields under wall-removal is broadly consistent with the BVC model, in that the likelihood of spatially localised firing seems to depend on the extent of barrier remaining around the field location. However, we also note that the unstable/dynamic responses of some cells in these conditions cannot be modelled by the current BVC model. In addition, responses like that in figure 3C would be even less likely in the model than the 1/25 indicated by our data, unless the firing threshold were reduced to allow a single BVC to drive place cell firing. Such variation in firing threshold would be consistent with a role for feed-back inhibition from other place cells.

Do BVCs really exist?

Are BVCs merely a useful construct, or might they really exist as a class of cell amongst the cortical inputs to the hippocampus? The BVC model imposes a number of functional constraints on its putative inputs, the BVCs. Foremost amongst these is that their fields should follow boundaries. This simple point predicts that in rectangular environments, BVC fields will tend to be ‘L’-shaped with sides parallel to the walls, and in circular environments, BVC fields will be more crescent-shaped. For example, in square environments, a preponderance of fields whose long axes were oriented at 45 degrees to the walls would entail revision of the model. Importantly, BVC fields should not only be found immediately adjacent to environmental boundaries, but broader fields should also be seen at longer distances. Secondly, the signal from a BVC should be stable with time. Thirdly, BVCs should be predominantly locational: responding to a boundary at a specific distance along an allocentric bearing, with little or no modulation by other factors such as the orientation of the animal. Elsewhere in the hippocampal formation elongated fields peaked at a distance from boundaries can sometimes be seen in other cell types, such as the presubicular place-by-direction cells/^64,65/. However, these cells clearly show a robust orientation signal; indeed, on average, they appear to signal information regarding orientation at a higher rate than information regarding location/⁶⁵/. Finally, the spatial tuning of BVCs would be expected to be broader than that of place cells, whose firing depends on several BVCs converging in sufficient strength to exceed the firing threshold.

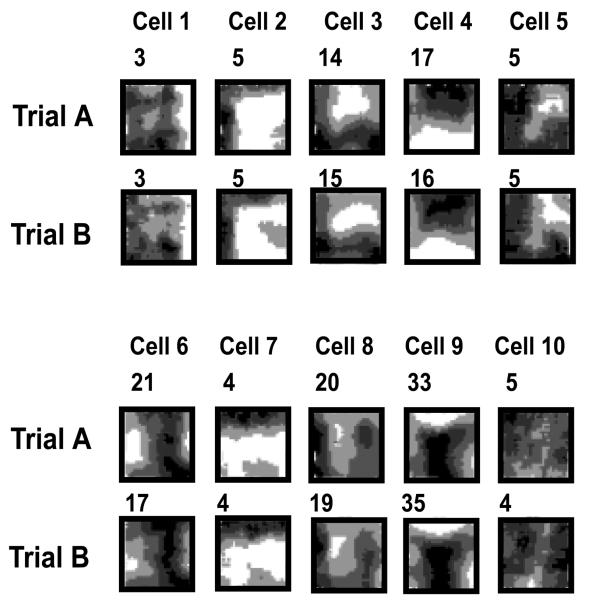
Intriguingly, we have observed that these criteria for BVCs are often met by neurons in the dorsal subiculum. (This may be somewhat surprising, since the subiculum is usually regarded as an output region of the hippocampal formation/⁶⁶/; this issue is considered later.) Figure 4 depicts our largest sample to date of simultaneously recorded subicular neurons. Firing rate maps are shown for 10 cells recorded as the rat foraged for rice grains during two exposures to the same square-walled environment. The two exposures were separated by about 20 minutes, during which the animal rested on a holding platform outside the recording chamber. Several points are evident from inspection of the firing. First, the spatial fields are generally less precise, and contain higher background firing, than the place fields of dorsal hippocampal place cells. Second, firing patterns are well reproduced across both trials. Third, the long axes of most fields are fairly straight and parallel to the rectangular boundaries. Finally, a fair proportion of the sampled cells show BVC-like field patterns, notably cells 2, 3, 4, 6, 7 and 9. The sample includes not only narrow boundary-proximal fields (e.g. cells 2, 7) but also, importantly, fields at intermediate and longer distances from boundaries (e.g. cells 6, 9).

Figure 4.

Firing rate maps of ten simultaneously-recorded dorsal subicular neurons in two trials in a square-walled environment. Cells 2, 6, 7, 8 and 9 show Boundary Vector Cell-like locational fields. The number at the top left of each firing rate map indicates the peak firing rate (Hz).

Do subicular cells show omnidirectional firing? We calculated the locational and directional information content/⁶⁷/ of the 10 subicular cells, and saw predominantly spatial correlates with little significant orientational modulation. When corrected for artefacts due to inhomogeneous sampling using a factorial maximum likelihood model or MLM/³¹/, the locational information /⁶⁸/ signalled by the BVC-like cells was on average 10 times greater than orientational information.

How should BVCs respond to environmental changes that are not purely geometric? Responses could be specific to particular types of boundary (e.g. extended surfaces such as walls or edges with a drop), and to juxtaposed materials (e.g. land and water). For now, we illustrate in two dorsal subicular neurons taken from different rats, preliminary evidence of remarkably pure geometry-dependent BVC responses in clearly different environments (figure 5). Environment A is a square-walled (62 × 62 cm × 50 cm high) enclosure, set within a circular testing arena partitioned from the room by black curtains (2.3 in diameter). These curtains are fully opened, revealing many room cues, in the Environment B condition, consisting of a cylinder (78 cm diameter × 50 cm high) made of different material from Box A. Environment C is an open-platform (90cm diameter) raised 25cm from the lab floor, that forms the floor of environments A and B. Environment C is set within the black-curtained arena of environment A. Environment D is the holding platform outside the standard testing space (for A, B, C), where the rats are placed during the inter-trial interval. These two candidate BVCs show a highly similar boundary vector response across four or more testing environments which differ significantly in ambient cues, environmental boundaries, and locational reference frame (A, B, C vs D). We know that at least some of these differences are salient, from behavioural registrations of novelty by the rats. For instance, rats showed a huge increase in rearing on their first introduction to environment B. They also respond as predicted to the introduction of a barrier. Figure 5 also shows this in further testing of one of these two cells, which fires at small distances from a western boundary; introduction of a north-south barrier creates a double field, in a manner predicted by the BVC model. The cell treats the barrier like another west wall.

Figure 5.

Geometry-dependent firing of potential subicular Boundary Vector Cells in response to extreme environmental manipulation. Left: Firing rate maps of two fields in four environments (A:curtained-off square walls; B: un-curtained with cylindrical walls of different material; C: no walls –boundary is a sheer drop; D on the small square holding platform – boundary is a sheer drop). Right: further testing of cell 1 in small and large square environments, including one with a barrier (in which cell shows doubled field). See main text for details. Trials are shown in order of testing (from top to bottom). Firing rate maps for open platform environments C and D include regions where the rats peer over the edges of the platform. Inset: Example of predicted BVC firing rate maps adapted from /¹²/).

In summary, some subicular cells show BVC-like fields, and some of these show a markedly environment-invariant or ‘pure’ boundary vector code. We are not the first to suggest that subicular cells show boundary-related firing. Sharp studied subicular firing in small- and large-square walled environments, and concluded that “environmental boundaries must play an important role in determining subicular firing patterns”/⁶⁹/. Sharp assumed that subicular cells follow a predominantly relative metric, the rat's distance from each wall being considered in proportion to the distance between the relevant enclosing walls. It remains to be shown whether Sharp's description provides a better fit of the subicular data than the fixed distance BVC model. Sharp found that expanded versions of small square firing rate maps were more highly correlated with large square rate maps, than the small square rate maps were correlated with the corresponding inner portion of the large-square rate maps /⁶⁹/. This is an important result, but is compatible with both relative and absolute distance-to-boundary interpretations of subicular firing patterns.

In summary, the suggestion that the BVC model fits important elements of the subicular cells seems quite reasonable. What was not anticipated is that the BVC model seems to better fit dorsal subicular cells than the most spatial cells of the entorhinal cortex, which provides the major cortical input to place cells. (Dorsocaudal medial entorhinal cells exhibit tightly peaked, multiple Gaussian fields spaced at regular intervals/⁷⁰/). After all, the classical view of the subiculum emphasises the massive CA1-subiculum projection and considers the subiculum as an output region of the hippocampal formation/⁶⁶/. However, various lines of evidence suggest that the classical view only partially captures subicular function. First, timeshift analysis at the millisecond scale suggests that subicular neurons tend to exhibit their best spatial signal before CA1 cells do/⁷¹/. Second, on a larger timescale, subicular cells may start firing in a novel environment more rapidly and robustly than CA1 cells/⁷²/. Third, preliminary evidence suggests some navigation tasks recruit direct entorhinal-subicular circuits, bypassing CA1/⁷³/. Fourth, feedback circuits through entorhinal cortex whereby subicular output is channelled into the hippocampus proper are being identified/^74,75/. It is also notable that major input to the presubiculum/⁷⁶/ and parasubiculum (unpublished data), which both project to the hippocampus via entorhinal cortex, comes from the subiculum. Fifth, recent electrophysiological studies indicate that CA1 pyramidal cells receive direct excitatory monosynaptic input from subicular cells/^77,78/ (see also /⁷⁹/). How important this direct projection is, however, remains unclear. In summary: spatial processing in the subiculum can be relatively independent of CA1 afferents, and might significantly contribute to input into the hippocampus proper. It will be important to examine the effect of subicular lesions and inactivation upon hippocampal place cell firing.

BVC-based models of behaviour

Can we relate our knowledge of the neural representation of spatial location to behaviour? First we assume that spatial memory depends, to some degree, on the storage of the BVC or place cell representation at the goal location, possibly via modification of synapses as in the ‘simple model’ of Burgess and O'Keefe/⁹/. Then, because of the systematic effects of geometric change on place cell firing/¹⁰/ we would expect to see specific systematic behavioural effects of geometric manipulations of the environment on behaviour in tasks that depend on a hippocampal representation of location. The BVC model gives us a quantitative basis for detailed, testable predictions about these effects. A complicating factor is that spatial learning and memory is supported by multiple neural representations operating in parallel/^8,80/, so that the hippocampal representation is obscured by conflicting information from other neural representations.

At present we have focussed on modelling behaviour in a human spatial memory paradigm where the geometric manipulations mirror those originally used by O'Keefe and Burgess to establish the geometric determinants of place cell firing. As mentioned earlier, place cells have recently been observed in the human hippocampus/²⁵/. Although their properties are much less well understood than rodent place cells, it is a reasonable working hypothesis that they will share the geometric properties seen in rats. Furthermore, neuropsychological and neuroimaging evidence supports the idea that, as in animals, the hippocampus plays a key role in human spatial behaviour. In particular where a task requires long-term memory, where there is a shift of view-point between learning and retrieval, or where the task requires information about the topology of a complex large-scale environment/⁸¹/.

In a previous experiment, Hartley, Trinkler and Burgess/¹⁵/ investigated the effects of varying the size and shape of a virtual environment in a simple spatial memory task. The virtual environment was a simple rectangular arena with low walls over which distant landmarks were visible. The distant landmarks provided cues for orientation (but not location, since they were projected at infinity). Subjects were asked to return to a location where they had previously seen a cue object (golf flag), having been temporarily moved from the environment and returned at a random location. We reasoned that if a representation based on BVCs controlled behaviour in this task, we would expect to see systematic and predictable distortions of search behaviour following geometric manipulations of the environment. The use of a virtual environment permitted us to vary the shape and size of the rectangular environment between presentation and testing (75% of trials), which allowed us to test whether the effects of geometric manipulations on behaviour were compatible with those suggested by a BVC-based representation of the unmarked goal location. This was an ambitious goal since complex behaviour in a task like this would normally be supported by several neural representations, including visual representations, path integrative and dynamically updated egocentric representations, as well as those reflecting the relative locations of environmental cues/⁸²/. However the subject's removal from the environment between presentation and testing, and their return at a random location would be expected to disrupt dynamically updated or path-integrative representations, and the results were not, as it turned out, compatible with a low-level visual representation.

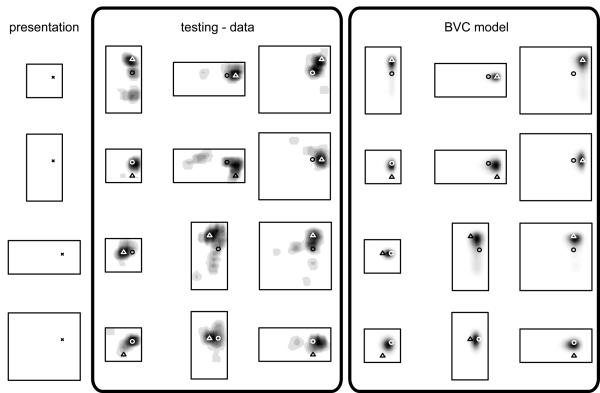
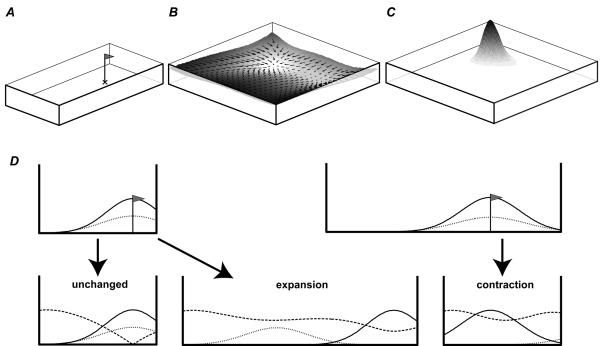
The distribution of search locations in this experiment were remarkably consistent (both within and between-subjects and across two independent experiments), and showed a reliable interaction between geometric changes and cue position. In trials where the environment changed size or shape, responses tended to lie somewhere between a location which preserved fixed distances to the two nearer walls and a location which conserved the ratios of distances between opposing walls (figure 6). In expansions of the environment and where the cued location was near to the walls of the arena, responses tended towards the fixed-distance location. In contractions of the arena, and where the cued location was nearer the centre of the arena, responses tended toward the fixed-ratio location. This pattern cannot be simply explained in terms of any single cue within the environment. Instead, responses seemed to be determined by the cue location with respect to the geometric configuration as a whole.

Figure 6.

Density of responses from a human spatial memory task (‘testing – data’) and prediction from simulation using BVC model (‘BVC model’). Human data (adapted from Hartley, Trinkler and Burgess /¹⁵/) – shows effects of geometric changes of the environment on response locations. The left column shows the location of a golf flag (X) in each of four virtual presentation environments. Subjects were briefly removed from the environment and then asked to place a marker at the cued location (the golf flag having been removed). On some trials the shape and size of the environment was changed during their absence. Response densities after changes of environmental shape are indicated by grey level. Some responses preserve fixed distances from the nearer walls (indicated by triangles), or the ratio of distances across the environment (circles). The final three columns show simulated density of responses corresponding to the experimental data, see main text.

How does this pattern fit with the BVC model? If responses were based on a place cell representation, one might naively expect them to maintain fixed distances to the nearer walls, since this is what the location of peak firing of a place cell tends to do. This would be a reasonable supposition if responses only depended on cells which fire strongly at the cued location. However, this would be to ignore the potentially valuable information which comes from cells which do not fire at the cued location. To take these into account, we used a Euclidean distance metric to compare the pattern of place cell activity seen at the goal location (in the first environment) with the pattern seen at any location (in the second, see figure 7B). This metric takes into account all firing rate changes. For example, a cell whose firing rate increases from 0 to 5Hz would be given equal weight to a cell whose firing rate decreases from 8 to 3Hz. Response density is then modelled as a decreasing function of the Euclidean metric (figure 7 C). Modelled responses thus cluster around locations that minimize the net change in activity from that seen at the cued location in the presentation environment. Following the gradient of this Euclidean metric (i.e., moving so as to maximally reduce the difference between the current and stored patterns of activity across the place cell population) would provide a crude model of navigation (figure 7B).

Figure 7.

BVC model of spatial memory. A. Cue location in presentation environment (marked by X). B. Surface showing the net difference in activity of a BVC population from that stored at the cue location in the presentation environment, as the subject moves around (using a Euclidean distance metric). Following the gradient of this surface leads back to the cue location, where the net change is minimized. C. The Softmax function is used to model the probability of a response at a given location given the difference in activity. D Above: BVCs firing at the cue location in a 1-D environment can be divided into those responding to East/left (net firing shown as dotted line) or West/right (net firing shown as solid line). This is shown for a small (i) and large (ii) presentation environment. Note the effect of proximity-weighting due to more sharply tuned (and more numerous) short range BVCs. Below: Dashed line shows the net difference in the firing of both populations from that at the cue location in the presentation environment as a function of the subject's location within the testing environment (using a Euclidean distance metric). The minimum of the dashed line shows the location of peak response: correct in an unchanged environment (left), maintaining a fixed distance to the nearer wall after environmental expansion (i -> middle), maintaining a fixed ration of distance between walls after environmental contraction (ii –> right). In contractions, the net change in activity from that at the stored location (dashed line), although strongly influenced by inputs tuned to the East wall (which was nearer at presentation), is also strongly influenced by increased firing in BVCs with short range tuning to the West wall which were inactive at the cue location (not shown).

Instead of directly modelling BVCs, our initial simulations/¹⁵/ showed that minimising the Euclidean distance between the current vector of the ‘proximities’ 1/(d+c) of the four walls and the vector stored at the presented goal location provided a good fit to these results. Notably, it predicts the same interaction between geometric change and cue location seen in the experimental data. The function we used for proximity is the same as that relating the width of tuning to preferred distance in the BVC model: in both models this reflects the greater influence of nearby wall compared to a distant one.

Although this boundary proximity model forms a useful link between neural and behavioural data, a neural model based directly on the activity of a population of BVCs (given by equations 1 and 2) is desirable and we present results of some recent simulations using this model below. To encode the cue location x, the pattern of BVC activity at the cue location (f_i(x) for all cells i) is stored. To return to the (now hidden) goal, the subject moves until the net change from the stored pattern is minimized, which in the absence of any geometric manipulation will again be at the cue location. When the environment is contracted or expanded, the BVCs tuned to a given wall will continue to fire at a fixed distance from that wall. The relative movement of the walls means that the set of BVC firing rates at the cue location in the presentation environment will no longer be exactly reproduced anywhere. Rather, response location y will be a compromise that minimizes the Euclidean difference of the current pattern of BVC firing $f_i^{\prime }\left(\underset{‒}{y}\right)$ and the pattern of firing at the cue location f_i(x) over all BVCs i (i.e. the location y that minimises ${\Sigma }_i{(f_i^{\prime }\left(\underset{‒}{y}\right)-f_i\left(\underset{‒}{x}\right))}^2$).

The more detailed neural model produces very similar results to the more abstract boundary proximity model, but is more faithful to the original BVC model and allows it to be extended to environments of any shape. An example of the results of the more recent BVC based simulation is shown in figure 6. The fit to the experimental data is impressive, and it shows that behaviour is at least compatible with a mechanism based on BVCs.

Figure 7 provides illustrative examples of how the model leads to the observed behaviour after expansions or contractions of a 1-D environment when the cue is nearer to one wall than the other, and in which all BVCs are either tuned to the “East” or “West” wall. One thing to note is that the majority of BVC firing will be in response to the nearer wall since short-range BVCs have a sharper tuning and are more densely packed/¹²/, in 2-D environments the nearer wall also subtends a larger angle: increasing the number of BVCs responding to it. Thus matching the distance to the nearer wall is more important than matching the distance to the farther one, and responses tend to maintain a fixed distance to it, especially in expansions of the environment. Where the cue is approximately equidistant from opposing walls (not shown in figure 7), the BVCs responding to each wall will contribute roughly equally to firing at the cue location. After an expansion of the environment, the BVC firing driven by each wall will exert approximately equal influence on the choice of response location. In this case the Euclidean difference will be minimised at an intermediate location to those maintaining fixed distances to each wall (the squared difference in the Euclidean metric means that two medium sized differences, one for each subset, amount to less than one large difference - as would be the case at either fixed-distance locations).

That this model reproduces the overall pattern of behaviour provides some encouragement that the BVC representation, or at least the way in which it favours proximal compared to distal boundaries, plays some role in human spatial memory. However, it also raises some questions as to the necessity of the place cell representation, as distinct from its putative inputs. Of course, BVCs may not actually exist or have the mnemonic role prescribed for them here, in which case the place cell population would produce qualitatively similarly behaviour (the application of threshold in equation 3 having little consequence). Beyond this, we previously argued/⁸³/, that mediation by the place cell representation adds the ability to control the generalisation of a spatial response learned in one environment to another environment: the availability of the same place cell representation in another environment depends on whether or not there is remapping between the two environments. One recent experiment in rats indicates that generalisation of knowledge of the goal being in the centre of one environment to a different shaped environment does indeed depend on the hippocampus /⁸⁴/, but see also /⁸⁵/.

Learning and the BVC model

As described so far, the BVC model incorporates only hard-wired feed-forward connections from BVCs to place cells. Thus, firing perturbations caused by changes in the topography of an environment are immediate and invariant. Although the model captures rotational or geometric changes in firing, there is good reason to believe that plasticity plays an important role in place cell firing/⁸⁶/. Place cell representations fail to stabilise in the presence of NMDAR block/⁸⁷/ or protein synthesis inhibition/⁸⁸/; both of which are essential for LTP. Also, experimental data from Lever et al./⁵⁰/ and Hayman et al./⁸⁹/ showed that a form of slow remapping can result from accumulated plastic changes occurring over several weeks/⁵⁰/. However, we think that the BVC model provides a good framework within which to investigate experience-dependent plasticity. In the section below we present data demonstrating the generation, stabilisation and subsequent persistence of place fields created as a result of deformation of a rat's environment. In conjunction, we describe an extension of the BVC model to incorporate an implementation of the BCM/¹⁶/ learning rule. Experience-dependent changes in the efficacy of BVC to place cell connections enable this model to describe the plastic process by which new place fields are created and maintained.

Plasticity induced by extending and opening a square environment

Recordings were made from 3 adult male Lister Hooded rats following the same procedure as the wall-removal experiment described earlier. In this experiment, which also took place in the ‘unbounded’ arena, the four walls were arranged in one of two configurations: a closed square with 60cm sides; or the same square with either the south or east wall moved out by 25cm to form a broken rectangle. In the broken rectangle configuration, rats were able to leave the local environment and explore the rest of the room, within the diameter determined by the auditory discouragement procedure (described earlier). A glow-in-the-dark sheet (60cm wide and 50cm high) attached to the north wall of the local environment served as a directional cue. Rotation of the cue was able to induce concordant rotation of place fields, confirming its efficacy as a directional cue. A single recording session consisted of alternating 5 minute trials in the square and 15 minute trial in the rectangle. Sessions always started and finished with a trial in the square environment. The three animals used in the experiment (r1, r2 & r3) experienced different numbers of trials and sessions: r1 and r3 each had a single recording session, consisting of 9 and 7 trials, respectively. Another rat, r2, had two consecutive days, experiencing 9 trials on the first day and 11 on the second. Spikes were acquired, analysed, and accepted using standard tetrode equipment and techniques/⁶³/. Only place fields contained within the local environment walls were analyzed further.

Fifteen place cells were identified from the 3 animals (r1: 5; r2: 8; r3: 2). Fields were considered to be ‘on’ if peak firing rate was greater than or equal to 1Hz. Six cells had place fields in all trials. A further 8 cells showed fields which either turned on or off in one of the two environments during the recording session. The remaining cell was unclassified: although it had stable fields in the square environment these became non-spatial in the rectangular environment.

The fields of the 6 cells that were active in all trials behaved like the majority of cells described by O'Keefe and Burgess/¹⁰/. In response to a deformation of the environment they maintained a fixed position relative to either the 3 unmoved walls (4 fields) or to the moved wall if close to it (2 fields, e.g. figure 8 cell A). The 8 cells with fields that turned on or off shared several characteristics. Importantly, they all had stable, persistent place fields in one of the two environments and the location of the new field was consistent with its location in the other shape (i.e. being the same distance from 3 of the walls). Six cells fired in the rectangular environment but were initially silent in the square, one cell fired in the square but was initially silent in the rectangle. Once a field turned on or off in one environment it remained in that state on subsequent exposures to the same environment (figure 8 cells B-D). Only 1 of the 8 cells stopped firing: after exposure to the rectangle, cell 4 (r1) stopped firing in the square environment (figure 8 cell D). Considering the time-course of the 7 cells with fields that turned on, 3 turned on after a single exposure to the alternative environment, a further 3 turned on after the second exposure to the alternative environment, and 1 turned on after a third exposure.

Figure 8.

Place fields recorded from four cells (A-D) over 9 trials, alternating between a closed square (65cm) environment and the same environment with the south wall moved out by 25cm. Trials in the square environment lasted 5 minutes, those in the open rectangle 15 minutes. When active, fields from the same cell occupied analogous positions in both conditions, consistent with the BVC model. Cell A fired continually throughout the session. Cells B-D exhibited experience-dependent plasticity: firing in the square starting (Cells B,C) or stopping after repeated exposure to the open rectangle.

Incorporating experience-dependent modification of BVC connections

Although the behaviour of the persistent cells is inline with model predictions and is similar to those described and modelled by Hartley et al. /¹²/. In its original form the model is unable to account for the changes in firing that were seen with successive exposure to the two environments. These changes imply that some form of plasticity had occurred as a result of the animal's experience. In order to address this we now describe an extension of the BVC model that incorporates learning and, as a result, is able to account for some of the changes we saw.

The model used here maintains the core components of the original formulation – see equations 1-3 above, and Ref /¹²/ for complete details. We simulated a population of 200 BVCs with preferred values selected from a range of distances covering the size of the environment and from a continuous distribution of directions. However, a variable strength (w_ji) was assigned to the connections from BVC i to place cell j, whose firing rate (see equation 3) becomes:

$$F_j\left(x\right)=A\Theta \left(\underset{i=1}{\Sigma }{f}_i\left(x\right)w_{\mathit{ji}}-T\right).$$ (4)

The weight matrix (w_ji) was initially seeded such that each of 100 place cells received presynaptic input from 10 random BVCs. These connections were of equal weight, as in the original model. The BCM rule was then used to update the weights between BVCs and place cells (w_ji), see Fuhs and Toursetzky/⁹⁰/ for a related approach. The BCM rule/¹⁶/ has several desirable characteristics that make it preferable to the basic Hebb rule for this application. First, it incorporates both positive and negative weight changes. Sustained activity of the postsynaptic cell above a defined threshold will result in an increase in efficacy of active synapses onto that cell. Activity below the threshold will result in a decrease in efficacy. Second, the position of the threshold itself is modulated by the recent activity of the postsynaptic cell. If a postsynaptic cell is highly active the threshold will move up, making it more likely that synaptic weight reduction will occur. Third, weight change only occurs if both the presynaptic and postsynaptic cells are active. Specifically, weight changes were implemented as follows:

$$\Delta w_{\mathit{ji}}=g_i\left(\underset{‒}{x}\right).\Phi (F_j\left(\underset{‒}{x}\right),\xi ),$$ (5)

where g_i(x) is the firing of BVC i at position x; F_j(x) is the firing of place cell j at position x; Φ(F, ξ) = [F(F-ξ)]_±0.02, where []_±0.02 indicates truncation of values above 0.02 or below −0.02. The threshold separating positive and negative weight changes is given by:

$$\xi ={\left(\frac{{\stackrel{-}{F}}_j}{F_0}\right)}^2{\stackrel{-}{F}}_j,$$ (6)

where F̄_j is the mean firing rate of place cell j across the current environment and F₀ is a positive constant. Finally, connections whose strength is zero (such as those between initially unconnected BVCs and place cell) will remain at zero.

BVC and place firing was simulated for two environments, a 65cm closed square and a 65cm × 90cm open rectangle. Firing was not simulated for areas outside of the walls. Learning was conducted iteratively: synaptic weights were updated according to presynaptic and postsynaptic firing; place cell firing was recalculated; weights were updated again, and so on. We first considered the behaviour of the model after training in an unchanging environment. With this goal in mind, 100 iterations of learning were simulated in the 65cm closed square. The first set of fields produced before learning were the same as those produced by the standard model and, as discussed earlier, resembled experimental data. Firing was localised in discrete areas of the environment, generally increased monotonically towards a single peak and a small proportion of cells (approximately 30%) did not fire.

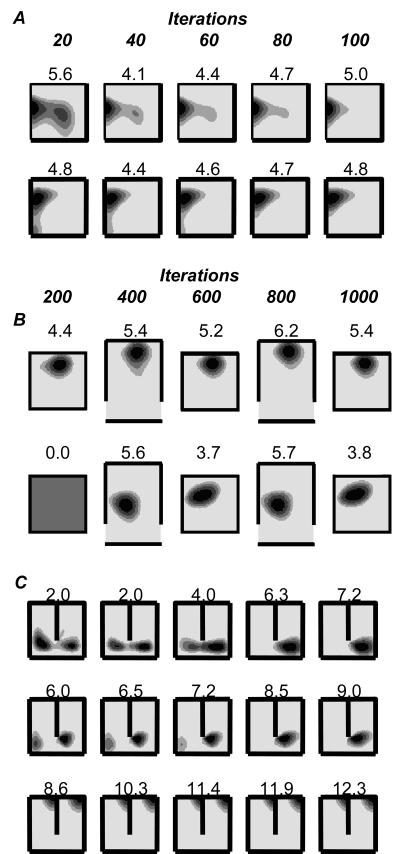
Inspection of firing fields after increasing numbers of learning iterations revealed several interesting characteristics (figure 9). First, there seemed to be a gradual ‘cleaning up’ of about one third of the fields which became smaller and more symmetrical (e.g. figure 9A). This process might best be represented as a ‘tidying of messy fields’. For example, large fields and those with extended, weak tails shrank in size, became more compact and generally came to more closely resemble typical place fields. Similarly a number of cells with weak subfields gradually lost those subfields. The BCM rule reduces the efficacy of BVC inputs to a place cell if they drive firing outside of the main place field, while inputs from BVCs that drive firing in the place field are strengthened. Second, a smaller number of fields remained relatively unchanged. Peak rate fluctuated slightly but field size and shape remained constant. Cells that remained unchanged were generally those that already had well-defined fields. Over larger numbers of learning iterations most cells reached a steady state. For example, after 500 iterations, most fields had been refined and remained stable for an additional 4500 iterations. The model's prediction of long term field stability fit the experimental data. Interestingly, experimental evidence also suggests that place fields experience a period of rationalisation similar to that seen here. For example, Wilson and McNaughton/²⁷/ recorded cells as a rat explored a novel area of its environment. Fields were initially unstable, providing an unreliable estimate of the animal's position. After 6 to 10 minutes, though, fields were sufficiently stable to provide an accurate reconstruction of the rat's path.

Figure 9.

Plasticity in the extended BVC model. Seven simulated cells are shown (one per row) after different amounts of learning (columns). A. Two place fields in an unchanging square (65cm) environment. Each column corresponds to 20 additional iterations of learning with the BCM rule, see main text for details. The fields are gradually ‘tidied up’. We also observed fields that remained unchanged after learning (not shown). B. Two place fields in alternating square (65cm) and open rectangle (90cm × 65cm) environments. Each column corresponds to an additional 200 iterations of BCM learning. The first place field maintains its position relative to the adjacent north wall in both environments. The second starts to fire in the square environment after exposure to the open rectangle, maintaining its position relative to the south wall. C. Simulated firing, learning was conducted in an unchanging environment (65 cm square with 40cm barrier). Again, each column represents 200 iterations. All cells initially exhibit double fields in the presence of the barrier. The first two cells progressively lost one of their fields with learning. The third cell essentially remained unchanged.

Next we examined the model's ability to account for the experimental results described above: plasticity resulting from alternating trials in the square and rectangular environment. We simulated the firing of 100 place cells over 1000 learning iterations. Learning was run in blocks of 200 iterations, after each block the ‘rat’ was moved to the alternative environment. Hence the simulation started with 200 iterations in the square environment then changed to the rectangular environment for 200 iterations and so on. In totally 600 iterations were run in the square environment and 400 in the rectangular environment.

The behaviour of the model accorded well with the experimental data. Fields initially present in both environments were generally stable and maintained their position relative to the environment walls (e.g. figure 9B above). A small number of cells were silent in both environments. Note, the BCM rule requires postsynaptic activity for any form of weight change to occur. Hence cells that are initially inactive in both environments will remain inactive. A smaller proportion of cells (approximately 10%) were inactive on first exposure to the square environment but fired robustly in the rectangle. On subsequent exposure to the square, after firing in the rectangle, all of these cells fired robustly (figure 9B below). This effect is produced because BVCs that drive place cell firing in the rectangle are strengthened. When the ‘rat’ is returned to the square, cells that were previously silent can now be driven above the firing threshold by the strengthened inputs. We saw fewer cells that initially fired in the square but not in the rectangle, as in the data (although this could result from an arousal effect in the data, see below). The model produced a single example of a cell that ceased firing.

The simulated firing did differ from experimental data in a few key regards. The first of these was that all cells that became active did so after a single exposure to the rectangle. In contrast, the experimental data contained a number of cells that became active only after multiple exposures to the rectangular environment. This is not a major discrepancy but indicates that a single trial corresponds to less than the 200 learning iterations used in simulations. A second point on which the model deviated from experimental observations was the proportion of cells that became active. Under the model 10% of cells behaved in this way, but experimentally the proportion was closer to 50%. It is possible that this is due to the non-parametric topological change in the environment, rather than parametric change in geometry (e.g., the broken rectangle, which allows the animal to escape the confines of the box, may have affected the excitability of individual cells via global change in the animal's arousal level). Unfortunately, the extent to which changes in arousal contributed to the plasticity seen in this experiment cannot be quantified or modelled. However, the more important aspect of the data with regard to the model is that when cells became active, they did so in the corresponding location (according to the model) in the two environments, and remained active thereafter.

The simulations presented here represent work in progress, and further work will be necessary to parameterize the model so that it fits quantitative aspects of the data more fully. However we have already demonstrated that in principal the BVC model coupled with the BCM rule can explain the main forms of experience dependent plasticity seen in our experimental data. Other changes, such as nonparametric remapping, remain to be understood. Nevertheless, capturing the qualitative character of experience-dependent parametric change in the place cell representation is an important step towards a more complete understanding of plasticity in the place cell representation.

Plastic Changes in Response to Barrier Insertion

We described earlier how the introduction of a barrier into an environment can cause immediate changes in place cell firing. In particular the barrier causes some place fields to double, displaying a field on either side of the barrier. But what happens after prolonged exposure to a barrier? If, as has been suggested/⁸/, place cells really do provide an allocentric representation of space then it is not desirable for two areas in the same environment to be represented by the same cell. With this is mind it might be thought that processes exist to resolve contradictions such as these. Indeed, data from Lever, albeit only 2 cells, showed that during a 10 minute trial one of a pair of doubled fields created by a barrier faded away/⁹¹/. To better understand this effect we recorded place cells on consecutive days as an animal repeatedly explored an environment, with and without the presence of a barrier.

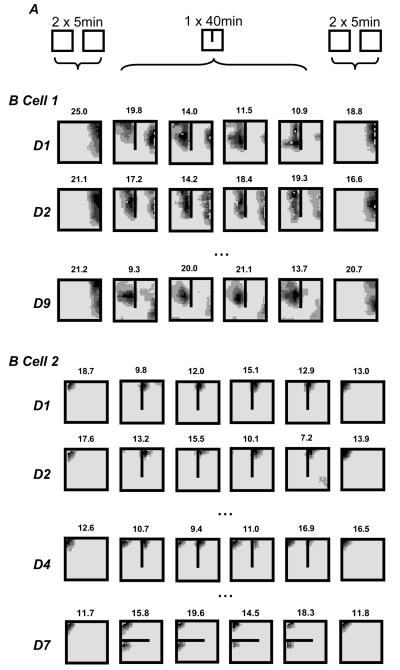
The barrier data described below was collected from a single animal. The place fields presented should be considered as qualitative examples of the possible outcomes of experience-dependent plasticity. Data was captured and analysed using standard procedures and equipment/⁶³/. The bulk of the recordings were made on 8 consecutive days with additional manipulations performed after the end of the experiment. Where possible, cells were followed across days. Recording sessions were conducted at the same time each day, allowing approximately 24 hours between sessions. Each session followed the same protocol, the first 2 trials saw the rat forage for rice in a square, walled environment for 5 minutes each. Laboratory equipment and furniture (e.g. computers) provided directional cues. The animal was returned to its home box between trials and the box was rotated pseudo-randomly by 90°, 180° or 270°. A barrier, made of the same material as the box, was then positioned in the centre of the environment with one end abutting the wall. The animal foraged continuously for 40 minutes with the barrier present and was then returned to its home box. The barrier was removed and a final two trials were conducted similarly to the first two, (see figure 10A).

Figure 10.

Firing rate maps from 2 place cells simultaneously recorded over several days (one per row) in the 65cm square enclosure with or without a 40cm North-South barrier. Each plot represents 10 minutes of exploration. The first column shows combined firing from 2, 5 minute trials recorded without a barrier. The next 4 columns show firing from a single continuous 40 minute trial (as 4 × 10 minute slices) in the presence of the barrier. The final column shows firing with the barrier removed. Cell 1 doubles its field when the barrier is introduced on day 1, while the Eastern field is gradually lost both within each day and over days, see main text. Cell 2 fired only on one side of the barrier for the first 3 days, then developed a field on both sides on day 4 and continued to do so on subsequent days (not shown), including in an East-West barrier configuration (day 7).

Cell 1, recorded on day 1, exhibited changes in firing similar to those reported by Lever et al./⁹¹/. Insertion of the barrier prompted the rapid appearance of an additional field adjacent to the West side of the barrier (figure 10, Cell 1, day1). Indeed, the cell fired on the rat's first pass through the new place field. The original field, adjacent to the East wall of the box, was initially more robust and fired more strongly than the new field but during the 40 minute trial it gradual shrank away while the new field was maintained. The peak rate of the new field was constant at about 14Hz whereas the rate of the original field fell from 23.6Hz in the first 5 minutes to 4.94Hz during the last 5 minutes. When the barrier was removed towards the end of the session, the original field was reinstated and the new field was lost.

Interestingly, when the barrier was placed in the box on the second day both the original field and new field were obvious during the first 5 minutes of the trial (figure 10, Cell 1, day2), with the cell firing on the first pass through each field. Again the initial (East) field became weaker through the session, but at a slower rate than on the first day. The main point here is that the fields did not return to the configuration they were in prior to the removal of the barrier at the end of the first day. We followed this cell over 10 days in total: the changes observed in one or other of the fields on one day were often not obviously present 24 hours later. There was some tendency for cumulative change however, with East field slowly weakening in the presence of the barrier, and moving South in the open box (figure 10, Cell 1, day 9). The time course of the changes seen here is reminiscent of the ‘slow remapping’ seen by Lever et al./⁵⁰/: changes that accumulated during the day being partially undone overnight in a ‘two steps forwards, one step back’ way/⁹¹/. It is interesting to note that Mehta, Barnes and McNaughton/⁹²/ also saw temporary changes in place field shape, and these were shown to be NMDAR dependent.

We also observed subfields appearing over time as well as disappearing. On the first 3 days cell 2 (recorded concurrently to cell 1 above) had a field in the Northwest corner of the box (figure 10, cell 2). When the barrier was inserted the field immediately shifted to the corner between the East side of the barrier and the North wall. On the fourth day of recording, insertion of the barrier provoked 2 fields in the corresponding Northwest corners on each side of the barrier (figure 10, cell 2, day 4). During 6 subsequent days of recording, the cell continued to exhibit a dual field when the barrier was present. Even with the barrier in an East-West orientation, the cell fired in both Northwest corners above and below the barrier (figure 10, cell 2, day 7).

In total we followed 11 cells for time courses varying from a day to the duration of the experiment. Although it is difficult to draw firm conclusions from such as small data set, nevertheless we can make some important observations that bear on the predictions of the BVC model, and our implementation of learning. First, the majority of the cells (6) exhibited some form of gradual plasticity. This was largely of the forms described above: duplication of a field, loss of a duplicate field or movement of field. Some cells showed all three forms at various stages. Second, there was no obvious relationship between changes observed concurrently in different cells. Third, cells we followed for longer seemed more likely to exhibit change. Two cells we held for the course of the experiment demonstrated plasticity, whereas, cells recorded for a single day remained unchanged. The implication of this is that these plastic changes are not coherent across cells, occurring at different times in different cells (Lever et al. saw this same effect/⁵⁰/).

The original BVC model was not designed to account for such effects of experience dependent plasticity. However, inclusion of the BCM learning rule allows the model to address some aspects of the experimental data. We simulated 1000 iterations of firing in a 65cm square environment with a barrier oriented North-South. Firing before learning was identical to that predicted by the standard BVC model; about 35% of cells were silent, of the remainder approximately 65% showed some form of doubled field. As described previously, learning conducted in a static environment results in fields that ‘tidy up’. We saw this effect again and it also extended to a rationalisation of some doubled fields, 44% of these cells showed a gradual loss of one field (figure 9C rows 1-2). The field with the lowest peak firing was usually the one that was removed (see also /⁹⁰/) although this was not always that case. In each case the retained field was largely unaffected by loss of the duplicate. The model does not predict that all double fields will be reduced to a single peak, even after 5000 learning iterations around half of the initial double fields remained (see figure 9C last row).

We note that some initially doubled fields end up as a single field near to the barrier (e.g. figure 9C middle row). This may relate to the experiment of Rivard et al./⁹³/ in which exposure to a cylindrical environment containing a barrier that moved between trials produced place fields that either fired with a fixed relationship to the cylinder or close to the barrier. It seems likely that, under the BCM rule, systematic movement of the barrier would cause most place fields to become driven solely by the barrier (if close enough) or the environment walls. That is, both observed effects would naturally result from the BVC model, without requiring Rivard's postulation of two distinct cell types (‘furniture cells’ and ‘room cells’). Indeed, if place cells start with a random set of connection weights, a small proportion will have the pattern of connections required to express this type of field before any learning (e.g. figure 1, A iv).

We did not, however, observe all of the effects that were seen in the experimental data. Learning under the model is continuous; predictably we did not see the overnight undoing of learning that was present in the experimental data. We also did not see any examples of fields being doubled as a result of learning rather than being present immediately following barrier insertion (cf figure 10 Cell 2). Indeed there seem to be a number of effects evident in the experimental data, the apparent independence of changes on different days, for example, that are not captured by the model.

Conclusion

The BVC model set out to explain place cell firing in terms of putative functional inputs to the hippocampus. In its original form, without learning, it is a very simple model, but can nonetheless account for observations such as the rapid formation of place fields in new environments /^27,94/ and the parametric changes of the place cell representation seen under geometric manipulations of the environment /^10,12/. The model captures the characteristic shapes of place fields in specific environment (e.g. elongated parallel to boundaries, such as crescent-shaped fields in cylinders), how specific fields will change shape in different environments, and how firing rates will change, (including the proportions of active place cells) in one shape but not another. Most strikingly, the model explained why the introduction of a barrier into a field will abolish it /⁴⁴/, but also predicted/⁹⁵/ that it will produce a doubled field /^12,91/ in many other circumstances. Field doubling was also expected in identical linked environments/⁶¹/ for the same reasons. The model predicts that normal spatial firing of place cells depends on the proportion of angle around the rat occupied by barriers. This effect is broadly confirmed for the first time in this paper by using aversive sound to constrain the animal's exploration while a walled environment is deconstructed.

We have found boundary vector cells be a useful construct, both in understanding experimental data and in formulating new experiments. But do they really exist, and if so where? Cells whose firing depends on barriers have previously been found in the subiculum /⁶⁹/ and we have now found further strong similarities with the predicted properties of BVCs in our own experiments. Most notably the firing fields of several subicular cells we observed followed the shape of the boundary of the animal's environment in the way expected of BVCs.

Extending the model to explain the numerous results showing experience-dependent plasticity in which depend on an animal's experience demands the addition of learning to the basic BVC model. By modifying feedforward connections from BVCs to place cells using the BCM learning rule/¹⁶/, the model can begin to account for a number of experimental observations. Here we showed that the model was compatible with the gross pattern of changes in place cell firing in response to repeated exposure to barrier insertion or environmental expansion. Further work will consider whether the BVC model can begin to explain the complex literature concerning partial/slow remapping (e.g. /^{96,61,50,97,98}/) , see /^90,58,99/ for alternative models. However, we suspect that the current feed-forward model may not be capable of accounting for the rapid, coherent remapping a population of place cells. At least in some situations /¹⁰⁰/ this type of remapping shows the attractor dynamics suggestive of a role for the recurrent modifiable connections between place cells in area CA3.

Mounting neuropsychological and functional neuroimaging evidence indicates that the human hippocampus (particularly in the right hemisphere) may play a similar role in spatial memory to the rat hippocampus, reviewed in /¹⁰¹/, see also /¹⁰²/. Although other neural systems (e.g. parietal or basal ganglia) undoubtedly play important roles in human spatial behaviour, their contributions almost certainly depends on the nature of the task at hand. Thus, following a long history of experiments designed to bias which representation is used (see e.g. /⁸⁰/) , we believe that it will be possible to test behavioural predictions of the BVC model in humans and other animals. For instance, in a walled virtual reality environment in which path integration was minimized and new object locations were used on each trial, the BVC model successfully predicted patterns of response in a spatial memory task in humans /¹⁵/. This would probably not be the case in tasks using single landmarks /¹⁰³/ or repeated route-learning /⁸⁰/). A future challenge will be to find behavioural evidence that tests predictions of our implementation of learning in the model.

In conclusion, our computational approach has allowed us to begin to understand the neural representation of space in the rat brain, and to be able to relate this knowledge to the potential mechanisms of human spatial memory. More generally, this work provides and example of the potential power of a combined computational and comparative approach to cognitive neuroscience.