Order effects in contingency learning: The role of task complexity

Abstract

Dennis and Ahn (2001) found that during contingency learning, initial evidence influences causal judgments more than does later evidence (a primacy effect), whereas López, Shanks, Almaraz, and Fernández (1998) found the opposite (a recency effect). We propose that in contingency learning, people use initial evidence to develop an anchoring hypothesis that tends to be underadjusted by later evidence, resulting in a primacy effect. Thus, factors interfering with initial hypothesis development, such as simultaneously learning too many contingencies, as in López et al., would reduce the primacy effect. Experiment 1 showed a primacy effect with learning contingencies involving only one outcome but no primacy effect with two outcomes. Experiment 2 demonstrated that the magnitude of the primacy effect correlated with participants' verbal working memory capacity. It is concluded that a critical moderator for exhibition of the primacy effect is task complexity, presumably because it interferes with initial hypothesis development.

Everyday life is experienced as a ceaseless series of sequential events. An essential step in understanding our environment is to be able to process this onslaught of events as they occur. In the present study, we examined how the learning of contingencies among events is influenced by the order in which information is experienced. For example, a graduate student might learn from one professor that teaching experiences are essential in getting a good job and then later learn from another professor that teaching experiences are not essential in getting a good job. How does the order in which people observe evidence affect their interpretation of contingency strength? In the present article, we examine what information in a sequence, early or late, is weighted more heavily, and under what conditions this weighting applies in the learning of contingency relationships.

Studies in which the effect of information order in contingency learning has been examined systematically have produced mixed results. Some studies have shown a recency effect: Information that is presented later in a sequence is more heavily reflected in judgments than is information that is presented earlier (see, e.g., Collins & Shanks, 2002; López, Shanks, Almaraz, & Fernández, 1998). Other studies have shown a primacy effect: Early-presented information is reflected in judgment more than is later information (e.g., Collins & Shanks, 2002; Dennis & Ann, 2001; Yates & Curley, 1986). The purpose of the present study was to investigate one potential source for these conflicting findings by comparing methods in Dennis and Ahn with those in López et al. (see the General Discussion section for other potential determinants of the order effects).

Primacy Effect in Contingency Learning

Dennis and Ahn (2001) found a primacy effect in causal strength judgments. Half of their participants first viewed a block of sequentially presented trials that mostly corroborated a generative causal relationship (e.g., ingesting of a plant paired with an allergic reaction and not ingesting a plant paired with the absence of an allergic reaction), followed by another block of sequentially presented trials that mostly suggested a preventive relationship (e.g., ingesting of a plant paired with the absence of an allergic reaction and not ingesting a plant paired with the presence of an allergic reaction). In a second condition, the order of the two blocks was switched. Although the participants in both conditions observed identical trials across the entire sequence, Dennis and Ahn found that final causal estimates were higher when positive information was presented first than when negative information was presented first during learning.

Such a primacy effect appears particularly remarkable because it is in opposition to a rational analysis. For instance, the updating of a hypothesis, if a Bayesian theorem is used, cannot be influenced by the order in which data are received (see Slovic & Lichtenstein, 1971, for more details). Dennis and Ahn (2001) accounted for their primacy effect in terms of a process of anchoring and adjustment, an account that served as a basis of the present study.

According to this account, the information that a person receives at the beginning of a learning sequence is used to construct a model about a possible causal relationship. This initial belief then provides an anchor point for future adjustments (Hogarth & Einhorn, 1992). In general, however, the anchor point will be underadjusted by later evidence (e.g., Kahneman & Tversky, 1973). For instance, people may prefer to focus on the evidence that confirms their initial hypothesis. In addition, they may interpret the later evidence in light of their initial hypothesis. For instance, if one starts by believing in a generative causal relationship between X and Y, later evidence of X paired with the absence of Y may be interpreted as simply a case in which a necessary precondition is not met, rather than as evidence against the held belief. Regardless of the specific mechanisms for underadjustments, one obvious implication of the anchoring and adjustment proposal is that the primacy effect is unlikely to be obtained if the anchor cannot be established early on during learning. Thus, we predict that the difficulty associated with developing an initial hypothesis will moderate the amount of primacy effect in contingency learning. Indeed, we will argue in the next section that López et al. (1998) found the recency effect because it was almost impossible to develop any hypothesis during the initial trials.

Recency Effect in Contingency Learning

López et al. (1998) employed a cue competition task to assess the influence of information order. They used learning sequences in which participants received information about an outcome (a disease in their experiments; henceforth, denoted by X) and several cues (symptoms in their experiments; henceforth, denoted by A, B, and C). Table 1 summarizes the design of their Experiment 1, which is the same design as that used in the present study. We will first explain how experimental trials were grouped into two types of blocks, followed by how learning sequences were created using these blocks.

Table 1. Number of Trials Used in Experiment 1 for Each Type of Possible Stimulus.

Learning Sequence	First Block	Second Block
Contingent-first	8 cases of AB with Disease X	8 cases of AC with Disease X
	2 cases of AB with no disease	2 cases of AC with no disease
	2 cases of B with Disease X	8 cases of C with Disease X
	8 cases of B with no disease	2 cases of C with no disease
Noncontingent-first	8 cases of A′C′ with Disease X′	8 cases of A′B′ with Disease X′
	2 cases of A′C′ with no disease	2 cases of A′B′ with no disease
	8 cases of C′ with Disease X′	2 cases of B′ with Disease X′
	2 cases of C′ with no disease	8 cases of B′ with no disease

Note—The target symptom in each condition (A and A′) is marked in bold. The notations for cues and diseases for the two learning sequences are slightly different (with an additional prime mark in the noncontingent-first sequence) to indicate that different symptoms and disorders were used, while keeping the letters of the alphabet the same to indicate the equivalence in the two blocks.

In the contingent block, A was always presented coupled with B, and this compound cue AB was generally accompanied by a disease. In contrast, B, when presented alone, was rarely accompanied by a disease. These pairings suggested that A was a better predictor of Disease X than was B, since B oftentimes appeared in the absence of the disease, whereas A rarely did. In the noncontingent block, A was always presented with a third cue C, whereas C could be presented without A. Both the compound cue (AC) and C alone were generally accompanied by the disease. According to the cue competition account advanced by López et al. (1998), this block suggested that A was a worse predictor than was C, because the presence of C could completely explain the occurrence of Disease X without any additional information being gained from the presence of A.

The order of these two blocks was manipulated so that in one condition, the contingent block was presented first (shown as the contingent-first learning sequence in Table 1), and in another condition, the noncontingent block was presented first (shown as the noncontingent-first learning sequence in Table 1). That is, throughout the learning sequence, identical trials were presented in both conditions, but in one condition, the participants first received the information that A is a good predictor, whereas in the other condition, they first received the information that A is a poor predictor. López et al. (1998) found that ratings of the relationship between Symptom A and the disease were higher in the noncontingent-first learning sequence than in the contingent-first learning sequence. This finding indicates that the participants were more influenced by recent information, contrary to Dennis and Ahn's (2001) findings.

Number of Relations to be Learned as a Determinant of Order Effects

We claim that the tasks required of López et al.'s (1998) participants were substantially more complex and demanding than those required of Dennis and Ahn's (2001) participants. We first will explain the complexity of the tasks in López et al. and then will argue that this increased complexity encouraged the recency effect.

As was described previously, there were two conditions in López et al. (1998). For each of the two conditions, two sets of stimulus materials were developed, each consisting of a disease and 3 symptoms. In López et al., these four sets of materials were intermixed and presented as a single sequence to the participants. Thus, during the same learning phase, the participants saw a total of four diseases and 12 symptoms. From this many symptoms and diseases, the participants would have been keeping track of 32 different types of trials: each of the four different combinations of symptoms (i.e., AB, B alone, AC, and C alone) for a disease paired with the absence and the presence of a disease for four different diseases.

Earlier, we argued that the primacy effect occurs because during initially observed trials, people form a hypothesis about the relationship between events (i.e., an anchor) and underadjust their initial hypothesis on the basis of later evidence. In accord with this account, we believe that increased cognitive demands, as in López et al. (1998), would lead to the recency effect. Being bombarded with too many different types of trials, participants would have struggled to put them together to reason about the most consistent hypotheses at the beginning of the learning phase. Similarly, De Houwer and Beckers (2003), who argued that contingency learning is like deliberate deductive reasoning processes, found a smaller forward blocking effect under high cognitive load than under low cognitive load, presumably because of the increased difficulty of engaging in such reasoning processes (see Waldmann & Walker, 2005, for similar findings).

Another factor, in addition to the difficulty in engaging in reasoning processes, was that López et al.'s (1998) participants received no information as to which symptoms could be paired with which disease prior to viewing trials. When B was accompanied by no disease, for instance, the implication of this trial would have been unclear to the participants (i.e., what symptom was B competing with and which of the four diseases could appear with B?) until the entire array of stimuli had been experienced. The beginning of every experimental block therefore became a learning period in which the participants had first to decide what symptoms could appear with a disease before they could begin to determine the strength of the relationship between a symptom and a disease. It might have been only later in the learning phase that the participants had fully memorized the stimulus materials and started to develop hypotheses. This would have resulted in a recency effect, as was found by López et al.

In contrast, consider a hypothetical case in which participants went through a learning phase similar to that in López et al. (1998), except that only one stimulus set (i.e., one disease and three symptoms) was presented. We would argue that hypothesis development is much more feasible in this case, and therefore, we would predict a primacy effect. We will provide a general account for this prediction first and then a concrete example below. Generally speaking, in the contingent-first condition, participants will initially develop the hypothesis that the target cue is contingent to the outcome in the first block and will underadjust this hypothesis during the second, noncontingent block. In the noncontingent-first condition, participants will initially develop the hypothesis that the target cue is noncontingent to the outcome and, again, will underadjust this hypothesis during the second, contingent block. If one compares the two conditions, participants' contingency strength estimates for the target cue at the end of the learning sequence will be higher in the contingent-first condition than in the noncontingent-first condition.

Below, we will provide one plausible process that concretely illustrates the general account above. In the contingent-first learning sequence (see the upper half of Table 1), one will be most likely to develop an initial hypothesis that A (the target cue) is a better predictor of the Disease X than is B (because B alone tends to be paired with no disease, leaving A to be the only explanation for trials in which AB appears with Disease X). In the following noncontingent block of this sequence, C alone is strongly associated with X (which might slightly lower confidence in A). This does not necessarily mean, however, that during trials in which Cues A and C were present along with Disease X that C is the only predictor of X (see De Houwer, Beckers, & Glautier, 2002, and Waldmann & Holyoak, 1992, for a similar interpretation); the observations can still be consistent with the interpretations that both A and C predict X. Thus, one may still hold on to the initial belief that A is a reasonably strong predictor for X.

Now consider the noncontingent-first learning sequence, shown in the bottom half of Table 1. In the first block, C′ is strongly associated with X′, but there is no support for A′ as a strong predictor of X′; A′ is a redundant cue during trials in which A′ and C′ are paired with the outcome X′, and unlike in the contingent-first sequence, there are no preceding trials that suggest that A′ is a good predictor. Consequently, one will be most likely to develop an initial hypothesis that A′ is a weak predictor of X′. In the following contingent block of this sequence, A′'s association with X′ has to be increased, because B′ alone is a weak predictor of X′, leaving A′ as the only possible predictor for X′. However, because one initially believed A′ to be a weak predictor, the overall assessment of A′'s efficacy will not be as strong as in the contingent-first sequence. In this way, when it is feasible to develop an initial hypothesis, we predict the primacy effect even in the cue competition paradigms.

In Experiment 1, we investigated whether a simplification of the overly complex procedure utilized by López et al. (1998) would result in the same recency finding. We predicted that when the number of contingencies to be simultaneously learned was grossly reduced, the primacy effect would be obtained, due to the ease with which hypothesis about contingency relationships could initially be formed. In a similar vein, Experiment 2 tested whether participants who had a large working memory capacity and, therefore, would have less of a problem tracking relatively complex evidence to form hypotheses would be more likely to show the primacy effect. Both experiments employed López et al.'s paradigm as closely as possible, in an attempt to demonstrate that manipulating task complexity alone is sufficient to obtain a primacy effect.¹

Experiment 1

In Experiment 1, we evaluated the possibility that a simplification of López et al.'s (1998) experimental design would promote a primacy effect. Specifically, in Experiment 1, a condition in which participants tracked only one set of materials (the one-disease condition) was compared with a condition in which they concurrently tracked two sets of materials (the two-disease condition). The latter would correspond to a level of cognitive load intermediate between that for the one-disease condition and that for the task in López et al.'s Experiment 1, which involved four disease sets. If task complexity were the critical determinant for obtaining the primacy effect, the primacy effect would be more likely to be found in the one-disease condition than in the two-disease condition.

Method

Participants

Twenty-seven undergraduates from Yale University participated in partial fulfillment of an introductory psychology course's requirements.

Design

The design of the experiment was a 2 (learning sequence: contingent-first vs. noncontingent-first) × 2 (condition: one-disease vs. two-disease) within-subjects factorial design. To provide an overview, each participant observed learning sequences that consisted of two types of blocks (contingent and noncontingent). The two learning sequences were developed by manipulating the order of the two blocks so that either a contingent block preceded a noncontingent block (referred to as a contingent-first learning sequence) or a noncontingent block preceded a contingent block (a noncontingent-first learning sequence). In the one-disease condition, each of these learning sequences was presented one at a time, whereas in the two-disease condition, information for both the contingent-first and the noncontingent-first learning sequences were intermixed and presented in a single sequence. Each of these manipulations will be explained below.

The contingencies for the contingent and noncontingent blocks were adopted from López et al.'s (1998) Experiment 1 (see Table 1). In the contingent block, the pairing of a target symptom (A) and another symptom (B) would almost always appear with the presence of the corresponding disease (X). However, when Symptom B was shown alone, the disease was almost always absent. In the noncontingent block, Disease X occurred as often with another symptom (C) alone as with the pairing of AC. Within each block, trials were randomized for each participant.

The two learning sequences were developed by manipulating the order of the contingent and noncontingent blocks as in López et al.'s (1998) Experiment 1. In the contingent-first sequence, the contingent block was presented first, and in the noncontingent-first sequence, the noncontingent block was presented first. The contingency information presented in each type of block was identical, regardless of learning sequence (i.e., the same contingency information was presented in the noncontingent block when it appeared in a contingent-first sequence as when it appeared in a noncontingent-first sequence). As a result, the two learning sequences consisted of 40 trials identical in contingencies, differing only in the order in which the blocking of the trials appeared in a sequence.

In addition to the manipulation of learning sequences, the second independent variable in Experiment 1 was how many sets of materials were concurrently presented to the participants (one-disease and two-disease conditions). The one-disease condition consisted of a learning sequence that represented information for only one disease and its three corresponding symptoms. Participants observed one one-disease condition in a contingent-first sequence and another one-disease condition in a noncontingent-first sequence. Each of these sequences was presented separately during different phases of the experiment.

In the two-disease condition, the contingent-first and the noncontingent-first sequences were intermixed and presented during the same learning phase, so that participants observed 80 trials during a single learning phase and had to simultaneously track contingency relations for two diseases. The two sequences were intermixed as follows. The first blocks of the contingent-first and noncontingent-first sequences were randomly intermixed and presented together. Following these trials, the second blocks of both sequences were randomly intermixed and presented for the two diseases.

To summarize, the participants experienced three separate experimental phases: the one-disease contingent-first sequence, the one-disease noncontingent-first sequence, and the two-disease intermixed contingent-first and noncontingent-first sequences. Note that the first two phases consist of 40 trials, whereas the third one consists of 80 trials. In order to equate the total number of trials for all three learning phases, 40 filler trials were added to each of the sequences in the one-disease condition.² These filler trials consisted of a 1,000-msec screen asking the participants to “Please wait…” and were randomly intermixed with actual trials. A momentary blank screen followed every trial, so that the participants saw a demarcation between trials. Therefore, the participants experienced 80 trials in each of the three learning phases.

Procedure

The experiment began with a general screen of instructions introducing the type of information that was going to be presented (e.g., diseases and symptoms). Then the participants received three learning phases (i.e., the one-disease contingent-first sequence, the one-disease noncontingent-first sequence, and the two-disease intermixed contingent-first and noncontingent first sequences) in a counterbalanced order. Each of these learning phases began with a specific screen of instructions denoting the disease(s) and target symptom for the subsequent trials. Each trial presentation screen started with the phrase, “A patient has the following symptoms…,” followed by a list of the symptoms for that trial. At the bottom of the screen, the diagnosis for that patient was indicated by the phrase, “The patient was diagnosed with (blank),” where the blank was either the name of the disease that corresponded to the given symptom set or the phrase “no disease.”³ In order to ensure sufficient viewing of the stimuli, each symptom–disease screen was shown for 1,000 msec before a participant was allowed to press the space bar in order to see the next trial. Within the same learning phase, the trials were presented as a single learning sequence without any explicit marking of blocks.

At the end of each experimental phase, the participants were presented with the question, “What is the degree of relationship between (target symptom) and (disease)?” as used in Experiment 1 in López et al. (1998). They were instructed to use a scale ranging from 0 (no relationship) to 100 (perfect relationship) and to enter their responses on the computer. The participants rated only the relationship between the target cue (indicated in bold in Table 1) and the disease and did not provide estimates for the other symptoms of that disease. In the two-disease condition, the questions regarding target symptoms associated with both diseases were presented at the end of the learning phase, and the order of answering for each of the target symptoms was randomized for each participant. The experiment was administered via SuperLab (Cedrus Corporation, 1999).

Stimulus Materials

Four different disease materials, taken from López et al.'s (1998) Experiment 1, were paired with the experimental conditions in a counterbalanced manner. Thus, the participants saw four different sequences instantiated in four different diseases. The diseases and their corresponding symptoms were fixed to be as follows, with the target symptom marked in italics: Cajal's disease was paired with the symptoms swollen gums, coughing, and painful breathing; Hocitosis was paired with the symptoms fever, excessive perspiration, and nausea;⁴ Ochoa's syndrome was paired with the symptoms headache, tremor, and baldness; and Beralgia was paired with the symptoms rapid heartbeat, sight loss, and itchiness.

Results and Discussion

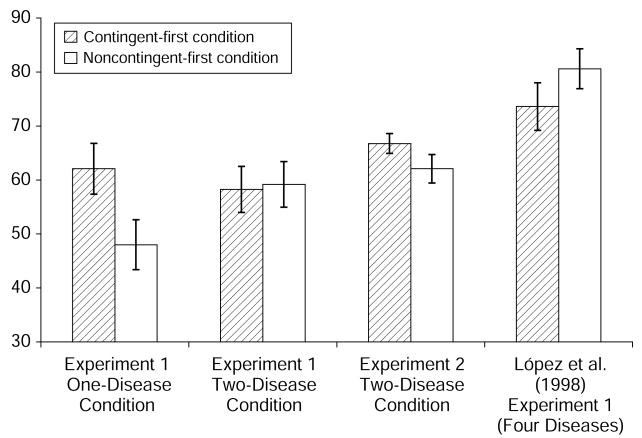
The key difference between our Experiment 1 and López et al.'s (1998) Experiment 1 was the number of cues the participants saw in a single learning sequence. When four stimulus sets were intermixed and presented to the participants in a single learning sequence, López et al. found a recency effect; ratings of the relationship between the target symptom and the disease were higher when a contingent block was last (see the last set of bars in Figure 1). In our Experiment 1, however, when only one symptom set and the corresponding disease were presented at a time, as in the one-disease condition, the opposite effect was found (see the first set of bars in Figure 1). In line with the claim that overall complexity is what modifies order effects, no such primacy effect was found in the two-disease condition (see the second set of bars in Figure 1).

Figure 1. Mean estimates of contingency strength for Experiments 1 and 2 and López, Shanks, Almaraz, and Fernández's (1998) Experiment 1. Error bars represent standard errors.

A 2 (condition: one-disease vs. two-disease) × 2 (sequence: contingent-first vs. noncontingent-first) repeated measures ANOVA was conducted on the participants' estimates on target symptoms. The only significant finding was a significant interaction effect [F(1,26) = 5.72, MS_e= 1,518.75, p < .03]. This interaction represents the fact that in the one-disease condition, ratings for the target symptom were higher in the contingent-first sequence (M = 62.07, SE = 4.72) than in the noncontingent-first sequence (M = 48.00, SE = 4.62) [t(26) = 2.41, p < .03].⁵ However, in the two-disease condition, there was no significant difference between the ratings for the contingent-first sequence (M = 58.26, SE = 4.27) and the noncontingent-first sequence (M = 59.19, SE = 4.22) (p > .80).

Therefore, Experiment 1 showed that a simplification of López et al.'s (1998) experimental design in our one-disease condition reversed their experimental findings to one of primacy. However, when the number of contingency relations to be learned was doubled, no primacy effect was found. This pattern of results supports the claim that the primacy effect failed to occur due to excessive cognitive demands caused by having to track too many relations.

Experiment 2

In Experiment 2, the participants tracked information for two stimulus sets simultaneously, as in the two-disease condition in Experiment 1. In addition, the individual participants' working memory capacities were measured. We have argued that the absence of a primacy effect in the two-disease condition in Experiment 1 was due to increased cognitive demands. That is, given too many different types of evidence, the participants failed to keep track of all the available information necessary to develop a hypothesis early on. If this was the case, it would be reasonable to predict that individuals who are better at dealing with cognitive demands would be better at concurrently monitoring different types of evidence so as to form a coherent hypothesis and, consequently, more likely to show the primacy effect. Thus, differences in working memory capacity could be expected to correlate with the amount of the primacy effect. Furthermore, because the task involved verbally coding hypotheses, rather than spatial reasoning, it could be hypothesized that the participants with a larger verbal working memory capacity (rather than those with a larger spatial working memory capacity) would be able to better track ongoing hypotheses under a moderately demanding task and would, therefore, demonstrate heavier utilization of early information in the contingency learning task.

Method

Participants

Sixty-five undergraduates from Vanderbilt University participated in partial fulfillment of an introductory psychology course requirement. One participant was dropped from the experiment due to marked incompetence in English, making the validity of his verbal working memory score questionable.

Overall Procedures

Each participant completed three working memory tasks, along with a new version of the contingency learning task. The three working memory tasks were taken from Shah and Miyake (1996). Two measures of spatial working memory were used: the spatial span and the simple arrow span tasks. A measure of verbal working memory, the sentence recall task, was also used. The order of the tasks was constant for all the participants, with the spatial span task being administered first, followed by the simple arrow span task, the contingency learning experiment, and finally the sentence recall task.⁶ The spatial working memory tasks and the contingency learning task were administered via SuperLab (Cedrus Corporation, 1999). The sentence recall task was presented on 5 × 7 in. index cards.

Spatial span task

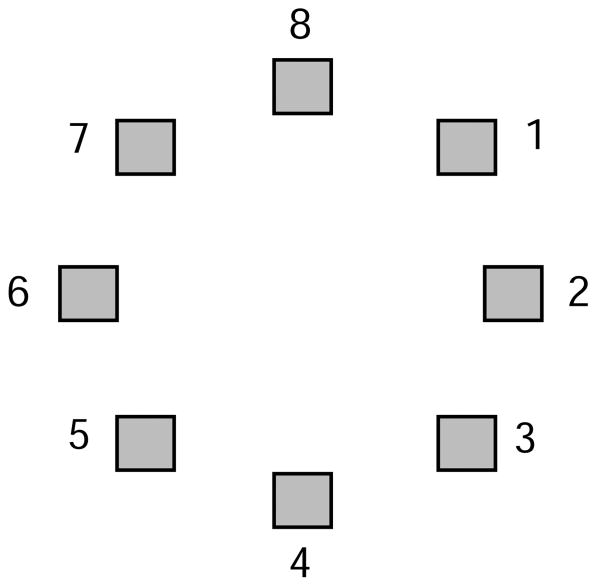
The basic procedure from Shah and Miyake (1996) was used. Generally, the participants observed a series of letters and made judgments as to whether the letters were shown in a normal or backward format during their presentation. After completing judgments on a set of letters, the participants were asked to recall the letters' orientations in the exact order of presentation. In this version of the task, the participants indicated the letters' orientation by using the circular grid shown in Figure 2. The participants entered the number corresponding to the orientation for each letter. The participants observed sets of increasing length over the course of the experiment, beginning at two letters per set presented before recall and ending with five letters per set. The participants saw a total of 20 sets: 5 different sets at each of four difficulty levels.

Figure 2. Response grid used in Experiment 2.

Simple arrow span task

The basic procedure was the same as that for Shah and Miyake's (1996) original task. The participants were asked to remember the orientation of sets of arrows. Five different set lengths were used, beginning at two arrows per set and increasing incrementally to six arrows per set. Three sets of arrows were presented at each set length, for a total of 15 sets. The participants recalled where the arrows' heads were pointing, using the same numbered grid and procedure as that in the previous task.

Sentence recall task

This task was taken from Shah and Miyake's (1996) adaptation of Daneman and Carpenter's (1980) classic reading span test. In the sentence recall task, the participants read aloud sentences varying in length from 13 to 16 words that were individually printed on index cards (e.g., “The assassin reached back to pull the coat free and a pair of handcuffs clattered to the floor,” “When at last his eyes opened, there was no gleam of triumph, no shade of anger,” and “The taxi turned up Michigan Avenue where they had a clear view of the lake”). The participants were instructed to verbally recall in order the last word of all the sentences that they had read in a set whenever they came to a blank card. For instance, in a set consisting of the previous three example sentences, the correct recall sequence would be “floor–anger–lake.”

Set length began at 2 sentences per set and increased to 5 sentences per set. The participants could complete 5 sets at each of four different set lengths, for a total of 20 sets (or 70 sentences). An experimenter sat in the room with a participant and recorded the participant's answers. If a participant did not correctly recall any of the 5 sets at a given length, the task was halted, and the participant was not required to move on to the next level of difficulty. One order of sentences was used for all the participants. All instructions were provided to the participants verbally by the experimenter. Three practice sets of sentences were provided.

Scoring for working memory tasks

The same scoring method as that in Shah and Miyake (1996) was used to score the three working memory tasks described above. In all three tasks, a set was considered correct only if all of the orientations/words for that set were recalled in the correct serial order. For both the spatial span task and the sentence recall task, the participants were given a score corresponding to the set length of the highest level at which they could correctly identify three of five sets. For example, if in the sentence recall task a participant correctly recalled three sets at a set length of four words and none at a set length of five words, the participant would be given a score of 4.0. If two sets at the next highest level were correctly identified, the score was increased by 0.5. (Therefore, in the previous example, if the participant had correctly identified two sets at a set length of five words, a score of 4.5 would have been recorded.) In the case in which a participant correctly identified two sets at more than one level above his or her proficiency level, the highest level at which two sets were accurately reported and the level at which three sets were reported were averaged to obtain a final score. If a participant did not reach proficiency at the lowest level, he or she was given a score of 1.0. Therefore, the range for both the spatial span and the sentence recall tasks was 1.0–5.0.

Since the simple arrow span task included only three sets per difficulty level, the participants were required to correctly identify two sets at a level to receive a score for that level and one set at a higher set length to earn the additional 0.5. The same procedures for averaging scores and for assigning a score of 1.0 were used as those in the other two working memory tasks. The range for this task was 1.0–6.0.

Contingency learning task

As in the previous experiment, the participants observed symptoms occurring either in the presence or in the absence of a corresponding disease and were later asked to make an estimate of the relationship between a target symptom and its disease. Participants completed one condition that was identical to the two-disease condition in Experiment 1, with the following exceptions. No timing delays were imposed on any of the trials, so the experiment was completely self-paced. In addition, the following changes were made to relieve the cognitive demands of the tasks, in an attempt to avoid the possibility that the task was so demanding that no participant could demonstrate a primacy effect. When a symptom or symptom pair was presented with the absence of its corresponding disease, the diagnosis phrase was changed to “The patient was not diagnosed with (blank),” where the blank was replaced with the name of the disease corresponding to the presented symptoms. This marking decreased the burden on the participants to determine which disease was absent, given a symptom. The participants also received a reminder sheet that listed the two diseases and their corresponding three symptoms, denoting the target symptom for each. After having seen all the trials for both diseases, the participants were asked to respond as in Experiment 1 to the degree of relationship between each disease and its target symptom.

Results and Discussion

We first will discuss the overall findings for the ratings of the disease and target symptom relationship, followed by analyses of individual participants' working memory capacity in relation to their displayed order effect. The mean rating on the relationship between the disease and the target symptom in the contingent-first condition (M = 66.75, SE = 1.84) was somewhat higher than that in the noncontingent-first condition (M = 62.09, SE = 2.64) [t(63) = 1.81, p = .075]. That is, a marginally significant primacy effect was obtained (see the third set of bars in Figure 1). This result differs from the results for the two-disease condition in Experiment 1, where virtually the same final estimates were supplied for the two learning sequences. Yet this move toward a primacy effect in Experiment 2 is consistent with our account, in that the cognitive demands in Experiment 2 were somewhat reduced from those in Experiment 1, as described in the Method section, in order to avoid floor effects for primacy findings.

A more critical question in Experiment 2 is whether the individual participant's working memory capacity correlated with the amount of primacy effect. A primacy effect measure was calculated as the participant's rating for the contingent-first disease minus the same participant's rating for the noncontingent-first disease. Each of the primacy effect scores was then correlated with the scores on the three working memory span tasks. There was no significant correlation between the primacy effect scores and the letter span task scores (r = −.11), nor was there a correlation between the primacy effect scores and the arrow span task scores (r = .19, ps > .10). That is, the primacy effect did not correlate with either of the measures of spatial working memory span. However, there was a significant positive correlation between the primacy effect scores and the sentence recall task scores (r = .26, p < .05). That is, the participants with larger verbal working memory capacities showed greater primacy effects in the contingency learning task.

Though significant, the size of the positive correlation between verbal working memory capacity and primacy effect was not large. Although this moderate correlation could have occurred because another cognitive capacity exists that can explain both primacy tendencies and working memory capacity, another highly likely reason could have been a truncated range problem in the verbal working memory data.⁷ As was explained earlier, the scores from the sentence recall task could range from 1 to 5, but our data ranged only from 2 to 4, with 72% of the data ranging from 2.5 to 3.5. To compensate for this, in another analysis, we examined only the participants with the lowest scores (i.e., 2; n = 12) and those with the highest scores (i.e., 4; n = 6) in the sentence recall task. Those who scored highest (M = 24.17, SE = 5.54) showed a much greater primacy effect than did those who scored lowest (M = −3.8, SE = 5.66) [t(16) = 3.12, p < .01].

General Discussion

The experiments described here have outlined conditions in which early observations will be used more than later observations as a source of judgment. When a version of López et al.'s (1998) experiment was simplified so that participants could easily develop hypotheses early on, primacy effects were found. No primacy effect was found as the number of cues increased. In addition, verbal working memory capacity was a good predictor of the amount of primacy effect an individual participant displayed.

Mechanism Underlying the Primacy Effect

Throughout this study, we have maintained the position that the primacy effect is obtained because people form a hypothesis from earlier data and underadjust this hypothesis. Thus, the move away from a primacy effect in López et al. (1998) can be explained in terms of the difficulty of producing hypotheses, due to the cognitive loads imposed by the task. Another potential mechanism can be derived on the basis of the serial position effect in memory research (e.g., Murdock, 1962). That is, people remember initial and recent trials better than middle items, and their memory for initial trials might be dampened when the total number of trials becomes too long, when there are too many different type of trials of which to keep track, or when a learner's working memory capacity is limited (e.g., Ward, 2002).

There are several limitations with this postulation. First, López et al. (1998; Experiment 2) tested participants' memory for cue–outcome pairings (i.e., which disease was paired with a given cue?) after all 160 trials had been observed. The participants provided fairly accurate answers even to the cues that were presented only during the first block. On the basis of these results, they concluded that their recency effect did not appear to be due to poor memory for initial trials. Second, in our Experiment 1, the number of trials for the one-disease and the two-disease conditions was equated, but a primacy effect was obtained only in the one-disease condition. Third, one might argue that the participants' memory for initial trials might still have been dampened in the two-disease condition because of some kind of retroactive interference; they experienced more information containing trials, which could have retroactively decreased memory for initial trials, resulting in a weakened primacy effect. However, this mechanism alone cannot explain why a primacy effect was obtained in the one-disease condition in Experiment 1. According to this argument, the participants' memory for both initial and recent trials should have been fairly accurate in the one-disease condition, and there is no reason why initial trials would have outdone recent trials. An additional process, such as a bias toward weighting initial trials more than later trials, is needed to account for the observed primacy effects. One plausible reason that a learner might weight initial trials more than recent trials would be that he or she is developing a hypothesis about a given relation; this is essentially the same as our original proposal.

Needless to say, more research is needed to determine the underlying processing mechanisms for the primacy effect. If an initial hypothesis is indeed used to reinterpret later contingency information, the details of this process need to be further delineated, such as when the hypothesis that serves as an anchor is first developed and what form it takes (e.g., would the hypothesis simply contain the direction of relations, or would it include strength information as well?).

Other Potential Determinants of Primacy and Recency Effects

Previous studies have suggested other factors that might moderate the direction of order effects. In this section, we will discuss some of these factors in light of the present findings.

Causal versus contingency learning

Another apparent difference between López et al. (1998) and Dennis and Ahn (2001) is that in the former, the participants were presented with an effect (e.g., symptoms) and had to learn its cause (e.g., a disease), whereas in the latter, the participants were presented with a cause and then with an effect. López et al. also asked their participants to judge relationship strength, whereas Dennis and Ahn explicitly asked their participants to estimate causal strengths. Given that associative models (e.g., Rescorla & Wagner, 1972) predict a recency effect (for more details, see Dennis & Ahn, 2001; López et al., 1998), it is tempting to conjecture that the differences in the types of learning involved (causal vs. contingency learning) might be a critical factor in obtaining a recency effect. However, the experiments that we have reported utilized procedures almost identical to those in López et al. and still showed the primacy effect. Thus, the distinction between causal and contingency learning does not appear to be a critical determinant for obtaining a recency effect.

Frequency of estimation

Another potential determinant for the recency effect is how frequently a learner is asked to explicitly estimate the strength of a relationship during learning (e.g., Collins & Shanks, 2002). It has been argued that a learner changes his or her anchor every time an explicit estimate of relationship strength is provided. Therefore, frequently providing an estimate causes the anchor to move toward recent trials, making a recency effect more likely (Hogarth & Einhorn, 1992). Indeed, Collins and Shanks claim to have found a recency effect, using Dennis and Ahn's (2001) procedure with the critical modification of increased estimation frequency.

However, Collins and Shanks's (2002) procedure may have inadvertently caused excessive pressure toward a recency effect. When an estimate is asked for only at the end of a sequence, as in Dennis and Ahn (2001), participants are implicitly cued to use all of the information they have seen thus far to make an estimate. However, when a judgment is asked for every 10 trials, as was the case in Collins and Shanks, participants can interpret this as a cue that the current, most recent information is the most important information to be used. Indeed, Collins and Shanks failed to take precautionary measures to prevent this type of misinterpretation.⁸ To the contrary, Dennis (2004) found that when participants were explicitly told to consider all trials, a primacy effect was obtained even when the participants had to make an estimate on every trial. More research is needed to further investigate this issue.

Prediction versus strength estimates

The present experiments measured the strengths of relations. However, Matute, Vegas, and De Marez (2002) have found that prediction tasks (“To what degree do you expect the outcome to occur in this particular trial?”) track temporally local events and are, therefore, more likely to display recency effects. Likewise, Collins and Shanks's (2002) Experiment 4 demonstrated that when the final judgment is to predict an outcome of a given trial, rather than to give an overall estimation of causal strengths, a robust recency effect is obtained. The recency effect in prediction tasks might stem from participants' assumption that the order of trials reflects the order of events (see below for more discussion on this), and thus, it would be rational to make predictions on the basis of the most recent trials. Future research can further examine whether the same type of recency effect will be obtained even when participants are explicitly told that the trial order does not reflect the event order.

It is also noteworthy that relationship judgments tend to reflect a recency effect when participants are asked to also make predictions during the learning phase about every trial's possible outcome before receiving feedback about the outcome (Collins & Shanks, 2002; López et al., 1998). One possible reason for this, in line with our present claim, is that having to make a prediction and incorporate subsequent feedback on every single trial could serve as another layer of cognitive demand. For example, in López et al., the participants first were presented with a list of the symptoms for a given patient and were asked to make a guess as to what disease was present in that patient. After making this guess, the participants were presented with a separate screen that provided feedback as to their response by providing the correct diagnosis for that patient. Therefore, the participants in López et al.'s study had to retain cue information for a given patient over multiple trial screens, had to determine whether and/or why their prediction in that trial was inaccurate, and then, finally, had to synthesize cue and outcome information. Also, as will be discussed more below, the prediction task in itself might have encouraged the participants to give more weight to recent events. The effect of requesting predictions during learning should be systematically studied in future research.

Information versus event order

One critical factor to be considered in studying the effect of order in contingency learning or causal induction is to be clear about what order it is that the experiment is manipulating. In all of the experiments on this issue, the implicit assumption has been that the manipulation of order pertained to the manipulation of information order (the order in which the participants received which type of information), rather than to event order (the temporal order in which the events actually took place in the world). Therefore, the trial that was presented last in a learning sequence, for example, did not necessarily correspond to the last event that occurred.

The recency effect might be more likely to be obtained when people interpret the manipulated order as the order in which the events took place. In particular, if information order is believed to be the actual order of events in the world that spans across a long period of time, it may be more rational to give extra weight to recent events. For instance, it would be more accurate to predict tomorrow's weather on the basis of this week's weather than to predict it on the basis of the weather of 6 months ago. Similarly, in judging the causal efficacy of a fertilizer on flower blooming, one might want to give more weight to recent data, rather than to data from 20 years ago. How the interpretation of the order manipulation influences order effects deserves future research.

Conclusion

The primacy effect was found to be moderated by the cognitive load required by the hypothesis-testing nature of the task and by the size of the verbal working memory capacity available to process information. The results of the described experiments point to the recency effect as being a by-product of overwhelming demands on the hypothesis-testing procedure. The possibility remains open that recency would be a dominating strategy in situations in which the temporal order of information is directly informative to the task at hand—for example, predictive judgments. Further research is needed to address whether the primacy effect can be overridden by more explicit domain theories of what evidence should be more heavily weighted.