Compartmental Neural Simulations with Spatial Adaptivity

Abstract

Since their inception, computational models have become increasingly complex and useful counterparts to laboratory experiments within the field of neuroscience. Today several software programs exist to solve the underlying mathematical system of equations, but such programs typically solve these equations in all parts of a cell (or network of cells) simultaneously, regardless of whether or not all of the cell is active. This approach can be inefficient if only part of the cell is active and many simulations must be performed. We have previously developed a numerical method that provides a framework for spatial adaptivity by making the computations local to individual branches rather than entire cells (Rempe and Chopp, 2006). Once the computation is reduced to the level of branches instead of cells, spatial adaptivity is straightforward: the active regions of the cell are detected and computational effort is focused there, while saving computations in other regions of the cell that are at or near rest. Here we apply the adaptive method to four realistic neuronal simulation scenarios and demonstrate its improved efficiency over non-adaptive methods. We find that the computational cost of the method scales with the amount of activity present in the simulation, rather than the physical size of the system being simulated. For certain problems spatial adaptivity reduces the computation time by up to 80%.

Introduction

Because of the success of Hodgkin and Huxley’s model of action potential propagation in the squid giant axon (Hodgkin and Huxley, 1952), and Rall’s formalization of cable theory (Rall, 1977), mathematical approaches to understanding neuron function have seen growing acceptance and popularity within the neuroscience community. Today, neural simulation environments such as NEURON (Hines and Carnevale, 2001) and GENESIS (Bower and Beeman, 1998) are commonly used by researchers to combine mathematical modeling with traditional experimental approaches.

These simulation environments can numerically solve the underlying system of equations with implicit numerical methods (Hines and Carnevale, 1997), which are advantageous because of their unconditional stability, even for large time steps. A trade-off of this unconditional numerical stability, however, is that the computations on all branches connected together in a cell are coupled; to update one branch in the cell, each branch must be updated, regardless of whether or not it is active. This is sometimes inefficient as some simulations exhibit large regions of the cell that are inactive, with only small portions active. This extra computational cost grows with the number of simulations performed; for example when a large number of simulations is performed when fitting the output of a model to experimental data. An alternative approach is to use a method that de-couples the update of individual branches from one another. Two different implementations of this idea have been developed previously (Mascagni, 1991; Rempe and Chopp, 2006) in order to parallelize neural simulations at the level of the individual cell and to introduce spatial adaptivity into neural simulations. Once the computation is reduced to the level of branches instead of cells, spatial adaptivity can be carried out by dynamically monitoring where activity is present and updating only those branches that are active, while saving computations in regions that are not active. Using this approach, we demonstrated the stability and convergence properties of our numerical method (Rempe and Chopp, 2006).

In this paper we apply this spatially adaptive numerical method to four scenarios in neuroscience. Some of these examples involve reproducing results from previous studies and others are new test problems. The objective of this study is to demonstrate the applicability and effectiveness of the spatially adaptive numerical method.

Materials and Methods

Background on the adaptive algorithm

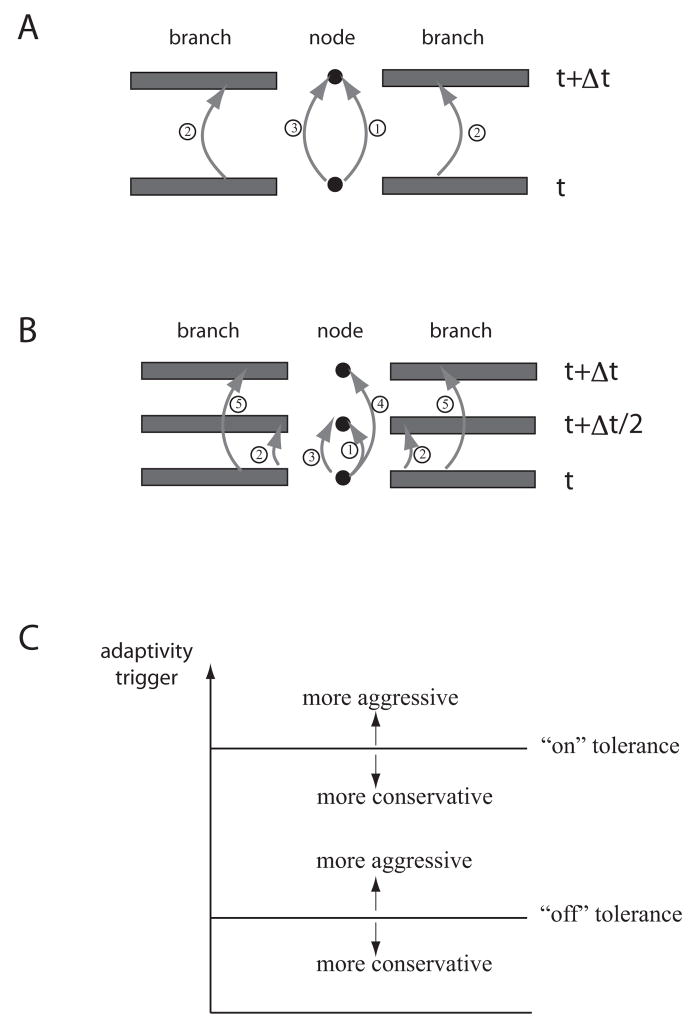
For each scenario the cable equations with Hodgkin-Huxley style ion channels were simulated on reconstructed cell morphologies of hippocampal neurons. The reconstructed morphologies can be found on the Spruston-Kath lab morphology database (www.northwestern.edu/dendrite/sk_models). Physical parameters such as channel densities used here were similar to those used in the original studies, and parameter values are given in each section. The numerical method used to update the equations is similar in spirit to that used in NEURON or GENESIS, but with an important added feature: the computations on individual branches are local in nature, meaning that select branches can be updated without doing so on every branch each time step of the simulation. To implement this local-updating scheme, we employed a predictor-corrector numerical approach to update the locations where branches connect to one another. The update schemes for the predictor-corrector method are given in Figure 1A and B for the methods corresponding to backward Euler and Crank-Nicolson, respectively. Each predictor-corrector method begins with an explicit step for the value at the nodes, those locations where branches connect to one another. This prediction is used in the boundary condition of the connecting branches. Finally, the nodes’ values are corrected with a step meant to mimic an implicit backward Euler or Crank-Nicolson step. This approach provides a natural framework for spatial adaptivity: only the branches that are active are updated at each time step.

Figure 1.

Overview of the numerical method. Each version of the method is illustrated on a simple configuration of two branches connected by a node. Both update schemes are designed to mimic an ordinary update using either backward Euler or Crank-Nicolson for the branches and nodes. A, Schematic of the backward Euler version of the predictor-corrector numerical method, indicating the three steps of the method: an explicit update for the nodes, an implicit update for the branches, and a corrector step for the nodes. Note that here “node” refers to any location where two or more branches connect. B, Schematic of the Crank-Nicolson version of the predictor-corrector numerical method. The first three steps are identical to the backward Euler predictor-corrector update except they are taken for only half of a time step. The additional two steps (steps 4 and 5) are explicit updates for the nodes and branches, consistent with performing Crank-Nicolson as a two-step update. This approach is meant to mimic the standard Crank-Nicolson update in a branch. See our previous work for details of the algorithm (Rempe and Chopp, 2006). Both update schemes were designed to de-couple the branches from one another. C A plot of the adaptivity trigger and sample values for the “on” and “off” tolerances. If the “on” tolerance is made larger, branches don’t turn on as quickly, making the adaptivity more aggressive. Smaller values of the “on” tolerance mean branches begin computing when a small trigger value is measured. This is referred to as conservative. For the “off” tolerance, making this value larger means branches will more easily be turned off, this is called more aggressive. If the “off” tolerance is made smaller a branch is not turned off until the trigger value is extremely small, this is considered more conservative. Modified from Rempe and Chopp, 2006.

To monitor the activity in each branch, and therefore whether or not that branch should be updated, the algorithm computes the value of a trigger that indicates activity within each branch. The trigger is computed as follows:

$$\text{trigger}=max\left(\mid \frac{\partial V^{\ast }}{\partial t}\mid ,\mid \frac{\partial m_i}{\partial t}\mid \right),$$

where

$$V^{\ast }=\frac{V-E_{\text{hyp}}}{E_{\text{dep}}-E_{\text{hyp}}},$$

m_i are the gating variables present in the model, E_dep is the most depolarized reversal potential of the ions present in the model, and E_hyp is the most hyperpolarized reversal potential of the ions present in the model. Since the membrane voltage, V, must remain between E_dep and E_hyp, the scaled voltage, V^* is between 0 and 1, just like the gating variables, and is dimensionless. This trigger responds to changes in the gating variables before they result in changes in the membrane voltage. Additional details of the numerical method, along with some examples, are provided in our intial description of the method (Rempe and Chopp, 2006). However, the trigger used here is an improvement to those described previously. For all of the following simulations a time step of 0.01 ms and a spatial grid size of Δx=12 μm were used. This choice of spatial grid is finer than is necessary for most simulations, but the performance of the spatially adaptive algorithm is not dependent on the choice of the spatial grid size. This is because turning off a branch makes the same relative reduction in the number of gridpoints used in the simulation, regardless of the grid spacing, as long as the spacing is approximately constant throughout the dendritic tree. Simulations performed with a larger grid spacing of 0.1 times the space constant at 100 Hz showed identical relative savings (data not shown) as the spatial adaptivity in the simulations shown in Figures 1 and 7, although the computing time was smaller for both the adpative and non-adaptive cases.

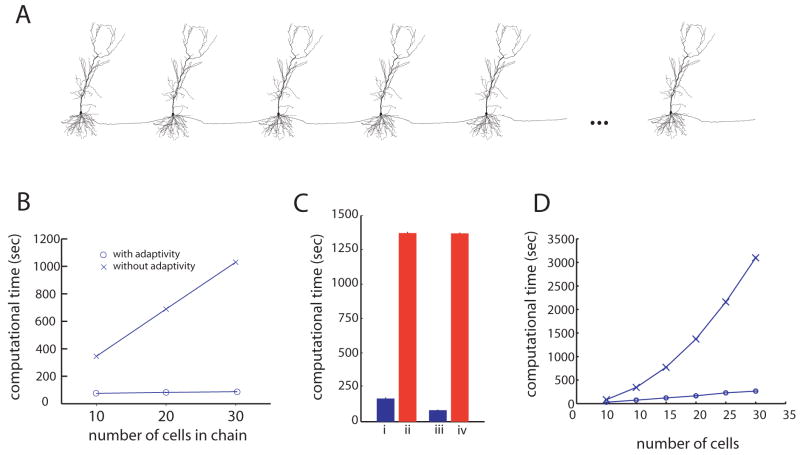
Figure 7.

The adaptive algorithm is highly efficient for simulating chains of cells connected by synapses. A, The chains are constructed by copying the morphology of one cell as many times as needed. B, Computing times for the algorithm with and without adaptivity (O and X respectively), on simulations of 10, 20 and 30 cells. In each simulation a synaptic-like input was injected into the first cell causing it to fire and initiate an action potential that travels down the length of the chain. Each simulation was run until 50 ms, just enough time for ten cells to fire. C, Computing times for the algorithm with and without adaptivity (blue and red bars, respectively), for simulations of a chain of 20 cells connected by strong synapses (4 nS). In each simulation, a synaptic-like input was injected into the first cell causing it to fire and initiate an action potential that travels down the length of the chain. In (i) and (ii) the synaptic connections were all the same strength, resulting in reliable propagation of activity down the length of the chain. In (iii) and (iv) the 10^th synapse was made weaker, (1 nS), resulting in propagation failure at the 10^th cell in the chain. Each simulation was run until 100 ms, just enough time for all 20 cells to fire if the propagation is reliable. If propagation is not reliable, the adaptive algorithm is faster, while the performance of the non-adaptive method is unchanged. D, Computing times for simulating chains of various lengths with and without adaptivity (O and X respectively). In each case the simulation was run just long enough for activity to propagate down the entire length of the chain. Each simulation used an “on” trigger of 0.015 and an “off” trigger of 0.007.

It is necessary here to define a few terms that will be used frequently hereafter. The tolerance used to determine if a branch is active, and therefore should be updated, will be called the “on” tolerance. Conversely, the tolerance used to determine if a branch is inactive and should be neglected instead of being updated will be called the “off” tolerance. For each simulation, the values chosen for the “on” and “off” tolerances are discussed. A large value for the “on” or “off” tolerance is considered “aggressive,” leading to a greater number of branches being made inactive. Small values for the tolerances are “conservative,” leading to fewer branches being made inactive. These terms are illustrated in Figure 1C. Also, to turn off a branch, two criteria must be met. The trigger must be below the “off” tolerance and the membrane potential must be within a separate tolerance, V_tol, of its resting value. This additional criteria ensures that the algorithm does not try to turn off a branch that has a constant voltage during some portion of a simulation, but is not close to the resting voltage. Unless otherwise indicated, V_tol was set to 5 mV. Note: to determine the resting potential, one simulation may need to be executed without adaptivity. The parameter V_tol is intended to be large enough that the exact resting membrane potential need not be found, yet small enough to only turn a branch off when it is truly at rest and not held at a depolarized potential for an extended period of time. For the bar graphs of computing time, each bar represents an average of 10 trials (see what follows for additional explanation), and the scale bars are standard deviations.

Synapse properties

For the simulations involving the gating of synaptic input, each synaptic conductance was modeled as the difference of two exponentials with τ_rise=0.2 ms and τ_fall=2 ms and a reversal potential of 0 mV. Each synapse had a conductance of 3 nS. For the simulations of chains of cells, the synapses had the same kinetics, but an amplitude of 4 nS, enough to elicit a spike in the soma of the next cell.

Gap junction modeling

To model a non-rectifying dendritic gap junction, we have added additional currents to the two locations that are connected by the gap junction. These currents are modeled as follows:

$$I_{\text{gap}}^1=G_{\text{gap}}(V_1-V_2)\text{and}{I}_{\text{gap}}^2=G_{\text{gap}}(V_2-V_1)$$

Here V₁ and V₂ are the voltages at the coupling site of cells 1 and 2, respectively, and G_gap is the conductance of the gap junction. Computationally, a gap junction is made up of two nodes, one for each cell connected by the gap junction. These nodes are updated in the same manner as ordinary nodes, with the addition of the two currents in this equation. As a result, the update of a gap junction is just as accurate as the update of a standard branch point. Algorithmic details for a gap junction can be found elsewhere (Rempe and Chopp, 2006).

Results

Demonstration of the algorithm

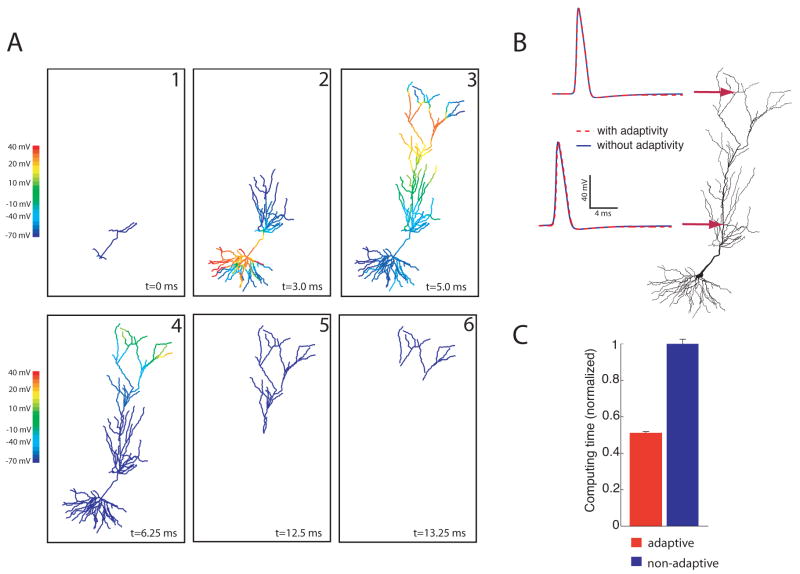
To illustrate the adaptive algorithm for a simple scenario, we simulated a subicular pyramidal cell (www.northwestern.edu/dendrite/sk_models). For the purpose of this simulation, Hodgkin-Huxley Na⁺ and K⁺ channels were placed throughout the dendritic tree. The cell was stimulated with a somatic current injection of 1 nA for 0.5 ms causing an action potential to be elicited and propagate into the dendrites. Figure 2A shows snapshots of the solution at different times; only those branches that are active are plotted. Despite the fact that many branches are turned off for much of the simulation, the resulting action potential is almost identical to that simulated in the non-adaptive simulation (Figure 2B).

Figure 2.

Spatial Adaptivity. A, Snapshots of response to a somatic current injection of 1 nA for 0.5 ms. Only the branches that are computing are plotted. B, Shown on the left is the computed voltage vs. time at the location marked with the arrow. Since the two traces overlay, the adaptive method is able to accurately resolve the voltage without introducing any additional errors. C, For this example the spatially adaptive method results in a 50% decrease in computing time

To quantify the savings brought about by the spatial adaptivity, we performed several simulations on this cell and calculated the computing time with and without adaptivity. When calculating the time it takes to run any computer program, this value will change slightly between executions of the program due to the activity of other computer processes running in the background. This variability in the computing time has nothing to do with the actual simulation being performed, and is not large, as indicated in the error bars. For this reason, average computing times are shown. The results, shown in Figure 2C, indicate a 50% decrease in computing time for this example.

Action-Potential Backpropagation in CA1 Pyramidal Neuron Dendrites

For the next example of the adaptive numerical algorithm, we reproduce some of the key results from a previous study of the strength with which action potentials invade the distal dendrites of CA1 pyramidal neurons (Golding et al. 2001). Typically in these cells, action potentials are initiated in the axon and backpropagate from their initiation point in the axon into the soma and then into the dendritic arbor (Stuart et al. 1997). The degree to which the action potential invades the dendritic arbor depends on a number of different biophysical properties of the cell, including dendrite diameter and the specific branching pattern (Goldstein and Rall 1974; Vetter et al. 2000) as well as the local densities of sodium and potassium channels (Llinas and Sugimori 1980; Stuart and Hausser 1994; Bischofberger and Jonas 1997; Chen et al. 1997; Martina et al. 2000; Hausser et al. 1995).

To investigate the extent of action potential backpropagation in CA1 pyramidal neurons, Golding et al. used a combination of paired somatic and dendritic whole-cell recordings, calcium-imaging techniques, quantitative anatomical analysis and compartmental modeling. One of the main results of the study is that pyramidal neurons in the CA1 region can largely be classified into two categories: those with weakly or strongly backpropagating action potentials (about 80% and 35% attenuation, respectively). These results were reproduced with compartmental modeling studies showing that even a small change in ion channel densities can determine whether an action potential backpropagates strongly or weakly in a particular cell. Specifically, the authors showed that introducing a slight spatial gradient in the Na⁺ or A-type K⁺ conductance can convert weak backpropagation to strong backpropagation (Golding et al. 2001).

We reproduced this modeling result using the adaptive algorithm with a similar CA1 pyramidal cell morphology, the same channel models (Na⁺, delayed-rectifier K⁺, and an A-type K⁺ conductances), and a similar stimulus (Figure 3). With these parameter values and the same constant value of Na⁺ channel density for the weak backpropagating case, we were able to obtain the same qualitative result, namely that an action potential started in the soma would not reach the distal dendrites. By changing the channel densities to include a slight gradient in the Na⁺ channel density, the action potential successfully invades the distal apical dendrites (Golding et al. 2001). The model employed here was somewhat less sophisticated than the one used previously (Golding et al. 2001), because we did not include an axon with nodes of Ranvier or a correction for dendritic spines. Our intention was to create a simple model that reproduced the previously reported effect.

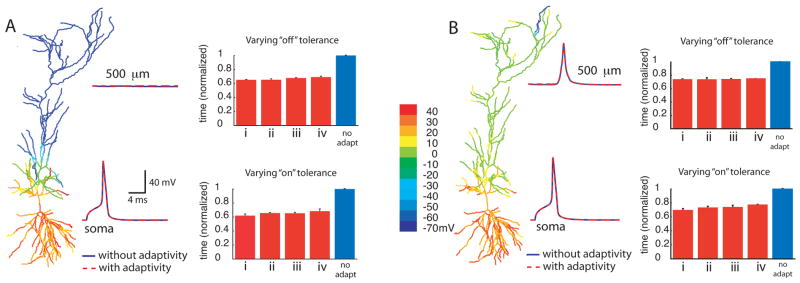
Figure 3.

Dichotomy of action potential backpropagation with adaptivity. In the case of weak backpropagation, A, an action potential initiated in the soma fails to invade the distal dendrites, but in the strongly backpropagating case, B, an action potential in the soma creates a dendritic spike, even in the distal dendrites. Peak voltage is shown color-coded in the morphological reconstruction. The voltage traces at the two locations in both cases were made without adaptivity (solid traces) and with adaptivity (dashed traces). The upper bar graph for each case shows normalized computing times for simulations done with fixed “on” tolerance, and various “off” tolerances. The “on” tolerance was fixed at 0.010 and V_tol was set to 5 mV. The“off” tolerances used were: (i) 0.007, (ii) 0.005, (iii) 0.003, and (iv) 0.001. The lower bar graphs for each case show computing times for simulations done with fixed “off” tolerance, and various “on” tolerances. The “off” tolerance was fixed at 0.005, and Vtol was set to 5 mV. The “on” tolerances used were: (i) 0.014, (ii) 0.012, (iii) 0.010 and (iv) 0.008. In both panels, the traces were made using an “on” tolerance of 0.008, an “off” tolerance of 0.005, and V_tol = 5 mV. The peak depolarization is indicated with color. In all bar graphs, each bar represents averages of 10 trials of simulations run until 10 ms. Scale bars are standard deviation.

To determine appropriate values for the “on” and “off” tolerances, we used the case with strong backpropagation and verified that the adaptive simulations gave the same results as the simulation without adaptivity. The same values used in the strong backpropagation case were then used in the weak backpropagation case. For the “on” tolerance, a value larger than 0.014 resulted in a 1 ms delay in the peak of the action potential, so 0.014 was chosen as an upper limit. With the “on” tolerance set to 0.008, there was perfect overlay in the traces, indicating that it was not necessary to use smaller “on” tolerance values. For the “off” tolerance, no improvement was seen either in accuracy for values smaller than 0.001, or in performance for values larger than 0.007. Therefore these values were used as the upper and lower bounds of the “on” and “off” tolerances for the simulations in this section.

Comparison of the voltage traces made at two different locations in the cell for the weak backpropagation case (Figure 3A) revealed that the simulations performed with spatial adaptivity were as accurate as those performed without adaptivity. The computing times for various levels of “off” and “on” tolerances are also compared to the non-adaptive case (Figure 3A), demonstrating that the adaptive algorithm resulted in computational savings of roughly 40% compared to the non-adaptive case.

For the strong backpropagation case (Figure 3B), spatial adaptivity results in a computational savings of about 30%. As expected, the method is less advantageous for the strong backpropagation case than for the weak backpropagation case, because activity spreads throughout the entire dendritic tree, so the algorithm cannot turn off as many branches as in the weak backpropagation case. Nevertheless, even though most branches are active at some point, the spatially adaptive algorithm is more efficient than computing every branch at each time step. Furthermore, in both the weak and strong backpropagation cases, the voltage responses computed with adaptivity correspond exactly to those made without adaptivity, provided that tolerances are set correctly.

A general characteristic of adaptive numerical methods is that there is a trade-off between error and efficiency: the larger the allowed error, the greater the improvement in efficiency. If the adaptive method is performed with very conservative tolerances the accuracy will be high, but the improvement in performance will usually be low. On the other hand, aggressive tolerances give significant improvements in speed, usually at the cost of reduced accuracy. Taken to an extreme, very aggressive tolerances used in any adaptive numerical method will yield incorrect results.

To illustrate this trade-off between accuracy and speed we calculated the errors introduced by spatial adaptivity and investigated their relationship with the “on” trigger value. We used the simulation that shows strong backpropagation of the action potential, (Figure 3B) and we categorized the errors into two different types. The first type is an error that causes the peak of the action potential to occur at a slightly later time than it would have without adaptivity. This will be referred to as a “phase” error and will be measured in milliseconds. The second kind of error is the difference in the shape of the traces made with and without adaptivity. To compute this error the trace made with adaptivity is shifted so that its peak voltage matches that of the trace made without adaptivity. Once the trace has been shifted the error is computed using the following formula:

$$\text{error}=\frac{\Vert {\mathbf{x}}_{\text{adapt}}-\mathbf{x}\Vert }{\parallel \mathbf{x}\parallel }$$

Where x_adapt is the solution computed with adaptivity, x is the solution computed without adaptivity. The symbol || || refers to a 2-norm and is calculated as follows:

$$\parallel \mathbf{x}\parallel ={\left(\sum _i\mid x_i{\mid }^2\right)}^{1/2}$$

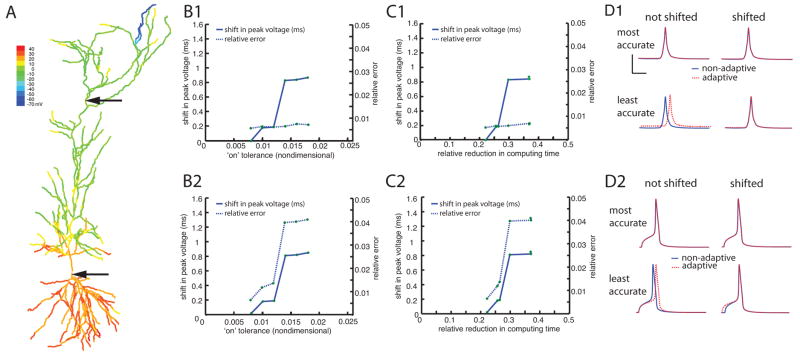
This second kind of error reflects artifacts introduced into the shape of the traces and will be referred to as “relative” error. Both kinds of errors increase as the “on” tolerance is made larger, both in the soma and in the primary apical dendrite (Figure 4 panels B1 and B2). For “on” tolerance values larger than those shown the action potential was not resolved in the primary apical dendrite. Note that for each value of the “on” tolerance the shift in peak voltage is less than 1ms and the shifted relative error is less than 5%.

Figure 4.

Trade-off between accuracy and performance when using the adaptive method on backpropagating action potential simulations. A, Color map of peak depolarization for the case with a strongly backpropagating action potential. B, The shift in peak voltage (solid line, left ordinate) and the relative error (dashed line, right ordinate) are plotted as functions of the “on” trigger for the location marked with the upper arrow (B1) and for the soma (B2). C, The shift in peak voltage (solid line, left ordinate) and the relative error (dashed line, right ordinate) are plotted as functions of the relative reduction in computing time for the location marked with the upper arrow (C1) and for the soma (C2). D, Voltage traces made with and without adaptivity (dashed traces and solid traces, respectively) for the location marked with the upper arrow (D1) and for the soma (D2). Shown are the most conservative tolerance (0.008, top row) and most aggressive tolerance (0.018, bottom row). The scale bars represent 4 ms and 4 mV. In each case the traces are shown shifted so the maximum voltage lines up (right-hand column) and without shifting (left-hand column). In each case the relative error was computed using the formula given in the text after artificially aligning the traces so its peak voltage lined up with the non-adaptive trace. For each simulation the “off” tolerance was 0.005 and V_tol was 1 mV.

Plotting the error vs. the relative reduction in computing time indicates that as the efficiency of the adaptivity goes up, so do the errors introduced (Figure 4 panels C1 and C2). For example, choosing the “on” tolerance such that the computing time is reduced by 25% would result in a 0.2 ms shift in the peak voltage at the soma and a 1% error in the shape of the voltage trace there. However, a more aggressive tolerance yielded a 35% reduction in computing time, but would introduce a 0.8 ms shift in the peak voltage at the soma and a 4% relative error. This illustrates the idea that the increased efficiency comes at a price of reduced accuracy.

Visual inspection of voltage traces for both locations indicates that the shift in peak voltage due to the adaptivity does not make a qualitative difference in the behavior for these values of the “on” tolerance (Figure 4 panels D1 and D2).

Gating of Dendritic Spikes in CA1 Hippocampal Pyramidal Neurons

As another test of the adaptive algorithm, we used it to reproduce a computational result from a recent study (Jarsky et al. 2005). In the previous study, synaptic input was simulated for both sources of excitatory synaptic input to CA1 pyramidal cells (Amaral 1993): the perforant-path, from layer III of entorhinal cortex, which innervate the apical dendritic tuft, and Schaffer-collaterals, which innervate more proximal apical dendrites as well as basal CA1 dendrites. Synapses from the perforant path were found to be ineffective in causing CA1 pyramidal cells to fire on their own, largely because these synapses are very far from the soma, and a depolarization in the apical tuft attenuates severely before reaching the soma. However, combining perforant-path input with a modest, appropriately timed Schaffer-collateral (SC) input in the region below the tuft can cause the dendritic spike to propagate forward, so that the soma fires an action potential when it would not have from either one of the inputs individually. In this way, the Schaffer-collateral synaptic input can act like a “gate” for the perforant path-evoked dendritic spike (Jarsky et al. 2005).

In the models used in that study, thousands of synapses were placed at random locations along branches in the upper apical tuft to represent perforant-path input and in slightly more proximal apical dendrites to represent Schaffer-collateral input. For each trial, a percentage of the perforant-path synapses and Schaffer-collateral synapses were chosen at random and activated. Tens of thousands of simulations were performed to investigate the effect of the relative timing of the two inputs and the percentage of each pool of inputs that were activated.

To reproduce this “gating” effect with our predictor-corrector algorithm, instead of using thousands of synapses and placing them randomly within a region, we chose to use a simplified version of the model, in which we placed one synapse at the end of each of the 33 branches in the apical tuft to represent perforant-path input, and one on the ends of each branch in 11 of the apical branches below the tuft to represent Schaffer-collateral input.

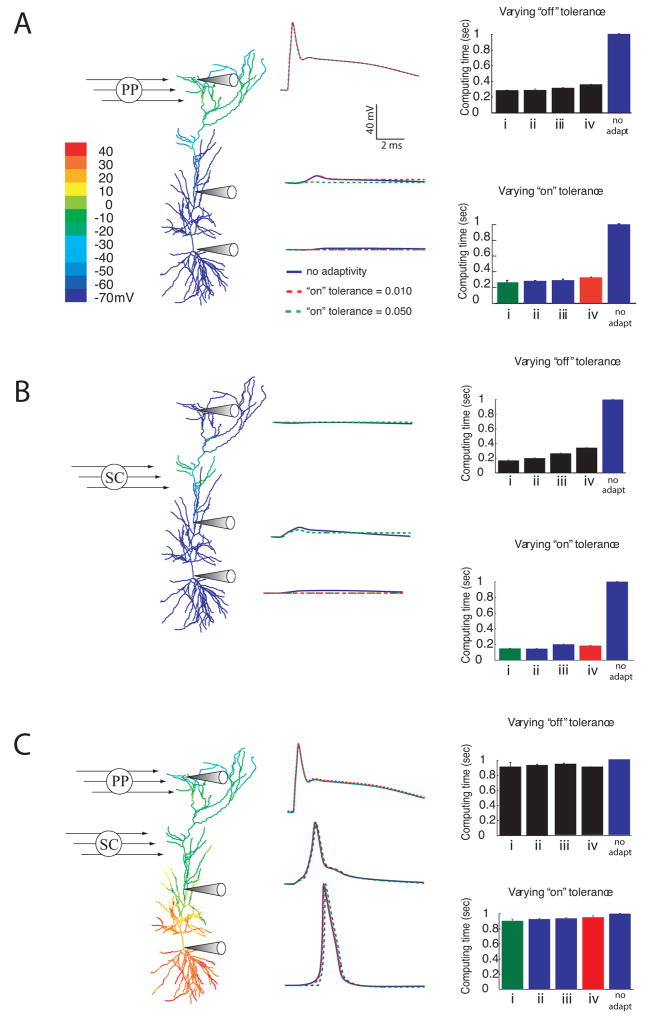
With this simplified approach, the gating behavior of the Schaffer-collateral input is clearly captured with and without spatial adaptivity, since the case with perforant-path input alone (Figure 5A) fails to elicit an action potential in the soma, as does the case with only modest Schaffer-collateral input (Figure 5B), but the case with both inputs causes an action potential to fire in the soma (Figure 5C).

Figure 5.

Spatial adaptivity brings about substantial savings when simulating the gating of dendritic spikes. A, Color map of peak depolarization and voltage versus time plots at three dendritic locations for activation of PP synapses only. B, Response to activation of Schaffer-collateral synapses. C, Response to activation of both inputs coincidentally. For each case, traces are shown without adaptivity (solid lines) and with two different levels of “on” tolerance: 0.010 (red dashed trace) and 0.050 (green dashed trace). Both adaptive traces used an “off” tolerance of 0.005, and a V_tol of 5 mV. The scale bars in panel A are appropriate for panels B and C as well. On the right hand side of each panel the relative computing times are plotted for various levels of “off” tolerance, (upper bar graph in each panel) and “on” tolerance (lower bar graph in each panel). In each case the upper bar graph used a constant “on” tolerance of 0.025 and the following “off” tolerances: i) 0.007, ii) 0.005, iii) 0.003, iv) 0.001. The lower bar graph for each case used a constant “off” tolerance of 0.005 and “on” tolerance values of i) 0.050, ii) 0.040, iii) 0.025, and iv) 0.010. The colored bars in the lower bar graphs for each scenario correspond to each panel’s colored voltage traces. The voltage scale bar in A is appropriate for all 3 cases.

In these simulations, since the activity is initiated by simulated synapses that decay slowly, the branches with synaptic input did not completely relax back to the resting voltage during the course of the simulation (10 ms, consistent with the simulations done in Jarsky et al. 2005). Therefore, the algorithm is not able to turn off many of the branches that had active synapses attached to them. As a result, the savings brought about by the adaptive algorithm for this problem came about primarily by leaving branches “off” that never depolarize, as in the case of perforant-path stimulation alone or the case of Schaffer-collateral stimulation alone.

For the adaptive algorithm to be useful for this problem the tolerances need to be set to capture the action potential in the soma if one occurs there. Optimally, the user should not have to re-adjust the tolerances depending on whether the synaptic inputs are enough to cause a spike in the soma or not. For these reasons, tolerances were chosen that sufficiently captured the case where both Schaffer-collateral inputs and perforant-path inputs were coincidentally activated, causing a spike in the soma. These tolerances, though not optimal for the cases where only one of the inputs was simulated, were able to capture the correct behavior for any of the three cases (perforant-path input alone, Schaffer-collateral input alone, or both).

To determine appropriate ranges for the “on” and “off” tolerances, the same procedure was used as in the last section. For “on” tolerances larger than 0.05 the action potential was not captured in the soma. With an “on” tolerance of 0.01 the traces perfectly overlaid the nonadaptive traces, so it was not necessary to make the tolerance any more conservative. These simulations used the same range of “off” tolerances as the simulations in the previous section.

First, we simulated the response to perforant-path input alone using the adaptive algorithm (Figure 5A). As expected, since many of the branches remain inactive throughout the simulation, including all the basal dendrites and many of the apical dendrites, the computational savings are substantial (about 70%). In this case, the performance gain shows little dependence on the exact choice of “on” and “off” tolerances, given that these values are in the appropriate range for this problem.

Next, we simulated the case with Schaffer-collateral activation alone and measured the efficiency of the adaptive algorithm. Similar to the case with only perforant-path activation, the spatial adaptivity is very effective, resulting in savings of up to 80% (Figure 5B). In contrast to the case with only perforant-path input, the computational time does show some dependence on the value of the “off” tolerance, with more aggressive values showing more computational savings because branches are turned off sooner.

Finally, we simulated the case where both inputs are active and combine to cause an action potential in the soma (Figure 5C). As expected for this case, since nearly all the branches in the cell are active throughout most of the simulation, the savings brought about by the adaptive algorithm are modest. Nevertheless, because a systematic parametric evaluation of these different cases would include instances where the extent or timing of Schaffer collateral activation did not produce successful gating, spatial adaptivity could provide some savings for this case as well.

As in the previous case we calculated the two types of errors introduced by the adaptivity: a shift in the peak voltage and an altering of the shape of the voltage trace. Again, both types of errors increase steadily as the “on” tolerance increases, both in the soma and in the main apical dendrite (Figure 6 panels B1 and B2). For “on” tolerance values larger than those shown the soma did not fire an action potential. Note that tolerance values larger than those shown are very aggressive and are not recommended as the first choice for any simulation.

Figure 6.

The adaptive algorithm exhibits a trade-off between accuracy and performance when used to simulate the gating of dendritic spikes. A, Color map of peak depolarization for the case with both inputs. B, The shift in peak voltage (solid line, left ordinate) and the relative error (dashed line, right ordinate) are plotted as functions of the “on” trigger for the location marked with the upper electrode (B1) and for the soma (B2). C, The shift in peak voltage (solid line, left ordinate) and the relative error (dashed line, right ordinate) are plotted as functions of the relative reduction in computing time for the location marked with the upper electrode (C1) and for the soma (C2). ). D, Voltage traces made with and without adaptivity (dashed traces and solid traces, respectively) for the location marked with the upper arrow (D1) and for the soma (D2). Shown are the most conservative tolerance (0.008, top row) and most aggressive tolerance (0.018, bottom row). In each case the traces are shown shifted so the maximum voltage lines up (right-hand column) and without shifting (left-hand column). The scale bars represent 4 ms and 4 mV. In each case the relative error was computed using the formula in the text after artificially aligning the trace computed with adaptivity so its peak voltage lined up with the non-adaptive trace. For each simulation the “off” tolerance was 0.005 and V_tol was 1 mV.

Plotting the errors vs. the relative reduction in computational cost indicates that the errors introduced by the adaptivity increase as the efficiency goes up (Figure 6 panels C1 and C2). Note that for this particular simulation the performance improvement is never very large since all of the branches need to be activated. For the most aggressive error tolerance that still captured the action potential in the soma the peak voltage is shifted by 0.25 mV and the error due to the change in shape is only about 2%. The improved efficiency of using the largest “on” tolerance came at a price of a much larger error while gaining little in terms of efficiency.

The shift in peak voltage due to the adaptivity does not make a qualitative difference in the behavior for these values of the “on” tolerance (Figure 6 panels D1 and D2).

For the cases with only one input, the soma did not turn on at all for many values of the “on” tolerance, resulting in a plots of error vs. tolerance that are flat (data not shown). If this algorithm were in a neural simulation program, an upper bound could be placed on the tolerance levels since choosing tolerance too aggressively can result in qualitatively wrong solutions,

To choose the tolerance values for the simulations shown in this study, we started each simulation with very conservative values for all tolerances and then gradually made them more aggressive until the adaptivity proved useful. To find an upper bound, we continued to make the tolerances more aggressive until the output began to deviate from the result without spatial adaptivity. This gave a range of suitable tolerance values. It is important to realize that in each scenario parameters were found for the adaptivity that are suitable regardless of the outcome of the simulation. It is not necessary to know beforehand whether the simulation will result in strong or weak backpropagation, for instance, or if the synaptic input would be strong enough to elicit a spike in the soma in the gating simulations.

Chains of Cells Connected by Synapses

As a third example to illustrate the effectiveness of the spatially adaptive method, we simulated long chains of full-morphology cell models connected together by simulated synapses. While this is a somewhat simplistic network, similar networks of morphologically-detailed cells have been modeled in other contexts (Lundqvist et al. 2006). The NEURON simulation environment has been extended to deal with large networks of morphologically-detailed cells (Migliori et al. 2006), and the Blue Brain Project was conceived in order to simulate very large networks of morphologically-detailed cells in the neocortex (Markram 2006).

For the simulations here, the ion channel densities were the same as those used in the strong backpropagation model of Golding et al. (2001), with a few minor simplifications. Instead of using a smooth linear gradient for the A-type K conductance in the apical dendrites, here we use a constant value for each region of dendrites: basal dendrites, apical dendrites, and distal dendrites (~500 μm from the soma) in the apical tuft. This was done to make it easier to set conductance values in all copies of the cell and is not a restriction of the algorithm itself. The constant values chosen for each section are the averages of the values used previously (Golding et al. 2001). In addition, the model used here did not have nodes of Ranvier in the axon and did not correct for dendritic spines. To create a chain of cells, we added an axon to the cell and then copied the morphology in such a way that each axon connected to the soma of the next cell in the chain. In this manner we were able to build long chains of full-morphology CA1 pyramidal cells (Figure 7A). When an action potential reached the end of the axon, creating a positive membrane potential, a synaptic conductance was triggered in the soma of the post-synaptic cell. The model for this synaptic input is described in the Methods and Materials section with an amplitude of 4 nS. This simulated synapse was sufficient to cause the post-synaptic cell to fire an action potential.

In reality, CA1 pyramidal cells do not connect to each other in this manner; however, the purpose of this model is to show the usefulness of the adaptive method for networks or chains of cells. The chain shown here is a simple one, but the technique presented could naturally be extended to more elaborate networks of cells with propagating activity.

The first simulations were chains of 10, 20, and 30 cells connected together as described above. Each simulation was run for 50 ms, long enough for 10 cells to fire (Figure 7B). Without adaptivity, the computing time grows linearly with the number of cells being simulated, even though the simulations of 20 and 30 cells have many cells that do not activate within the first 50 ms of the simulation. This is consistent with the characteristics of the method we described previously (Rempe and Chopp 2006), namely that the number of calculations performed is of the same order as the number of compartments in the model. In mathematical terms, the method is said to be “order N”, i.e., O(N), meaning that the computational cost is proportional to N, the number of compartments in the model. Performing the same simulations with adaptivity, however, results in only a slight increase in computing time as the chain of cells is lengthened. This is because the adaptive method does not simulate any of the inactive cells in the chain in front of the action potential, and stops updating a cell once it has fired and recovered. For the same reason, there is also a significant reduction in computing time when using the adaptive method on the chain of 10 cells. The adaptive method is significantly faster because at any given point in the simulation it is updating only active branches, which in this case is roughly the number of branches in one cell since the cells fire action potentials one after another. The nonadaptive method, however, updates all branches in each cell, even those ahead and behind the active cell. This illustrates the fact that the computational cost of the adaptive method scales with activity. Even though the three chains have different physical sizes, they all have the same amount of activity, and therefore take the same amount of time to simulate.

As another test we ran both the adaptive and non-adaptive algorithms on a chain of 20 cells, allowing the simulation to run long enough for an action potential to propagate all the way down the length of the chain (100 ms). Then we ran the same simulation again, except this time the tenth cell in the chain had a weaker synapse (1 nA instead of 4 nA), thus stopping propagation along the chain (Figure 7C). Using the adaptive method on this experiment resulted in a more efficient simulation when the action potential didn’t propagate than when it did, whereas without adaptivity, the cases with and without successful propagation required the same amount of time to simulate. This further demonstrates the key fact that the computational cost of the adaptive method is determined by the amount of activity present in a simulation, rather than its physical size.

We also simulated chains of various lengths just long enough for activity to propagate down the length of the chain (Figure 7D). For chains of 5, 10, 15, 20, 25, and 30 cells, the simulations were run for 25, 50, 75, 100, 125, and 150 ms, respectively. Without adaptivity, the computing time grows quadratically [O(N²)] since each time the number of cells is increased, so does the duration of the simulation. With adaptivity, however, these simulations scale linearly since the same amount of activity is simulated in each case; the only variable changing is the duration of the simulation, resulting in a linear increase in computing time for larger (and longer) simulations.

Cells Connected by Gap Junctions Including Closed Loops

Many neurons in the nervous system are interconnected via direct electrical connections instead of chemical synapses (Sohl et al. 2005). These electrical connections, called gap junctions, significantly affect network dynamics (Hormuzdi et al. 2004), and modeling studies with networks of cells connected by gap junctions have shown diverse network behavior including bursting, antiphase spiking, and phase-locked states (Connors and Long, 2004). The particular network behavior predicted by these models depends on both the choice of intrinsic properties for the cells and the location and strength of the gap junction connections (Saraga and Skinner 2004; Saraga et al. 2006).

The models used to simulate networks of cells connected by gap junctions range from simple integrate-and-fire models (Skinner et al. 1999; Kopell and Ermentrout 2004; Manor et al. 1997), to full compartmental models (Traub and Bibbig 2000; Traub et al. 2001; Traub et al. 2005). A recent study used full-morphology neural models to examine how active properties in dendrites contribute to the dynamics that arise from gap-junction coupling (Saraga et al. 2006). This study could not have been done with single compartment neural models.

An important consideration in performing these detailed gap junction modeling studies using programs like GENESIS or NEURON is whether or not the gap junction-connected cells form a closed loop. The reason this is an issue is due to the way that the branches of the cell are organized within many neural simulators. If the network of cells contains a closed loop formed by gap junctions and an implicit integration method is used, the linear system solved in these simulation programs is no longer of a special structure that allows it to be solved in O(N) operations, but instead its solution may require O(N³) operations (Hines 1984). It may be possible to modify these algorithms so that they handle closed loops without a substantial computational penalty, but we know of no published study that has done so. One alternative is to use an explicit update scheme, but these methods require a smaller time step to remain accurate (Bower and Beeeman 1998). This restriction on closed loops in networks of gap junction-connected cells is a limitation of existing modeling software as closed loops have been shown experimentally to exist in networks of interneurons in the visual cortex (Fukuda et al. 2006) and are proposed to exist in the hippocampus (Zsiros et al. 2007).

Here we use a few simple examples to illustrate the fact that closed loops of gap-junction-connected cells don’t present any difficulties for the predictor-corrector numerical method we have developed (Rempe and Chopp 2006). We also show that the addition of closed loops does not change the efficiency of the numerical method.

We first show simulations of a pair of cells connected with one or two gap junction connections, where the case with two gap junctions forms a closed loop. Also, we simulate ten cells connected with gap junctions forming many closed loops (Figure 8). In all cases, the model shape used is that of a hippocampal interneuron with morphology similar to a basket cell, whose morphology can be found on the Spruston-Kath lab morphology database. This morphology is copied as many times as needed. The channel properties used in each of the model cells are identical to those used in Saraga et al. (2006), namely Hodgkin-Huxley-like Na⁺ and K⁺ channels and a leak current. The soma was given active properties and the dendrites were passive. With this choice of channels a single neuron spontaneously fires action potentials at a rate of approximately 15 Hz.

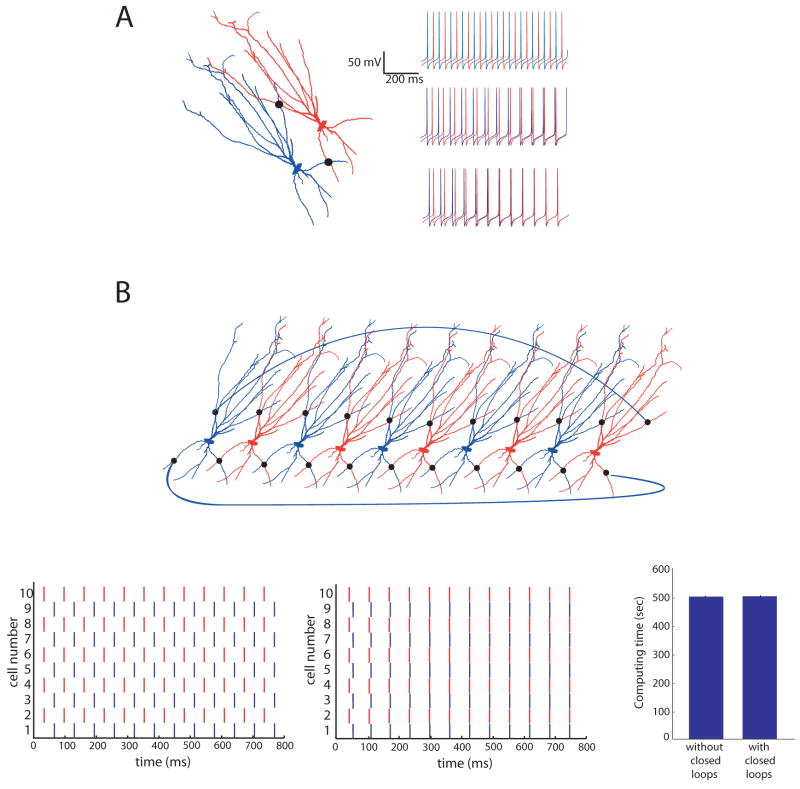
Figure 8.

The predictor-corrector numerical method easily allows for networks of cells connected by gap junctions, including closed loops. A, Two basket cells were simulated using the same morphology and channels. Shown in the insets are traces of each cell, with colors corresponding to the cells shown above. With no gap junctions, (top trace), since one cell is started at a slightly hyperpolarized potential, the two cells fire out of phase with one another. If the two cells are connected by one gap junction of 200 pS located approximately 200 μm from each cell’s soma (indicated with a black dot), the connection acts to synchronize the firing of the two cells (middle trace). If an additional gap junction is inserted in the basal dendrites, approximately 150 μm from each soma, the two cells synchronize sooner (lower trace). The scalebars apply to all three traces. B, A network of ten cells interconnected by gap junctions. The black dots indicate gap junctions. To further illustrate the closed loops, two additional gap junctions connect the last cell in the chain to the first cell. Odd-numbered cells in the chain were started at a hyperpolarized potential. Shown at the bottom left is a raster plot of ten cells’ firing pattern without any gap junction connections. The middle is a raster plot with the gap junctions present. The high degree of interconnectivity results in fast synchronization of the network. The bottom right shows computing times for the 10-cell network shown in the top panel with and without gap junctions, indicating that the presence of closed loops does not affect the computation time. Each simulation was run for 400 ms. In each case the average computing time was calculated from 5 trials.

For these simulations, alternating cells were started at a slightly hyperpolarized potential (−75 mV as compared to −65 mV), resulting in even and odd-numbered cells firing exactly out of phase with one another when they are unconnected. Without this change, each cell would have an identical firing pattern, even when they are unconnected. This alteration allowed us to see more clearly the effect of the gap junctions.

We first simulated two basket cells connected by 0, 1, or 2 gap junctions (Figure 8A). If the two cells are not connected with any gap junctions they fire out of phase (top trace). When the two cells are connected with one distal gap junction (~200 μm from each cell’s soma measured along the branches) of 15 nS, the firing patterns synchronize after about 400 ms (middle trace). When an additional gap junction of the same strength is placed in the basal dendrites (~150 μm from each soma), the two cells synchronize much more quickly (lower trace).

To simulate a small network of neurons with multiple closed loops, we made 10 copies of the cell and connected them so that each pair of cells formed a closed loop. In addition, two more gap junction connections were constructed linking the first and last cells in the chain (Figure 8B). Half of the cells were started at a hyperpolarized potential, setting them out of phase with the other half of the cells in the chain. When connected by relatively weak gap junctions (200 pS), all ten cells synchronized very quickly (Figure 8B, middle plot).

Finally, we compared computational times for the 10-cell network with and without gap junction connections. We found that the computational time is independent of whether or not closed loops exist in the simulation (Figure 8B), confirming the notion that the number of computations performed by the method does not change from O(N) to O(N³) when closed loops are included. This simulation demonstrates that our numerical method allows for the exploration of complex gap junctionally connected networks without a computational penalty.

In each of these simulations with gap junctions, the model results in spontaneous firing without a stimulus, so the spatial adaptivity algorithm proved to be ineffective, regardless of the choice of trigger. If the simulation was started with only a few branches “on”, the remaining branches never activated, regardless of the value of the “on” tolerance. If the simulation was started with all of the branches “on”, none of the branches ever inactivated. Trying to use the spatially adaptive method on this problem illustrates an important characteristic of the algorithm: spatial adaptivity is not well-suited to problems that involve tonic firing or other kinds of incessant activity. If none of the branches in a cell are ever at rest, the algorithm will not be able to turn off any branches, and therefore will not bring about any savings as compared to nonadaptive methods. Therefore, spatial adaptivity was not used for these simulations. However, some studies have shown interesting network activity on rings of connected one-compartment neuron models. For instance, on a ring of integrate-and-fire neurons with nearest-neighbor connections plus a few random, non-local connections, activity can either persist or be extinguished (Roxin et al. 2004). In the case where activity dies out completely, the adaptive method could prove very useful, since the algorithm would stop updating cells that are no longer active. Nevertheless, the predictor-corrector algorithm is still very useful for these simulations, even without adaptivity, because it can handle closed loops formed by gap junctions without any additional computational burden, while other simulation methods cannot.

Discussion

The results presented here improve upon our spatially adaptive predictor-corrector numerical algorithm as well as establish its usefulness for realistic simulations. In contrast to the previous study, here we present a more realistic model for the gap junctions, a more robust trigger for the adaptivity, and more realistic examples.

One of the most important characteristics of the spatially adaptive algorithm is that its computational cost scales with activity in a simulation, not with the physical size of the problem. In simulations of single cells, if all or nearly all of the branches are active throughout the simulation, spatial adaptivity is not very beneficial. However, in simulations with less activity and a portion of the branches either remaining near their resting voltage throughout the simulation or returning to rest before the simulation is complete, the spatially adaptive method offers significant computational savings. This was true for the simulations of weakly backpropagating action potentials, the simulations with Schaffer-collateral or perforant-path input alone, and simulations of chains of cells connected by synapses. The predictor-corrector algorithm also handles closed loops of gap junction connections easily and efficiently.

This algorithm could be very useful when many simulations are needed to tune various parameters in a model. When exploring a parameter space, varying even just a few parameters over a relatively small range can add up to many simulations. A computational algorithm with even modest performance improvements would result in significant reductions in overall computing time. To begin a parameter study the algorithm could be used with fairly aggressive tolerances in an effort to reduce the size of the parameter space while giving a feel for the behavior of the solution in different parameter regimes. The trade-off in accuracy may be acceptable it if the intent is to see general behavior and not precise quantitative results. This initial exercise could be followed up with a more precise algorithm on the simulations of interest.

As a rule of thumb, when performing a simulation for the first time, especially one designed to explore the parameter dependence of a phenomena, it is best to first use the method without spatial adaptivity. With the non-adaptive method demonstrating the phenomenon of interest, the adaptive method may then be utilized and tolerance values can be chosen by comparing simulation results with and without adaptivity. Care must be taken in choosing the tolerances. As with any adaptive numerical method, if a tolerance is chosen to be too aggressive, the results can be incorrect. Once it has been determined that the tolerances are appropriate, a series of simulations can be performed with the tolerances fixed.

As an alternative approach, instead of detecting activity by monitoring the time derivative of the state variables, the algorithm could be paired with a standard error-control method such as CVODE. Presumably with this approach it may not be necessary to first perform the simulation without spatial adaptivity. The main benefit of the numerical method proposed is the computational savings brought about by spatial adaptivity, regardless of the choice of method to dynamically determine which branches are active.

For most of the simulations shown in this study, the absolute voltage requirement was not invoked. That is, when the trigger value became small enough to turn off a branch, its voltage was within V_tol of its resting value, so the absolute voltage criteria was satisfied and the branch was turned off. However, in two scenarios (simulations with perforant-path or Schaffer-collateral input alone) this was not the case. After depolarizing because of the synaptic input, branches in the mid-apical region of the cell decay back to their resting values very slowly, as indicated by the center traces in the top two panels of Figure 4. As a result, the trigger indicated that these branches should be turned off, but they did not satisfy the absolute voltage requirement, so they were left on. As a result, the absolute voltage tolerance, V_tol, keeps the algorithm from turning off branches that are not at rest, but are simply changing very slowly.

In each case, it was easy to choose which branches to start in the “on” state at the beginning of the simulation. The simulations in Figures 2 and 3 were started with the soma and a few branches connected to it in the “on” state since the soma is where current was injected. For the simulations in Figure 4 all branches without a synapse attached were started in the “off” state, while those with synapses attached were started in the “on” state. In the simulations of chains of cells in Figure 6, each simulation was started with only a few branches near the soma of the first cell in the “on” state.

Often in neural simulations one does not know beforehand how many of the cells being simulated will be active during the course of the simulation. For instance, when simulating activity in networks of integrate-and-fire neuron models, many different kinds of network states may arise, including self-sustained persistent activity or a brief transient followed by failure (Roxin et al. 2004). Also, it is common in neural modeling to perform many simulations of a cell or a network of cells, while adjusting certain physical parameters at the beginning of each simulation. Altering these physical parameters may result in a change of the network behavior, like faulty propagation of a signal. This adaptive method would be very beneficial for those scenarios as it would detect the faulty propagation and not update cells that are not changing. Simulation of the chain of synaptically connected neurons (Figure 5) clearly illustrates that our method scales with activity, not the physical size of the problem, whereas the conventional method scales with the number of cells (branches) being simulated, regardless of activity.

It should be noted that to obtain the original results for the simulations of the gating of dendritic spikes (Jarsky et al. 2005), the authors used the NEURON simulation environment and ran over 170,000 simulations on a 64-processor Beowulf cluster. While individual simulations were not time-consuming, running all 170,000 of them resulted in several days of computing time. Thus, an adaptive algorithm could result in an overall savings that could be measured in days. Even greater savings would be possible for large-scale network simulations.

The adaptive method presented here is not intended to improve the performance of every neural simulation, but rather should be thought of as a tool, one that can be very helpful for some tasks but not for others. In cases where every branch of every cell is active for the duration of the simulation, the algorithm will probably not be very useful. In fact, in this case it could actually be slightly less efficient than a non-adaptive method due to the overhead involved with adaptivity. This could be true for simulations involving cells that are constantly bombarded with synaptic input, causing tonic firing in the soma and constant activity in all of the dendrites. The fact that a spatially adaptive method could actually be slower than a non-adaptive one is analogous to the idea that adaptive time-step numerical methods are slightly less efficient than fixed step methods if the time step must remain small throughout the simulation. However, as shown in this study, there are a number of cases where the activity in a simulation is spatially localized and the method is beneficial because of the computational efficiency. For other simulations where gap junctions form closed loops, the method is attractive because of the way it easily handles such loops. It is our hope that numerical methods like this one will open up new possibilities in terms of large scale neural simulations that are now difficult because of the high computational cost.