Working memory dynamics and spontaneous activity in a flip-flop oscillations network model with a Milnor attractor

Abstract

Many cognitive tasks require the ability to maintain and manipulate simultaneously several chunks of information. Numerous neurobiological observations have reported that this ability, known as the working memory, is associated with both a slow oscillation (leading to the up and down states) and the presence of the theta rhythm. Furthermore, during resting state, the spontaneous activity of the cortex exhibits exquisite spatiotemporal patterns sharing similar features with the ones observed during specific memory tasks. Here to enlighten neural implication of working memory under these complicated dynamics, we propose a phenomenological network model with biologically plausible neural dynamics and recurrent connections. Each unit embeds an internal oscillation at the theta rhythm which can be triggered during up-state of the membrane potential. As a result, the resting state of a single unit is no longer a classical fixed point attractor but rather the Milnor attractor, and multiple oscillations appear in the dynamics of a coupled system. In conclusion, the interplay between the up and down states and theta rhythm endows high potential in working memory operation associated with complexity in spontaneous activities.

Introduction

During the past 60 years, despite seminal observations suggesting the existence and the importance of complex dynamics in the brain (Nicolis and Tsuda 1985; Skarda and Freeman 1987; Babloyantz and Destexhe 1986), fixed point dynamics has been the predominant regime used to describe brain information processing and more precisely to code associative memories (Amari 1977; Hopfield 1982; Grossberg 1992). More recently, the increasing power of computers and the development of new statistical mathematics demonstrated less equivocally the necessity to rely on more complex dynamics (e.g. Varela et al. 2001; Kenet et al. 2003; Buzsaki and Draguhn 2004). In that view, by extending classical Hopfield networks to encode cyclic attractors, the authors demonstrated that cyclic and chaotic dynamics could encompass several limitations of fixed point dynamics (Molter et al. 2007a, b).

During working memory tasks, tasks requiring the ability to maintain and manipulate simultaneously several chunks of information for central execution (Baddeley 1986), human scalp EEG (Mizuhara and Yamaguchi 2007; Onton et al. 2005) and neural firing in monkeys (Tsujimoto et al. 2003; Rainer et al. 2004) suggested that the theta rhythm (4–8 Hz) plays an important role. The neural basis of the working memory has been widely investigated in primates by using delay to matching tasks. In these tasks, the primate has to retain specific information during a short period of time to guide a forthcoming response. Single cell recordings has shown that during this delay period, some cells located in specific brain areas had increased firing rates (Fuster and Alexander 1971; Rainer et al. 1998).

How these cells can maintain sustained activity is not solved. However, while the coding of information in long-term memory is mediated by synaptic plasticity (e.g. Whitlock et al. 2006), it seems that working memory and more generally short-term memory relies on different mechanisms, potential candidates being that the information is maintained in the network’s dynamics itself (Goldman-Rakic 1995). Recent related observations reported the existence of slow oscillations in the cortex associated with ‘flip-flop’ transitions between bistable up- and down-states of the membrane potential; Up-states, or depolarized states, being associated with high firing rates of the cells during seconds or more. The transition between up and down states as well as the maintenance of high activity during up states could be the result of network interactions, and the neural basis for working memory (McCormick 2005).

Different models of working memory have been proposed. According to the classification proposed by Durstewitz et al. (2000), one type of model is based on a cellular mechanism of bistability (e.g. Lisman and Idiart 1995). Another type follows to the tradition of classical rate coding scheme proposed by (Amari 1977; Hopfield 1982; Grossberg 1992). In these models (e.g. Brunel et al. 2004; Mongillo et al. 2005), the associative memories are coded by cell assemblies in a recurrent network where the synaptic weights are usually pre-encoded according to a Hebbian rule (Hebb 1949). As a result, the recovery of a memory, i.e. of a cell assembly, leads to persistent activity of that cell assembly through recurrent excitation. This could be described as an up-state, while the attractor to the resting state would be the down-state. Flip-flop transitions between up- and down-states are regulated by applying transient inputs.

Remarkably, these models neglect the presence, and accordingly the possible contribution, of the theta rhythm observed during working memory tasks. However, many physics studies have demonstrated the powerful impact of rhythms and oscillations on synchronization which in turn could play an important role during working memory tasks. Here, to conciliate the cell assembly theory with the presence of brain rhythms, we hypothesize that during up-states the firing rate is temporally modulated by an intrinsic cellular theta rhythm. Synchronization among cellular rhythms leads to dynamical cell assembly formation in agreement with observation of EEG rhythms. Grounding on two previous reports (Colliaux et al. 2007; Molter et al. 2008), we propose here the “flip-flop oscillation network” characterized by two different temporal and spatial scale. First, at the unit scale, a theta oscillation is implemented, second, at the network scale, cell assemblies are implemented in the recurrent connections. We demonstrate how the intrinsic cellular oscillation implemented at the unit level can enrich, at the network level, the dynamics of the flip-flop associative memory.

In the following section, we first formulate the flip-flop oscillation network model. Then, we show that the dynamics for a single cell network has an interesting attractor in term of the Milnor attractor (Milnor 1985). Following that, network dynamics in two coupled system is further analyzed. Finally, associative memory networks are elucidated by focusing on possible temporal coding of working memory.

Model

To realize up- and down-states where up-states are associated with oscillations, two phenomenological models are combined. First, in tradition of Hopfield networks and the theory of associative memories, each cell i is characterized by its membrane potential S_i, and is modulated by the activity of other cells through recurrent connections (Hopfield 1982). Second, to account for the presence of an intrinsic oscillation, each cell is characterized by a phase ϕ_i. The phase follows a simple phase equation defining two stable states: a resting state and a periodic motion (Yamaguchi 2003; Kaneko 2002; Molter et al. 2007c). These two variables are coupled such that, first, an oscillation component cos ϕ_i produces intrinsic oscillation of the membrane potential, second, the evolution of the phase depends on the level of depolarization. As a result, the cell’s dynamics results from the non linear coupling between two simpler dynamics having different time constant. Thus, in a network of N units, the state of each cell is defined by 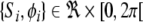(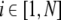) and evolves according to the dynamics:

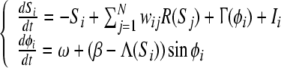1

with w_ij, the synaptic weight between cells i and j, R(S_j), the spike density of the cell j, and I_i represents the driving stimulus which enables to selectively activate a cell. In the second equation, ω and β are respectively the frequency and the stabilization coefficient of the internal oscillation.

The spike density is defined by a sigmoid function:

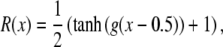2

The couplings between the two equations, Γ and Λ appear as follows:

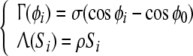3

where ρ and σ modulates the coupling between the internal oscillation and the membrane potential, and ϕ₀ is the equilibrium phase obtained when all cells are silent (S_i = 0); i.e. .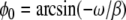

The following set of parameters was used: ω = 1, β = 1.2 and g = 10. Accordingly, 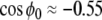. ρ, σ and w_ij are adjusted in each simulations. A C++ Runge–Kutta Gill integration algorithm is used with a time step set to h = 0.01 in first simulations and to h = 0.1 in Section “Working memory of cell assemblies” simulations (to fasten the computation time). The variation of h leaded to no visible dynamical change. If we consider that ω = 1 represents the 8 Hz theta oscillation, one computational time step represents 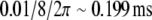in first simulations and ∼1.99 ms in last section.

One unit

For one unit, the dynamics in Eq. 1 simplifies to:

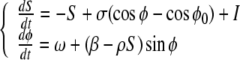4

Next paragraph analyzes the dynamics in absence of any external input (I = 0). Then, to understand how information is processed by a neural unit, we observe the dynamics in response to different patterns of stimulation.

Fixed point attractors

When I = 0, since ω < β, the dynamics defined by Eq. 1 has two fixed points, M₀ = (0, ϕ₀) and M₁ = (S1, ϕ₁). The linear stability of M₀ is analyzed by developing the Jacobian of the coupled Eq. 4 at M₀:

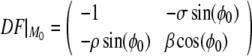5

The eigenvalues are given by:

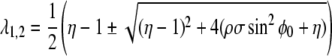6

where 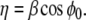The linear stability of the fixed point M₀ is a function of the internal coupling between S and ϕ, μ = ρσ. With our choice of ω = 1 and β = 1.2, one eigenvalue becomes positive and M₀ becomes unstable for 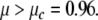Since μ is the crucial parameter for the stability of the resting state, we fixed here ρ = 1 and we analyzed the dynamics according to σ.

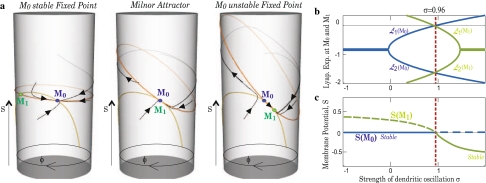
Figure 1a shows trajectories and nullclines in the three possible scenario (μ < μ_c, μ = μ_c and μ > μ_c). The two fixed points M₀ and M₁ (defined by the intersection of the two nullclines) merge for μ = μ_c. To have a better understanding of the dynamics, Fig. 1b shows the evolution of the Lyapunov exponents at M₀ and M₁ when σ1 is varied. Figure 1c shows how the two fixed points exchange their stability at criticality. This corresponds to a transcritical bifurcation. Around the bifurcation our two equations (Eq. 1) can be reduced to the normal form of the bifurcation:

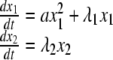7

Fig. 1.

Fixed points analyses for one cell. a Cylinder space (S,ϕ) with nullclines (orange for dS/dt = 0, yellow for dϕ/dt) and some trajectories. Left to right shows the three possible scenario: M₀ is stable fixed-point for μ < μ_c, M₀ is the Milnor attractor for μ = μ_c and M₀ is unstable fixed-point for μ > μ_c. b Evolution of the two Lyapunov exponents of the system at M₀ (in blue) and M₁ (in green) in function of σ (ρ = 1). As expected, one exponent becomes null at σ = μ_c. c Evolution of the two fixed points, M₀ and M₁, when σ is varied. μ = μ_c corresponds to a transcritic bifurcation

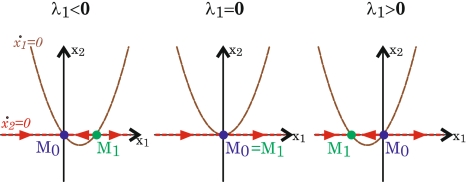
Figure 2 shows how the fixed points changed stability according to the variation of λ₁.

Fig. 2.

Normal form reduction near μ_c. The two nullclines 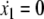and 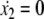appear. Plain arrows indicate the direction of the trajectories for x₂ = 0

For the fixed point M₀:

• μ < μ_c: both Lyapunov exponents are negative. All trajectories converge to the trajectories M₀ which is accordingly stable. The other fixed point, M₁, is unstable with ϕ₁ < ϕ₀ and S₁ > S₀;

• μ > μ_c: one Lyapunov exponent is negative while the other is positive. It corresponds to the co-existence of both attracting and diverging trajectories. Trajectories attracted to M₀ escape directly from it. M₀ corresponds to an unstable fixed point. M₁ is stable with ϕ₁ > ϕ₀ and S₁ < S₀;

• μ = μ_c one Lyapunov exponent is negative. Accordingly, the basin of attraction of M₀ has a positive measure and many trajectories are attracted to it. However, since the other Lyapunov exponent equals zero, it exists an ‘unstable’ direction along which the dynamics can escape due to infinitesimal perturbation. Accordingly, M₀ does not attract all trajectories from an open neighborhood and does not define a classical fixed point attractor. However, it is still an attractor if we consider Milnor’s extended definition of attractors (Milnor 1985). At M₀, the two nullclines becomes tangent and the two fixed points merge, M₀ = M₁.

The particularity and interest of the Milnor attractor is the following. For all values of μ, any initial state of our system is attracted and converges to a fixed point of the system (M₀ or M₁). To escape from that fixed point, and to perform an oscillation, a given amount of energy has to be provided, e.g. as a transient input. The more 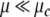or 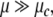the more the amount of energy required to escape from that fixed point is important. By contrary, at the Milnor attractor (or for 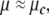) the dynamics becomes very receptive and an infinitesimal perturbation can push the dynamics to iterate through an oscillation.

Response to a constant input

Under constant inputs, the dynamics of the system 4 can either converge to a fixed point, either converge to a limit cycle. To obtain a fixed point 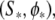dϕ/dt must be equal to zero in Eq. 4, which requires:

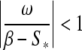8

and Eq. 4 becomes:

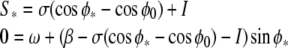9

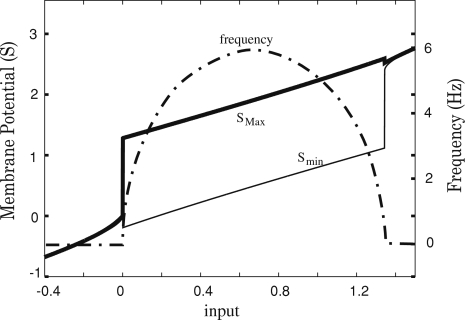
Figures 3 and 4a show the evolution of the dynamics for various levels of input. Fixed points are obtained either for small values of I (S < (β−ω) in Condition 8), either for large values of I (S > β in Condition 8). In between, oscillatory dynamics occurs. The period of the oscillation can be approximated by identifying S with its temporal average, 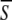and by solving the integral 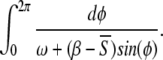This approximation gives an oscillation at frequency 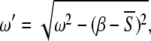which is in good agreement with computer experiments (Fig. 3).

Fig. 3.

Evolution of the maximum and minimum values of S, and of the dominant frequency obtained by FFT when the input current is varied

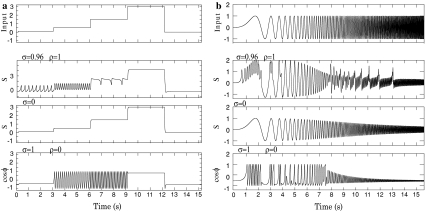
Fig. 4.

Voltage response to input currents. a for current steps, b for oscillatory input of increasing frequency. Upper figures show the input pattern. Then, from up to down, the voltage response is shown for our complex unit, then for a unit without phase modulation, finally, when only the phasic output is considered

In Fig. 4a, the dynamics of our system of two equations is compared with the dynamics obtained for σ = 0 (i.e. for a simple integrating unit as in the rate model) and for the current output from the phase model (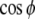). As expected from Fig. 3, the coupling of the phase adds oscillation in a large range of inputs, and, as a first order approximation, our unit’s dynamics appears as a non-linear combination of both dynamics.

Response to oscillatory input

Since the output of a unit can become the input to other units and can contain oscillations, it is interesting to see how a unit reacts to oscillatory inputs. Figure 4b shows the dynamics obtained when considering an oscillating currents having an increasing frequency. The input current follows the ZAP function, as proposed in (Muresan and Savin 2007): 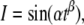with 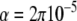and β = 3.

Again the two limit cases are considered. First, when σ = 0 (third row), the unit becomes an integrating unit and the membrane potential oscillates at the input frequency but with exponential attenuation in amplitude. Second, for the phase impact (fourth row), at slow input frequency (lower than ω), one or several oscillations are nested in the up-state. When the input frequency is larger than ω (t > 650 ms), oscillations follows the input frequency which leads to faster oscillations with attenuation.

When the two dynamics are coupled (second row), at very low frequencies (lower than 2 Hz), the dynamics goes from fixed point dynamics to limit-cycle dynamics during up-states. We propose that these oscillations at the theta frequency occurring for positive currents could model the increase of activity during ‘up-states’. For faster frequencies of the input signal, but still slower than the phase frequency ω, one oscillation occurs during the up-state, leading to higher depolarization of the membrane potential, and an attenuation function of the frequency appears as a result of the integration. At frequencies faster that the phase frequency ω, interference occur and generate higher mode resonances.

Two coupled units

For sake of simplicity, we will discuss results obtained for symmetrical connections (w₁₂ = w₂₁ = w). In the two following simulations, the dynamics of the network is analyzed after a transient excitation is applied to one unit. Figure 5 analyzes the dynamics by looking at the extrema of the membrane potential and by quantifying the phase difference between the two units. The measure of synchrony is obtained by dividing the time between the maximum of the membrane potential of the two units, 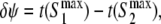by the period of the signal, T. Accordingly, 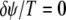corresponds to the two units oscillating at same phase (phase locked), and 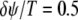corresponds to the two units being antiphase locked.

Fig. 5.

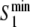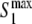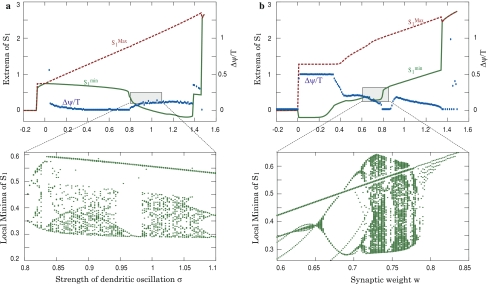
Extrema of the membrane potential during the up-state ( and ) and normalized phase difference (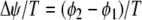) for a two-unit network when either the internal coupling strength (a) or the synaptic weight (b) is varied. Lower figures demonstrate the presence of complex dynamics in specific region of the upper figures by showing the bifurcation diagram for the local minima of the membrane potential. For (a), w = 0.75. For (b), σ = 0.9

The impact of different type of inputs is beyond the scope of this paper and only the impact of a transient input applied to one unit is considered.

From an Hopfield network to a flip flop network

For σ = 0, the membrane potential is not influenced by the phase and the system of two equations simplifies to a classical recurrent network. Since Hopfield, that system is well known for its ability to encode patterns as associative memories in fixed point attractors (Hopfield 1982; Amit 1989; Durstewitz et al. 2000). In our two units network, if the coupling strength w is strong enough (w larger than 0.68), the dynamics is characterized by two stable fixed points, a down state (S₁ = S₂ = 0) and an up-state (visible in Fig. 5a with S₁ ∼ 0.65). Applying a positive transient input to one of the two cells suffices to move the dynamics from the down-state to the up-state. In return, a negative input can bring back the dynamics to the down state.

When increasing σ, a small oscillation characterizes the up-state and associative memory properties (storage and completion) are preserved. The two cells oscillate at nearly identical phases.

For large values of σ (i.e. large internal coupling), the membrane potential saturates. The region of interest lies before saturation when the membrane returns transiently near the resting state and accordingly not so far from the Milnor attractor. This leads to complex dynamics as shown by the fractal structure of the local minima of S₁ (lower part of Fig. 5a). In that situation, a transient input applied simultaneously to the two units would synchronize the two units’ activity and after one oscillation, when the membrane potentials cross the resting state, they stop their activity and remain in the fixed point attractor (not shown here).

Influence of the synaptic weight

Figures 5b and 6 show the impact of varying the synaptic weight on the dynamics of the two units after transient stimulation of one unit.

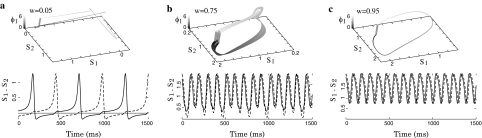
Fig. 6.

S_i temporal evolution, (S₁,S₂) phase plane and (S_i, ϕ_i) cylinder space. a Up-state oscillation for strong coupling. b Multiple frequency oscillation for intermediate coupling. c Down-state oscillation for weak coupling

For small synaptic weights, the two units oscillate anti-phase (Fig. 6a) and their membrane potentials periodically visit the resting state for a long time. The frequency of this oscillation increases with the synaptic weights and for strong synaptic weights (Fig. 6c), rapid in-phase oscillation appear. In that situation, the oscillation does not cross anymore the fixed point attractor, the dynamics remains in up-state. For intermediate coupling strength, an intermediate cycle is observed and more complex dynamics occur for a small range of weights (0.58 < w < 0.78 with our parameters, Fig. 5b). The bifurcation diagram shows multiple roads to chaos through period doubling (Fig. 6b).

Working memory of cell assemblies

In this section, a network of N = 80 cells containing eight strongly overlapped cell assemblies is simulated. Each cell assembly contained 10 cells among which seven were overlapping with other cell assemblies. The intersection between two cell assemblies was limited to two cells. The connectivity of the network was chosen bimodal: The synaptic weights between cells lying in the same cell assembly were chosen from the normal distribution (μ = 0.8 and σ = 0.15), while the other weights were chosen from the normal distribution (μ = 0.2 and σ = 0.1).

To avoid saturation, a global inhibition unit has been added to the network. This unit computes the total activity of the network 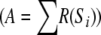and inhibits all cell with the following negative current:

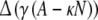10

where Δ(x) = −x for x > 0 and 0 elsewhere; γ defines the strength of the inhibitory cell (here 0.1) and κ (in %) defines a threshold triggering the inhibition (here 0.03, meaning that inhibition starts when more than 3% of cells are activated).

Spontaneous activity

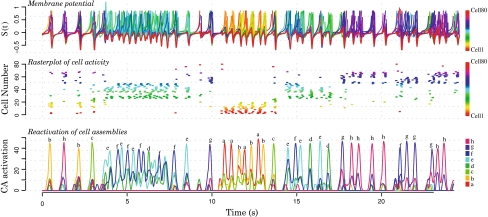
Figure 7 shows the spontaneous activity of the network, i.e. in absence of any external stimuli. The upper part of the figure shows the evolution of the membrane potential for the 80 cells (each cell is represented by a different color). The membrane potential is maintained around the Milnor attractor (nearby the stable fixed point). The middle part in Fig. 7 shows rasterplot of cells activity. Global inhibition was tuned to prevent the simultaneous activation of multiple cell assemblies and each period is associated with the activation of a specific subset of cells. Lower part in Fig. 7 quantifies the proportion of each cell assembly activated at each time step. During the observed period, all cell assemblies (characterized in the figure by a different color and letter) are reactivated. It has to be noted that since cell assemblies are overlapping, the total reactivation of a cell assembly is necessarily associated with the partial reactivation of other cell assemblies.

Fig. 7.

Spontaneous activity in a 80 units network containing eight overlapped cell assemblies of 10 cells each. The upper and the middle figures show respectively the membrane potential and a rasterplot of the activity of each individual cell (one color per cell). The lower figure shows the reactivation of the different cell assemblies (each assembly has its own color and letter). Periods of no-activity alternate with periods of activity during which specific cell assemblies are preferentially activated

The activity of the network can be explained in the following way: when one cell is activated, it tends to activate the cells belonging to the same cell assembly and the activated cells undergo one oscillation before going back to the resting state, nearby to the Milnor attractor. At the Milnor attractor, any cell can be kicked out of the attractor leading to the activation of a different or the same cell assembly. As a result, the spontaneous activity of the system is characterized by the Milnor attractor which provides a kind of reset of the entire network, enabling the activation of the different stored memories. The system itinerates among the previously stored memories, with the passage from one memory to a new one characterized by the “ruin of the Milnor attractor” leading to a kind of “chaotic itinerancy” (Tsuda 1992; Kaneko 1992).

The overlapping structure of the cell assemblies can influence the sequence of reactivation: The reactivation of one specific cell assembly will tend to reactivate the cell assemblies sharing common cells.

Working memory

In this section, after applying external stimuli during short time periods to part of one or several cell assemblies embedded in the network, we observe the network’s ability to sustain the activity of these cell assemblies in agreement with the theory of working memory. To reflect biologically plausible conditions, cell assemblies were sequentially activated during 100 computational time steps; i.e. approximately 200 ms.

In the previous section, we saw that after the reactivation of one cell assembly, all cell assemblies are equally probable to be reactivated. To modify this probability and to increase the probability of selected cell assemblies to be reactivated, as previously proposed (Molter et al. 2008), we simulated a transient period of Hebbian synaptic plasticity during the presentation of the stimuli. Practically, at each computational step, weights between cells reactivated during that period were increased by 0.01. We believe that the proposed mechanism can be related with growing evidence showing that attention-like processes are associated with period of short term plasticity (van Swinderen 2007; Jaaskelainen et al. 2007).

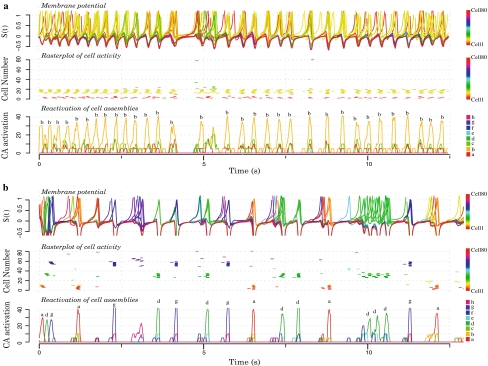
In Fig. 8a, part (40%) of one cell assembly was stimulated. In Fig. 8b, part (40%) of three cell assemblies were sequentially stimulated. First, we observe that in agreement with the theory of associative memories, in both scenario, rasterplot figures indicate that the stimulation of 40% of a cell assembly results in its complete reactivation. Second, it appears that in both cases, the transient stimulation of a cell assembly leads to its preferential reactivation and to a form of sustained activity.

Fig. 8.

Working memory in a 80 units network containing eight overlapped cell assemblies of 10 cells each. In both a and b, upper figures show the membrane potential of each individual cell (each cell one color). Middle figures show rasterplots of individual cells activity (a cell is said to be in an active state if its spike density is larger than 0.5). Lower figures show the reactivation of the different cell assemblies (one color and letter per cell assembly). a An external stimulus was impinging part (40%) of one cell assembly during a short transient (10 computational time steps). As a result, this cell assembly is continuously activated as a short term memory. b External stimuli are successively applied to part (40%) of three cell assemblies (each CA is stimulated during 100 computational time steps; i.e. approximately 200 ms). After stimulation, we observe that these three cell assemblies have sustained activity

The explanation is the following. After external stimulation, the network is attracted to its resting state, and again the dynamics reflects the presence of diverging orbits crossing attracting orbits. When one cell assembly was reactivated (Fig. 8a), its recurrent connections were increased during the attention-like reactivation, and that cell assembly is now more likely to win the competition and to be reactivated. Since the rapid weight increase due to attention is not balanced by a slow decrease, no dynamics transition is expected and short term memory is expected to last forever (as in Brunel et al. 2004; Mongillo et al. 2008). To implement a slow extinction of the working memory (after dozens of seconds), a mechanism of slow weight decrease could be implemented.

When three cell assemblies were reactivated (Fig. 8b), the balance between excitation and inhibition results in the competition of these three cell assemblies which leads to complex patterns of activity. As a result, the three cell assemblies show clear sustained activity, and these reactivations occur at different times. This result appears important since their simultaneous reactivation would mix them and would prevent any possibility to decode the utile information embedded in the network. Together, these results confirm that our model satisfies one important defining feature of the working memory: The ability to maintain simultaneously multiple chunks of information in short term memory.

Discussion

Recent neuroscience emphasized the importance of the brain dynamics to achieve higher cognitive functions. From a computational perspective, it gave straightforward directions for the development of new type of models where dynamics played more central roles (Kozma and Freeman 2003; Molter et al. 2007). In this paper, to conciliate the classical Hopfield network (Hopfield 1982) with the need of more complex dynamics, we propose a new biologically motivated network model, called “flip-flop oscillation network”.

In this model, each cell is embedded in a recurrent network and is characterized by two internally coupled variables, the cell’s membrane potential and the cell’s phase of firing activity relatively to the theta local field potential.

In a first study, we demonstrate theoretically that in the cylinder space, the Milnor attractor (Milnor 1985) appears at a critical condition through forward and reverse saddle-node bifurcations for a one-cell network (Figs. 1, 2). Near the critical condition, the pair of saddle and node constructs a pseudo-attractor, which leads to Milnor attractor-like properties in computer experiments. Nearby the attractor, the dynamics of the cell is characterized by high sensitivity: infinitesimal transient perturbation can activate an oscillation of the membrane potential.

Simulations of a two-cell network revealed the presence of numerous complex dynamics. We observed that semi-stability of the Milnor attractor dynamics characterizing one cell dynamics, combined in a two cell-network leads to oscillations and chaotic dynamics through period doubling roads (Fig. 5). The important role played by the Milnor attractor for the apparition of the chaotic attractor suggests chaotic itinerancy (Tsuda 2001).

Finally, we tested our model during spontaneous activity (Fig. 7) and for selective maintenance of previously stored information (Fig. 8). In agreement with the cell assembly theory (Hebb 1949), multiple overlapping cell assemblies were phenomenologically embedded in the network to simulate chunks of information.

During spontaneous activity, the network is dynamically switching between the different cell assemblies. After the reactivation of a specific cell assembly, the quasi-stable state of the Milnor attractor provides receptivity to second order dynamics of the internal state and to external stimuli. During that “receptive” or “attention-like” state, a different information can be reactivated. This is supported by recent biological reports; for example, the spatiotemporal pattern of activity of cortical neurons observed during thalamically triggered events are similar to the ones observed during spontaneous events (MacLean et al. 2005). From a dynamics perspective, the presence of the Milnor attractor prevents the network to be “occulted” by one information and leads to chaotic itinerancy between the previously stored cell assemblies.

To simulate working memory tasks, we analyzed if the network could transiently hold specific memories triggered by external stimuli. To reliably and robustly enforce the maintenance of triggered cell assemblies, short period of synaptic plasticity was simulated, reproducing attention-like processes (van Swinderen 2007; Jaaskelainen et al. 2007). As a result, one or multiple cell assemblies could selectively be maintained. An important feature brought by the addition of the theta rhythm to the classical Hopfield network is that different cell assemblies are separately reactivated at different theta oscillations. At each theta cycle, cells from a unique cell assembly are synchronously reactivated. That enables our network to solve the binding problem by reactivating at different phases different overlapping cell assemblies.

If the addition of an internal oscillation to classical rate coding model (e.g. Brunel et al. 2004; Mongillo et al. 2008) can solve the binding problem, it can still not explain in an easy way the limited memory capacity of working memory [e.g. the magical number seven (Miller 1956)]. In that sense, it differs from the seminal paper from Idiart et al. (Lisman and Idiart 1995) where it was proposed that memories are stored in gamma cycles embedded in theta cycles, and that the magical number seven is explained by the number of gamma cycles which can be embedded in a theta cycle. Further studies should focus more deeply on the capacity problem. More precisely, the reactivation of multiple items at different phase of a same theta cycle should be tested.

To summarize, we are proposing a compact, effective, and powerful “flip-flop oscillations network” whose dynamical complexity can be of interest for further analysis of integrative brain dynamics. First attempts to solve working memory tasks gave promising results were different chunks of information were reactivated at different theta cycles. Finally, in our model, the information conveyed during spontaneous activity and working memory tasks appeared similar, reminding the famous quote from Rodolfo Llinas: “A person’s waking life is a dream modulated by the senses” (Llineas 2001).