Abstract
We follow up on a suggestion by Rolls and co-workers, that the effects of competitive learning should be assessed on the shape and number of spatial fields that dentate gyrus (DG) granule cells may form when receiving input from medial entorhinal cortex (mEC) grid units. We consider a simple non-dynamical model where DG units are described by a threshold-linear transfer function, and receive feedforward inputs from 1,000 mEC model grid units of various spacing, orientation and spatial phase. Feedforward weights are updated according to a Hebbian rule as the virtual rodent follows a long simulated trajectory through a single environment. Dentate activity is constrained to be very sparse. We find that indeed competitive Hebbian learning tends to result in a few active DG units with a single place field each, rounded in shape and made larger by iterative weight changes. These effects are more pronounced when produced with thousands of DG units and inputs per DG unit, which the realistic system has available, than with fewer units and inputs, in which case several DG units persists with multiple fields. The emergence of single-field units with learning is in contrast, however, to recent data indicating that most active DG units do have multiple fields. We show how multiple irregularly arranged fields can be produced by the addition of non-space selective lateral entorhinal cortex (lEC) units, which are modelled as simply providing an additional effective input specific to each DG unit. The mean number of such multiple DG fields is enhanced, in particular, when lEC and mEC inputs have overall similar variance across DG units. Finally, we show that in a restricted environment the mean size of the fields is unaltered, while their mean number is scaled down with the area of the environment.
Keywords: Hippocampus, Entorhinal cortex, Place cells, Grid cells, Competitive learning
Place fields in the age of grid cells
Until a few years ago the representation of space in terms of place cells, discovered by John O’Keefe and collaborators in the rodent hippocampus (O’Keefe and Dostrovsky 1971; O’Keefe 1976), was often seen as approaching an apparently unique, necessary and fundamental Platonic ideal, and as such embedded in brain-inspired models of navigation and spatial cognition. Note, however, that abundant experimental evidence points at departures from the Platonic ideal, e.g. in terms of modulation of the place-dependent response by the animal’s own velocity and even by that of other moving objects (Ho et al. 2008). With the discovery of grid cells (Fyhn et al. 2004; Hafting et al. 2005), at least as striking in their geometrical beauty, grid and place cells have appealed together for the “conceptual primacy” formerly enjoyed by place cells alone. They have appeared as dual representations in a scheme akin to that of orthogonal bases in frequency and real space, respectively. Correspondingly, it has been proposed that place cell responses may be generated by grid cell responses through a sort of Fourier transformation, where a limited number of sines and cosines of different spatial frequency suffice to generate, if summed with appropriate coefficients, an approximately localized bump of activity approaching a delta-function (Solstad et al. 2006). The nearly periodic grid cells, close to delta-functions in frequency space, would lead to a similar set of near delta-functions in real space, such that the position of the animal, represented by a distributed ensemble of many grid cells, could be equivalently represented by a much more restricted, hence sparser ensemble of place cells.
Loosely speaking, the metaphor of a Fourier transform does seem fitting, and the drastically enhanced sparsity of the code describes the main effect of the transform, even if implemented through a different algorithm, such as Independent Component Analysis (Franzius et al. 2007b). In detail, however, a few tens of grid-cell-like units can summate their activity into the single broad peak of a place-cell-like unit only if their spatial phases are precisely aligned on their one surviving peak, and the connection weights are such as to suppress the extra peaks. The connection weights and input sampling that are required in the established transformation (Solstad et al. 2006; Franzius et al. 2007a) could conceivably emerge from a self-organizing plasticity process, but this needs to be fleshed out. A step in this direction has been taken by Rolls et al. (2006), who have proposed that simple competitive learning on the connections from grid cells in medial entorhinal cortex (mEC) to granule cells in the dentate gyrus (DG) might turn the DG cells, which have multiple scattered tiny fields with the initial random connection weights, into proper place cells with a single peak. In their model, each DG unit receives inputs solely from mEC units, 100 in their 1D simulation and 125 in their 2D simulation, and competitive learning is implemented through a variety of simple “learning rules” inspired by Hebb’s principle (Hebb 1949). If the learning rules used include a “trace”, i.e. a temporal smoothing factor, the resulting DG fields are broader.
This simulation study has been published before new experimental recordings (Leutgeb et al. 2007) confirmed that DG granule cells, a very small proportion of which had been shown to be active in any given environment (Jung and McNaughton 1993; Chawla et al. 2005), in fact often present multiple firing fields, when active. The distribution of the number of firing fields per active DG cells reported in Leutgeb et al. (2007) can be well fitted by a Poisson distribution with mean 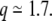 Preliminary data also suggest that in larger environments the average number of these DG fields scales up with the environment, and their average size might also tend to scale up (Jill K. Leutgeb, personal communication). Unlike the single fields typical of the hippocampus proper, particularly the CA3 region, DG does not therefore seem to match the Platonic ideal of a place cell in the delta-function sense. The transformation from mEC to DG cannot be really idealized as a transformation from frequency to real space.
Preliminary data also suggest that in larger environments the average number of these DG fields scales up with the environment, and their average size might also tend to scale up (Jill K. Leutgeb, personal communication). Unlike the single fields typical of the hippocampus proper, particularly the CA3 region, DG does not therefore seem to match the Platonic ideal of a place cell in the delta-function sense. The transformation from mEC to DG cannot be really idealized as a transformation from frequency to real space.
Aside from perhaps “overdoing” the tendency to produce single DG fields, the notion of competitive Hebbian learning advanced by Rolls et al., while very appealing in its simplicity and in not invoking any ad hoc ingredient, has not been found completely convincing. For example, it has been criticized for resulting in implausibly small fields (Molter and Yamaguchi 2008) and for not explaining how a mere realignment of grid activity, in a changed context, could lead to global remapping in the hippocampus (Hayman and Jeffery 2008), as indeed observed experimentally (Fyhn et al. 2007). Both these recent modelling studies envisage a specific mechanism to select out a cluster of mEC inputs that tightly overlap in spatial phase: in the Molter and Yamaguchi (2008) model it is coincident theta phase, whereas in the Hayman and Jeffery (2008) model it is coincident location on the granule cell’s dendritic tree.
We have been intrigued by these more structured suggestions, which fit into interesting ideas about the role of theta oscillations and dendritic structure (see e.g. Burgess et al. 2007; Igarashi et al. 2007; Wagatsuma and Yamaguchi 2007); but at the same time we have wondered whether the simple notion of competitive learning advocated by Rolls and colleagues had expressed its full potential in their simulations. In particular, we have asked what is the effect, simulating the emergence of DG firing activity in a new environment, of incorporating three basic facts: (i) there are not few, but of the order of millions, DG granule cells in the rodent (Amaral et al. 1990); (ii) they receive from over a thousand, not just over a hundred, of mEC layer II units; and (iii) they also receive from over a thousand units in lateral entorhinal cortex (lEC), which do not present with a clear spatial modulation, but appear to be able to distinguish one context or environment from others, for example by representing the presence of particular objects, as suggested again by Rolls et al. (2005; see also Suzuki and Amaral 2003).
This short paper thus reports the effects of competitive Hebbian learning in what is essentially an upgraded version of the simulation by Rolls and colleagues, restricted to the emergence of DG fields in a single new environment.
Model
Grid unit activity
The firing rate of a grid unit, as a simplified model of real grid cells, is defined as
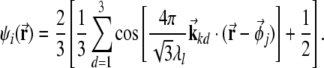 |
1 |
Here index i is the combination of j, k and l; the symbol · denotes the inner product; 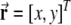 is the location of the virtual rodent;
is the location of the virtual rodent; 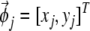 is a spatial phase;
is a spatial phase; 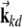 is the direction onto which the location is projected, with d = 1,2,3 and
is the direction onto which the location is projected, with d = 1,2,3 and
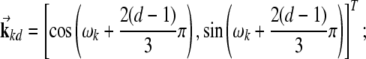 |
2 |
λl is the distance between two peaks of 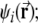 and ωk is the orientation of the grid.
and ωk is the orientation of the grid.
Grid units are organized into 200 local ensembles. Each ensemble has 100 grid units with the same orientation ωk and spacing λl. ωk is uniformly sampled within [0, 2π] (i.e., within [0, π/3], as our grids present an exact π/3 rotation symmetry around any of their peaks). λl is either linearly or logarithmically sampled within the range [30, 70] (arbitrary spatial units, meant to roughly correspond to cm); the figures are drawn from the linear sampling simulations, but results were virtually indistinguishable. Within each ensemble, the 100 grid cells have different spatial phases, with xj and yj uniformly sampled in the range [0, 100].1
Network model
The firing rate 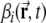 of a DG unit is determined through a simple linear-threshold transfer function. The total number of DG units is M = 1,000. Each DG unit receives input from N = 1,000 different units randomly selected from the entire population of 20,000 mEC grid units.
of a DG unit is determined through a simple linear-threshold transfer function. The total number of DG units is M = 1,000. Each DG unit receives input from N = 1,000 different units randomly selected from the entire population of 20,000 mEC grid units.
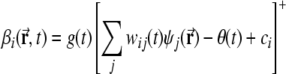 |
3 |
Here j is the index that labels grid units which are connected to DG unit i, through synaptic weights wij(t); [·]+ denotes the threshold-linear transform that leaves positive arguments intact and sets negative arguments to zero; further, ci denotes the sum of all lEC inputs, which are taken to provide context information from lateral entorhinal cortex, but no spatial information coding for position within the environment. In the model, each value ci is sampled from a Gaussian distribution with standard deviation σ. The mean of the distribution is not relevant as it can be lumped together with the threshold θ(t). For each DG unit i, ci can be positive or negative, but is fixed during simulations. Finally, in fact, g(t) and θ(t) are the (uniform) gain and threshold of the DG network, chosen at each time t to ensure that the mean and sparsity of the DG activity are both equal to a pre-specified constant a
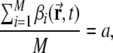 |
4 |
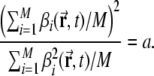 |
5 |
Learning rules
Learning proceeds as follows. First, the current location 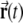 along the virtual trajectory is determined, and the activity of all mEC units is calculated according to Eq. 1, given the current location. Then, the activity of all DG units is determined by their threshold-linear transfer function (Eq. 3). The weights are then updated according to a Hebbian rule
along the virtual trajectory is determined, and the activity of all mEC units is calculated according to Eq. 1, given the current location. Then, the activity of all DG units is determined by their threshold-linear transfer function (Eq. 3). The weights are then updated according to a Hebbian rule
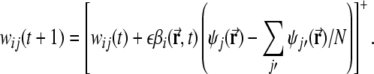 |
6 |
Here the negative weights are cut to zero by the threshold-linear function [·]+. 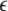 is a positive learning rate. In all the following simulations,
is a positive learning rate. In all the following simulations, 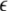 is set to 0.00001.
is set to 0.00001.
Before learning, the weights are initialized as uniform random numbers in the range [0,1]. At each time step, the weights are further normalized into unitary length
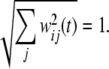 |
7 |
Results
The effect of learning
First, we run standard simulations with each DG unit receiving input from a random sample of 1,000 mEC units. A simulation entails 20 learning epochs in each of which the virtual rat simply visits each of the 10,000 nodes of a 100 × 100 grid representing the 1 sqm environment. After visiting each node, activity is propagated from the input array to the DG units, the threshold and gain are adjusted to produce the required mean DG activation and sparsity, and the (feedforward) weights are updated according to Eqs. 6 and 7. Visiting each node orderly does not alter the character of the results with respect to simulations where a virtual rat follows a more realistically varied trajectory, as we checked in control simulations (not shown), but it does reduce fluctuations substantially, enabling a clearer appreciation of small differences. With the small learning rate we used, there is no difference between the characteristics of the firing fields of DG units activated earlier and later within one epoch.
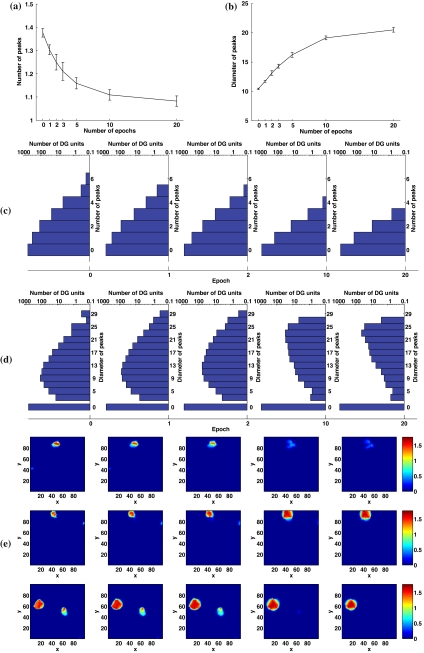
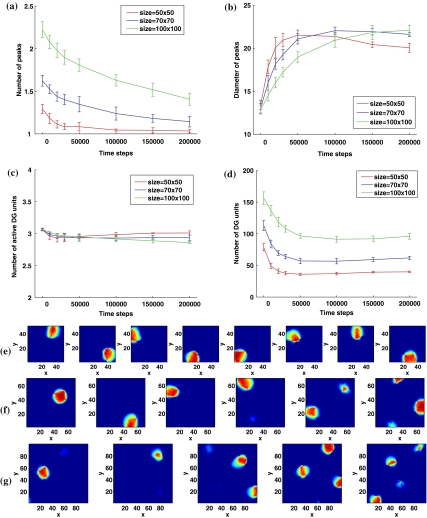
Figure 1a reports the mean number of fields, or more exactly of peaks, of DG units that show at least one peak after thresholding, at different stages of learning. A peak of a DG field is extracted as a continuous region where the maximal firing rate of the DG unit is larger than 0.3 and its mean firing rate in the region is larger than 0.2 (corresponding to about 15% and 10% of the maximal firing rate of all DG units respectively). The multiplicity distribution, i.e. the distribution in the number of peaks per unit, is shown in Fig. 1c as semi-log histograms at five different time points. At time 0, before any learning occurs, a substantial fraction of DG units show two or more peaks (detailed distribution averaged over six simulations: 561.17 units with no peaks, 304.5 with 1 peak, 108.83 with 2, 20.83 with 3, 4.17 with 4 and 0.5 with 5 or more). As learning proceeds, most of the smaller and lower peaks disappear and others coalesce, leading to an eventual distribution highly concentrated on single-peak units (after 20 learning epochs, 862.5 units with no peaks, 128.83 with 1 peak, 8.33 with 2, only 0.33 with 3 and none with more).
Fig. 1.
Competitive Hebbian learning reduces the number of DG fields and increases their size. a Mean number of peaks per active DG unit, averaged over 6 simulations, as a function of learning epoch. b Mean diameter of peaks, extracted as a continuous region with maximal firing rate above 15% and mean firing rate above 10% of the maximal firing rate of all DG units. c Multiplicity distributions, i.e. distributions in the number of peaks per unit, after 0, 1, 2, 10, 20 learning epochs. The means of the positive multiplicity distributions, i.e. bars with ≥1 peaks, are shown in (a). d Size distributions generating the means in (b). e Example fields of three DG units at time 0, 1, 2, 10, 20 epochs. Sparsity a = 0.003
In parallel to the reduction in the number of peaks, their average size increases. The size of a peak is quantified as the diameter of the minimal circle bounding the region. Figure 1b indicates an over two-fold mean increase in area, which, as shown in panel (e), is accompanied by a significant rounding and smoothing of the shape of the field—this is of course highly variable from field to field. As indicated in the histograms of Fig. 1d, most of the smallest fields disappear with learning, and those that remain tend to have a large diameter (the mode of the distribution ends up at 23–24 nodes, or “cm”); whereas before learning, most peaks have a small diameter (mode at 9–10 nodes). Competitive Hebbian learning, therefore, reduces the number of peaks of active DG units, while making them larger, smoother and rounder, as earlier found by Rolls et al. (2006).
Learning in small networks is not quite the same
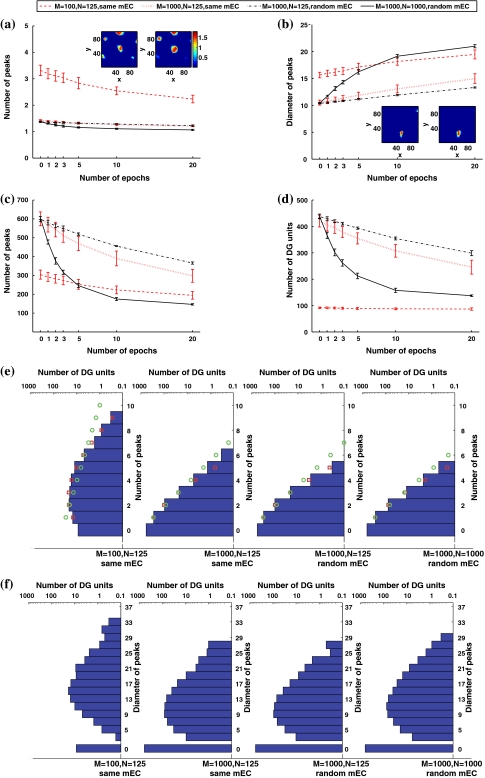
Interestingly, while the effects are qualitatively the same in a network of smaller number of units and connections, such as the one studied by Rolls et al. (2006), quantitatively there are large differences. Figure 2 compares the results just described above with those obtained in a network with the same structure as used by Rolls et al. (2006), and with those obtained in two networks with intermediate structures.
Fig. 2.
Fewer DG units and mEC inputs lead to more fields per unit, due to less competition and insufficient averaging. a Mean number of peaks per active DG unit (solid line), as in Fig. 1, but also in simulations with 125 mEC inputs per DG unit. Inset: example of a DG unit with multiple peaks from a simulation with 100 DG units and 125 inputs before learning (left) and after 20 learning epochs (right). b The difference in the size of the peaks vanishes gradually with learning. Inset: example of a DG unit with irregular peaks from a network with 1,000 DG units and 125 random mEC inputs per unit before learning (left) and after 20 learning epochs (right). Color code is the same as in (a). c The total number of peaks decreases with learning. d The number of active DG units. Most of the DG units in the small network are active in order to represent the 10,000 locations. e Multiplicity distributions generating the means in (a), after 1 learning epoch. The square and circle markers show the best-fit Poisson distributions and exponential distributions respectively. f Size distributions generating the means in (b), after 1 learning epoch
When considering only 100 DG units, each connected to the same 125 mEC units (chosen at random; with the DG sparsity set to a = 0.03, so that a similar number of DG units, about 3, are active at any time, as in the previous simulations) the network structure is essentially the same as used by Rolls et al. (2006). The average number of peaks per active DG unit is then about twice as many as those in larger networks with 1,000 DG units (Fig. 2a). Before any learning, most units have more than three peaks, as the example shown in the inset of Fig. 2a, and even after many learning epochs the average decreases only to ca. 2.5 peaks per active DG unit. This is simply due to the small number of DG units: with about 3 required to be active at any one place, almost all of them get a chance to win the competition at least somewhere in the environment, and usually more than once. In fact, the total number of peaks, summed over all DG units, is much smaller than in equivalent simulations with 1,000 DG units, as shown in Fig. 2c; those peaks are however forced onto an insufficient number of units.
While the main difference between the results obtained by Rolls et al. (2006) and those reported in Fig. 1 is due to the different number of DG units, the two intermediate simulations in Fig. 2 clarify that also the number of mEC inputs to each DG unit has a significant effect. When a DG unit receives only 125 inputs, as in the study by Rolls et al. and unlike the 1,000 inputs used in Fig. 1, less averaging makes individual fields more irregular and rigid (see the inset in Fig. 2b), so they increase in size less and decrease in number less than in our standard simulation (see Fig. 2b, c). More DG units remain active (Fig. 2d) but, still, nearly all active DG present a single field (Fig. 2a). Whether the fewer mEC inputs are the same across all DG units or a random sample for each unit, on the other hand, makes almost no difference.
Figure 2e shows that with a small DG population, the peak multiplicity distribution can be well fitted to a positive Poisson distribution. When the DG population is large, instead, the multiplicity distribution lies between a positive Poisson distribution and a positive discrete exponential distribution2. The size distribution after 1 learning epoch is similar across all simulations (Fig. 2f).
Although the effects of learning are largely similar, we see that scaling up the model to a more realistic size, in particular the size of DG population and the number of mEC inputs per DG unit, leads to a rather different scenario, where DG units come to have essentially a single place field, in contrast to experimental findings (Jung and McNaughton 1993; Leutgeb et al. 2007).
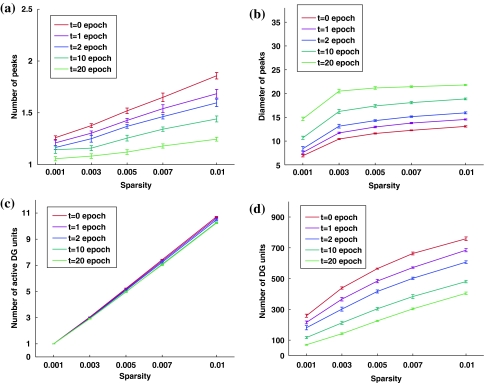
While obtained in simulations in which we set a = 0.003, the above conclusion is valid for other sparsity values as well, with only quantitative variations. We run control simulations also with a = 0.001, 0.005, 0.007 and 0.01, all in the “realistic” DG sparse coding regime, in which only a few percent of granule cells are observed to be active somewhere in a typical experimental box (Chawla et al. 2005) and of these only a fraction at any particular location in the box (Leutgeb et al. 2007). Figure 3 shows that less sparse activity implies more as well as larger peaks per active DG unit, while maintaining the earlier trends with training: training decreases the mean number of peaks, and increases their size. The fraction of active DG units also increases with less sparse representations, so if one counts the total number of active DG units in the environment (Fig. 3d) one finds an enhanced version of the increase in the number of peaks per active units (Fig. 3a). Remarkably, if one counts instead the number of active DG units at any particular location in the environment (Fig. 3c) one finds that they do not vary with training, and almost exactly match the naïve guess aM.
Fig. 3.
Results are similar however sparse the DG representation: a Mean number of peaks per active DG unit, as a function of sparsity. b Mean diameter of the peaks of DG fields. c Mean number of DG units which have fields at any particular location (counting only firing rates ≥15% of the maximal firing rate of all DG units). d Total number of DG units active anywhere in the environment
The effect of additional lEC inputs
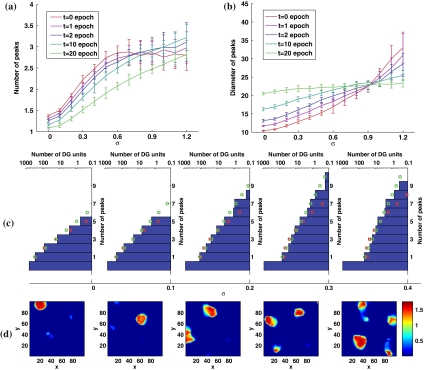
The scenario changes once more, however, if we consider that real DG granule cells receive also a substantial fraction of their afferents from lateral entorhinal cortex, where cells have been described as having weak spatial modulation or none at all (Hargreaves et al. 2005). In our model, we assume lEC inputs not be spatially modulated; hence the sum of all lEC inputs to a given DG unit is a randomly assigned quantity, constant in space, which we take to be normally distributed across DG units, with standard deviation σ. The simulations above therefore correspond to σ = 0, whereas σ = 0.3–0.4 yields a total lEC input with similar variance, across DG units and at any given position, as the total mEC input they receive. Figure 4 describes the effect of running simulations (with 1,000 DG units and 1,000 mEC inputs per DG unit) at different σ values.
Fig. 4.
Adding lEC input increases the number of DG fields. a Mean number of peaks per active DG unit, after 0, 1, 2, 10 and 20 learning epochs, as a function of the lEC signal width σ. b Mean diameter of peaks, for the simulations in (a). c Multiplicity distributions generating some of the means in (a), after 1 learning epoch. The square and circle markers show the best-fit Poisson distributions and exponential distributions respectively. d Examples of the maps expressed by DG units after 1 learning epoch
As shown in Fig. 4a, adding the model lEC input substantially increases the mean number of peaks per active DG unit. The effect is easy to understand: a subset of DG units are made more likely to be activated anywhere in the environment, those that receive the larger (constant) lEC input, so they tend to display more peaks, at the expense of units that would have had a field in the environment but are driven below threshold by a lack of lEC drive. Therefore strong lEC inputs help break the homogeneity across DG units, contrasting the effects of competitive learning. The addition of lEC inputs concurrently increases somewhat the mean size of DG fields, at least at initial and intermediate stages of training, though after 20 epochs this effect nearly vanishes, and in fact for large σ training in itself decreases the size of the fields (Fig. 4b).
The detailed distribution in the number of peaks per DG unit (Fig. 4c) is not dissimilar, after 1 learning epoch, from that reported experimentally (Leutgeb et al. 2007), although closer to exponential (a sloped line in the semi-log histograms) than to Poisson when σ is larger than 0.1. The appearance of the fields, for the “realistic" value σ = 0.3, is also broadly similar (Fig. 4d).
Scaling down the environment
Finally, we performed identical simulations in environments scaled down by a factor of 2 (a 70 × 70 grid, corresponding to roughly 0.5 sqm) and by a factor of 4 (a 50 × 50 grid, corresponding to roughly 0.25 sqm).
The effects are clear: the mean number of peaks is reduced, whereas their average size does not change significantly (Fig. 5a,b). In particular, after 1 learning epoch, in the three sets of simulations the number of DG units was distributed as follows: in the 100 × 100 environment, 863.5 DG units with no fields, 69 with 1, 27.67 with 2, 18.5 with 3, 11.33 with 4 and 10 with more than 4; in the 70 × 70 environment, 903.17 DG units with no fields, 61.33 with 1, 22 with 2, 9 with 3, 3.67 with 4 and 0.83 with more than 4; in the 50 × 50 environment, 930.67 DG units with no fields, 53.83 with 1, 12.83 with 2, 2.16 with 3, 0.17 with 4 and 0.33 with more than 4.
Fig. 5.
Scaling down the environment reduces the number of fields per DG unit, with no effect on their size. a Mean number of peaks per active DG unit, in 3 sets of simulations differing in the size of the environment. b Mean diameter of each field, in the same 3 sets. c The mean number of DG unit active at any given location does not scale down—it remains roughly equal to aM. d The total number of active DG units scales sublinearly with the size of the environment. (e–g) Representative examples of DG fields in environments of three sizes, after 100,000 steps of learning. Here results are shown as functions of time steps, because in environments with different size 1 learning epoch corresponds to different number of time steps. Sparsity a = 0.003, σ = 0.3
When counting the total number of active DG units in each environment (Fig. 5d), the decrease in the smaller ones seems sublinear, stabilizing after training around 97 (100 × 100), 55 (70 × 70) and 35 (50 × 50). The sublinearity appears to be due to border effects, in that fields with an average diameter around 20 units may be counted if they fall within larger areas, of e.g. 1.44 (120 × 120), 0.81 (90 × 90) and 0.49 (70 × 70) sqm—in fact, the number of DG units active at each location remains constant at the value set by the sparsity, Fig. 5c. Examples of the fields in the three environments are given in Fig. 5e–g.
Discussion
In conclusion, we find that the experimentally observed appearance, size and number of DG fields are broadly compatible with those that are produced by a simple model in which DG units receive mEC and lEC inputs of similar strength, and have their mean activity and sparsity tightly regulated by inhibition. The effect of competitive Hebbian learning on the feedforward connections they receive from mEC is to decrease the fields of active DG units, while making them larger and more regular in shape, as envisaged by Rolls et al. (2006). We obtain results that largely replicate those of their simulations, but as a consequence of the near cancellation of two factors of a distinct nature: we consider a larger and more realistic number of DG units and mEC inputs per unit, which tends in itself to produce DG units with a single field, and we also consider additional lEC inputs, which brings back the mean number of DG fields to higher values. What we do not find anymore, in this more realistic model, is the appearance of the resilient, underlying periodicity of the grid inputs, which was evident in earlier models (Solstad et al. 2006).
Although other complex factors, such as the theta rhythm (Hayman and Jeffery 2008) may well contribute to shape DG fields, we find that these additional factors are probably not required for a first appraisal of the EC-DG transformation. In this sense, this little study fits within the general view that much of the relevant learning and memory dynamics in the rodent hippocampus may be understood even neglecting the prominent rhythmicity at theta and faster scales, and the beautiful geometry in the circuitry, and resorting to extremely simplified network models like the one employed here. In a similar spirit, we have discussed how grid cell activity could emerge itself purely as a single-cell process, from learning on feedforward weights combined with firing rate adaptation (Kropff and Treves 2008). In a forthcoming publication (Cerasti and Treves, in preparation), we discuss the amount of information that multiple DG fields can impart to a new CA3 representation, in which active CA3 units typically have, instead, a single field. Thus, the overall transformation from multiple regularly arranged fields in mEC to fewer multiple but irregular fields in DG to essentially single fields in CA3 appears both natural and information efficient, and to require no dynamical sophistication at all. In previous reports (see e.g. Papp et al. 2007) we have discussed the main properties of simplified models of the CA3 recurrent network, which are extremely interesting even at a rather abstract level of analysis: fragmentation of would-be continuous attractors, tendency to coalesce, storage capacity.
We have limited the analysis reported here to the learning of a single environment, even though understanding the EC-DG transformation crucially hinges on understanding how the apparent universality of EC maps can be translated into hippocampal remapping (Fyhn et al. 2007) and in particular into the exquisite sensitivity to context of DG fields (Leutgeb et al. 2007), which appears to depend on Hebbian learning in the DG network (McHugh et al. 2007). The type of correlations which result between the activity of DG units in different environments, as well as the fundamental issue of the role of new DG units, produced by neurogenesis within the previous few weeks (Aimone et al. 2006), are left for future reports.
Acknowledgements
We are grateful for enlightening discussions to all colleagues in the Kavli Institute and in the Spacebrain EU collaboration, which has funded this work; Jill Leutgeb and Emilio Kropff have been particularly helpful with advice and access to preliminary data.
Footnotes
Note that the exact type of λ sampling is not essential. What is important is that many different spacings, as well as orientations and spatial phases, are sampled. We also run simulations with the same sampling of spacings and phases but a unique orientation of the grids, and results were quite different, as that orientation remained quite salient in the nearly periodic responses of many of the DG units (not shown).
The positive Poisson distribution is defined as 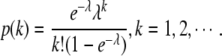 The positive discrete exponential distribution is defined as
The positive discrete exponential distribution is defined as 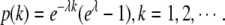 The maximum likelihood estimation of the parameter λ is fitted according to the actual distribution of the peaks.
The maximum likelihood estimation of the parameter λ is fitted according to the actual distribution of the peaks.
Contributor Information
Bailu Si, Phone: +39-040-3787630, FAX: +39-040-3787615, Email: bailusi@sissa.it.
Alessandro Treves, Email: ale@sissa.it.
References
- Aimone J, Wiles J, Gage F (2006) Potential role for adult neurogenesis in the encoding of time in new memories. Nat Neurosci 9:723–727 [DOI] [PubMed]
- Amaral D, Ishizuka N, Claiborne B (1990) Neurons, numbers and the hippocampal network. Prog Brain Res 83:1–11 [DOI] [PubMed]
- Burgess N, Barry C, O’Keefe J (2007) An oscillatory interference model of grid cell firing. Hippocampus 17(9):901–812 [DOI] [PMC free article] [PubMed]
- Chawla M, Guzowski J, Ramirez-Amaya V, Lipa P, Hoffman K, Marriott L, Worley P, McNaughton B, Barnes C (2005) Sparse, environmentally selective expression of arc rna in the upper blade of the rodent fascia dentata by brief spatial experience. Hippocampus 15:579–586 [DOI] [PubMed]
- Franzius M, Sprekeler H, Wiskott L (2007a) Slowness and sparseness lead to place, head-direction, and spatial-view cells. PLoS Comput Biol 3:1605–1622 [DOI] [PMC free article] [PubMed]
- Franzius M, Vollgraf R, Wiskott L (2007b) From grids to places. J Comput Neurosci 22:297–299 [DOI] [PubMed]
- Fyhn M, Molden S, Witter M, Moser E, Moser M-B (2004) Spatial representation in the entorhinal cortex. Science 305:1258–1264 [DOI] [PubMed]
- Fyhn M, Hafting T, Treves A, Moser M-B, Moser E (2007) Hippocampal remapping and grid realignment in entorhinal cortex. Nature 446:190–194 [DOI] [PubMed]
- Hafting T, Fyhn M, Molden S, Moser M-B, Moser E (2005) Microstructure of a spatial map in the entorhinal cortex. Nature 436:801–806 [DOI] [PubMed]
- Hargreaves E, Rao G, Lee I, Knierim J (2005) Major dissociation between medial and lateral entorhinal input to the dorsal hippocampus. Science 308:1792–1794 [DOI] [PubMed]
- Hayman R, Jeffery K (2008) How heterogeneous place cell responding arises from homogeneous grids—a contextual gating hypothesis. Hippocampus 18:1301–1313 [DOI] [PubMed]
- Hebb D (1949) The organization of behavior: a neuropsychological theory. New York: Wiley
- Ho S, Hori E, Kobayashi T, Umeno K, Tran A, Ono T, Nishijo H (2008) Hippocampal place cell activity during chasing of a moving object associated with reward in rats. Neuroscience 154:254–270 [DOI] [PubMed]
- Igarashi J, Hayashi H, Tateno K (2007) Theta phase coding in a network model of the entorhinal cortex layer II with entorhinal-hippocampal loop connections. Cogn Neurodyn 1:169–184 [DOI] [PMC free article] [PubMed]
- Jung M, McNaughton B (1993) Spatial selectivity of unit activity in the hippocampal granular layer. Hippocampu 3:165–182 [DOI] [PubMed]
- Kropff E, Treves A (2008) The emergence of grid cells: intelligent design or just adaptation? Hippocampus 18:1256–1269 [DOI] [PubMed]
- Leutgeb J, Leutgeb S, Moser M-B, Moser E (2007) Pattern separation in the dentate gyrus and CA3 of the hippocampus. Science 315, 961–966 [DOI] [PubMed]
- McHugh T, Jones M, Quinn J, Balthasar N, Coppari R, Elmquist J et al (2007) Dentate gyrus nmda receptors mediate rapid pattern separation in the hippocampal network. Science 319:94–99 [DOI] [PubMed]
- Molter C, Yamaguchi Y (2008) Entorhinal theta phase precession sculpts dentate gyrus place fields. Hippocampus 18:919–930 [DOI] [PubMed]
- O’Keefe J (1976) Place units in the hippocampus of the freely moving rat. Exp Neurol 51:78–109 [DOI] [PubMed]
- O’Keefe J, Dostrovsky J (1971) The hippocampus as a spatial map. preliminary evidence from unit activity in the freely-moving rat. Brain Res 34:171–175 [DOI] [PubMed]
- Papp G, Witter M, Treves A (2007) The CA3 network as a memory store for spatial representations. Learn Mem 14:732–744 [DOI] [PubMed]
- Rolls E, Xiang J, Franco L (2005) Object, space, and object-space representations in the primate hippocampus. J Neurophysiol 94:833–844 [DOI] [PubMed]
- Rolls E, Stringer S, Elliot T (2006) Entorhinal cortex grid cells can map to hippocampal place cells by competitive learning. Netw: Comput Neural Syst 15:447–465 [DOI] [PubMed]
- Solstad T, Moser E, Einevoll G (2006) From grid cells to place cells: a mathematical model. Hippocampus 16:1026–1031 [DOI] [PubMed]
- Suzuki W, Amaral D (2003) Perirhinal and parahippocampal cortices of the macaque monkey: cytoarchitectonic and chemoarchitectonic organisation. J Comp Neurol 463:67–91 [DOI] [PubMed]
- Wagatsuma H, Yamaguchi Y (2007) Neural dynamics of the cognitive map in the hippocampus. Cogn Neurodyn 1:119–141 [DOI] [PMC free article] [PubMed]